Abstract
With the expansion of vehicle-to-everything (V2X) networks and the rising demand for intelligent services, vehicle edge computing encounters heightened requirements for more efficient task offloading. This study proposes a task offloading technique that utilizes federated collaboration and multi-agent deep reinforcement learning to reduce system latency and energy consumption. The task offloading issue is formulated as a Markov decision process (MDP), and a framework utilizing the Multi-Agent Dueling Double Deep Q-Network (MAD3QN) is developed to facilitate agents in making optimal offloading decisions inside intricate environments. Secondly, Federated Learning (FL) is implemented during the training phase, leveraging local training outcomes from many vehicles to enhance the global model, thus augmenting the learning efficiency of the agents. Experimental results indicate that, compared to conventional baseline algorithms, the proposed method decreases latency and energy consumption by at least 10% and 9%, respectively, while enhancing the average reward by at least 21%.
1. Introduction
With the advancement of vehicle intelligence, high-real-time tasks such as autonomous driving and automatic navigation require rigorous service quality standards [1,2]. Conventional cloud computing services face challenges in achieving millisecond-level response times. Vehicle Edge Computing (VEC) mitigates this issue by allocating computing resources to Road Side Units (RSUs) [3,4], which theoretically facilitates substantial decreases in service response times. In resource-constrained VEC systems, edge nodes face challenges in evenly distributing high-concurrency, heterogeneous computational demands. The ambiguity of task requirements and the critical nature of latency characteristics present considerable challenges to the performance of task offloading [5,6]. Centralized optimization methods rely on the sharing of global states, which necessitates the transmission of sensitive information, including vehicle trajectories, thereby presenting a risk of privacy leakage. The achievement of efficient, secure, and reliable task offloading in dynamic environments presents a significant challenge that limits the effectiveness of vehicle-road collaboration.
Deep Reinforcement Learning (DRL) serves as an effective method for optimizing task offloading and resource allocation in dynamic vehicle networks [7,8,9,10,11], primarily due to its capacity for policy optimization independent of predefined models. Nonetheless, DRL-based methods encounter challenges in managing task offloading within dynamic network environments that necessitate additional focus. Quality of Experience (QoE) is a dynamic performance metric that indicates user satisfaction, necessitating a balance between task processing latency and terminal energy consumption constraints. While some studies have investigated the trade-off between delay and energy consumption, they have insufficiently addressed user needs and have failed to meet QoE requirements [12,13,14,15]. Additional studies have employed a reinforcement learning framework utilizing deep Q-networks to concurrently optimize task offloading and resource allocation [16,17].
The combination of FL and DRL has gradually become an important research direction for task offloading and resource management in V2X networks. In [18], a task offloading scheme combining federated deep reinforcement learning with power control was proposed. This method achieves joint optimization of power control and task allocation in a vehicle edge computing environment, thereby improving system performance while reducing energy consumption. In [19], an online task offloading and resource allocation method based on federated deep reinforcement learning was proposed to address the task offloading problem in mobile edge computing under harsh environments. This method significantly enhances the robustness and adaptability of the system in complex dynamic network environments. In [20], focusing on the 6G-V2X network scenario, a task offloading and resource management framework combining federated learning is proposed. This framework addresses the challenges of computational resource scheduling and load balancing in large-scale V2X networks. Additionally, ref. [21] investigates V2X edge intelligence based on federated learning and proposes an adaptive parallel design to enhance training efficiency, thereby providing new insights for intelligent task offloading and resource optimization in V2X environments. In [22], a multi-objective evolutionary algorithm (SONG) is proposed for facility localization problems in vehicle-based fog computing networks, effectively reducing network energy consumption while maintaining task execution efficiency. In [23], a task-driven, priority-aware offloading scheme based on deep reinforcement learning technology was proposed. This method focuses on optimizing task offloading decisions based on task priority and deadline, thereby improving task completion efficiency while minimizing energy consumption. The joint optimization problem of task offloading and resource allocation is an NP-hard problem. Although existing research has made significant progress in this field, optimizing offloading decisions remains challenging, and conventional DRL algorithms often struggle to identify the global optimal solution for such problems. Especially in complex V2X environments, the strategies of various devices continue to evolve during training, which may lead to competition for resources such as bandwidth, computing power, and storage [24], thereby affecting the overall system performance.
A multi-agent DRL algorithm is proposed to optimize task offloading decisions in complex environments to address these issues. MAD3QN effectively mitigates the effects of non-stationarity and resource limitations in single-agent settings. The algorithm improves the stability of state value evaluation by decomposing Q-values into state values and action advantages [25]. Implementing FL helps address the challenges posed by non-independent and identically distributed (Non-IID) data during model training, while safeguarding privacy and improving overall model efficacy. Non-IID data is common in car edge computing, as many vehicles exhibit varied task kinds, computational capabilities, and data distributions, potentially resulting in inconsistent gradients and sluggish convergence during model training. This study presents the FL technique, which successfully alleviates the adverse impacts of non-IID data via distributed training and weighted aggregation. As a distributed machine learning approach, federated learning enables agents to share solely the trained model parameters during the training process. This paper presents the following key contributions:
- For VEC situations, develop communication, computation, and system cost models predicated on task processing deadlines and energy limitations, and articulate the task offloading problem as a Markov Decision Process (MDP). This approach takes into account the dynamic attributes of RSU and MEC server workloads, formulates an effective reward mechanism, and emphasizes enhancing performance in MEC systems.
- To mitigate the expenses associated with prolonged task processing, we developed a task offloading approach utilizing multi-agent deep reinforcement learning. This approach employs a dual network design to partition the Q-function into a state value function and an action advantage function, hence augmenting the program’s learning efficacy in intricate situations and facilitating the agent’s ability to make optimal offloading decisions.
- The MAD3QN algorithm employs a distributed training approach that necessitates the handling of substantial data transport. Federated learning was implemented to enhance training efficiency. During this process, agents exchange training parameters following model aggregation and updates, which mitigates the effects of non-IID data while safeguarding data privacy and security, thereby enhancing the convergence rate and optimization efficacy of the model.
2. System Model
Figure 1 illustrates a vehicle traffic scenario on urban roads, featuring a VEC system that includes vehicles, RSUs, Mobile Edge Computing (MEC) servers, and base stations. Deploying MEC servers in proximity to RSUs is essential for enhancing the computational resource capacity and, consequently, the quality of service for vehicles. Each MEC server implements an agent utilizing deep reinforcement learning. Agents obtain revised global model parameters from base stations to enhance their local model training. Post-training, the models are disseminated to adjacent RSUs through wireless connections. RSUs utilize the trained models to determine optimal offloading decisions for each vehicle. It is assumed that all RSUs are administered by base stations and linked to RSU facilities through fiber optic cables. Let represent the set of cars, and designate the set of RSUs located along the roadside. Let denote the set of T time intervals, each enduring τ seconds. Each vehicle evaluates two distinct queues: the computational queue and the transmission queue. During time slot , the RSU acquires task requests from vehicles within its coverage area and determines binary offloading based on the vehicles’ status information. Designate the RSU coverage radius as r and the CPU clock frequency as . Tasks are arranged according to a first-in, first-out methodology for local processing on the vehicle or designated for processing at the RSU. The RSU scheduler is responsible for allocating newly arrived tasks to each queue at the start of the time slot. Assume that each RSU comprises I queues, with each queue representing a vehicle . Upon arrival at the RSU, a task is assigned to the appropriate queue. Let denote the index of the computational work arriving at the RSU during time slot . Let be the magnitude of the task, quantified in bits. The magnitude of task corresponds to a discrete set , whereby denotes the scenario in which no task is received. Let denote the processing density of the task, indicating the number of CPU cycles required for a unit to perform (1000 cycles per bit). Let represent the task’s deadline, indicating that the task must be finalized before this time frame; otherwise, it will be forfeited. Let the binary variable represent the offloading choice, indicating whether the task is allocated to the computation queue () or the transmission queue.
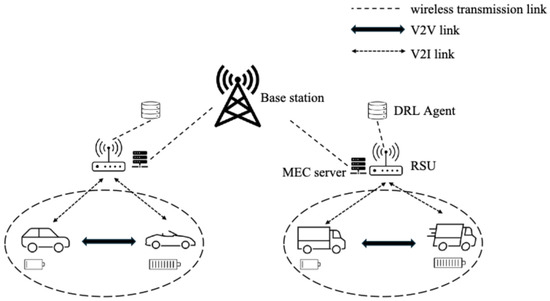
Figure 1.
System model.
2.1. Communication Model
The RSU persistently gathers real-time vehicle status data, including task queue, vehicle speed, position, and available wireless resources. Every wireless communication link utilizes Orthogonal Frequency Division Multiple Access (OFDMA) [26] technology to provide communication among vehicles and between vehicles and infrastructure. Assuming the transmission channels possess perfect channel state information and that the vehicle’s wireless channels stay stable during task transmission. In the vehicle-to-RSU channel, tasks in the transmission queue are allocated to the corresponding RSU using the wireless communication link. In time slot , if task is allocated to the transmission queue for offloading, let denote the time slot in which the task is assigned to the RSU or rejected. Let represent the number of time slots the task remains in the transmission queue; the vehicle computes the value of before task offloading.
denotes the timeframe before which other tasks in the transmission queue were allocated or abandoned. If, during time slot , the task of vehicle is allocated to the transmission queue, then in the subsequent time slot , the task is either scheduled or rejected.
denotes the communication latency necessary for transmitting task from vehicle to RSU . Let denote the transmission rate from to . Shannon’s formula articulates the communication rate of the uplink task from to as follows:
represents the channel gain, while denotes the communication transmission power from the vehicle to the RSU. The channel capacity is , and the Gaussian white noise power is , where denotes co-channel interference. Consequently, the communication latency and transmission energy expenditure of task from vehicle to are articulated as
2.2. Computation Model
Computational tasks may be performed locally on the vehicle or at the RSU. Define the binary variable to denote the offloading target, showing if the work is offloaded to the RSU; assign accordingly, otherwise assign . Given the brevity of the time slot , it may be presumed that the quantity of vehicles monitored by the RSU during this interval remains constant, represented as
where denotes the maximum capacity of vehicles that may be accommodated in the area, and and signify the average speed and maximum speed limit of vehicles on the route, respectively.
2.2.1. Local Execution
Simulate a queuing system comprising a computational queue and a vehicle processor. At the commencement of time slot , task of vehicle is allocated to the local computing queue. Let be the time interval during which task is executed or abandoned. If , then the computational queue is empty. Let be the number of time slots that the task must wait for processing in the computing queue.
denotes the time slot preceding which other tasks in the computation queue were executed or abandoned. If task is allocated to the compute queue for processing during time slot , then is denoted as
If task is not finalized before the conclusion of time slot , the task is promptly abandoned. denotes the computing latency necessary for task processing within the queue. Let represent the processing capability of the vehicle , and denote the number of CPU cycles required to process a single bit of data; thus, the local computational delay of the vehicle is
denotes the CPU frequency used by vehicle during task execution. The energy usage of vehicle within the time interval is articulated as
2.2.2. Edge Execution
Each RSU possesses several active queues and performs multiple tasks concurrently. The computational resources of the RSU fluctuate over time, and the computational capability of during time slot is . Assume that vehicle allocates task to RSU during time slot . Let denote the unique index of the task, represent the size of the task in active queue of , indicate the length of the active queue after the time slot, and signify the number of bits of discarded tasks in the active queue at the end of the time slot. Let the collection of active queues of RSU during time slot .
Let be the time interval during which task is either executed or abandoned following its transfer to the active queue. If , then the active queue is empty. Let denote the number of time slots that task must wait before being processed in the current queue.
denotes the time slot during which tasks in the active queue are either processed or rejected before time slot . During the time slot , the task is either executed or discarded.
If the conclusion of slot does not finalize task , it is promptly discarded. Furthermore, each RSU performs tasks alone and does not distribute computational load with neighboring nodes. Upon execution of task on its designated RSU, the requisite computational latency and energy consumption are as follows:
represents the CPU frequency utilization when RSU performs the task. Furthermore, take into account the energy expenditure while the vehicle awaits mission completion and return, articulated as
The whole energy consumption of task performed at the edge is articulated as
3. Problem Formulation and Algorithm Design
3.1. Problem Formulation
The system model aims to enhance task offloading decisions, thereby reducing processing costs associated with latency, energy consumption, and task loss rates, and ultimately elevating vehicle service quality. The vehicle model takes into account the battery power, which has become a crucial issue in the era of new energy cars. Before executing the ideal offloading option, the agent assesses the vehicle’s status and battery power, and then determines the optimal selection upon arrival of a new job. The expense associated with task processing can be articulated as
denotes the battery power of the vehicle. denotes the delay of the task following the agent’s decision—the cumulative duration of time slots from time slot t until the task is executed. Upon task abandonment, . represents the energy consumption of the task after the agent has made its decision. Mathematically expressed as
3.2. Markov Decision Process
To reduce the long-term task processing costs of the system, it is essential to transform this optimization issue into a Markov decision process, thereby elucidating the decision-making process of task offloading. Subsequently, we shall elucidate the state space, action space, and reward function within the Markov decision process.
State space: At the commencement of time slot t, the agent gathers vehicle status data within the vicinity, denoted as vector , including the magnitude of freshly arriving tasks, battery power, queue information, and RSU workload history.
where is the queue duration in the preceding time slot of , and represents the battery power of vehicle during time slot . To forecast the future workload of RSU, is depicted as historical load data. This data is documented in the matrix for the time interval , spanning from to . For in the time slot of , is delineated as
Action space: Exemplifies the conduct and choices of agents. Let denote the action executed by vehicle during time slot . This step encompasses the choice to unload the task and the identification of the unloading node. Among these, is the designated RSU for the unloading task.
Reward function: Characterize the task-unloading choice of vehicle as a function that maps its state to the associated action, denoted as . Let denote the reward function corresponding to task . Considering the observed state and the chosen action , the reward function is denoted as
where signifies the execution of task , indicates the rejection of task ; represents the cost incurred when opting for action in state ; depicts the energy expenditure associated with selecting action in state ; indicates the fixed reward for task completion, if , then . In the following sections, the reward function is referred to as . In the observed environmental state , the vehicle executes action by policy . The agent seeks to identify the optimal policy , to minimize long-term task processing costs.
represents the discount factor, and the predicted considers the time-dependent system environment. To address the optimization challenge presented in Formula (26) inside a dynamic environment, we propose a Deep Reinforcement Learning (DRL) optimization approach to ascertain the relationship between each state-action combination and the long-term task processing cost.
Figure 2 illustrates that each agent is outfitted with a neural network including five layers: an input layer, a dense layer, an advantage value layer, and an output layer. Let represent the parameter vector of the neural network, which is utilized to preserve the connection weights and neuron biases across all layers. The input layer consists of six neurons that receive state information, with each neuron representing a specific parameter, which is subsequently transmitted to the hidden layer. The dense layer comprises a collection of neurons employing the rectified linear unit (ReLU) as the activation function. The initial dense layer establishes connections from the input layer’s neurons to each neuron in the dense layer, which subsequently connects to each neuron in the following dense layer. In the second dense layer, the output of each neuron is interconnected with all neurons in the A&V layer. The A&V layer is a novel element introduced by Dueling DDQN into the neural network, comprising two separate dense networks: the action advantage vector (A) and the state value (V). The neural network independently learns these outputs, which are then aggregated through summation to obtain the Q-value. For each agent, let represent the state value and designate the action advantage value of action in the context of state . The parameter vector is responsible for ascertaining these values and is modified during the training of the MAD3QN algorithm. The A&V layer and the output layer together establish , namely
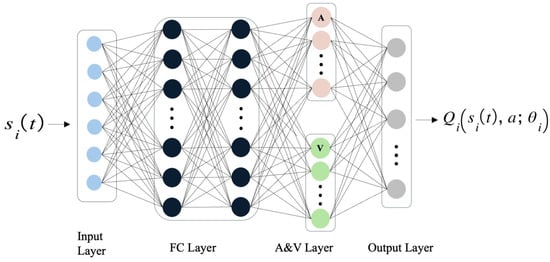
Figure 2.
Neural network structure of Dueling DDQN.
3.3. MAD3QN Optimization with Enhanced Q-Values
In this section, the proposed MAD3QN algorithm effectively minimizes task processing costs. Based on the dueling network architecture, MAD3QN consists of two key components: the evaluation network () and the target network (). These components share the same neural network structure but differ in their parameter vectors, and . is responsible for real-time learning and decision offloading, taking the current state, , as input and outputting the Q-value, . selects the optimal action , based on the maximum Q-value. The target Q-value of is , representing the long-term reward caused by a specific action under the observed state. The target Q-value serves as a reference for updating the network parameter vector , which is achieved by minimizing the difference between the Q-values in and . The replay experience buffer is responsible for recording observed experiences, . In Algorithm 1, each agent initializes the experience replay buffer D using neural networks and . At the start of each iteration, the initial state is set, and an update parameter request is generated. The agent selects the following action using an ε-greedy strategy:
In the ε-greedy strategy, a random action is selected with probability ; otherwise, the agent chooses the action with the highest Q-value based on the assessment network settings. Following the evaluation network’s update of the parameter vector, this experience is recorded in D. For each experience , it computes , denoting the reward value of experience and the discounted Q-value of the action executed by the neural network in the subsequent state of experience , i.e.,:
where denotes the ideal action selection determined by the maximum Q-value in under state , i.e.,:
This value reflects the reward noted in and the estimated projected reward value. The agent trains its neural network using previous experience samples, concurrently updating the parameters of the evaluation network and computing the vector . The update is performed by calculating the loss function through evaluating the Q-values of both the network and the target network. The loss function is as follows:
| Algorithm 1: MAD3QN training process |
| 1: Input: Observed environmental state ; Output: parameters |
| 2: Initialization: empirical replay buffer D, evaluation network and target , parameters and |
| 3: for episode i = 1, 2, …, M do |
| 4: Initialize the state |
| 5: for each agent in a time slot do |
| 6: According to the current state , randomly select an action or choose to |
| 7: Perform the action to obtain and the reward |
| 8: Store the experience , , , ) in D. |
| 9: for agent do |
| 10: Obtain a set of experience samples from D. |
| 11: for each experience do |
| 12: Get the experience |
| 13: Calculate according to (29) |
| 14: end for |
| 15: Setting |
| 16: Update parameters by minimizing the loss function (Equation (31)) |
| 17: Update parameters for each agent |
| 18: end for |
| 19: if end of episode then |
| 20: Update target network parameters: |
| 21: Perform model aggregation |
| 22: end if |
| 23: end for |
| 24: end for |
3.4. Complexity Analysis
The amount of experience needed to find the best offloading approach determines MAD3QN’s computational complexity. Each training event requires backpropagation computations with a computational complexity of , where is the number of neural network multiplication operations. In each training iteration initiated by a new task, a sample set of experiences is extracted from D. The training method incorporates training sets, each including predicted tasks, resulting in a total computational complexity of , characterized by polynomial complexity.
3.5. FL-Based Optimization Method for MAD3QN Models
During model training, frequent data transfers significantly consume network bandwidth, complicating resource allocation and increasing the risk of data leakage during transmission. To resolve these challenges, FL technology is utilized during model training. Unlike traditional dispersed training, federated learning facilitates collaborative model training while safeguarding data privacy and security, improving model performance. In federated learning, the heterogeneity of data distribution among various devices, such as automobiles, roadside units, or mobile edge computing servers, frequently renders gradient consistency a critical aspect influencing model stability and convergence. Each agent trains the model with local input, and the computed gradients may disagree, resulting in instability and protracted convergence during the global model update process. This study utilizes a weighted average method for model parameter aggregation to alleviate the effects of non-IID data on gradient consistency, and implements a soft update strategy to facilitate gradual and smooth convergence of the global model.
As illustrated in Figure 3, during the model initialization phase, the MEC server acquires the global MAD3QN model from the base station and sets the model parameters. Each MEC server utilizes local data to conduct preliminary training on model during the training process. Upon the completion of local training, the revised model parameters, instead of the original data, are transmitted to the base station. The base station conducts weighted computations on the model according to the ratio of each MEC server’s local data utilization to the total data to achieve the updated global model . The revised model parameters are subsequently communicated to each MEC server for the forthcoming training cycle. Upon acquisition of the new model, the MEC servers execute a soft update of the model parameters to mitigate the influence of extraneous parameters on the overall model. This federated learning approach guarantees data privacy while enhancing model stability and convergence velocity by tackling challenges like data distribution heterogeneity and gradient inconsistency among agents. The equations for local updates and global aggregation are as follows:
where denotes the soft update weight, represents the overall number of training samples, and represents the quantity of locally trained samples associated with the MEC server. Algorithm 2 presents the pseudocode for the MAD3QN model aggregation approach grounded in FL.
| Algorithm 2: FL-based MAD3QN model training |
| 1: Input: Global model parameters ; Local model parameters |
| 2: Output: updated global model parameters |
| 3: Initialization: In time slot , the base station initializes the MAD3QN model ; each agent initializes the local |
| 4: MAD3QN model . |
| 5: for round i = 1, 2, …, M do |
| 6: for agent do |
| 7: Download global parameters from base station |
| 8: Update local parameters according to (32) |
| 9: Perform local training based on local data |
| 10: Update the trained parameters and upload to the base station |
| 11: end for |
| 12: Base station aggregates the uploaded by the agents according to Equation (33) |
| 13: Each smart body receives the updated weighted average parameters |
| 14: end for |
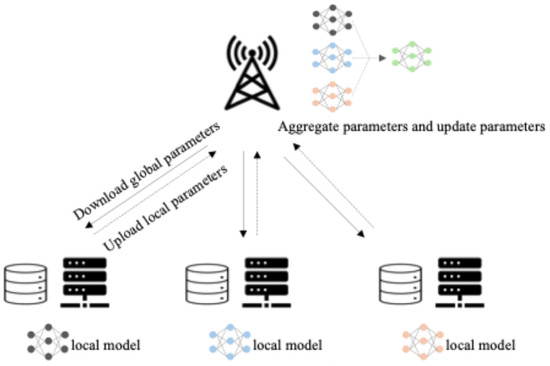
Figure 3.
Federated learning training process.
4. Experimental Results
4.1. Parameter Settings
Consider an urban two-way road vehicle traffic scenario with 1 base station, 6–10 RSU devices, and 10–50 vehicles in the RSU coverage region. As per 3GPP R15 [27] and C-V2X vehicle-to-everything and vehicle-to-infrastructure (V2I) essential technologies [28], the primary simulation parameters [29] and hyperparameters are shown in Table 1 and Table 2. The and components of each intelligent agent consist of two layers of fully connected neural networks, featuring 128 neurons in the first layer and 64 neurons in the second layer, employing ReLU as the activation function. The RMSProp optimizer is employed to train and adjust the weights of the neural network iteratively. The algorithm undergoes training throughout 10,000 episodes. Each episode comprises 100 time slots, each lasting 0.1 s. The learning rate is established at 0.001, and the discount factor is determined to be 0.9. The likelihood of random exploration commences at an initial value and progressively diminishes by 1, converging around 0.01. Simulation tests were conducted using Python 3.8.19 and TensorFlow 2.0.0 to assess the efficacy of the FL-MAD3QN algorithm in a VEC context.

Table 1.
Hyperparameters of the FL-MAD3QN algorithm.

Table 2.
Simulation parameters.
To assess the efficacy of the suggested algorithm, the subsequent algorithms were compared:
- Local computation (LC): Vehicles utilize their inherent computing capabilities to execute all computational operations.
- Full offloading (FO): All vehicle tasks are transferred to the RSU for remote execution.
- FL-DQN: Achieves the ideal offloading technique through integration with federated learning.
- DDPG: A task offloading algorithm utilizing an evaluation network and a target network architecture.
4.2. Convergence Analysis and Performance Comparison
Convergence Analysis: Figure 4 depicts the rewards of several algorithms and the corresponding benefits based on differing agent quantities within each algorithm. The convergence efficacy of the FL-MAD3QN method is compared with that of MAD3QN and MADQN Figure 4a. Initially, each agent trains its model, leading to minimal variations in average payouts. With the escalation of training cycles, the experience replay buffer data expands steadily, gradually enhancing and stabilizing the agents’ average rewards. As illustrated Figure 4a, MAD3QN encounters substantial reward variability during the initial training phases, resulting in a reduced convergence rate in the absence of federated learning. This signifies that gradient inconsistency, resulting from non-IID input, impacts the model’s training process. Conversely, following the implementation of federated learning, FL-MAD3QN significantly alleviates the effects of non-IID data during global model aggregation, resulting in more consistent updates among various agents. As a result, the global model exhibits accelerated convergence and diminished reward fluctuations. Following a specified number of training iterations, FL-MAD3QN initiates model aggregation, causing agents to diverge from local optima progressively. Consequently, the average reward escalates more consistently, and the convergence performance surpasses that of MAD3QN and MADQN without FL. Figure 4b, the convergence performance of FL-MAD3QN with varying agent quantities is illustrated. As the quantity of agents escalates, the dimensions of both the state space and action space expand, resulting in an initial decline in the average reward of FL-MAD3QN. Nevertheless, once the model converges and stabilizes, it continues to yield a satisfactory average reward.
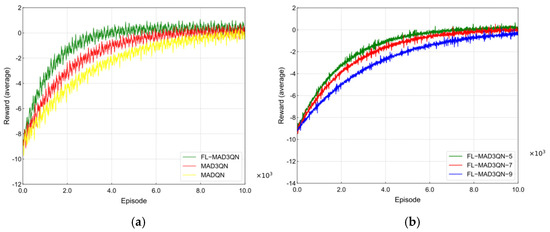
Figure 4.
(a) Rewards for different algorithms; (b) rewards for different numbers of agents.
Performance Comparison: Figure 5 illustrates a performance comparison across different task arrival rates. Figure 5a, the proposed methodology consistently outperforms current techniques as the task arrival rate fluctuates. As the task arrival rate increases, the performance advantage of the proposed approach becomes more apparent. At a task arrival rate of 300, the proposed technique achieves 18.06% and 58.29% higher task completions compared to FL-DQN and DDPG, respectively. Figure 5b, for a task arrival rate of 300, the proposed solution reduces the average delay by at least 10.12% and 18.20% relative to FL-DQN and DDPG, respectively. When the task arrival rate surpasses 500, the proposed algorithm may demonstrate elevated average latency, which is ascribed to its superior task completion rate relative to other methods. Figure 5c, At diminished task arrival rates, the total energy consumption across all techniques is similar. At a task arrival rate of 500, the proposed solution reduces total energy consumption by 9.08% compared to FL-DQN and by 13.72% relative to DDPG. The FL-MAD3QN approach utilizes extensive computational resources, while the LC and FO methods depend exclusively on local and edge node resources, respectively. Thus, their task completion rates are far lower than the FL-MAD3QN algorithm, resulting in lower energy consumption. Figure 5d, depicts the average reward at different task arrival rates. At a task arrival rate of 300, the proposed method achieves an average reward improvement of 18.25% and 38.78% compared to FL-DQN and DDPG, respectively.
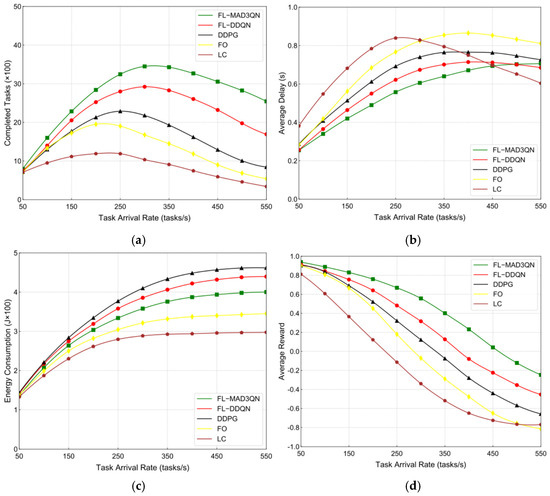
Figure 5.
Performance comparison at different task arrival rates: (a) completed tasks; (b) average delay; (c) energy consumption; (d) average reward.
Figure 6a illustrates that with an increase in the number of cars, the suggested algorithm consistently outperforms alternative techniques in terms of task completion rate. Once the vehicle count reaches 50, the work requires considerable processing resources, enabling the agent to arrange tasks efficiently. The FL-MAD3QN algorithm attains a minimum of a 12.91% enhancement in task completion rate. Figure 6b indicates that the overall average delay has a tendency to increase. Upon reaching a vehicle count of 100, the FL-MAD3QN algorithm decreases the average delay by a minimum of 11%. LC exclusively executes tasks locally, resulting in a consistent average delay. Figure 6c, when the quantity of cars rises, the system’s processing resources expand, resulting in an upward trajectory in total energy usage. The suggested technique decreases total energy usage by a minimum of 15.78% and 24.03% when compared to FL-DQN and DDPG, respectively. The FL-MAD3QN algorithm employs comprehensive computational resources, whereas LC and FO rely solely on local and edge nodes for task processing, resulting in reduced energy consumption. Figure 6d illustrates the average payoff as the quantity of vehicles escalates. Upon reaching a count of 100, the strain on edge nodes escalates, and the suggested algorithm achieves an average reward enhancement of at least 21% compared to FL-DQN and DDPG. As LC continually executes tasks locally, the average reward remains constant.
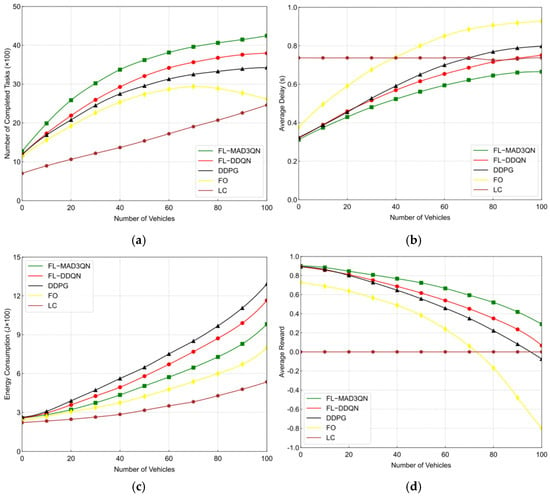
Figure 6.
Performance comparison with different numbers of vehicles: (a) number of completed tasks; (b) average delay; (c) energy consumption; (d) average reward.
5. Conclusions
This study presents an enhanced deep reinforcement learning task offloading strategy within the context of vehicular edge computing to minimize latency and energy expenditure while adhering to task processing deadlines and energy limitations. Initially, in light of the dynamic and unpredictable characteristics of mobile settings, communication and computational models are established, and the costs associated with task processing are evaluated. Secondly, utilizing the previously mentioned models, an optimization target is formulated, and the task offloading issue is represented as a Markov decision process. A method based on the MAD3QN framework is developed to reduce the system’s task processing costs, allowing the agent to make optimal offloading decisions independently of other task models or agent offloading choices. Ultimately, FL is integrated with the MAD3QN framework to improve model training efficiency while safeguarding user data privacy. Experiments indicate that the proposed algorithm exhibits favorable performance in terms of model convergence, latency, energy consumption, and task completion rate.
Subsequent efforts will enhance the algorithm’s efficacy by utilizing prioritized experience replay and implementing weight allocation techniques to improve the model’s learning efficiency. Furthermore, the interrelations among tasks may be taken into account to enhance the task model.
Author Contributions
Conceptualization, H.Z.; methodology, H.Z.; software, Y.L.; validation, Y.L.; formal analysis, Y.L.; investigation, Z.P.; resources, Z.P.; data curation, Z.M.; writing—original draft preparation, Y.L.; writing—review and editing, Y.L.; visualization, Z.M.; supervision, Z.M.; project administration, H.Z.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (42471213) and Northeast Geoscience and Science and Technology Innovation Center Regional Innovation Fund Project (QCJJ2023-49).
Data Availability Statement
Derived data supporting the findings of this study are available from the corresponding author on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Panigrahy, S.K.; Emany, H. A survey and tutorial on network optimization for intelligent transport system using the internet of vehicles. Sensors 2023, 23, 555. [Google Scholar] [CrossRef]
- Gong, T.; Zhu, L.; Yu, F.R.; Tang, T. Edge intelligence in intelligent transportation systems: A survey. IEEE Trans. Intell. Transp. Syst. 2023, 24, 8919–8944. [Google Scholar] [CrossRef]
- Luo, G.; Shao, C.; Cheng, N.; Zhou, H.; Zhang, H.; Yuan, Q.; Li, J. Edge Cooper: Network-aware cooperative LiDAR perception for enhanced vehicular awareness. IEEE J. Sel. Areas Commun. 2023, 42, 207–222. [Google Scholar] [CrossRef]
- Yin, L.; Luo, J.; Qiu, C.; Wang, C.; Qiao, Y. Joint task offloading and resources allocation for hybrid vehicle edge computing systems. IEEE Trans. Intell. Transp. Syst. 2024, 25, 10355–10368. [Google Scholar] [CrossRef]
- Dong, S.; Tang, J.; Abbas, K.; Hou, R.; Kamruzzaman, J.; Rutkowski, L.; Buyya, R. Task offloading strategies for mobile edge computing: A survey. Comput. Netw. 2024, 254, 110791. [Google Scholar] [CrossRef]
- Ren, J.; Hou, T.; Wang, H.; Tian, H.; Wei, H.; Zheng, H.; Zhang, X. Collaborative task offloading and resource scheduling framework for heterogeneous edge computing. Wirel. Netw. 2024, 30, 3897–3909. [Google Scholar] [CrossRef]
- Zabihi, Z.; Moghadam, A.M.E.; Rezvani, M.H. Reinforcement learning methods for computation offloading: A systematic review. ACM Comput. Surv. 2023, 56, 17. [Google Scholar] [CrossRef]
- Luo, Z.; Dai, X. Reinforcement learning-based computation offloading in edge computing: Principles, methods, challenges. Alex. Eng. J. 2024, 108, 89–107. [Google Scholar] [CrossRef]
- Xue, J.; Wang, L.; Yu, Q.; Mao, P. Multi-Agent Deep Reinforcement Learning-based Partial Offloading and Resource Allocation in Vehicular Edge Computing Networks. Comput. Commun. 2025, 234, 108081. [Google Scholar] [CrossRef]
- He, H.; Yang, X.; Mi, X.; Shen, H.; Liao, X. Multi-Agent Deep Reinforcement Learning Based Dynamic Task Offloading in a Device-to-Device Mobile-Edge Computing Network to Minimize Average Task Delay with Deadline Constraints. Sensors 2024, 24, 5141. [Google Scholar] [CrossRef]
- Zhao, P.; Kuang, Z.; Guo, Y.; Hou, F. Task offloading and resource allocation in UAV-assisted vehicle platoon system. IEEE Trans. Veh. Technol. 2024, 74, 1584–1596. [Google Scholar] [CrossRef]
- Sun, G.; He, L.; Sun, Z.; Wu, Q.; Liang, S.; Li, J.; Niyato, D.; Leung, V.C.M. Joint task offloading and resource allocation in aerial-terrestrial UAV networks with edge and fog computing for post-disaster rescue. IEEE Trans. Mob. Comput. 2024, 23, 8582–8600. [Google Scholar] [CrossRef]
- Farimani, M.K.; Karimian-Aliabadi, S.; Entezari-Maleki, R.; Egger, B.; Sousa, L. Deadline-aware task offloading in vehicular networks using deep reinforcement learning. Expert Syst. Appl. 2024, 249, 123622. [Google Scholar] [CrossRef]
- He, H.; Yang, X.; Huang, F.; Shen, H.; Tian, H. Enhancing QoE in Large-Scale U-MEC Networks via Joint Optimization of Task Offloading and UAV Trajectories. IEEE Internet Things J. 2024, 11, 35710–35723. [Google Scholar] [CrossRef]
- Zhu, K.; Li, S.; Zhang, X.; Wang, J.; Xie, C.; Wu, F.; Xie, R. An Energy-Efficient Dynamic Offloading Algorithm for Edge Computing Based on Deep Reinforcement Learning. IEEE Access 2024, 12, 127489–127506. [Google Scholar] [CrossRef]
- Zhai, L.; Lu, Z.; Sun, J.; Li, X. Joint task offloading and computing resource allocation with DQN for task-dependency in multi-access edge computing. Comput. Netw. 2025, 263, 111222. [Google Scholar] [CrossRef]
- Wu, J.; Du, R.; Wang, Z. Deep reinforcement learning with dual-Q and Kolmogorov–Arnold Networks for computation offloading in Industrial IoT. Comput. Netw. 2025, 257, 110987. [Google Scholar] [CrossRef]
- Moon, S.; Lim, Y. Federated deep reinforcement learning based task offloading with power control in vehicular edge computing. Sensors 2022, 22, 9595. [Google Scholar] [CrossRef]
- Xiang, H.; Zhang, M.; Jian, C. Federated deep reinforcement learning-based online task offloading and resource allocation in harsh mobile edge computing environment. Clust. Comput. 2024, 27, 3323–3339. [Google Scholar] [CrossRef]
- Hasan, M.K.; Jahan, N.; Nazri, M.Z.; Islam, S.; Khan, M.A.; Alzahrani, A.I.; Alalwan, N.; Nam, Y. Federated learning for computational offloading and resource management of vehicular edge computing in 6G-V2X network. IEEE Trans. Consum. Electron. 2024, 70, 3827–3847. [Google Scholar] [CrossRef]
- Qiang, X.; Chang, Z.; Ye, C.; Hämäläinen, T.; Min, G. Split federated learning empowered vehicular edge intelligence: Concept, adaptive design, and future directions. IEEE Wirel. Commun. 2025, 32, 90–97. [Google Scholar] [CrossRef]
- Hussain, M.; Azar, A.T.; Ahmed, R.; Amin, S.U.; Qureshi, B.; Reddy, V.D.; Alam, I.; Khan, Z.I. SONG: A multi-objective evolutionary algorithm for delay and energy aware facility location in vehicular fog networks. Sensors 2023, 23, 667. [Google Scholar] [CrossRef]
- Hao, H.; Xu, C.; Zhang, W.; Yang, S.; Muntean, G.-M. Task-Driven Priority-Aware Computation Offloading Using Deep Reinforcement Learning. IEEE Trans. Wirel. Commun. 2025. [Google Scholar] [CrossRef]
- Pang, S.; Wang, T.; Gui, H.; He, X.; Hou, L. An intelligent task offloading method based on multi-agent deep reinforcement learning in ultra-dense heterogeneous network with mobile edge computing. Comput. Netw. 2024, 250, 110555. [Google Scholar] [CrossRef]
- Du, R.; Wu, J.; Gao, Y. Dual-Q network deep reinforcement learning-based computation offloading method for industrial internet of things. J. Supercomput. 2024, 80, 25590–25615. [Google Scholar] [CrossRef]
- Tan, L.; Kuang, Z.; Zhao, L.; Liu, A. Energy-efficient joint task offloading and resource allocation in OFDMA-based collaborative edge computing. IEEE Trans. Wirel. Commun. 2021, 21, 1960–1972. [Google Scholar] [CrossRef]
- Shen, J.; Du, Z.; Zhang, Z.; Yang, N.; Tang, H. 5G NR and Enhancements: From R15 to R16; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Jiang, J. Key Technologies of C-V2X Internet of Vehicles and Vehicle-Road Coordination; China Science and Technology Publishing & Media Co., Ltd.: Beijing, China, 2024. [Google Scholar]
- Zhu, L.; Zhang, Z.; Liu, L.; Feng, L.; Lin, P.; Zhang, Y. Online distributed learning-based load-aware heterogeneous vehicular edge computing. IEEE Sens. J. 2023, 23, 17350–17365. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).