Identification of Interacting Objects and Evaluation of Interaction Loss from Wideband Double-Directional Channel Measurement Data by Using Point Cloud Data

Abstract

This paper proposes an approach to identify interacting objects (IOs) and determine their interaction losses (ILs) using point cloud data from wide-band double-directional channel sounding data. The scattering points (SPs) were identified using the maximum likelihood-based approach applied to the high-resolution path parameters estimated from the channel sounding data, and then IOs were identified via visual inspection of SPs within a 3D point cloud. The proposed approach utilizes all path parameters to calculate the approximate likelihood function for all candidate SPs to determine the SP, regardless of the propagation mechanism. The proposed technique was demonstrated at a suburban residential site with a frequency of 11 GHz. The results show that IOs that are not usually considered in the ray-tracing simulation were identified.

1. Introduction

The utilization of the high-frequency band in mobile communication requires a detailed investigation of the radio channel characteristics. The ray tracing (RT) technique, which is based on the reflection and diffraction laws represented by geometrical optics (GO) and geometrical theory of diffraction (GTD), respectively, has been widely used for the prediction of radio channel characteristics in urban and indoor scenarios, and many implementations are already available [1,2,3,4]. It is also known that the RT technique has some limitations in modeling complex environments. The most significant phenomenon is diffuse scattering owing to random surface irregularities beyond the application range of GO. An effective modeling approach has been proposed [5] and is widely used nowadays, although some empirical parameter tuning is required. Another source of discrepancy is the violation of the applicable range of the GO and GTD in terms of the size of the objects. In the SHF band, deterministic surface irregularities, due to window frames, metal boxes, sewage pipes, door knobs, and so on, significantly affect channels.

Ordinary RT techniques rely on a three-dimensional (3D) representation of the propagation environment using polygons. On the other hand, state-of-the-art technologies for capturing 3D structures, such as laser scanning and photogrammetry, output point cloud data. Three alternative approaches were considered for utilizing 3D point cloud data for RT techniques. One approach is to reconstruct simplified polygons that are suitable for conventional ray tracing [6]. Another approach is to directly apply GO to point cloud data [7,8]. The last approach is to use the diffuse scattering model for point cloud data [9,10].

Directional channel sounding is an effective technique for experimentally investigating the identification of interacting objects (IOs) in radio propagation channels. A simple visualization of the angle of arrival/departure on the photo has been used to identify IOs [11,12]. However, it is not easy to identify IOs when (1) the angular resolution or accuracy is not sufficiently high because of the available size of the antenna array or (2) scatterers are far away, and IOs cannot be resolved on the photo. Moreover, this approach utilizes only single-directional parameters and discards the other parameters.

Another approach to identify IOs from wideband double-directional channel responses and a 3D map of the measurement site is known as measurement-based ray tracer (MBRT) [13,14,15,16]. MBRT traces the rays along the directions of departure and arrival to identify propagation paths, including IOs, by considering the propagation delay. MBRT takes an inverse approach to the ordinary RT technique to identify IOs from the ray parameters obtained from measurements. MBRT identifies not only IOs but also their interaction losses (ILs) from the ray amplitude values. However, conventional MBRT considers GO and GTD as the governing mechanisms of propagation, and small or irregular objects that cannot be appropriately handled by conventional ray tracing may not be properly identified as IOs.

The application of 3D point clouds to MBRT is still limited, but 3D point clouds have an advantage over polygons in representing small or irregular objects. It was found that IOs cannot be identified by tracing the rays from both Tx and Rx when the angular resolution or accuracy of the direction of arrival (DoA) at the Rx site and the direction of departure (DoD) at the Tx site are not sufficiently high.

This paper proposes a measurement-based ray tracer (MBRT) for 3D point cloud data, taking into account the directions of departure and arrival as well as the delay time, to identify interacting objects (IOs) and to evaluate the interaction loss (ILs) from ray path parameters estimated from wideband double-directional channel measurement data. To consider the accuracy of the ray path parameters in the estimation process, the maximum likelihood approach was applied to identify scattering points that represent IOs. ILs are straightforwardly determined by comparing the ray path weights and free-space losses corresponding to the delay time. Preliminary results were presented for the measurement results in a suburban microcellular environment at 11 GHz. The remainder of this paper is organized as follows: Section 2 describes the representation of wideband double-directional propagation paths corresponding to rays in RT. Section 3 proposes the concept of MBRT for point cloud data to identify IOs. Section 4 presents the identified IOs and ILs for a dataset measured in a suburban microcellular environment at 11 GHz. Section 5 discusses the measurement results from the prediction perspective. Finally, conclusions are presented in Section 6.

2. Representation of Wideband Double-Directional Propagation Paths

It is quite common to introduce a ray path model to represent the propagation channel as the post-processing of channel sounding to de-embed the effects of antenna patterns and waveform from the measured data [17,18]. As shown in Figure 1, a ray path from the transmitter (Tx) to a point $\mathrm{P}({\mathrm{x}}_p,{\mathrm{y}}_p,{\mathrm{z}}_p)$ in the cloud is represented by five parameters, i.e., $\left({\phi }^{\mathrm{T}},{\vartheta }^{\mathrm{T}},{\phi }^{\mathrm{R}},{\vartheta }^{\mathrm{R}},\tau \right)$. ${\phi }^{\mathrm{T}}$ and ${\vartheta }^{\mathrm{T}}$ represent the azimuth and zenith at the transmitter (Tx) side, known as the direction of departure (DoD); ${\phi }^{\mathrm{R}}$ and ${\vartheta }^{\mathrm{R}}$ are the azimuth and zenith at the receiver (Rx) side, known as the direction of arrival (DoA). These two directions are locally defined in the coordinate systems associated with Tx and Rx, respectively. $\tau$ represents the propagation delay from Tx to Rx.

A narrowband double-directional MIMO channel response at frequency f is represented by the following channel matrix [19]:

$$\mathbf{H}\left(f\right)=\sum _{l=1}^L{\mathbf{a}}_{\mathrm{R}}({\phi }_l^{\mathrm{R}},{\vartheta }_l^{\mathrm{R}},f){\mathsf{\Gamma }}_l{\mathbf{a}}_{\mathrm{T}}^{\mathrm{T}}({\phi }_l^{\mathrm{T}},{\vartheta }_l^{\mathrm{T}},f)·e^{-\mathrm{j}2\pi f{\tau }_l},$$

(1)

where l is the index of the propagation path, and L is the total number of paths, ${\mathbf{a}}_{\mathrm{R}}$ and ${\mathbf{a}}_{\mathrm{T}}$ are the array antenna responses of the Rx and Tx, respectively. ${\mathsf{\Gamma }}_l$ is the dual-polarized complex path weight for the l-th path, given by

$${\mathsf{\Gamma }}_l=\left[\begin{array}{cc}{\gamma }_{\mathrm{VV},l}& {\gamma }_{\mathrm{VH},l}\\ {\gamma }_{\mathrm{HV},l}& {\gamma }_{\mathrm{HH},l}\end{array}\right],$$

(2)

where subscripts V and H represent the vertical and horizontal polarizations, which are parallel to ${\vartheta }_l$ and ${\phi }_l$, respectively. ${\gamma }_{\mathrm{VV},l}$ and ${\gamma }_{\mathrm{HH},l}$ represent the co-polarized path weights, whereas ${\gamma }_{\mathrm{VH},l}$ and ${\gamma }_{\mathrm{HV},l}$ are the cross-polarized path weights. These path parameters are estimated from the channel sounding data using a maximum likelihood-based technique [17,18,19]. These paths are hereafter simply called measured paths, and their parameters are referred to as measured path parameters (MPPs).

3. Measurement-Based Ray Tracing (MBRT) for Point Cloud Data

Conventional MBRT utilizes polygon data to represent the 3D geometry of the environment. In the case of a single-bounce path, two rays are traced from the Tx toward the measured DoD and from the Rx toward the measured DoA. When they hit the same polygon, the DoD and DoA are adjusted from the measured values to satisfy the reflection or diffraction law for the identification of the reflection or diffraction point. This technique is robust for high-angular-resolution measurements so that two rays can hit the same polygon. However, it is difficult to identify the scattering point if two rays hit different polygons, because of the low angular resolution.

The MBRT developed in this study was used to identify the scattering point (SP) of a single-bounce path corresponding to a measured path among 3D point clouds of objects within the propagation environment. Unlike conventional MBRT for 3D polygons, it was not necessary to consider ordinary ray-tracing rules such as reflection and diffraction laws. Instead, for each of the candidate scattering points (CSPs), a single-bounce ray was considered along Tx-CSP-Rx, and the error metric from MPPs was evaluated. The minimizer of the error metric among the CSPs was chosen as the SP with the tolerance of the measurement and parameter estimation errors.

3.1. Determination of the Single-Bounce Scattering Point for a Measured Path

The single-bounce scattering point corresponding to a measured path is determined as follows:

• m-th point $P_m$ is assumed to be a candidate scattering point (CSP) within the point cloud. For each $P_m$, we have the following:

  (a)

  Single-bounce path parameters

  $${\mathsf{\Theta }}_{\left(P_m\right)}=({\phi }_{\left(P_m\right)}^{\mathrm{T}},{\vartheta }_{\left(P_m\right)}^{\mathrm{T}},{\phi }_{\left(P_m\right)}^{\mathrm{R}},{\vartheta }_{\left(P_m\right)}^{\mathrm{R}},{\tau }_{\left(P_m\right)})$$

  are evaluated by assuming a single-bounce path Tx-CSP-Rx as follows:

  • ${\phi }_{\left(P_m\right)}^{\mathrm{T}}$ and ${\vartheta }_{\left(P_m\right)}^{\mathrm{T}}$ are calculated by drawing a straight line between Tx and CSP;
  • ${\phi }_{\left(P_m\right)}^{\mathrm{R}}$ and ${\vartheta }_{\left(P_m\right)}^{\mathrm{R}}$ are calculated by drawing a straight line between CSP and Rx;
  • ${\tau }_{\left(P_m\right)}$ is calculated as the sum of the lengths of two lines, Tx-CSP and CSP-Rx, divided by the free space velocity of the radio wave c.

  (b)

  The error between the measured path parameters $({\phi }^{\mathrm{T}},{\vartheta }^{\mathrm{T}},{\phi }^{\mathrm{R}},{\vartheta }^{\mathrm{R}},\tau )$ and the single-bounce path parameter for the CSP $({\phi }_{\left(P_m\right)}^{\mathrm{T}},{\vartheta }_{\left(P_m\right)}^{\mathrm{T}},{\phi }_{\left(P_m\right)}^{\mathrm{R}},{\vartheta }_{\left(P_m\right)}^{\mathrm{R}},{\tau }_{\left(P_m\right)})$ is

  $$\left\{\begin{array}{c}{ϵ}_{{\phi }_{\left(P_m\right)}^{\mathrm{T}}}={\phi }^{\mathrm{T}}-{\phi }_{\left(P_m\right)}^{\mathrm{T}}\hfill \\ {ϵ}_{{\vartheta }_{\left(P_m\right)}^{\mathrm{T}}}={\vartheta }^{\mathrm{T}}-{\vartheta }_{\left(P_m\right)}^{\mathrm{T}}\hfill \\ {ϵ}_{{\phi }_{\left(P_m\right)}^{\mathrm{R}}}={\phi }^{\mathrm{R}}-{\phi }_{\left(P_m\right)}^R\hfill \\ {ϵ}_{{\vartheta }_{\left(P_m\right)}^{\mathrm{R}}}={\vartheta }^{\mathrm{R}}-{\vartheta }_{\left(P_m\right)}^{\mathrm{R}}\hfill \\ {ϵ}_{{\tau }_{\left(P_m\right)}}=\tau -{\tau }_{\left(P_m\right)}\hfill \end{array}\right.$$

  (3)

• The standard deviations of the estimation errors of measured path parameters are defined as $({\sigma }_{{\phi }^{\mathrm{T}}},{\sigma }_{{\vartheta }^{\mathrm{T}}},{\sigma }_{{\phi }^{\mathrm{R}}},{\sigma }_{{\vartheta }^{\mathrm{R}}},{\sigma }_{\tau })$. It is assumed that each standard deviation is proportional to the resolution of the parameter estimation, such as the antenna beamwidth or delay domain mainlobe, which is determined by the measurement condition, and the errors of the individual parameters are uncorrelated with each other. Under such assumptions, the Euclidean error of the five-dimensional error space is represented by the sum of the square errors, normalized by their standard deviations.

  $${ϵ}^2\left(P_m\right)={\displaystyle \frac{{ϵ}_{{\phi }_{\left(P_m\right)}^{\mathrm{T}}}^2}{{\sigma }_{{\phi }^{\mathrm{T}}}^2}}+{\displaystyle \frac{{ϵ}_{{\vartheta }_{\left(P_m\right)}^{\mathrm{T}}}^2}{{\sigma }_{{\vartheta }^{\mathrm{T}}}^2}}+{\displaystyle \frac{{ϵ}_{{\phi }_{\left(P_m\right)}^{\mathrm{R}}}^2}{{\sigma }_{{\phi }^{\mathrm{R}}}^2}}+{\displaystyle \frac{{ϵ}_{{\vartheta }_{\left(P_m\right)}^{\mathrm{R}}}^2}{{\sigma }_{{\vartheta }^{\mathrm{R}}}^2}}+{\displaystyle \frac{{ϵ}_{{\tau }_{\left(P_m\right)}}^2}{{\sigma }_{\tau }^2}}.$$

  (4)
  When the error is assumed to be Gaussian distributed, $-{ϵ}^2\left(P\right)$ is equivalent to a log-likelihood function.
• The scattering point P is identified by minimizing the value of ${ϵ}^2\left(P_m\right)$, i.e.,

  $$P=arg\underset{m}{min}{ϵ}^2\left(P_m\right).$$

  (5)

3.2. Clustering

Because of the spatial diffusivity of the scattering and the modeling error of the path parameter estimation, a single interacting object (IO) might be associated with multiple paths. Therefore, the SPs obtained in the previous subsection were clustered in terms of individual IOs by visual inspection of the point cloud data.

k-th cluster power ${\overline{G}}_{{\mathcal{C}}_k}$ is defined as the power sum of the individual path weights, as follows:

$${\overline{G}}_{{\mathcal{C}}_k}=\sum _{l\in {\mathcal{C}}_k}{G}_l,$$

(6)

where ${\mathcal{C}}_k$ is a set of path indices in cluster k, and $G_l$ is the polarization-averaged power of l-th path, which is expressed using Equation (2) as

$$G_l={\displaystyle \frac{|{\gamma }_{\mathrm{VV},l}{|}^2+|{\gamma }_{\mathrm{VH},l}{|}^2+|{\gamma }_{\mathrm{HV},l}{|}^2+{\left|{\gamma }_{\mathrm{HH},l}\right|}^2}{2}}.$$

(7)

k-th cluster delay ${\tau }_{{\mathcal{C}}_k}$ is defined as the power-weighted average of the individual path delay.

$${\tau }_{{\mathcal{C}}_k}={\displaystyle \frac{{\sum }_{l\in {\mathcal{C}}_k}{G}_l{\tau }_l}{{\overline{G}}_{{\mathcal{C}}_k}}}.$$

(8)

3.3. Interaction Loss

The interaction loss of each cluster is defined against its free space path gain with cluster delay $G_{{\mathcal{C}}_k}^{\mathrm{FS}}$ as follows:

$$G_{{\mathcal{C}}_k}^{\mathrm{F}}={\left({\displaystyle \frac{1}{4\pi f_0{\tau }_k}}\right)}^2,$$

(9)

where $f_0$ denotes carrier frequency. Therefore, the interaction loss of the k-th cluster $L_k^{\mathrm{I}}$ is defined as

$$L_{{\overline{G}}_{{\mathcal{C}}_k}}^{\mathrm{I}}={\displaystyle \frac{G_{{\mathcal{C}}_k}^{\mathrm{F}}}{{\overline{G}}_{{\mathcal{C}}_k}}}.$$

(10)

4. Results for a Suburban Microcellular Environment at 11 GHz

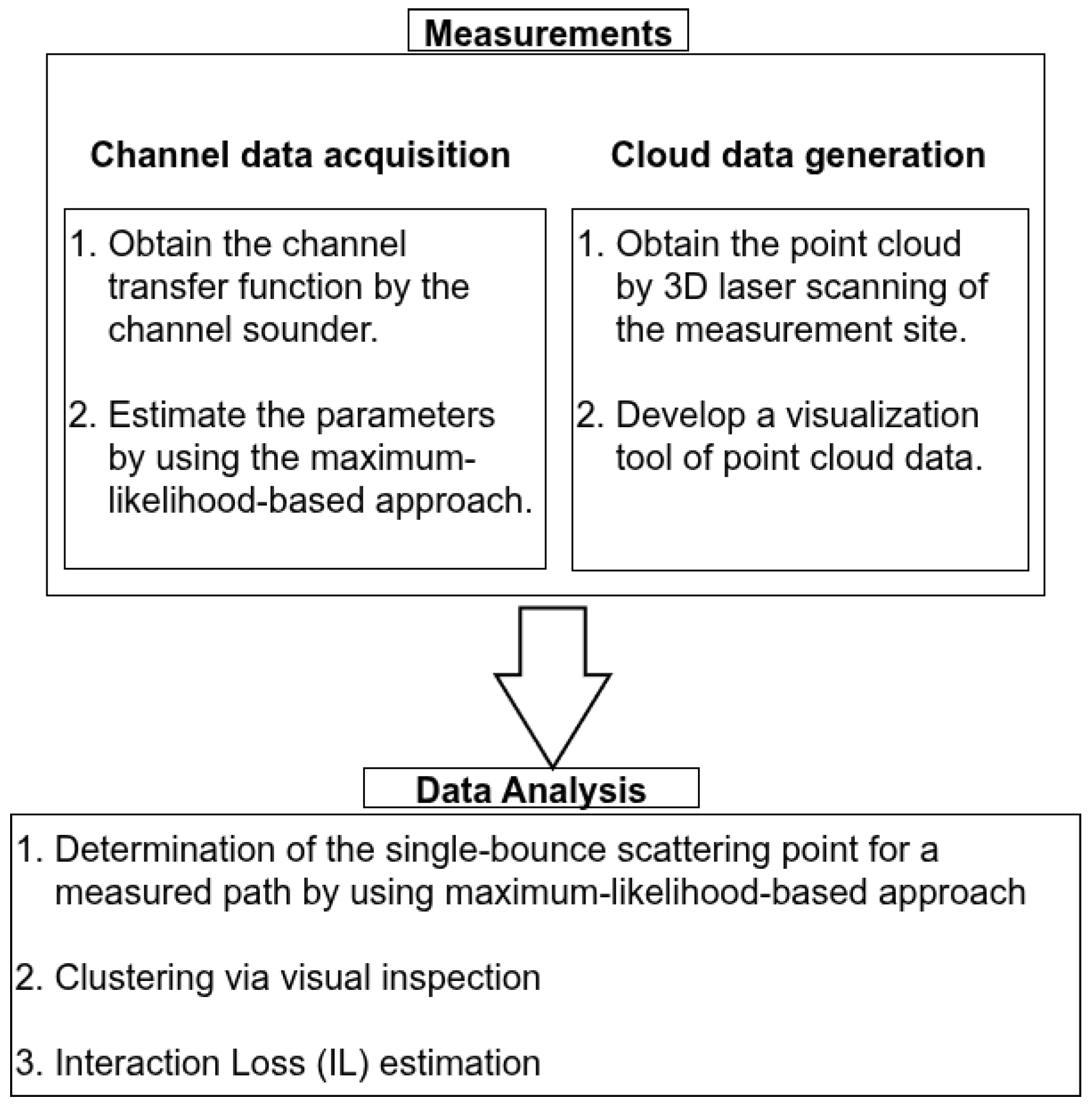
The proposed technique was applied to a suburban microcellular environment at 11 GHz [20]. Figure 2 shows the flowchart of this research. The choice of the frequency of 11 GHz was due to the availability of the spectrum for the propagation measurement, when the authors planned the measurement in 2008. It was the lowest frequency band above 6 GHz, where a 400 MHz bandwidth was available. It is noted that the frequency was not of interest for 5G, as Frequency Range 2 for IMT was identified above 24 GHz. After more than 15 years, the 11 GHz band within Frequency Range 3, which has become more promising than Frequency Range 2, which was not yet commercially successful in 5G.

4.1. Description of Measurement Data

Measurements were conducted in an outdoor residential area in Ishigaki City, Okinawa, Japan. The Rx antenna representing a base station (BS) was mounted on the balcony on the third floor of an apartment, approximately 9 m above the ground, as shown in Figure 3. The Tx antenna representing a mobile station (MS) was mounted on top of the vehicle approximately 3 m above the ground, as shown in Figure 4.

A 24 × 24 MIMO channel sounder at 11 GHz was used to measure the double-directional channel [20].

Table 1. Channel sounding parameters.

Parameter	Value
Carrier frequency	11 GHz
Signal bandwidth	400 MHz
Power per antenna	10 mW
Number of tones	2048
Tone spacing	195 KHz
Symbol duration	146.88 μs
Delay resolution	2.5 ns
Maximum delay	4 μs
Uniform Circular Array	Dual-polarized patch element Radiation pattern -H-plane: 100 degree beamwidth, -V-plane: 65 degree beamwidth Gain: 6 dBi Tx,Rx: 12 dual-polarized patches (12 VP/12 HP) (UCA spaced by 0.44 $\mathsf{\lambda }$)

lists the parameters used in the measurement. A nonlinear conjugate gradient approach was applied to the measured data to identify the path parameters [19].

The Tx position selected for the analysis was in the obstructed line of sight (OLoS) by the electric box, and the distance between the MS and BS was approximately 10 m.

Point cloud data of the 3D townscape were captured separately using laser scanners at the measurement site. The specified system error of the laser scanner was 35 mm.

4.2. Results

Four clusters were identified through visual inspection. Figure 5 and Figure 6 illustrate these clusters in perspective and orthographic views, respectively.

Table 2. Identified interacting objects (IOs) and their interaction losses (ILs).

IO	IL [dB]	Color
Electric box	5.26	yellow
Building facade	14.85	blue
Around BS	15.05	red
Power line	21.16	green

summarizes the IOs, their ILs, and the colors of the lines used in the figures.

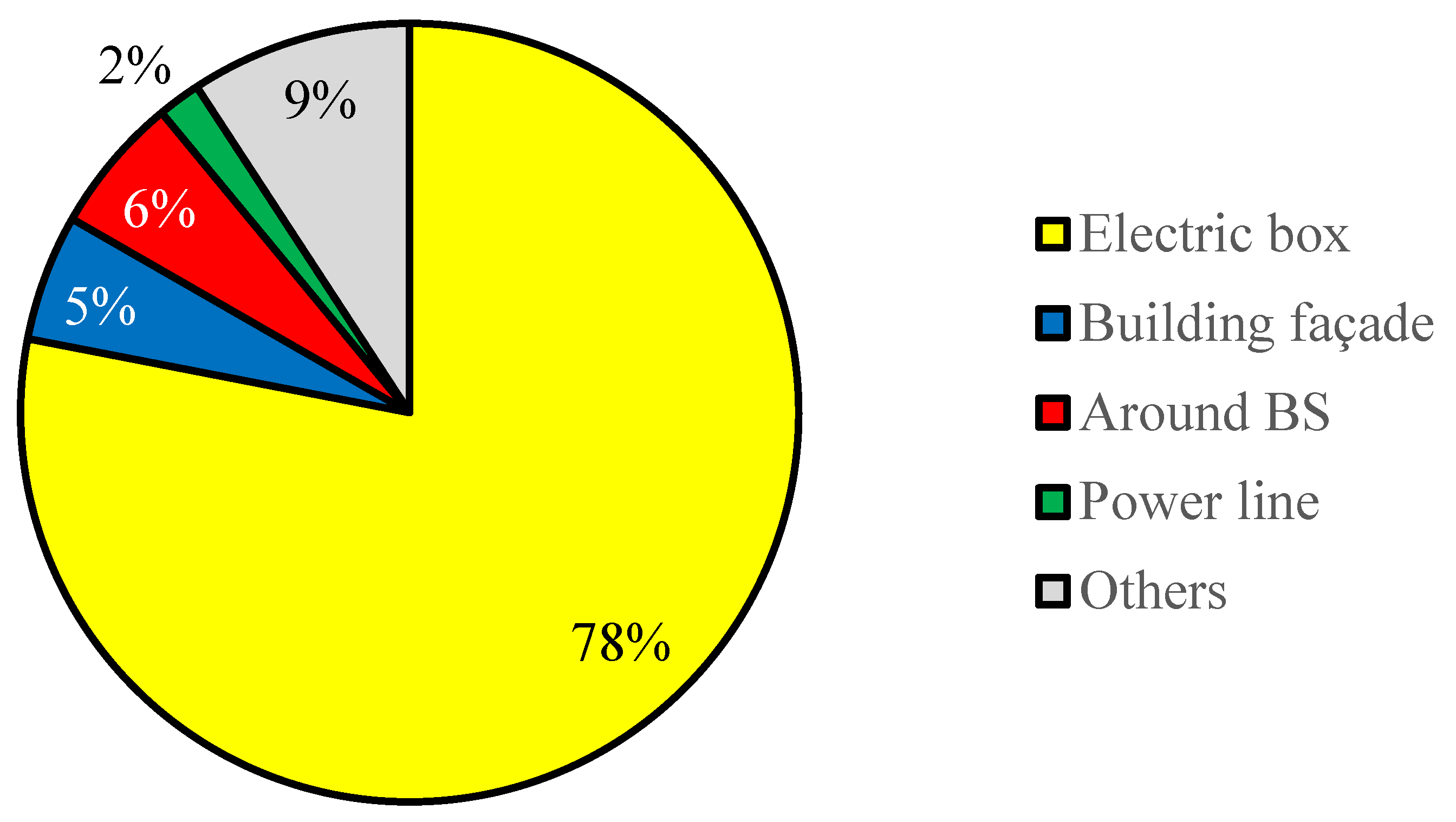
• Electric box: The yellow lines in Figure 5, Figure 6 and Figure 7 depict the electric box on the utility pole. It consisted of the largest number of SPs with the smallest IL, 5.26 dB, in this measurement scenario. Because the line-of-sight (LoS) component was obstructed by this electric box, the forward-scattering component should be dominant.
• Building facade: The blue lines in Figure 5, Figure 6 and Figure 7 depict the facades of the adjacent buildings. The building facade is the most commonly interacting object in urban and suburban areas, but it is unusual to observe single-bounce paths on the same side of the street as the base station antenna. IL of 14.85 dB was observed, which was relatively large if specular reflection was assumed. This might be due to scattering at the surface irregularity of the facade.
• Around the base station: The red lines in Figure 5, Figure 6 and Figure 7 depict the scattering points surrounding the BS. Although it is rather difficult to identify the scattering mechanism, an IL of 15.05 dB was observed.
• Power lines: The green lines in Figure 5, Figure 6 and Figure 7 depict a power line installed 6 m above the sidewalk. IL of 21.16 dB was observed.

5. Discussion

All the IOs identified by the proposed technique are hardly modeled or even identified by the conventional ray-tracing simulation, considering specular reflection and edge diffraction. It should be noted that all these objects are much larger than the wavelength (2.7 cm) and are not negligible. However, they cannot be represented using simple polygons.

Figure 8 illustrates the distribution of the power ratio from the individual IOs identified in this scenario as follows:

$$r_{{\mathcal{C}}_k}={\displaystyle \frac{{\overline{G}}_{{\mathcal{C}}_k}}{{\sum }_k{\overline{G}}_{{\mathcal{C}}_k}}}.$$

(11)

Because the LoS was slightly obstructed by the electric box, the forward-scattering path through the electric box was dominant. The contributions from the other three IOs were not very large, but were not negligibly small. This result shows that such metallic objects are sources of a significant amount of scattering in urban and suburban microcell propagation channels.

6. Conclusions

This paper proposed an approach to identify interacting objects and evaluate the interaction losses from wideband double-directional channel measurement data using point cloud data. This approach utilizes a maximum likelihood estimation of the scattering point for each path by assuming a single-bounce propagation. The proposed approach was applied to a suburban microcell environment. At the selected site, there were four scattering objects, namely the electric box, building facade, antenna surrounding objects, and power line, some of which cannot be appropriately treated in conventional ray-tracing simulators. These results suggest that refinement of the simulation technique from conventional ray tracing to deal with more complicated objects is necessary.