Importance Measure Analysis of Output Performance of Multi-State Flexoelectric Structures Based on Variance
Abstract
1. Introduction
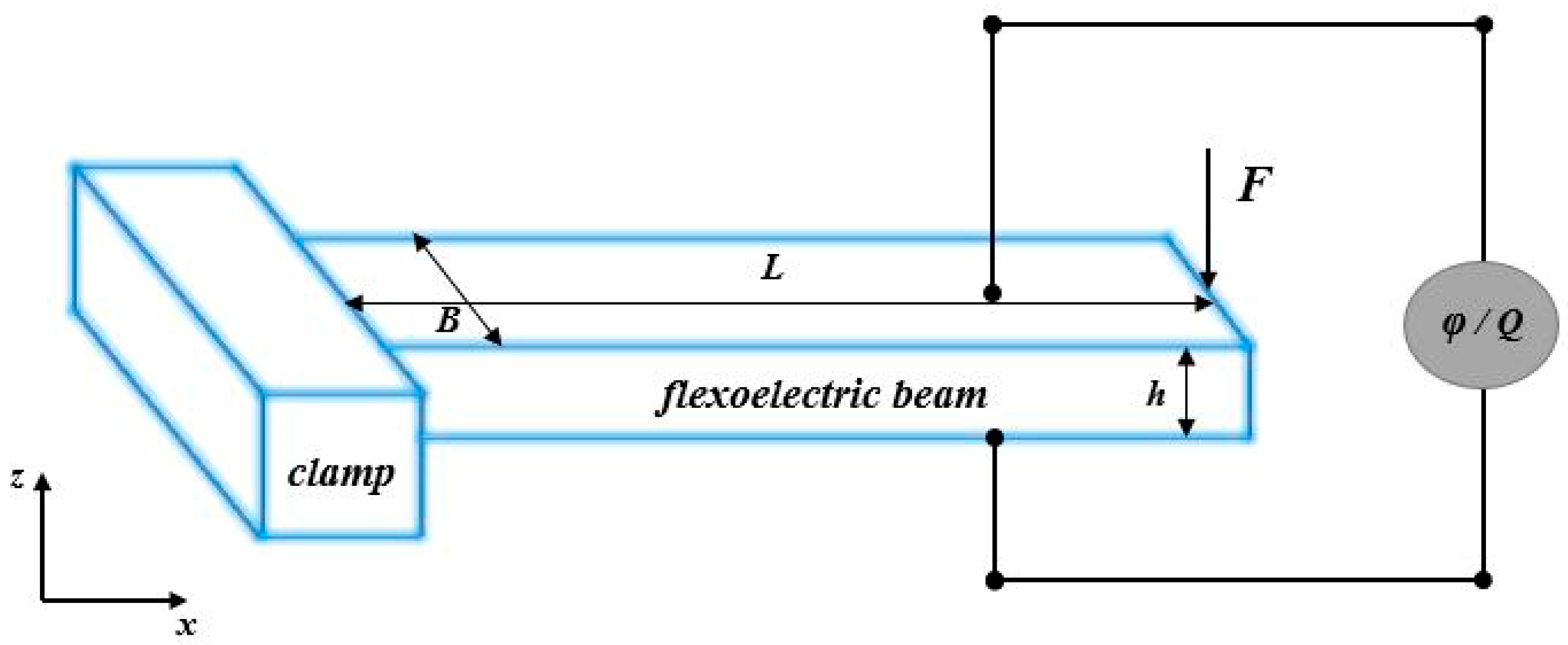
2. Output Response Model of Multi-State Flexoelectric Beams
2.1. Displacement Description
2.2. Constitutive Relation
2.3. Apply Load
2.4. The Output of Electrical Signals in Various Electrical Conditions
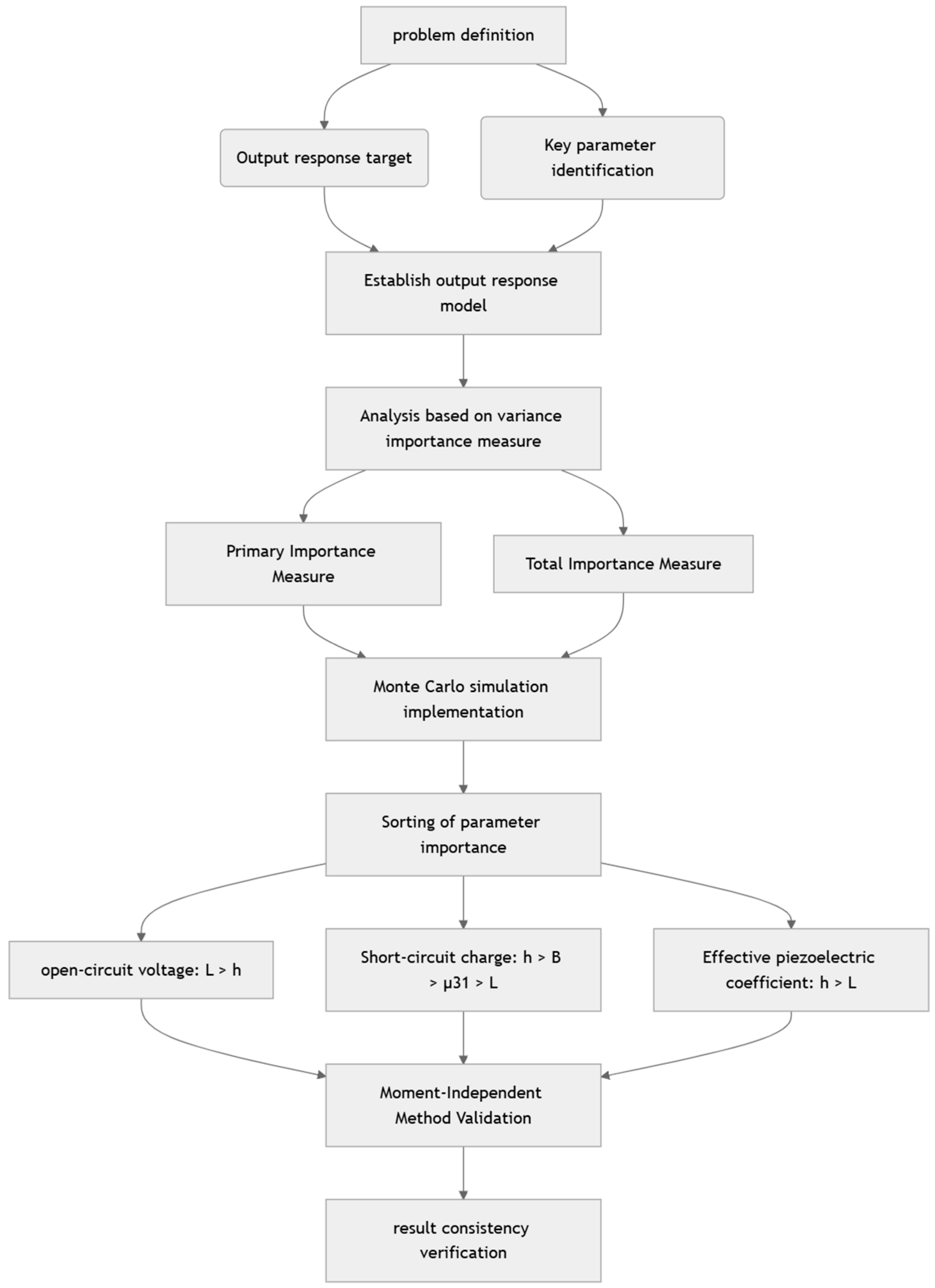
3. The Importance Measure Analysis Theory Based on Variance
3.1. Variance Decomposition and Importance Measure Index
3.2. The Computation Steps of Importance Measure Based on Monte Carlo Simulation
4. The Importance Measure Analysis of Multi-State Flexoelectric Structures
4.1. Parameter Uncertainty of Multi-State Flexoelectric Structures
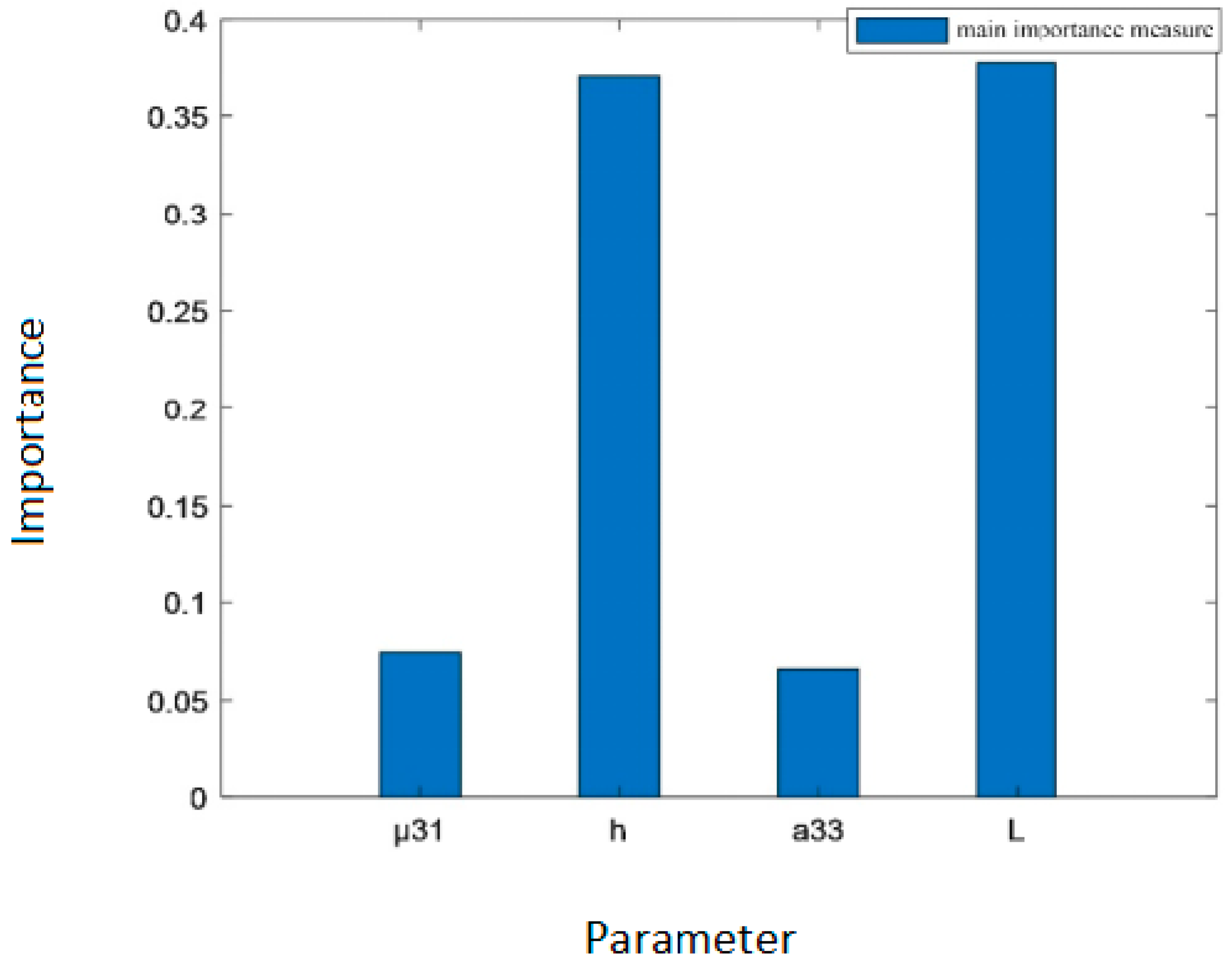
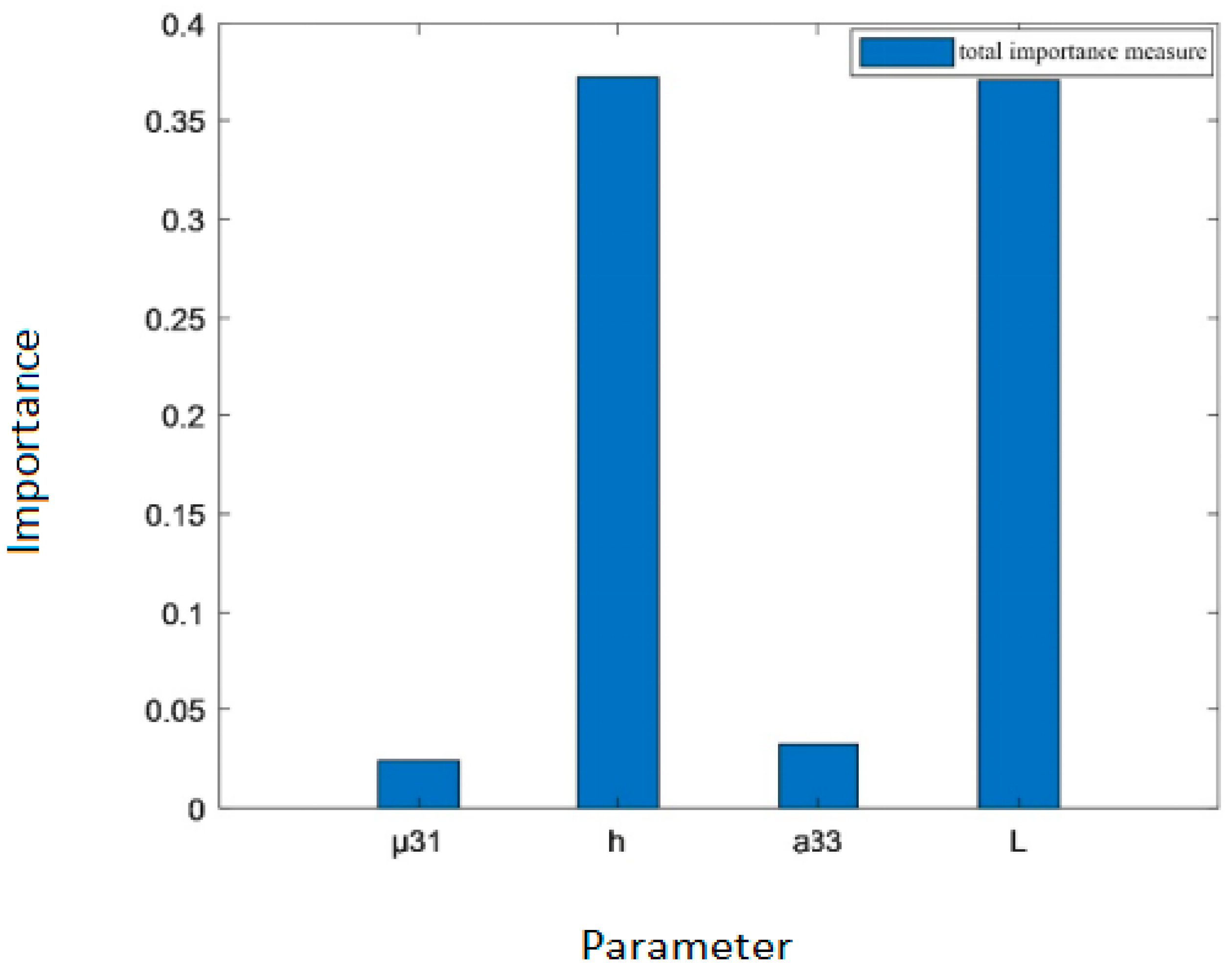
4.2. The Importance Measure Analysis of Multi-State Flexoelectric Structures Based on Variance
4.3. Analysis and Verification of the Importance Measure of Flexure Electric Beam Parameters Based on Moment Independence
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bera, S.; Guerin, S.; Yuan, H.; O’Donnell, J.; Reynolds, N.P.; Maraba, O.; Ji, W.; Shimon, L.J.W.; Cazade, P.-A.; Tofail, S.A.M.; et al. Molecular engineering of piezoelectricity in collagen-mimicking peptide assemblies. Nat. Commun. 2021, 12, 2634. [Google Scholar] [CrossRef]
- Wu, C.; Niu, R. Current research status of electrorheological fluids and electrorheological effects. Commun. Power Technol. 2020, 37, 163–165. [Google Scholar]
- Han, T.; Liu, H.; Wang, J.; Gao, C.; Han, Y. Electrostrictive Effect of Materials under High Pressure Revealed by Electrochemical Impedance Spectroscopy. J. Phys. Chem. 2021, 125, 8788–8793. [Google Scholar] [CrossRef]
- Gupta, N.; Pandey, A.; Vanjari, S.R.K.; Dutta, S. Influence of residual stress on performance of AIN thin film based piezoelectric MEMS accelerometer structure. Microsyst. Technol. 2019, 25, 3959–3967. [Google Scholar] [CrossRef]
- Shu, L.; Liang, R.; Yu, Y.; Huang, W.; Wei, X.; Li, F.; Jiang, X.; Yao, X.; Wang, Y. Flexoelectric effects in crystalline materials: Current situation and prospects. Mod. Technol. Ceram. 2018, 39, 223–246. [Google Scholar]
- Friswell, M.I.; Adhikari, S. Sensor shape design for piezoelectric cantilever beams to harvest vibration energy. J. Appl. Phys. 2010, 108, 014901. [Google Scholar] [CrossRef]
- Yang, X.; Zhou, Y.; Wang, B.; Zhang, B. A finite-element method of flexoelectric effects on nanoscale beam. Int. J. Multiscale Comput. Eng. 2019, 17, 545–552. [Google Scholar] [CrossRef]
- Omidian, R.; Beni, Y.T.; Mehralian, F. Analysis of size-dependent smart flexoelectric nanobeams. Eur. Phys. J. Plus 1 2017, 132, 481. [Google Scholar] [CrossRef]
- Mao, S.; Purohit, P.K.; Aravas, N. Mixed finite-element formulations in piezoelectricity and flexoelectricity. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20150879. [Google Scholar] [CrossRef]
- Bhaskar, U.K.; Banerjee, N.; Abdollahi, A.; Wang, Z.; Schlom, D.G.; Rijnders, G.; Catalan, G. A flexoelectric microelectromechanical system on silicon. Nat. Nanotechnol. 2016, 11, 263–266. [Google Scholar] [CrossRef]
- Zhang, H.; Hua, T.; Wang, C. Research progress of flexural effect and its application. J. Ceram. 2023, 51, 812–830. [Google Scholar]
- Chen, W. Forced Vibration Analysis and Grain Size Effect of a Flexoelectric Beam. Master’s Thesis, Xi’an JiaoTong University, Xi’an, China, 2021. [Google Scholar]
- Wang, B.; Gu, Y.; Zhang, S.; Chen, L. Flexoelectricity in solids: Progress, challenges, and perspectives. Prog. Mater. Sci. 2019, 106, 100570. [Google Scholar] [CrossRef]
- Ahmadpoor, F.; Sharma, P. Flexoelectricity in two-dimensional crystalline and biological membranes. Nanoscale 2015, 7, 16555–16570. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Chen, T.; Shu, L.; Wang, Z.; Huang, W.; Fei, L.; Li, F.; Rao, Z.; Ke, S.; Li, B.; et al. Flexoelectric fatigue in (K,Na,Li)(Nb,Sb)O3 ceramics. Appl. Phys. Lett. 2018, 113, 182901. [Google Scholar] [CrossRef]
- Krichen, S.; Sharma, P. Flexoelectricity: A Perspective on an Unusual Electromechanical Coupling. J. Appl. Mech. 2016, 83, 030801. [Google Scholar] [CrossRef]
- Abdollahi, A.; Vásquez-Sancho, F.; Catalan, G. Piezoelectric Mimicry of Flexoelectricity. Phys. Rev. Lett. 2018, 121, 205502. [Google Scholar] [CrossRef]
- Wei, P.; Lu, Z.; Hao, W.; Feng, J.; Wang, B. Efficient sampling methods for global reliability sensitivity analysis. Comput. Phys. Commun. 2012, 183, 1728–1743. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity analysis for importance assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef]
- Bjerager, P.; Krenk, S. Parametric Sensitivity in First Order Reliability Theory. J. Eng. Mech. 1989, 115, 1577–1582. [Google Scholar] [CrossRef]
- Campolongo, F.; Saltelli, A. Sensitivity analysis of an environmental model: An application of different analysis methods. Reliab. Eng. Syst. Saf. 1997, 57, 49–69. [Google Scholar] [CrossRef]
- Borgonovo, E.; Hazen, G.B.; Plischke, E. A Common Rationale for Global Sensitivity Measures and Their Estimation. Risk Anal. 2016, 36, 1871–1895. [Google Scholar] [CrossRef]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Iooss, B.; Lemaître, P. A review on global sensitivity analysis methods. In Uncertainty Management in Simulation-Optimization of Complex systems: Algorithms and Applications; Dellino, G., Meloni, C., Eds.; Springer: Boston, MA, USA, 2015; pp. 101–122. [Google Scholar]
- Wei, P.; Lu, Z.; Song, J. Variable importance analysis: A comprehensive review. Reliab. Eng. Syst. Saf. 2015, 142, 399–432. [Google Scholar] [CrossRef]
- Chabridon, V. Analyse de Sensibilité Fiabiliste Avec Prise en Compte d’ Incertitudes sur le Modèle Probabiliste-Application aux Systèmes Aérospatiaux. Ph.D. Thesis, Université Clermont Auvergne (2017–2020), Clermont-Ferrand, France, 2018. [Google Scholar]
- Maume-Deschamps, V.; Niang, I. Estimate of quantile-oriented sensitivity indices. Stat. Probab. Lett. 2017, 134, 122–127. [Google Scholar] [CrossRef]
- Lemaître, P.; Sergienko, E.; Arnaud, A.; Bousquet, N.; Gamboa, F.; Iooss, B. Density modification-based reliability sensitivity analysis. J. Stat. Comput. Simul. 2015, 85, 1200–1223. [Google Scholar] [CrossRef]
- Perrin, G.; Defaux, G. Efficient evaluation of reliability-oriented sensitivity indices. J. Sci. Comput. 2019, 79, 1433–1455. [Google Scholar] [CrossRef]
- Yun, W.; Lu, Z.; Jiang, X. An efficient method for moment-independent global sensitivity analysis by dimensional reduction technique and principle of maximum entropy. Reliab. Eng. Syst. Saf. 2019, 187, 174–182. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J.; Guo, X.; Cheng, Y.; Xu, Y.; Yuan, X. Sensitivity analysis of flexoelectric materials surrogate model based on the isogeometric finite element method. Front. Phys. 2022, 10, 1111159. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Flexoelectricity of Barium titanate. Appl. Phys. Lett. 2006, 88, 232902. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. Surface and flexoelectricity effects on size-dependent thermal stability analysis of smart piezoelectric nanoplates. Struct. Eng. Mech. Int. J. 2018, 67, 143–153. [Google Scholar]
- Lv, Z.; Song, S.; Li, H. Reliability and Reliability Sensitivity Analysis of Structural Mechanism; Science Press: Beijing, China, 2009. [Google Scholar]
- Sun, X.; Croke, B.; Roberts, S.; Jakeman, A. Comparing methods of randomizing Sobol′ sequences for improving uncertainty of metrics in variance-based global sensitivity estimation. Reliab. Eng. Syst. Saf. 2021, 210, 107499. [Google Scholar] [CrossRef]
- Derennes, P.; Morio, J.; Simatos, F. Simultaneous estimation of complementary moment independent and reliability-oriented sensitivity measures. Math. Comput. Simul. 2021, 182, 721–737. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Zhang, K. Sensitivity analysis of stochastic and fuzzy structural systems based on variance. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2018. [Google Scholar]
| Parameter Name | Parameter Symbol | Variable | Unit | Distribution | Mean Value | Standard Deviation |
|---|---|---|---|---|---|---|
| Flexure electric coefficient | Normal distribution | |||||
| Beam thickness | Normal distribution | |||||
| Dielectric coefficient | Normal distribution | |||||
| Beam length | Normal distribution | |||||
| Young’s modulus | Normal distribution | |||||
| Beam width | Normal distribution |
| Variable | ||||
|---|---|---|---|---|
| Main importance measure | 0.0746 | 0.3701 | 0.0662 | 0.3769 |
| Variable | ||||
|---|---|---|---|---|
| Total importance measure | 0.0241 | 0.3731 | 0.0323 | 0.3715 |
| Variable | ||||
|---|---|---|---|---|
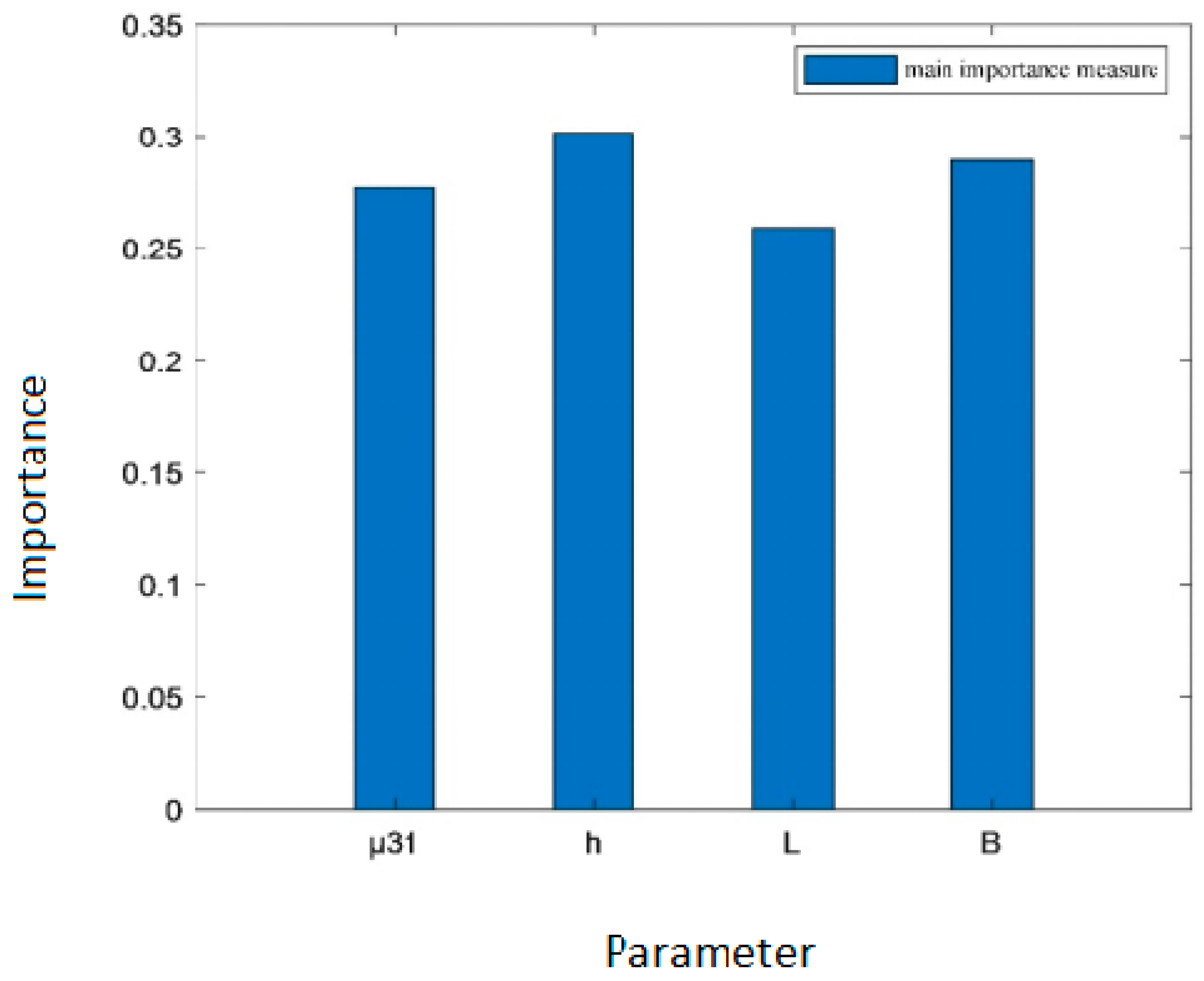
| Main importance measure | 0.2768 | 0.3016 | 0.2592 | 0.2892 |
| Variable | ||||
|---|---|---|---|---|
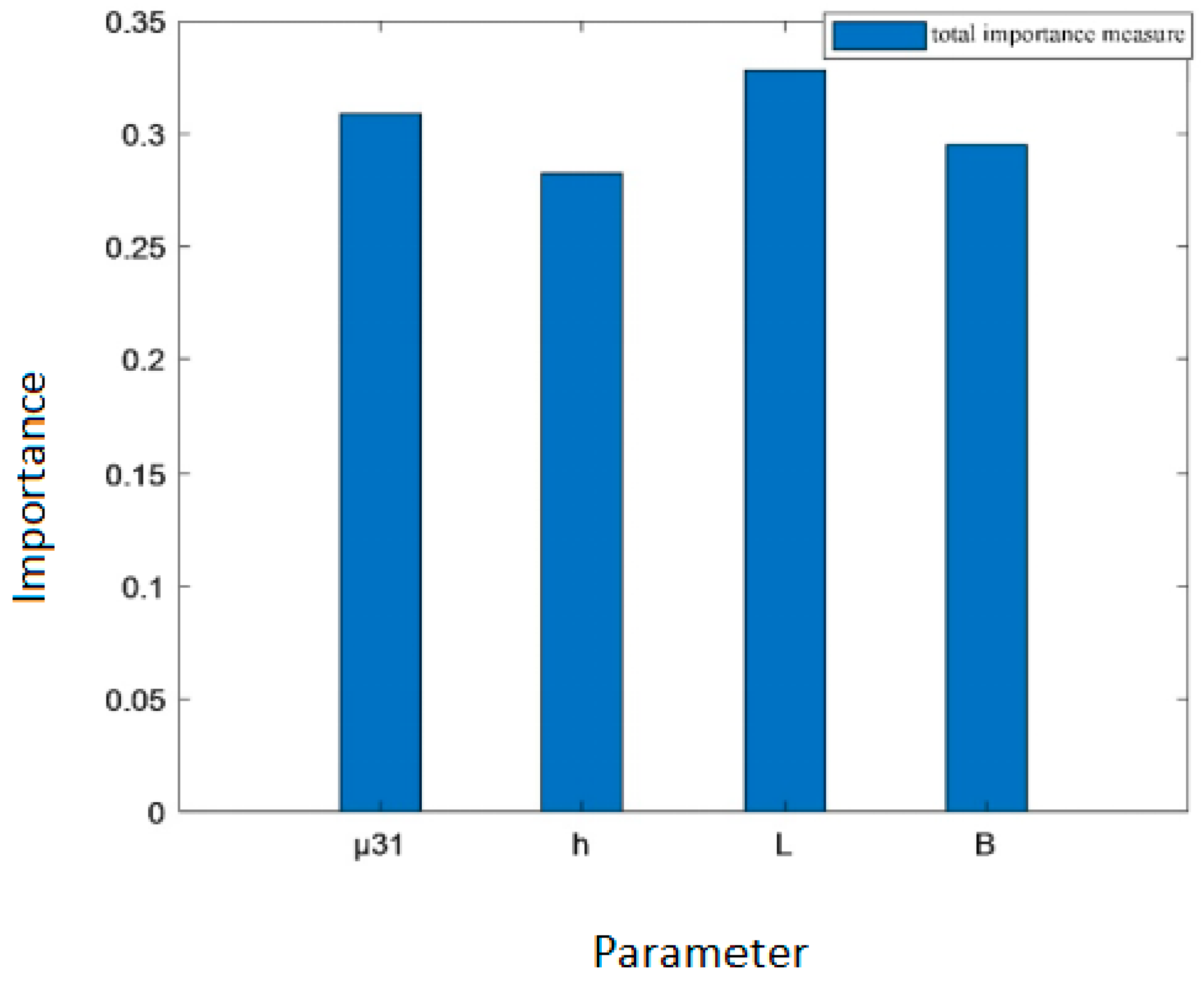
| Total importance measure | 0.3089 | 0.2825 | 0.3282 | 0.2952 |
| Variable | ||||
|---|---|---|---|---|
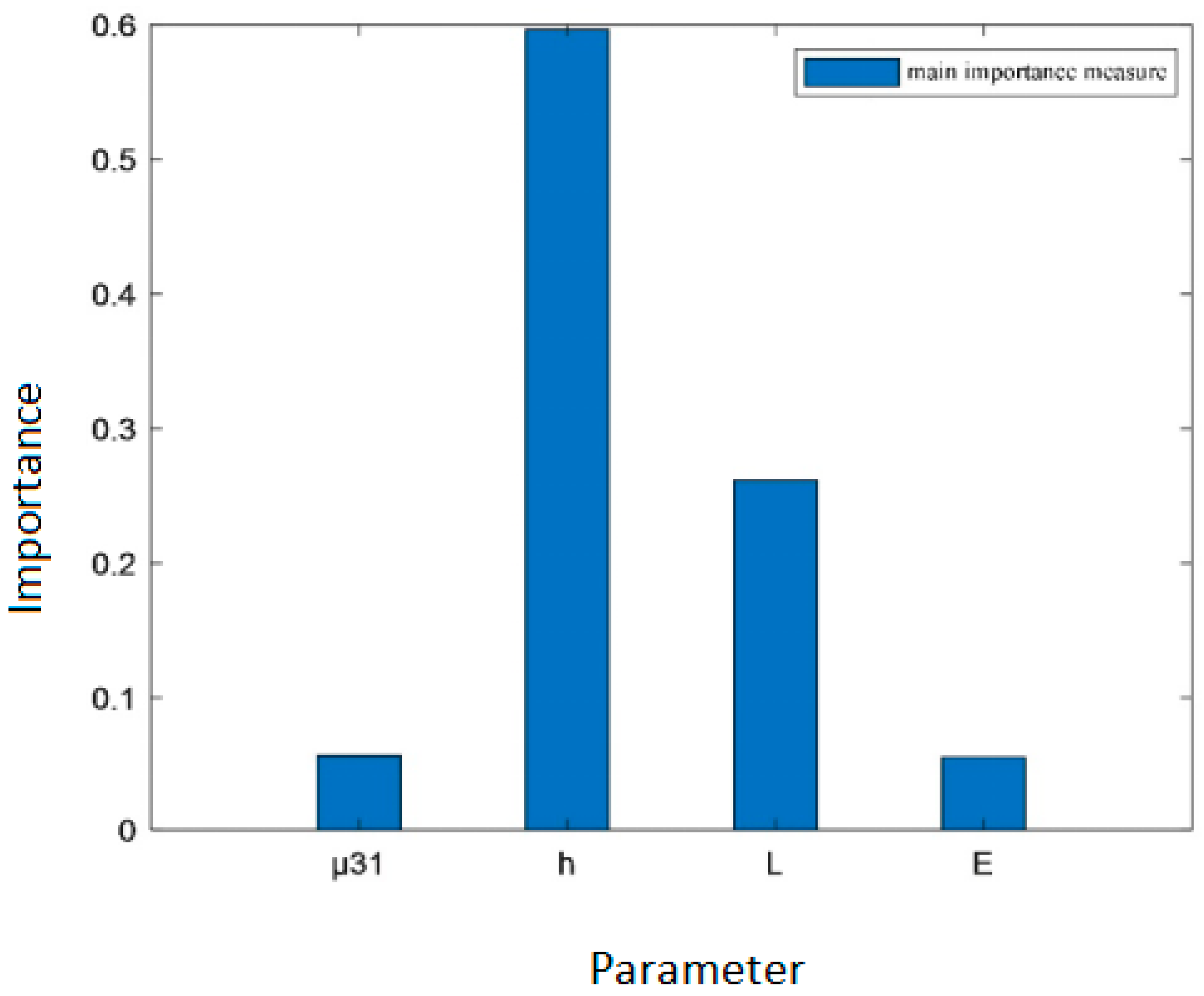
| Main importance measure | 0.0571 | 0.5965 | 0.2616 | 0.0557 |
| Variable | ||||
|---|---|---|---|---|
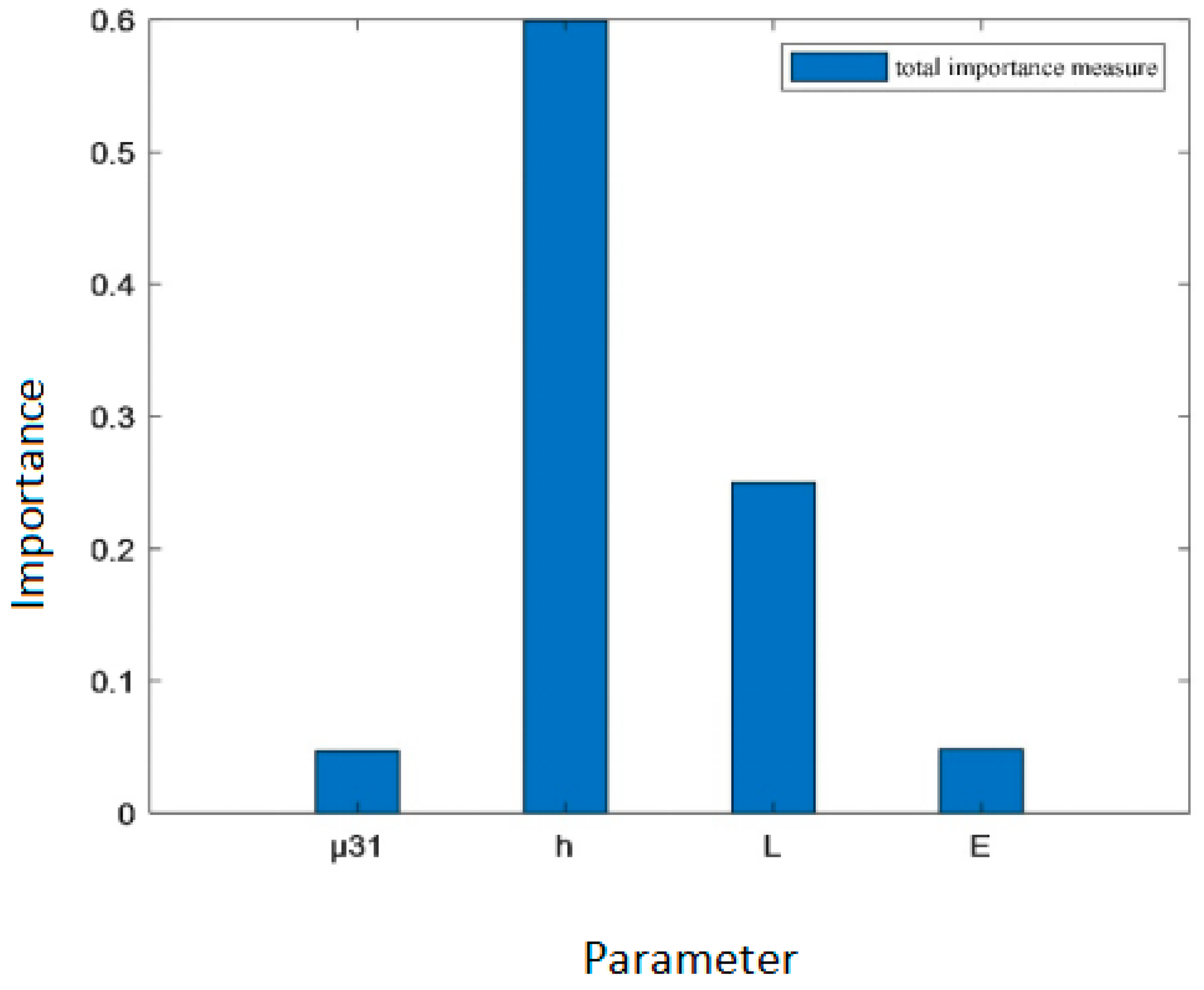
| Total importance measure | 0.0470 | 0.5991 | 0.2498 | 0.0485 |
| Variable | ||||
|---|---|---|---|---|
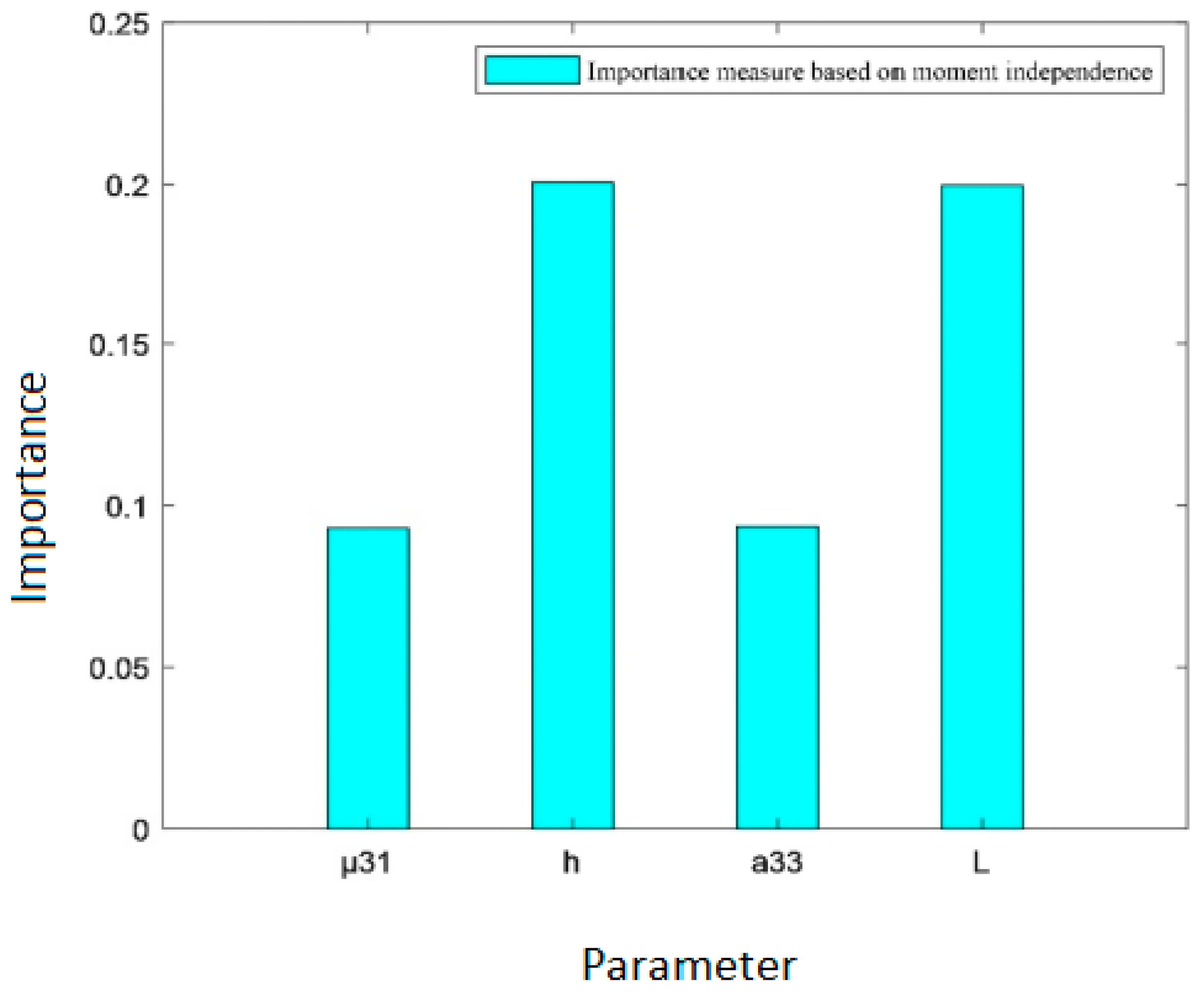
| Importance measure index | 0.0929 | 0.2007 | 0.0934 | 0.1997 |
| Variable | ||||
|---|---|---|---|---|
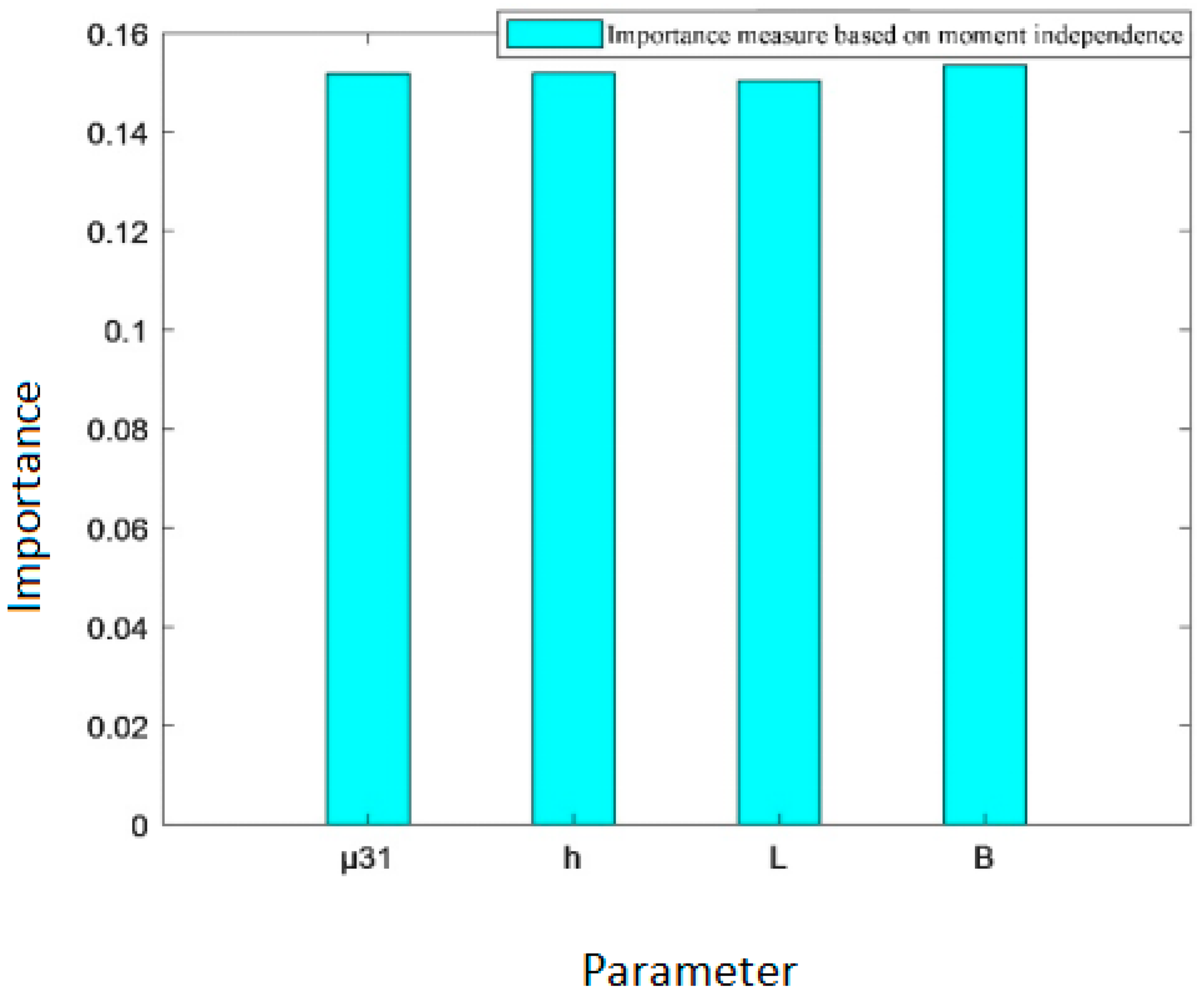
| Importance measure index | 0.1519 | 0.1520 | 0.1504 | 0.1535 |
| Variable | ||||
|---|---|---|---|---|
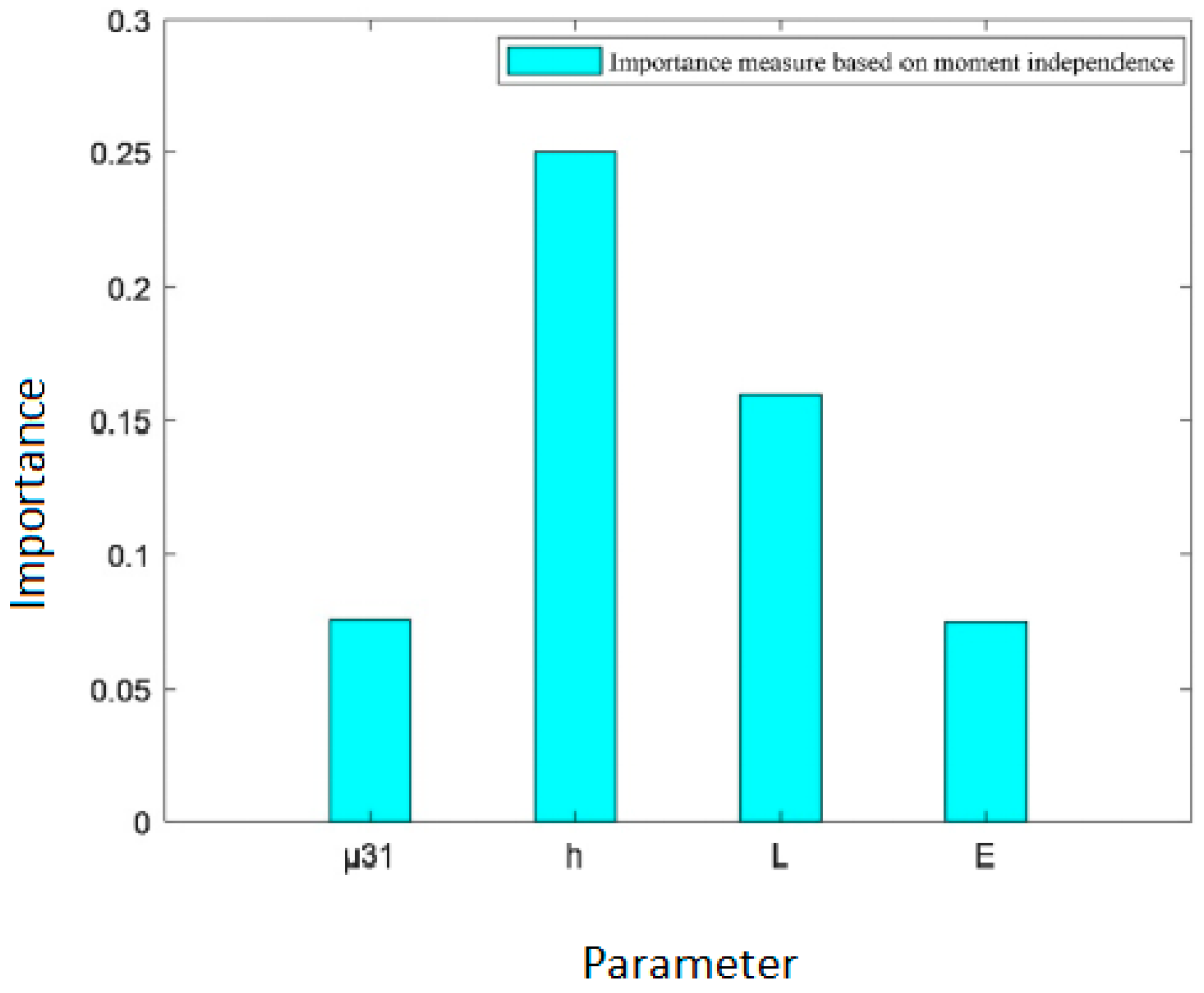
| Importance measure index | 0.0753 | 0.2502 | 0.1594 | 0.0745 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Xu, Y.; Tian, Y.; Han, C.; Hu, Y.; Liu, X. Importance Measure Analysis of Output Performance of Multi-State Flexoelectric Structures Based on Variance. Electronics 2025, 14, 3481. https://doi.org/10.3390/electronics14173481
Zhang F, Xu Y, Tian Y, Han C, Hu Y, Liu X. Importance Measure Analysis of Output Performance of Multi-State Flexoelectric Structures Based on Variance. Electronics. 2025; 14(17):3481. https://doi.org/10.3390/electronics14173481
Chicago/Turabian StyleZhang, Feng, Yuxiao Xu, Yuxiang Tian, Cheng Han, Yitao Hu, and Xiaoxiao Liu. 2025. "Importance Measure Analysis of Output Performance of Multi-State Flexoelectric Structures Based on Variance" Electronics 14, no. 17: 3481. https://doi.org/10.3390/electronics14173481
APA StyleZhang, F., Xu, Y., Tian, Y., Han, C., Hu, Y., & Liu, X. (2025). Importance Measure Analysis of Output Performance of Multi-State Flexoelectric Structures Based on Variance. Electronics, 14(17), 3481. https://doi.org/10.3390/electronics14173481






