Abstract
In recent years, digital twin technology has demonstrated remarkable potential in intelligent transportation systems, leveraging its capabilities of high-precision virtual mapping and real-time dynamic simulation of physical entities. By integrating multi-source data, it constructs virtual replicas of vehicles, roads, and infrastructure, enabling in-depth analysis and optimal decision-making for traffic scenarios. In vehicular networks, existing information caching and transmission systems suffer from low real-time information update and serious transmission delay accumulation due to outdated storage mechanism and insufficient interference coordination, thus leading to a high age of information (AoI). In response to this issue, we focus on pairwise road side unit (RSU) collaboration and propose a digital twin-integrated framework to jointly optimize information caching and communication power allocation. We model the tradeoff between information freshness and resource utilization to formulate an AoI-minimization problem with energy consumption and communication rate constraints, which is solved through deep reinforcement learning within digital twin systems. Simulation results show that our approach reduces the AoI by more than 12 percent compared with baseline methods, validating its effectiveness in balancing information freshness and communication efficiency.
1. Introduction
With the development of Internet of Vehicles (IoV) technology and its increasingly broad application prospects, IoV and its related technologies have garnered significant attention from both the automotive industry and academia. IoV technology enhances transportation safety, efficiency, and intelligence, serving as a foundational technology for vehicle dispatching and autonomous driving while delivering diverse services and application experiences to passengers [1]. In the IoV system, vehicles acquire high-frequency and heterogeneous data from road unit side (RSU) and cloud platforms to obtain traffic condition and entertainment data. Therefore, information cache stands as a core technology for ensuring real-time response and high reliability by enabling seamless data flow among vehicles, roads, and clouds [2,3]. To more effectively support IoV applications and improve the quality of service (QoS), it is necessary to optimize the cache and communication resource allocation, which can synergistically achieve a multi-objective enhancement of system throughput, information freshness, and energy efficiency, thus supporting the large-scale intelligent development of the IoV [4].
Digital twin, alternatively referred to as a cyber twin, has emerged as a pivotal technology for constructing future smart cities and the industrial metaverse, garnering escalating global attention from both industry and academic circles. At its core, a digital twin is a virtual replica of a real-world physical system, process, or various abstract concepts. It can be implemented through a computer program or encapsulated within a software model that enables real-time interaction and synchronization with its physical counterpart [5]. The integration of digital twin with deep learning and generative artificial intelligence (AI) has become mainstream, addressing dynamic resource optimization and intelligent decision-making in scenarios such as vehicle networking, spacecrafts, and industrial equipments [6,7].
The application of digital twins in vehicle networking remains in the exploratory stage. The authors of [8] constructed a digital twin-based IoV framework and assigned nearby Internet-of-Things gateways for vehicular communication, addressing the issues of insufficient RSU coverage and high latency. A digital twin-driven remote vehicle data-sharing platform was built in [9], which integrated federated learning and blockchain to design privacy-preserving mechanisms and dynamic incentive contracts. Digital twin was utilized in [10] to introduce a data-driven framework to improve traffic efficiency and minimize flow-table overflow in software-defined vehicular networks. Furthermore, existing studies have begun to explore the collaboration between digital twin and multi-dimensional resources. In [11], the authors introduce a two-tier digital twin architecture with multi-agent reinforcement learning to optimize edge computing resource allocation, and the authors of [12] proposed a digital twin-assisted framework of edge resource allocation with adaptive federated multi-agent reinforcement learning in IoV to minimize the energy consumption and service cost. For dynamic IoV environments, the researchers of [13] combined semantic sensing and digital twin to optimize the QoS with a reduction in system cost, ensuring stable and efficient services with high vehicle mobility and fast-changing network topology. In [14], the authors proposed an edge intelligence collaboration scheme based on digital twin, which optimized task offloading decisions through a virtual mirror, but only considered communication delay optimization in a single-RSU scenario. Moreover, actor–critic learning was used in [15] to solve the joint network selection and power level allocation problem in digital twin data synchronization, minimizing the long-term cost of delays and energy consumption. Although these studies built digital twin-based frameworks in vehicular networks for resource optimization, they did not consider the cooperation of RSUs and joint optimization of multiple resources.
To quantify the freshness of information, the authors of [16] proposed the concept of age of information (AoI) and designed an application-layer broadcast rate adaptation algorithm to minimize the system AoI. The AoI of an information block at a certain moment refers to the time elapsed from the generation of that information block to that moment. The authors of [17] pointed out that minimizing the AoI of the information acquired by the receiver was neither equivalent to maximizing the utilization of communication systems nor equivalent to minimizing transmission delay. Numerous studies have explored the application of AoI in vehicular networks. The authors of [18] proposed a greedy algorithm for vehicular beacon scheduling to minimize expected sum AoI. In [19], the authors investigated the problem of minimizing vehicle power under stringent latency and reliability constraints in terms of probabilistic AoI, and derived the relationship between AoI and the data queue length distribution. The authors of [20] proposed a cache-aided delayed update and delivery scheme for the joint optimization of content update, delivery, and radio resource allocation to meet the AoI requirements of various applications, while in [21], the researchers built an AoI analysis framework for vehicular social networks based on mean field theory and jointly optimized the information update frequency and transmission probability to minimize the average peak AoI. Ref. [22] conducted a comprehensive performance evaluation of the main broadcast rate control algorithm from the aspects of channel load, throughput, and AoI, and revealed that controlling congestion only based on channel load or AoI would lead to suboptimal performance. Moreover, the AoI for vehicular networks was analyzed in [23] through a spatiotemporal model, which revealed the correlation between communication and computing capabilities but did not involve information cache allocation.
With the objectives of minimizing latency, AoI, or maximizing throughput, extensive research has been conducted on optimizing communication power in vehicular networks. The authors of [24] proposed a joint scheduling and power control scheme based on greedy algorithms for vehicular links, reducing the service interruption rate and maintaining throughput fairness among vehicles. Based on the analysis of the queuing system for vehicle-to-vehicle (V2V) links, Ref. [25] put forward an optimal power allocation scheme for each pair of spectrum-reusable links. In vehicular networks, the rapid mobility of vehicles leads to dynamic channel variations, making it difficult to obtain real-time channel state information and thus posing challenges to wireless resource allocation. To address this issue, the authors of [26] proposed a power allocation scheme to reduce the interference in V2V communication, maximizing the number of communicating vehicles while meeting latency and reliability requirements. In [27], the researchers achieved optimal power allocation in vehicular networks by minimizing system outage probability to enhance cooperative communication performance. The authors of [28] proposed an optimization method for energy consumption and AoI in the IoV system by adjusting vehicular transmission intervals and power via a deep reinforcement learning (DRL) algorithm. In spite of the consideration of channel changes caused by vehicle movement, the existing studies mostly relied on traditional algorithms or simplified models for power adjustment, making it difficult to adapt to the rapidly changing vehicular environment. Moreover, most of them optimized power for local links or partial regions, lacking global mechanisms such as multi-link collaboration and interference coordination, which easily led to suboptimal power allocation due to interference accumulation in dense scenarios. Different from these works [19,20,25,28], we combine a digital twin for joint caching and power allocation with a DRL approach to achieve a global and adaptive solution in vehicular networks.
Despite the progress made in existing research regarding the integration of digital twin with IoV, notable gaps persist, particularly in supporting the highly efficient utilization of caching space and communication resource. Firstly, there is a lack of focus on the collaborative scenario of RSUs, which hinders the support for short-range cooperative services among adjacent RSUs. Secondly, communication power and information caching are seldom regarded as joint optimization objectives in the resource allocation of vehicular networks, and digital twin technology has not been incorporated to realize dynamic adaptation between these factors. In response to these issues, we propose a digital twin-integrated framework for pairwise RSU collaboration, which jointly optimizes information caching and communication power allocation to minimize the total AoI in vehicular networks. This framework leverages a multi-agent DRL approach with the multi-agent twin delayed deep deterministic policy gradient (MATD3) algorithm to address the dynamic and non-convex nature of the optimization problem and enable efficient caching and power allocation strategies through virtual interactions within the digital twin environment. The main contributions of this work are summarized as follows:
- We establish a system where the vehicles obtain information from edge storage servers and develop a queuing model for information transmission from RSUs to vehicles. A scalable pairwise RSU collaboration model is proposed, leveraging digital twins for real-time scenario-mirroring of RSUs. Based on these models, we derive the expression of the total AoI in the system.
- To boost real-time information acquirement in vehicular networks, we formulate an optimization problem for minimizing the total AoI by allocating information cache and controlling transmission power, constrained by energy consumption and data rate requirement. To solve this problem, a multi-agent DRL approach is developed with a double Q-network-based MATD3 algorithm, mitigating overestimation bias in the training.
- The simulations demonstrate superior performance of the proposed approach in terms of convergence speed, AoI optimization, and resource efficiency compared with baseline methods, underscoring the framework’s adaptability to real-world vehicular network dynamics.
The remainder of this paper is organized as follows. Section 2 builds a vehicular network and AoI model, Section 3 formulates an optimization problem to minimize total AoI via RSU power control and cache allocation, and Section 4 proposes a MATD3-based multi-agent deep reinforcement learning method for obtaining solutions. Section 5 sets the simulation scenario parameters and analyzes the experiment results. Finally, the paper concludes in Section 6.
2. System Model
2.1. Scenario Description
We constructed a vehicular network model, as shown in Figure 1. There are U pairs of RSUs in the system, i.e., there are RSUs. The edge storage server connected to each pair of RSUs stores I types of real-time information with different functions and in the form of information blocks. Each type of information is updated at a fixed time interval in the server. Assume that the sizes of information blocks of the same type are equal. The number of vehicles in the system model is V, and each vehicle is simultaneously connected to the nearest pair of RSUs, through which the vehicle obtains the information in the storage server. Let , and denote the set of RSU pairs, the set of vehicles, and the set of information types, respectively. Let be the set of vehicles connected to the u-th pair of RSUs. Each pair of RSUs is connected to a fog server. Therefore, there are a total of U fog servers in the system model. The fog server can be used to control and manage the communication power and information storage allocation of the two connected RSUs. There is a base station in the system, and it is connected to a server, which is used to run the digital twin system. Each fog server in the physical space has a corresponding digital mirror in the digital twin. The fog server maintains contact with its digital mirror through the base station.
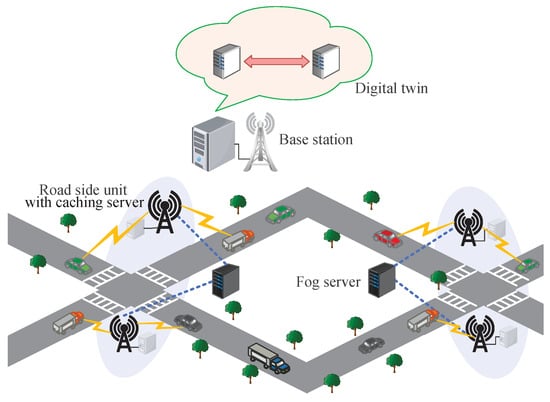
Figure 1.
System model.
2.2. Channel Model
Since the vehicular network is dynamic, the communication channel is considered to be time-varying [29] and subject to block fading. The block fading is composed of path loss, frequency-selective Rayleigh fading, and shadowing fading. The path loss is modeled as , where is the path loss exponent, d denotes the distance between the vehicle and RSU, and is the preferred distance. The frequency-selective Rayleigh fading follows a Rayleigh distribution with a standard deviation of . The shadowing fading takes the form of , where is a random variable that follows a normal distribution with a mean of 0 and a variance of [30].
2.3. Age of Information Model
Assume that the message blocks are instantly arranged to be transmitted from the server connected to the RSU to the vehicles connected to that RSU after its generation. The messages undergo a queueing process, and each message waits for the prior messages to be sent first. The AoI of a message at time slot t is defined as the elapsed time from the generation to time t. Let denote the AoI at time t for the i-th type of information downloaded by vehicle v from the u-th pair of RSUs. To facilitate the calculation and optimization of the AoI of the total system, the AoI is decomposed into three components, including the average queuing time before transmission in the u-th pair of RSUs, the time for downloading the message block, and the elapsed time from the moment the message block is received by vehicle v to time t. The AoI is expressed as
where denotes that the i-th type of information is stored in RSU 1 of the u-th pair of RSUs, and denotes that it is stored in RSU 2. Figure 2 shows the curve of over time, where , , represents the area of the corresponding regions in the figure; , , indicates the moment when the j-th block of information type i is generated in the storage server, and represents the moment when this message block is received by vehicle v. Let and . Assume that vehicles download information at a fixed rate. Since each type of information is updated at fixed time intervals in the server and the message blocks of the same type of information are of equal size, we can deduce
where represents the update frequency of information type i. As illustrated in Figure 2, can be expressed as
Consequently, is satisfied. The average AoI for information type i downloaded by vehicle v over the time T is calculated by
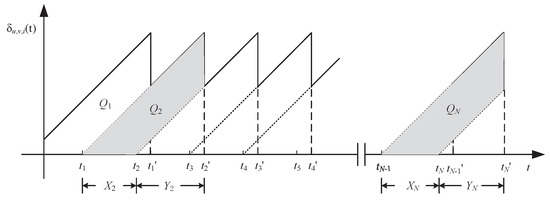
Figure 2.
The AoI for the information.
Substituting (1) into (5), we get
By the geometric meaning of a definite integral, the expression in (6) satisfies
where represents the number of blocks of information type i received by vehicle v up to time T, i.e., . Substituting (2)–(4) into (7) gives
Consider the practical scenario that the information is continuously downloaded during long-term operation; time T is assumed to be infinite for achieving the steady and statistical character of AoI. Since , , and , we have
Therefore, as T is enlarged infinitely, AoI for the information type i downloaded by vehicle v is calculated by
Due to the particular delay between the digital twin and the physical environment, there is a deviation between the data in the digital twin and the physical environment. Let be the channel used for communication between vehicle v and RSU k of the u-th pair of RSUs. Assume that is the estimated value of the channel gain in the digital twin when vehicle v is connected to RSU k of the u-th pair of RSUs, and is the deviation between the estimated value and the actual value. Then, the actual value of the channel gain is expressed as
Let be the power for communication between RSU k of the u-th pair of RSUs and vehicle v. is the interference that vehicle v receives from other vehicles and RSUs when connected to RSU k of the u-th pair of RSUs, calculated by
Therefore, the actual value of the signal-to-interference-plus-noise ratio when vehicle v is connected to RSU k of the u-th pair of RSUs is expressed by
where represents the power of additive white Gaussian noise (AWGN). Let the system channel bandwidth be W; then the corresponding download rate is calculated by
Therefore, the downloading time can be calculated by
where represents the size of the information block of the i-th type of information.
According to queuing theory, the sum of the average number of information blocks generated per unit time for all types of information in RSU 1 and RSU 2 of the u-th pair of RSUs is represented as
Assume that the information transmitted from the same RSU to the vehicle is in the same queue when information is queuing for transmission. It can be obtained that
where is the average number of information blocks that RSU k transmits to vehicle v per unit time. The expression is given as
In (19), is the average size of information blocks in RSU k of the u-th pair of RSUs, which is calculated by
We can express the sum of the average AoI of all types downloaded by vehicle v through the u-th pair of RSUs as
where indicates that vehicle v is connected to the u-th pair of RSUs, otherwise .
3. Problem Formulation
Aiming to enhance the real-time performance of information retrieval in the vehicular network, an optimization problem of minimizing the total AoI in the system by allocating information cache and controlling the transmission power of RSUs is formulated as
where is the set of information cache allocation variable, and represents the set of transmission power between RSUs and vehicles. C1 indicates that the download rate of each vehicle should not be less than to ensure the quality of service. C2 means that the sum of transmission power allocated by each RSU should not exceed the maximum power. C3 and C4 indicate that the total size of information in the caching server should not exceed the overall capacity of the server. C5 is formulated to prevent the queue from becoming infinitely long.
This optimization problem is non-linear and non-convex, and the power control of RSUs is interrelated. Therefore, it is difficult to solve the power and storage allocation of each RSU by traditional optimization methods. In contrast, RL can learn optimal multi-variable collaborative decision-making strategies through interactive trial-and-error attempts between agents and the environment. It is particularly suitable for such dynamic, non-convex, and high-dimensional coupled optimization scenarios.
4. Multi-Agent Deep Reinforcement Learning Method
Due to the existence of multiple pairs of RSUs, a multi-agent DRL-based method is proposed to solve problem (23). The process of this algorithm is described in detail below.
4.1. Markov Decision Process
Problem (23) is formulated as a multi-agent extended Markov decision process to describe the decision-making on information cache and communication power allocation based on the MATD3 algorithm. Below, we introduce the settings of the state space, action space, and reward function of the Markov decision process, respectively.
4.1.1. State Space
We define the state space of fog server u as
where is the number of vehicles in the set . Therefore, the global state of the system is represented as
4.1.2. Action Space
Since the MATD3 algorithm is only applicable to a continuous action space, a continuously valued variable in (0, 1) is defined as . Let
The action space of fog server u is defined as
Therefore, the joint action space of all fog servers is defined as
4.1.3. Reward Setting
A reward function for each fog server is set to guide the algorithm to minimize the total AoI in the system under the constraints given in problem (23). In the reward function, constraints C1 to C4 are designed as penalty terms. For fog server u, its reward function is designed as
where , , and are penalty coefficients. When constraint C5 is not satisfied, becomes negative or infinite. To avoid it, a penalty is enforced by
where L is a relatively large value. The optimization problem (23) aims to minimize the total AoI. Therefore, it is a cooperative problem for all fog servers. Let the reward functions of all fog servers be the same, i.e., . The total reward of all fog servers in the system is defined by
4.2. MATD3-Based Cache and Power Allocation Algorithm
The MATD3 algorithm is a multi-agent extension of the TD3 algorithm, employing centralized training with a decentralized execution (CTDE) framework. It inherits TD3’s enhancements that mitigate DDPG’s Q-value overestimation bias via clipped double-Q learning, target policy smoothing, and delayed policy updates. Compared to the DDPG algorithm, the MATD3 algorithm converges faster and achieves more stable and higher rewards.
The framework of the power and storage allocation algorithm based on MATD3 is shown in Figure 3. Each fog server’s digital mirror acts as an agent, yielding U agents. They interact with the virtual environment in the digital twin during training to learn optimal strategies. Agent u comprises an actor network (parameterized by ) and two critic networks (parameterized by ), with corresponding target networks . An experience replay buffer stores tuples , and mini-batches are sampled to decorrelate sequential dependencies for training stability.
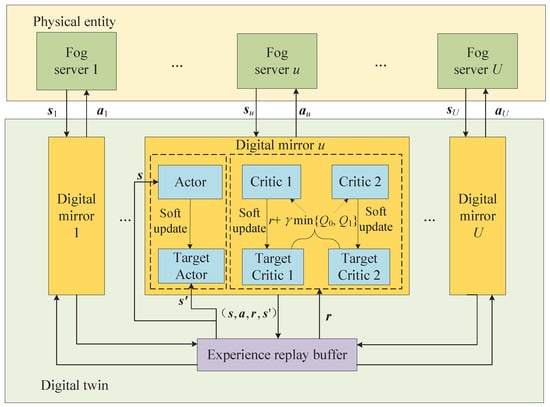
Figure 3.
Framework of the MATD3-based cache and power allocation algorithm.
The agents cooperate to achieve global optimization through environment information sharing and local policy update. During training of the CTDE paradigm, critic networks leverage global state and joint actions of all agents to estimate the Q-value, and the actor network is updated using gradients computed from critic networks. At execution time, each agent learns a local actor policy based on its own state and the evaluation from critic networks. The dual-critic networks are employed to mitigate overestimation bias, and the unified reward with a global goal is taken to transform the independent decision to coordination.
The training mechanisms include the critic update and actor update. The critic networks , , are optimized by minimizing the loss function
where represents the Q-value estimate for the state–action pair in the k-th critic network of the u-th agent. With the definition of as the discount factor, y is expressed as
The action space in (33) is obtained by
where and denote the lower and upper bounds of the action, respectively. and h represent the lower and upper bounds of the noise , .
The cumulative reward of agent u is expressed by . The actor network is updated via a policy gradient to maximize the expected cumulative reward by
Assume that M denotes the number of training iteration and F represents the training step number. The centralized training procedure is presented in Algorithm 1, where d indicates the update frequency of the actor network and represents the action noise with . Algorithm 2 illustrates the distributed execution process after centralized training. In this algorithm, each agent only needs to use its actor network, and each agent u can quickly obtain the optimal action solely based on its observed state .
| Algorithm 1 Centralized training for cache and power allocation based on MATD3 |
|
| Algorithm 2 Distributed execution for cache and power allocation based on MATD3 |
|
4.2.1. Computational Complexity Analysis
In Algorithm 1, the core computations originate from the updates of the actor and critic networks. Let and denote the number of layers in the actor network and the critic network, respectively. Let , , and , , represent the number of neurons in the -th layer of the actor network and the -th layer of the critic network. The computational complexity of the -th layer in the actor network is . Thus, the total computational complexity of the entire actor network is . Similarly, the total computational complexity of the critic network is . The overall computational complexity of Algorithm 1 obeys . Since only the actor networks are applied in Algorithm 2, its total computational complexity amounts to .
4.2.2. Scalability and Response Capability Analysis
The MATD3 model demonstrates excellent scalability through its distributed architecture. This framework decomposes the centralized solution into a collaborative solving process involving multiple distributed agents. Each agent generates decisions through a policy network based on local state information, which not only reduces computational complexity but also supports parallel computation among agents. Coupled with environmental information sharing within the digital twin system, the design effectively balances global coordination and local execution so as to adapt to the large city-wide deployment of vehicular networks.
Moreover, the MATD3 algorithm ensures a real-time response capability through the cooperation mechanism. Due to the adoption of CTDE architecture, each agent generates action independently through a lightweight actor network based on observed state and asynchronous parameter updates, avoiding the large communication overhead of centralized decision-making. Furthermore, the adoption of dual-critic networks effectively mitigate the Q-value overestimation, suppressing the value function fluctuation and significantly accelerating the policy optimization process.
5. Simulation Results
5.1. Simulation Scenario Setup
In the simulation, the scenario shown in Figure 1 is set up. First, the RSUs and vehicles are configured to be randomly and uniformly distributed in the area. Then, an IoV model based on a realistic road structure and vehicle mobility is constructed with non-uniform deployment of RSUs. Referring to [31,32], a road network covering a square area of 2 km is built with urban traffic characteristics, dynamic vehicular flow, and varying vehicle density. The traffic density ranges from 30 to 60 vehicles per , with vehicle speed varying from 20 km/h to 60 km/h. Non-uniform RSU deployment is achieved through variance spacing with 200~300 m for high-density segments and 500~800 m for low-density segments. During the training process of the algorithms, each episode consists of 200 steps. Both the actor network and the critic network contain three fully connected layers and two hidden layers, each having 256 neurons. All linear rectification functions are used as the activation function for all hidden layers, and all neural networks are updated using the adaptive moment estimation optimizer. The warm-up size of the experience replay buffer is 25,600. Other parameter settings are summarized in Table 1.

Table 1.
Simulation parameter settings.
5.2. Analysis of Simulation Results
We analyze the convergence performance of the MATD3 and DDPG algorithms in Figure 4. In the simulation scenario, there are 12 RSUs, 120 vehicles, and 60 channels, and the number of information types is 10. The common hype parameters of the two algorithms are set to be the same, and the learning rate of the critic network is 0.01 and 0.005, respectively. It can be seen from the figure that the rewards obtained by the algorithms generally increase with the episode number. When the learning rate of the critic network is 0.01, the MATD3 algorithm converges after about 370 episodes of training, while the DDPG algorithm requires about 650 episodes of training to converge. When the learning rate of the critic network is 0.005, the MATD3 algorithm converges after about 600 episodes of training, while the DDPG algorithm requires about 750 episodes of training to converge. Thus, it can be obtained that the MATD3 algorithm converges faster. The figure also shows that the convergence curve of the MATD3 algorithm has less fluctuation and achieves a higher final reward.
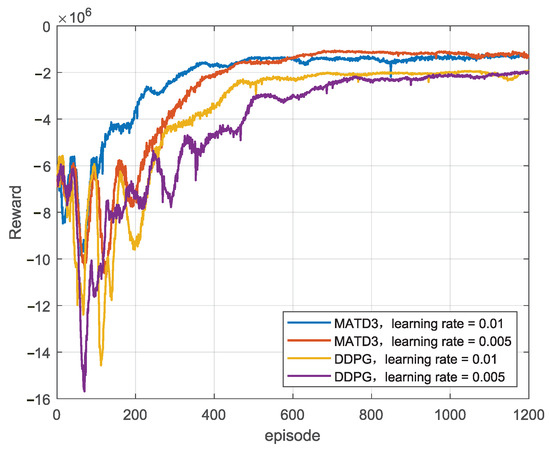
Figure 4.
Reward value versus the number of episode.
Figure 5 illustrates the trend of the total AoI in the system, which is obtained by the MATD3 and DDPG algorithms and in relation to an increasing channel gain prediction deviation of the digital twin. In this simulation, each vehicle occupies a distinct channel, and the communication between vehicles and RSUs is free from interference by other communication links. It can be seen from the figure that the total AoI decreases with increasing deviation. This is because in (13) in the absence of interference, and the value of (13) changes as increases. Consequently, the download rate of the vehicle increases, which reduces both the information download time and the queuing time for information transmission, thereby decreasing the AoI. In addition, Figure 5 demonstrates that the proposed MATD3 algorithm achieves superior AoI performance compared to the DDPG algorithm in this scenario. Furthermore, as the number of vehicles increases, the performance gap between the two algorithms widens. The MATD3 algorithm maintains stable AoI performance, while the DDPG algorithm exhibits a more significant degradation in AoI.
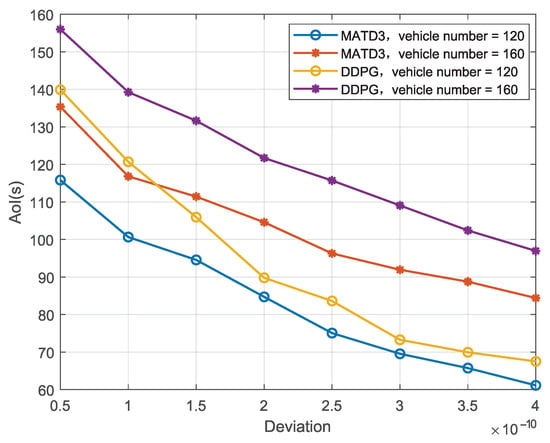
Figure 5.
Total AoI versus channel gain estimation deviation in a digital twin.
The total AoI of the system achieved by the MATD3 algorithm and that by the DDPG and greedy algorithms are shown in Figure 6, in relation to different vehicle numbers versus the number of system channels. For the greedy algorithm, the RSUs select the maximal transmission power, while a random strategy is adopted for information cache allocation. It is observed that the total AoI decreases as the number of system channels increases.
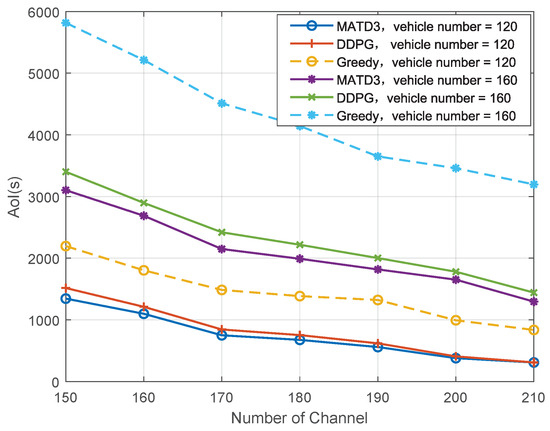
Figure 6.
Total AoI versus the number of channels.
Figure 7 depicts the total AoI variation versus the number of vehicles with a channel number of 100, revealing that the total AoI rises alongside both the growing count of vehicles and the increasing number of information type. This occurs because a greater number of information type leads to more queued information, which extends the queuing waiting time. Moreover, it places a heavier download load on vehicles, lengthening the overall download time and thus driving up the total AoI.
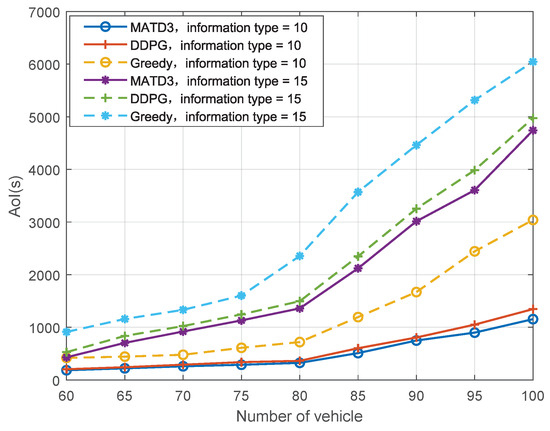
Figure 7.
Variation in total AoI versus the number of vehicle.
Both Figure 6 and Figure 7 demonstrate that the MATD3 algorithm exhibits better AoI performance than the DDPG and greedy algorithms. Since the greedy algorithm not only selects the total maximal transmission power of RSUs, increasing communication interference, but also uses random information storage allocation, a worse storage location is obtained for certain information types. This reduces the information transmission rate and increases both transmission delay and queuing waiting time. In contrast, the MATD3 algorithm obtains transmission power and information cache allocation through training so as to reduce the queuing time and transmission delay.
We compare AoI performance under the uniform and non-uniform deployment of RSUs in Figure 8. It can be seen that the AoI is smaller under non-uniform RSU distribution than uniform RSU distribution. This is because the non-uniform configuration adjusts the distribution interval according to the vehicle density so as to reduce the AoI of the vehicles in a high-density area. Moreover, the AoI decreases with the RSU number because the distance from the vehicle to the RSU becomes smaller with increasing RSU configuration.
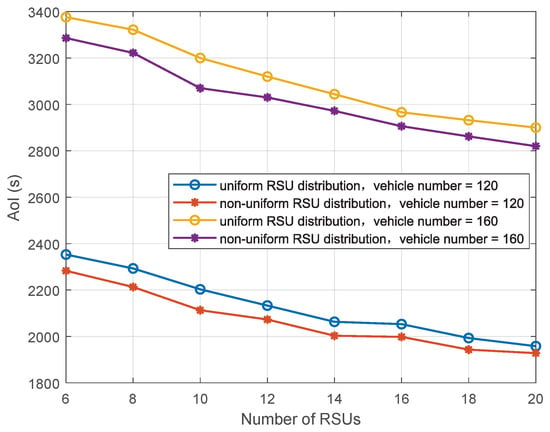
Figure 8.
Performance comparison of uniform and non-uniform RSU distribution.
6. Conclusions
We established a vehicular network model where vehicles obtained information through paired RSUs and the resource allocation of RSUs was controlled through a fog server and digital twin system. An optimization problem for information cache and communication power was formulated with the aim to minimize the AoI of the system. Subsequently, a MATD3-based algorithm was proposed to solve this problem. Finally, simulation results showed that the proposed method improved the system AoI performance compared with baseline approaches. Additionally, they revealed that the total system AoI increased with the number of vehicles, channels, and information types, which gave significant guidance on network construction and configuration.
Author Contributions
Conceptualization, G.Z. and F.K.; methodology, G.Z.; software, J.S.; validation, J.S. and Y.L.; formal analysis, Y.L.; investigation, C.Z.; resources, C.Z.; data curation, J.S.; writing—original draft preparation, C.Z.; writing—review and editing, G.Z.; visualization, J.S.; supervision, G.Z.; project administration, G.Z.; funding acquisition, G.Z. and F.K. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Guangdong Basic and Applied Basic Research Foundation (2023A1515140003) and the National Natural Science Foundation of China (62171188).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Junran Su was employed by the company China Telecommunications Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| AoI | Age of Information |
| RSU | Road Side Unit |
| CV | Connected Vehicle |
| IoV | Internet of Vehicles |
| QoS | Quality of Service |
| DRL | Deep Reinforcement Learning |
| V2I | Vehicle-to-Infrastructure |
| V2V | Vehicle-to-Vehicle |
| MATD3 | Multi-agent Twin Delayed Deep Deterministic Policy Gradient |
| CTDE | Centralized Training with Decentralized Execution |
| AWGN | Additive White Gaussian Noise |
References
- Chen, F.; Hao, B.; Yang, S.; Chen, W.; Duan, Q.; Zhou, F. A Review of Internet of Vehicle Technology in Intelligent Connected Vehicle. In Proceedings of the IEEE International Conference on Industrial Informatics (INDIN), Bari, Italy, 10–12 July 2024. [Google Scholar] [CrossRef]
- Choi, Y.; Lim, Y. Deep Reinforcement Learning for Edge Caching with Mobility Prediction in Vehicular Networks. Sensors 2023, 23, 1732. [Google Scholar] [CrossRef] [PubMed]
- Pappalardo, M.; Virdis, A.; Mingozzi, E. Energy-Optimized Content Refreshing of Age-of-Information-Aware Edge Caches in IoT Systems. Future Internet 2022, 14, 197. [Google Scholar] [CrossRef]
- Yang, J.; Ni, Q.; Luo, G.; Cheng, Q.; Oukhellou, L.; Han, S. A Trustworthy Internet of Vehicles: The DAO to Safe, Secure, and Collaborative Autonomous Driving. IEEE Trans. Intell. Veh. 2023, 8, 4678–4681. [Google Scholar] [CrossRef]
- Gao, J.; Peng, C.; Yoshinaga, T.; Han, G.; Guleng, S.; Wu, C. Digital Twin-Enabled Internet of Vehicles Applications. Electronics 2024, 13, 1263. [Google Scholar] [CrossRef]
- Ebadpour, M.; Jamshidi, M.B.; Talla, J.; Hashemi-Dezaki, H.; Peroutka, Z. A Digital Twinning Approach for the Internet of Unmanned Electric Vehicles (IoUEVs) in the Metaverse. Electronics 2023, 12, 2016. [Google Scholar] [CrossRef]
- Liao, X.; Wang, Z.; Zhao, X.; Liu, Y.; Jia, L. Cooperative Ramp Merging Design and Field Implementation: A Digital Twin Approach Based on Vehicle-to-Cloud Communication. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4490–4500. [Google Scholar] [CrossRef]
- Qian, C.; Qian, M.; Hua, K.; Liang, H.; Xu, G.; Yu, W. Digital Twin based Internet of Vehicles. In Proceedings of the 33rd International Conference on Computer Communications and Networks (ICCCN), Vancouver, BC, Canada, 22–25 July 2024. [Google Scholar] [CrossRef]
- Tan, C.; Li, X.; Gao, L.; Luan, T.H.; Qu, Y.; Xiang, Y.; Lu, R. Digital Twin Enabled Remote Data Sharing for Internet of Vehicles: System and Incentive Design. IEEE Trans. Veh. Technol. 2023, 72, 13474–13489. [Google Scholar] [CrossRef]
- Shahriar, M.S.; Subramaniam, S.; Matsuura, M.; Hasegawa, H.; Lin, S.-C. Digital Twin Enabled Data-Driven Approach for Traffic Efficiency and Software-Defined Vehicular Network Optimization. In Proceedings of the 2024 IEEE 100th Vehicular Technology Conference (VTC2024-Fall), Washington, DC, USA, 22–25 September 2024. [Google Scholar] [CrossRef]
- Li, M.; Gao, J.; Zhou, C.; Shen, X.; Zhuang, W. Digital Twin-Driven Computing Resource Management for Vehicular Networks. In Proceedings of the 2022 IEEE Global Communications Conference (GLOBECOM), Rio de Janeiro, Brazil, 4–8 December 2022. [Google Scholar] [CrossRef]
- Singh, P.; Hazarika, B.; Singh, K.; Huang, W.-J.; Duong, T.Q. Digital Twin-Assisted Adaptive Federated Multi-Agent DRL with GenAI for Optimized Resource Allocation in IoV Networks. In Proceedings of the 2025 IEEE Wireless Communications and Networking Conference (WCNC), Sydney, Australia, 13–16 April 2025. [Google Scholar] [CrossRef]
- Rawlley, O.; Oshin, B.; Gupta, S.; Bhattacharyya, T.; Singh, S. Optimizing Quality-of-Service (QoS) using Semantic Sensing and Digital-Twin in Pro-dynamic Internet of Vehicles (IoV). In proceeding of the 2024 IEEE 100th Vehicular Technology Conference (VTC2024-Fall), Washington, DC, USA, 7–10 October 2024. [Google Scholar] [CrossRef]
- Liu, T.; Tang, L.; Wang, W. Resource Allocation in DT-Assisted Internet of Vehicles via Edge Intelligent Cooperation. IEEE Internet Things J. 2022, 9, 17608–17626. [Google Scholar] [CrossRef]
- Zheng, J.; Luan, T.H.; Hui, Y.; Yin, Z.; Cheng, N.; Gao, L. Digital Twin Empowered Heterogeneous Network Selection in Vehicular Networks With Knowledge Transfer. IEEE Trans. Veh. Technol. 2022, 71, 12154–12168. [Google Scholar] [CrossRef]
- Kaul, S.; Gruteser, M.; Rai, V.; Han, C. Minimizing Age of Information in Vehicular Networks. In Proceedings of the 8th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, Salt Lake City, UT, USA, 27–30 June 2011. [Google Scholar] [CrossRef]
- Kaul, S.; Yates, R.; Gruteser, M. Real-Time Status: How Often Should One Update? In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM), Orlando, FL, USA, 25–30 March 2012. [Google Scholar] [CrossRef]
- Ni, Y.; Cai, L.; Bo, Y. Vehicular Beacon Broadcast Scheduling Based on Age of Information (AoI). China Commun. 2018, 15, 67–76. [Google Scholar] [CrossRef]
- Abdel-Aziz, M.K.; Liu, C.-F.; Samarakoon, S.; Bennis, M.; Saad, W. Ultra-Reliable Low-Latency Vehicular Networks: Taming the Age of Information Tail. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM), Abu Dhabi, United Arab Emirates, 9–13 December 2018. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Luo, H.; Gao, J.; Zhao, L.; Shen, X.S. Towards Fresh and Low-Latency Content Delivery in Vehicular Networks: An Edge Caching Aspect. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018. [Google Scholar] [CrossRef]
- Li, Z.; Xiang, L.; Ge, X. Age of Information Modeling and Optimization for Fast Information Dissemination in Vehicular Social Networks. IEEE Trans. Veh. Technol. 2022, 71, 5445–5459. [Google Scholar] [CrossRef]
- Turcanu, I.; Baiocchi, A.; Lyamin, N.; Filali, F. An Age-Of-Information Perspective on Decentralized Congestion Control in Vehicular Networks. In Proceedings of the 2021 19th Mediterranean Communication and Computer Networking Conference (MedComNet), Athens, Greece, 16–18 June 2021. [Google Scholar] [CrossRef]
- Jiang, N.; Yan, S.; Liu, Z.; Hu, C.; Peng, M. Communication and Computation Assisted Sensing Information Freshness Performance Analysis in Vehicular Networks. In Proceedings of the 2022 IEEE International Conference on Communications Workshops (ICC Workshops), Seoul, Republic of Korea, 16–20 May 2022. [Google Scholar] [CrossRef]
- Nguyen, B.L.; Ngo, D.T.; Dao, M.N.; Duong, Q.T.; Okada, M. A Joint Scheduling and Power Control Scheme for Hybrid I2V/V2V Networks. IEEE Trans. Veh. Technol. 2020, 69, 15668–15681. [Google Scholar] [CrossRef]
- Guo, C.; Liang, L.; Li, G.Y. Resource Allocation for High-Reliability Low-Latency Vehicular Communications With Packet Retransmission. IEEE Trans. Veh. Technol. 2019, 68, 6219–6230. [Google Scholar] [CrossRef]
- Hisham, A.; Yuan, D.; Ström, E.G.; Pettersson, M. Adjacent Channel Interference Aware Joint Scheduling and Power Control for V2V Broadcast Communication. IEEE Trans. Intell. Transp. Syst. 2021, 22, 443–456. [Google Scholar] [CrossRef]
- Ji, Y.; Sun, D.; Zhu, X.; Wang, N.; Zhang, J. Power Allocation for Cooperative Communications in Non-Orthogonal Cognitive Radio Vehicular Ad-Hoc Networks. China Commun. 2020, 17, 91–99. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Q.; Fan, P.; Cheng, N.; Chen, W.; Letaief, K.B. DRL-Based Optimization for AoI and Energy Consumption in C-V2X Enabled IoV. IEEE Trans. Green Commun. Netw. 2025. early access. [Google Scholar] [CrossRef]
- Li, S.; Lin, S.; Cai, L.; Shen, X.S. Joint Resource Allocation and Computation Offloading with Time-Varying Fading Channel in Vehicular Edge Computing. IEEE Trans. Veh. Technol. 2020, 69, 3384–3398. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, H.; Han, Z.; Liu, W. Spectrum Allocation and Power Control in Full-Duplex Ultra-Dense Heterogeneous Networks. IEEE Trans. Commun. 2019, 67, 4365–4380. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, L.; Zhang, L.; Zhang, X.; Sun, D. An RSU Deployment Scheme for Vehicle-Infrastructure Cooperated Autonomous Driving. Sustainability 2023, 15, 3847. [Google Scholar] [CrossRef]
- Cao, X.; Cui, Q.; Zhang, S.; Jiang, X.; Wang, N. Optimization Deployment of Roadside Units with Mobile Vehicle Data Analytics. In Proceedings of the 2018 24th Asia-Pacific Conference on Communications (APCC), Jeju Island, Republic of Korea, 15–17 October 2018. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).