Shielding Effectiveness Evaluation of Wall-Integrated Energy Storage Devices

Abstract

A homogenisation procedure for energy-buffering structural layers with integrated electrical energy storage systems (capacitors) is described with the aim of calculating their shielding effectiveness to the electromagnetic waves when they are installed inside building walls. In fact, these storage systems may attenuate electromagnetic fields in the frequency ranges employed by mobile telephony, radio broadcasting, and wireless data transmission, thus impairing the operation of Internet of Things infrastructures. The capacitors inside the individual energy-buffering modules have a multilayered structure, in which the layers have very small thicknesses, making an analytical solution of the electromagnetic field for this kind of object practically impossible. Similarly, numerical solutions may not be practical due to the very small thickness of the layers compared to the overall object size. Therefore, this paper presents a simple and effective analytical method to model multilayered structures consisting of homogenising the whole capacitor, which can then be treated as a unique block of material with fictitious (but effective) electric and magnetic parameters. The method is based on multi-section transmission lines, and a quick and reliable analytical methodology is proposed to evaluate the shielding capabilities using the homogenised capacitor’s effective parameters. Moreover, experimental measurements on a real prototype have also been carried out to validate the methodology. Results show that the trend of the simulated and measured SE is the same, proving that the method can be employed to obtain a conservative estimation of the SE from numerical simulations.

1. Introduction

Electrical energy storage is the key solution to optimise the exploitation of renewable energy resources, as enshrined in the objectives of the European governments’ strategic initiatives aiming at the green transition and climate neutrality in the next years [1]. In particular, as the energy sector transitions from centralised fossil-fuel-based production to decentralised renewable generation, the ability to buffer electrical energy becomes essential for ensuring grid stability, load balancing, and energy availability in both residential and commercial sectors. At the same time, the increasing electrification and digitalisation of modern buildings have introduced new challenges related to electromagnetic compatibility (EMC). Contemporary structures are densely populated with electrical and electronic systems, making them increasingly exposed to both intentional and unintentional electromagnetic fields (EMFs). Energy-efficient buildings are especially characterised by the widespread deployment of sensors, controllers, and communication modules, which are orchestrated through software platforms forming the backbone of Internet of Things (IoT) infrastructures. 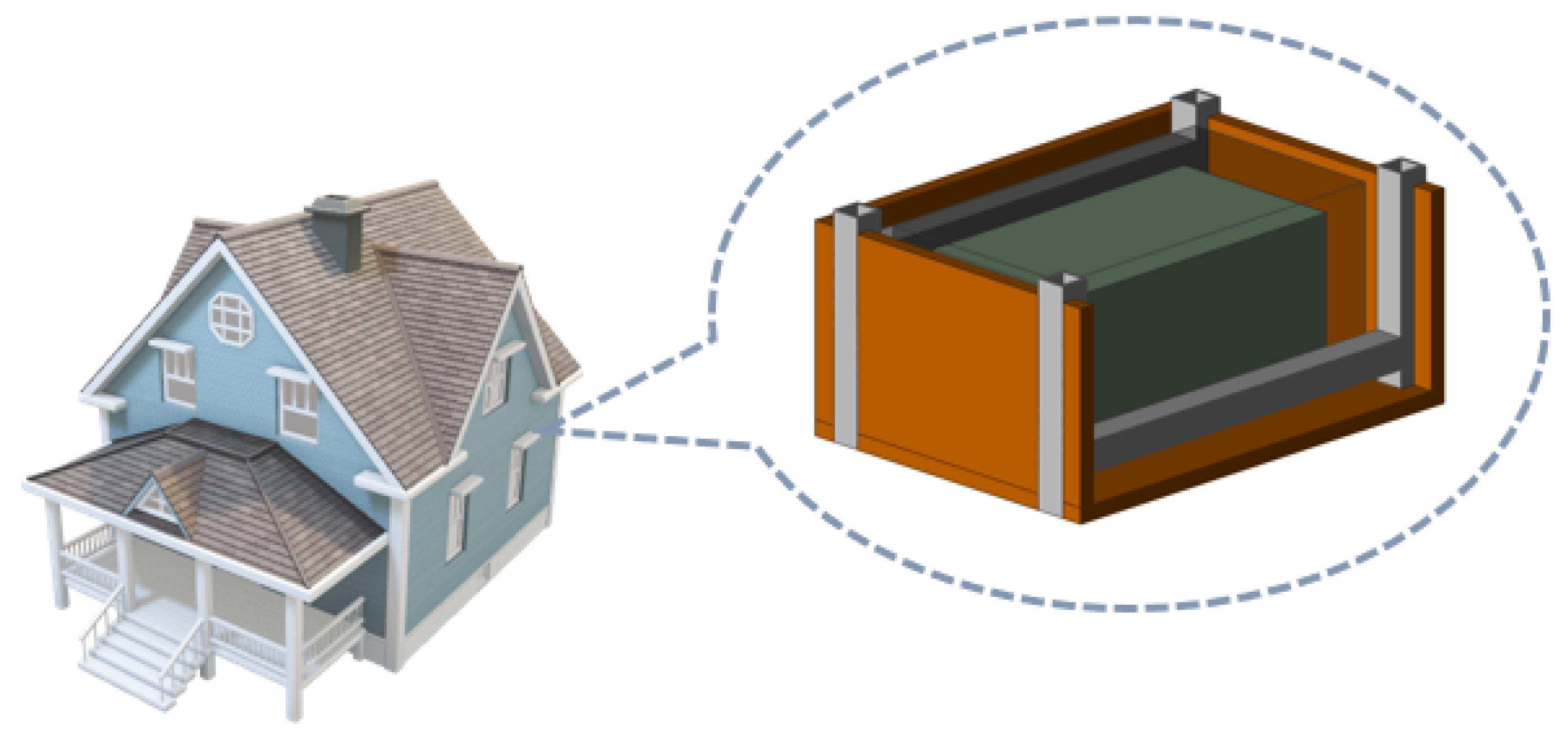These IoT systems constitute the operational intelligence of so-called smart cities, that are digitally advanced urban environments designed to optimise resource use and reduce environmental impact [2]. In this evolving technological context, the concept of energy-buffering structural layers (modular units that simultaneously fulfil structural, thermal, and electrical functions) emerges as a promising solution. These multifunctional components, as investigated in the present work and illustrated in Figure 1, offer a compelling solution to the integration of electrical energy storage directly within the building envelope [3]. By embedding energy storage elements within walls or other architectural elements, it becomes possible to reduce transmission losses, facilitate demand-side management, and support decentralised energy systems.

However, the introduction of energy-buffering structural layers also necessitates a careful analysis of their interaction with electromagnetic fields, particularly in the frequency ranges employed by mobile telephony, radio broadcasting, and wireless data transmission. Since these electromagnetic fields permeate living spaces and are critical for the functioning of IoT networks, it is crucial to assess whether integrated energy storage systems may interfere with or, conversely, mitigate electromagnetic propagation. The interaction with low-frequency fields, such as those at 50–60 Hz typically associated with power lines, is considered negligible in this context. This is due to the extremely large wavelength of such fields (on the order of several thousand kilometres), which allows them to penetrate thin conductive materials such as the metallic layers used in capacitors or the mounting brackets found in building assemblies.

Moreover, intentional electromagnetic interference (IEMI) poses a significant and emerging threat to energy-efficient storage buildings and other critical infrastructures in modern urban areas. Intentional attacks by criminals or malicious actors, which can target power electronics through conducted and radiated susceptibility mechanisms, are gaining increased attention in both civilian and military sectors. IEMI attacks fall into two main categories: radiated interference, which involves electromagnetic fields radiating and affecting wireless devices, and conducted interference, which involves injecting malicious signals into power or signal lines. The propagation paths of the two attack modes are different, and they call for different defence and assessment strategies. Conducted immunity testing assesses how power electronic devices withstand interference conducted along physical connections such as power leads or communication cables. These tests often involve injecting specific transient signals through coupling transformers or probes to simulate switching transients, bursts, surges, and spikes that may be introduced intentionally or naturally. To assess device immunity levels, a series of conducted susceptibility tests (e.g., CS115 for fast transients, CS116 for damped sinusoidal transients) are defined by common test standards like MIL-STD-461G [4]. Testing setups typically involve calibrated injection devices, and the evaluation includes verifying that the device maintains proper operation under these conditions. Relevant standards also include IEC 61000-4-6 [5], which describes immunity testing under conducted disturbance conditions in the frequency range relevant to power and signal lines. These tests help manufacturers identify vulnerabilities in device designs and improve resilience against malicious attacks conducted on critical power electronics equipment. Radiated immunity testing evaluates the ability of electronic devices to operate without significant degradation when exposed to externally generated electromagnetic fields. It is performed in controlled environments such as anechoic chambers where devices under test (DUTs) are exposed to frequency sweeps (commonly 80 MHz to 1000 MHz per IEC 61000-4-3 [6]). The objective is to identify the threshold at which malfunction is caused by radiated fields. Concerns about radiation immunity are particularly important because adversaries can deteriorate or interfere with device functionality by using continuous wave signals or high-power electromagnetic pulses. Recent research also includes advanced methods for evaluating worst-case radiated interference on linear multiport systems like wiring harnesses, optimising assessment of the voltage peaks induced on devices by intentionally radiated electromagnetic fields [7]. This research provides a theoretical and practical framework for modelling and mitigating radiated electromagnetic threats to power electronics in critical infrastructures.

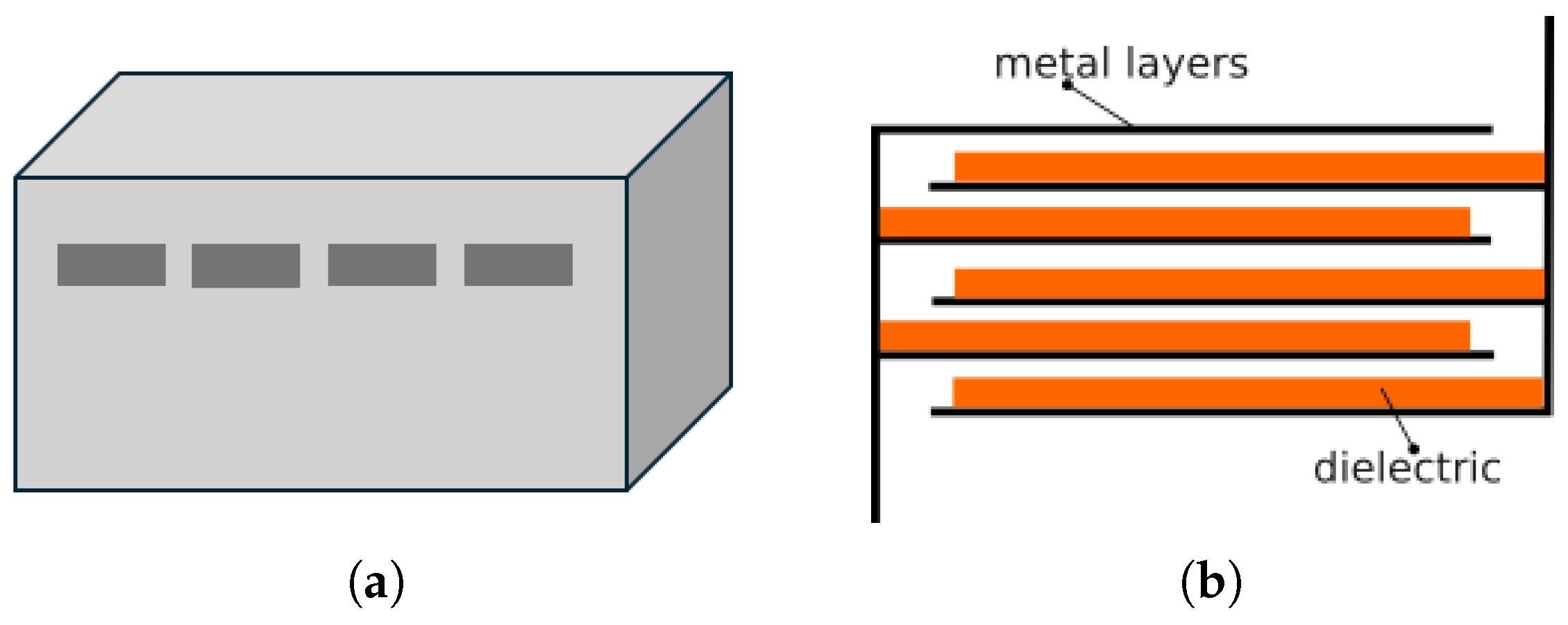
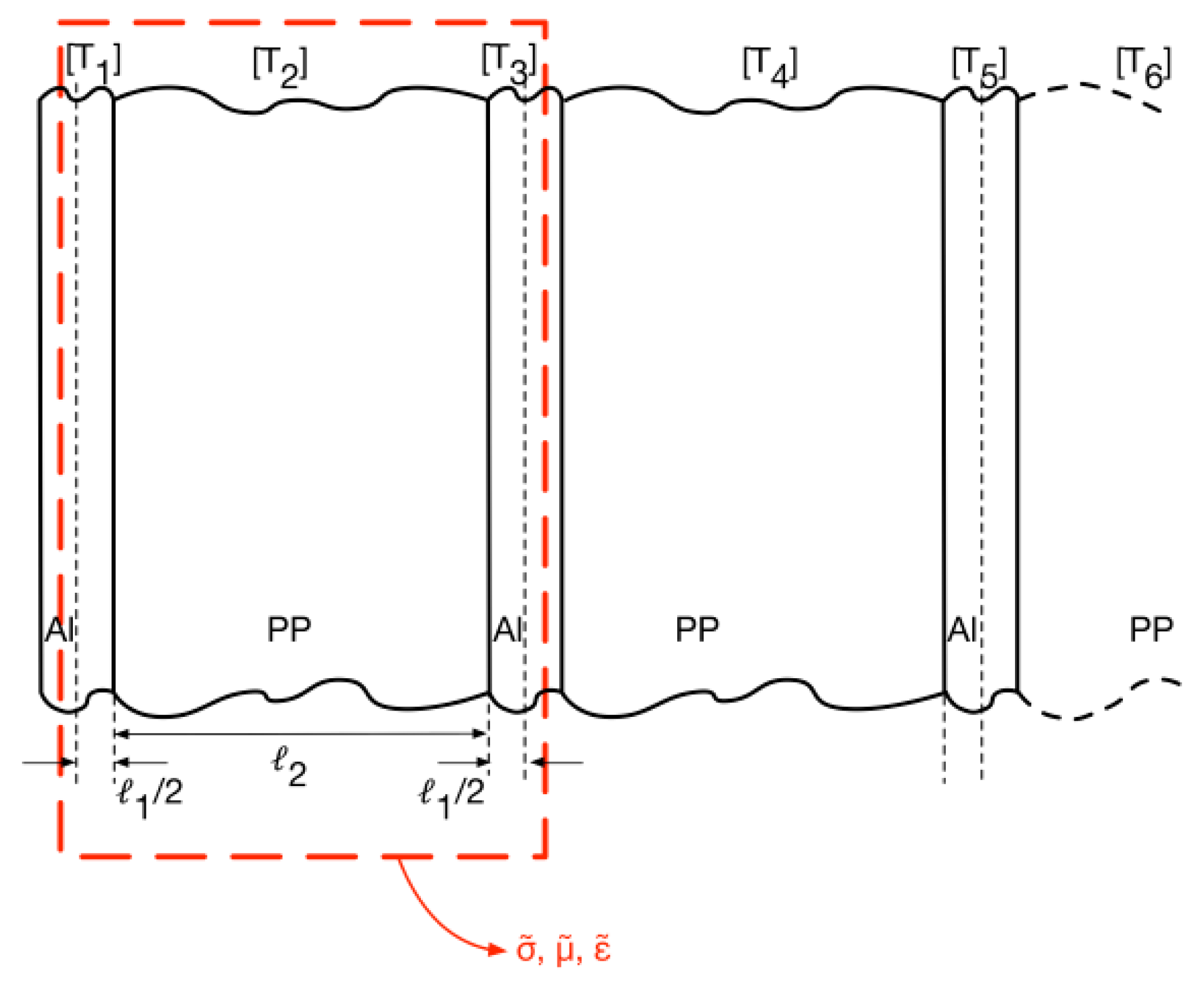
The electrical energy storage system analysed in this study is based on a multilayer capacitor comprising multiple stacks of metallised dielectric sheets, arranged in compact configurations. These capacitive modules are embedded within structural elements, forming the core of the energy-buffering layers. The sheets are oriented parallel to the surface of the capacitor enclosure, a configuration that not only supports efficient energy storage but also enhances thermal insulation and reduces the transmission of acoustic vibrations in the direction normal to the wall surface. This dual functionality positions the capacitor as a multifunctional element capable of storing electrical energy while also contributing to thermal and acoustic regulation. The primary objective of this paper is to explore a third potential function: the ability of these embedded capacitors to provide electromagnetic shielding. Given their multilayered structure and the presence of conductive surfaces, these devices may attenuate or reflect incident electromagnetic waves, offering a passive EMC benefit in environments increasingly dominated by wireless communication technologies.

The work presented herein focuses on the characterisation of the capacitor’s electromagnetic behaviour and its implications for integration in smart building environments. The broader aim is to evaluate the feasibility of using such multifunctional components to support not only the energy needs but also the electromagnetic compatibility of future sustainable buildings.

2. Energy-Buffering Structural Layers with Integrated Electrical Energy Storage Systems

The energy-buffering structural layers consist of modular units, namely functional building blocks designed to form the walls of modern sustainable buildings. Each unit incorporates embedded capacitors that serve not only as energy storage elements but also contribute to the thermal and acoustic performance of the building envelope. The integrated capacitor of each building block is composed of four parallel-connected elements, each consisting of a thin-film cylinder. A schematic diagram of the capacitor is shown in Figure 2b, highlighting the composition of one or more stacks of thin metallised dielectric sheets. The dielectric is polypropylene (PP), and the metallisation is aluminium (Al) in the active area and zinc in the contact area. The metallisation has a variable thickness which on one side can be around 150 nm and on the active part around 10–15 nm. The overall thickness of the flattened cylinder (given by twice the sum of the thicknesses of the three parts) is approximately 23.6 mm. The parameters of the capacitor layers are shown in

Table 1. Parameters of the capacitor real layers.

Layer	σ (S/m)	ε (F/m)	${\mathit{\mu }}^{\prime },{\mathit{\mu }}^{″}$ (H/m)	Thickness (μm)	Frequency GHz
Al	$3.5\times {10}^7$	1	1	$15\times {10}^{-3}$	any
PP	$5.5\times {10}^{-14}$	2.2	1	4.8	any

.

3. Calculation of the Shielding Effectiveness

For the frequencies of interest, ranging from tens of MHz to GHz, the shielding effectiveness (SE) of a shield is defined in terms of the electric field as follows:

$$S{E}_{\mathrm{dB}}=-20log{\displaystyle \frac{\left|E^P\right|}{\left|E_0^P\right|}},$$

(1)

where $E^P$ and $E_0^P$ at a generic point P of space are the magnitudes of the shielded and unshielded electric field intensities, respectively. A similar definition holds also for the magnetic field, and it coincides with (1) considering a plane wave as the incident field [8]. Due to the complex structure of the electrical energy storage system, the prediction of its SE is not an easy task. Indeed, the capacitor presents a multilayered structure with thousands of alternate thin layers of dielectric and metal. While an analytical solution of the electromagnetic field in a domain with this kind of object is practically impossible, the numerical solution obtainable through finite element method (FEM) codes results in being not practical due to the very small thickness of the layers compared to the overall object size. Indeed, a huge mesh would be required to calculate the field values and estimate the SE accurately. Moreover, the presence of dielectric-metal interfaces may lead to numerical instabilities due to the dramatic discontinuities the field undergoes in that portion of the domain (i.e., the electric conductivity is nearly null in the dielectric and very large in the metal). To overcome these numerical issues, some strategies may be adopted, always based on numerical codes. A simple and effective alternative to modelling multilayered structures consists in homogenising the whole capacitor, which can then be treated as a unique block of material with fictitious (but effective) electric and magnetic parameters.

Parameter Extraction Based on Transmission-Line Method

Some of the methods in the literature are homogenisation techniques which allow the extraction of the actual parameters of the materials (for example, magnetic permeability and permittivity) from experimental measurements of S parameters [9,10]; other methods [11,12,13] are applied to the synthesis of a single layer of artificial material having the same electromagnetic properties as a conductive shield with the aim of avoiding a fine discretisation of the material, thus reducing calculation times. Since the considered capacitor has a multilayered structure, it was necessary to identify methodologies that would allow this type of structure to be effectively represented, such as those based on the transmission matrix [8,11,14]. According to the methodology illustrated in [8], it is possible to establish an analogy between the propagation of electric and magnetic field waves through a medium layer and the propagation of voltage and current waves in a transmission line. An n-layered structure can be represented as a single-layer structure by a transmission matrix calculated as the product of the transmission matrices representing each kth layer, written as follows:

$$\widehat{\mathbf{T}}={\widehat{\mathbf{T}}}_n{\widehat{\mathbf{T}}}_{n-1}\dots {\widehat{\mathbf{T}}}_1=\prod _{k=1}^n{\widehat{\mathbf{T}}}_k$$

(2)

where ${\widehat{\mathbf{T}}}_k$ is the transmission matrix associated to the kth layer and is defined as follows:

$${\widehat{\mathbf{T}}}_k=\left[\begin{array}{cc}\cosh \left({\widehat{\gamma }}_k{l}_k\right)& -{\widehat{\eta }}_k\sinh \left({\widehat{\gamma }}_k{l}_k\right)\\ -(1/{\widehat{\eta }}_k)\sinh \left({\widehat{\gamma }}_k{l}_k\right)& \cosh \left({\widehat{\gamma }}_k{l}_k\right)\end{array}\right]$$

(3)

with $l_k$ as the thickness of the generic kth layer and ${\widehat{\gamma }}_k$ and ${\widehat{\eta }}_k$ as the propagation constant and intrinsic impedance, respectively. In an alternating layer structure, the matrices of the type (3), if multiplied in odd numbers with (2), give a total transmission matrix which is again of the type (3), written as follows:

$$\widehat{\mathbf{T}}=\left[\begin{array}{cc}\cosh \left(\widehat{\gamma }l\right)& -\widehat{\eta }\sinh \left(\widehat{\gamma }l\right)\\ -(1/\widehat{\eta })\sinh \left(\widehat{\gamma }l\right)& \cosh \left(\widehat{\gamma }l\right)\end{array}\right]=\left[\begin{array}{cc}{\widehat{T}}_{11}& {\widehat{T}}_{12}\\ {\widehat{T}}_{21}& {\widehat{T}}_{22}\end{array}\right].$$

(4)

By enforcing that the matrix $\widehat{\mathbf{T}}$ has an effective propagation constant $\widehat{\tilde{\gamma }}$, an effective intrinsic impedance $\widehat{\tilde{\eta }}$ and thickness l, it is possible to determine the parameters of the homogenised capacitor as follows:

$$\widehat{\gamma }={\displaystyle \frac{{\cosh }^{-1}\left({\widehat{\mathbf{T}}}_{11}\right)}{l}}$$

(5)

and

$$\widehat{\eta }=-{\displaystyle \frac{\sinh \left[{\cosh }^{-1}\left({\widehat{\mathbf{T}}}_{11}\right)\right]}{{\widehat{\mathbf{T}}}_{12}}}.$$

(6)

Starting from a three-layer structure of the capacitor (aluminum–polypropylene–aluminum, shown in Figure 3), in which the layer thicknesses and real physical parameters of the capacitor are considered, the transmission matrix (4) can be determined, whose elements allow the propagation constant (5) and the characteristic impedance (6) to be found. The transmission line parameters for the homogenised structure are then defined as follows:

$$\widehat{\tilde{\gamma }}=\sqrt{j\omega \widehat{\tilde{\mu }}(\tilde{\sigma }+j\omega {\widetilde{ϵ}}^{\prime })}$$

(7)

$$\widehat{\tilde{\eta }}=\sqrt{{\displaystyle \frac{j\omega \widehat{\tilde{\mu }}}{\tilde{\sigma }+j\omega {\widetilde{ϵ}}^{\prime }}}}$$

(8)

from which the effective parameters of the electrical conductivity $\tilde{\sigma }$, the magnetic permeability $\widehat{\tilde{\mu }}$, and the permittivity ${\widetilde{ϵ}}^{\prime }$ of the homogeneous single-layer (homogenised) structure can be estimated considering the following:

$${\displaystyle \frac{\widehat{\tilde{\gamma }}}{\widehat{\tilde{\eta }}}}=\tilde{\sigma }+j\omega {\widetilde{ϵ}}^{\prime }$$

(9)

$${\displaystyle \frac{\widehat{\tilde{\eta }}\widehat{\tilde{\gamma }}}{j\omega }}=\widehat{\tilde{\mu }}.$$

(10)

These relations allow the extraction of the effective parameters $\tilde{\sigma }$, $\widehat{\tilde{\mu }}$, and ${\widetilde{ϵ}}^{\prime }$, written as follows:

$$\tilde{\sigma }=\mathrm{Re}\left[{\displaystyle \frac{\widehat{\tilde{\gamma }}}{\widehat{\tilde{\eta }}}}\right]$$

(11)

$${\widetilde{ϵ}}^{\prime }=\mathrm{Im}\left[{\displaystyle \frac{\widehat{\tilde{\gamma }}}{\widehat{\tilde{\eta }}}}\right]$$

(12)

$$\widehat{\tilde{\mu }}={\displaystyle \frac{\widehat{\tilde{\eta }}\widehat{\tilde{\gamma }}}{j\omega }}.$$

(13)

Through this procedure, the multilayered capacitor can then be reduced to an equivalent homogeneous structure consisting of a single layer having the same thickness as the squeezed capacitor (obtained by multiplying the base cell thickness, i.e., $l_1+l_2$, by the number of layers), to which the extracted effective parameters are assigned.

4. Implementation and Results

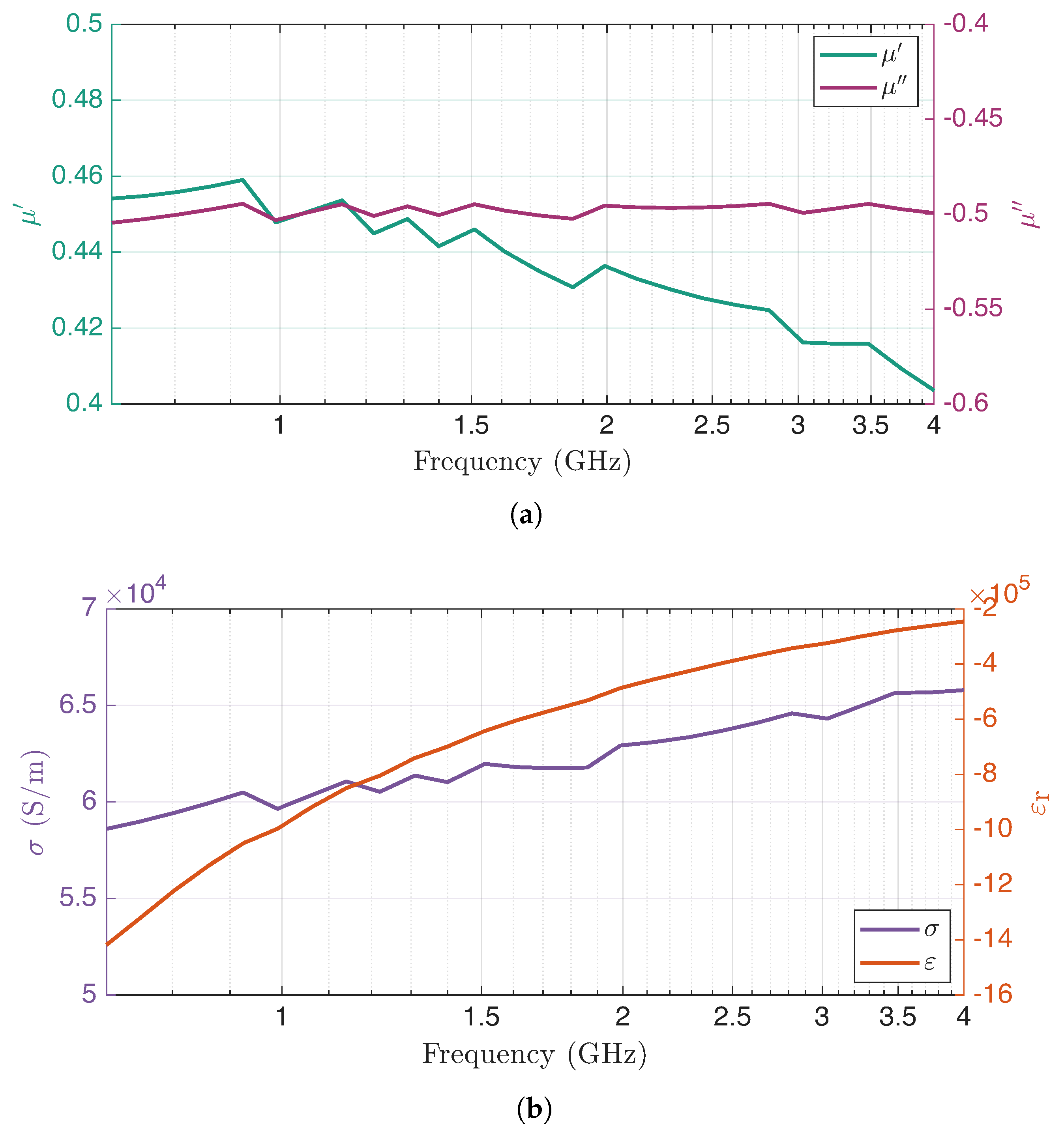
The effective parameters of the homogenised capacitor obtained as a function of frequency are shown in Figure 4. The energy-buffering structural layer containing the capacitor, namely the brick, is then formed by a wooden structure (brown part in Figure 1) supported by square cross-section steel tubes (grey in Figure 1), which also serve as electrical connectors. The capacitor is housed inside the brick together with elements for acoustic and thermal shielding, which, however, do not influence the electromagnetic field at the frequencies of interest.

4.1. Numerical Simulations

To numerically evaluate the shielding effectiveness of the homogenised capacitor, it is necessary to illuminate it with a plane wave and evaluate the attenuation of this wave downstream of the shield. FEM simulations with Ansys Maxwell© were carried out. In analogy with the experimental tests, described in the next section, the SE is evaluated through the power transferred between the regions upstream and downstream of the homogenised capacitor calculating the S parameters relevant to a two-port network representing the homogenised capacitor. The S matrix (scattering matrix) is defined as follows:

$$\left[\begin{array}{c}{\widehat{b}}_1\\ {\widehat{b}}_2\end{array}\right]=\left[\begin{array}{cc}{\widehat{S}}_{11}& {\widehat{S}}_{12}\\ {\widehat{S}}_{21}& {\widehat{S}}_{22}\end{array}\right]\left[\begin{array}{c}{\widehat{a}}_1\\ {\widehat{a}}_2\end{array}\right]$$

(14)

where the terms ${\widehat{a}}_1$ and ${\widehat{a}}_2$ represent the power waves incident on ports 1 and 2 of the two-port network, respectively, and ${\widehat{b}}_1$ and ${\widehat{b}}_2$ represent the power waves reflected back from ports 1 and 2, respectively.

The shielding effectiveness therefore corresponds to the difference between the parameter ${\widehat{S}}_{21}$, which represents the transmission coefficient, calculated without and with the shield (i.e., the homogenised capacitor). Being interested in the interaction of the object with the wave in its propagation direction only, a parallelepiped domain of 26.9 cm × 15.5 cm (rectangular cross-section) × 160 cm (length of the simulation waveguide) has been used. The boundary conditions were chosen in such a way to impose the propagation of the plane wave in the waveguide along the positive x-direction, i.e., by imposing the following:

• Surfaces parallel to the plane $xy$ perfectly electrically conductive;
• Surfaces parallel to the $xz$ plane of very high magnetic permeability.

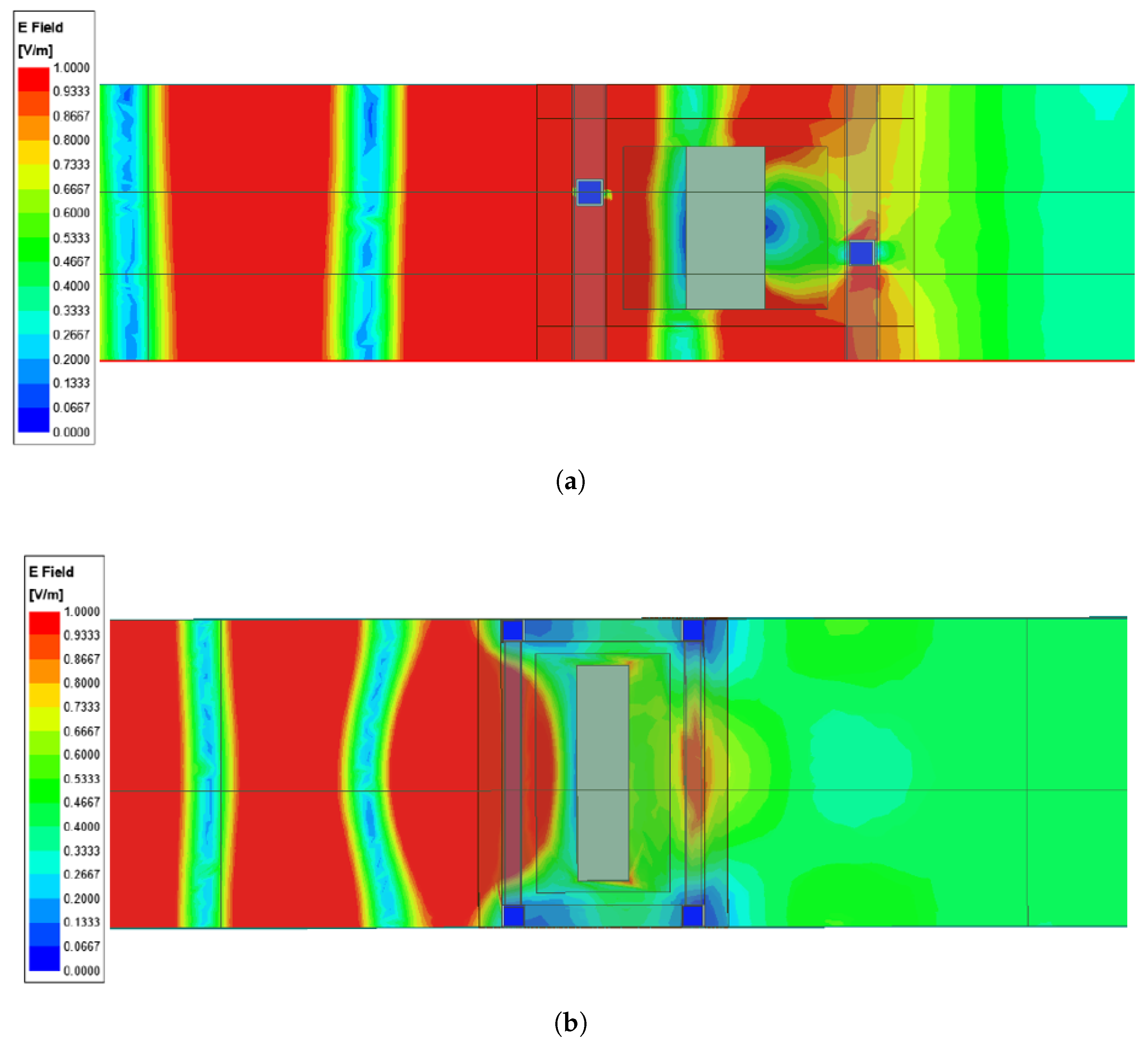
The simulated electric field is plotted in Figure 5a,b for planes cutting the brick in half, considering the side and the top views, respectively. Its value is normalised with respect to the input one (the one obtained without the shield) and clearly shows the presence of standing waves. The vertical plane (Figure 5a, i.e., the side view) indicates that the homogenised capacitor contributes the most to the shielding because the electric field is very low at the interface. From the horizontal plane (Figure 5b, i.e., the top view), it can be seen that also the metallic parts of the supporting structure play a role in the shielding, since they alter the electric field distribution.

4.2. Experimental Setup

Measurements of the shielding effectiveness on a single energy-buffering system prototype were carried out with reference to the IEEE Std 299:2006 standard [15]. The selected frequency range was 800 MHz–3.6 GHz, a range covering part of frequency bands commonly employed by 2G–3G–4G–5G cellular telephony. The range was limited by the available instrumentation. The method illustrated in [15] makes use of two twin antennas, one transmitting (TX) and another receiving (RX), connected to the output and input ports of a Vector Network Analyser (VNA), respectively. The measurement of the SE consists in calculating the ratio between the electromagnetic field received by the RX antenna with and without the shield between the antennas.

A schematic diagram illustrating the measurement setup for the SE is shown in Figure 6a. The shield can thus be characterised in terms of the “insertion loss” caused by the shield interposed between the TX and RX antennas. The laboratory measurement setup is shown in Figure 6b, where a screened enclosure of dimensions 1 m × 1 m × 1.1 m with an aperture and the brick sample prototype positioned on the aperture is used. The transmitting horn antenna is visible, too. Horn antennas are preferred due to their enhanced directivity.

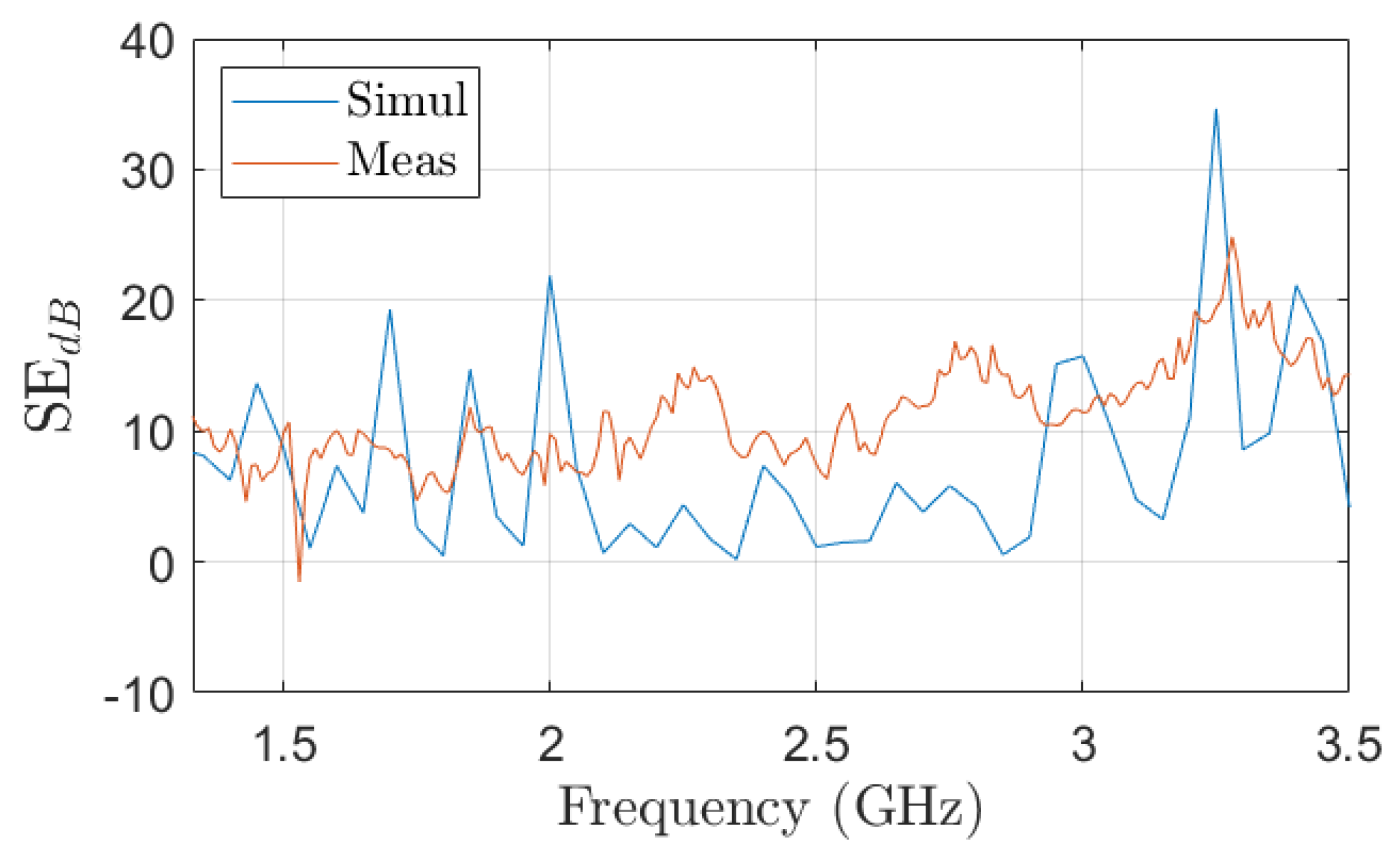
The comparison of the simulated and measured SE is shown in Figure 7. Although the simulations indicate higher values for many frequencies of the frequency range, the trend of the SE as the frequency increases is similar. It has to be noticed that comparison is purely indicative, as the simulation results are obtained exploiting a plane wave in a waveguide, whereas in the measurement twin antennas were used, generating a field configuration which approximates that of a plane wave depending on the frequency and distance. Thus, differences between simulated and measured values can be reasonably expected. In any case, being the predicted SE lower than the measured one, it can be concluded that the simulation provides a conservative estimation of the capability of the energy-buffering system to provide attenuation to electromagnetic fields. In any case, the measured/simulated SE of the energy-buffering system is below 20 dB over the whole frequency range, and thus the shielding provided by the energy-buffering system is very limited.

5. Discussion and Conclusions

An analytical procedure for the extraction of the electromagnetic parameters of a wall-integrated capacitor energy storage device has been developed to simplify the calculation of the SE that these devices present when embedded in building walls. Accurate electromagnetic simulations can be performed without having to reproduce numerous and very thin layers in the FEM model. Experimental measurements on a real prototype have also been carried out to validate the simulations. Despite some discrepancies in the value of the peaks, the trend of the simulated and measured SE is the same, proving that the method can be employed to obtain a conservative estimation of the SE from FEM models. Results show that the SE of the energy-buffering system is below 20 dB over the whole frequency range, and thus the shielding provided by the energy-buffering system is very limited compared to what is achievable by purposely designed shielding solutions. The proposed approach for the SE evaluation was revealed to be simple and effective, with possible extension to cover the following:

• Extending the frequency range of analysis;
• Integrating the model with aperture and vent effects in irregular structures;
• Exploration of design strategies to achieve a target SE using the proposed homogenisation approach.