Workload Prediction for Proactive Resource Allocation in Large-Scale Cloud-Edge Applications

Abstract

Accurate workload prediction is essential for proactive resource allocation in large-scale Content Delivery Networks (CDNs), where traffic patterns are highly dynamic and geographically distributed. This paper introduces a CDN-tailored prediction and autoscaling framework that integrates statistical and deep learning models within an adaptive feedback loop. The framework is evaluated using 18 months of real traffic traces from a production multi-tier CDN, capturing realistic workload seasonality, cache–tier interactions, and propagation delays. Unlike generic cloud-edge predictors, our design incorporates CDN-specific features and model-switching mechanisms to balance prediction accuracy with computational cost. Seasonal ARIMA (S-ARIMA), Long Short-Term Memory (LSTM), Bidirectional LSTM (Bi-LSTM), and Online Sequential Extreme Learning Machine (OS-ELM) are combined to support both short-horizon scaling and longer-term capacity planning. The predictions drive a queue-based resource-estimation model, enabling proactive cache–server scaling with low rejection rates. Experimental results demonstrate that the framework maintains high accuracy while reducing computational overhead through adaptive model selection. The proposed approach offers a practical, production-tested solution for predictive autoscaling in CDNs and can be extended to other latency-sensitive edge-cloud services with hierarchical architectures.

1. Introduction

Large-scale applications deployed across distributed cloud-edge infrastructures, hereafter referred to as cloud-edge applications, must dynamically adapt to fluctuating resource demands to maintain high availability and reliability. Such adaptability is typically achieved through elasticity, in which the system automatically adjusts its resource allocation based on workload intensity. Operationally, elasticity is commonly realized via auto-scaling mechanisms that enable application components to autonomously scale either vertically (adjusting resource capacity of individual instances) or horizontally (modifying the number of component instances), thereby ensuring efficient and resilient service provisioning. Traditional auto-scaling approaches (e.g., those provided by default in commercial platforms such as Amazon AWS (https://aws.amazon.com/ec2/autoscaling/) (accessed on 30 April 2025) and Google Cloud (https://cloud.google.com/compute/docs/autoscaler) (accessed on 30 April 2025) are reactive, adjusting resources only after performance thresholds are breached. In contrast, proactive auto-scaling anticipates future workload changes and allocates resources in advance. This predictive capability hinges on accurate workload forecasting, typically enabled by machine learning or statistical models trained to capture patterns in resource demand [1,2,3]—a task that is inherently challenging because it requires not only sophisticated forecasting techniques but also a deep understanding of workload dynamics and their temporal evolution.

Workloads in cloud-edge applications are predominantly driven by external request patterns and are often geographically distributed to satisfy localized demand. To effectively model such workloads, key performance indicators, such as “the number of client requests to an application” [3] or the corresponding volume of generated network traffic, are commonly employed. These workload traces are typically captured as time series [4], enabling temporal analysis and forecasting. Classical statistical models, particularly AutoRegressive Integrated Moving Average (ARIMA) and its variants, Seasonal ARIMA (S-ARIMA) [5] and elastic ARIMA [6], have been widely used for this purpose. These methods have demonstrated reasonable predictive accuracy at low computational cost across a variety of workload types [6,7,8]. In addition, modern machine learning (ML) techniques, particularly Recurrent Neural Networks (RNNs), have been extensively applied to workload modeling and prediction due to their ability to capture complex, non-linear temporal patterns. These models offer improved accuracy over traditional approaches for both short- and long-term forecasting [9,10], making them well suited to dynamic and bursty workload scenarios.

However, in distributed systems such as cloud-edge environments, operational data streams are inherently non-stationary, i.e., they exhibit temporal dynamics and evolve over time due to both external factors (e.g., changes in user behavior, geographical load variations) and internal events (e.g., software updates, infrastructure reconfiguration) [11,12,13]. This evolution often results in a mismatch between the data used to train prediction models and the data encountered during inference, a phenomenon commonly known as concept drift [14]. As a consequence, the accuracy of predictive models deteriorates over time, necessitating regular retraining. Both ARIMA and RNN-based models rely on access to up-to-date historical data for training and updates. While effective, maintaining these models across large-scale distributed systems, where millions of data points are processed per time unit, poses significant challenges in terms of scalability and timeliness. To address these issues, online learning techniques have emerged and been integrated into various modeling algorithms, such as Online Sequential Extreme Learning Machine (OS-ELM) [15], Online ARIMA [16], and LSTM-based online learning methods [17]. These approaches enable models to incrementally adapt to streaming data using relatively small updates, making them well suited for dynamic environments where workloads and system conditions evolve over time. Among these techniques, OS-ELM has gained attention due to its ability to combine the benefits of neural networks and online learning while maintaining low computational complexity, which enhances its practicality in large-scale cloud-edge systems.

Building on this foundation, we present a framework for constructing predictive workload models designed to support proactive resource management in large-scale cloud-edge environments. Unlike most prior work, our framework is trained and validated on operational traces collected from a live, production CDN serving millions of daily requests. This real-world dataset captures authentic traffic variability, seasonal effects, and sudden spikes, making it a strong basis for practical evaluation. The targeted application, i.e, a multi-tier Content Delivery Network, is representative of large-scale, latency-sensitive services deployed at the cloud-edge interface. The framework is validated through a practical use case involving CDNs, a class of applications characterized by highly variable and large-scale traffic patterns.

To accommodate the multi-timescale nature of CDN workloads, we systematically investigate both offline and online learning methods. The evaluation spans a range of modeling techniques, including statistical forecasting, Long Short-Term Memory (LSTM) networks, and OS-ELM, all trained on real operational CDN datasets. Further, these models are integrated into a unified prediction framework intended to provide workload-forecasting capabilities to autoscalers and infrastructure-optimization systems, enabling proactive and data-driven scaling decisions. We conduct a thorough performance evaluation based on prediction accuracy, training overhead, and inference time, in order to assess the applicability and efficiency of each approach within the context of the CDN use case.

Ultimately, the goal of this work is to develop a robust and extensible framework for transforming workload forecasts into actionable resource-demand estimates, leveraging system profiling, machine learning, and queuing theory.

The main contributions of this work are as follows:

(i)

A comprehensive workload characterization based on operational trace data collected from a large-scale real-world CDN system.

(ii)

The development of a predictive modeling pipeline that combines statistical and machine learning methods, both offline and online, to capture workload dynamics across different time scales.

(iii)

A unified framework that links workload prediction with resource estimation, enabling proactive auto-scaling in cloud-edge environments.

(iv)

Empirical validation of the framework on real-world CDN traces, measuring prediction fidelity, computational efficiency, and runtime adaptability.

The remainder of the paper is organized as follows: Section 2 surveys related work; Section 3 introduces the targeted application, i.e., the BT CDN system (https://www.bt.com/about) (accessed on 30 April 2025), its workload, and workload-modeling techniques utilized in our work; Section 4 introduces datasets, outlines workflows and methodologies, and presents the produced workload models along with an analysis of results; Section 5 presents a framework composed of the produced workload models and a workload-to-resource requirements calculation model; Section 6 discusses future research directions; and Section 7 concludes the paper.

2. Related Work

Understanding system performance, application behavior, and workload characteristics is fundamental to enabling elasticity and proactive resource allocation. Consequently, these topics have received extensive attention in the literature over the past decade, as reviewed in several comprehensive surveys [3,18,19]. This section discusses related work with a particular emphasis on workload-modeling and -prediction techniques, as well as auto-scaling mechanisms.

2.1. Workload Modeling and Prediction

Workload modeling and prediction in large-scale distributed applications and datacenter infrastructure have been addressed using classical statistical models such as auto-regression, Markov models, and Bayesian models [7,20,21]. Rossi et al. [20,21] propose a Hybrid Bayesian Neural Network (HBNN) that integrates a Bayesian layer into an LSTM architecture to model both epistemic and aleatoric uncertainty in CPU and memory workload prediction. Using variational inference, the model outputs a Gaussian distribution over future demand, enabling computation of confidence-based upper bounds for proactive resource allocation. Experiments on Google Cloud trace data show that HBNN achieves comparable point-prediction accuracy to standard LSTM while reducing overprovisioning and total predicted resources for the same QoS targets. Also targeting proactive workload prediction, the work in [22] first clusters virtual machines (VMs) into different groups exhibiting particular workload patterns. The authors next build a Hidden Markov model-based method leveraging the temporal correlations in workloads of each group to predict the workload of each individual VM. The method reportedly improves prediction accuracy by up to 76% compared to traditional methods using only the individual-server level (i.e., single time series-based methods). Sheng et al. propose a Bayesian method in [23] to predict the average resource utilization in terms of CPU and memory for both long-term intervals (e.g., up to 16 h) and consecutive short-term intervals (e.g., every 2 min). Through experiments with Google’s data traces, the proposed method is shown to achieve a high accuracy regardless of the degree of workload fluctuation and to outperform existing auto-regression and filter-based methods. With the same targeted domain as the focus in this present work, we employ S-ARIMA to model the workload of a CDN cache server [7]. The obtained predictive model basically meets our main requirement of workload predictions for the targeted CDN. Moreover, the preliminary results—including the workload analysis, the statistical workload model and the application model—presented in that work lay the foundation for the present study.

Apart from classical statistical methods, ML techniques have recently been widely adopted for workload prediction in the highly distributed computing platforms [24,25,26]. Kumar et al. propose an online workload-prediction model based on the ELM technique [24]. The model adopts the rapid yet highly accurate learning process of ELM to forecast the workload arrival in very short time intervals. Extensive experiments using Google workload traces show that the proposed ELM outperforms the state-of-the-art techniques, including ARIMA, Support Vector Regression (SVR), by surprisingly reducing the mean prediction error from 11% up to 100%. Another online resource utilization predictive model using a spare Bidirectional LSTM (Bi-LSTM) is proposed in [25]. The authors improve the learning time of a classical Bi-LSTM by constructing a Bi-LSTM model with fewer parameters that is more efficient for online prediction. The model is evaluated through experiments with Google and PlanetLab data, and the results show that besides a high prediction accuracy, the model’s training time is reduced by 50–60% compared to the classical Bi-LSTM model. The aforementioned techniques rely on the analysis of just a single server or application workload, which may be inefficiently in the context of highly distributed cloud-edge platforms. With a consideration of the user mobility behavior in such cloud-edge computing environments, Nguyen et al. propose a location-aware workload-prediction model for edge datacenters (EDCs) [26]. The proposed multivariate-LSTM-based model exploits the correlation in workload changes among EDCs within close proximity to each other so as to forecast the future workload for each of them. Experiments demonstrate robust performance with considerably improved prediction accuracy compared to other recent advanced methods.

2.2. Elasticity in Large-Scale Cloud-Edge Systems

Aiming at reliable, cost- and energy-efficient computing platforms, diverse techniques and methodologies have been devised to implement elasticity or auto-scaling (sub)systems. Existing implementations rely on either a rule-based or a model-based approach in tackling the elasticity in a reactive or proactive manner. While the rule-based approach has been more popular and widely adopted in many commercial products thanks to its straightforward deployment and high reliability, the proactive one, backed by aforementioned modeling and prediction techniques, is shown to be more complicated and advanced, hence drawing more attention from the research community.

By adopting the rule-based elasticity, commercial cloud-based resource providers simply offer a user interface enabling clients to define performance metric thresholds of, e.g., resource utilization, rejection rates, or service response times, and corresponding scaling plans to be executed. Based on these settings, resources are then automatically allocated for the applications in order to reactively adapt to their performance changes. Examples for this approach include Kubernetes [27] and Amazon AWS [28] that rely on their rule-based autoscalers to perform horizontal auto-scaling.

A recent work proposing a hybrid proactive auto-scaling mechanism, namely Chameleon, has been presented in [29]. Its auto-scaling framework incorporates multiple proactive methods coupled with a reactive mechanism to facilitate the resource allocation. The framework adopts time series analysis to forecast the arriving load intensity and relies on queuing theory to estimate resource demands. The authors of the work next propose Chamulteon, an enhanced version of Chameleon, enabling the coordinated scaling of microservice applications [30]. The Chamulteon auto-scaling framework is implemented with two sub-functions: a reactive one to perform scaling tasks for the microservices respecting the resource demand in short time intervals, and a proactive one relying on workload prediction to proactively perform such tasks in longer time intervals. The framework is shown to outperform notable autoscalers through experiments using real-world data traces, and conducted in various environments with different virtualization technologies.

In a related effort, Bhardwaj et al. [31] introduces a performance-aware resource allocator that learns resource-to-performance mappings online and incorporates uncertainty through ARMA-based load forecasting with 90% confidence bounds. Its modular design supports both multi-tenant and microservice workloads and demonstrates improved utility and tail latency compared to existing baselines. Building on the theme of SLO-driven autoscaling, Jeon et al. [32] proposes a system tailored for fixed-size on-premises ML inference clusters, allowing developers to specify latency SLOs directly. Faro dynamically autoscales inference job replicas to maximize cluster-wide utility, integrating with Ray Serve on Kubernetes, and achieves significantly fewer SLO violations, i.e., 2.3× to 23× improvement over prior methods under real-world workloads. Complementing these works, Liu et al. [33] addresses elasticity challenges in serverless platforms by decoupling prediction from scheduling to reduce overhead and employing dual-staged scaling to enable fast, low-cost resource adjustments. This design improves deployment density and resource utilization while significantly reducing cold start latency and scheduling costs compared to state-of-the-art schedulers. In another line of work, Nguyen et al. [34] present a location-aware proactive elastic controller for dynamic resource provisioning targeting latency-intolerant mobile edge applications. Their controller comprises four components: a multivariate LSTM-based location-aware workload predictor capturing correlations across adjacent edge data centers (EDCs); a queuing theory-based performance modeler; a group-based resource provisioner for scaling resources at each EDC; and a weighted round-robin load balancer for real-time user request distribution. Extensive experiments with real user-mobility data demonstrate significant improvements in scaling capability and resource-provisioning efficiency over state-of-the-art reactive controllers.

3. CDN Systems and Workloads

This section examines workload modeling and prediction for large-scale distributed cloud-edge applications, with CDNs serving as a real-world case study. We analyze the architecture and operational workload characteristics of a production-scale multi-tier CDN system operating globally, identifying key spatiotemporal patterns. Based on these insights, we then explore both time series statistical modeling approaches, specifically S-ARIMA, and ML techniques—including LSTM-based RNNs and OS-ELM—as candidates for robust predictive models.

3.1. A Large-Scale Distributed Application and Its Workload

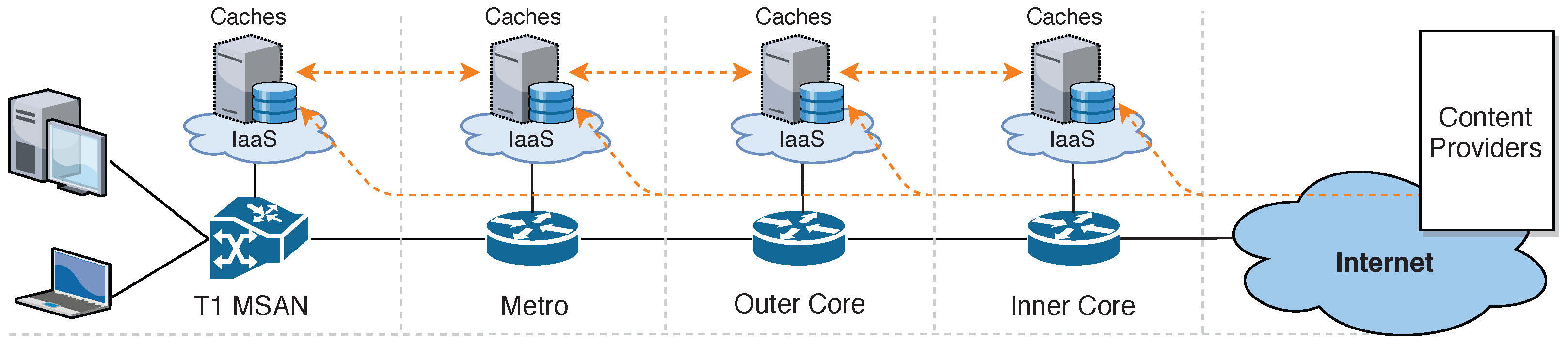
CDNs efficiently distribute internet content using large networks of cache servers (or caches), strategically placed at network edges near consumers. This content replication benefits all stakeholders, i.e., consumers, content providers, and infrastructure operators, by improving Quality of Experience (QoE) and reducing core network bandwidth consumption.

Production CDNs are typically organized as multi-tier hierarchical systems (e.g., edge, metro/aggregation, and core tiers). Each tier contains caches sized and located to serve different scopes of users: edge caches are positioned close to end-users to minimize latency; metro caches aggregate requests from multiple edge sites; and core caches handle large-scale regional or national demand. This hierarchical design enables both horizontal scaling, i.e., adding new caches in any tier to increase capacity, and vertical scaling, i.e., upgrading resources within existing caches. Such flexibility allows CDNs to adapt quickly to demand surges, shifts in content popularity, and geographic changes in traffic distribution.

In recent years, many CDNs have adopted virtualized infrastructures, deploying software-based caches (vCaches) in containers or VMs across cloud-edge resources. Virtualization facilitates the flexible and rapid deployment of multi-tier caching networks for large-scale virtual CDNs (vCDNs) [7]. Leveraging the hierarchical nature of networks, this multi-tier model significantly enhances CDN performance [35,36,37]. For instance, Figure 1 illustrates a conceptual model of BT’s production vCDN system, where vCaches are deployed across hierarchical network tiers (T1, Metro, Core).

To provide a concrete basis for our analysis, this paper investigates the BT CDN and its operational workloads. This CDN employs a hierarchical caching structure where each cache possesses at least one parent cache in a higher network tier, culminating in origin servers as the ultimate source of content objects. Content delivery adheres to a read-through caching model, i.e., a cache miss triggers a request forwarding to successive upper vCaches until a hit is achieved or the highest tier vCache is reached. Should no cache hit occur within the CDN, content objects are retrieved from their respective origin servers and are subject to local caching for subsequent demands (see Section 3.2 below for more details).

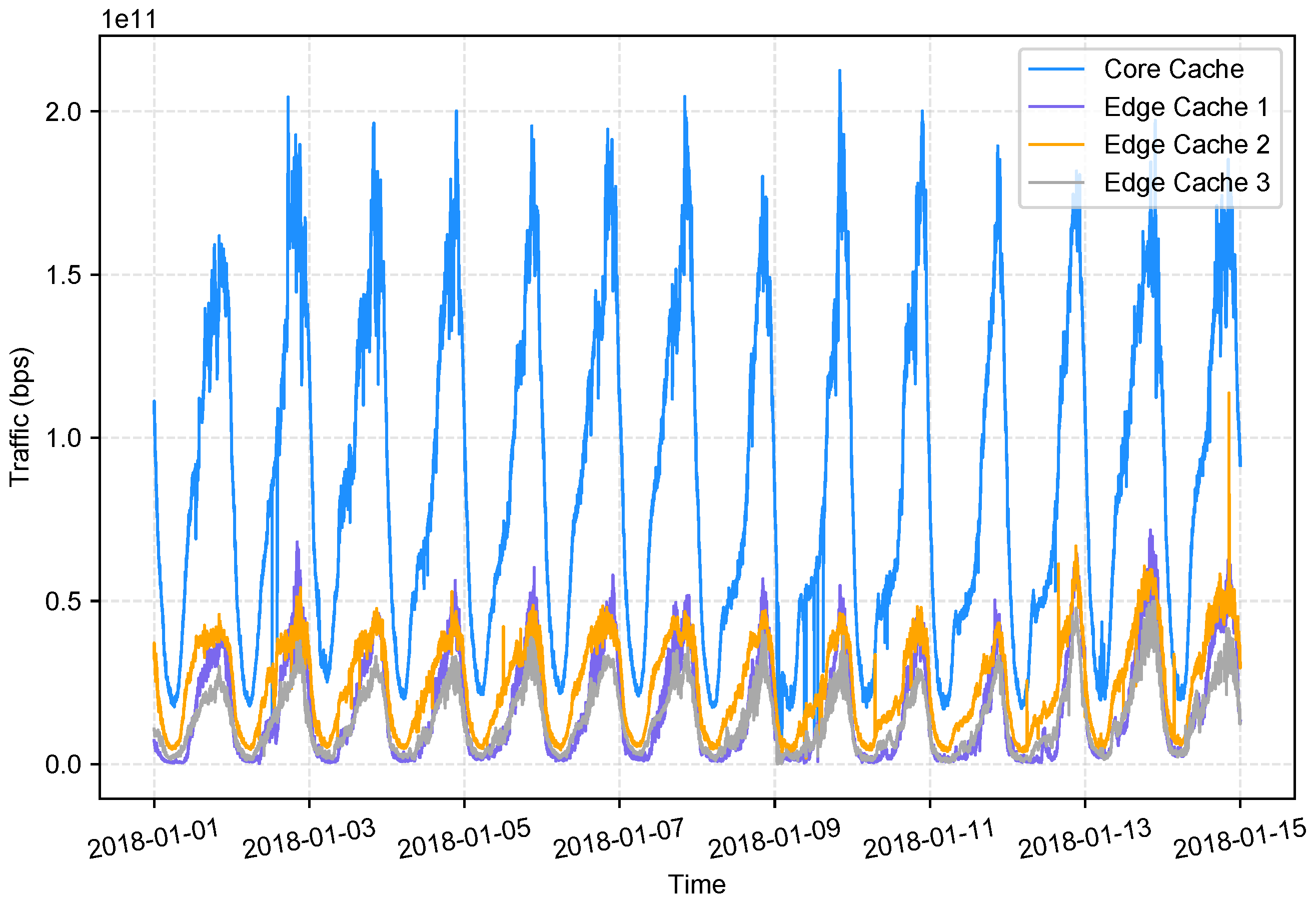
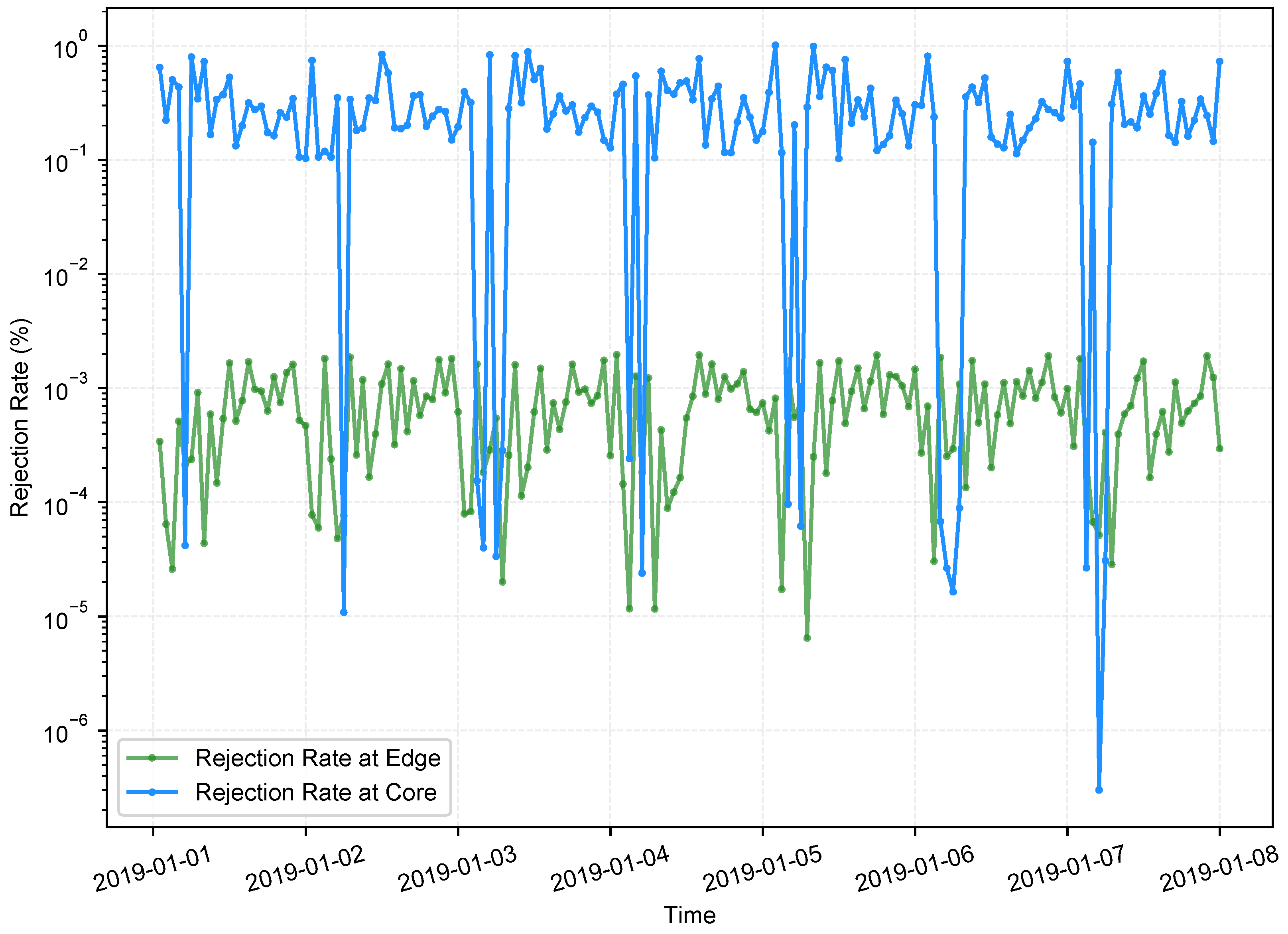
Because scaling decisions can be made independently at different tiers, workload distribution is dynamic rather than fixed. For example, operators may expand edge capacity to reduce upstream load, or scale metro/core tiers to handle heavy aggregation traffic. These strategies influence cache hit ratios, inter-tier traffic patterns, and ultimately the workload characteristics we seek to predict. Understanding these dynamics requires empirical analysis of production workloads, which we conduct using datasets collected from the BT CDN. Consistent with the read-through model, workload at core network vCaches is significantly higher than at edge vCaches, a characteristic evident in our exploratory data analysis and visually represented in Figure 2. Furthermore, our analysis reveals a distinct daily seasonality in the workload data: minimum traffic volumes are recorded between 01:00 and 06:00, while peak traffic occurs from 19:00 to 21:00. This pattern aligns with typical user content access behaviors and supports our previous findings on BT CDN workload characteristics [7].

3.2. Governing Dynamics

From a high-level perspective, CDN caches can be seen to adhere to the governing dynamics of read-through caches. Requests are served locally if caches contain requested content items, or forwarded to another node (typically at the same level or higher) in the cache hierarchy if not. Once a request reaches a cache or an origin server (located at the root of the cache hierarchy) that contains the requested data the request is served, and a response is sent back to the client. Cache nodes update their caches based on perceived content popularity, request patterns, or instructions for the cache system control plane. Content data is typically sent in incremental chunks, and some systems employ restrictions on requests and delivery, e.g., routing restrictions or timeout limits, Statistically, cache content can be seen as subsets of the content catalogue (the full data set available through the CDN), and statistical methods modeling and predicting the popularity (the relative likelihood that a specific content item will be requested) can be used to influence cache scaling and placement both locally (for specific cache sites or regions) or globally (for the entire CDN system).

The request forwarding algorithms of CDNs can be seen to adhere to distinct styles, e.g., naive forwarding sends requests to (stochastically or deterministically selected) cache nodes at the same or higher levels in the cache hierarchy, topology-routed schemes use information on the cache system topology to route requests to specific paths (e.g., using network routing and topology information, or mappings of content id hashes to cache subsegments), and content-routed and gossiping schemes distribute cache content information among nodes to facilitate more efficient request routing similar to peer-to-peer systems. In general, the goals of these approaches typically aim at some combination of minimization of network bandwidth usage, load balancing among resource sites, maximization of cache hit ratios, or control of response time to end-users.

While mechanisms such as these can improve the performance of CDNs [7], they also complicate construction of generalizable workload-prediction systems as they dynamically skew request patterns. For reasons of simplicity in prediction and workload modeling in this work, CDN content delivery is here modeled as naive read-through caches where individual nodes are considered independent, and autonomously update their caches based on locally observed content popularity patterns (i.e., cache content is periodically evicted to make room for more frequently requested data when such is served). Further information about alternative styles of modeling and use of network topology to improve routing and prediction of workload patterns can be found in [4,7]. Combination of these mechanisms with the framework developed in this work is subject for future work.

3.3. Statistical Workload Modeling

For time series analysis, especially with seasonal data, S-ARIMA is a well-established and computationally efficient method for constructing predictive models [5,7]. Given the pronounced daily seasonality in the BT CDN workload datasets, we use S-ARIMA to generate short-term workload predictions.

As described in [5], an S-ARIMA model comprises three main components: a non-seasonal part, a seasonal part, and a seasonal period (S) representing the length of the seasonal cycle in the time series. This model is formally denoted as $\mathrm{SARIMA}(p,d,q)(P,D,Q)\left[S\right]$. Here, the hyperparameters $\{p,d,q\}$ specify the orders for the non-seasonal auto-regressive, differencing, and moving-average components, respectively, while $\{P,D,Q\}$ denote these orders for the seasonal part. S-ARIMA models are constructed using the Box-Jenkins methodology, which relies on the auto-correlation function (ACF) and partial auto-correlation function (PACF) for hyperparameter identification. Model applicability is then validated using the Ljung-Box test [38] and/or by comparing the time series data against the model’s fitted values. Finally, the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC) serves as the primary metric for optimal model selection.

3.4. Machine Learning Based Workload Modeling

In contrast to traditional statistical methods, ML techniques derive predictive models by learning directly from data, without requiring predetermined mathematical equations. Given the necessity for solutions that support resource allocation and planning across varying time scales, and that meet stringent requirements for practicality, reliability, and availability, we employ two specific ML candidates for our workload modeling: LSTM-based RNNs and OS-ELM.

3.4.1. LSTM-Based RNN

Artificial Neural Networks (ANNs) are computational models composed of interconnected processing nodes with weighted connections. Based on their connectivity, ANNs are broadly categorized into two forms [39]: Feed-forward Neural Networks (FNNs), which feature unidirectional signal propagation from input to output, and Recurrent Neural Networks (RNNs), characterized by cyclical connections. The inherent feedback loops in RNNs enable them to maintain an internal “memory” of past inputs, significantly influencing subsequent outputs. This temporal persistence provides RNNs with distinct advantages over FNNs for sequential data. In this work, we adopt two prominent RNN architectures, LSTM and Bidirectional LSTM (Bi-LSTM), widely recognized for their efficacy in capturing temporal dependencies within time series data.

• LSTM: With the overall rapid learning process and the efficiency in handling the vanishing gradient problem, LSTM has been preferred and achieved record results in numerous complicated tasks, e.g., speech recognition, image caption, and time series modeling and prediction. In essence, an LSTM includes a set of recurrently connected subnets; each of which contains one or more self-connected memory cells, and three operation gates. The input, output and forget gates respectively play the roles of write, read and reset operations for memory cells [40]. An LSTM RNN performs its learning process in a multi-iteration manner. For each iteration, namely epoch, given an input data vector of length T, the vectors of gate units and memory cells, with the same length, are updated through a two-step process including the forward pass recursively updating elements of each vector one by one from the 1st to the $T^{th}$ element, and the backward pass carrying out the update recursively in reverse direction.
• Bi-LSTM: It is an extension of the traditional LSTM in which for each training epoch, two independent LSTMs are trained [41]. During training, a Bi-LSTM effectively consists of two independent LSTM layers: one processes the input sequence in its original order (forward pass), while the other processes a reversed copy of the input sequence (backward pass). This dual processing enables the network to capture contextual information from both preceding and succeeding elements in the time series, leading to a more comprehensive understanding of its characteristics. Consequently, Bi-LSTMs often achieve enhanced learning efficiency and superior predictive performance compared to unidirectional LSTMs.

3.4.2. OS-ELM

OS-ELM is distinguished as an efficient online technique for time series modeling and prediction. It delivers high-speed forecast generation, often achieving superior performance and accuracy compared to certain batch-training methods in various applications. OS-ELM’s online learning paradigm allows for remarkable data input flexibility, processing telemetry as single entries or in chunks of varying sizes.

Unlike conventional iterative learning algorithms, OS-ELM’s core principle involves randomly initializing input weights and then rapidly updating output weights via a recursive least squares approach. This strategy enables OS-ELM to adapt swiftly to emergent data patterns, which often translates to enhanced predictive accuracy over other online algorithms [42]. In essence, the OS-ELM learning process consists of two fundamental phases:

(i)

Initialization: A small chunk of training data is required to initialize the learning process. The input weights and biases for hidden nodes are randomly selected. Next, the core of the OS-ELM model including the hidden layer output matrix and the corresponding output weights are initially estimated using these initial input parametric components.

(ii)

Sequential Learning: A continuous learning process is applied to the collected telemetry iteratively. In each iteration, the output matrix and the output weights are updated using a chunk of new observations. The chunk size may vary across iterations. Predictions can be obtained continuously after every sequential learning.

Comprehensive details regarding OS-ELM implementation, including calculations and procedures, are available in [15].

4. Workload Modeling and Prediction

This section provides a detailed account of our approach to workload modeling and prediction for large-scale distributed cloud-edge applications. We begin by describing the real-world dataset collected from a core BT CDN cache, which serves as the empirical foundation for our analysis. Subsequently, we outline the workflow guiding our data processing, model construction, and prediction phases. We then establish our methodology, detailing crucial steps from data resampling and training dataset selection to multi-criteria continuous modeling and model validation. Finally, we present and discuss experimental results, including performance evaluations across various models and metrics.

4.1. Dataset

We use a real-world workload dataset collected from multiple cache servers of the BT CDN [43], spanning 18 consecutive months from 2018 to 2019. Each record is sampled at one-minute intervals and represents traffic volume (bits per second, bps) served by the caches. For the experiments, we select a single core-network cache, which consistently exhibits the highest workloads and thus offers the most challenging and representative prediction scenario.

4.2. Workflow

The workflow for our workload-modeling and -prediction process is illustrated in Figure 3. The process begins with the workload collector, which instruments production system servers and infrastructure networks across multiple locations to gather metrics and Key Performance Indicator (KPI) measurements as time-series data. Subsequently, exploratory data analysis (EDA) is regularly performed offline on the collected data to gain insights into workload and application behaviors, identify characteristics, and reveal any data anomalies for cleansing.

Knowledge derived from the EDA is then fed to a workload characterizer, responsible for extracting key workload features and characteristics. This extracted information directly informs the parameter settings for modeling algorithms within the workload modelers. Multiple workload modelers, employing various algorithms, train and tune models to capture the governing dynamics of the workloads, storing these models for identified states in model descriptions.

Finally, a workload predictor utilizes these model descriptions, incorporating semantic knowledge of desired application behavior, to interpret and forecast future states of monitored system workloads. Workload predictors are typically application-specific, request-driven, and serve as components in application autoscalers or other infrastructure-optimization systems. Further details about the workflow pipeline, including the mapping of the conceptual services to architecture components as well as a concrete example of usage of the framework are available in Section 5.1.

4.3. Methodology

High-quality workload modeling and prediction for the BT CDN require a preliminary understanding of the application structure (Section 3.1) and an exploratory data analysis (EDA) of its telemetry data. This section outlines the data preparation, modeling techniques, and validation procedures applied in our study.

4.3.1. Resampled Datasets

To enable near real-time horizontal autoscaling with short-term predictions, we target a 10 min prediction interval. While past studies reported large variations in VM startup times across platforms [44], modern virtualization and orchestration platforms have reduced initialization delays to sub-minute levels [45,46,47]. However, in large-scale CDN deployments, end-to-end readiness involves more than infrastructure spin-up, including application warm-up, cache synchronization, and routing stabilization, often requiring several minutes before new instances reach a steady state. Empirical analysis of our CDN workloads reveals both sub-hour fluctuations and recurring daily cycles (see Figure 2). Based on these observations, we create two resampled datasets from the original 1 min traces:

• The 10-min dataset supports fine-grained, short-term scaling decisions.
• The 1-h dataset captures broader trends for longer-term planning.

We refer to these as the original datasets in the following discussion.

4.3.2. Appropriate Size of Training Datasets

Analysis of the original datasets confirms that training on time-localized chunks yields more accurate and representative models than training on the full dataset, consistent with our earlier work [7] and other studies [13,48]. We therefore segment each dataset into multiple chunks and train a separate model on each. After systematically evaluating various chunk sizes, we adopt a single chunk size for all techniques to ensure fair comparison:

• a chunk sizes of 2 months for the 10 min dataset.
• a chunk sizes of 4 months for the 1 h dataset.

These segments, referred to as data chunks (e.g., “10 min data chunk”), serve as our training datasets.

4.3.3. Multi-Criteria Continuous Workload Modeling

As described in Section 3, we employ a portfolio of modeling techniques, each chosen for its specific advantages. S-ARIMA and OS-ELM are applied to both the 10 min and 1 h training datasets. LSTM is used exclusively for the 1 h dataset, while Bi-LSTM is applied only to the 10 min dataset.

Each technique fulfills a distinct role:

• S-ARIMA: Low training cost with competitive accuracy compared to learning-based methods.
• LSTM-based models: Highest expected predictive accuracy, capturing complex temporal dependencies.
• OS-ELM: Fastest training and inference, well suited for near real-time scaling or as a fallback option.
• Bi-LSTM: Selected for the 10 min dataset due to its ability to capture short-range dependencies without explicit seasonality, outperforming standard LSTM in this context.

Models are referred to as 1-h models or 10-min models according to their training dataset (e.g., 1 h S-ARIMA model, 10 min OS-ELM model).

For practical deployments, we adopt a continuous modeling and prediction approach in which models are regularly retrained with newly collected data to preserve accuracy. This is implemented using a sliding window over the original datasets. Based on the chunk sizes defined in Section 4.3.2, the window advances in one-month steps, ensuring each model is used for at most one month before retraining. This schedule balances responsiveness and computational overhead while providing a robust evaluation framework. Operational systems may choose shorter intervals (e.g., weekly or daily) if needed. For each modeling technique, this process yields a sequence of models, one per data chunk, spanning the entire dataset.

4.3.4. Model Validation

We validate the models using a rolling-forecast technique that produces one-step-ahead predictions iteratively. For each ML model, a series of real data values, corresponding to a number time-steps, is given to retrieve the next time-step prediction in each iteration. In contrast, an S-ARIMA model produces the next time-step prediction and is then tuned with the real data value observed at that time-step so as to be ready for the forthcoming predictions.

To illustrate the model validation, we perform predictions, precisely out-of-sample predictions, continuously for every 10 min in one day and every one hour in one week using each of the 10 min models and the 1 h models, respectively. In other words, we collect workload predictions for 144 consecutive 10 min time periods and 148 consecutive 1 h periods for each of the corresponding models. Next, the set of predictions obtained by each model is compared to a test dataset of real workload observations extracted from the corresponding original dataset at the relevant time period of the predictions. This means in order to facilitate such a comparison for each case of model construction, after retrieving a training dataset, a test dataset consisting of consecutive data points at the same periods is reserved.

Because every ML model requires an input data series to produce a prediction, in order to accomplish the model validation, we form a validation dataset by appending the test dataset to the input series of the last epoch of the training process. Next, a sliding window of size m is defined on the validation dataset to extract a piece of input data for every prediction retrieval from the model, where m denotes the size or the number of samples of the input series for each training epoch, which is generally called the size of the input of an ML model. The structure of such a validation dataset together with a sliding window defined on it is illustrated in Figure 4.

In case of S-ARIMA, our implementation requires a model update after each prediction retrieval, thus we keep updating the model with observations in the test dataset one by one during the model validation process.

4.4. Experimental Results

With the selected chunk sizes of two months and four months (see Section 4.3.2), we obtain two sets of training data: 16 chunks from the 10 min dataset and 14 chunks from the 1 h dataset. For each chunk, we construct models using three different techniques:

• S-ARIMA: The 1 h S-ARIMA models are constructed with seasonality $S=24$ to capture the daily traffic pattern. We apply the same seasonality to the 10 min models (capturing 4 h patterns), as our EDA reveals no explicit within-hour seasonality in the 10 min data. The rest of hyperparameters are identified using the method presented in Section 3.3.
• LSTM-based: Given the relative simplicity of the patterns in both datasets, we use a single hidden layer for LSTM and Bi-LSTM models, with 24 and 32 neurons, respectively. The input layer size is fixed at 40 neurons, and learning rates remain constant throughout training. Empirically, Bi-LSTM converges faster (150 epochs) than LSTM (270 epochs).
• OS-ELM: We use a single hidden layer across all OS-ELM configurations. For the 1 h dataset, models are trained with 48 input neurons and 35 hidden neurons to capture strong daily seasonality. For the 10 min dataset, hyperparameters are varied across chunks to account for workload fluctuations.

To account for randomness in ML-based models and ensure robustness, each experiment is repeated 10 times per technique and data chunk. Thus, we obtain 10 model variants for every configuration, and all are used in subsequent predictions. All experiments are executed on a CPU-based cluster without GPU support, ensuring consistent computational conditions.

Model accuracy is evaluated using the symmetric mean absolute percentage error (SMAPE), a widely adopted regression metric [49,50,51]:

$$\mathrm{SMAPE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{|y_i-{\widehat{y}}_i|}{\left(\right|y_i|+|{\widehat{y}}_i\left|\right)/2}}100\%$$

where n is the number of test data points, and $y_i$ and ${\widehat{y}}_i$ denote the observed and predicted values, respectively. Lower SMAPE values indicate higher predictive accuracy.

To summarize, each original dataset produces a corresponding result set comprising the trained models, their predictions, associated errors, and measured training and inference times. Accordingly, we obtain two result sets: one for the 10 min dataset and one for the 1 h dataset. Each result set contains multiple models trained on different data chunks. Due to space constraints, we focus our discussion on representative subsets of these results—specifically, the best-performing and worst-performing models for each technique and dataset—while still considering the full result sets in our quantitative comparisons.

4.4.1. Performance Comparison Within Each Modeling Technique

We select two representative model groups for detailed analysis: (i) best-case models, defined as the top-performing instance of each technique (S-ARIMA, LSTM-based, and OS-ELM), and (ii) worst-case models, corresponding to the poorest-performing instance of each type.

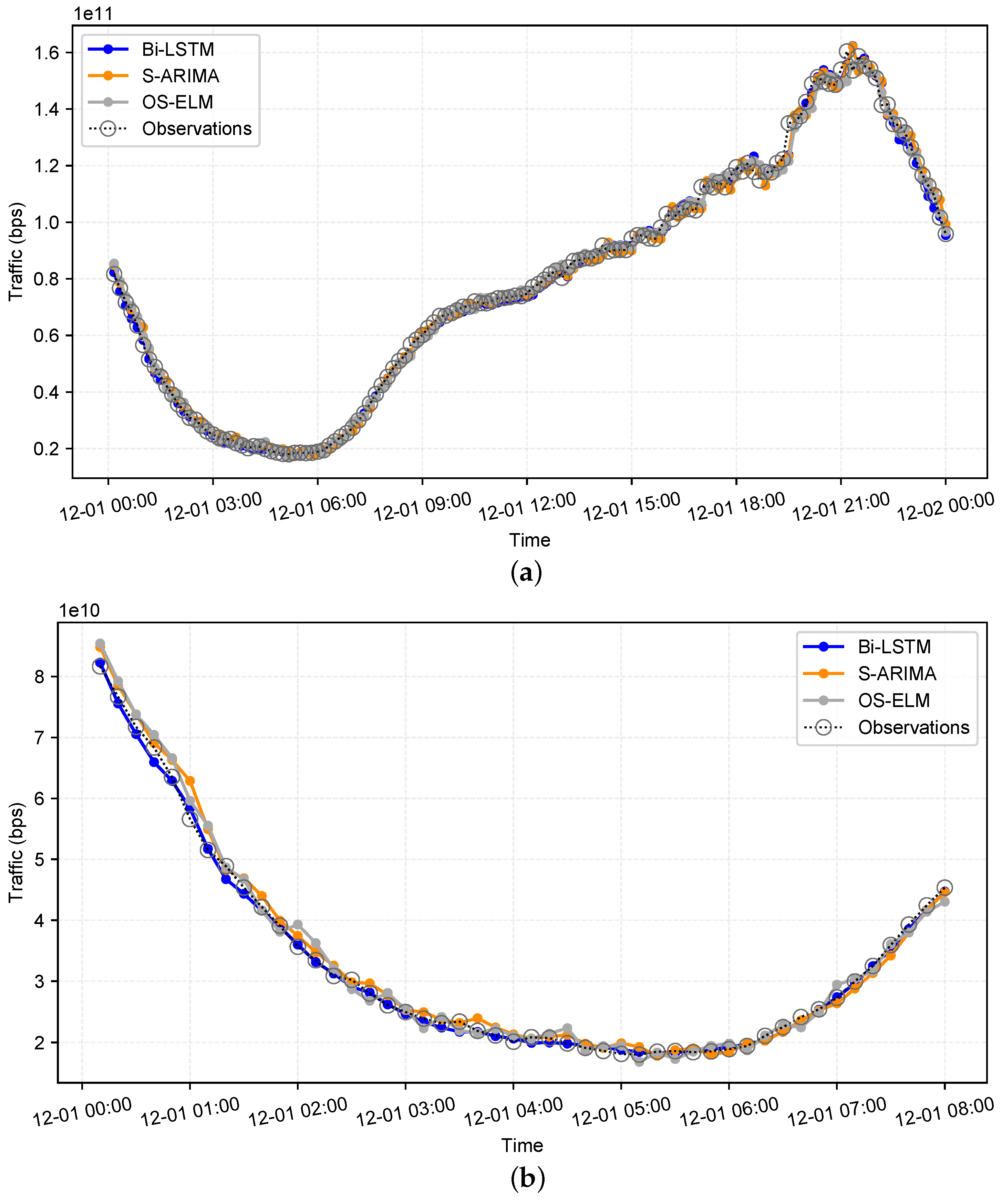
Accordingly, for the 10 min dataset, Figure 5 illustrates the worst-case models, derived from the representative data chunk March–April 2018. In contrast, Figure 6 illustrates the best-case models, derived from the representative data chunk October–November 2018. In both figures, Figure 6a presents the complete prediction series across the entire test period, while Figure 6b provides a zoomed-in 48 h segment for fine-grained comparison.

The observations from Figure 5 and Figure 6 indicate that, while the 10 min dataset exhibits clear seasonal patterns, the traffic dynamics vary substantially across different time periods. These variations support the use of smaller, time-localized training chunks rather than the entire dataset, as localized training enables more accurate short-term predictions. Furthermore, the figures reveal notable performance differences among models of the same type when trained on different chunks. For example, models trained on March–April 2018 systematically underperform compared to those trained on October–November 2018, underscoring the sensitivity of prediction accuracy to temporal context.

A similar analysis is conducted on the 1 h dataset, where representative cases are selected from the 1st and 9th chunks, corresponding to January–April 2018 and September–December 2018, respectively. The results, shown in Figure 7 and Figure 8, exhibit the same trend as observed in the 10 min models: performance varies considerably across different time periods, with certain chunks yielding systematically weaker models. This further confirms the importance of localized training in capturing the temporal variability of workload dynamics.

Takeaway. 

Workload behavior varies significantly across time, even within the same seasonal cycle. Training on time-localized data chunks enables models to adapt to these dynamics, yielding more reliable short-term predictions.

4.4.2. Cross-Technique Performance Evaluation Across Modeling Methods and Training Data

Effective proactive scaling requires a clear understanding of the relative strengths and limitations of alternative modeling approaches. To this end, we conduct a systematic comparison of models built with different prediction techniques and training data granularities, aiming to inform model selection across diverse operational conditions.

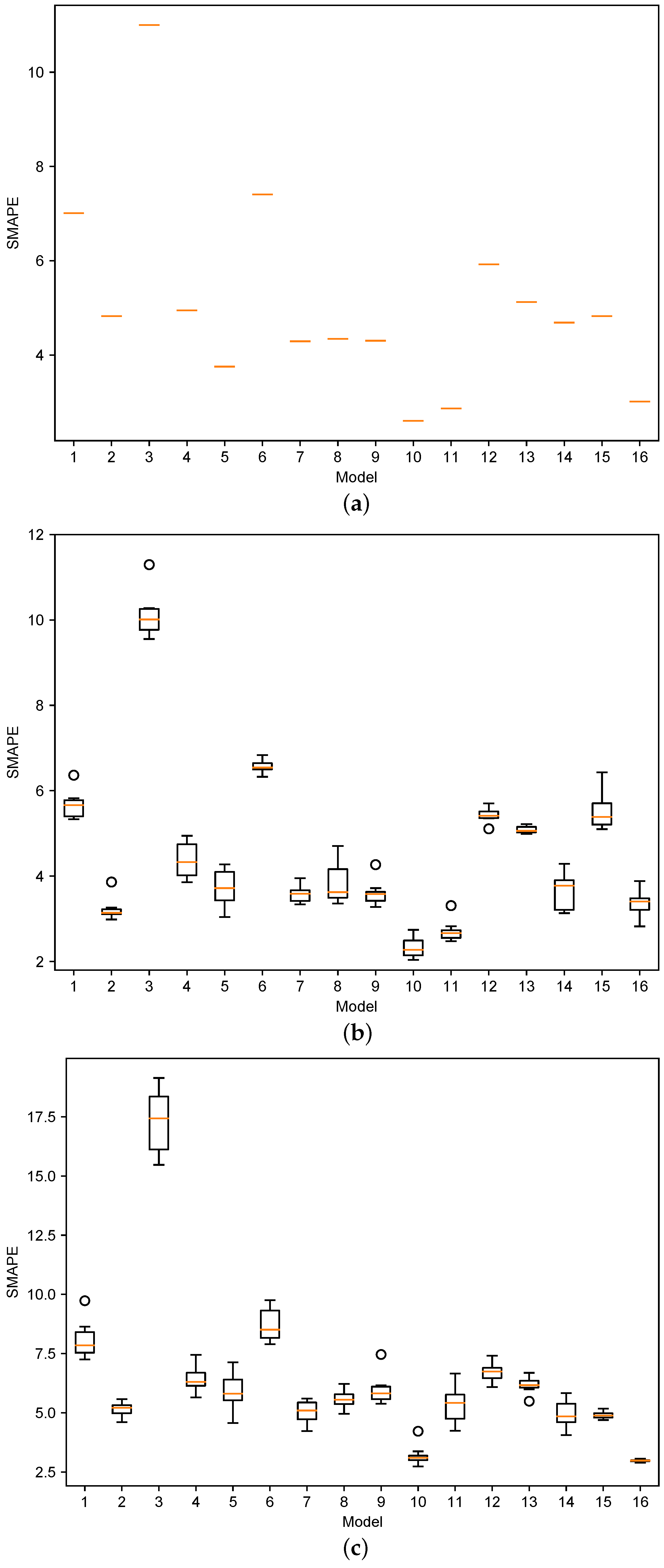
We evaluate the prediction error in terms of SMAPE for S-ARIMA, LSTM, and OS-ELM models, and summarize the results in Figure 9 and Figure 10, corresponding to the 10 min and 1 h datasets, respectively.

The comparative illustrations in Figure 9 and Figure 10 reveal several clear trends. First, LSTM-based models consistently achieve the highest accuracy: more than 90% of the trained models yield prediction errors below 6% (10 min) and 7.25% (1 h). Second, OS-ELM exhibits the weakest performance, with prediction errors approaching 9% and 13% for the same proportion of models. Finally, while S-ARIMA generally produces slightly higher errors than LSTM, it remains a competitive baseline, delivering reliable predictions with low error bounds and occasionally surpassing LSTM in particular cases.

Furthermore, the boxplots in Figure 9 and Figure 10 highlight a key difference between statistical and ML-based approaches. S-ARIMA yields nearly identical errors across runs (with a notably slim box), consistent with its deterministic formulation that involves no randomness during training. By contrast, the ML-based methods (LSTM and OS-ELM) exhibit noticeable variability in error, reflecting their stochastic nature: each run begins with randomly initialized parameters and relies on iterative optimization.

The dispersion in prediction errors is most pronounced in the 1 h models: LSTM exhibits a relatively narrow spread of approximately 1.5%, whereas OS-ELM shows a wider spread of up to 5% (see Figure 10b,c). Despite these differences, the error bounds remain within acceptable limits, underscoring the robustness and reliability of the models for the targeted workload-prediction task.

Across all modeling techniques, the average prediction error remains below 8% in nearly all configurations, with best-case errors dropping to under 3%. These results demonstrate that both S-ARIMA and LSTM are robust candidates for reliable workload forecasting in support of proactive autoscaling. While OS-ELM exhibits higher error rates, it remains valuable in scenarios that demand rapid retraining and low-latency adaptation to workload drift, as discussed in the following section.

Although the 10 min and 1 h models are trained on different data granularities and target distinct objectives, a broad comparison shows that the 10 min models generally achieve higher predictive accuracy than their 1 h counterparts when evaluated on comparably sized test sets. This advantage likely stems from the reduced variability of workload dynamics over shorter time horizons, which minimizes deviations between predictions and observations and thereby lowers error rates.

Takeaway. 

LSTM-based models deliver the highest prediction accuracy in most cases, while S-ARIMA achieves comparable performance in certain scenarios. OS-ELM yields somewhat higher errors but remains practical for settings requiring rapid retraining and fast adaptation. Overall, both statistical and learning-based models reliably capture workload patterns, with 10 min models consistently outperforming 1 h models due to their finer temporal resolution.

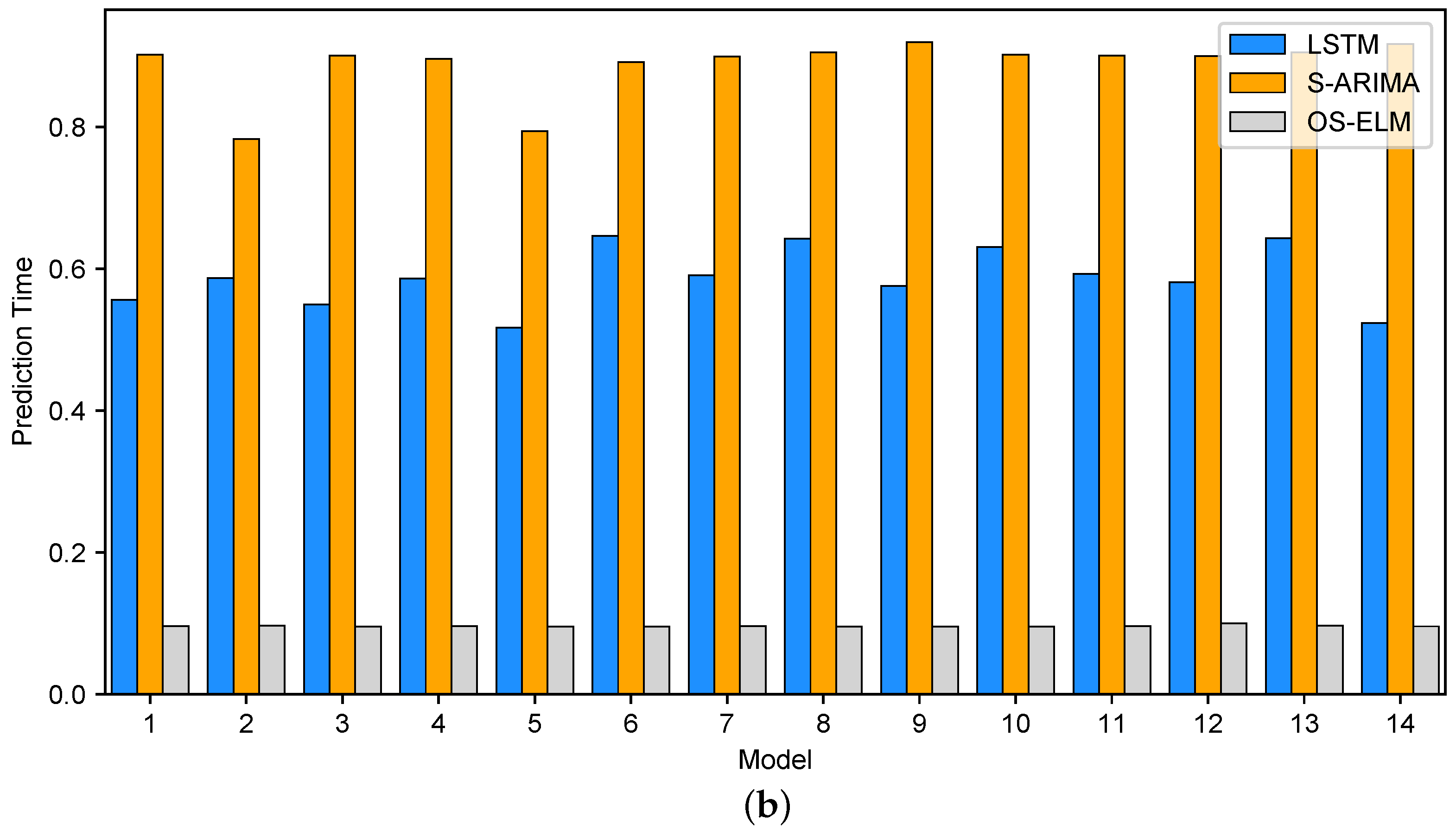
4.4.3. Training Time and Prediction Time of the Models

Beyond accuracy, model training and prediction times are also critical factors in our use case. To enable fair comparison, we measured and recorded both metrics for all models during our experiments. Figure 11 reports the results for the 10 min dataset, with Figure 11a showing training times and Figure 11b showing prediction times. Similarly, Figure 12 presents the corresponding results for the 1 h dataset. All measurements are reported in seconds. The prediction time shown in the figures corresponds to the total computation required to generate 144 predictions (10 min models) and 168 predictions (1 h models). From our experiments, each tuning step requires on average 11 s for the 10 min models and 4 s for the 1 h models. Although this overhead is non-negligible relative to inference time, it remains acceptable for our use case, where predictions are made 10 min or 1 h ahead, allowing sufficient time for tuning.

As shown in Figure 11a and Figure 12a, training time dominates the overall computational cost across all evaluated techniques. Among the three approaches, LSTM-based models incur the highest training overhead, whereas OS-ELM achieves the fastest training performance. Specifically, LSTM and Bi-LSTM models are approximately 15–20× and 40–80× slower than S-ARIMA under the 10 min and 1 h configurations, respectively.

For the 1 h models, OS-ELM maintains a stable training time of approximately 0.4 s across all workloads, owing to the use of a fixed hyperparameter configuration. In contrast, the 10 min models employ varying hyperparameter settings, leading to moderate fluctuations in OS-ELM training time, ranging from below one second to slightly above three seconds. Despite this variability, OS-ELM remains substantially more efficient, with training times that are 40× to several hundred times lower than those of the corresponding S-ARIMA models.

A notable observation in Figure 12a concerns the training time of the first two 1 h S-ARIMA models, both trained on data chunks of nearly identical size (2880 samples). A single-parameter increase in the non-seasonal auto-regressive component and the seasonal moving-average component causes the first model to require nearly 10× longer training time than the second. A similar effect also explains the comparatively short training time observed for the fifth model. By contrast, this strong sensitivity to hyperparameter choices is not evident in Figure 11a for the 10 min models, even when trained on substantially larger datasets (over 8000 samples). On average, however, the 10 min models still exhibit training times approximately 6–8× longer than those of the 1 h models, owing to the larger training data volume, excluding the aforementioned 1 h models with unusually low training times.

Across both the 10 min and 1 h model sets, prediction times remain relatively stable within each model type, as each applies a fixed computational cost per prediction. As shown in Figure 11b and Figure 12b, Bi-LSTM models incur approximately twice the prediction time of standard LSTM models. This overhead arises from the bidirectional architecture, which nearly doubles the computation required, despite generating fewer predictions overall (144 for the 10 min Bi-LSTM models versus 168 for the 1 h LSTM models).

The smaller number of predictions in the 10 min models also contributes to the lower overall inference times observed for S-ARIMA and OS-ELM compared to their 1 h counterparts. Notably, Figure 12b shows that the prediction time of each S-ARIMA model exceeds that of the corresponding LSTM model. This indicates that a single inference step in LSTM—dominated by activation through one hidden layer—entails lower computational cost than the statistical forecasting step in S-ARIMA.

Takeaway. 

OS-ELM consistently achieves the lowest training and prediction times, making it particularly attractive for scenarios that demand rapid model updates or adaptation to concept drift. Its training overhead is minimal—often more than 40× lower than S-ARIMA and orders of magnitude faster than LSTM-based models—enabling efficient retraining without noticeable delay. By contrast, LSTM and Bi-LSTM, while offering superior predictive accuracy, incur substantially higher training costs that may hinder responsiveness in real-time environments requiring frequent retraining.

5. Resource Allocation

Workload models provide insight into application workload characteristics and behaviors and can be used to generate workload predictions as demonstrated in the previous section. With mechanisms of workload-to-resource transformation, such workload predictions can, in turn, be used to estimate or compute resource demands of the applications beforehand to enable proactive resource allocation—a key capability for proactive autoscaling and system elasticity. This section presents a layered architecture of our workload-prediction framework realizing the workflow shown in Figure 3, a workload-to-resource transformation model, and describes how we incorporate the above models to form a workload predictor serving the auto-scaling component or the application autoscaler with workload predictions. A discussion on the execution of each model under particular scenarios is also revealed.

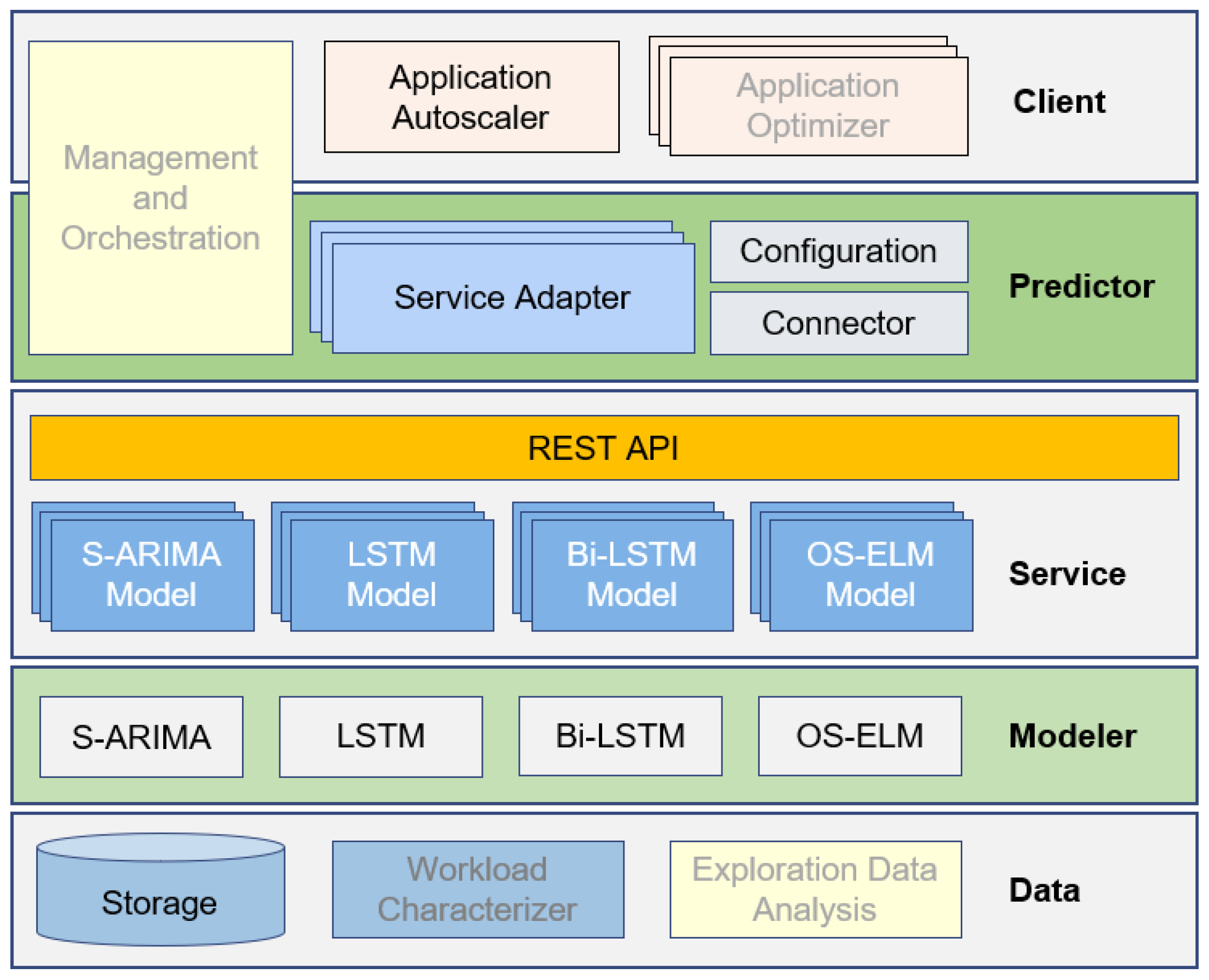
5.1. Prediction Framework

Figure 13 illustrates the architecture of our prediction framework, consisting of components structured in five layers that constitute the foundation of the CDN autoscaling system. An automation loop controls these components to construct and update workload models and to serve requests for workload predictions. Components in the three lower layers dealing with data analysis and modeling are implemented using Python because of feature-rich libraries, both built-in and add-on, attached to its API. The predictor, autoscaler, and supporting components in the upper layers are implemented in Java to integrate with the RECAP automated resource-provisioning system [52]. Below are further details of each layer and its functional building blocks.

• Data: The bottom layer provides data storage via InfluxDB (https://www.influxdata.com (accessed on 30 April 2025)) where collected workload time series from the CDN are persisted and served. The workload characterizer and EDA are outside the automation loop and are executed manually to prepare complete usable workload datasets and to serve workload modelers with datasets, features, and parameter settings or model configurations.
• Modeler: This layer contains workload modelers implemented with Python libraries and APIs, including S-ARIMA (in statsmodels (https://www.statsmodels.org (accessed on 30 April 2025) module [53]), LSTM and Bi-LSTM (in Keras (https://keras.io (accessed on 30 April 2025)) and OS-ELM.
• Service: this service layer accommodates the workload models provided by the modeler layer. Each model is wrapped as a RESTful service, and then served its clients through a REST API implemented using Flask-RESTful (https://flask-restful.readthedocs.io (accessed on 30 April 2025).
• Predictor: the key component of this layer is a workload predictor built upon a set of service adapters facilitating access to the corresponding prediction services running in the lower layer. The adapter is interfaced with the underlying REST API through blocks enabling configuration and connection establishment.
• Client: the layer hosts client applications (e.g., the autoscaler and application-specific optimizers) querying and consuming the workload predictions generated by the underlying predictor.
  There is a management and orchestration (MO) subsystem designated to allow users or operators to configure, control, manage and orchestrate the operations as well as the life cycle of components within the framework. This MO is running across two top layers in order to synchronize the operations between clients and the predictor and to adapt the requirements of clients to the configuration and/or the operations of the predictor.

Components in the modeler, service and predictor layers constitute the core of the automation loop. Each workload modeler in the modeler layer is designed to be able to construct different models using different datasets, including the 1 h and 10 min datasets retrieved from the data storage, and various data features and parameter settings recommended by the process of workload characterization and EDA. The automation loop requires the CDN system to be continuously monitored for a regular workload data collection so as to enable refreshing the constructed models with recent workload behaviors. Accordingly, after producing initial workload models based on historical data, the modelers are responsible for periodically updating the models with new data at run-time based on given schedules.

To flexibly serve prediction requests from applications of different types and platforms, the models are encapsulated according to the microservice architecture [54] and then exposed to clients through a REST API Gateway implemented in the service layer. On top of the service layer, we add a predictor adaptation layer, with a predictor that provides client applications with predictions retrieved from the underlying services. The predictor serves each client request using an aggregated value from an ensemble of prediction models. The MO configures this ensemble.

For simplicity and transparency when using the prediction services, a set of service adapters is implemented to provide native APIs in order to accommodate the implementation of the aforementioned main predictor as well as any client applications or even any other versions of a predictor demanding workload predictions from any single model or any ensemble of the models. Note that there could be multiple predictors implemented in this predictor layer using different technologies and/or different configurations for the model ensemble. Accordingly, various sets of adapters are also provided. It is obvious that the adoption of microservices and the adaptation layer in the proposed architecture of our prediction framework enables the extensibility and adaptability of the framework to the arrival of new client applications as well as new workload models.

5.2. Workload Model Execution

The constructed models have different characteristics, costs, and performance. The performances of the models are also fluctuated for different training datasets. Leveraging every single model or some ensemble of these models to achieve accurate predictions in different conditions under different scenarios is really needed. This work aims at a proactive auto-scaling system which highly relies on short-term workload predictions. Accordingly, we need model-selection procedures that exploit accuracy yet remain simple, fast, and low-complexity. In this section, we discuss the usage of the constructed models in general while the decision on the model selection and implementation for real cases is left to the realization of predictors. It is worth noting that the below illustration is obtained from the models for our CDN use case, but the discussion is generally applied to any scenarios of using our workload models.

Because of the low prediction error rates, S-ARIMA and LSTM-based models are two candidates to be used as the single model for predictions in most of the cases. One practical approach is to select a model at random initially, measure the error rates for a fixed number of steps, and then switch to the lower-error model. Switching occurs during the models’ life cycle until new models are trained and ready. Note that the approach is applied to every pair of models constructed using the same training dataset.

An ensemble approach likewise considers S-ARIMA and LSTM-based models. The simplest method applies aggregate functions (minimum, maximum, or average) to the two predictions obtained from the two models. This logic is implemented within the predictors so as to return the aggregated value as the workload prediction to the autoscaler. Taking the maximum deliberately over-provisions resources and is likely to minimize SLA violations. Contrarily, taking the minimum value brings advantages in resource saving which is crucial for resource-constrained EDCs. For those reasons, an assessment on the trade-off between the resource cost and the penalty for SLA violations is needed to flexibly make decision on which predictors to be used in real scenarios.

Another simple aggregation method that we aim to implement in the framework is to adapt the workload-prediction computation to the continuous evaluation of the error rates of the two models over time. Specifically, a weighted computing model is applied to perform a linear combination of the sets of predictions provided by the two models together with corresponding weighting coefficients. Coefficients are adaptively adjusted based on the error rates of the models. Note that we target at a simple and fast mechanism of coefficient adjustment for our use case of an auto-scaling system in this work. Let $w_t^s$ and $w_t^m$ denote the predictions given by the S-ARIMA and LSTM-based models at time t, respectively; and $c_t^s$ and $c_t^m$ denote the coefficients applied to the corresponding predictions. The workload prediction $w_t$ produced by the ensemble model is given by:

$$w_t=w_t^s{c}_t^s+w_t^m{c}_t^m$$

where $c_t^s+c_t^m=1$, $c_t^s=1-{\displaystyle \frac{e_t^s}{e_t^s+e_t^m}}\mathrm{and}{c}_t^m=1-{\displaystyle \frac{e_t^m}{e_t^s+e_t^m}}$, where $e_t^s$ and $e_t^m$ are the mean absolute error (MAE) of the S-ARIMA and LSTM-based models respectively, and the MAE is measured as the difference between the predictions and the actual observations, which is given by:

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n|y_{t-i}-{\widehat{y}}_{t-i}|$$

where $y_{t-i}$ and ${\widehat{y}}_{t-i}$ denote the observation and the prediction at time $(t-i)$ respectively, and n is the number of prediction steps to be considered.

Apparently, this weighted computing model simply gives a higher significance to a model that performs better than the other on average in the past n prediction steps, hence the greater weight/coefficient. Figure 14 illustrates the results obtained by our ensemble model leveraging on such a weighted computing model for two different scenarios that have been presented above in Figure 7 and Figure 8.

Table 1. Prediction error (SMAPE) of the models.

Scenario	10 min Models			1 h Models
	S-ARIMA	Bi-LSTM	Ensemble	S-ARIMA	LSTM	Ensemble
Best	2.60	2.04	2.02	3.82	3.79	3.17
Worst	11.00	9.55	9.98	8.09	6.77	6.44

shows the prediction errors of the two selected individual models and the ensemble model with $n=1$ for all the aforementioned cases.

Because the performance gap between LSTM-based and S-ARIMA models is small, the ensemble offers no significant improvement. Nevertheless, the ensemble model is applicable with an acceptable performance in different cases. In the worst scenario of 10 min models, the ensemble model fails to leverage the great performance of Bi-LSTM, hence producing the higher error rate than the single Bi-LSTM. This indicates that under highly fluctuating workloads, S-ARIMA and LSTM-based models alternate in performance. It is thus recommended to stick to the LSTM-based models, which yield the best performance in most of the cases, instead of using the proposed ensemble model for decision making support.

Predictive models, especially ML models, suffer the performance degradation in terms of the prediction accuracy due to various reasons, namely model drift, during their life cycle [55,56,57], thus require a periodic re-construction after some time periods when new datasets are collected or a unacceptable accuracy, defined by the the applications or business, is observed in prediction results. In such a case, due to a long training time (see Figure 11a and Figure 12a) and the requirement of a large dataset for accurate modeling, LSTM-based models could be disqualified from the ensemble. In other words, we can switch to use the single S-ARIMA model until a new qualified LSTM-based model is ready to be added to the ensemble. Note that besides the relative low training time, our S-ARIMA models are updated with new observations if existed right after producing every prediction, hence having a high possibility to retain a longer life cycle than LSTM-based models.

Given their lower accuracy, OS-ELM models are a last resort when S-ARIMA and LSTM-based models are unavailable. In addition, OS-ELM models come with extremely low training time and decent degrees of accuracy represented by a below 9% (for 10 min models) and 13% (for 1 h models) error rates in most of the cases, hence suitable for applications without strict constraints in workload prediction or resource provisioning. Capable of online learning, OS-ELM models are refreshed with new observations during their life cycle, i.e., no need for a re-construction. Therefore, with the acceptable error rates OS-ELM models could be an appropriate candidate for near real-time auto-scaling system that requires workload predictions in minutes; or at least there are still some gaps in time for OS-ELM models to be utilized, for example, when both S-ARIMA and LSTM-based models are under construction or in their updating phases.

Takeaway. 

Effective model selection and combination strategies are critical for reliable short-term workload prediction in dynamic environments. While LSTM-based and S-ARIMA models provide high accuracy, their performance may fluctuate across datasets. A lightweight ensemble approach, e.g., weighted averaging based on recent error history, offers robustness with minimal complexity. In highly volatile settings, sticking with LSTM may be preferable. For real-time adaptability during model retraining or drift, OS-ELM serves as a fast, low-cost fallback, enabling continuous prediction with acceptable accuracy.

5.3. Workload to Resource Requirements Transformation and Resource Allocation

To accomplish the autoscaler in our framework, a model of workload to resource requirements transformation is required to compute the amount of resource needed to handle certain workload at specific points in time. This model is realized as the key logic in the autoscaler, and the results in terms of the amount of resource produced by the autoscaler is enacted through a resource-provisioning controller of the caching system of the CDN operator. The core of the model is a queuing system derived from our previous work presented in [34]. In this model, the amount of resource represents the number of server instances to be deployed in the system by the controller. This work aims at a simple model only for an illustrative purpose, i.e., a demonstration of the applicability and feasibility of the constructed models as well as the proposed framework, because at the moment it is impossible to obtain a full system profiling and fine-grain workload profiles from production servers of any CDNs, inclusive of BT CDN.

5.3.1. System Profiling

Video streaming services including video on demand and live video streaming are forecast to dominate the global Internet traffic with about 80% of the total traffic [58,59]. Among them, Netflix and YouTube are the two popular large streaming service providers in the world which leverage CDNs to boost their video content delivery [60,61]. Accordingly, for the sake of simplicity in our workload-to-resource modeling, we assume that the collected workload data in this work represents the traffic generated by caches when serving video contents to users via streaming applications or services. Therefore, most of parameter settings utilized in our model are derived based on the existing work of application/system profiling and workload characterization of these two content providers. As shown in [61], the peak throughput of a Netflix server is 5.5 Gbps, which is assumed to be the processing capability of a server instance of our considered CDN. Note that this is the throughput of a catalog server that could be lower than the one of a cache server deployed in Netflix or any CDN providers nowadays.

In addition, existing work including [61,62,63] pointed out that these two content providers adopt the Dynamic Adaptive Streaming over HTTP (DASH [64,65]) standard in their systems. With DASH, a video is encoded at different bit rates to generate multiple “representations” of the video with different qualities in order to adaptively serve users using various devices and attached to network infrastructures with different qualities in terms of speed, bandwidth, throughput, etc. Each representation is then chunked into multiple segments with a fixed time interval, which are fed to the user devices. A user device downloads, decodes, and plays the segments one by one; and such a segment is considered as a unit of content to be cached at CDNs. There have been different implementations of the time interval in commercial products, for example, 2 s in Microsoft Smooth Streaming and Netflix system and 10 s in Apple Inc. HTTP Live Streaming as shown in [66,67]. For our workload-to-resource modeling, we utilize the time interval of 2 s for every segment cached and served by the CDN. Moreover, recent years has observed the growing popularity of high-definition (HD) contents that require high bit rate encoding. Thus, this paper assumes the video contents served by the CDN are with 1080p resolution (i.e., Full HD contents), hence encoded at 5800 Kbps as per the implementation of Netflix [68]. This means in our model the size of a segment is 11.6 Mbits. With the throughput of 5.5 Gbps, the estimated average serving time per segment is about 2.1 ms.

Studies on user experience show that a below 100 ms server response time (SRT) gives users a feeling of an instantly responding system and is required by highly interactive games including first-person shooter and racing games [69,70,71]. Assuming BT CDN serves the video contents to users in the UK and around Europe with a requirement of high quality of service, i.e., an approximately 100 ms SRT. With the network latency of about 30–50 ms on the Internet throughout a continent [69,72], by neglecting other factors, e.g., client buffering, TCP hand-shaking and acknowledgements, we roughly estimate the acceptable limit of the serving time per segment at 50 ms for a server instance in our model. In case the segments are served by a CDN’s local (edge) cache located closer than 100 m away from the users, with the network throughput of 44 Mbps estimated by Akamai [35], time for a user to download a segment is estimated at 264 ms. To ensure every next segment arrives at the user device within 2 s, the upper limit of the serving time can be relaxed to 1700 ms, assuming requests for the segments received by the cache server before the segments are processed and returned. Note that longer acceptable serving time indicates a low resource demand. Therefore, it is worth considering such a high limit of serving time because this is practical for CDN operators in the sense that the local cache utilizes the edge resource which is costly and limited. All these parameter settings are summarized in

Table 2. Parameters used in the workload-to-resource model.

Parameter	Value	Description
Core server instance
$T_s$	2.1 ms	Average serving time
$T_m$	50 ms	Maximum acceptable serving time
Edge server instance
$T_s$	21 ms	Average serving time
$T_m$	1700 ms	Maximum acceptable serving time

.

5.3.2. Workload-to-Resource Transformation Model

The model is constructed to estimate the number of server instances required to serve the arrival workload with an aim at securing predefined service-level objectives (SLOs), e.g., the targeted service response time or the service rejection rate. All server instances at a certain DC are assumed to have the same hardware capacity, hence delivering the same performance. It is also assumed that at any given time there is only one request being served by a specific instance, and the subsequent requests are queued. To this end, a caching system at a DC is modeled as a set of m instances of $\mathit{M}/\mathit{M}/\mathit{1}/\mathit{k}/\mathit{FIFO}$ queues, where m denotes the total number of server instances. Let $T_m$ and $T_s$ be the acceptable maximum service response time defined by the SLOs and the average response time required to perform a single request in a server instance, respectively; and let k denote the maximum number of requests that a server instance can admit under a guarantee that they are served within an acceptable serving time, then k is given by: $k=\lfloor \frac{T_m}{T_s}\rfloor$.

Besides the predefined SLOs, from the infrastructure resource provider’s perspective, the average resource utilization threshold is also defined, above which the resource utilization of a cache server in constrained to remain. This threshold is set to 80% in our experiments. The given values of the threshold together with the workload arrival rate and the current number of available server instances are the inputs to the transformation model in order to estimate the desired number of instances that should be allocated for each time interval using the equations defined for the $M/M/1/k$ queue [73].

5.3.3. Experimental Results

We conduct experiments in two scenarios with different configurations of server instances provided by the underlying infrastructures to the CDN. Specifically, the caching server system is assumed to be deployed in a high-performance core DC or in a low-performance edge DC with limited resource capacity. Capability of server instances in corresponding DCs is illustrated through parameter settings defined in Table 2.

Figure 15 illustrates the estimation of resource demands under two aforementioned parameter settings according to the workload observed from cache servers at the monitored network site of BT CDN. It is observable that in order to serve the same amount of workload, thanks to the high performance equipment, the number of server instances allocated in the core DC (below 50 instances) is significantly lower than that of the edge DC (up to approximately 360 instances). Figure 16 depicts the resource estimation, in terms of the number of server instances, based on the workload-prediction results made by the 1 h ensemble model (shown as resource allocation through the blue line) and its counterpart corresponding to the real observed workload (shown as resource demand through the red line) within the same time period. Resulted from the highly accurate predictions given by the proposed model, the estimated resource allocation, shown in Figure 16, enables the auto-scaling system to elastically provision an amount of resources closely matched the current resource demands in a proactive manner.

Experimental results also show under-provisioned and over-provisioned states of the auto-scaling system at some points in time, illustrated through Figure 16, where the number of allocated server instances is lower and higher than the actual demand, respectively. Due to the workload-prediction models always come along with certain error rates, i.e., it is impossible to obtain 100% accurate predictions all the time, such deviations between the resource demand and the resource allocation are inherently inevitable. However, the deviations obtained from our experiments are insignificant, thus do not induce any noticeable impact to the system’s reliability. To confirm this argument, we further collect the service rejection rates from the experiments. Figure 17 illustrates the average service rejection rates according to the resource-allocation behaviors under experimental scenarios with core DC and edge DC settings. In general, the observed average rejection rates are pretty low, just up to approximately 1% and 0.001% corresponding to the use of server instances in the core and edge DCs, respectively. Such low rejection rates prove the efficiency and reliability in resource allocation of the auto-scaling system, which once again confirms the high prediction accuracy of our predictive model.

Given the same targeted server utilization, the caching system at the edge DC allocates many more server instances than the one at core DC as discussed above. With such a high number of allocated server instances, the edge-DC caching system can obviously serve many more requests simultaneously, resulting in a lower service rejection rate. In essence, the service rejection rate is proportional to, but conflicts with the server utilization [8,34], because the expectation usually includes a high server utilization together with a low rejection rate; hence, one would sacrifice the service rejection rate to improve server utilization, and vice versa. As evident through the experimental results in both scenarios, our autoscaler persistently guarantees a predefined high server utilization at 80% while retains such low service rejection rates. This facilitates an efficient and reliable caching system or the overall CDN system. With the cheap and “unlimited” resources at the core DCs, the service rejection rate of a CDN system deployed at such a core DC can be improved by lowering the targeted resource utilization, i.e., a provision of a larger number of server instances.

Takeaway. 

A lightweight queue-based transformation model effectively bridges workload predictions to resource-allocation decisions, enabling accurate and efficient autoscaling. Despite using simplified profiling assumptions, the model delivers close-to-optimal provisioning for both edge and core CDN environments, as evidenced by low service rejection rates (≤1%). This demonstrates the practical viability of combining predictive modeling with queue theoretic resource estimation in latency-sensitive, resource-constrained caching systems.

6. Discussion

While the evaluated models, particularly LSTM-based and S-ARIMA, demonstrate strong predictive accuracy across most cases, especially with 10 min datasets, occasional performance degradation is observed under highly volatile workload conditions (e.g., Figure 5 and Figure 7). These cases highlight the limitations of current models in capturing abrupt shifts and suggest that more sophisticated techniques, such as deep neural networks or ensemble-based methods, could enhance robustness. However, any gains in accuracy must be carefully weighed against the additional computational and operational overhead these methods introduce.

In practice, large-scale distributed systems like CDNs frequently contend with workload and concept drift in operational data streams [11,12,13]. While “offline” ML models consistently yield higher predictive accuracy in most scenarios (particularly those with strong seasonality and recurring patterns), their performance can degrade over time due to this drift. Maintaining their reliability, therefore, requires periodic retraining, which often incurs significant computational overhead and delay. This highlights the complementary strengths of online learning approaches. Among the evaluated techniques, OS-ELM emerges as a particularly compelling candidate due to its ability to retrain quickly and deliver low-latency predictions with minimal overhead. These properties make it well suited for highly responsive resource-management scenarios, such as autoscaling containerized CDN components (e.g., vCaches), where sub-minute provisioning decisions are critical.

In addition to short-term forecasting, this work also initiates an exploration of long-term workload prediction, spanning months to years. Long-term prediction is required by multiple use cases and/or stakeholders including BT in our large RECAP (https://recap-h2020.github.io/ (accessed on 30 April 2025)) project [52] in order to accommodate the future resource planning and supplying in both hardware and software. Our current approach is to apply S-ARIMA to different resampled datasets with monthly or yearly interval. These results require further stakeholder evaluation and are therefore not presented here. LSTM could also be a candidate, but building LSTM models using a large dataset or the entire collected dataset is extremely time-consuming and out of the scope of the paper, and hence subject to future work.

As observed in Section 5.3, we are using a coarse-grained model/profile of a service system together with various assumptions in our estimation of the resource demands. Even though the assumptions have been made based upon existing studies on real applications/systems, our estimation can be considered as a basic reference for limited and specific cases in which resources are homogeneous and no diversity in traffic is experienced. Nowadays, every CDN system accommodates a mix of content services such as web objects and applications, video on demand, live streaming media, and social media; hence, its workload includes different types of traffic. Therefore, more complex and fine-grained models are required. To meet this requirement, more effort has been put on collecting data deep inside heterogeneous computing systems in cloud-edge environments to build such fine-grained system profiles of the CDN as well as its workloads so as to achieve more accurate estimations in resource demands. Moreover, we are aiming at an extension of our work to cover the modern 5G communication systems that share properties with CDNs, for instance, the support of different types of traffic and the use of heterogeneous resources in cloud-edge computing.

7. Conclusions

This paper presents a practical framework for proactive resource allocation, demonstrating advantages over reactive approaches in latency, availability, and cost efficiency in cloud-edge environments. Grounded in real-world CDN traces, our evaluation of statistical (S-ARIMA), deep learning (LSTM), and online learning (OS-ELM) models confirms that predictive autoscaling can effectively capture workload patterns. By translating forecasts into resource requirements with a queuing theoretic model, our system achieves low rejection rates (≤1%) and high resource utilization. The framework’s feasibility was further validated through its integration into the RECAP architecture [52], proving its adaptability for distributed applications.

The broader implications of this work support the development of more intelligent, autonomous, and cost-efficient distributed systems, with clear applications beyond CDNs in areas like media streaming and IoT platforms. This research opens several avenues for future study. Promising directions include exploring hybrid forecasting models, applying reinforcement learning for more adaptive policies, and developing archetype-aware strategies that apply specialized models to different workload patterns. Furthermore, future work should incorporate richer metrics beyond CPU utilization and address the complexity of microservice dependencies to prevent performance interference and cascading failures in cloud native environments.