Research on the Robustness of Boolean Chaotic Systems

Abstract

Boolean chaotic systems solely composed of logic devices have been successfully applied in fields such as random number generation, reservoir computing, and radar detection because of their simple structure and amenability to integration. However, noise in a circuit makes Boolean chaotic systems less robust, which means noise transforms the outputs from chaotic to periodic. In this paper, the characteristics of the process through which logic devices respond to input signals are called device response characteristics. A device’s response characteristic parameters can adjust its response speed and the results it yields to the same input signal. The relationship between logical device response characteristic parameters and the time delay parameter was studied. The results indicate that the distribution range and continuity of chaos in the time delay parameter space can be enhanced by reducing the logical device response characteristic parameters, thereby improving the robustness of a Boolean chaotic system. This research is significant for the hardware design of Boolean chaotic system, as it details the selection of appropriate devices for enhancing chaotic time delay parameter space and robustness.

1. Introduction

Boolean chaos is generated by autonomous Boolean networks, consisting of interconnected nodes that update autonomously. Each node’s input is a Boolean variable—0 or 1—and performs Boolean operations. In recent years, these networks have been widely studied and successfully applied in fields such as information security [1,2], reservoir computing [3,4,5], radar detection [6,7], and physically unclonable functions [8,9].

Unlike classical Boolean networks, which use control signals to update all nodes synchronously or asynchronously [10], the update time of each node in autonomous Boolean networks is uncertain and depends on its own response characteristics, thus generating more complex chaotic signals. In 2009, Zhang et al. developed an autonomous Boolean network by coupling XOR logic gates with XNOR logic gates and observed chaotic signals in a corresponding experiment [11]. The bandwidth of Boolean chaos is about GHz (−10 dB), offering great advantages relative to existing electrical chaos. Therefore, it has undergone rapid development in many fields, especially random number generation [12,13,14]. In 2013, Rosin et al. proposed a Boolean chaotic system composed of three input logic devices. It was found that Boolean chaotic systems cannot generate chaotic signals when there are fewer than five logic devices. The entropy value of the chaotic sequence increased as the number of logic devices increased. Therefore, a Boolean chaotic system consisting of 16 devices was realized, generating random numbers at 100 Mbit/s [15]. In 2019, Zhang Qiqi et al. developed a Boolean chaotic system with 15 two-input logic devices and generated random numbers at 100 Mbit/s [16]. Research on the effects of the number of logic devices on the system showed that the system could not output an oscillating signal when there were only three logic devices, while it could produce a chaotic output when the number was greater than 6. As the number increased, the entropy value of the chaotic sequence output by the system increased alongside it. At the same time, many researchers have conducted theoretical research on Boolean chaos. In 2010, Cavalcante et al. found that the time delay between different nodes and the device response characteristics of logic gates are the key factors affecting the generation of Boolean chaos [17]. The stability and unpredictability of Boolean chaos are key to ensuring the safe generation of random numbers. In 2019, Gong Lishuang et al. used theoretical simulations to demonstrate that noise makes Boolean chaotic sequences unpredictable [18]. In 2021, Liu Haifang et al. studied the influence of noise on Boolean chaos under the influence of different time delay parameters [19]. It was found that small Boolean chaotic systems lack robustness to noise. Accordingly, the authors proposed a method for improving robustness by increasing the number of logic devices. In 2025, Sil, Priyotosh et al. examined the dynamics of Boolean networks, finding that the dynamics of Boolean networks tend towards a more chaotic regime as network connectivity or size increases [20]. However, increasing the number of logic devices will increase the power consumption and volume of the system. Reducing the number of components is very important, especially in the high-speed generation random numbers with a large number of parallel Boolean chaotic entropy sources [15].

In summary, to date, the research on Boolean chaotic systems has mainly focused on the topological structures of networks, enhancing the performance of Boolean chaotic systems by increasing the number of devices and improving circuit structures. There is relatively little research on the response characteristics of logic devices, although previous studies [17] have shown that the response characteristics of devices are a key factor in the generation of chaos. It is assumed that the stability of Boolean chaotic systems can be enhanced by optimizing the response characteristics of logic devices without increasing the number of devices. In order to verify this hypothesis and propose a method for enhancing the robustness of small Boolean chaotic systems, we conducted the following research.

We studied a small Boolean chaotic system composed of three two-input logic devices, carrying out a numerical simulation of how Boolean chaos robustness changes with the variation trend of time delay parameters and device response characteristic parameters. Permutation entropy was employed to characterize chaos. The simulation results indicate that the distribution of Boolean chaos in the time delay parameter space is small and discontinuous, and Boolean chaos lacks robustness at the boundary between chaos and the period. We further investigated the impact of logic device response characteristics on the robustness of Boolean chaos. A simulation experiment verified the effectiveness of this method, showing that reducing the device response characteristic parameters can improve the distribution range and continuity of chaos in the time delay parameter space, thereby enhancing the robustness of Boolean chaos.

Robustness lays the foundation for Boolean chaos in safe random bit generation. The method described in this paper can be used to select logic devices with appropriate response characteristics to reduce the size of the system in the hardware design of Boolean chaotic systems.

2. Boolean Chaotic System Model

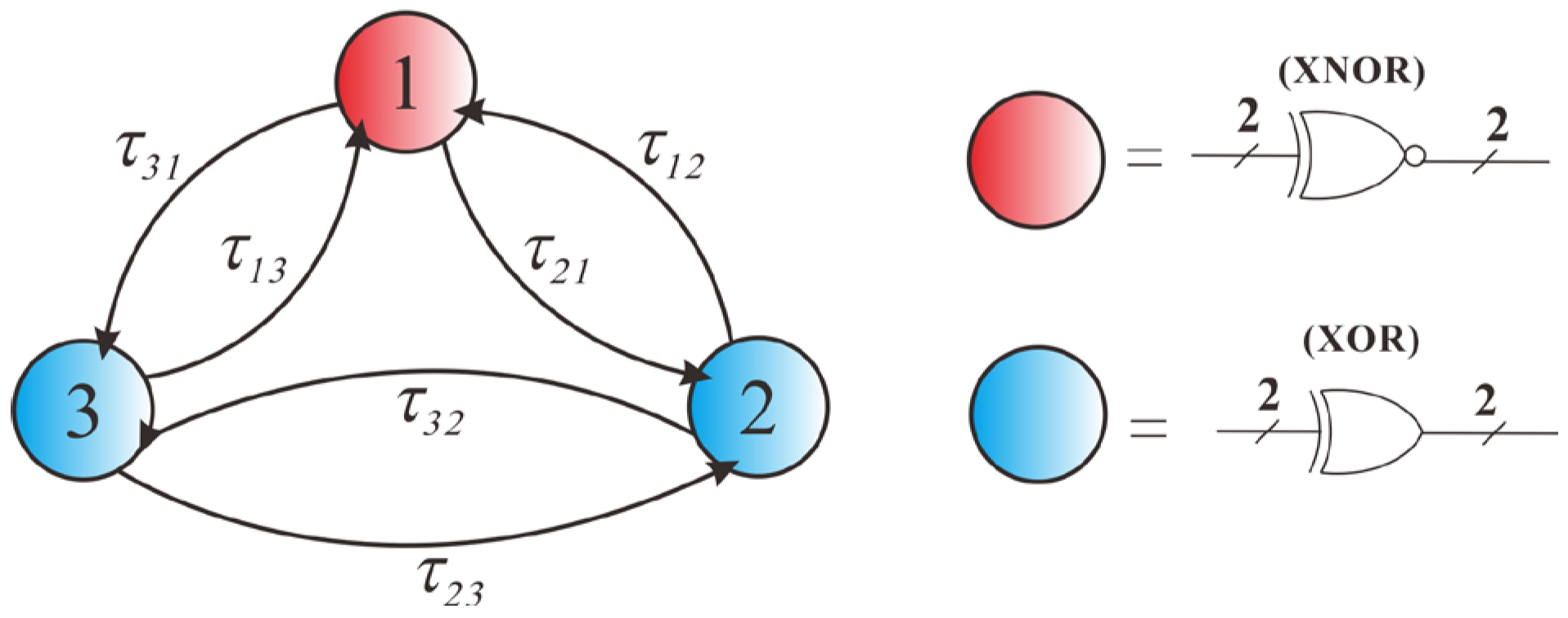
A schematic of a small Boolean chaotic system with three nodes is shown in Figure 1. Node 1 performs the XNOR operation, while nodes 2 and 3 perform the XOR operation. Each node has two inputs from the outputs of the previous and next adjacent nodes, respectively. Boolean delay piecewise-linear differential equations are the improved versions of the Boolean delay equations. Differential equations can describe the continuous temporal evolution of the continuous output state of Boolean chaotic systems [21,22]. Therefore, Boolean delay piecewise-linear differential equations were used to describe the small Boolean chaotic system depicted in Figure 1. Differential Equations (1a) and (1b) are mathematical models of the small Boolean chaotic system. The differential terms dx₁/dt, dx₂/dt, and dx₃/dt can be used to simulate logic devices’ response processes. The coefficients τ_lp,1, τ_lp,2, and τ_lp,3 can be used to adjust the speed of the response process; hence, they are called the device response characteristic parameters. The variable x_i(t) is the output of node i, X_i(t) denotes the quantitative results of x_i(t) obtained using Equation (1a), and xth = 0.5 V is the threshold voltage, which is determined by the characteristics of the logic devices themselves. The time delay parameter τ_ij denotes the signal transmission delay between devices.

$$\left\{\begin{array}{c}{\tau }_{lp,1}{\displaystyle \frac{d{x}_1(t)}{dt}}=-x_1(t)+X_2(t-{\tau }_{1,2})\odot X_3(t-{\tau }_{1,3})\\ {\tau }_{lp,2}{\displaystyle \frac{d{x}_2(t)}{dt}}=-x_2(t)+X_3(t-{\tau }_{2,3})\oplus X_1(t-{\tau }_{2,1})\\ {\tau }_{lp,3}{\displaystyle \frac{d{x}_3(t)}{dt}}=-x_3(t)+X_1(t-{\tau }_{3,1})\oplus X_2(t-{\tau }_{3,2})\end{array}\right.$$

(1a)

$$X_i(\mathrm{t})=\left\{\begin{array}{cc}1,\hfill & x_i(\mathrm{t})>x_{\mathrm{th}}\\ 0,\hfill & x_i(\mathrm{t})<=x_{\mathrm{th}}\end{array}\right.\hspace{1em}i=1,2,3$$

(1b)

Permutation entropy can be used to characterize the complexity of a sequence, offering advantages in terms of calculation simplicity and speed. It is a commonly used method for characterizing chaotic sequences [19,23]. Equations (2a)–(2c) were used to calculate H. In these equations, Y(t) is the sequence obtained via reconstruction of the output sequence x(t), the reconstruction dimension d is set to 5, and the reconstruction dimension τ_e is set to 5 ns. By arbitrarily arranging the elements in the d-dimensional data Y(t), d! arrangements can be obtained, and C_e represents one of the arrangements: e = 1, 2, 3… d!. The value of f(Y(t)) is 1 when the arrangement of elements in datum Y(t) at time t is consistent with C_e; otherwise, it is 0. P_Ce is the probability of arranging C_e. Obviously, the range of the permutation entropy value H is 0–1, and the higher the permutation entropy value, the greater the complexity of the output x(t). Permutation entropy H reaches its maximum value of 1 when the data in Y(t) that conform to any arrangement C_e have an equal probability distribution: P_Ce = 1/d!.

$$Y(t)=\{x(t),x(t+{\tau }_e),x(t+2{\tau }_e),\dots ,x(t+(d-1)\times {\tau }_e)\},$$

(2a)

$$\left\{\begin{array}{c}{P}_{C_e}={\displaystyle \frac{{\displaystyle {\sum }_{t=1}^{n-d+1}f(Y(t))}}{n-d+1}}\\ f(Y(t))=\left\{\begin{array}{cc}1\hfill & \mathrm{permutation} \mathrm{of} Y(t)\in C_e\\ 0\hfill & \mathrm{permutation} \mathrm{of} Y(t)\notin C_e\end{array}\right.\end{array}\right.,$$

(2b)

$$H=-{\displaystyle \frac{{\displaystyle {\sum }_{e=1}^{d!}{P}_{C_e}\log (P_{C_e})}}{\log (d!)}}$$

(2c)

3. Results

Chaos is extremely sensitive to initial values, and small changes in initial values can result in the complete separation of chaotic trajectories. In hardware implementation for Boolean chaotic systems, the noise in the circuit is equivalent to constantly changing initial values, causing the system output to constantly change. Time delay and logic devices’ nonlinear response characteristics are the source of Boolean chaos [18]. So, we studied the impact of noise on the system under the influence of these two different parameters. Permutation entropy H was employed to characterize chaos (with a high permutation entropy value) and periods (with low permutation entropy values) [19,23]. The variation in the entropy value can be used to characterize the robustness of chaos. In the experiment, node 1 was used as the output; the time delay parameter values are shown in

Table 1. Time delay parameters of the small Boolean chaotic system.

τ12/ns	τ13/ns	τ21/ns	τ23/ns	τ31/ns	τ32/ns
0.2	1.1	2	1	1.2	1.2

.

The impact of noise on the dynamics of Boolean chaos is shown in Figure 2. Figure 2 shows map graphs of the permutation entropy H of output x₁(t) in two-dimensional parameter space (τ_lp, τ₁₃). Figure 2a is a map of the permutation entropy H of x₁(t) without noise. Figure 2b is a map of the permutation entropy H_noise of x₁(t) with noise. Figure 2c is a map of permutation entropy difference H_noise − H. Parameter τ_lp represents the values of τ_lp,1, τ_lp,2, and τ_lp,3. The more complex the sequence x₁(t), the higher the H value. Therefore, a high H value represents chaos, while a low H value represents periodicity. A permutation entropy H greater than 0.95 was used to identify chaotic sequences in this study based on experience. In Figure 2a,b, the red pixels represent high permutation entropy, the green pixels represent low permutation entropy, and the black dashed line is the boundary where the permutation entropy value is 0.95. Evidently, the high-H regions are distributed in areas with small τ_lp or τ₁₃. Moreover, the distribution of high-entropy regions is discontinuous; that is, there are low-H regions mixed in with the high-H regions. A comparative analysis of Figure 2a,b shows that noise can easily cause drastic changes in permutation entropy near the boundary. Figure 2c illustrates the changes more intuitively. In Figure 2c, the color gradient from black to white represents the value of H_noise − H from 1 to −1; the dashed line is consistent with the black dashed line in Figure 2b. Red pixels represent chaotic degradation regions. The results indicate that chaotic degradation often occurs at the boundaries.

In order to depict the phenomenon of chaotic degradation intuitively, Figure 3 shows the outputs transitions of the Boolean chaotic system in the red area in Figure 2c. Figure 3a,b show the output sequence x₁(t) and its spectrum without noise interference. The output sequence x₁(t) in the figure is a complex sequence without periodicity, with a flat spectrum and no obvious peaks. Figure 3c,d show the output sequence x₁^noise(t) and its spectrum with noise. The sequence x₁^noise(t) in the figure changes from chaotic to periodic over time, and clear peaks can be seen in its spectrum. The results indicate that noise causes the system output to degrade from chaotic to periodic at the boundary of chaos and periodicity, indicating the small Boolean chaotic system lacks robustness.

In reference [19], the lack of robustness in Boolean chaotic systems was found to be due to the fact that edge jitter caused by noise changes the value of the time delay parameter. Therefore, a small change in the time delay parameter τ₁₃ causes chaotic degradation at the boundary of chaos and periodicity, as shown in Figure 3. Figure 4 is a schematic diagram of the noise-induced changes in the time delay parameter. In Figure 4, x₃ represents the output signal of node 3. Signal x₃ changes from 0 to 1 at time t₁, generating a rising edge. It is assumed that the rising edge is transmitted to node 1 and generates a falling edge in the signal of node 1 at t₂. Obviously, the time delay parameter τ₁₃ = t₂ − t₁. The black line represents the ideal position for edge flipping. Noise can cause an edge to deviate from the ideal position, as shown in the gray area in the figure. Thus, the actual value of the time delay parameter τ₁₃ changes to τ₁₃ + noise. The variation in the delay parameter τ₁₃ leads to changes between chaotic sequences in the continuous chaotic space, but it can easily lead to the degradation of chaos towards periodicity at the boundary.

The analysis above indicates that enhancing the distribution range and continuity of chaos in the time delay parameter space can improve the robustness of a small Boolean chaotic system. Figure 2 shows that the distribution range and continuity of chaos in the time delay parameter space, indicating that the distribution range of chaos on the τ₁₃ axis and continuity increase as the device response characteristic parameters decrease.

In order to enhance the robustness of Boolean chaotic systems, we studied the influence of device response characteristics on output x₁. Figure 5 shows the impact of noise on output x₁ in the time delay parameter space (τ₁₂, τ₁₃) under the influence of different device response characteristic parameters. Figure 5a–e show the distribution of the permutation entropy of x₁ in the time delay parameter space (τ₁₂, τ₁₃) when τ_lp = 0.05, 0.1, 0.2, 0.3, and 0.4 ns, respectively. The first column depicts the permutation entropy H of the x₁(t) without noise. The second column indicates the permutation entropy H_noise of the x₁(t) with noise. The third column indicates the permutation entropy difference H_noise − H. The colors in Figure 5 serve the same function as they do in Figure 2. A comparison between Figure 5a1–e1 shows that the smaller the value of the device response time τ_lp, the larger the high-permutation-entropy region. Correspondingly, a comparison between Figure 5a3–e3 shows that the permutation entropy difference caused by noise becomes increasingly smaller as τ_lp decreases. This is particularly true for the chaotic degradation area depicted in red, which becomes increasingly smaller until it disappears at τ_lp = 0.05 ns. The results indicate that the sensitivity of chaos to time delay parameters can be reduced by reducing the device response characteristic parameter τ_lp, thereby improving chaos robustness.

In the continuous Boolean chaotic space, as shown in Figure 5e1, noise does not generate drastic changes in permutation entropy, but it does cause changes in the chaotic trajectory, making the chaotic sequence unpredictable. Figure 6 shows the influence of noise on the output x₁ in a stable Boolean chaotic system with τ_lp = 0.05 ns, τ₁₂ = 1.1 ns, and τ₁₃ = 0.96 ns (Figure 6a). In Figure 6a, the red curve represents the chaotic sequence x₁ without noise, and the blue curve represents the chaotic sequence x₁^noise with noise, while the black line in Figure 6b represents the difference x₁^noise − x₁. Evidently, the chaotic sequence separates into completely different trajectories over time, which makes the output chaotic sequence x₁(t) unpredictable.

4. Discussion and Conclusions

In classical chaos, noise can cause the output to vary between different chaotic trajectories by changing the initial value, making the output unpredictable. However, the experimentally obtained results shown in Figure 2 indicate that noise reduces the robustness of small Boolean chaotic systems, meaning that the output randomly varies between being chaotic and periodical. Analysis reveals that noise causes small shifts in chaotic parameters, leading to a transition from chaos to periodicity in the output.

Previous studies have shown that the nonlinear response characteristics of logic devices are the fundamental cause of Boolean chaos. So, we studied the influence of the response characteristics of logic devices on the robustness of Boolean chaos. The results indicate that the distributions of chaos in the device response characteristic parameter space and time delay parameter space are interdependent. Reducing the device response characteristic parameters can enhance the distribution range and continuity of chaos in the time delay parameter space, and vice versa. Therefore, the sensitivity of Boolean chaos to noise-induced changes in time delay parameters can be reduced by reducing the device response characteristic parameters, thereby enhancing the robustness of small Boolean chaotic systems.

This study lays a theoretical foundation for the hardware design of Boolean chaotic systems. By selecting high-speed response devices, the robustness of small Boolean chaotic systems can be enhanced, and the number of logic devices can be reduced. This work is expected to result in smaller Boolean chaotic systems with high-speed devices.