UWB Radar-Based Human Activity Recognition via EWT–Hilbert Spectral Videos and Dual-Path Deep Learning
Abstract
1. Introduction
2. Literature Review
2.1. Radar Modalities for Human Activity Recognition
2.2. Signal Processing Approaches
2.3. Machine Learning Integration
2.4. Existing UWB Radar-Based Approaches
2.5. Research Gaps and Limitations
3. Methodology
3.1. Overview of the Proposed Method
3.2. Characteristics of UWB Radar Signals and Data Acquisition Process
3.3. Processing Radar Signals Using Data-Adaptive Multiresolution Analysis and Hilbert Transform
3.3.1. EMD Applied to Radar Frames
3.3.2. EWT Applied to Radar Frames
3.3.3. Hilbert Spectrum Transformation of Mode Components
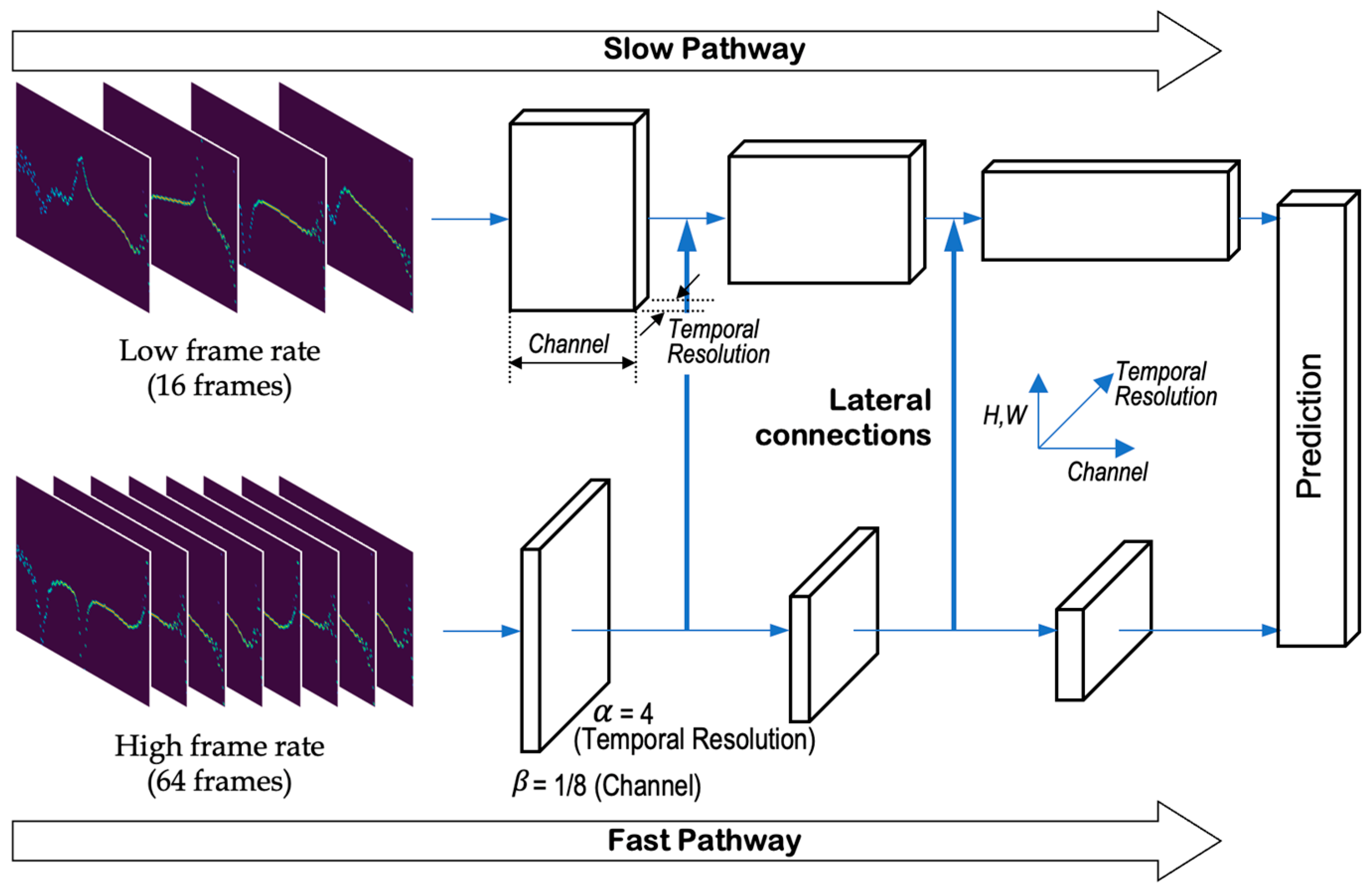
3.4. Deep-Learning-Based Human Motion Classification Using Video Data
3.4.1. Generation of Video-Format Data for Deep Learning
3.4.2. Human Motion Classification Using a Video-Based Deep Learning Model
4. Experiments and Results
4.1. Experimental Overview
- Arm_wave refers to the swinging of one arm sideways while it is extended forward.
- Bowing refers to the bending of the upper body forward and then returning the body to an upright position.
- Raise_hand refers to lifting one arm vertically upward and then lowering it.
- Stand_up describes the action of rising from a seated position and then sitting down.
- Twist refers to rotating the upper body to one side while standing and then returning to the original posture.
4.2. Preliminary Experiment
4.2.1. Experimental Methodology
4.2.2. Preliminary Experimental Results
4.3. Cross-Validation
4.4. Comparative Performance Analysis
4.4.1. Ablation Study Results
4.4.2. Comparison with Existing Methods
4.4.3. Computational Performance Metrics
4.5. Cross-Subject Validation
4.6. Environmental Robustness Analysis
5. Discussion
5.1. Principal Findings and Theoretical Implications
5.2. Practical Implications
5.3. Limitations and Future Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UWB | Ultra-Wideband |
| CW | Continuous Wave |
| FMCW | Frequency-Modulated Continuous Wave |
| ToF | Time-of-Flight |
| STFT | Short-Time Fourier Transform |
| CWT | Continuous Wavelet Transform |
| EMD | Empirical Mode Decomposition |
| IMF | Intrinsic Mode Function |
| EWT | Empirical Wavelet Transform |
| CNN | Convolutional Neural Network |
| I3D | Inflated 3D |
| LSTM | Long Short-Term Memory |
| WRTFT | Weighted Range-Time–Frequency Transform |
| PCA | Principal Component Analysis |
| KNN | K-Nearest Neighbor |
| RMDL | Random Multimodal Deep Learning |
| DNN | Deep Neural Network |
| RNN | Recurrent Neural Network |
| MIMO | Multiple-Input Multiple-output |
| SFCW | Stepped-Frequency Continuous Wave |
| MRA | Multiresolution Analysis |
| PRF | Pulse Repetition Frequency |
| EIRP | Effective Isotropic Radiated Power |
| HHT | Hilbert–Huang Transform |
| SGD | Stochastic Gradient Descent |
References
- Bilich, C.G. Bio-Medical Sensing Using Ultra-Wideband Communications and Radar Technology: A Feasibility Study. In Proceedings of the 1st International Pervasive Health Conference and Workshops, Innsbruck, Austria, 29 November 2006; pp. 1–9. [Google Scholar]
- Cho, H.S.; Choi, B.; Park, Y.J. Monitoring Heart Activity Using Ultra-Wideband Radar. Electron. Lett. 2019, 55, 878–880. [Google Scholar] [CrossRef]
- Lee, Y.; Park, J.Y.; Choi, Y.W.; Park, H.-K.; Cho, S.-H.; Cho, S.H.; Lim, Y.-H. A Novel Non-Contact Heart Rate Monitor Using Impulse-Radio Ultra-Wideband (IR-UWB) Radar Technology. Sci. Rep. 2018, 8, 13053. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, X.; Ding, Y.; Wang, Y.; Zhou, J.; Zhang, L. Contactless Simultaneous Breathing and Heart Rate Detections in Physical Activity Using IR-UWB Radars. Sensors 2021, 21, 5503. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Ebrahim, M.P.; Hasan, K.; Heydari, F.; Howley, P.; Yuce, M.R. Accurate Heart Rate and Respiration Rate Detection Based on a Higher-Order Harmonics Peak Selection Method Using Radar Non-Contact Sensors. Sensors 2022, 22, 83. [Google Scholar] [CrossRef] [PubMed]
- Rong, Y.; Bliss, D.W. Remote Sensing for Vital Information Based on Spectral-Domain Harmonic Signatures. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3454–3465. [Google Scholar] [CrossRef]
- Malešević, N.; Petrović, V.; Belić, M.; Antfolk, C.; Mihajlović, V.; Janković, M. Contactless Real-Time Heartbeat Detection via 24 GHz Continuous-Wave Doppler Radar Using Artificial Neural Networks. Sensors 2020, 20, 2351. [Google Scholar] [CrossRef]
- Cardillo, E.; Caddemi, A. Radar Range-Breathing Separation for the Automatic Detection of Humans in Cluttered Environments. IEEE Sens. J. 2021, 21, 14043–14050. [Google Scholar] [CrossRef]
- Lv, W.; He, W.; Lin, X.; Miao, J. Non-Contact Monitoring of Human Vital Signs Using FMCW Millimeter-Wave Radar in the 120 GHz Band. Sensors 2021, 21, 2732. [Google Scholar] [CrossRef] [PubMed]
- Turppa, E.; Kortelainen, J.M.; Antropov, O.; Kiuru, T. Vital Sign Monitoring Using FMCW Radar in Various Sleeping Scenarios. Sensors 2020, 20, 6505. [Google Scholar] [CrossRef]
- Court of Justice of the European Union. Judgment in Case C-212/13; Court of Justice of the European Union: Luxembourg, 2014. [Google Scholar]
- European Union Agency for Fundamental Rights. Surveillance by Intelligence Services: Fundamental Rights Safeguards and Remedies in the European Union; Publications Office of the European Union: Luxembourg, 2023. [Google Scholar]
- Wang, M.; Cui, G.; Yang, X.; Kong, L. Human Body and Limb Motion Recognition via Stacked Gated Recurrent Units Network. IET Radar Sonar Navig. 2018, 12, 1046–1051. [Google Scholar] [CrossRef]
- Ding, C.; Hong, H.; Zou, Y.; Chu, H.; Zhu, X.; Fioranelli, F.; Le Kernec, J.; Li, C. Continuous Human Motion Recognition with a Dynamic Range-Doppler Trajectory Method Based on FMCW Radar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6821–6831. [Google Scholar] [CrossRef]
- Maitre, J.; Bouchard, K.; Bertuglia, C.; Gaboury, S. Recognizing Activities of Daily Living from UWB Radars and Deep Learning. Expert Syst. Appl. 2021, 164, 113994. [Google Scholar] [CrossRef]
- Ding, C.; Zhang, L.; Gu, C.; Bai, L.; Liao, Z.; Hong, H.; Li, Y.; Zhu, X. Non-Contact Human Motion Recognition Based on UWB Radar. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 8, 306–315. [Google Scholar] [CrossRef]
- Qi, R.; Li, X.; Zhang, Y.; Li, Y. Multi-Classification Algorithm for Human Motion Recognition Based on IR-UWB Radar. IEEE Sens. J. 2020, 20, 12848–12858. [Google Scholar] [CrossRef]
- Pardhu, T.; Kumar, V. Human Motion Classification Using Impulse Radio Ultra Wide Band Through-Wall Radar Model. Multimed. Tools Appl. 2023, 82, 36769–36791. [Google Scholar] [CrossRef]
- An, Q.; Wang, S.; Zhang, W.; Lv, H.; Wang, J.; Li, S.; Hoorfar, A. RPCA-Based High-Resolution Through-the-Wall Human Motion Feature Extraction and Classification. IEEE Sens. J. 2021, 21, 19058–19068. [Google Scholar] [CrossRef]
- Mitra, S.K. Digital Signal Processing: A Computer-Based Approach, 2nd ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Mallat, S. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Gilles, J. Empirical Wavelet Transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Hahn, S.L. Hilbert Transforms in Signal Processing; Artech House: Boston, MA, USA, 1996. [Google Scholar]
- Feichtenhofer, C.; Fan, H.; Malik, J.; He, K. SlowFast Networks for Video Recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27–28 October 2019; pp. 6202–6211. [Google Scholar]
- Tran, D.; Bourdev, L.; Fergus, R.; Torresani, L.; Paluri, M. Learning Spatiotemporal Features with 3D Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 4489–4497. [Google Scholar]
- Carreira, J.; Zisserman, A. Quo Vadis, Action Recognition? A New Model and the Kinetics Dataset. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4724–4733. [Google Scholar]
- Kim, Y.; Ling, H. Human activity classification based on micro-Doppler signatures using a support vector machine. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1328–1337. [Google Scholar]
- Zhang, J. Basic gait analysis based on continuous wave radar. Gait Posture. 2012, 36, 667–671. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, A.; Li, H.; Le Kernec, J.; Fioranelli, F. Continuous human activity classification from FMCW radar with Bi-LSTM networks. IEEE Sens. J. 2020, 20, 13607–13619. [Google Scholar] [CrossRef]
- Cao, L.; Liang, S.; Zhao, Z.; Wang, D.; Fu, C.; Du, K. Human activity recognition method based on FMCW radar sensor with multi-domain feature attention fusion network. Sensors 2023, 23, 5100. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, H.; Wu, Y.; Wang, B.; Yang, D. FMCW radar human action recognition based on asymmetric convolutional residual blocks. Sensors 2024, 24, 4570. [Google Scholar] [CrossRef]
- Abratkiewicz, K. Radar detection-inspired signal retrieval from the short-time Fourier transform. Sensors 2022, 22, 5954. [Google Scholar] [CrossRef]
- Song, M.-S.; Lee, S.-B. Comparative study of time-frequency transformation methods for ECG signal classification. Front. Signal Process. 2024, 4, 1322334. [Google Scholar] [CrossRef]
- Guo, J.; Hao, G.; Yu, J.; Wang, P.; Jin, Y. A novel solution for improved performance of time-frequency concentration. Mech. Syst. Signal Process. 2023, 185, 109784. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, L.; Diao, M. LPI radar waveform recognition based on time-frequency distribution. Sensors 2016, 16, 1682. [Google Scholar] [CrossRef]
- Konatham, S.R.; Maram, R.; Cortés, L.R.; Chang, J.H.; Rusch, L.; LaRochelle, S.; de Chatellus, H.G.; Azaña, J. Real-time gap-free dynamic waveform spectral analysis with nanosecond resolutions through analog signal processing. Nat. Commun. 2020, 11, 3309. [Google Scholar] [CrossRef]
- Kim, Y.; Moon, T. Human detection and activity classification based on micro-Doppler signatures using deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2015, 13, 1–5. [Google Scholar] [CrossRef]
- Li, Z.; Le Kernec, J.; Abbasi, Q.; Fioranelli, F.; Yang, S.; Romain, O. Radar-based human activity recognition with adaptive thresholding towards resource constrained platforms. Sci. Rep. 2023, 13, 3473. [Google Scholar] [CrossRef]
- Seyfioğlu, M.S.; Gürbüz, S. Deep neural network initialization methods for micro-Doppler classification with low training sample support. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2462–2466. [Google Scholar] [CrossRef]
- Li, H.; Shrestha, A.; Heidari, H.; Le Kernec, J.; Fioranelli, F. Bi-LSTM network for multimodal continuous human activity recognition and fall detection. IEEE Sens. J. 2019, 20, 1191–1201. [Google Scholar] [CrossRef]
- Hernangomez, R.; Santra, A.; Stanczak, S. Human activity classification with frequency modulated continuous wave radar using deep convolutional neural networks. In Proceedings of the 2019 International Radar Conference, Toulon, France, 23–27 September 2019; pp. 1–6. [Google Scholar]
- Chen, D.; Xiong, G.; Wang, L.; Yu, W. Variable length sequential iterable convolutional recurrent network for UWB-IR vehicle target recognition. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–11. [Google Scholar] [CrossRef]
- Hung, W.-P.; Chang, C.-H. Dual-mode embedded impulse-radio ultra-wideband radar system for biomedical applications. Sensors 2024, 24, 5555. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Deng, J.; Zhang, H.; Gulliver, T.A. Ultra-wideband impulse radar through-wall detection of vital signs. Sci. Rep. 2018, 8, 13367. [Google Scholar] [CrossRef] [PubMed]
- Novelda. NVA620x Preliminary Datasheet; Novelda: Oslo, Norway, 2013. [Google Scholar]
- Breed, G. A Summary of FCC Rules for Ultra Wideband Communications. High. Freq. Electron. 2005, 4, 42–44. [Google Scholar]
- Gabor, D. Theory of Communication. J. Inst. Electr. Eng. 1946, 93, 429–457. [Google Scholar] [CrossRef]
- Fairchild, D.P.; Narayanan, R.M. Classification of Human Motions Using Empirical Mode Decomposition of Human Micro-Doppler Signatures. IET Radar Sonar Navig. 2014, 8, 425–434. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, S.S.P. (Eds.) Hilbert–Huang Transform and Its Applications, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Soomro, K.; Zamir, A.R.; Shah, M. UCF101: A Dataset of 101 Human Actions Classes from Videos in the Wild. arXiv 2012, arXiv:1212.0402. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Kay, W.; Carreira, J.; Simonyan, A.; Zhang, B.; Hillier, C.; Vijayanarasimhan, S.; Viola, F.; Green, T.; Back, T.; Natsev, P.; et al. The Kinetics Human Action Video Dataset. arXiv 2017, arXiv:1705.06950. [Google Scholar] [CrossRef]
- Kosson, A.; Messmer, B.; Jaggi, M. Rotational Equilibrium: How Weight Decay Balances Learning Across Neural Networks. OpenReview 2024. Available online: https://openreview.net/forum?id=Kr7KpDm8MO (accessed on 12 June 2025).
- Available online: https://github.com/leftthomas/SlowFast (accessed on 12 June 2025).
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Fan, H.; Murrell, T.; Wang, H.; Alwala, K.V.; Li, Y.; Li, Y.; Xiong, B.; Ravi, N.; Li, M.; Yang, H.; et al. PyTorchVideo: A Deep Learning Library for Video Understanding. In Session 26: Open Source Competition, Proceedings of the 29th ACM International Conference on Multimedia, Chengdu, China, 20–24 October 2021; ACM: New York, NY, USA, 2021. [Google Scholar]


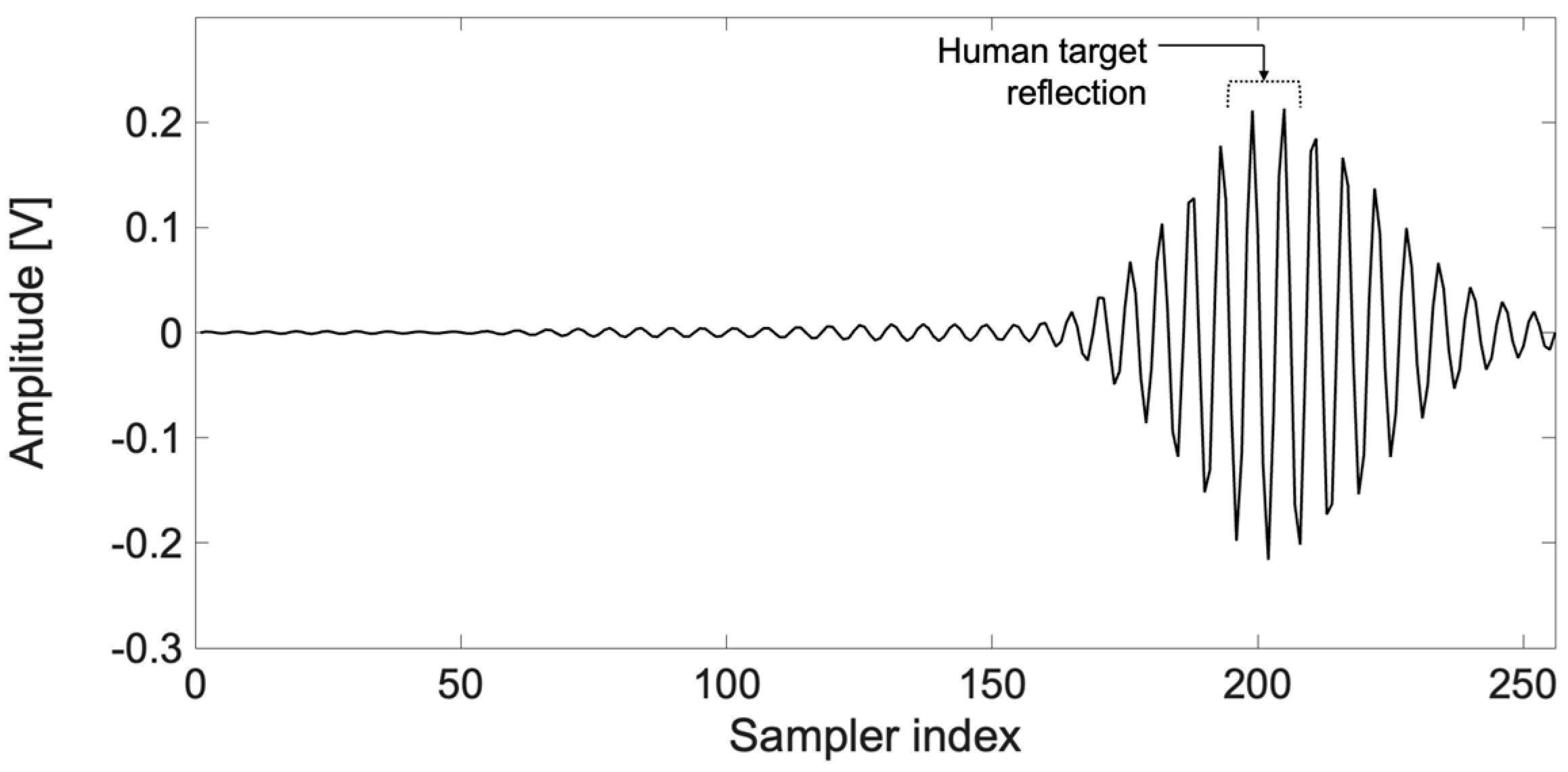
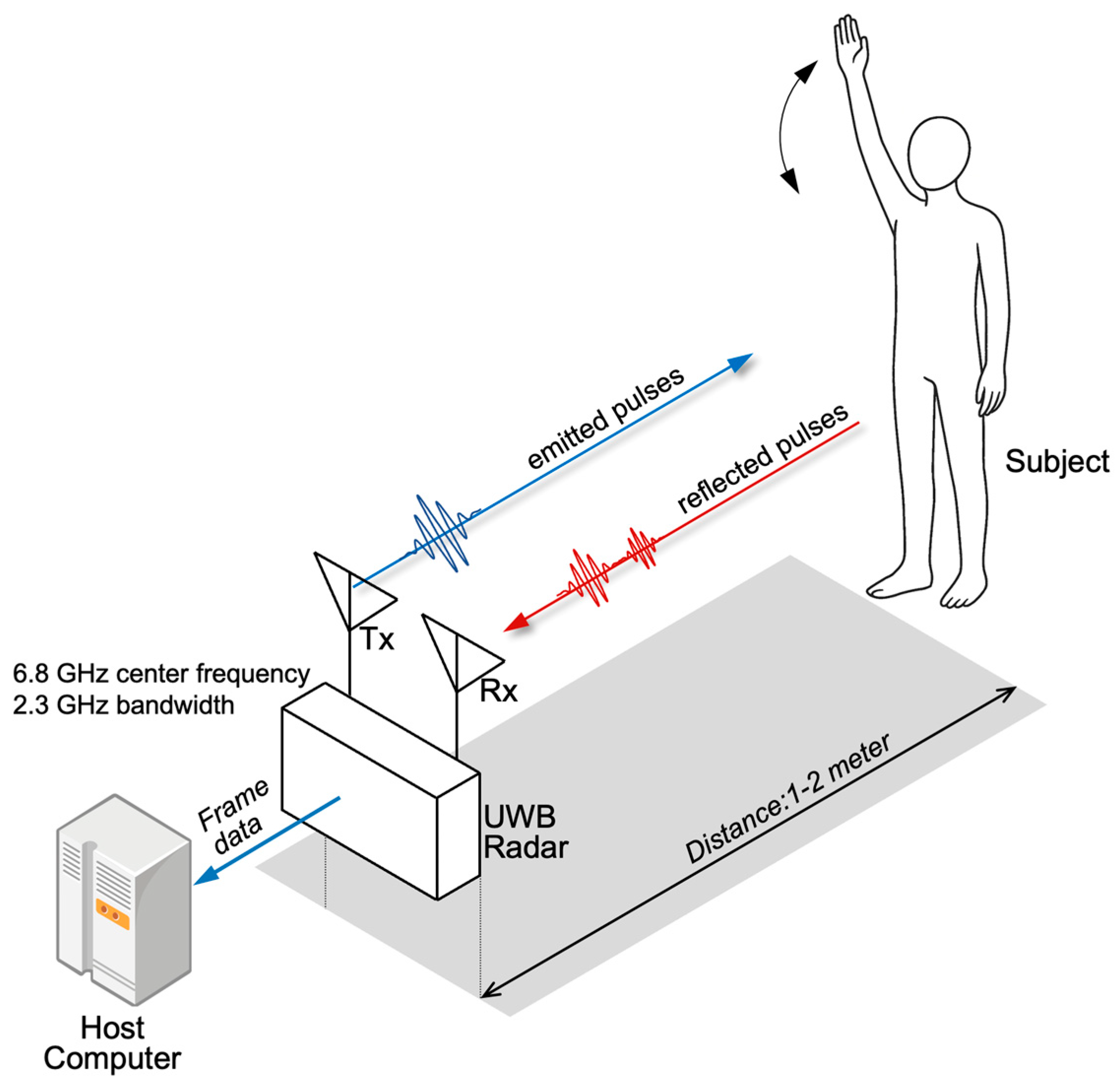

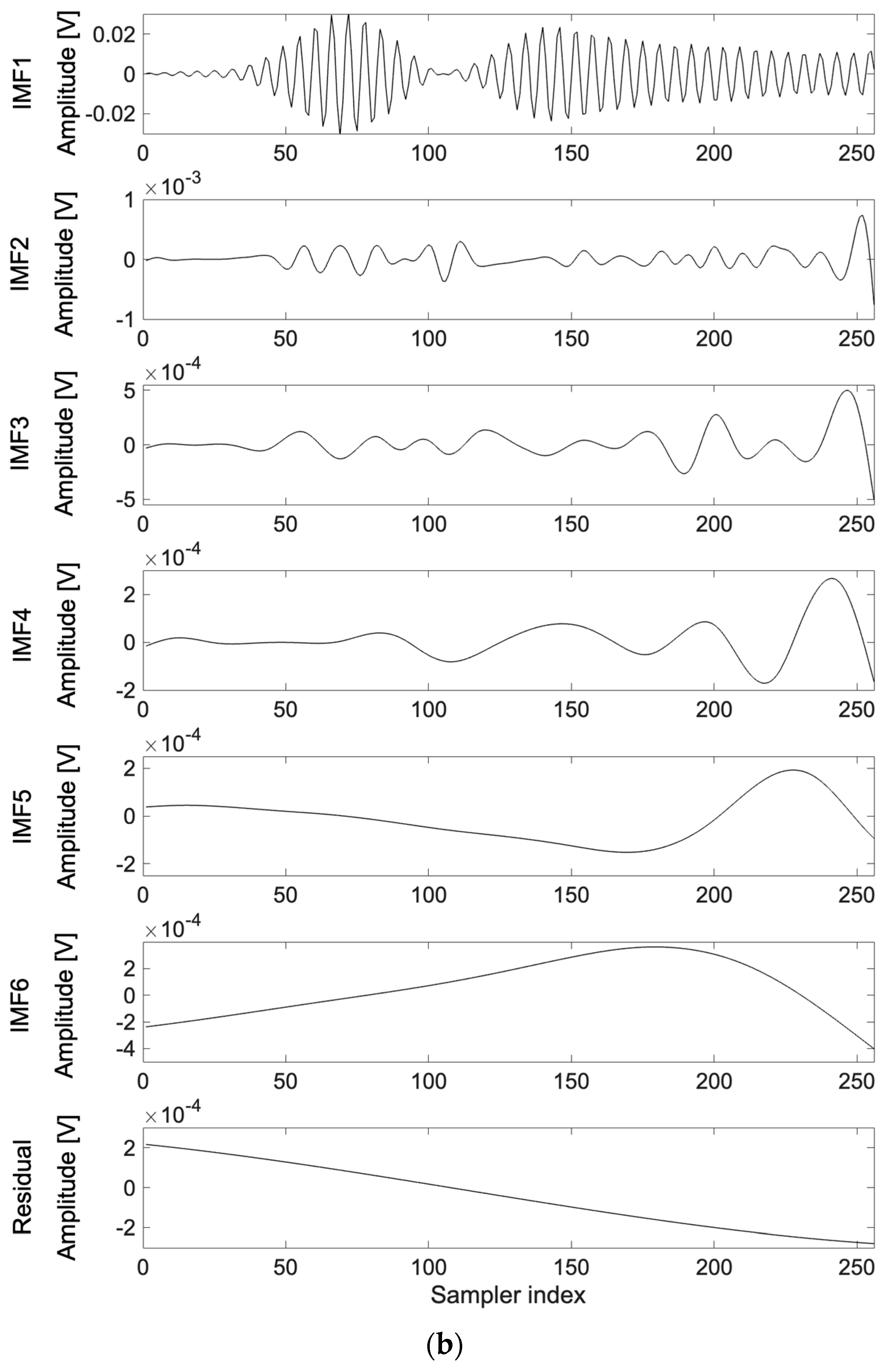
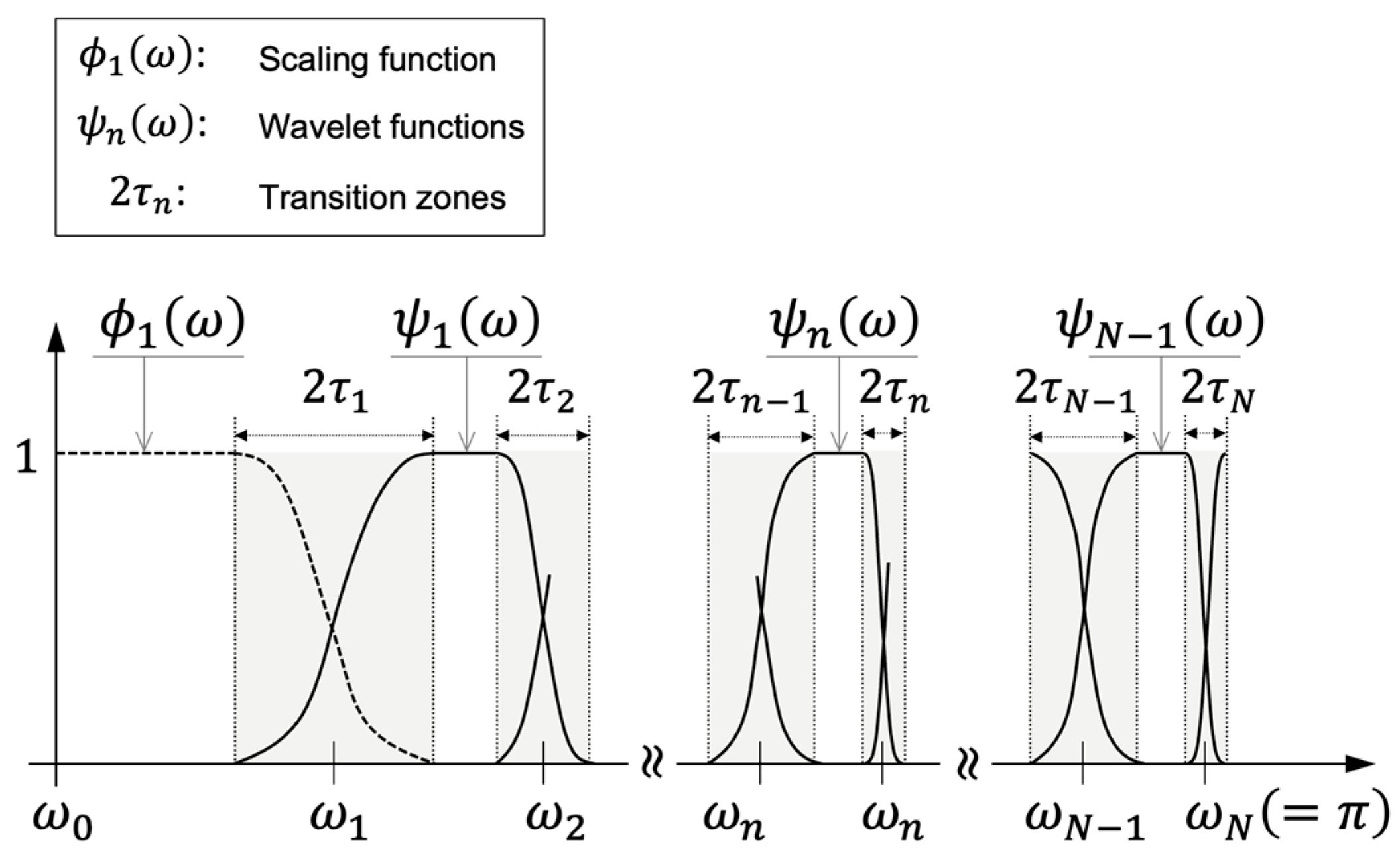
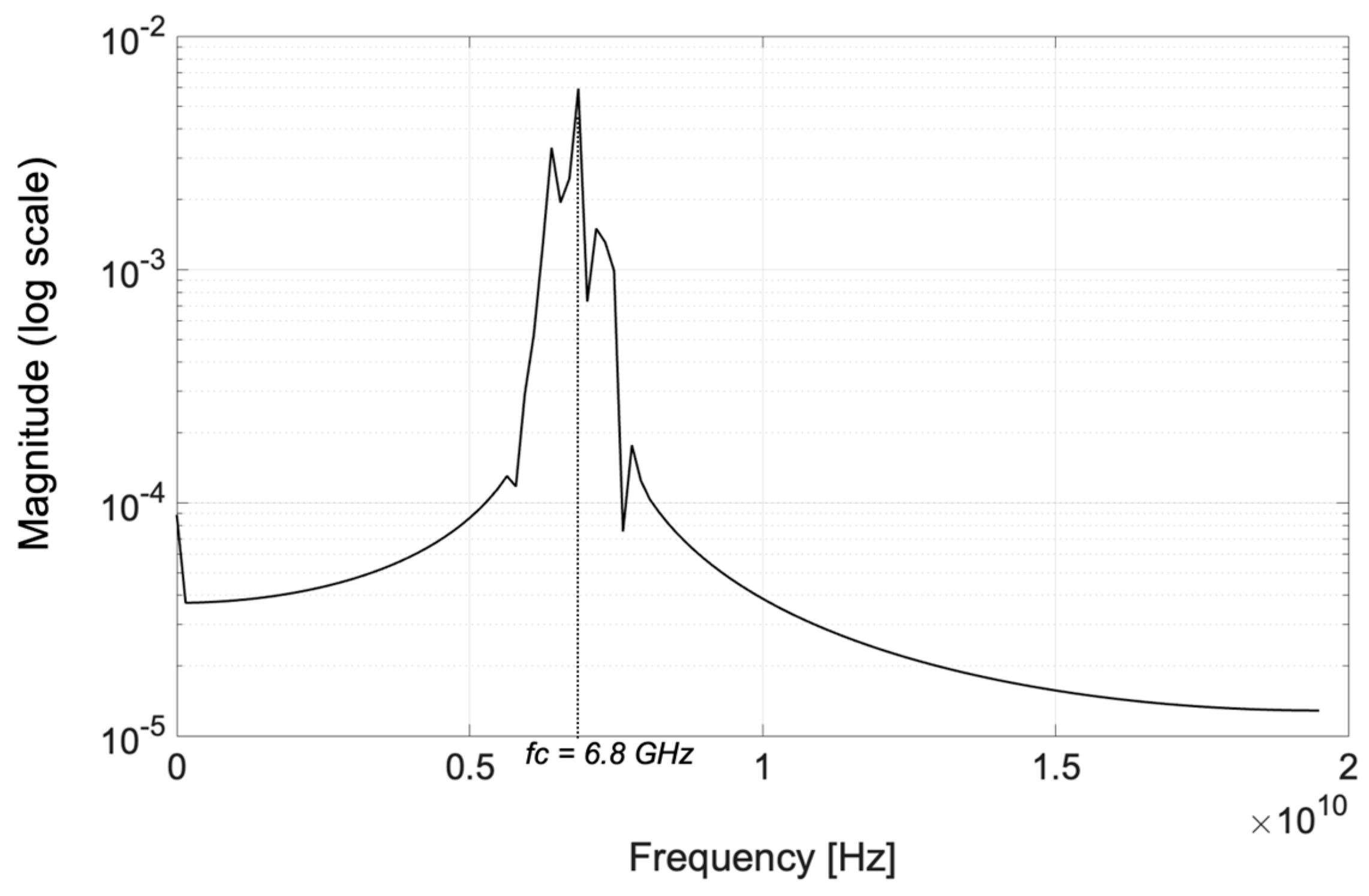
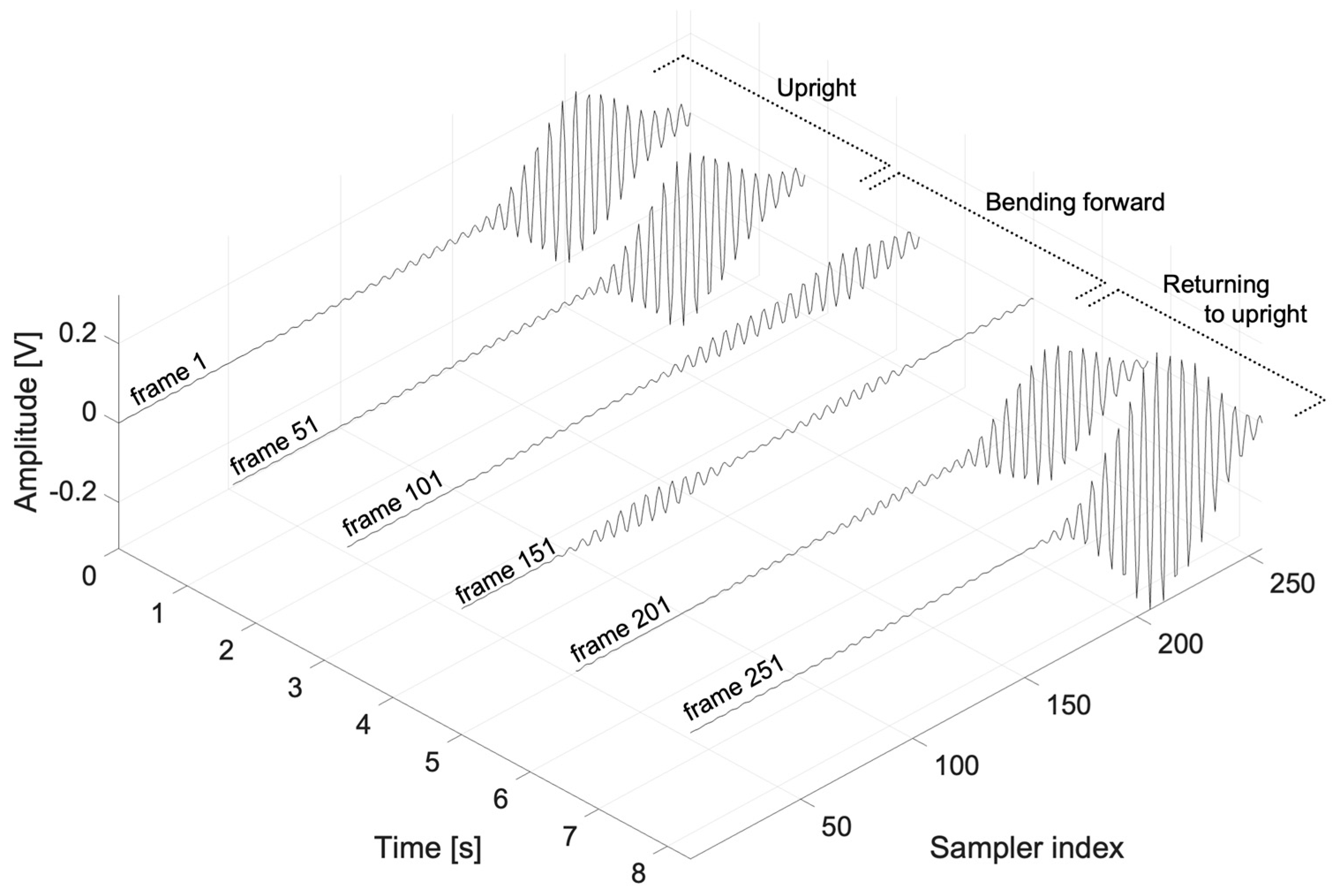

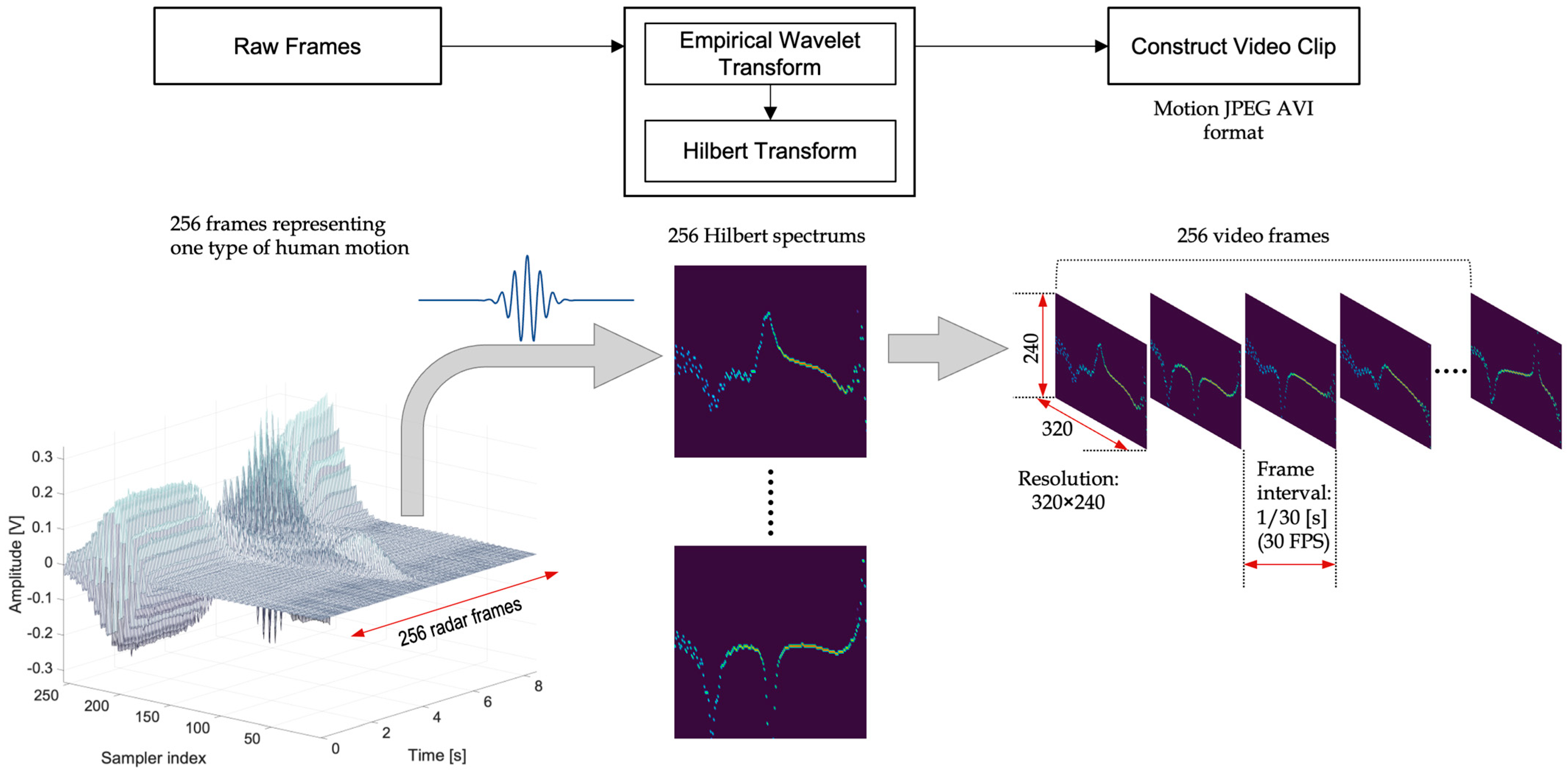
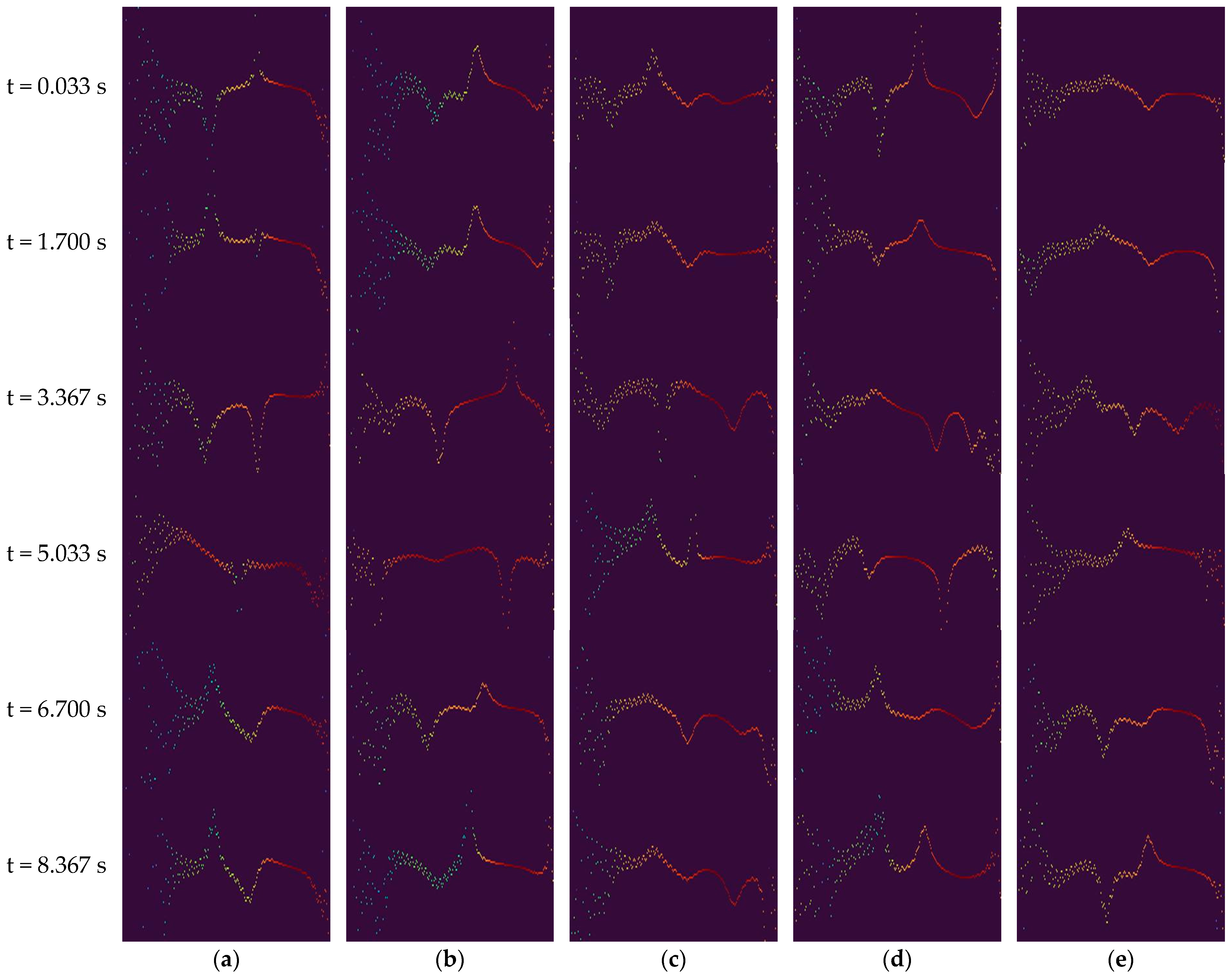
| Decomposition Mode | Frequency [GHz] | Relative Energy [%] |
|---|---|---|
| IMF1 | 6.34–7.21 | 99.90 |
| IMF2 | 1.20–6.83 | 0.02 |
| IMF3 | 0.52–3.38 | 0.01 |
| IMF4 | 0.25–1.35 | 0.00 |
| IMF5 | 0.08–0.70 | 0.01 |
| IMF6 | 0.04–0.35 | 0.04 |
| Residual | 0.05–1.48 | 0.02 |
| Decomposition Mode | Frequency [GHz] | Relative Energy [%] |
|---|---|---|
| (approximation) | 6.34–7.21 | 99.98 |
| (detail) | 11.80–11.89 | 0.02 |
| EMD | EWT | |||
|---|---|---|---|---|
| Frame Index | Frequency [GHz] | Relative Energy [%] | Frequency [GHz] | Relative Energy [%] |
| 1 | 6.33–7.15 | 99.92 | 6.33–7.15 | 99.99 |
| 51 | 6.34–7.14 | 99.94 | 6.34–7.14 | 99.99 |
| 101 | 6.34–7.03 | 99.72 | 6.33–7.02 | 99.96 |
| 151 | 6.30–7.16 | 99.97 | 6.30–7.16 | 100.00 |
| 201 | 6.37–7.20 | 99.98 | 6.37–7.20 | 100.00 |
| 251 | 6.36–7.15 | 99.95 | 6.36–7.15 | 100.00 |
| Label | Arm_Wave | Bowing | Raise_Hand | Stand_Up | Twist | Total |
|---|---|---|---|---|---|---|
| Number | 108 | 104 | 110 | 120 | 111 | 553 |
| Software | Hardware | ||
|---|---|---|---|
| OS | Ubuntu 20.04 | CPU | Intel core i9-10980XE 3.00 GHz |
| PyTorch | 1.8.0 (TorchVision 0.9.0) | RAM | 32 GB |
| Python | 3.7 | GPU | Nvidia GeForce RTX 3090 Ti 24 GB |
| CUDA | 11.1 (CuDNN 8.0.5) | ||
| Experiment Number | Pretrained Model | Batch | Scheduler | Learning Rate | Weight Decay | Normalization | Top-1 Accuracy (%) |
|---|---|---|---|---|---|---|---|
| E-1 | slowfast_r50 | 4 | SGD | 1 × 10−4 | 1 × 10−5 | kinetics-400 | 82.14 |
| E-2 | slowfast_r101 | 4 | SGD | 1 × 10−4 | 1 × 10−5 | kinetics-400 | 85.71 |
| E-3 | slowfast_r101 | 4 | SGD | 1 × 10−3 | 1 × 10−5 | kinetics-400 | 90.18 |
| E-4 | slowfast_r101 | 4 | SGD | 1 × 10−3 | 1 × 10−5 | radar-5 | 91.07 |
| E-5 | slowfast_r101 | 4 | SGD | 1 × 10−3 | 5 × 10−4 | radar-5 | 91.96 |
| E-6 | slowfast_16 × 8_R101 | 2 | SGD | 1 × 10−3 | 5 × 10−4 | radar-5 | 99.11 |
| E-7 | slowfast_16 × 8_R101 (freeze) | 2 | SGD | 1 × 10−3 | 5 × 10−4 | radar-5 | 75.00 |
| Fold Number | Train Size | Test Size | Accuracy (%) | 95% Confidence Interval | Standard Error |
|---|---|---|---|---|---|
| 1 | 441 | 112 | 99.11 | [96.82, 99.87] | 0.0087 |
| 2 | 442 | 111 | 99.10 | [96.79, 99.86] | 0.0088 |
| 3 | 442 | 111 | 100.00 | [98.42, 100.00] | 0.0000 |
| 4 | 443 | 110 | 99.09 | [96.75, 99.85] | 0.0089 |
| 5 | 444 | 109 | 99.08 | [96.72, 99.84] | 0.0090 |
| Configuration | Accuracy (%) | Key Enhancement |
|---|---|---|
| Raw + 2D CNN | 76.3 | Baseline |
| STFT + 2D CNN | 82.1 | Time–frequency analysis |
| EWT + 2D CNN | 89.5 | Adaptive decomposition |
| EWT-Hilbert + 2D CNN | 91.8 | Phase information |
| EWT-Hilbert + SlowFast | 99.28 | Temporal modeling |
| Method | Radar Type | Activities | Accuracy (%) | Validation |
|---|---|---|---|---|
| Maitre et al. [15] | 3 × UWB | 15 | 95.0 | Multi-subject |
| Ding et al. [16] | UWB | 12 | 95.3 | Multi-subject |
| Qi et al. [17] | UWB | 12 | ~85.0 | Multi-subject |
| Pardhu et al. [18] | UWB | 3 | 95.6 | Limited |
| An et al. [19] | UWB-MIMO | 6 | 98.7 | Multi-subject |
| Our Method | 1 × UWB | 5 | 99.28 | 5-fold cross-validation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, H.-S.; Park, Y.-J. UWB Radar-Based Human Activity Recognition via EWT–Hilbert Spectral Videos and Dual-Path Deep Learning. Electronics 2025, 14, 3264. https://doi.org/10.3390/electronics14163264
Cho H-S, Park Y-J. UWB Radar-Based Human Activity Recognition via EWT–Hilbert Spectral Videos and Dual-Path Deep Learning. Electronics. 2025; 14(16):3264. https://doi.org/10.3390/electronics14163264
Chicago/Turabian StyleCho, Hui-Sup, and Young-Jin Park. 2025. "UWB Radar-Based Human Activity Recognition via EWT–Hilbert Spectral Videos and Dual-Path Deep Learning" Electronics 14, no. 16: 3264. https://doi.org/10.3390/electronics14163264
APA StyleCho, H.-S., & Park, Y.-J. (2025). UWB Radar-Based Human Activity Recognition via EWT–Hilbert Spectral Videos and Dual-Path Deep Learning. Electronics, 14(16), 3264. https://doi.org/10.3390/electronics14163264






