Optimization of Parallel Fourier Transform in YHGSM Based on Computation–Communication Overlap

Abstract

Spectral models, due to their stability and efficiency, have become one of the most popular approaches for implementing numerical weather prediction systems. Given the complexity of these models, they often require the use of multi-node computing resources for parallel processing to meet the stringent real-time requirements. However, as the number of nodes increases, the efficiency of inter-node communication becomes a critical bottleneck. In the case of the Yin-He Global Spectral Model (YHGSM), developed by the National University of Defense Technology, communication overhead is very high during the Fourier transform section, which consists of the transform itself and the subsequent transposition from the z-μ decomposition to the z-m decomposition. To address this challenge, we introduce an optimized scheme that overlaps communication with computation. By grouping corresponding communication and computation tasks, this approach leverages non-blocking communication techniques within MPI, combined with the use of asynchronous communication progress threads. Our experimental results demonstrate that this scheme can reduce execution time by up to 30% compared to the non-overlapped version, thereby significantly hiding communication overhead and enhancing the efficiency of YHGSM.

1. Introduction

Weather forecasting is closely linked to our production activities and daily life. Against the backdrop of global warming, extreme weather and climate events are occurring with increasing frequency [1]. For instance, China has experienced a significant rise in extreme heavy rainfall and large-scale extreme heat events in recent years, characterized by extended durations and more frequent record-breaking occurrences [2]. Research by AghaKouchak et al. highlights that extreme weather events globally are exhibiting characteristics that diverge from historical patterns [3]. Consequently, timely and accurate weather forecasting is essential for protecting lives and property.

Despite the growing influence of machine learning in weather forecasting, numerical models remain the primary tool for weather prediction. Depending on the spatial discretization schemes employed, numerical models can be divided into two categories: grid-point models and spectral models. While spectral models involve more complex forecasting processes, they offer more stable integrations and more accurate results. These advantages make spectral models widely used in operational forecasting systems [4]. The Yin-He Global Spectral Model (YHGSM) developed by the National University of Defense Technology is a spectral model.

YHGSM is designed for high-resolution forecasting and climate research. It features advanced parallel computing techniques to greatly improve computational efficiency and scalability. By integrating the finite volume method (FVM), YHGSM reduces spectral transform costs while maintaining forecast accuracy. It effectively simulates extreme weather events and supports model coupling, extending its applications to atmosphere–ocean interactions and climate trend analysis [5]. With good performance in both accuracy and efficiency, YHGSM plays a vital role in modern weather and climate modeling.

Spectral models rely on parallel computing technologies to meet the stringent real-time demands of weather forecasting. Improving the efficiency of these models on multi-node systems has long been a key area of research. As hardware scales continue to grow, the proportion of communication overhead has also increased. In the realm of parallel optimization, the technique of overlapping communication with computation has gained prominence. Effective strategies for hiding communication overhead can lead to substantial performance gains, making it a critical focus for optimizing the performance of spectral models [6,7,8,9,10].

MPI (Message Passing Interface) is the mainstream communication interface used in parallel programming, supported by most multi-node systems and networks. The MPI Forum introduced non-blocking communication mechanisms in the MPI-2 standard [11] and non-blocking collective communication in the MPI-3 standard [12]. These features facilitate the overlapping of computation with communication [13]. However, the effectiveness of such overlapping, from a performance perspective, depends on the specific implementation and the underlying system architecture. Non-blocking operations enable the possibility of overlapping communication with computation, but do not guarantee it [14].

For YHGSM, based on restructuring interpolation arrays and overlapping communication with computation across subarrays, the efficiency of the semi-Lagrange interpolation has been significantly enhanced recently [15]. However, the method does not consider how to progress non-blocking operations, leaving it to the parallel computer, and it has not been extended to other parts of the model. In fact, the spectral transform involves a significant volume of communication as well. Therefore, if we can effectively hide this communication overhead within computation time, the runtime of the model can be significantly reduced further, boosting the operational efficiency of YHGSM.

In this paper, we analyze the spectral transform of YHGSM, with a particular focus on the Fourier transform section. This section involves significant communication overhead due to the three-dimensional data transposition. By grouping and interleaving communication and computation and leveraging MPI’s asynchronous communication, the communication overhead is significantly reduced. Experiments conducted on a multi-node cluster demonstrate that the runtime of this section is reduced by about 30%, highlighting the effectiveness of the proposed method.

The remainder of this paper is organized as follows: Section 2 provides background information on YHGSM and MPI non-blocking communication. Section 3 details the implementation of the strategy for overlapping communication with computation. Section 4 outlines the experimental results. Finally, Section 5 summarizes the work and draws conclusions.

2. Background

2.1. Three-Dimensional Data Transposition in YHGSM

YHGSM is a global, medium-range numerical weather prediction system developed by the National University of Defense Technology. This model employs spectral modeling technology, integrating advanced dynamic frameworks and physical processes to enhance the accuracy and reliability of weather forecasts. Additionally, it incorporates four-dimensional variational assimilation (4D-VAR) techniques to improve the initial conditions and, consequently, the forecast quality [16].

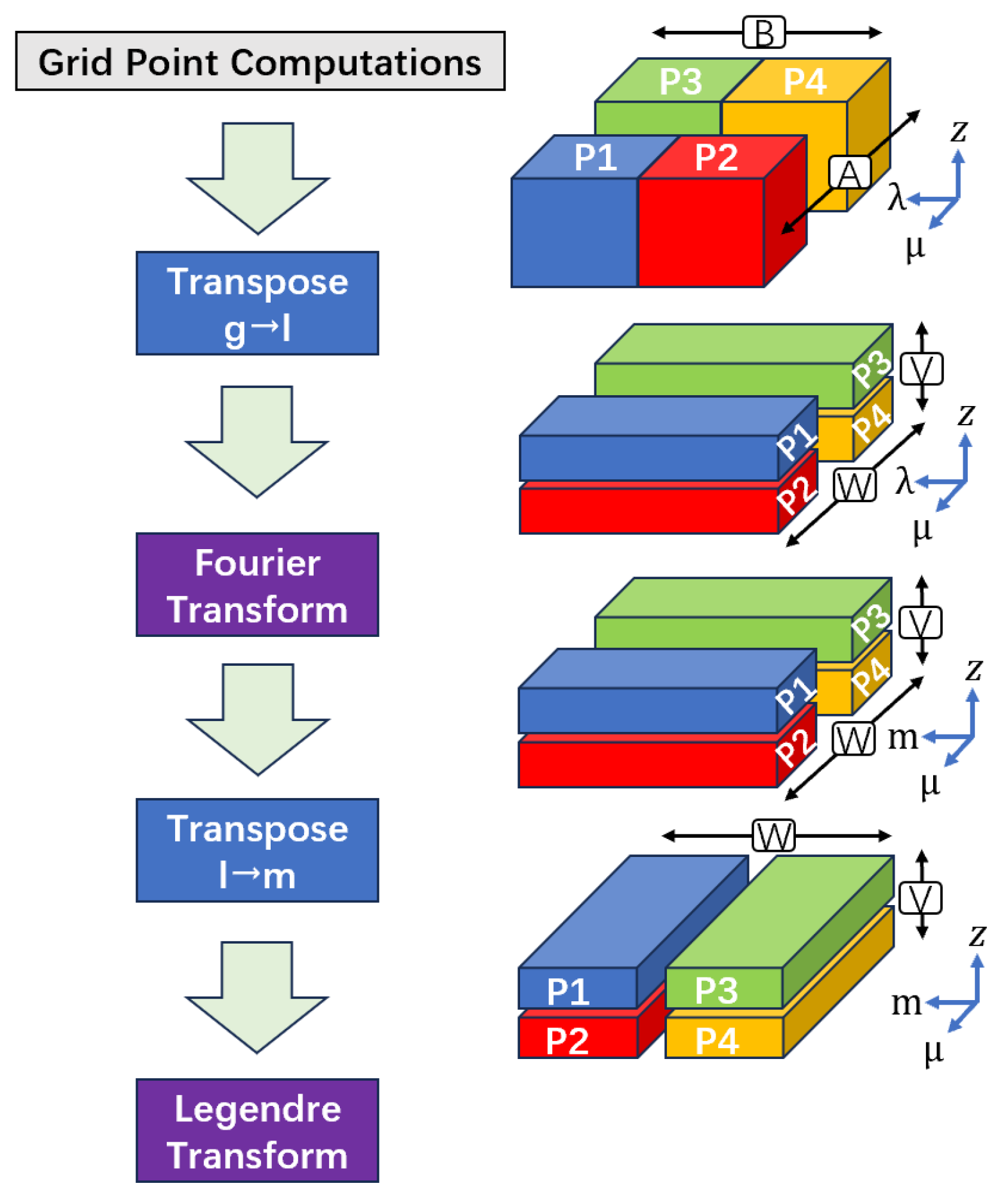
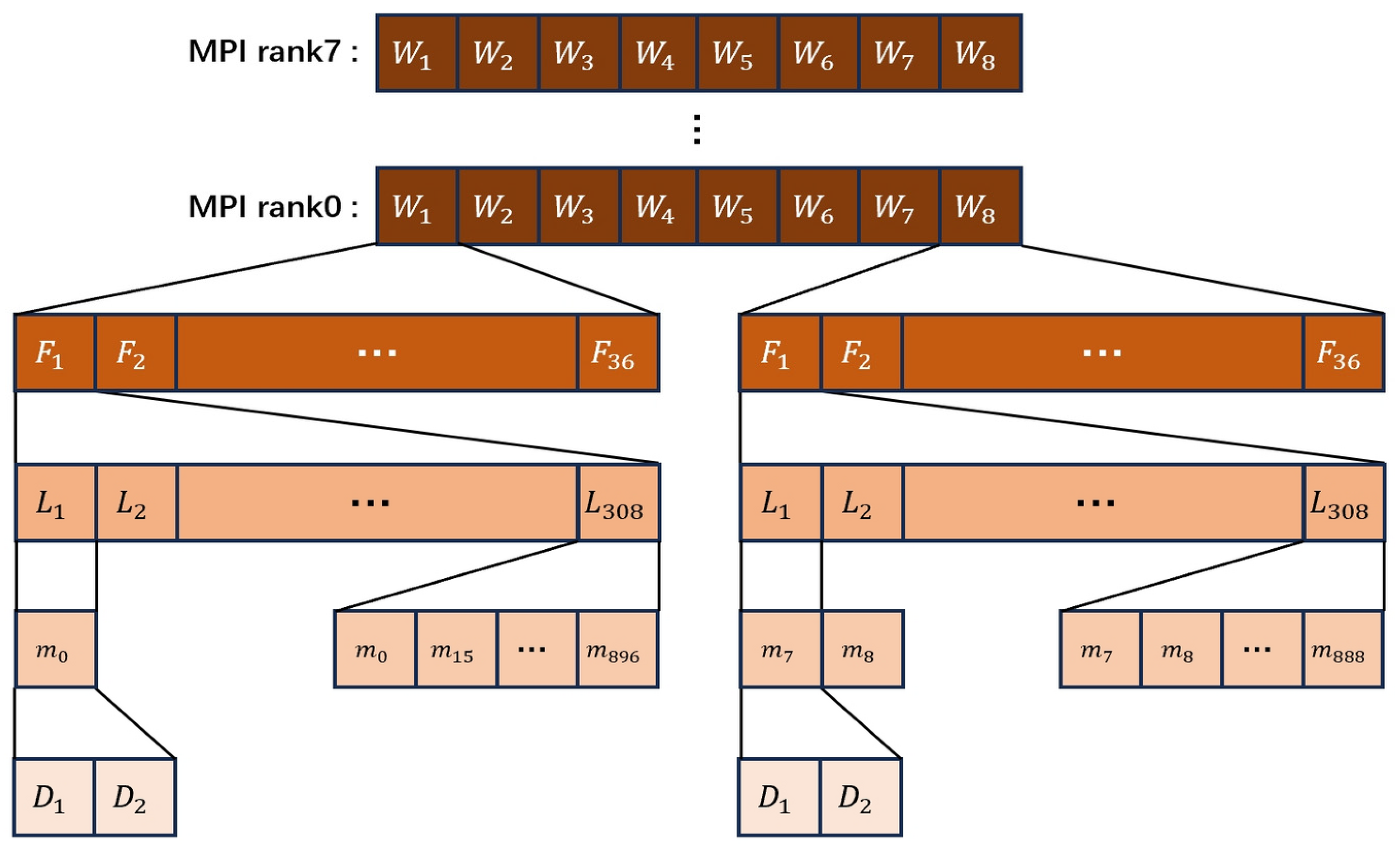
In YHGSM, forecast variables are transformed from grid data to spectral coefficients, and the forecast state is advanced in spectral space. This process involves data transpositions between grid space, Fourier space, and spectral space, as shown in Figure 1. This procedure is carried out across four main stages.

The first stage is the Initial Grid Partitioning. During the grid-space computations, data are partitioned along the horizontal dimensions. In the μ (zonal) direction, data are divided into multiple A sets. For instance, processes P1 and P2 belong to the same A1 set. In the λ (meridional) direction, data are divided into multiple B sets. For example, P1 and P3 belong to the same B1 set.

The second stage is the First Data Transposition. Before the Fourier transform, a 3D transposition is needed to rearrange the data layout. This transposition enables data alignment along the vertical (z) and zonal (μ) directions and involves intra-A set communication. After this step, the data are restructured into V sets and W sets.

The third is the Fourier transform. The Fourier transform maps the λ dimension to the m dimension.

The last is the Second Data Transposition. Prior to the Legendre transform, a second transposition is performed to prepare the data for spectral-space operations. This step involves communication within each V set, reorganizing data into W sets across the m dimension. To achieve load balancing, m values are distributed cyclically across the W sets. For instance, in Figure 1, m0 and m2 may be assigned to W1, while m1, m3, and m4 are handled by W2.

Throughout the above procedure, each data transposition involves significant communication overhead. If this communication overhead can be hidden within the preceding and subsequent computation stages, the program’s execution efficiency can be improved.

2.2. MPI Non-Blocking Communication

MPI is a parallel computing programming model and library standard that defines a set of specifications and functions for enabling communication and parallel computation on distributed memory systems. MPI is widely used in large-scale scientific and engineering computational applications [17,18].

The MPI programming model is based on a message-passing mechanism, and programmers need to explicitly define parallel tasks, message-passing operations, and synchronization between processes [19]. MPI supports two fundamental modes of communication: point-to-point communication and collective communication.

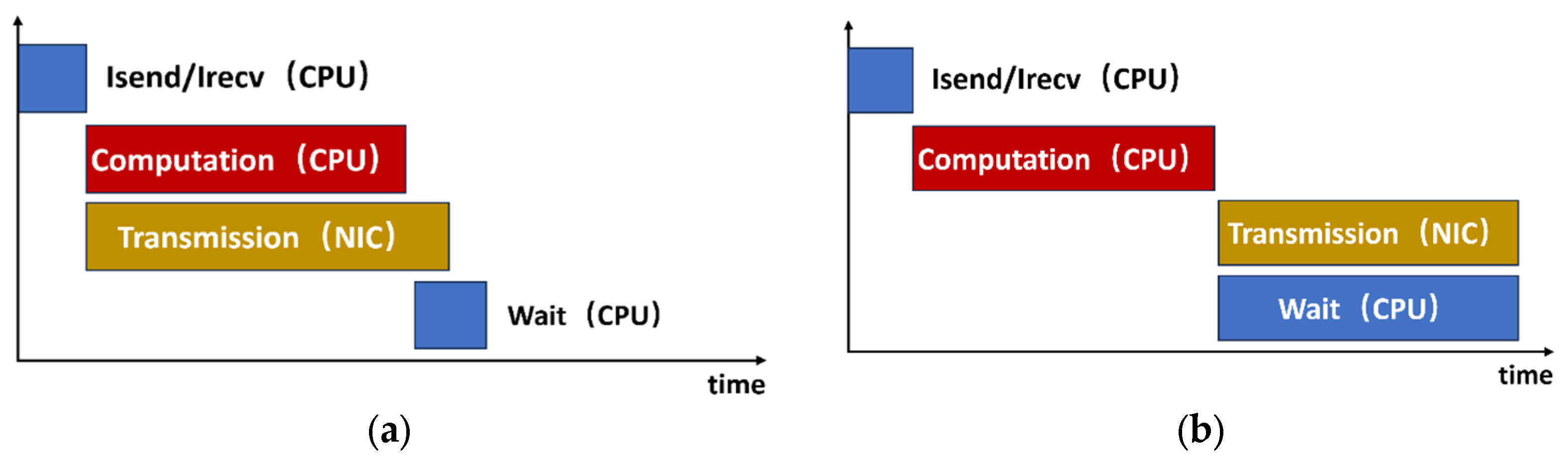
To prevent deadlock issues and facilitate the overlapping of communication with computation, the MPI Forum introduced non-blocking communication functions. Non-blocking communication essentially splits blocking communication into two parts: initiation and completion. Once a non-blocking communication call is made, control is returned immediately to the process, allowing it to continue with computation tasks. Only when it is necessary to ensure that the communication has completed, the MPI_WAIT function is called to finalize the communication [20]. Although non-blocking communication calls return immediately, the MPI standard does not guarantee that communication will occur concurrently with computation. Therefore, in practical implementations, simply using non-blocking communication may fail to achieve effective computation–communication overlapping [21]. As illustrated in Figure 2, communication may not actually begin until the MPI_WAIT function is invoked.

To ensure the quality of communication, the MPI standard employs two different protocols for handling small and large messages: the eager protocol for small messages and the rendezvous protocol for large messages. The MPI standard also uses a communication progress model to ensure the completion of communication operations. When a process initiates a communication, it must actively manage the progress of the communication to ensure its eventual completion [22,23]. Overlapping communication with computation is particularly important when using the rendezvous protocol to transfer large messages. However, the rendezvous protocol involves multiple interactions between the sender and receiver, requiring more active management of communication progress. At certain points, advancing communication progress necessitates invoking specific functions, such as MPI_WAIT and MPI_TEST [24]. In the case of blocking communication, this is equivalent to calling MPI_WAIT immediately after starting the communication, continuously polling for progress until it is complete. For non-blocking communication, achieving communication progress becomes an implementation-dependent issue, which is crucial for effectively overlapping communication with computation.

To achieve communication progress and overlap it with computation in non-blocking situations, three common approaches are typically employed.

The first method involves significantly modifying the program. As illustrated in Figure 3, it requires inserting multiple calls to the MPI_TEST function at regular intervals within the computation segment intended to overlap with communication. According to the MPI standard, MPI_TEST not only checks if a specified communication operation has completed but also advances the communication to the next stage if it detects that progress is needed. However, a major drawback of this approach is that the placement and frequency of MPI_TEST calls are entirely controlled by the programmer [25]. Since communication progress is opaque to programmers, they must rely on trial and error to determine the optimal timing for these calls. Furthermore, in practical applications, computational segments often depend on scientific computing libraries, making it challenging to insert MPI_TEST calls appropriately and achieve effective computation–communication overlap.

The second method, offloading MPI communication entirely to dedicated hardware, is the optimal solution. This approach requires no additional effort from the programmer to manage progress and avoids wasting hardware resources [26,27]. However, it requires the system to be designed with this capability in mind, making it highly dependent on effective software–hardware coordination. Due to the need for specialized system implementations, which are not yet widely available, this method is rarely used in practice to achieve efficient overlap between computation and communication.

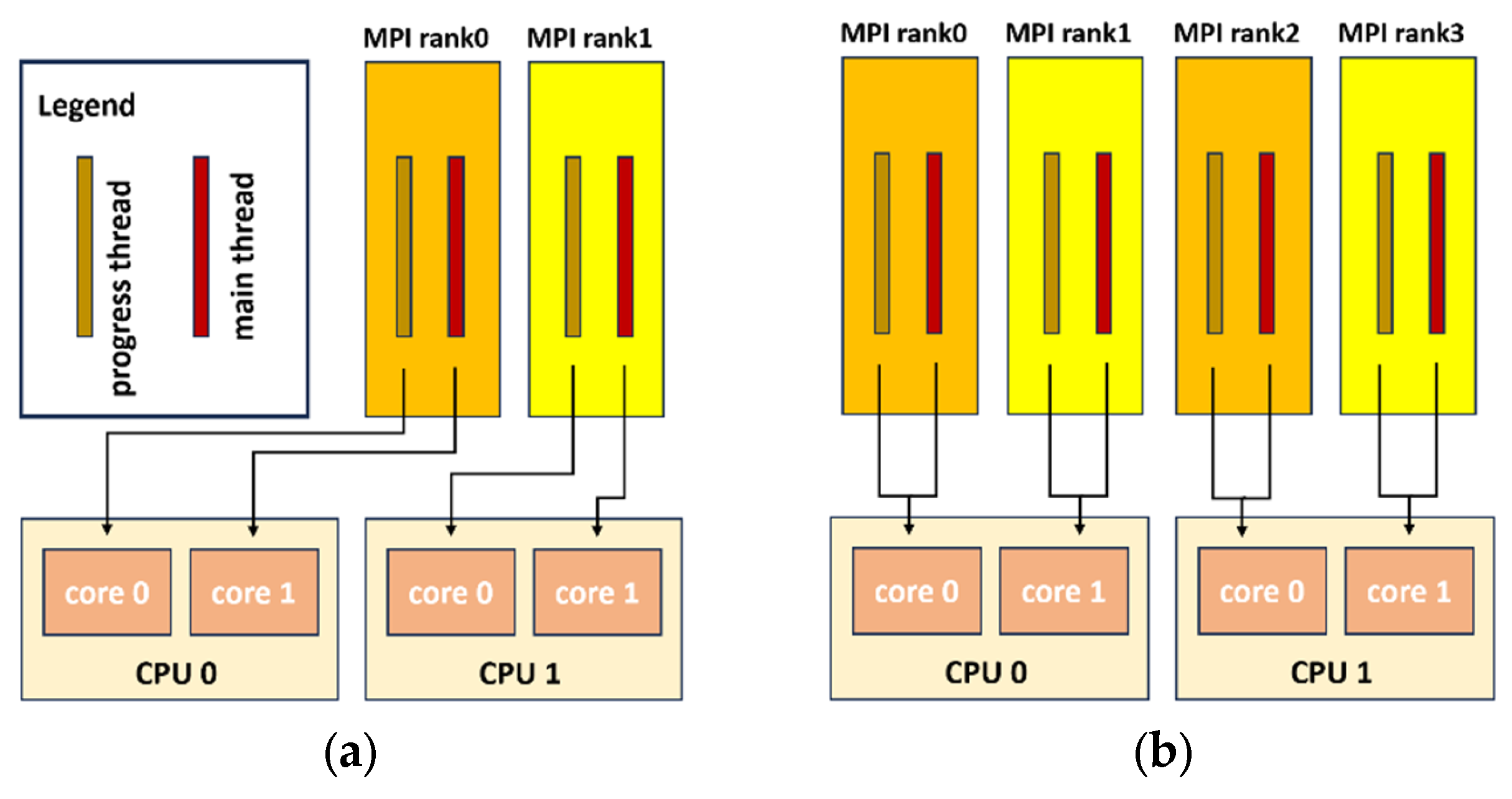
The third method, using asynchronous progress threads, offers a practical and balanced approach to overlapping communication with computation. This extension is widely supported in general-purpose MPI implementations and requires minimal code changes, making it suitable for most systems. For instance, in MPICH v3.2, setting the environment variable MPICH_ASYNC_PROGRESS = 1 enables this feature. MPI then automatically creates a dedicated communication thread for each process. The main thread continues with computation after initiating communication, and the progress thread handles communication advancement in the background.

However, CPU core contention must be considered. If both threads share a core (see Figure 4), performance may suffer due to competition for CPU cycles. To avoid this, it is recommended to assign a dedicated core to the progress thread whenever resources are available [28].

2.3. Recent Advances in Parallel Optimization for YHGSM

In recent years, with the rapid advancement of HPC, numerical models such as YHGSM have undergone continuous parallel optimization to meet the increasing demands of high-resolution global numerical weather prediction [29,30,31]. By addressing various parallel bottlenecks, multiple advanced parallel strategies have been introduced and refined, significantly improving the model’s computational efficiency and scalability.

Extensive efforts have been made to improve the parallel performance of the YHGSM model. To optimize the semi-Lagrangian scheme in YHGSM, one-sided communication was introduced to enhance the efficiency of the model. Tests show that the number of communication operations was reduced by approximately 50%, significantly improving parallel efficiency while preserving interpolation accuracy [32].

Another work in optimizing YHGSM’s parallel performance was undertaken in 2021, when researchers introduced a variable-based subarray grouping strategy for the semi-Lagrangian interpolation scheme [15]. Instead of processing all prognostic variables together, the fields were partitioned into independent subarrays—each interpolated and communicated separately.

Building on this, Liu et al. proposed a further refinement through a communication–computation overlapping strategy with grouping of vertical levels. Recognizing that the 93 vertical layers in YHGSM exhibit weak inter-layer dependencies, the scheme divides these layers into three groups [16]. Each group performs non-blocking communication and interpolation in a staggered manner, allowing the communication of one group to overlap with the computation of another. This approach effectively reduces the idle time during the semi-Lagrangian interpolation and achieved a 12.5% reduction in runtime on a 256-core system.

While YHGSM has achieved considerable progress in parallel optimization—particularly in semi-Lagrangian schemes—certain components of the model, such as the spectral transform, remain communication-intensive. Among these, the Fourier transform stage poses a significant performance bottleneck due to the large volume of data transposition across three dimensions. If this communication overhead can be effectively hidden within computation through careful program restructuring and system-level tuning, the runtime of the model can be further reduced.

3. Implementation and Optimization Strategy

3.1. Analysis of the Original Scheme

We focus on the Fourier transform and the subsequent three-dimensional data transpose.

Table 1. Brief description of the original Fourier transform program.

Original Program
1 DO LAT FROM MYFSTLAT TO MYLSTLAT 2 CALL FFT(LAT, FBUF) 3 CALL FOUT(LAT, FBUF, FOUBUF_IN) 4 ENDDO 5 CALL MPI_ALLTOALLV(FOUBUF IN, FOUBUF, MPI_ALLW_COMM)

shows a simplified structure of the original program executed by each MPI process. Initially, each MPI process computes the FFT for its assigned latitude rows, as illustrated in Figure 1. Each MPI process belongs to a specific V set and W set. Within a V set, all latitude rows are processed collectively, with each W set handling a subset of rows. The computed data are initially stored in FBUF. After computing each latitude row, the corresponding result is transferred from FBUF to the send buffer FOUBUF_IN via the FOUT subroutine, according to the requirements of the three-dimensional data transposition. Once all latitude rows have been traversed, the Fourier transform computation task for the current MPI process is completed. Subsequently, inter-process data exchange is performed using MPI collective blocking communication. The final data arrangement in the receive buffer FOUBUF represents the transposed three-dimensional structure. The data exchange occurs only among the MPI processes belonging to different W sets within the same V set, under the MPI_ALLW_COMM communication domain, meaning that no communication occurs between different V sets, which simplifies the communication process to some extent. It can be stated that the calls to FOUT and MPI_ALLTOALLV subroutines together form the three-dimensional data transpose section. For each MPI process, the computation part consists of the FFT and FOUT subroutines, while communication is primarily handled by the MPI_ALLTOALLV subroutine.

After the computation phase, the structure of the local send buffer FOUBUF_IN for each MPI process is depicted in Figure 5. On the basis of Figure 1, we assume a division of V × W = 8 × 8, where each MPI process is assigned a specific pair of V set and W set and is responsible for the corresponding data segment. FOUBUF_IN is logically organized into eight W-blocks (W1–W8), each destined for one of the eight processes within the same V set but with different W sets. Within each W-block,

• Data is arranged in increasing order of latitude rows.
• If a process handles 308 latitude rows, each W-block is divided into 308 L-blocks (L1–L308).
• Each L-block is further subdivided by wave number. To balance load, wave numbers are cyclically distributed across W-blocks (e.g., m0 and m15 in W1; m7 and m8 in W8).
• The innermost dimension is the field dimension, combining vertical level and physical field dimensions. For example, if the process handles 36 fields, each m-block is subdivided into 36 F-blocks (F1–F36), and each F-block holds two DOUBLE values: D1 and D2.

In the current implementation of YHGSM, field data are statically distributed across processes along the field dimension, which generally ensures load balancing, where each field involves similar computation. However, our analysis reveals that the MPI collective blocking communications at this stage may introduce substantial communication overhead. To address this issue, we introduce an optimized strategy in the following section, which has the potential to significantly improve performance further under the condition of load balancing.

3.2. Pipelined Strategy for Communication–Computing Overlap

Due to the interdependence between the Fourier transform computation and the subsequent three-dimensional data transposition, communication cannot begin until the computation is complete, making it impossible to directly overlap communication with computation. However, since both communication and computation involve large amounts of data, they can be grouped separately, and the concept of pipelining can be used to hide part of the communication overhead. As shown in Figure 1, the data layout along both horizontal dimensions alters after the three-dimensional transposition. Therefore, grouping the communication part along the vertical dimension is relatively straightforward.

In the computation section, it is evident that only the longitude dimension maps to the wave number dimension after the Fourier transform, while the vertical dimension remains unchanged. In the model, the vertical dimension is merged into the field dimension. The field dimension is naturally independent across different variables, resulting in minimal inter-group data dependencies and providing a favorable condition for implementing pipelined execution. Furthermore, the existing data layout in YHGSM is naturally organized by field, making this grouping both efficient and convenient for implementation. Therefore, grouping data along the physical field dimension is the most suitable approach.

To group communication according to the field dimension, two primary challenges must be addressed in YHGSM. First, although the data in FOUBUF_IN spans several dimensions, as shown in Figure 5, it is physically stored as a one-dimensional array. This necessitates restructuring the data layout, along with corresponding adjustments to the receive buffer FOUBUF. Second, the communication buffer parameters for different MPI processes are computed dynamically at runtime to accommodate diverse hardware configurations. To address these challenges, the data structure can be modified as described in Figure 6.

In the proposed approach, the send and receive buffer parameters, such as the offset and length for each MPI process, are not hardcoded but are instead computed dynamically based on the local data size and the number of fields handled by each process. This design ensures adaptability to different problem sizes and hardware configurations. Furthermore, communication grouping is achieved by reorganizing the data layout so that the data are first grouped along the field dimension. This allows both computation and communication to be segmented into multiple groups, enabling pipelined execution.

As shown in Figure 6, the field dimension, which was originally the innermost, has been elevated to a position between the W-set dimension and the latitude row dimension, while the other dimensions are preserved. This reordering enables communication to be grouped effectively by field and simplifies the computation of the parameters required by the communication routines.

A simplified description of the modified program is given in

Table 2. Simplified description of the modified Fourier transform program using non-blocking communication and pipelined execution.

Modified Program
1 DO FIELDS FROM 1 TO N 2 DO LAT FROM MYFSTLAT TO MYLSTLAT 3 CALL FFT(LAT, FBUF, FIELDS) 4 CALL FOUT(LAT, FBUF, FIELDS, FOUBUF_IN) 5 ENDDO 6 IF (FIELDS .NE. 1) THEN 7 CALL MPI_WAIT(REQ) 8 ENDIF 9 CALL MPI_ALLTOALLV_NONBLOCKING(FOUBUF_IN, FOUBUF, MPI_ALLW_COMM, FIELDS, REQ) 10 ENDDO 11 CALL MPI_WAIT(REQ)

, which omits some details and only presents grouping and non-blocking communication. The modified program first divides the fields into N groups. For example, if there are a total of 36 fields in this MPI process, they are divided into three groups, with each group handling the communication and computation for 12 fields. The program first calls the FFT subroutine to perform the Fourier transform computation for the first group, then invokes the FOUT subroutine to arrange the data into the send buffer FOUBUF_IN. Next, it initiates non-blocking communication for the first group and immediately starts computation for the second group. After completing the second group’s computation, the program uses MPI_WAIT to ensure the first group’s communication has finished before starting communication for the second group. In the subsequent performance experiments, we fixed the number of groups at N = 3, based on prior experience from our earlier work [15], which effectively demonstrated the potential benefits of overlapping communication with computation.

Figure 7 illustrates the proposed mechanism for overlapping communication with computation through pipelining. In this scheme, the computation of each group is executed concurrently with the communication of the preceding group, forming a pipeline that effectively hides part of the communication overhead. Building upon this idea, Figure 8 presents the modified workflow. It demonstrates how the original sequential pattern of communication followed by computation is reorganized into a staged execution model and highlights the key differences from the original version.

4. Experiment

The numerical experiments presented in this paper were conducted on a cluster with 85 nodes, each equipped with two 18-core Intel(R) Xeon(R) Gold 6150 CPUs (Intel Corporation, Santa Clara, CA, USA) running at 2.7 GHz and 192 GB of RAM (cores were allocated on demand according to each experimental configuration, rather than fully occupying all available cores in every run). The nodes are interconnected via a high-speed InfiniBand network. The operating system used was Linux 3.10.0–862.9.1 (available at https://www.kernel.org/), and the compiler was Intel 19.0.0.117 (Intel Corporation, Santa Clara, CA, USA). MPICH 3.3.2 was employed for inter-process communication. To implement the overlap of communication with computation based on MPI non-blocking operations, we set the environment variable MPICH_ASYNC_PROGRESS = 1 and allocated two cores for each MPI process. Comparative experiments between the optimized and initial schemes were performed using the YHGSM TL1279 version with an integration time of 600 s. A two-dimensional parallelization scheme was adopted, with the total number of processes determined by the product of the process counts in the W and V directions. Each runtime measurement was averaged over five trials. Since the three-dimensional data transposition involves coordination among processes within the same V-set communication domain, the MPI_BARRIER function was used to synchronize the processes within this domain before entering the Fourier transform section, ensuring the accuracy of wall-clock time measurements.

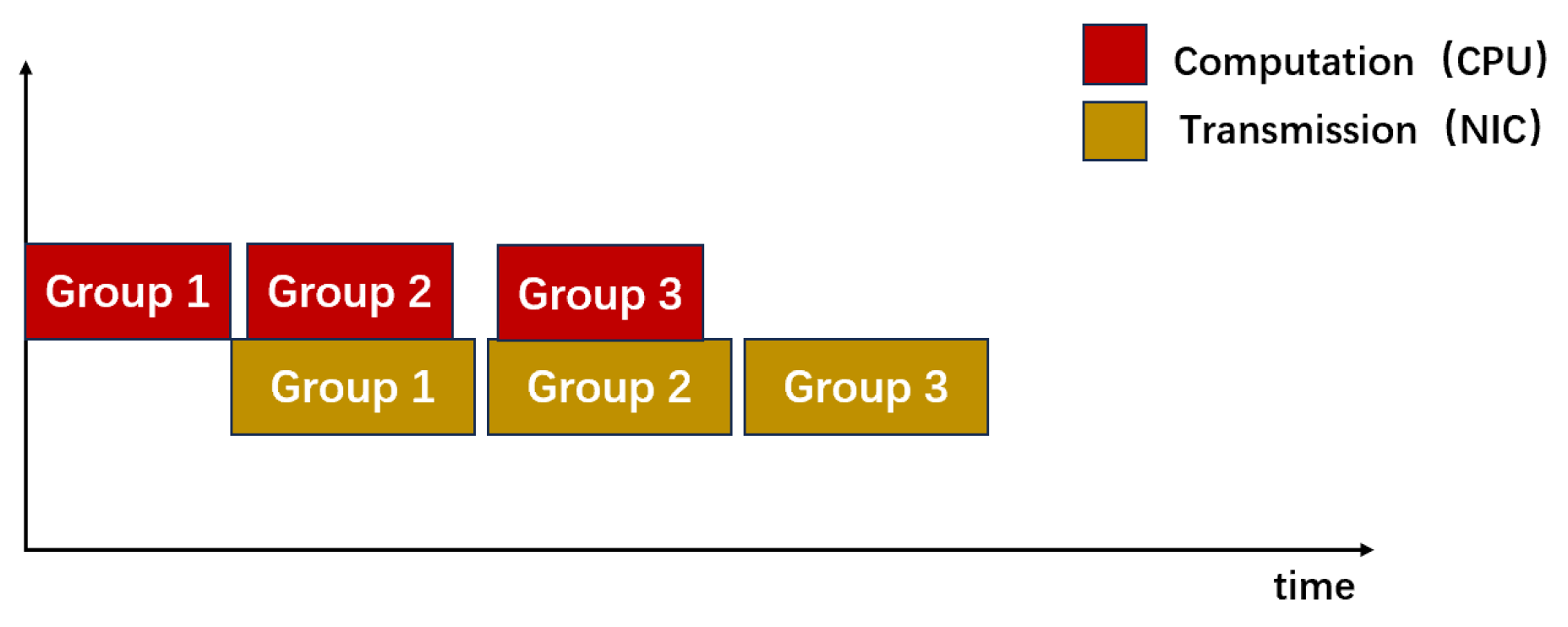
To measure the runtime of the Fourier transform section, the number of V and W sets was varied. Communication and computation were divided into three groups, and the YHGSM was run for six steps. The performance of three implementations—blocking collective communication, non-blocking point-to-point communication, and non-blocking collective communication—was compared.

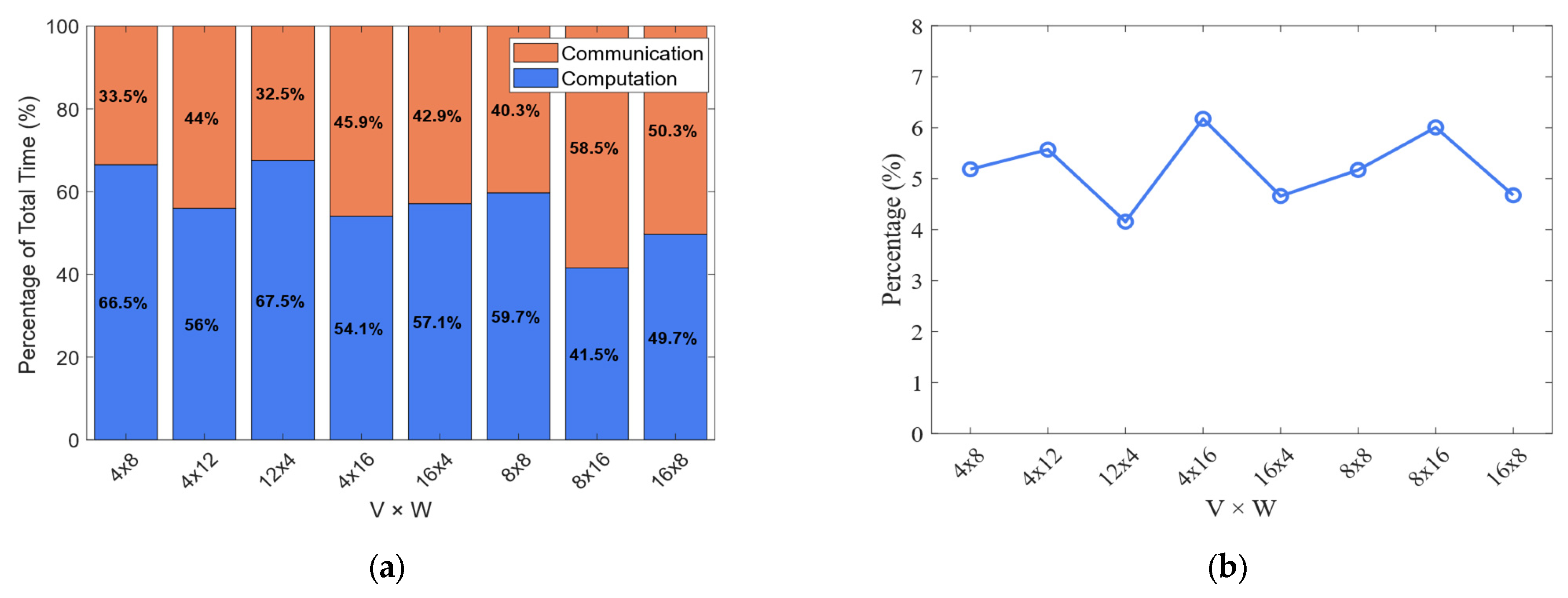
Figure 9a illustrates the time distribution between the computation and communication phases within the Fourier transform component of the YHGSM model. As shown in the figure, communication overhead constitutes a substantial portion of the total runtime across most configurations. Notably, in the 8 × 16 case, communication accounts for as much as 58.5% of the total execution time. This highlights communication as a major performance bottleneck. To address this challenge, dedicated communication optimizations are essential. As shown in Figure 9b, the Fourier transform stage accounts for approximately 5% of the total model runtime. Although this proportion may appear small, it should be noted that the wall-clock time of YHGSM run includes multiple components such as I/O, physics parameterizations, and other computations. In this context, a 5% share is non-negligible. Moreover, optimizations in this stage yield performance benefits in every single time step of the model integration and can be readily generalized to other spectral models.

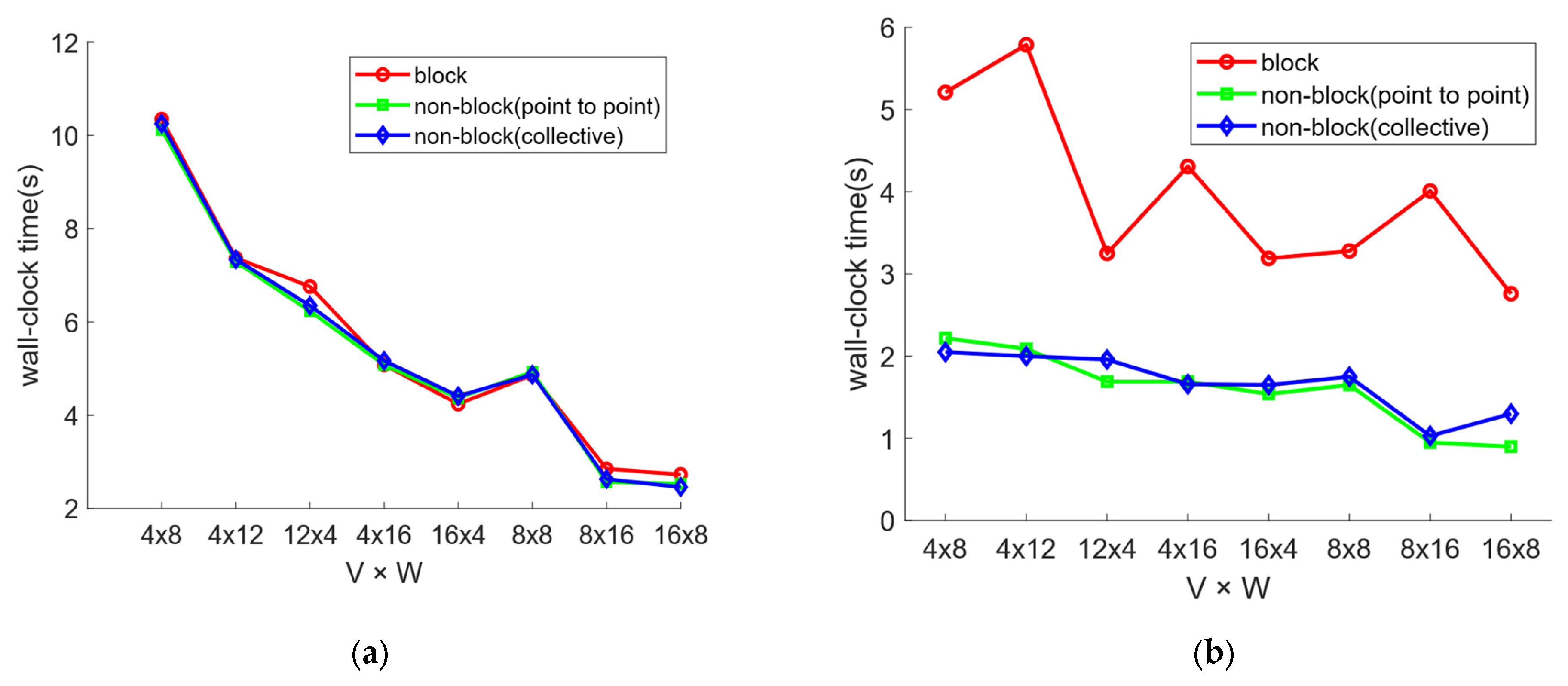
Figure 10a illustrates how computation times change with varying V × W configurations across the three implementations. In the latter two implementations, which use non-blocking communication, communication and computation can overlap. It can be observed that as the total number of processes increases, the overall computation time for the Fourier transform decreases. This trend is primarily due to the fact that a higher number of processes reduces the workload per process. Additionally, regardless of whether communication is overlapped or computation is grouped, the measured computation time remains relatively unchanged, as the total computation workload per MPI process remains fixed once the values of V and W are determined.

Figure 10b shows how communication times change with varying V × W configurations across the three implementations. For the blocking case, the data represent the actual communication overhead, whereas in the non-blocking cases, the measurement includes the overhead of both the MPI non-blocking communication initiation and completion functions across all communication groups. The results indicate that using asynchronous progress threads to overlap communication with computation is clearly effective, leading to a significant reduction in communication overhead.

It is important to note that the MPI non-blocking communication initiation and completion functions themselves introduce some overhead. Therefore, non-blocking communication yields performance benefits only when the original communication cost is greater than this overhead. The extent of the benefits also depends on the ratio of computation to communication overhead, as well as the efficiency of hardware–software coordination on the execution platform.

As the number of processes increases, there is a general trend of decreasing communication time in Figure 10b. This is influenced by two factors: first, the increase in the number of communication operations results in greater invocation overhead; second, each communication operation involves less data. However, the total communication overhead is dominated by the latter, thereby it is reduced step by step. Additionally, it can be observed that for most V × W configurations, the point-to-point non-blocking operation incurs less overhead compared to the collective version. This may be due to the relatively small total number of processes, which limits the ability of collective operations to fully leverage their advantages.

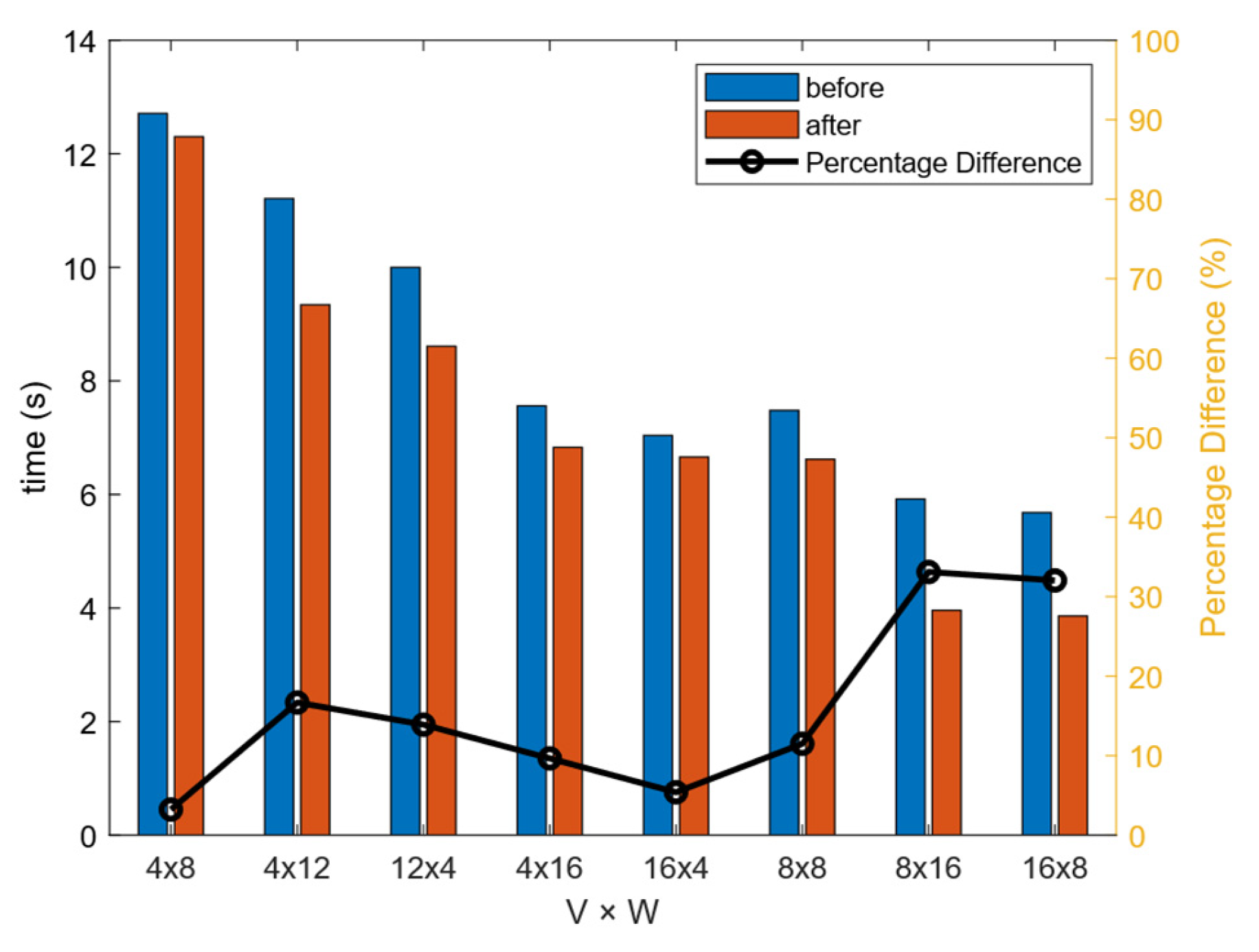
Figure 11 presents the total runtime of the Fourier transform section before and after optimization, with YHGSM running 6 steps, each with a time step of 600 s. The results demonstrate that the computation–communication overlap strategy significantly reduces runtime in this section. This improvement is attributed to the use of pipelining, which effectively hides part of the communication overhead. Notably, the optimization yields the greatest benefit at 128 processes, achieving up to a 30% reduction in execution time. Moreover, the overall runtime shows a decreasing trend as the number of processes increases, demonstrating a certain level of scalability.

To assess the performance impact of the proposed optimization, we measured the runtime components in both the original and optimized implementations. In the baseline version, communication during the Fourier transform stage accounted for approximately 30% to 60% of the total execution time, revealing a communication bottleneck that constrained both scalability and overall performance.

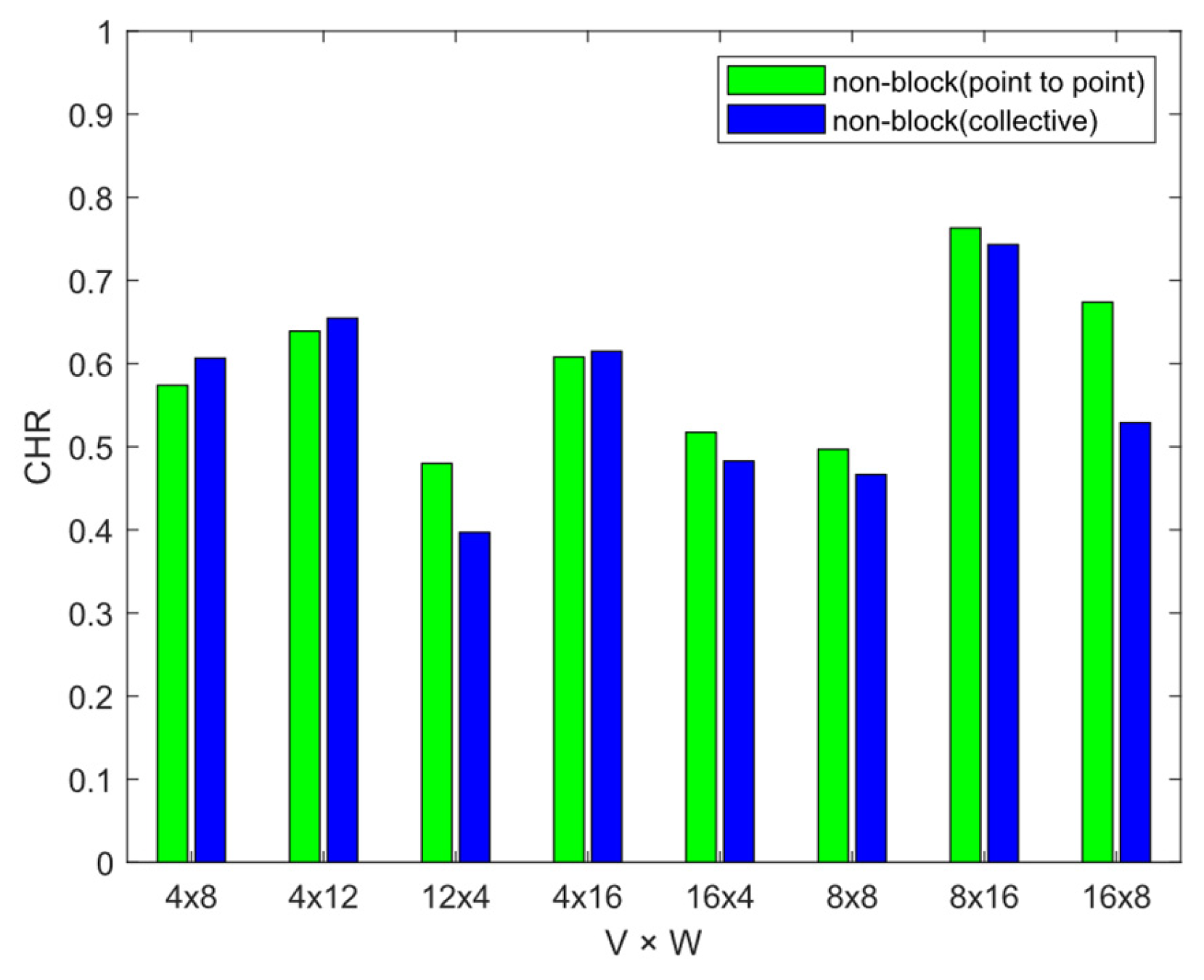
To quantify the benefit of the overlap strategy, we introduce the Communication Hiding Ratio (CHR), defined in Equation (1). Here, ${Comm}_{origin}$ refers to the total communication time in the blocking implementation without any overlap, and ${Comm}_{noverlap}$ denotes the portion of communication time that is not overlapped by computation. A CHR value close to 1 indicates that most of the communication time has been successfully hidden behind computation:

$$CHR=({Comm}_{origin}-{Comm}_{noverlap})/{Comm}_{origin}$$

(1)

Figure 12 shows that the CHR varies between 40% and 75% across different configurations, demonstrating that a significant portion of the communication latency has been successfully overlapped with computation.

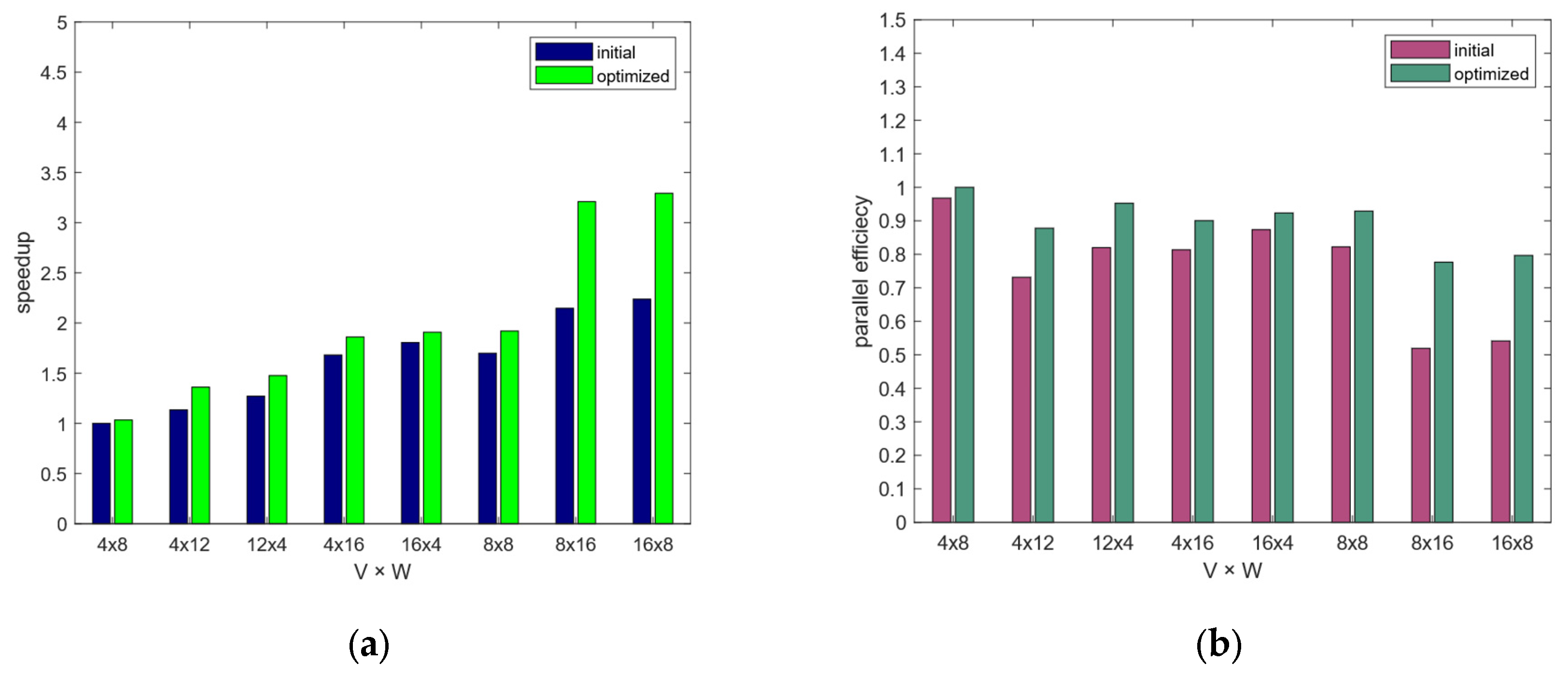
Figure 13a,b show the speedup and parallel efficiency of the Fourier transform section before and after optimization. It can be observed that across various V × W configurations, both speedup and parallel efficiency have improved, further demonstrating the effectiveness of the optimization strategy. The baseline uses 32 MPI processes without computation–communication overlap, each mapped to a physical core (the model cannot run correctly with a single process). We do not count the asynchronous progress threads as additional computational resources because they are active only during the computation–communication overlap phases and do not contribute to other parts of the execution.

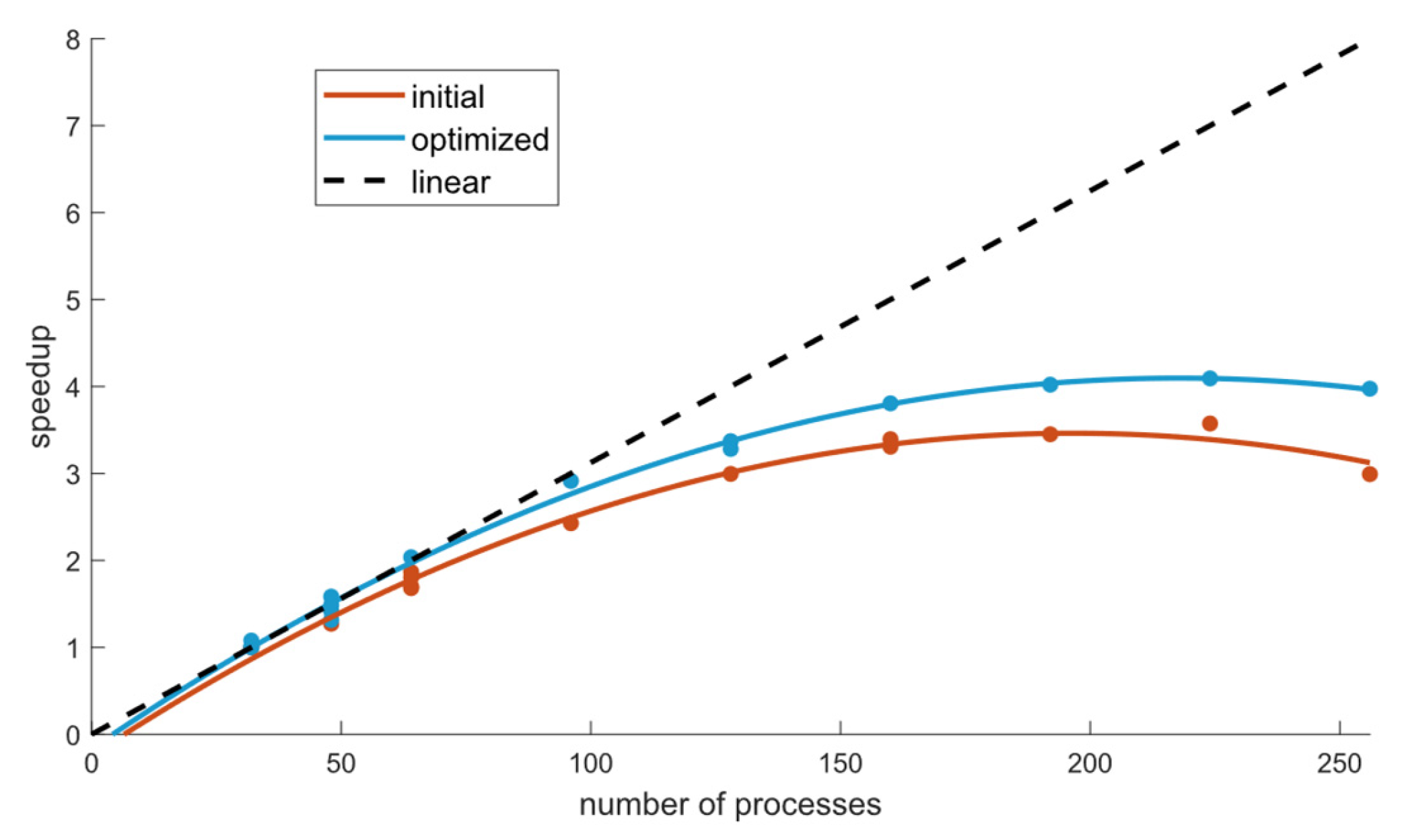
Figure 14 illustrates the speedup of the Fourier transform section before and after applying the computation–communication overlap optimization, using the 32-process configuration as the baseline. The results demonstrate a clear improvement in speedup after optimization, with the curve approaching ideal linear behavior more closely than the unoptimized version. This confirms the effectiveness of the proposed overlap strategy in this communication-intensive section. This experiment focuses on the Fourier transform stage of the model, which is inherently constrained in scalability due to its intensive all-to-all communication. By applying the optimization, we achieved a clear performance improvement. Extending this strategy to other similarly constrained components is expected to enhance the overall scalability of the model.

5. Conclusions

In YHGSM, frequent transformations between grid space and spectral space are required, particularly three-dimensional data transpositions between Fourier transforms and Legendre transforms. These operations involve significant communication overhead across multiple processes. To address this issue and improve runtime efficiency, we analyzed the data dependencies and program structure between the Fourier transform computations and communication tasks. Based on this analysis, we proposed a method that achieves partial overlap of communication and computation by grouping them along the field dimension and executing in a pipelined manner.

In our implementation, we adopted MPI non-blocking communication and leveraged asynchronous progress threads supported by MPICH to enable effective overlap. Experimental results demonstrated that the optimized scheme, which groups operations by field dimension, successfully reduced the runtime of the Fourier transform section in YHGSM. Compared to the original scheme, we observed improvements in speedup and parallel efficiency. Specifically, with a process configuration of V × W = 8 × 16, the optimized scheme reduced runtime by up to 30%. These results confirm the effectiveness of our computation–communication overlap strategy in YHGSM and suggest potential applications for other parts of YHGSM with significant communication costs or even for other spectral models.

Looking forward, the proposed approach shows strong potential for generalization. It could be extended to other components of YHGSM where communication costs dominate, such as Legendre transforms or semi-Lagrangian interpolation stages. Furthermore, the grouping and pipelining strategy can be applied to other spectral models that face similar computational and communication bottlenecks. More broadly, this method contributes to ongoing efforts in high-performance computing to optimize tightly coupled parallel applications and may inspire future research on automated task reorganization, hybrid communication strategies, and adaptive overlap mechanisms in large-scale scientific simulations.

That said, generalizing the proposed method to other modules may present additional challenges due to differences in data dependencies, communication patterns, and memory access behaviors. These factors could affect the feasibility and effectiveness of pipelined execution and will be important considerations in our future work.