Rotation- and Scale-Invariant Object Detection Using Compressed 2D Voting with Sparse Point-Pair Screening

Abstract

The Generalized Hough Transform (GHT) is a powerful method for rigid shape detection under rotation, scaling, translation, and partial occlusion conditions, but its four-dimensional accumulator incurs prohibitive computational and memory demands that prevent real-time deployment. To address this, we propose a framework that compresses the 4-D search space into a concise 2-D voting scheme by combining two-level sparse point-pair screening with an accelerated lookup. In the offline stage, template edges are extracted using an adaptive Canny operator with Otsu-determined thresholds, and gradient-direction differences for all point pairs are quantized to retain only those in the dominant bin, yielding rotation- and scale-invariant descriptors that populate a compact 2-D reference table. During the online stage, an adaptive grid selects only the highest-gradient pixels per cell as a base points, while a precomputed gradient-direction bucket table enables constant-time retrieval of compatible subpoints. Each valid base–subpoint pair is mapped to indices in the lookup table, and “fuzzy” votes are cast over a 3 × 3 neighborhood in the 2-D accumulator, whose global peak determines the object center. Evaluation on 200 real industrial parts—augmented to 1000 samples with noise, blur, occlusion, and nonlinear illumination—demonstrates that our method maintains over 90% localization accuracy, matches the classical GHT, and achieves a ten-fold speedup, outperforming IGHT and LI-GHT variants by 2–3×, thereby delivering a robust, real-time solution for industrial rigid object localization.

1. Introduction

Machine vision has become indispensable for industrial workpiece localization. Although deep learning methods introduced since 2012 have dramatically improved accuracy [1,2,3,4], their heavy data demands, extensive offline training, and inference latency often hinder real-time deployment on the factory floor. Traditional gray-level template matching—e.g., Sum of Absolute Differences (SAD) [4], Sum of Squared Differences (SSD) [5], and Normalized Cross-Correlation (NCC) [6]—remains fast and reliable under controlled conditions, but it degrades sharply in the case of large rotations, scale changes, illumination shifts, noise, or occlusion. Shape-based matching methods [7,8] improve robustness to lighting and clutter by matching object contours, yet they require separate templates at multiple scales and orientations, leading to prohibitive matching times when parts overlap or are partially hidden. Feature-point techniques such as SIFT and SURF [9,10] deliver rotation and scale invariance, but their high-dimensional descriptors and need for dense keypoints limit throughput; textureless or weakly textured parts often yield too few reliable matches [11].

The Generalized Hough Transform (GHT) [12] addresses many of these shortcomings by voting edge points into a multi-parameter space to locate arbitrary shapes despite rotation, scaling, translation, and even partial occlusion. However, its four-dimensional accumulator—covering the rotation angle, scale factor, and 2-D translation—imposes heavy computational and memory overhead, rendering the standard GHT impractical for high-resolution images or complex geometries in real-time systems. Prior work has proposed numerous methods of acceleration—the Randomized GHT to sample votes stochastically, hierarchical pyramids to trade resolution for speed, and displacement-vector or invariant GHTs to collapse one or more parameters—but they either sacrifice robustness, reintroduce per-pair computational redundancy, or remain sensitive to noise and occlusion.

To overcome these limitations, we present an improved GHT framework that collapses the 4-D search into a concise 2-D voting scheme via two-level sparse point-pair screening and accelerated lookup. In the offline stage, template edge-point pairs whose gradient-direction differences fall outside the dominant quantization bin are discarded, and each retained pair contributes a rotation- and scale-invariant descriptor to a compact 2-D lookup table. In the online stage, an adaptive grid prunes base points to only the strongest gradients, and a precomputed gradient-direction bucket table enables O(1) subpoint retrieval. “Fuzzy” 3 × 3 neighborhood votes in the 2-D accumulator further enhance robustness, while integral-image peak detection accelerates center localization. In summary, the key contributions of this paper are as follows:

• Two-level sparse point-pair screening. We introduce an offline quantization of gradient-direction differences to retain only the most discriminative template point pairs then apply an online adaptive grid to select only the highest-gradient base points—drastically reducing both template and image candidate pairs before voting.
• Rotation- and scale-invariant 2-D lookup-table construction. Each surviving point pair is encoded by its interior angle (rotation-invariant) and side-length ratio (scale-invariant) and quantized into a compact 2-D reference table, collapsing the conventional 4-D accumulator into a simple 2-D index space.
• O(1) subpoint retrieval via precomputed gradient buckets. We replace expensive per-pair angle computations with constant-time hash lookups into a precomputed gradient-direction bucket table, enabling rapid identification of compatible subpoints during matching.
• Robust fuzzy voting accelerated by integral-image peak detection. Votes are cast over a 3 × 3 neighborhood in the 2-D accumulator to enhance resilience against noise and occlusion, and an integral-image technique is used to quickly locate the global peak.
• Validated real-time performance on complex industrial parts. Through experiments on 200 real workpieces (augmented to 1000 under noise, blur, occlusion, and nonlinear illumination conditions), our method achieves over 90% localization accuracy—on par with the classical GHT—while delivering an order-of-magnitude speedup and outperforming IGHT/LI-GHT variants by 2–3×.

The rest of this paper is organized as follows. Section 2 surveys related efforts to speed up the GHT; Section 3 details our two-level screening and lookup pipeline; Section 4 presents experimental validation with noise, occlusion, illumination, and scale/rotation changes; and Section 5 concludes.

2. Related Work

The original Generalized Hough Transform (GHT) excels at detecting arbitrarily shaped objects under rotation, scaling, translation, and partial occlusion conditions, but its four-dimensional accumulator—spanning rotation, scale, and 2-D translation—imposes heavy computational and memory costs. Fung et al. [13] address this in the Randomized GHT (RGHT) by stochastically sampling the Hough space, which lowers the average number of votes yet remains vulnerable to dense noise and requires careful tuning of the sampling rate. Ulrich and Nourbakhsh’s hierarchical pyramid schemes [14,15] compress memory via a coarse-to-fine, multi-resolution voting strategy; however, they still traverse the full 4-D parameter space, and there is a trade-off between speed and robustness when adapting pyramid levels.

A related family of methods reduces dimensionality by encoding feature-point displacements. Nixon’s Displacement-Vector GHT (DV-GHT) and its refinements [16,17] collapse one translation dimension by converting edge or corner points into displacement vectors relative to a chosen reference. While this yields a 3-D accumulator (rotation and scale still unresolved), these approaches cannot directly recover full similarity parameters without additional voting stages. Kassim’s Invariant GHT (I-GHT) [17] builds rotation-invariant contour-pair descriptors to eliminate the rotation vote yet remains sensitive to occlusion and background clutter because it still requires voting over scale and translation. Lin et al. [18] propose the Radial Gradient Angle (RGA) descriptor for rotation invariance, but it lacks inherent scale invariance and must recompute the RGA for every candidate pair—adding considerable per-pair overhead.

More complex local-triangle or spectral descriptors aim to achieve full similarity invariance at the cost of heavier computation. Polygon-IGHT [19] leverages triangle-based invariants to handle 2-D translation, rotation, and scale simultaneously, but the O(N³) combinatorics of triplet selection make it impractical for large point sets. Remote-sensing approaches such as ORSIM [20] and Fourier-HOG frameworks [21] employ multi-channel histograms and spectral transforms to encode geometric invariance; however, the convolutional and Fourier-transform steps introduce significant runtime and memory overhead on high-resolution imagery.

Other strategies focus on reference-point selection or local shape attributes to shrink the vote space. Lee and Chen [22] propose using a single boundary point as a reference—minimizing storage but forfeiting robustness when that point is occluded or missing. Tsai and Huang [23] replace gradient-angle tables with curvature- and radius-based lookups to adapt to local shape variations, yet curvature estimation on noisy edges often yields unstable votes. Artolazabal et al.’s LI-GHT [24] employs local Fourier descriptors for strong noise resistance but requires long, continuous edge segments, making it unsuitable for small or fragmented shapes. Aguado [25] and Ser [26] independently exploit the gradient-difference of point pairs to achieve full 2-D (rotation + scale) invariance, collapsing the GHT accumulator to a simple 2-D voting scheme. While these techniques dramatically reduce memory and speed requirements, their reliance on pairwise consistency degrades performance under occlusion conditions or in scenes with multiple overlapping instances.

In summary, existing GHT variants either retain a high-dimensional accumulator, introduce complex invariants that incur substantial overhead, or exhibit brittleness under occlusion and noise conditions. In the next section, we present a novel method that combines adaptive two-level point-pair screening with precomputed gradient-direction lookup to achieve robust, real-time 2-D voting without sacrificing accuracy.

3. Our Method

Unlike previous GHT variants that perform full 4-D voting with gradient-difference templates at every image location, our pipeline introduces three fundamental innovations that together yield orders-of-magnitude speedups and greater noise resilience:

• Two-Level Screening. A coarse grid-filtering stage rapidly discards ≥90% of background positions by testing only object-size consistency, reducing the effective search space from $O(W\times H\times A\times \Phi )$ to $O\left(G\right)$, where $G\ll W\times H$.
• Precomputed Gradient Lookup. Instead of on-the-fly interpolation or expensive trigonometric rotations, we store all $\Delta \theta \times \Delta \varphi$ gradient templates in a constant-time lookup table, replacing per-vote arithmetic with $O\left(1\right)$ table access and achieving a ∼$5\times$ speedup.
• Fuzzy Neighborhood Voting. A $3\times 3$ Gaussian-weighted vote spread counters edge jitter and quantization noise, whereas the standard GHT votes at a single bin.

To overcome the GHT’s 4-D bottleneck, we organize our method into two phases:

• Offline phase: Extract edge-point pairs, filter by adaptive gradient-difference quantiles, and build a 2-D rotation/scale-invariant lookup table.
• Online phase: Grid-filter base points, look up valid sub-points, then perform 2-D voting with fuzzy $3\times 3$ maxima.

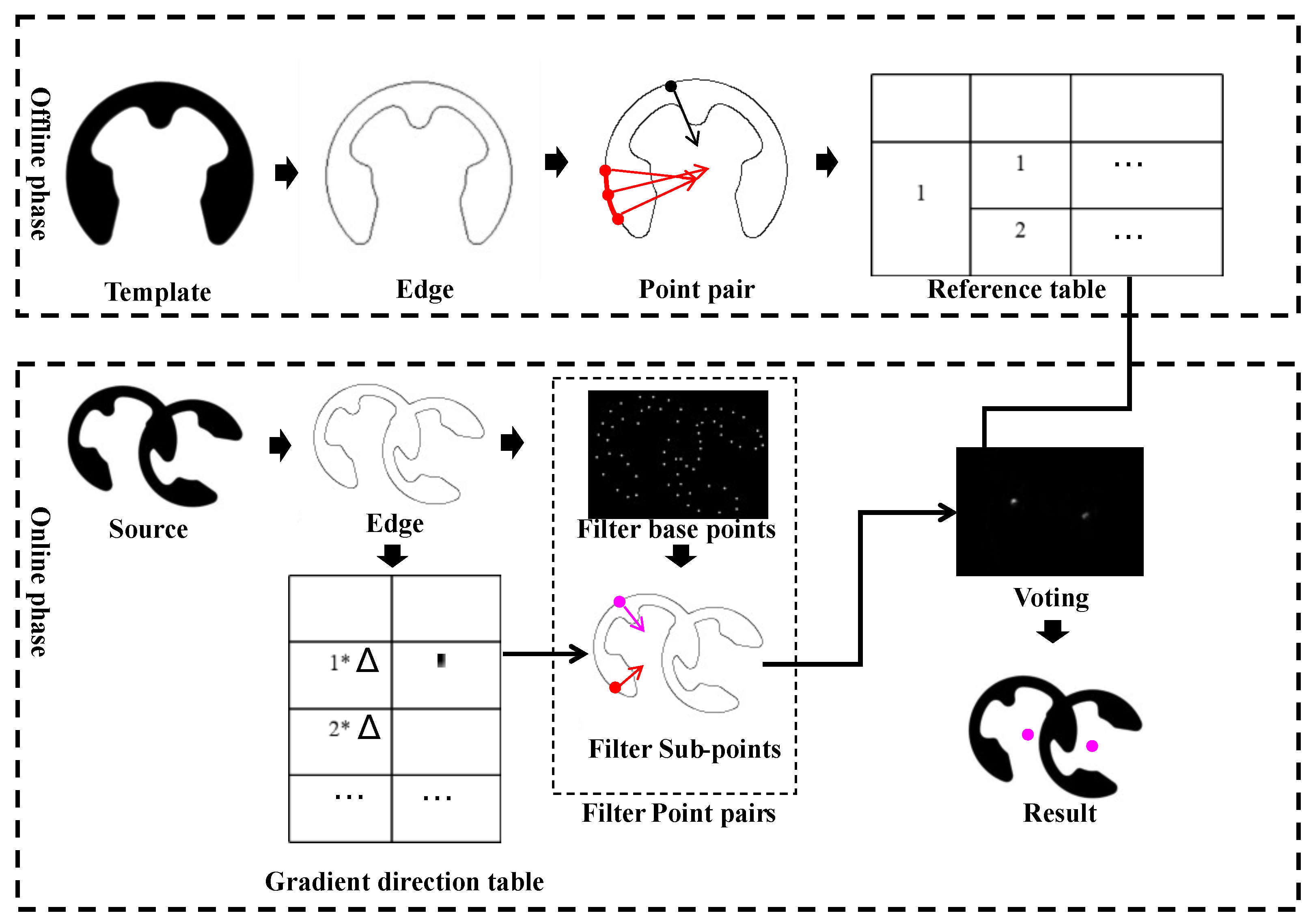
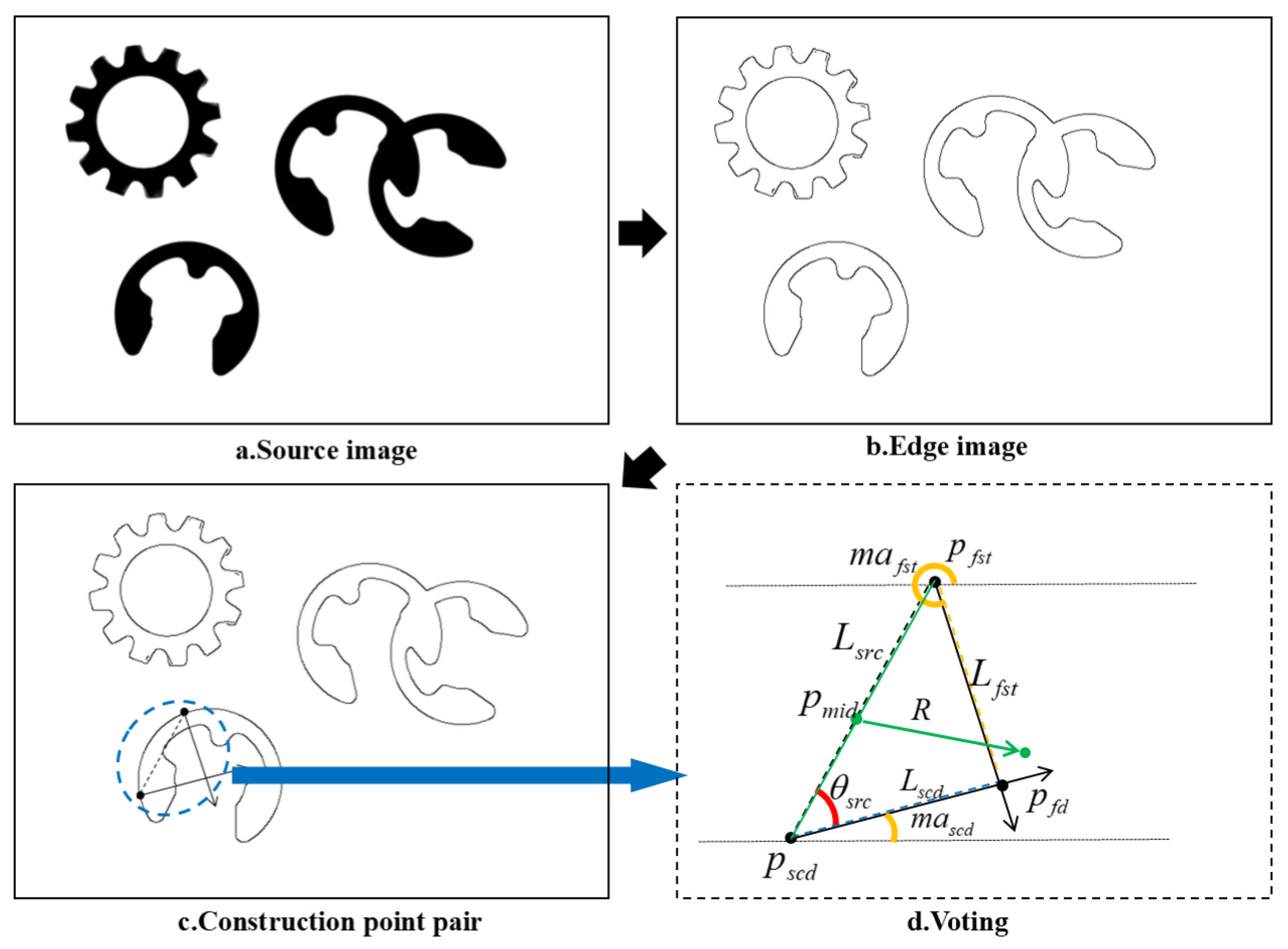
Figure 1 illustrates this two-stage workflow.

We begin by detecting edge points with an adaptive Canny filter, deriving strong and weak thresholds automatically. Next, we form point pairs from these edges and compute their gradient-difference values, which we quantize. We retain only those pairs falling in the most populated quantization bin. From these filtered pairs we extract rotation- and scale-invariant features to populate our 2-D reference table.

For each new image, we detect edges as before and index every point by its gradient direction in a lookup table. We apply an adaptive grid to select a sparse set of base points then for each base point retrieve compatible sub-points via the gradient-direction index (respecting the offline quantization bin). From each resulting pair we recompute invariant features to query the reference table and cast “fuzzy” votes (3 × 3 neighborhood) for the target center. Finally, we locate the global peak—using an integral-image speedup—to determine the object’s position.

3.1. Offline Template Construction

In the offline phase, we preprocess the template to enable rapid, robust matching in the subsequent online stage. Specifically, we first extract edge points with an adaptive Canny operator whose thresholds are set via Otsu’s method. We then screen the candidate point pairs using a two-level strategy—first by their gradient-direction difference, and then by adaptive quantization of that difference to retain only the most stable, information-rich pairs. Finally, these filtered pairs are used to populate a 2-D rotation- and scale-invariant reference table, collapsing the traditional 4-D voting space into a compact lookup structure. Together, these steps lay the foundation for high-speed, accurate matching under rotation, scale change, and partial occlusion conditions.

3.1.1. Adaptive Canny Edge Extraction

We first extract the template’s edge information using an adaptive Canny edge operator. Its dual thresholds are set automatically via Otsu’s maximum inter-class variance method: The gray level that maximizes inter-class variance becomes the strong threshold $Thr{e}_{\mathrm{strong}}$, and half of that value is used as the weak threshold $Thr{e}_{\mathrm{weak}}$. Applying the Canny operator with these thresholds yields the set of edge points $E_K=\{P_1,P_2,\dots ,P_n\}$, which are then used for subsequent point-pair screening and reference table construction.

3.1.2. Gradient-Difference-Based Point-Pair Screening

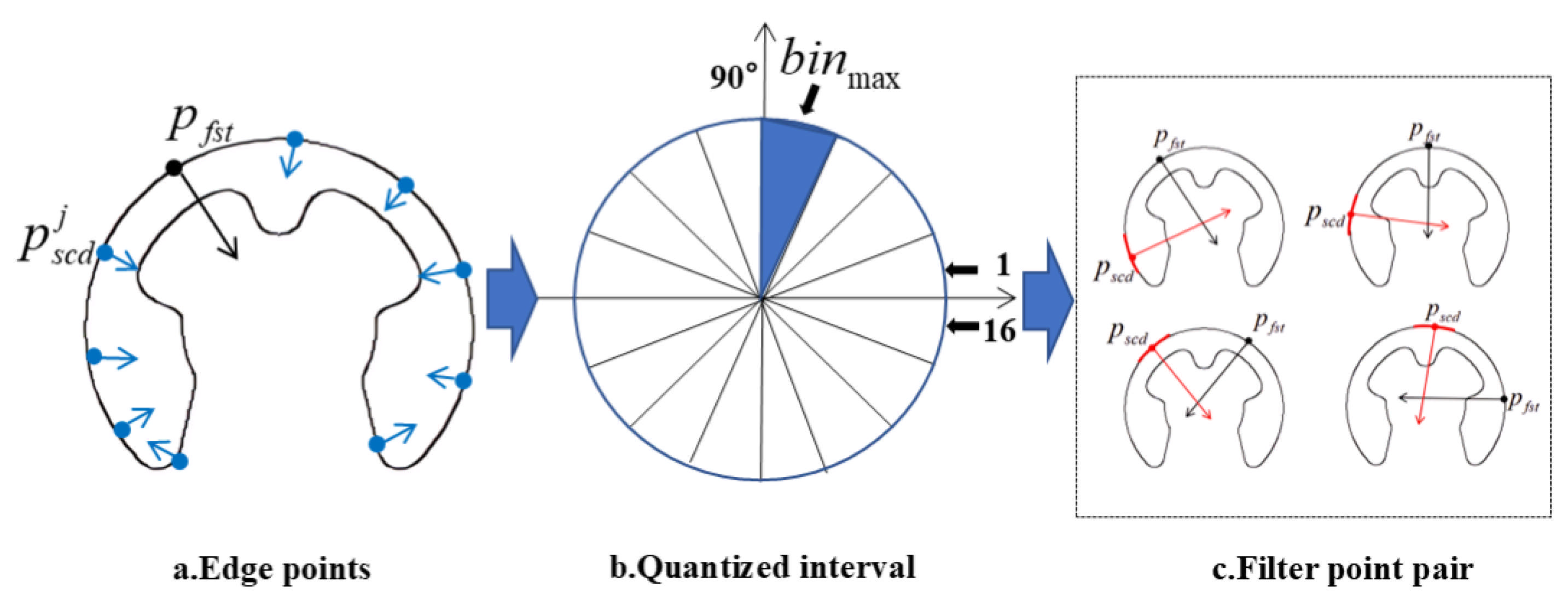
Once the edge points are extracted, they must be paired to derive rotation- and scale-invariant features. Pairing every possible combination, however, incurs heavy redundant computation and degrades matching efficiency. To address this, we constrain candidate pairs by their gradient-direction difference, retaining only those whose angular difference falls within a chosen quantization interval. This yields a sparse, yet robust, set of point pairs and substantially reduces computational load.

Specifically, after obtaining edge points from the template image, we construct the initial set of candidate point pairs. For each edge point considered as a base point, all remaining edge points are regarded as potential sub-points to form point pairs. The candidate point pair set can be formally defined as follows:

$$CP=\left\{\begin{array}{c}\{c{p}_1^2,c{p}_1^3,\dots ,c{p}_1^n\},\hfill \\ \{c{p}_2^1,c{p}_2^3,\dots ,c{p}_2^n\},\hfill \\ ⋮\hfill \\ \{c{p}_n^1,c{p}_n^2,\dots ,c{p}_n^{n-1}\}\hfill \end{array}\right\}$$

(1)

Here, $c{p}_i^j$ denotes a point pair consisting of the i-th point as the base point and the j-th point as the sub-point.

Using the gradient-direction information from the template image, the gradient directions of the base point ($m{a}_{base}$) and sub-point ($m{a}_{sub}$) are obtained, respectively. Then the gradient-direction difference ($m{a}_{diff}$) between these two points is calculated counterclockwise using the following:

$$m{a}_{diff}=(m{a}_{base}-m{a}_{sub}+360)\mathrm{mod}360$$

(2)

The gradient-direction difference is inherently rotation-invariant, so we use it to prune redundant point pairs (Figure 2). Since this difference ranges over $[0,360°)$, we divide it into quantization bins of width ${\Delta }_{\mathrm{bin}}$, yielding $\frac{360}{{\Delta }_{\mathrm{bin}}}$ discrete intervals. Only point pairs whose angular difference that falls within the most populated bin are retained.

Figure 2b highlights the quantization bin ${\mathrm{bin}}_{\max }$ that contains the largest number of gradient-difference values. We define the subset ${\mathrm{CP}}_{\mathrm{req}}$ as all point pairs whose angular differences fall into this dominant bin.

Using the full candidate set $CP$ for both reference-table construction and online matching introduces substantial redundancy and dramatically increases computation time.

To address this, we employ the adaptive bin-based screening strategy illustrated in Figure 2. By focusing solely on ${\mathrm{bin}}_{\max }$, we prune out less informative pairs while retaining enough valid point pairs for robust matching, thus achieving an effective balance between speed and stability.

3.1.3. Rotation/Scale-Invariant Reference Table Construction

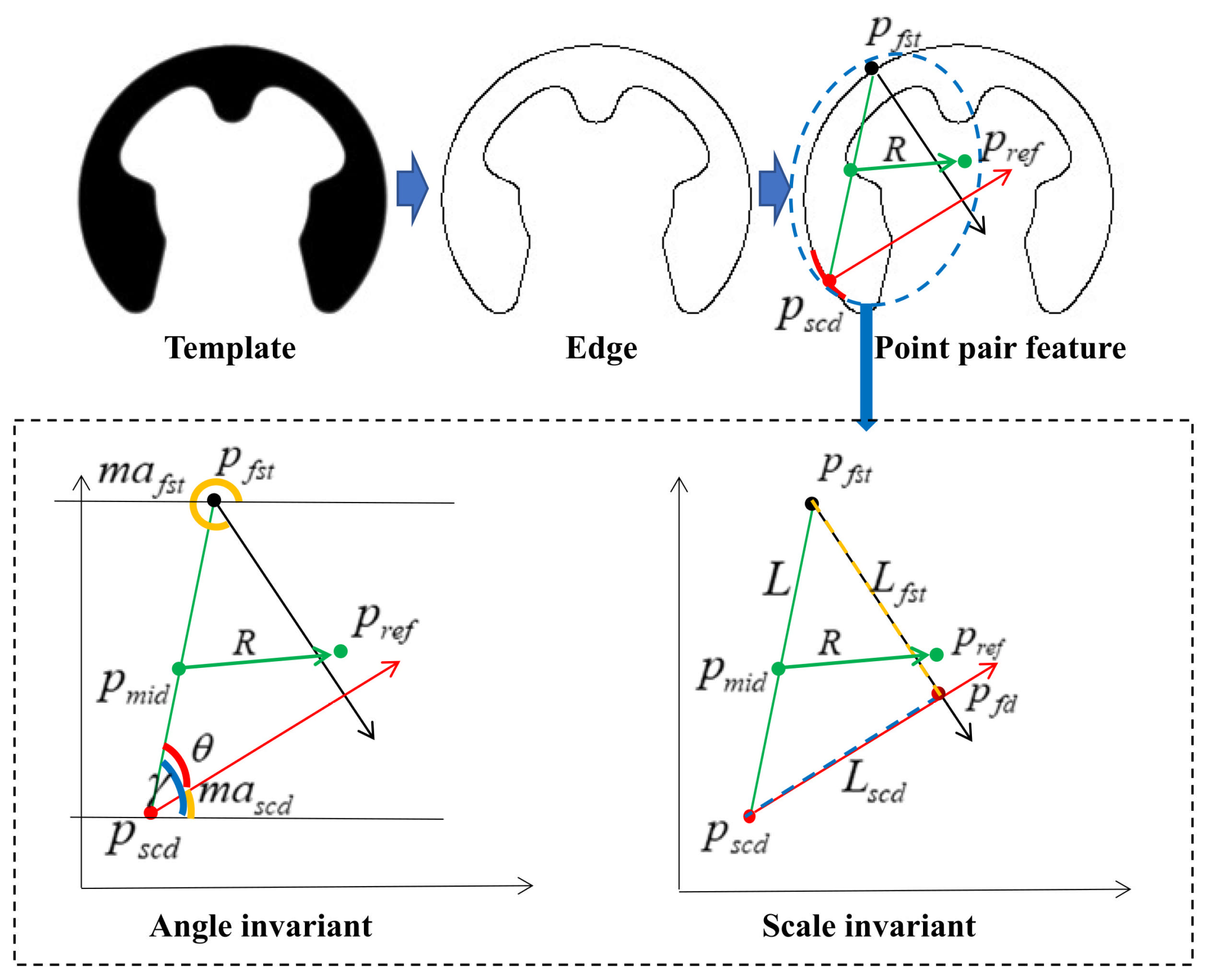
To collapse the 4-D voting space, we extract rotation- and scale-invariant descriptors from each selected point pair. Each pair forms a local triangle whose interior angle $\theta$ and side-length ratio $\varphi$ serve as the primary and secondary indices, respectively. We quantize $\theta$ and $\varphi$ into discrete bins $({\theta }_{\mathrm{index}},{\varphi }_{\mathrm{index}})$, and for each bin we record the following:

• The pair’s gradient directions $(m{a}_{\mathrm{fst}},m{a}_{\mathrm{scd}})$;
• The Euclidean length $L_j^i$ of the point pair;
• The 2-D displacement vector ${\mathbf{R}}_j^i(x,y)=\left(x_{\mathrm{ref}}-x_{\mathrm{ctr}},y_{\mathrm{ref}}-y_{\mathrm{ctr}}\right)$ from the pair’s midpoint to the template’s reference point.

The vector ${\mathbf{R}}_j^i(x,y)$ is computed as

$$R_j^i(x,y)=\mathrm{referPt}(x,y)-{\mathrm{centerPt}}_j^i(x,y)$$

(3)

where ${\mathrm{centerPt}}_j^i(x,y)$ denotes the midpoint of the $i-j$ point pair.

We use each filtered point pair to form a local triangle (Figure 3): and from the base point $P_i^{\mathrm{fst}}$ we draw a ray along its gradient direction $m{a}_{\mathrm{fst}}$, from the sub-point $P_j^{\mathrm{scd}}$ we draw another ray along its gradient direction $m{a}_{\mathrm{scd}}$ and connect $P_i^{\mathrm{fst}}$ to $P_j^{\mathrm{scd}}$ to complete the triangle. The interior angle at $P_j^{\mathrm{scd}}$, denoted $\theta$, is invariant to rotation and scale. We compute this angle as

$$\theta =\left|m{a}_{\mathrm{scd}}-\gamma \right|,$$

(4)

where

$$\gamma =\arctan \left({\displaystyle \frac{y_{P_i^{\mathrm{fst}}}-y_{P_j^{\mathrm{scd}}}}{x_{P_i^{\mathrm{fst}}}-x_{P_j^{\mathrm{scd}}}}}\right)$$

(5)

is the azimuth from $P_i^{\mathrm{fst}}$ to $P_j^{\mathrm{scd}}$. This invariant angle $\theta$ is then quantized into bins to serve as the first-level index in the reference table.

The interior angle $\theta$ is inherently rotation-invariant and thus serves as our first-level index. Since $\theta \in (0,180°)$, we quantize it into bins of width $\Delta \theta$. The resulting bin index is computed as

$${\theta }_{\mathrm{index}}=\mathrm{round}\left({\displaystyle \frac{\theta }{\Delta \theta }}\right)$$

(6)

We denote the two side lengths of the local triangle by $L_i^{\mathrm{fst}}$ and $L_j^{\mathrm{scd}}$. Their ratio

$${\mathrm{Ratio}}_L={\displaystyle \frac{L_i^{\mathrm{fst}}}{L_j^{\mathrm{scd}}}}$$

(7)

is invariant to rotation and scaling, and therefore serves as our second-level index. Quantizing this ratio into bins of size $\Delta \varphi$ yields the index

$${\varphi }_{\mathrm{index}}=\mathrm{round}\left({\displaystyle \frac{{\mathrm{Ratio}}_L}{\Delta \varphi }}\right).$$

(8)

Table 1. Reference table of improved point pair features.

${\mathit{\theta }}_{\mathit{index}}$	${\mathit{\varphi }}_{\mathit{index}}$	$\mathit{Value}$$\mathbf{(}{\mathit{ma}}_{\mathit{fst}}\mathbf{,}{\mathit{ma}}_{\mathit{scd}}\mathbf{,}{\mathit{R}}_{\mathit{j}}^{\mathit{i}}\mathbf{(}\mathit{x}\mathbf{,}\mathit{y}\mathbf{)}\mathbf{,}{\mathit{L}}_{\mathit{j}}^{\mathit{i}}\mathbf{)}$
1	1	$\{\cdots |\theta =\Delta \theta ,Rati{o}_L=\Delta \varphi \}$
1	2	$\{\cdots |\theta =\Delta \theta ,Rati{o}_L=2\Delta \varphi \}$
2	1	$\{\cdots |\theta =2\Delta \theta ,Rati{o}_L=\Delta \varphi \}$
2	2	$\{\cdots |\theta =2\Delta \theta ,Rati{o}_L=2\Delta \varphi \}$
⋮	⋮	⋮

summarizes the reference table entries, each indexed by the quantized angle and ratio bins $({\theta }_{\mathrm{index}},{\varphi }_{\mathrm{index}})$.

3.2. Online Matching Pipeline

In the online stage, we first prune the full set of edge pixels to a sparse collection of high-gradient base points via an adaptive grid, then build a gradient-direction lookup table to rapidly retrieve compatible sub-points. Next, each base–sub pair is converted into a local triangle from which rotation- and scale-invariant descriptors are computed and quantized. Finally, these quantized indices are used to fetch precomputed template descriptors for 2-D voting in an accumulator, yielding the object’s estimated center position.

3.2.1. Adaptive Grid-Filtering of Base Points

We first detect edge points

$$E_{\mathrm{source}}=\{E_K^1,E_K^2,\dots ,E_K^S\}$$

(9)

using the same adaptive Canny operator as in the offline stage, where S denotes the number of edge pixels. Recall that during template processing, we identified the gradient-difference bin ${\mathrm{bin}}_{\max }$ that contains the most point-pairs. Thus, for matching we only form and vote on target point-pairs whose gradient-direction difference lies within ${\mathrm{bin}}_{\max }$, significantly reducing unnecessary computations.

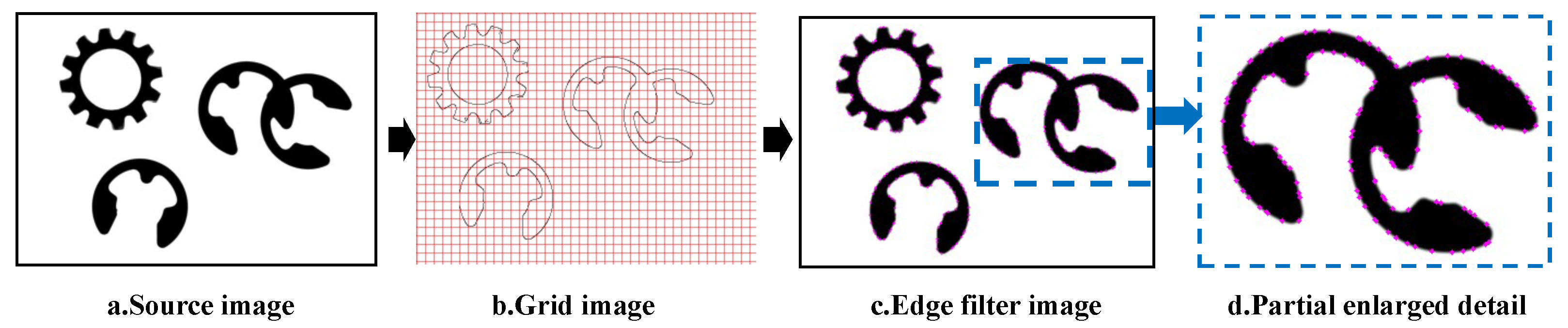
Typically, verifying whether each edge-pixel pair’s gradient-difference falls into the chosen bin ${\mathrm{bin}}_{\max }$ would require treating every edge pixel as a base point and pairing it with all others—an approach that incurs massive redundancy. To address this, we adopt an adaptive grid-filtering strategy: we overlay a grid on the image and, in each cell, select only the edge pixel with the highest gradient magnitude as a base point. By drastically reducing the number of base points, this method cuts down on unnecessary point-pair constructions and significantly accelerates the matching process.

In the online phase, we adopt an adaptive grid-filtering strategy to prune base points (Figure 4). First, we compute the grid cell size ${\mu }_{wh}$ by solving

$${\mathrm{Thre}}_{size}={\log }_2{\displaystyle \frac{\min (W_T,H_T)}{{\mu }_{wh}}}$$

(10)

where $W_T$ and $H_T$ are the template’s width and height, and ${\mathrm{Thre}}_{size}=4$. This divides the image into a $2^{{\mathrm{Thre}}_{size}}\times 2^{{\mathrm{Thre}}_{size}}$ grid. Within each cell containing edge points, only the pixel with the highest gradient magnitude is retained as a base point. Because this filtering is applied only to the target image (the offline reference table still uses all template edge points), we preserve matching completeness while dramatically cutting redundant computations and accelerating the matching process.

3.2.2. Gradient-Direction Lookup Table Construction

To avoid the costly pairwise angular comparisons, we prebuild a lookup table that indexes edge points by their gradient directions. The process is as follows:

• Quantize and bucketize. For each edge point in the target image, compute its gradient direction $m{a}_{\mathrm{src}}$ and quantize it to an integer index:    

  $$m{a}_{\mathrm{idx}}=\mathrm{round}\left(m{a}_{\mathrm{src}}\right).$$

  (11)
  Insert the point into bucket $\mathrm{Table}\left[m{a}_{\mathrm{idx}}\right]$ (see

  Table 2. Gradient-direction lookup table.

  Index	Points
  0	$p_1,p_5,p_7,\dots$
  1	$p_3,p_8,p_9,\dots$
  2	$p_2,p_4,p_6,\dots$
  ⋮	⋮
  358	$p_{12},p_{15},p_{17},\dots$
  359	$p_{11},p_{13},p_{16},\dots$

  ).
• Determine valid angular range. Given a grid-filtered base point of direction $m{a}_{\mathrm{fst}}$, compute the permissible sub-point angular interval around the precomputed bin $bi{n}_{\max }$:

  $$\left\{\begin{array}{cc}\hfill m{a}_{sub}^{left}& =bi{n}_{max}-{\displaystyle \frac{\Delta bin}{2}},\hfill \\ \hfill m{a}_{sub}^{right}& =bi{n}_{max}+{\displaystyle \frac{\Delta bin}{2}}\hfill \end{array}\right.$$

  (12)

  and thus the condition

  $$m{a}_{fst}-m{a}_{sub}^{right}<m{a}_{scd}<m{a}_{fst}-m{a}_{sub}^{left}$$

  (13)
• Lookup sub-points. Retrieve all candidate sub-points from the buckets whose indices fall in the above range, then apply a distance-based filter to enforce the expected pairwise separation.

This transforms an $O\left(N^2\right)$ angular-difference loop into a handful of constant-time hash lookups plus one distance check per candidate, dramatically accelerating point-pair construction.

3.2.3. Invariant Feature Extraction in Target Image

To ensure consistent lookup in the reference table, we replicate the same rotation- and scale-invariant descriptors in the target image. Given a filtered point pair $(P_{\mathrm{fst}}^i,P_{\mathrm{scd}}^i)\in C{P}_{\mathrm{source}}$, we proceed as follows:

• Form the local triangle. Let

  $$P_{\mathrm{mid}}^i=\frac{1}{2}\left(P_{\mathrm{fst}}^i+P_{\mathrm{scd}}^i\right).$$

  (14)
  The three vertices $\{P_{\mathrm{fst}}^i,P_{\mathrm{mid}}^i,P_{\mathrm{scd}}^i\}$ are shown in Figure 5d.
• Compute the interior angle ${\theta }_{\mathrm{src}}$.

  $${\theta }_{\mathrm{src}}=\left|m{a}_{\mathrm{scd}}-\gamma \right|,$$

  (15)

  $$\gamma =\arctan \left(y_{P_{\mathrm{fst}}^i}-y_{P_{\mathrm{scd}}^i}/x_{P_{\mathrm{fst}}^i}-x_{P_{\mathrm{scd}}^i}\right).$$

  (16)
• Quantize the angle.

  $${\theta }_{\mathrm{index}}=\mathrm{round}\left({\theta }_{\mathrm{src}}/\Delta \theta \right).$$

  (17)
• Compute the side-length ratio ${\varphi }_{\mathrm{src}}$.

  $${\varphi }_{\mathrm{src}}={\displaystyle \frac{∥P_{\mathrm{mid}}^i-P_{\mathrm{fst}}^i∥}{∥P_{\mathrm{mid}}^i-P_{\mathrm{scd}}^i∥}},$$

  (18)

  $${\varphi }_{\mathrm{index}}=\mathrm{round}\left({\varphi }_{\mathrm{src}}/\Delta \varphi \right).$$

  (19)
• Retrieve descriptors. Retrieve $\left(m{a}_{\mathrm{fst}},m{a}_{\mathrm{scd}},R_j^i,L_j^i\right)$ from RefTable[${\theta }_{\mathrm{index}},{\varphi }_{\mathrm{index}}$].

In summary, Equations (14)–(19) collectively define the rotation-invariant interior angle, the scale-invariant side-length ratio, and their quantized indices, providing the descriptors needed for efficient lookup in the subsequent voting stage.

3.2.4. Reference Table Lookup and 2-D Center Voting

Each entry in the reference table stores the displacement vector of a template point pair relative to its reference point. During matching, we retrieve this vector and use the estimated rotation ${\tau }_{\mathrm{angle}}$ and scale ${\tau }_{\mathrm{scale}}$ to map it into the target image. Given a point pair in the source image with midpoint $\left(x_{\mathrm{src}}^i,y_{\mathrm{src}}^i\right)$ and a stored displacement ${\mathbf{R}}_j^i=(x^R,y^R)$, the computed object center $\left(x_{\mathrm{src}}^r,y_{\mathrm{src}}^r\right)$ is

$$\left[\begin{array}{c}{x}_{\mathrm{src}}^r\\ y_{\mathrm{src}}^r\end{array}\right]={\tau }_{\mathrm{scale}}{R}_{\mathrm{matrix}}\left({\tau }_{\mathrm{angle}}\right)\left[\begin{array}{c}{x}^R\\ y^R\end{array}\right]+\left[\begin{array}{c}{x}_{\mathrm{src}}^i\\ y_{\mathrm{src}}^i\end{array}\right].$$

(20)

Here, ${\left[x_{\mathrm{src}}^r,y_{\mathrm{src}}^r\right]}^{\mathsf{T}}$ is the chosen center, ${\left[x^R,y^R\right]}^{\mathsf{T}}$ is the stored displacement, and ${\left[x_{\mathrm{src}}^i,y_{\mathrm{src}}^i\right]}^{\mathsf{T}}$ is the midpoint of the detected pair. The rotation matrix $R_{\mathrm{matrix}}\left({\tau }_{\mathrm{angle}}\right)$ is given by

$$R_{\mathrm{matrix}}\left({\tau }_{\mathrm{angle}}\right)=\left[\begin{array}{cc}\cos {\tau }_{\mathrm{angle}}& -\sin {\tau }_{\mathrm{angle}}\\ \sin {\tau }_{\mathrm{angle}}& \cos {\tau }_{\mathrm{angle}}\end{array}\right],$$

(21)

and the pair midpoint is

$$\left[\begin{array}{c}{x}_{\mathrm{src}}^i\\ y_{\mathrm{src}}^i\end{array}\right]=\frac{1}{2}\left(\left[\begin{array}{c}{x}_{\mathrm{fst}}^i\\ y_{\mathrm{fst}}^i\end{array}\right]+\left[\begin{array}{c}{x}_{\mathrm{scd}}^i\\ y_{\mathrm{scd}}^i\end{array}\right]\right),$$

(22)

where $\left[x_{\mathrm{fst}}^i,y_{\mathrm{fst}}^i\right]$ and $\left[x_{\mathrm{scd}}^i,y_{\mathrm{scd}}^i\right]$ are the coordinates of the base and sub-points, respectively. Each calculated $\left(x_{\mathrm{src}}^r,y_{\mathrm{src}}^r\right)$ casts a vote in the 2-D accumulator, and the global maxima correspond to the estimated object centers.

4. Experiment

4.1. Experimental Environment

We conducted experiments using 200 real RGB images (1024 × 1280) of five distinct industrial components and additionally augmented them into 1000 images with varying levels of noise, blur, occlusion, and illumination conditions. We compared our proposed algorithm against the traditional GHT, I-GHT, and LI-GHT to comprehensively evaluate its performance.

To demonstrate that our method remains reliable under the most damaging real-world conditions in industrial vision, we selected four representative interference modes—blur, noise, occlusion, and nonlinear illumination—that together encompass the dominant failure causes in our target scenario:

• Blur simulates defocus and motion blur due to vibration or rapid part movement on an assembly line.
• Noise emulates sensor readout noise and compression artifacts in low-light or high-ISO imaging.
• Occlusion reflects partial blocking of the target by fixtures, tooling, or crossing parts.
• Nonlinear illumination models specular highlights and uneven lighting from strong point sources or reflective surfaces.

These four modes were each applied at multiple severity levels (low/medium/high) to our base set of five workpiece classes (see sample images in Figure 6). Alternative distortions—such as geometric warp or scale changes—either occur far less frequently in our assembly-line setup or are already handled by the GHT’s inherent scale-invariance. By focusing on these four interference types, we ensure a fair, practical, and targeted assessment of robustness. All algorithms (GHT, I-GHT, LI-GHT, and ours) were then evaluated on the same distorted dataset and compared accordingly.

4.2. Hyperparameter Sensitivity Analysis

To quantify how each tuning parameter affects detection accuracy, we ran single-variable trials on our dataset (1000 augmented images), measuring localization precision (P) only. All other parameters were held at their default values. The results are summarized in

Table 3. Hyperparameter sensitivity: precision (P) for each tested value.

Parameter	Value	Precision (%)
${\Delta }_{\mathrm{bin}}$	2	88.5
	4	91.2
	6	90.3
$\Delta \theta$	3°	89.7
	5°	91.2
	7°	90.1
$\Delta \varphi$	0.05	89.4
	0.10	91.2
	0.15	90.0
Thre_size	3	90.5
	4	91.2
	5	90.8
Neighborhood size	$3\times 3$	91.2
	$5\times 5$	90.9

.

From Table 3, the peak precision of 91.2% occurs at

$${\Delta }_{\mathrm{bin}}=4,\Delta {\theta }^{\prime }=5°,\Delta \varphi =0.10,\mathrm{Thre}\_\mathrm{size}=4,\mathrm{NeighborhoodSize}=3\times 3,$$

which we therefore adopted as our default configuration.

4.3. Point-Pair Screening Test

Our method’s robustness depends on reliably extracting and screening edge points to form rotation- and scale-invariant point pairs. Here, we assess the stability of grid-filtered base points under increasing occlusion conditions.

Figure 7 compares base-point selection on unobstructed versus randomly occluded workpieces. Each pair shows the original image (top) and the grid-filtered base points (bottom; white = retained, red = dropped). Even with 50% of the area occluded, over 93% of the base points remain.

Table 4. Proportion of stable base points at different shading intensities.

Occlusion (%)	Stable Points (%)
0	100
10	96.8
20	94.5
30	94.1
40	94.3
50	93.7

reports the percentage of stable base points—i.e., those retained from the unobstructed reference—across occlusion levels from 0% to 50%. While stability decreases slightly as occlusion rises, it stays above 90%, demonstrating that our grid-filtering strategy effectively preserves informative edge points and filters out redundancy.

4.4. Time Consuming Test

We separately evaluated runtime efficiency for rotations (0–360°) and scales (0.5–1.5), using images sized 1408 × 1024 with single and multiple targets.

Figure 8 presents the runtime evaluation across different angle and scale intervals. Specifically, Figure 8a,b illustrate the runtime for single and multiple target matching at various angle ranges. As the angle search range increases, the computational cost of the traditional GHT method grows proportionally due to the need to create additional templates at different orientations. In contrast, the runtime of the proposed method remains stable and significantly lower, requiring approximately 15 ms for single-target localization and about 40 ms for multiple-target scenarios. This stable performance arises from the rotation and scale invariance of the extracted features, ensuring consistent runtime regardless of increasing angle search intervals.

Figure 8c,d demonstrate the runtime performance of single and multiple targets for varying scale ranges. As the scale search range expands, the runtime of all methods gradually increases. The runtime of the traditional GHT method grows most significantly due to the exponential increase in templates required. Methods such as the I-GHT and LI-GHT, which possess scale invariance, experience a relatively moderate rise in runtime. In comparison, our proposed method maintains the lowest runtime increase because the carefully selected point pairs efficiently limit redundancy, despite the gradual rise in the total number of point pairs with increased scale.

4.5. Stability Test

Stability testing primarily evaluates the robustness of each method with various types of interference commonly encountered in industrial scenarios. In real-world production lines, workpieces frequently occlude one another. Additionally, noise and blur introduced by imaging equipment, as well as nonlinear or uneven illumination caused by complex lighting conditions, are common challenges in visual localization tasks.

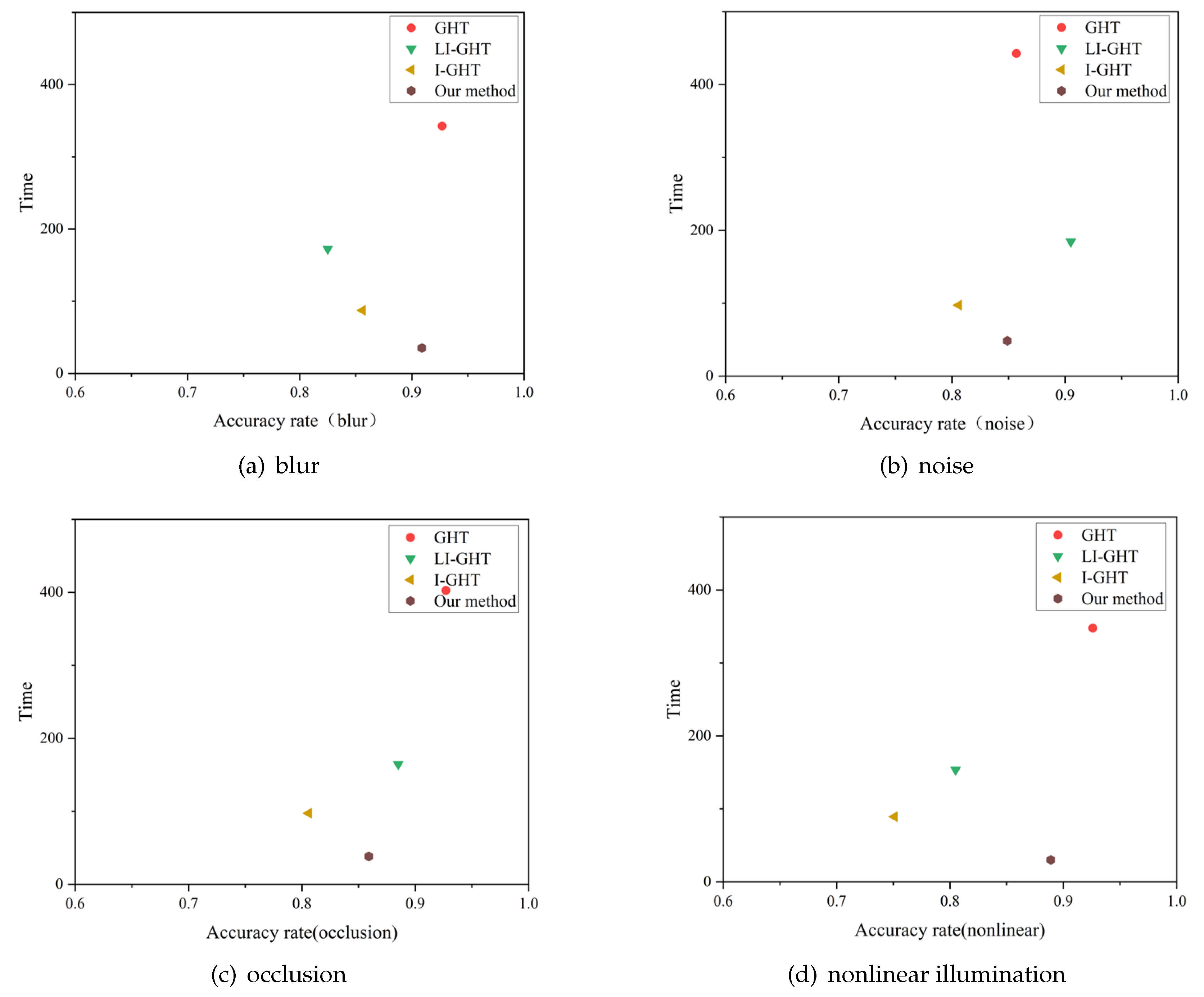
To evaluate robustness, we conducted stability tests under four representative conditions: blur, noise, occlusion, and nonlinear illumination, maintaining a controlled false detection rate (approximately 3%). For each condition, we recorded both the positioning accuracy and the runtime.

Figure 9 summarizes the performance of various methods under these interference conditions. The traditional GHT consistently achieves the highest accuracy across all conditions, maintaining around 90%. The LI-GHT performs comparably well under noise and occlusion conditions but is significantly impacted by blur and nonlinear lighting. Our proposed method, built upon the traditional GHT framework, maintains accuracy close to that of the standard GHT while being approximately 10× faster in matching and 2–3× faster than the improved GHT and LI-GHT variants.

4.6. Anti-Interference Test

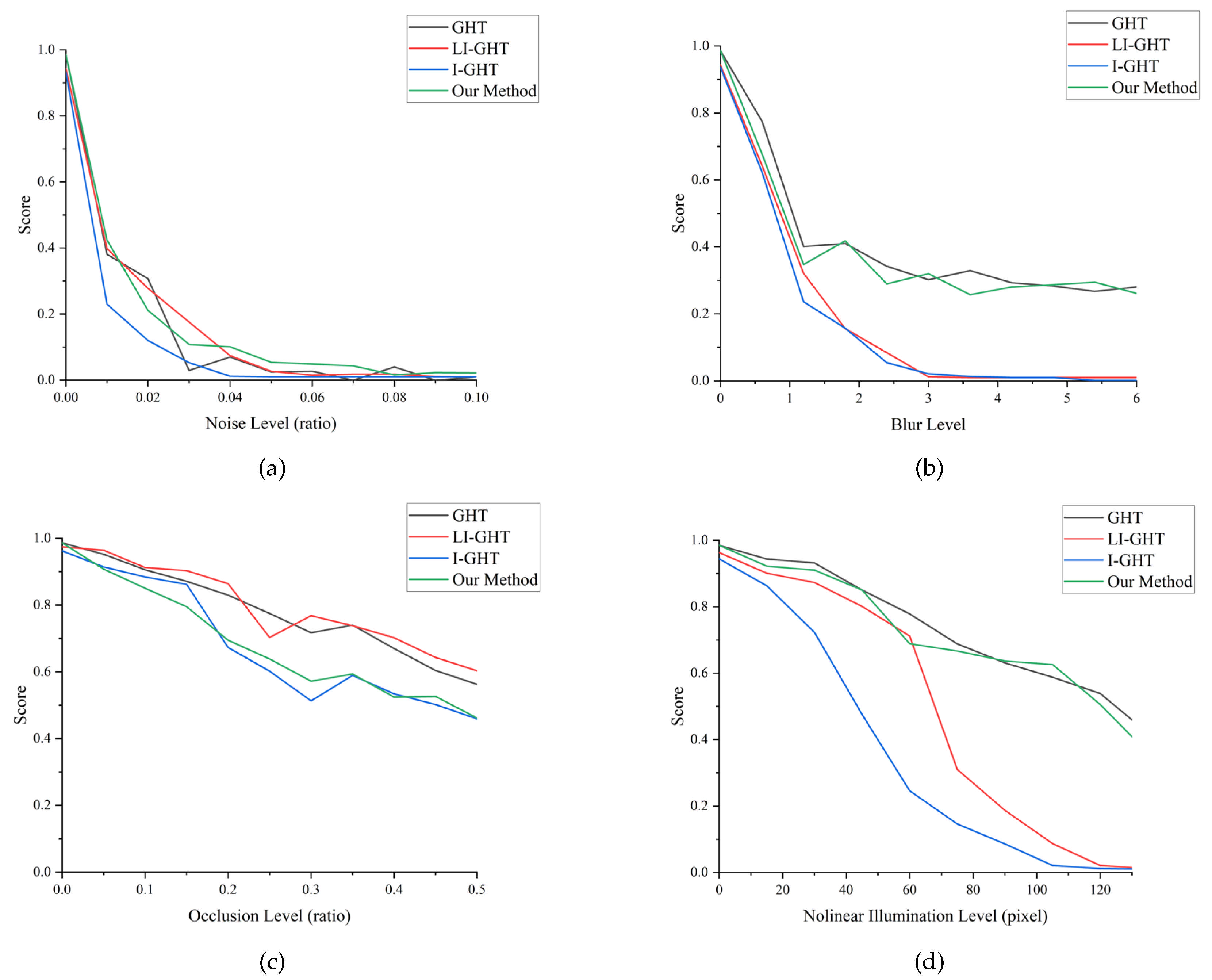
Target identification in our method is based on similarity scores obtained through matching. A high similarity score indicates a stable match, while a low score—below a predefined threshold—leads to rejection. As such, similarity scores directly influence matching accuracy. To evaluate the algorithm’s robustness, we analyzed how similarity scores at target positions change with varying levels of interference.

Figure 10 presents representative target images with four types of interference: (a) noise, (b) blur, (c) occlusion, and (d) nonlinear illumination. The corresponding similarity score variations for each scenario are summarized in Figure 11a–d.

The results in Figure 11 show that the traditional GHT exhibits strong robustness across all interference types. However, noise has the most significant impact on both the GHT and improved variants as it degrades edge quality and affects reliable matching. Despite introducing speed optimizations, our method maintains similarity scores comparable to the traditional GHT as it still leverages gradient direction and edge information during voting. This demonstrates that the proposed method achieves significant acceleration without compromising anti-interference performance.

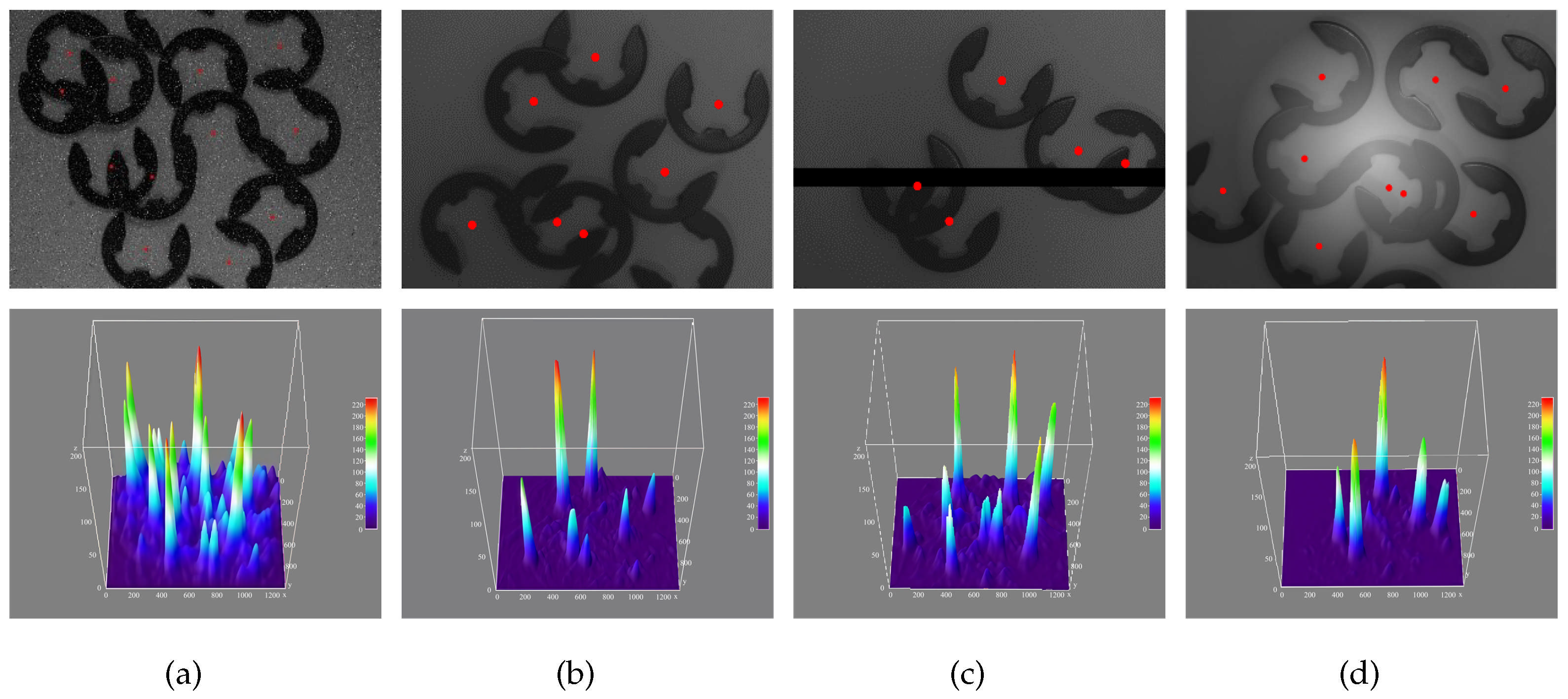
4.7. Location Result

This method uses point pair information to construct features, so it has the invariance of rotation scale change, and the positioning speed is one order of magnitude faster than that of the traditional GHT method. Additionally, our method employs the gradient direction voting, maintaining stability comparable to the traditional GHT without compromising accuracy despite significantly improved runtime. Figure 12b shows the positioning results of this method applied under different workpiece testing conditions, and Figure 12c shows the voting results of this method for different workpieces.

The method in this paper can locate different artifacts by a voting strategy through the screening points and can also detect multiple targets with different postures. Figure 13 shows the positioning results of this method under different interference conditions, and (a) to (d) are the positioning results for noise, blur, occlusion, and nonlinear illumination interference conditions and voting visualization results in turn. In the face of some interference situations, the algorithm in this paper can also maintain good positioning results.

5. Conclusions

This paper introduces a two-level point-pair screening strategy (based on gradient-difference quantization and adaptive grid-filtering) combined with a precomputed lookup mechanism, effectively collapsing the 4-D search space of the traditional GHT into a simplified 2-D voting procedure with fuzzy 3 × 3 maxima. The proposed method achieves rotation and scale invariance, operates approximately an order of magnitude faster than the traditional GHT, and maintains accuracy above 90% under various challenging conditions, including noise, occlusion, blur, and uneven illumination.

The experimental results demonstrate that the proposed method achieves rotational and scale invariance. In terms of computation time, this method significantly outperforms the traditional GHT by approximately 10 times and is 2–3 times faster than other improved methods (LI-GHT, I-GHT) while maintaining comparable accuracy (above 90%) under various interference conditions. Stability tests under various interference conditions show that our point-pair screening strategy achieves robustness comparable to the traditional GHT, confirming that the speed improvements do not compromise matching stability.

6. Future Work

While our two-level screening GHT has shown strong robustness and real-time performance under blur, noise, occlusion, and nonlinear illumination conditions, there remain several promising avenues for further research:

• Automatic hyperparameter tuning. Developing a lightweight calibration module (e.g., Bayesian optimization or gradient-free search) that can automatically select ${\Delta }_{\mathrm{bin}},\Delta \theta ,\Delta \varphi ,\mathrm{Thre}\_\mathrm{size}$, and neighborhood size for a new industrial setup.
• Multi-modal integration. Extending the pipeline to fuse RGB with depth or infrared data—this could further mitigate failure cases under extreme lighting conditions or when the target’s texture matches the background.
• Adaptive region proposal. Investigating the possibility of combining our grid-filtering with fast, learned region proposals (e.g., lightweight transformer encoders) to further prune irrelevant areas before voting.
• Embedded deployment. Porting and optimizing the lookup-table implementation for microcontroller or FPGA platforms to achieve true on-device inference without any GPUs or NPUs.
• Benchmark expansion and failure case study. Broadening evaluation to geometric distortions (e.g., viewpoint changes, scale variation) and building a public repository of “hard” examples to encourage comparison and future method development.

By pursuing these directions, we aim to further enhance both the versatility and the deployment flexibility of our accelerated GHT framework.