A Quantitative Analysis Framework for Investigating the Impact of Variable Interactions on the Dynamic Characteristics of Complex Nonlinear Systems
Abstract
1. Introduction
2. System Modeling and Dynamic Analysis
2.1. Approximate Solutions for System Responses
2.2. Nonlinearity Influence Indices
2.2.1. Fundamental Modes
2.2.2. System Response
- Nonlinear Overall Contribution Index Si
- Composite Mode Contribution Index Ir,kl
- Post-disturbance Modal Analysis: Accurate identification of dominant modes critical for stability evaluation.
- Control Design Optimization: Prioritized selection of high-impact modes for strategic improvements.
- Predictive Modeling Enhancement: Comprehensive incorporation of intermodal interactions for precise system dynamic judgment.
3. Case Study
3.1. DC Microgrid System
3.1.1. System Modeling
3.1.2. Result Analysis
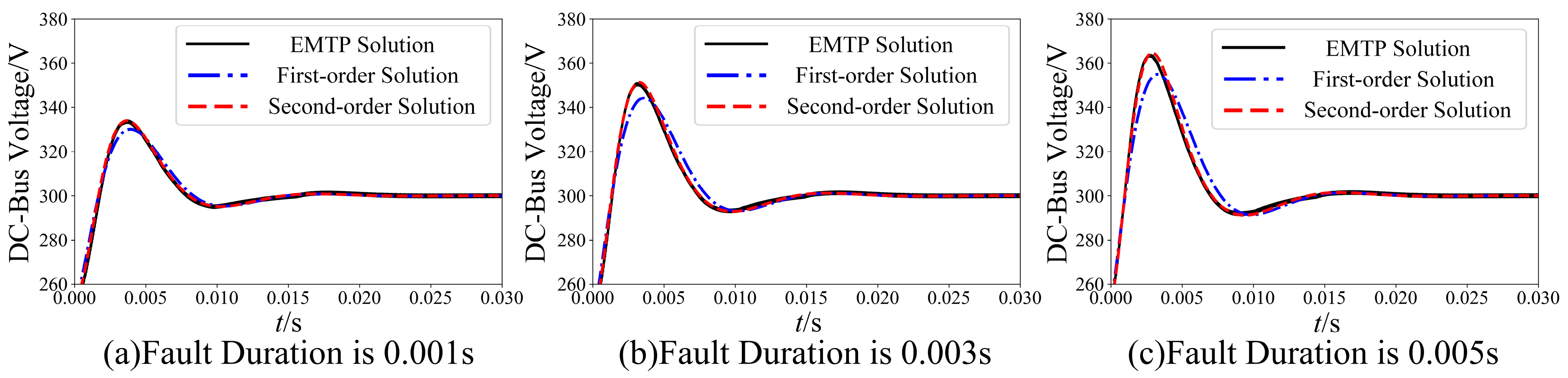
- Accuracy Analysis of Analytical Solutions
- Fixed duration with varying severity (Figure 8).
- 2.
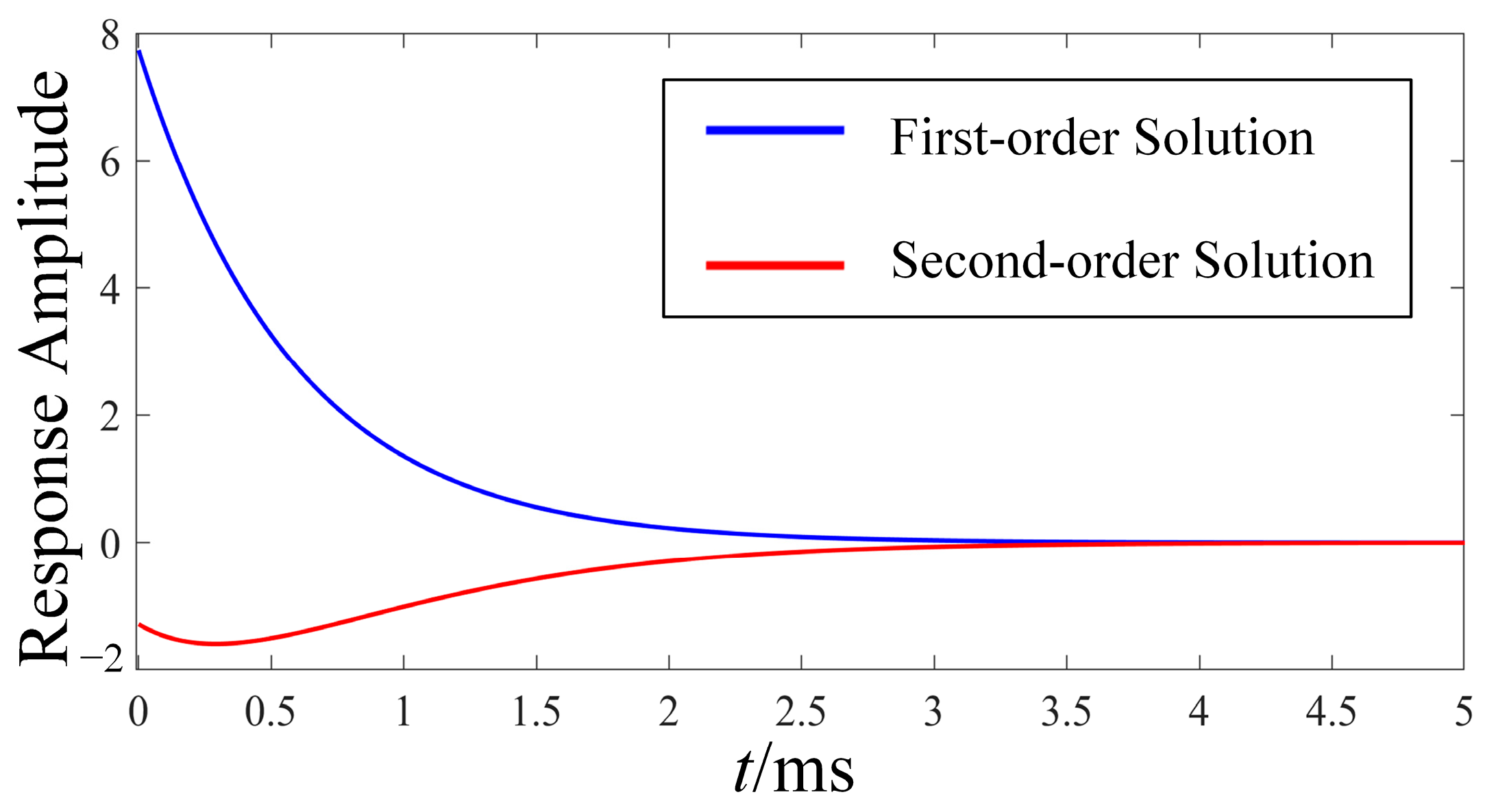
- Analysis of the Impact of Nonlinear Modal Interaction on System Response
- Divergent initial amplitude-phase characteristics of identical modes;
- Distinct state transition patterns;
- Non-negligible variations in dynamic response signatures.
- Cross-coupling between fundamental modes through pairwise combinations (e.g., λ6 + λ7, λ7 + λ8, λ8 + λ9)
- Self-coupling phenomena where individual modes interact with themselves (e.g., λ8 + λ8, λ9 + λ9)
- Reference voltage deviations activate Boost switching adjustments;
- Switching transients directly excite modes λ8 + λ9 through inductor-capacitor resonance;
- Modal energy redistribution stabilizes DC voltage fluctuations.
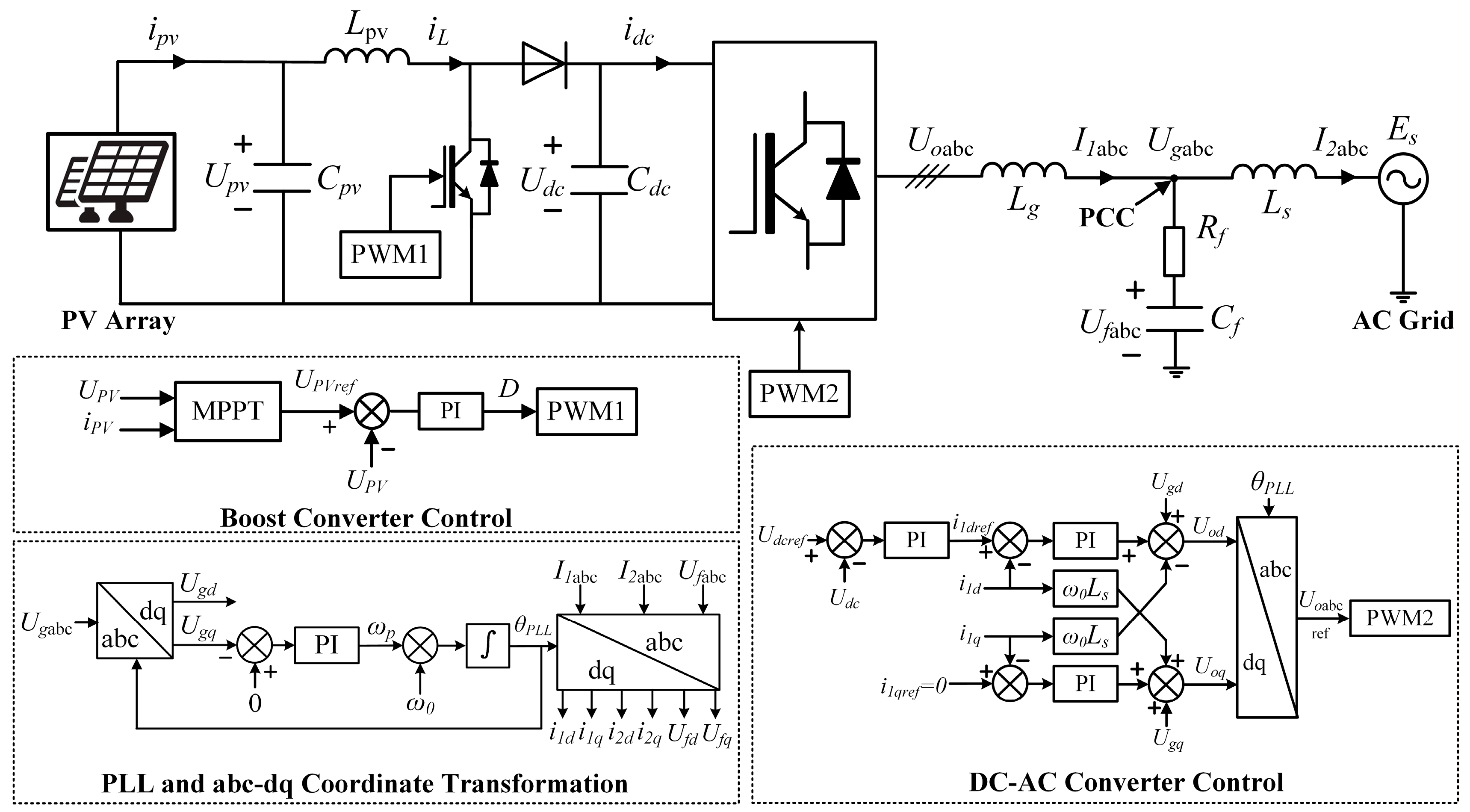
3.2. PV DC-AC System
- PV/DC Stage: xpv (boost converter integral control output); Upv (PV array voltage); iL (Lpv inductor current), Udc (DC-link voltage).
- AC Stage: i1d, i1q (inverter-side dq current); i2d, i2q (grid-side dq current); Ufd, Ufq (Cf filter capacitor voltage).
- Control States: θPLL (PLL output angle); xdc (outer-loop DC voltage control integral state); xid, xiq inner-loop current control integral state.
- DC-Link Voltage Control Dominance: Modal analysis shows that the most influential mode involves the DC-link voltage (Udc) and its integral controller state (xdc). This mode dominates transient responses during PCC faults due to its role in power balance regulation. The sudden loss of AC power output rapidly charges Cdc, while the PI controller (kpdc, kidc) struggles to restore equilibrium.
- Critical Converter Current Coupling: The secondary dominant mode links Udc with converter-side dq-currents (i1d, i1q). This reflects the interaction between DC-link dynamics and the inverter’s power injection capability.
- Significant PCC/Filter Network Dynamics: The third major mode encompasses PCC currents (i2d, i2q), filter voltages (Ufd, Ufq), and converter currents (i1d, i1q). It captures the interaction between the LCL filter’s resonant dynamics and fault-induced voltage collapse at the PCC.
- Negligible PV/Boost Dynamics and Model Reduction Opportunity: Photovoltaic states (xPV, UPV) and boost converter variables (iL) are absent from dominant modes. PV-side dynamics have minimal influence on fault-induced DC transients due to the slow response of the PV system. Consequently, the PV generation and DC-DC conversion stage can be simplified to a constant power source (PPV) or an ideal current source (iPV ≈ const) for fault stability studies, reducing computational complexity while preserving accuracy in modeling critical DC-AC interactions.
4. Conclusions
- System Nonlinear Dynamics
- Second-order solution superiority: Accurately captures multi-mode oscillations/damping distortion under 5~15% disturbances, outperforming linearization—critical for modeling fault-induced transients like rapid DC-link capacitor charging during PCC faults.
- Modal dominance inversion: Nonlinear coupling induces amplitude/phase modifications in fundamental modes, potentially reversing modal dominance hierarchies identified through linear methods.
- Composite mode emergence: Specific fundamental mode combinations (e.g., modes λ6, λ7, λ8, and λ9 in the DC microgrid system) generate composite modes that critically govern system output characteristics.
- Critical Interaction Mechanisms
- DC Microgrid Voltage Regulation: Composite modes formed by λ8 + λ8 and λ9 + λ9 regulate DC voltage through dual mechanisms: (1) boost converter switching excites LC resonance to activate modal responses, and (2) storage capacitor buffering enables energy redistribution for stabilization.
- PV System Fault Dynamics: Three dominant interactions govern PCC faults: (1) Udc-xdc coupling maintains power balance, (2) Udc-i1d/i1q synergy constrains inverter current capability, (3) LCL filter resonance (i2d/i2q-Ufd/Ufq-i1d/i1q) drives voltage collapse.
- Design Implications And Scalability
- Control System Synthesis: Requires amplitude-aware compensation for modal clusters (e.g., modes λ6, λ7, λ8, and λ9 in DC microgrid system) and adaptive gain scheduling for DC-AC converter current coupling.
- Model Reduction: PV array and Boost converter dynamics (xPV, UPV, iL) are negligible during faults, enabling replacement with constant power sources.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MSM | Model series method |
| NFM | Normal form method |
| EMTP | Electromagnetic transients program |
| MPPT | Max power point tracking |
| PCC | Point of common coupling |
Appendix A
| Parameters | Value | |
|---|---|---|
| DC-side filters | Cpv/F | 1 × 10−3 |
| Lpv/H | 3.9375 × 10−3 | |
| Cdc/F | 4296.875 × 10−6 | |
| Boost Control | kpb/p.u. | 0.0053 |
| kib/p.u. | 0.0015 | |
| fPWM1/kHz | 10 | |
| Udcref/V | 800 | |
| AC-side filters | Lg/H | 800 × 10−6 |
| Ls/H | 1 × 10−6 | |
| Cf/F | 500 × 10−6 | |
| Rf/Ω | 5 | |
| Inverter Control | kppll/p.u. | 10 |
| kipll/p.u. | 50,000 | |
| kpdc/p.u. | 0.85 | |
| kidc/p.u. | 68 | |
| kpd/p.u. | 8.657 | |
| kid/p.u. | 16.3579 | |
| kpq/p.u. | 8.657 | |
| kiq/p.u. | 16.3579 | |
| fPWM2/kHz | 10 | |
| iqref/A | 0 | |
| ω1/rad | 314 | |
References
- IRENA. Global Renewables Outlook: Energy Transformation 2050, 2020th ed.; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2020. [Google Scholar]
- Lew, D.; Bartlett, D.; Groom, A.; Jorgensen, P.; O’sUllivan, J.; Quint, R.; Rew, B.; Rockwell, B.; Sharma, S.; Stenclik, D. Secrets of Successful Integration: Operating Experience With High Levels of Variable, Inverter-Based Generation. IEEE Power Energy Mag. 2019, 17, 24–34. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, Y. Overview of the Analysis and Mitigation Methods of Electromagnetic Oscillations in Power Systems With High Proportion of Power Electronic Equipment. J. Proc. CSEE 2020, 40, 7185–7201. [Google Scholar] [CrossRef]
- Alam, S.; Al-Ismail, F.S.; Salem, A.; Abido, M.A. High-Level Penetration of Renewable Energy Sources Into Grid Utility: Challenges and Solutions. IEEE Access 2020, 8, 190277–190299. [Google Scholar] [CrossRef]
- Shu, D.; Xie, X.; Rao, H.; Gao, X.; Jiang, Q.; Huang, Y. Sub- and Super-Synchronous Interactions Between STATCOMs and Weak AC/DC Transmissions With Series Compensations. IEEE Trans. Power Electron. 2018, 33, 7424–7437. [Google Scholar] [CrossRef]
- Liu, Y.; Shuai, Z.; Li, Y.; Cheng, Y.; Shen, Z. Harmonic Resonance Modal Analysis of Multi-inverter Grid-connected Systems. J. Proc. CSEE 2017, 37, 4156–4164+4295. [Google Scholar] [CrossRef]
- Hasan, K.N.M.; Rauma, K.; Luna, A.; Candela, J.I.; Rodriguez, P. Study on harmonic resonances and damping in wind power plant. In Proceedings of the 2012 4th International Conference on Intelligent and Advanced Systems (ICIAS2012), Kuala Lumpur, Malaysia, 12–14 June 2012; pp. 418–423. [Google Scholar] [CrossRef]
- Hong, L.; Shu, W.; Wang, J.; Mian, R. Harmonic Resonance Investigation of a Multi-Inverter Grid-Connected System Using Resonance Modal Analysis. IEEE Trans. Power Deliv. 2019, 34, 63–72. [Google Scholar] [CrossRef]
- Tahim, A.P.N.; Pagano, D.J.; Lenz, E.; Stramosk, V. Modeling and Stability Analysis of Islanded DC Microgrids Under Droop Control. IEEE Trans. Power Electron. 2015, 30, 4597–4607. [Google Scholar] [CrossRef]
- Anand, S.; Fernandes, B.G. Reduced-Order Model and Stability Analysis of Low-Voltage DC Microgrid. IEEE Trans. Ind. Electron. 2013, 60, 5040–5049. [Google Scholar] [CrossRef]
- Marx, D.; Magne, P.; Nahid-Mobarakeh, B.; Pierfederici, S.; Davat, B. Large Signal Stability Analysis Tools in DC Power Systems with Constant Power Loads and Variable Power Loads—A Review. IEEE Trans. Power Electron. 2012, 27, 1773–1787. [Google Scholar] [CrossRef]
- Kabalan, M.; Singh, P.; Niebur, D. Large Signal Lyapunov-Based Stability Studies in Microgrids: A Review. IEEE Trans. Smart Grid 2017, 8, 2287–2295. [Google Scholar] [CrossRef]
- Sanchez-Gasca, J.; Vittal, V.; Gibbard, M.; Messina, A.; Vowles, D.; Liu, S.; Annakkage, U. Inclusion of higher order terms for small-signal (modal) analysis: Committee report-task force on assessing the need to include higher order terms for small-signal (modal) analysis. IEEE Trans. Power Syst. 2005, 20, 1886–1904. [Google Scholar] [CrossRef]
- Thapar, J.; Vittal, V.; Kliemann, W.; Fouad, A. Application of the normal form of vector fields to predict interarea separation in power systems. IEEE Trans Power Syst. 1997, 12, 844–850. [Google Scholar] [CrossRef]
- Pariz, N.; Shanechi, H.; Vaahedi, E. Explaining and validating stressed power systems behavior using modal series. IEEE Trans. Power Syst. 2003, 18, 778–785. [Google Scholar] [CrossRef]
- Shanechi, H.; Pariz, N.; Vaahedi, E. General nonlinear modal representation of large scale power systems. IEEE Trans. Power Syst. 2003, 18, 1103–1109. [Google Scholar] [CrossRef]
- Wu, F.; Wu, H.; Han, Z.; Gan, D. Comparison between methods for power system nonlinear modal analysis. J. Proc. CSEE 2007, 34, 19–25. [Google Scholar]
- Rodríguez, O.; Medina, A.; Andersson, G. Closed-form analytical characterisation of non-linear oscillations in power systems incorporating unified power flow controller. IET Gener. Transm. Distrib. 2015, 9, 1019–1032. [Google Scholar] [CrossRef]
- Zhang, H.; Yi, C.; Wei, T. Non-linear modal analysis of transient interaction behaviours in SEPIC DC–DC converters. IET Power Electron. 2017, 10, 1190–1199. [Google Scholar] [CrossRef]
- Zeinali, R.; Ghazi, R.; Pariz, N. Nonlinear interaction problems of large capacity wind farms. In Proceedings of the Iranian Conference of Smart Grids, Tehran, Iran, 24–25 May 2012; pp. 1–6. [Google Scholar]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Buragohain, U.; Mir, A.S.; Senroy, N. Transient Stability Assessment of a DFIG-WTG System Using Trajectory Sensitivity Analysis. IEEE Trans. Power Syst. 2024, 39, 5818–5828. [Google Scholar] [CrossRef]

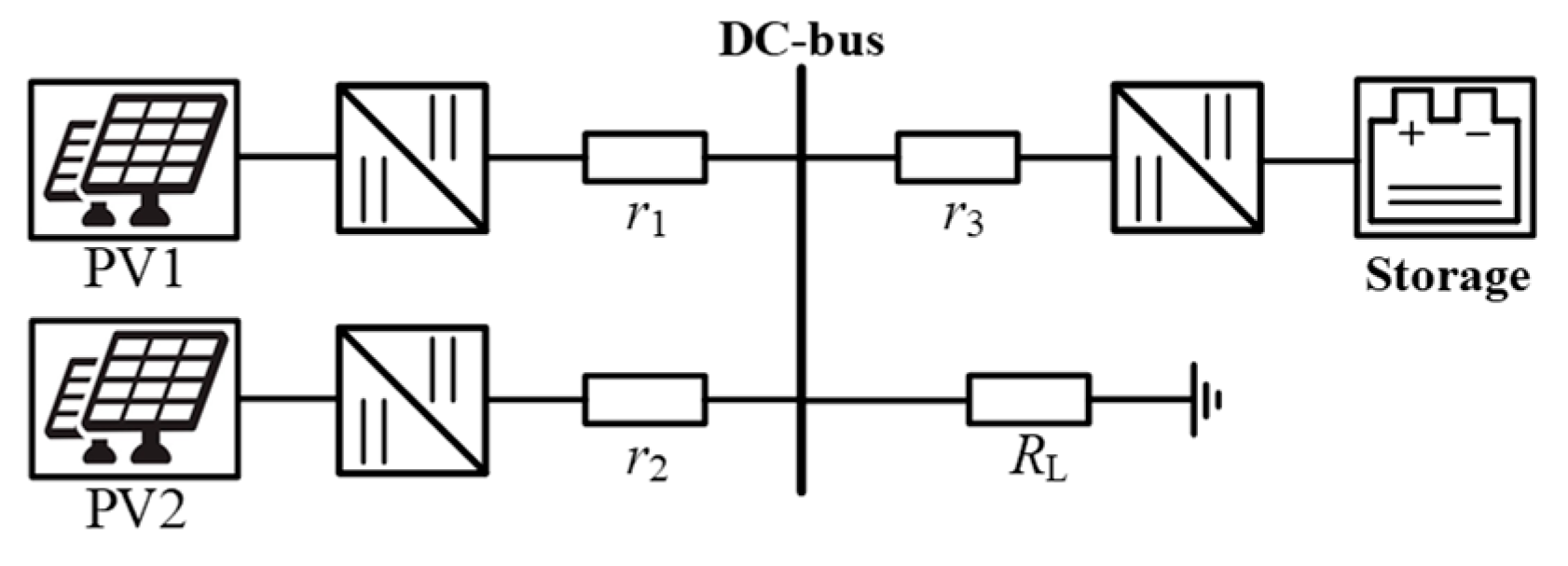







| Parameters | PV1 | PV2 | |
|---|---|---|---|
| Filter | Cpv/mF | 0.3 | 0.5 |
| Lc/mH | 1.5 | 2 | |
| Cc/mF | 0.5 | 0.8 | |
| Line Resistance | r1,2/mΩ | 0.4 | 0.5 |
| Control System | kPc | 0.05 | 0.05 |
| kIc | 5 | 5 | |
| Parameters | Value | Parameters | Value | ||
|---|---|---|---|---|---|
| Filter | Cv/mF | 3 | Battery Voltage | Us/V | 200 |
| Lv/mH | 1.5 | Control System | kPv | 0.01 | |
| Voltage Reference | Uoref/V | 300 | kIv | 10 | |
| Line Resistance | r3/mΩ | 0.5 | Rv | 0.02 | |
| Disturbance Magnitude/% | 2.34 | 5.305 | 7.162 | 12.833 |
| First-order Error/% | 9.523 | 11.506 | 14.046 | 15.879 |
| Second-order Error/% | 3.856 | 5.221 | 6.284 | 7.539 |
| Disturbance Magnitude/% | 15.253 | 18.985 | 23.418 | 25.524 |
| First-order Error/% | 20.682 | 22.789 | 26.357 | 30.143 |
| Second-order Error/% | 12.233 | 14.755 | 19.406 | 24.484 |
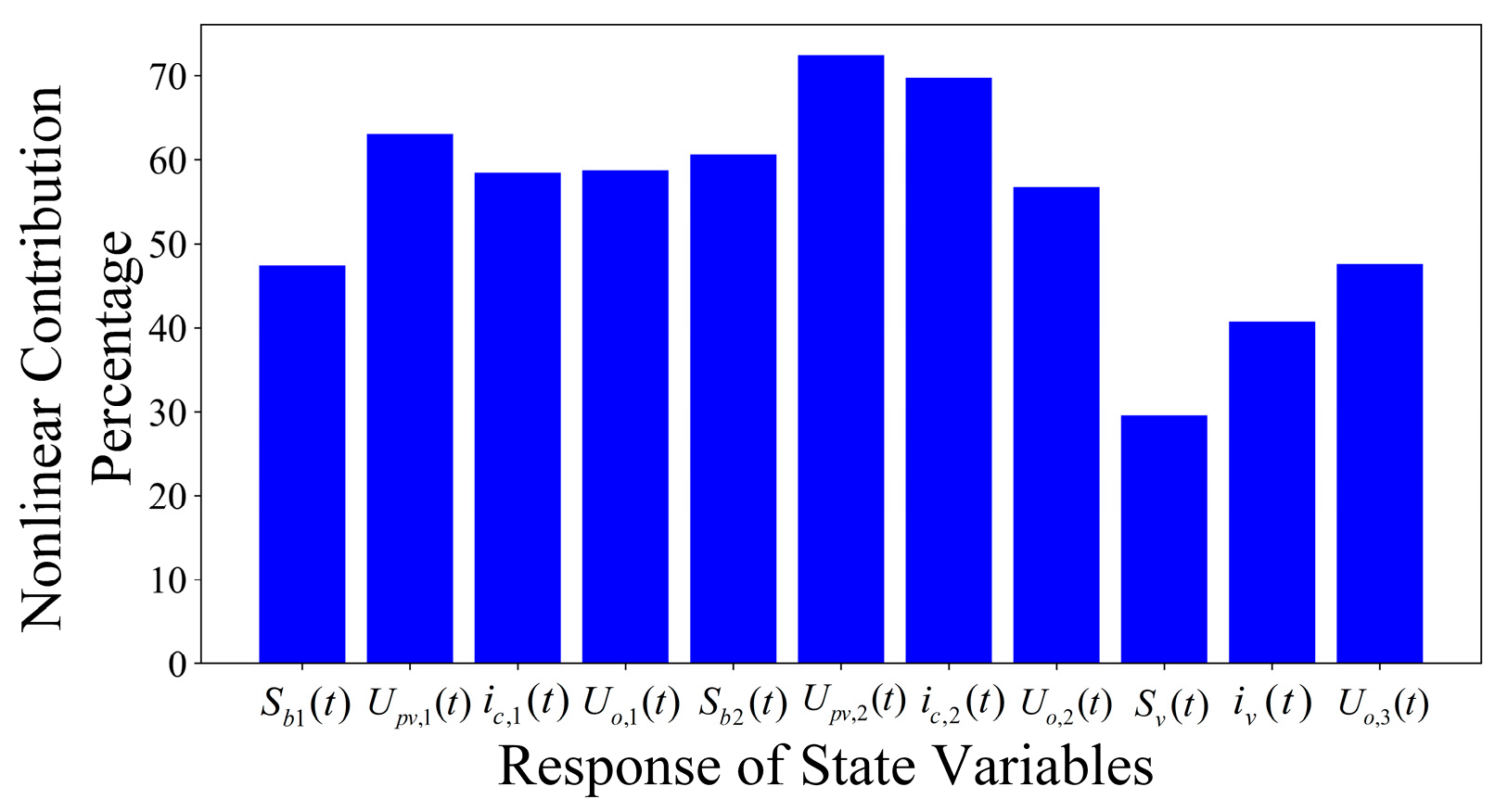
| Fundamental Modal Number | Eigenvalue | State Variable with High Degree of Participation | Disturbance Magnitude 5.305/% | Disturbance Magnitude 15.253/% | Disturbance Magnitude 20.524/% | |||
|---|---|---|---|---|---|---|---|---|
| |I1,j|/p.u. | θj/rad | |I1,j|/p.u. | θj/rad | |I1,j|/p.u. | θj/rad | |||
| λ1,2 | −2512.83 ± 2791.91i | Upv,1, ic,1 | 1.0402 | ∓0.4127 | 1.0446 | ∓0.4734 | 1.0011 | ∓0.2400 |
| λ3 | −4141.43 | Uo,1 | 1.6349 | 2.2721 | 2.3929 | |||
| λ4,5 | −3084.30 ± 1831.27i | Upv,2, ic,2 | 2.0029 | ∓0.6730 | 2.9383 | ∓1.0300 | 2.3255 | ∓1.3313 |
| λ6,7 | −1782.69 ± 230.847i | Uo,2, iv, ic,2 | 1.1911 | ±1.5024 | 2.5805 | ±1.9125 | 4.0171 | ±1.9594 |
| λ8,9 | −124.617 ± 570.608i | Sv, iv, Uo,3 | 1.0481 | ±0.0222 | 1.0209 | ±0.0658 | 0.9734 | ±0.1225 |
| λ10 | −48.332 | Sb1 | 0.9473 | 0.9138 | 0.8832 | |||
| λ11 | −98.630 | Sb2 | 0.8881 | 0.7992 | 0.7023 | |||
| Fundamental Mode Pair (λk + λl) | Eigenvalue Sum | N2,ikl | Ir,kl | |
|---|---|---|---|---|
| Amplitude/V | Amplitude Percentage/p.u. | |||
| 8 + 8 | −249.3 + 1141.0i | 10.638 | 18.09 | 0.0481 |
| 9 + 9 | −249.3 − 1141.0i | |||
| 7 + 8 | −1906.0 + 338.5i | 27.734 | 47.17 | 0.0161 |
| 6 + 9 | −1906.0 − 338.5i | |||
| 8 + 9 | −249.3 | 1.711 | 2.90 | 0.0076 |
| 6 + 8 | −1906.0 + 802.8i | 11.526 | 19.60 | 0.0067 |
| 7 + 9 | −1906.0 − 802.8i | |||
| 6 + 7 | −3563 | 5.163 | 8.78 | 0.0016 |
| 6 + 6 | −3563.0 + 464.2i | 2.021 | 3.44 | 0.00063 |
| 7 + 7 | −3563.0 − 464.2i | |||
| Fundamental Mode Pair (λk + λl) | State Variable with High Degree of Participation | N2,ikl | Ir,kl | |
|---|---|---|---|---|
| Amplitude/V | |Re(λk + λl)| | |||
| 9 + 9/10 + 10 | Udc, xdc | 14.34 | 114.42 | 0.1478 |
| 5 + 9/6 + 10 | Udc, xdc, i1d, i1q, i2d, i2q | 8.21 | 382.53 | 0.0239 |
| 5 + 10/6 + 9 | 7.14 | 382.53 | 0.0207 | |
| 5 + 14/6 + 15 | i1d, i1q, i2d, i2q, Ufd, Ufq | 2.19 | 621.36 | 0.0039 |
| 5 + 15/6 + 14 | 1.12 | 621.36 | 0.0020 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Liu, C.; Su, C. A Quantitative Analysis Framework for Investigating the Impact of Variable Interactions on the Dynamic Characteristics of Complex Nonlinear Systems. Electronics 2025, 14, 2902. https://doi.org/10.3390/electronics14142902
Tang Y, Liu C, Su C. A Quantitative Analysis Framework for Investigating the Impact of Variable Interactions on the Dynamic Characteristics of Complex Nonlinear Systems. Electronics. 2025; 14(14):2902. https://doi.org/10.3390/electronics14142902
Chicago/Turabian StyleTang, Yiming, Chongru Liu, and Chenbo Su. 2025. "A Quantitative Analysis Framework for Investigating the Impact of Variable Interactions on the Dynamic Characteristics of Complex Nonlinear Systems" Electronics 14, no. 14: 2902. https://doi.org/10.3390/electronics14142902
APA StyleTang, Y., Liu, C., & Su, C. (2025). A Quantitative Analysis Framework for Investigating the Impact of Variable Interactions on the Dynamic Characteristics of Complex Nonlinear Systems. Electronics, 14(14), 2902. https://doi.org/10.3390/electronics14142902





