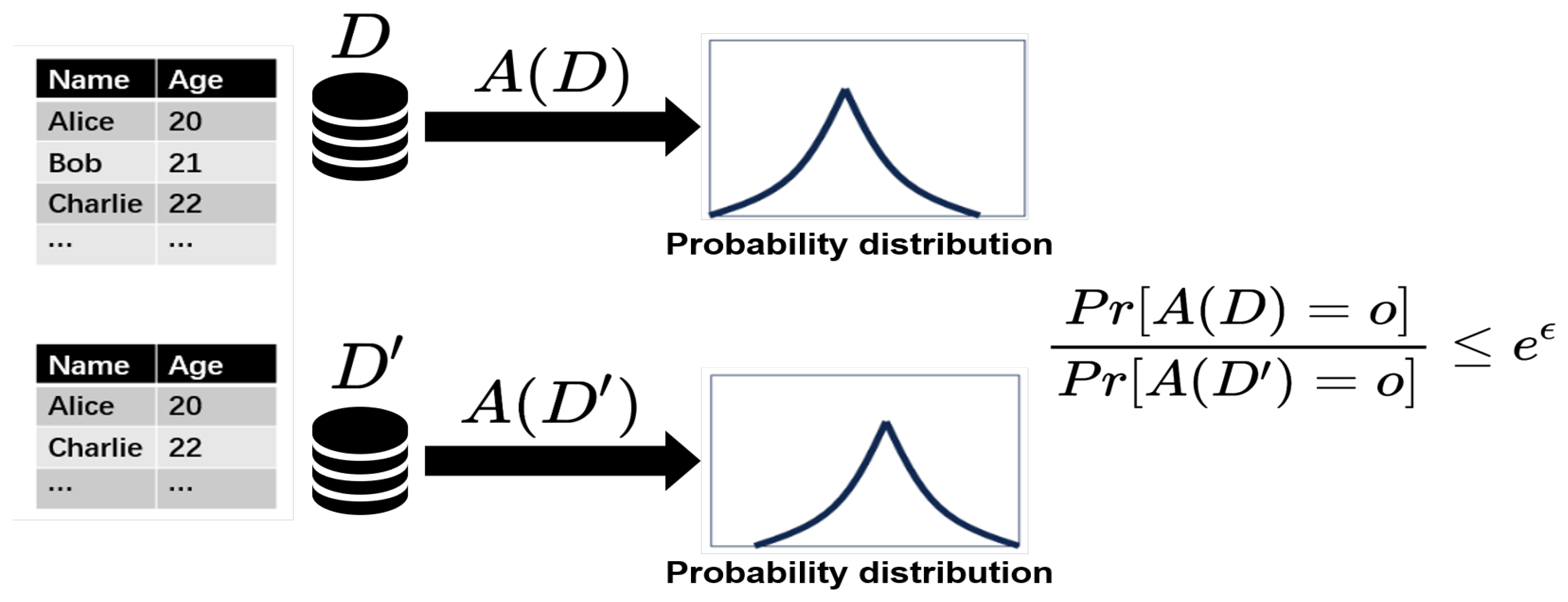
Appendix A.2. Hyperparameter Selection
In this section, we focus on supplementing the hyperparameter selection strategy. We mainly analyze and in Formula (7), the privacy budget , and the relaxation parameter .
The selection of requires balancing the rate of privacy budget decay with the stability of model convergence. A value that is too large may cause the budget to deplete rapidly, introducing excessive noise; a value that is too small may result in decay occurring too slowly, failing to meet later privacy requirements. primarily ensures that the gradient weights of clients participating for the first time are not affected by decay. Its decay logic is primarily implemented using exponential decay, achieving the principle that “the longer the delay, the lower the weight.”
The choice of must match the dataset complexity and privacy requirements. For example, simple datasets (e.g., MNIST) are robust to noise, and is sufficient for convergence; in contrast, complex datasets (e.g., CIFAR100) require to avoid noise interference. The choice of follows the “low probability of failure” principle to avoid individual information being identified separately. For example, CIFAR100 contains 60,000 samples, and 1.7 × 10−5, so setting it to 1 × 10−5 meets the safety constraints.
Based on the above selection strategy,
Table A2 shows the hyperparameter tuning process, value basis, and effect comparison for CIFAR100 (Transformer model), covering different scenario requirements.
Table A2.
Hyperparameter tuning process and comparative analysis for CIFAR100 (Transformer).
Table A2.
Hyperparameter tuning process and comparative analysis for CIFAR100 (Transformer).
| Scenario Requirement | | | | | Accuracy | Convergence Rounds |
|---|
| Unoptimized Baseline | 0.1 | 1 | 10 | 1 × 10−5 | 58.23 | 60 |
| High-Privacy | 0.15 | 1 | 5 | 1 × 10−6 | 54.55 | 75 |
| Balanced | 0.1 | 1 | 10 | 1 × 10−5 | 62.34 | 55 |
| High-Utility | 0.08 | 1 | 20 | 1 × 10−5 | 65.82 | 45 |
| Unstable Network | 0.1 | 1 | 10 | 1 × 10−5 | 61.55 | 58 |
Based on the aforementioned selection strategy,
Table A2 presents the hyperparameter tuning process, value selection criteria, and performance comparisons for the CIFAR100 dataset using the Transformer model, covering various scenario requirements.
Based on the data in the table, we can summarize the following:
(1) In the baseline scenario, default values are selected based on theoretical constraints, resulting in moderate model accuracy; however, privacy risks and convergence speed are not aligned with the scenario requirements.
(2) In the high-privacy scenario, strict control of privacy leakage is required (e.g., medical image data), so is increased, and and are decreased to ensure “privacy first”;
(3) In the balanced scenario, , , and = 1 × 10−5 make the algorithm more general;
(4) In the high-utility scenario, non-sensitive data can relax privacy constraints, so reducing and increasing reduces noise interference, ensuring controllable risks and maximum efficiency;
(5) In the unstable network scenario, due to high network latency, adjust from 0.1 to 0.9 to avoid frequent discarding of valid gradients.
Appendix A.3. Actual Deployment Analysis
We can analyze the adaptability of ADP-FL on real devices from the experimental computational complexity results in
Table 5:
1. Client computing power requirements: In simulation experiments, the training time for a single client ranged from 22 to 295 min (depending on the dataset), but the computing power of actual edge devices (such as smartphones and IoT sensors) is typically lower than that of experimental servers. Further optimization can be achieved through model lightweighting (e.g., pruning, quantization). For example, after compressing the model parameters of VGG9 by half, we observed an approximately 40% reduction in simulation time on CIFAR10 through testing. We speculate that ADP-FL meets real-time requirements on mainstream chips in mobile devices.
2. Server load: In simulation experiments, the aggregation time for 50 clients was less than 1 s. Based on linear scaling, supporting 1000 clients would result in an aggregation time of approximately 20 s, which aligns with the concurrent processing capabilities of cloud servers.
3. Weak network adaptation: If a client fails to upload gradients due to network interruption, the lag-based sparse reset mechanism enables it to reconnect without requiring retraining from scratch.
4. Communication Volume: Taking the VGG9 model as an example, the gradient of the VGG9 model is approximately 1.2 MB per client, which aligns with real-world usage scenarios. Additionally, in actual deployment, gradient sparsification can be employed to reduce the communication volume further.
Based on the simulation results analyzing computational time and communication volume, our algorithm is feasible for practical deployment.
Appendix A.4. Multi-Metric Performance Analysis
In this section, we have added multiple metrics, including precision, recall, and F1 score, to analyze the algorithm’s performance.
Table A3,
Table A4 and
Table A5 compares precision, recall, and F1-Score under different privacy budgets.
Table A6 and
Table A7 compare metrics under the Laplace mechanism and the Gaussian mechanism.
Under both the Gaussian mechanism and the Laplace mechanism, the ADP-FL algorithm outperforms the Baseline algorithm in most scenarios, particularly demonstrating consistent advantages in precision, recall, and F1 scores, thereby validating the effectiveness of its “dynamic adjustment of privacy budget + weighted aggregation” strategy.
Table A3.
Precision of baseline and ADP-FL algorithms under different privacy budgets .
Table A3.
Precision of baseline and ADP-FL algorithms under different privacy budgets .
| Algorithm | MNIST | CIFAR10 | CIFAR100 | EMNIST |
|---|
| Non | 86.92 | 55.76 | 53.62 | 66.89 |
| Baseline | 50.87 | Nan | Nan | Nan |
| Baseline | 85.89 | 56.43 | 52.83 | 65.01 |
| Baseline | 85.93 | 61.78 | 61.02 | 63.78 |
| ADP-FL | 65.98 | Nan | Nan | Nan |
| ADP-FL | 87.05 | 53.92 | 52.31 | 64.23 |
| ADP-FL | 91.98 | 63.42 | 60.65 | 69.12 |
Table A4.
Recall of baseline and ADP-FL algorithms under different privacy budgets .
Table A4.
Recall of baseline and ADP-FL algorithms under different privacy budgets .
| Algorithm | MNIST | CIFAR10 | CIFAR100 | EMNIST |
|---|
| Non | 87.15 | 55.92 | 53.85 | 67.12 |
| Baseline | 51.22 | Nan | Nan | Nan |
| Baseline | 86.11 | 56.78 | 53.05 | 65.32 |
| Baseline | 86.18 | 62.03 | 61.25 | 64.05 |
| ADP-FL | 66.51 | Nan | Nan | Nan |
| ADP-FL | 87.32 | 54.21 | 52.54 | 64.51 |
| ADP-FL | 92.27 | 63.71 | 60.88 | 69.43 |
Table A5.
F1-Score of baseline and ADP-FL algorithms under different privacy budgets .
Table A5.
F1-Score of baseline and ADP-FL algorithms under different privacy budgets .
| Algorithm | MNIST | CIFAR10 | CIFAR100 | EMNIST |
|---|
| Non | 87.03 | 55.84 | 53.73 | 67.00 |
| Baseline | 51.04 | Nan | Nan | Nan |
| Baseline | 85.99 | 56.60 | 52.94 | 65.16 |
| Baseline | 86.05 | 61.90 | 61.13 | 63.91 |
| ADP-FL | 66.24 | Nan | Nan | Nan |
| ADP-FL | 87.18 | 54.06 | 52.42 | 64.37 |
| ADP-FL | 92.12 | 63.56 | 60.76 | 69.27 |
Table A6.
Performance metrics of baseline and ADP-FL algorithms under Gaussian mechanism.
Table A6.
Performance metrics of baseline and ADP-FL algorithms under Gaussian mechanism.
| Dataset | Algorithm | | Precision | Recall | F1-Score |
|---|
| MNIST | Baseline | 10 | 72.98 | 73.25 | 73.11 |
| ADP-FL | 10 | 74.56 | 74.89 | 74.72 |
| Baseline | 20 | 85.37 | 85.68 | 85.52 |
| ADP-FL | 20 | 86.45 | 86.78 | 86.61 |
| Baseline | 30 | 81.82 | 82.15 | 81.98 |
| ADP-FL | 30 | 81.76 | 82.09 | 81.92 |
| Baseline | 40 | 82.80 | 83.13 | 82.96 |
| ADP-FL | 40 | 84.41 | 84.74 | 84.57 |
| Baseline | 50 | 79.78 | 80.11 | 79.94 |
| ADP-FL | 50 | 80.10 | 80.43 | 80.26 |
| CIFAR10 | Baseline | 10 | 27.25 | 27.58 | 27.41 |
| ADP-FL | 10 | 27.51 | 27.84 | 27.67 |
| Baseline | 20 | 40.65 | 40.98 | 40.81 |
| ADP-FL | 20 | 41.91 | 42.24 | 42.07 |
| Baseline | 30 | 48.10 | 48.43 | 48.26 |
| ADP-FL | 30 | 49.61 | 49.94 | 49.77 |
| Baseline | 40 | 47.18 | 47.51 | 47.34 |
| ADP-FL | 40 | 45.84 | 46.17 | 46.00 |
| Baseline | 50 | 50.90 | 51.23 | 51.06 |
| ADP-FL | 50 | 53.06 | 53.39 | 53.22 |
| CIFAR100 | Baseline | 10 | 29.61 | 29.94 | 29.77 |
| ADP-FL | 10 | 32.51 | 32.84 | 32.67 |
| Baseline | 20 | 42.65 | 42.98 | 42.81 |
| ADP-FL | 20 | 46.08 | 46.41 | 46.24 |
| Baseline | 30 | 47.95 | 48.28 | 48.11 |
| ADP-FL | 30 | 45.61 | 45.94 | 45.77 |
| Baseline | 40 | 46.57 | 46.90 | 46.73 |
| ADP-FL | 40 | 47.84 | 48.17 | 48.00 |
| Baseline | 50 | 50.93 | 51.26 | 51.09 |
| ADP-FL | 50 | 53.06 | 53.39 | 53.22 |
| EMNIST | Baseline | 10 | 88.01 | 88.34 | 88.17 |
| ADP-FL | 10 | 89.98 | 90.31 | 90.14 |
| Baseline | 20 | 96.65 | 96.98 | 96.81 |
| ADP-FL | 20 | 97.23 | 97.56 | 97.39 |
| Baseline | 30 | 97.55 | 97.88 | 97.71 |
| ADP-FL | 30 | 96.76 | 97.09 | 96.92 |
| Baseline | 40 | 97.35 | 97.68 | 97.51 |
| ADP-FL | 40 | 97.50 | 97.83 | 97.66 |
| Baseline | 50 | 97.90 | 98.23 | 98.06 |
| ADP-FL | 50 | 98.41 | 98.74 | 98.57 |
Under the Gaussian mechanism, the advantage of ADP-FL is more stable, outperforming the Baseline in most scenarios (e.g., F1 score of 53.22 for CIFAR10 with , compared to 51.06 for the Baseline), especially under high privacy budgets (), where the optimization effect on complex datasets is more pronounced. This is due to the continuity of Gaussian noise, which is more suitable for ADP-FL’s dynamic budget adjustment strategy. In the Laplace mechanism, performance fluctuates significantly. In some scenarios, ADP-FL performs worse than the baseline (e.g., EMNIST with an F1 score of 95.24, baseline 98.04), but it shows significant optimization for CIFAR100 in the = 30–40 range (F1 improvement of 6.4%). This is related to the discreteness of Laplace noise, which can introduce local biases during dynamic budget allocation.
Table A7.
Performance metrics of baseline and ADP-FL algorithms under Laplace mechanism.
Table A7.
Performance metrics of baseline and ADP-FL algorithms under Laplace mechanism.
| Dataset | Algorithm | | Precision | Recall | F1-Score |
|---|
| MNIST | Baseline | 10 | 80.48 | 80.81 | 80.64 |
| ADP-FL | 10 | 82.28 | 82.61 | 82.44 |
| Baseline | 20 | 81.81 | 82.14 | 81.97 |
| ADP-FL | 20 | 80.42 | 80.75 | 80.58 |
| Baseline | 30 | 82.36 | 82.69 | 82.52 |
| ADP-FL | 30 | 83.17 | 83.50 | 83.33 |
| Baseline | 40 | 84.24 | 84.57 | 84.40 |
| ADP-FL | 40 | 86.09 | 86.42 | 86.25 |
| Baseline | 50 | 86.87 | 87.20 | 87.03 |
| ADP-FL | 50 | 86.74 | 87.07 | 86.90 |
| CIFAR10 | Baseline | 10 | 49.76 | 50.09 | 49.92 |
| ADP-FL | 10 | 35.52 | 35.85 | 35.68 |
| Baseline | 20 | 28.41 | 28.74 | 28.57 |
| ADP-FL | 20 | 46.14 | 46.47 | 46.30 |
| Baseline | 30 | 42.80 | 43.13 | 42.96 |
| ADP-FL | 30 | 46.14 | 46.47 | 46.30 |
| Baseline | 40 | 51.03 | 51.36 | 51.19 |
| ADP-FL | 40 | 51.41 | 51.74 | 51.57 |
| Baseline | 50 | 48.89 | 49.22 | 49.05 |
| ADP-FL | 50 | 48.91 | 49.24 | 49.07 |
| CIFAR100 | Baseline | 10 | 43.29 | 43.62 | 43.45 |
| ADP-FL | 10 | 36.20 | 36.53 | 36.36 |
| Baseline | 20 | 30.81 | 31.14 | 30.97 |
| ADP-FL | 20 | 42.70 | 43.03 | 42.86 |
| Baseline | 30 | 42.17 | 42.50 | 42.33 |
| ADP-FL | 30 | 48.57 | 48.90 | 48.73 |
| Baseline | 40 | 50.06 | 50.39 | 50.22 |
| ADP-FL | 40 | 52.44 | 52.77 | 52.60 |
| Baseline | 50 | 46.49 | 46.82 | 46.65 |
| ADP-FL | 50 | 50.33 | 50.66 | 50.49 |
| EMNIST | Baseline | 10 | 97.30 | 97.63 | 97.46 |
| ADP-FL | 10 | 97.33 | 97.66 | 97.49 |
| Baseline | 20 | 97.88 | 98.21 | 98.04 |
| ADP-FL | 20 | 95.08 | 95.41 | 95.24 |
| Baseline | 30 | 97.80 | 98.13 | 97.96 |
| ADP-FL | 30 | 98.06 | 98.39 | 98.22 |
| Baseline | 40 | 97.83 | 98.16 | 97.99 |
| ADP-FL | 40 | 97.91 | 98.24 | 98.07 |
| Baseline | 50 | 97.74 | 98.07 | 97.90 |
| ADP-FL | 50 | 97.40 | 97.73 | 97.56 |
Appendix A.5. Comparisons of Performance Under Different Noise Mechanisms
Intuitive experimental results are shown in
Figure A1,
Figure A2,
Figure A3 and
Figure A4. The red line represents the accuracy of the baseline algorithm, and the green line represents the accuracy of the ADP-FL algorithm.
Figure A1.
On the MNIST dataset, adaptive differential privacy algorithms based on Laplace and Gaussian mechanisms were tested against the baseline algorithm, with privacy budgets set to 10, 20, 30, 40, and 50 from top to bottom.
Figure A1.
On the MNIST dataset, adaptive differential privacy algorithms based on Laplace and Gaussian mechanisms were tested against the baseline algorithm, with privacy budgets set to 10, 20, 30, 40, and 50 from top to bottom.
Figure A2.
On the CIFAR10 dataset, adaptive differential privacy algorithms based on Laplace and Gaussian mechanisms were tested against the baseline algorithm, with privacy budgets set to 10, 20, 30, 40, and 50 from top to bottom.
Figure A2.
On the CIFAR10 dataset, adaptive differential privacy algorithms based on Laplace and Gaussian mechanisms were tested against the baseline algorithm, with privacy budgets set to 10, 20, 30, 40, and 50 from top to bottom.
Figure A3.
On the CIFAR100 dataset, adaptive differential privacy algorithms based on Laplace and Gaussian mechanisms were tested against the baseline algorithm, with privacy budgets set to 10, 20, 30, 40, and 50 from top to bottom.
Figure A3.
On the CIFAR100 dataset, adaptive differential privacy algorithms based on Laplace and Gaussian mechanisms were tested against the baseline algorithm, with privacy budgets set to 10, 20, 30, 40, and 50 from top to bottom.
Figure A4.
On the EMNIST dataset, adaptive differential privacy algorithms based on Laplace and Gaussian mechanisms were tested against the baseline algorithm, with privacy budgets set to 10, 20, 30, 40, and 50 from top to bottom.
Figure A4.
On the EMNIST dataset, adaptive differential privacy algorithms based on Laplace and Gaussian mechanisms were tested against the baseline algorithm, with privacy budgets set to 10, 20, 30, 40, and 50 from top to bottom.