An Evolutionary Algorithm for Multi-Objective Workflow Scheduling with Adaptive Dynamic Grouping
Abstract
1. Introduction
2. Problem Description
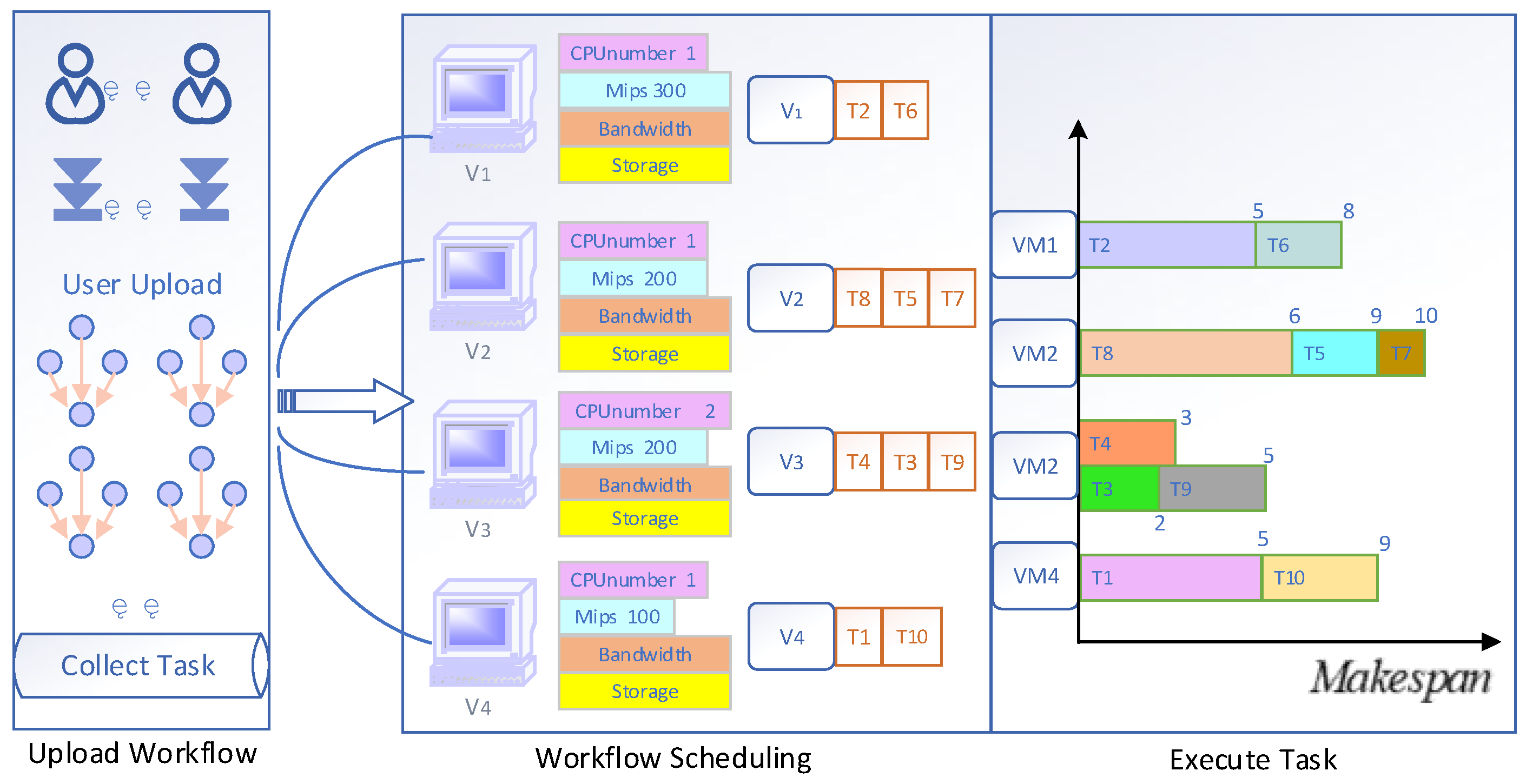
2.1. Cloud Computing Workflow Scheduling Model
2.2. Optimization Goals
2.2.1. The Calculation of Makespan
2.2.2. Task Execution Cost
2.2.3. Energy Consumption for Virtual Machines
3. An Evolutionary Algorithm for Workflow Scheduling with Adaptive Dynamic Grouping
| Algorithm 1 The pseudocode of ADG |
| 1: G ← GroupDecisionVariables 2: Initialize a population P 3: Calculate on the non-dominated solutions of P 4: for g = 1 → |G| do 5: Get a new population by re-generating values on decision variables of for P 6: P′ ← Regenerate Population on group based P 7: Non—dominate sorting of and calculate 8: ∆ ← max[ 9: end for 10: while Stop condition is not reached do 11: ← Roulette wheel selection based on ΔC 12: for = 1 → L do 13: if Δ + Δ = 0 then 14: ← Subdivide() 15: replace in G 16: TC ← 0 17: end if 18: Q ← Reproduction() 19: 20: Update the non-dominated solutions using 21: 22: Δ ← −, 23: ← 24: TC = Δ + TC 25: end for 26: Δ ← max[TC/L,0] 27: end while |
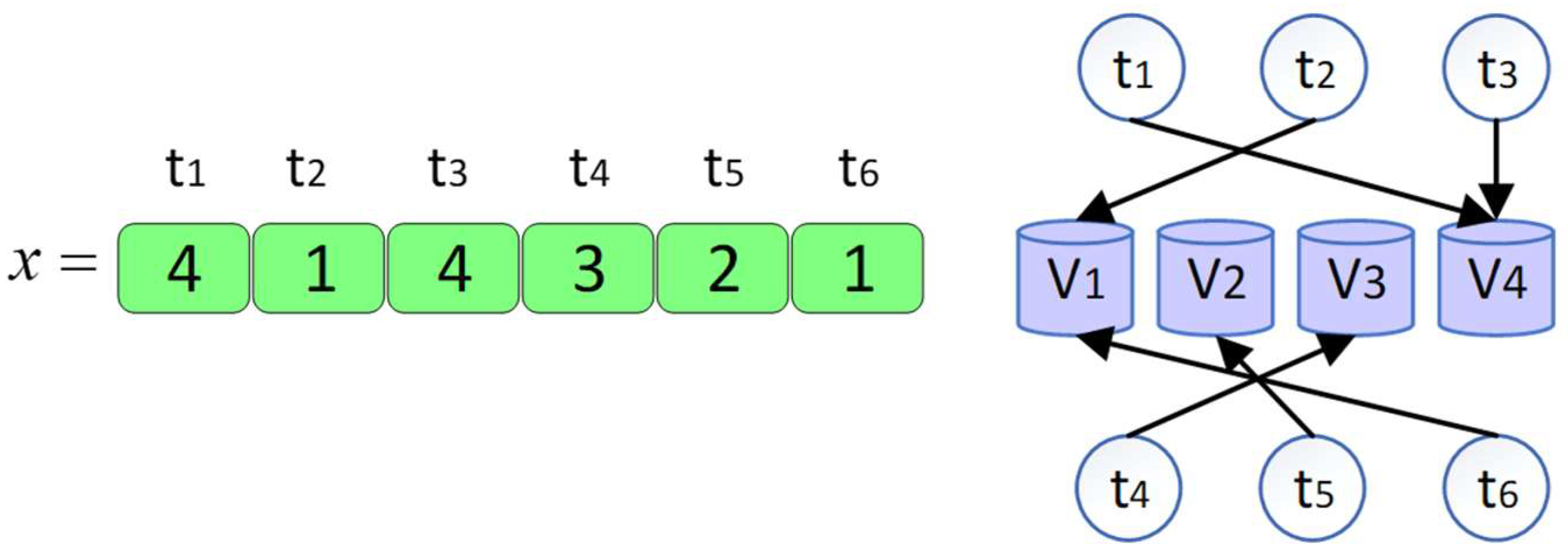
3.1. The Encoding Method
3.2. The Framework of ADG
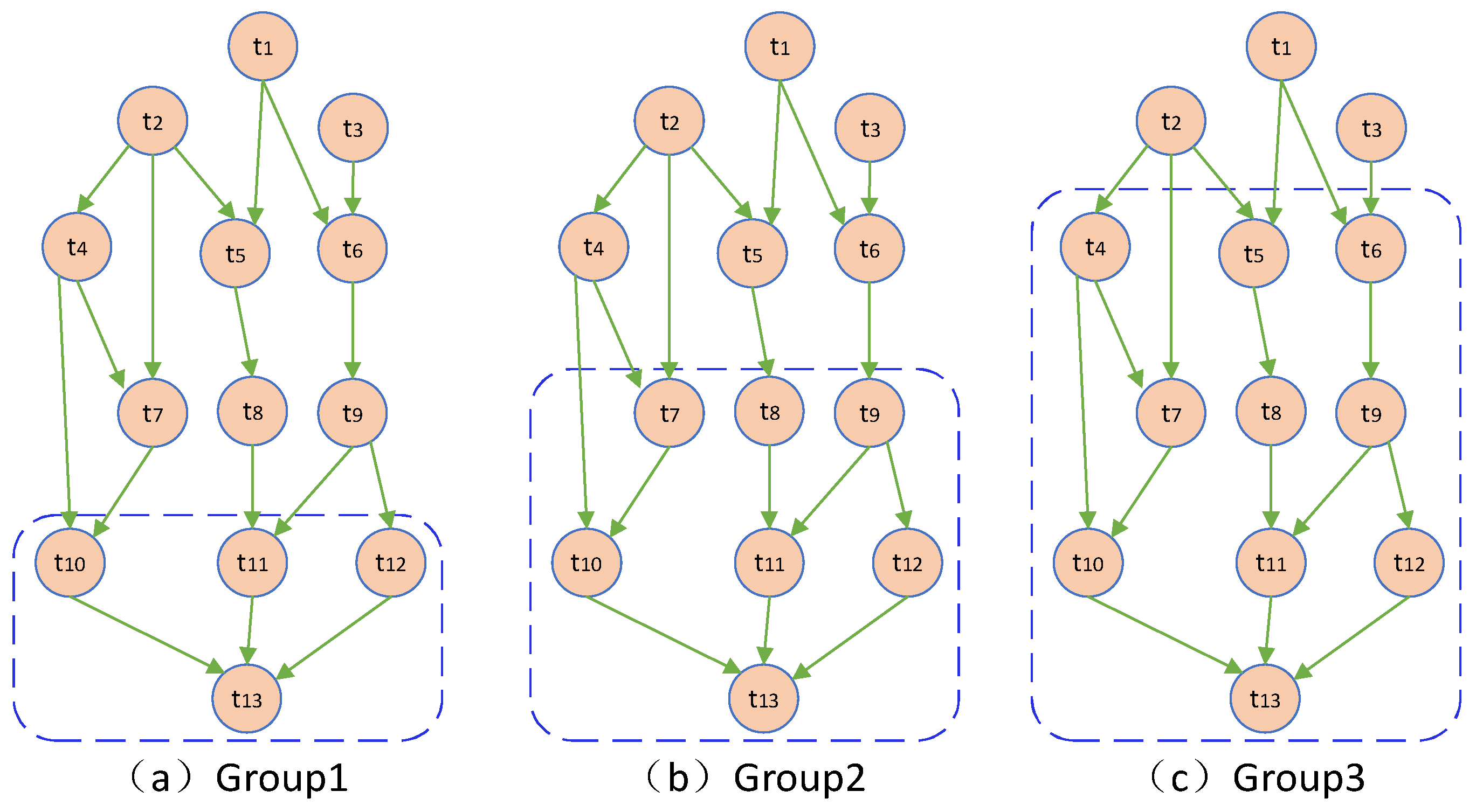
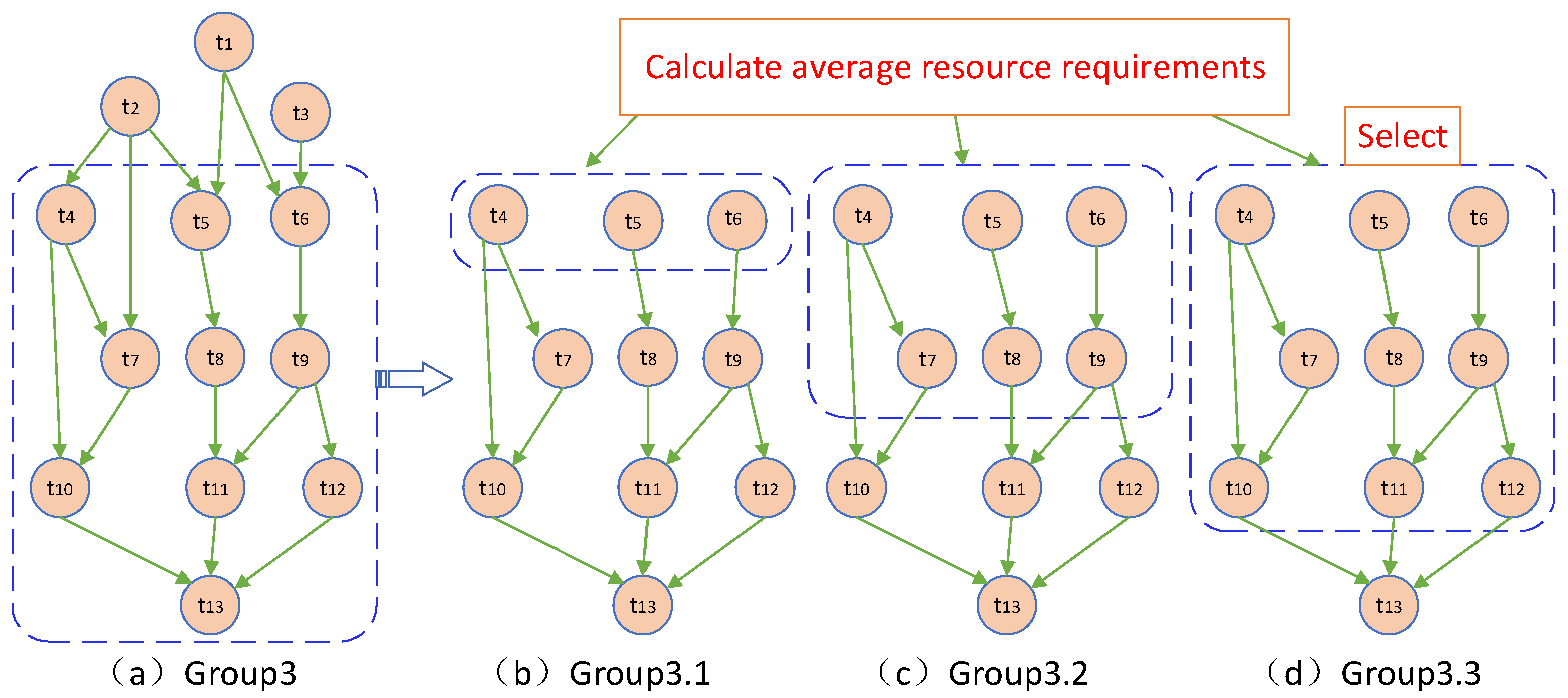
3.3. Dynamic Decision Variable Grouping Mechanism Based on Workflow Structure Decomposition
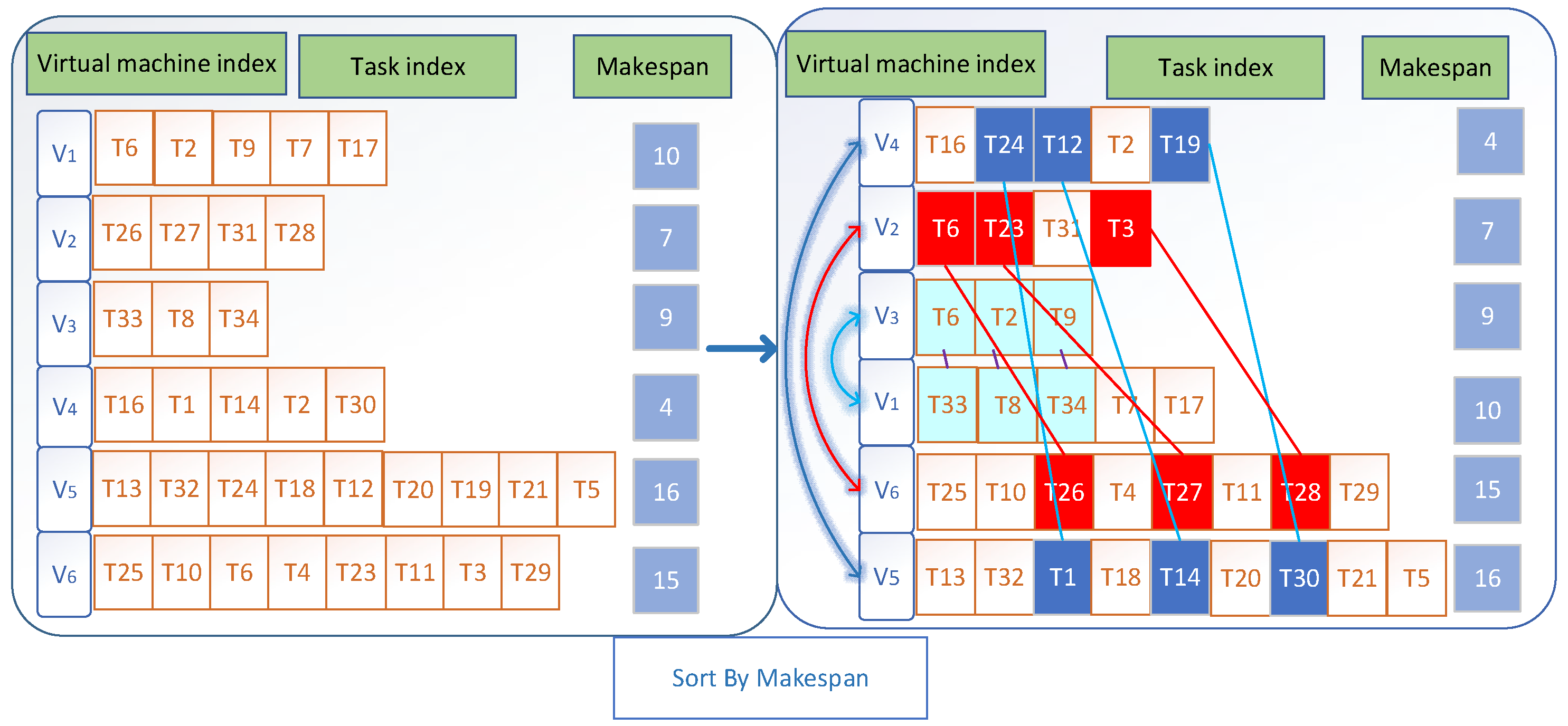
3.4. Task Priority Scheduling Policy and Group Task-VM Mapping Reproduction Policy
4. Experiment
4.1. Experimental Setup
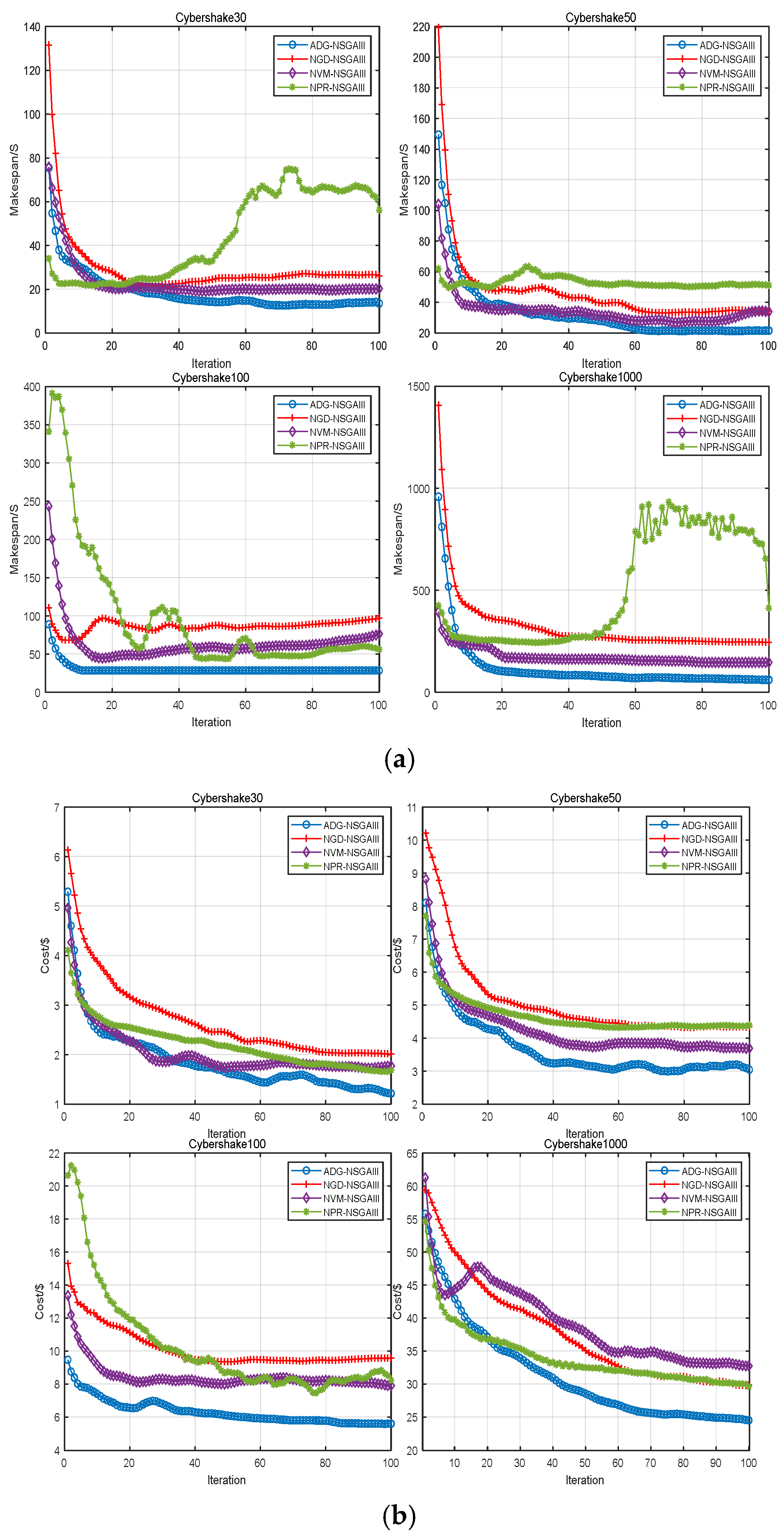
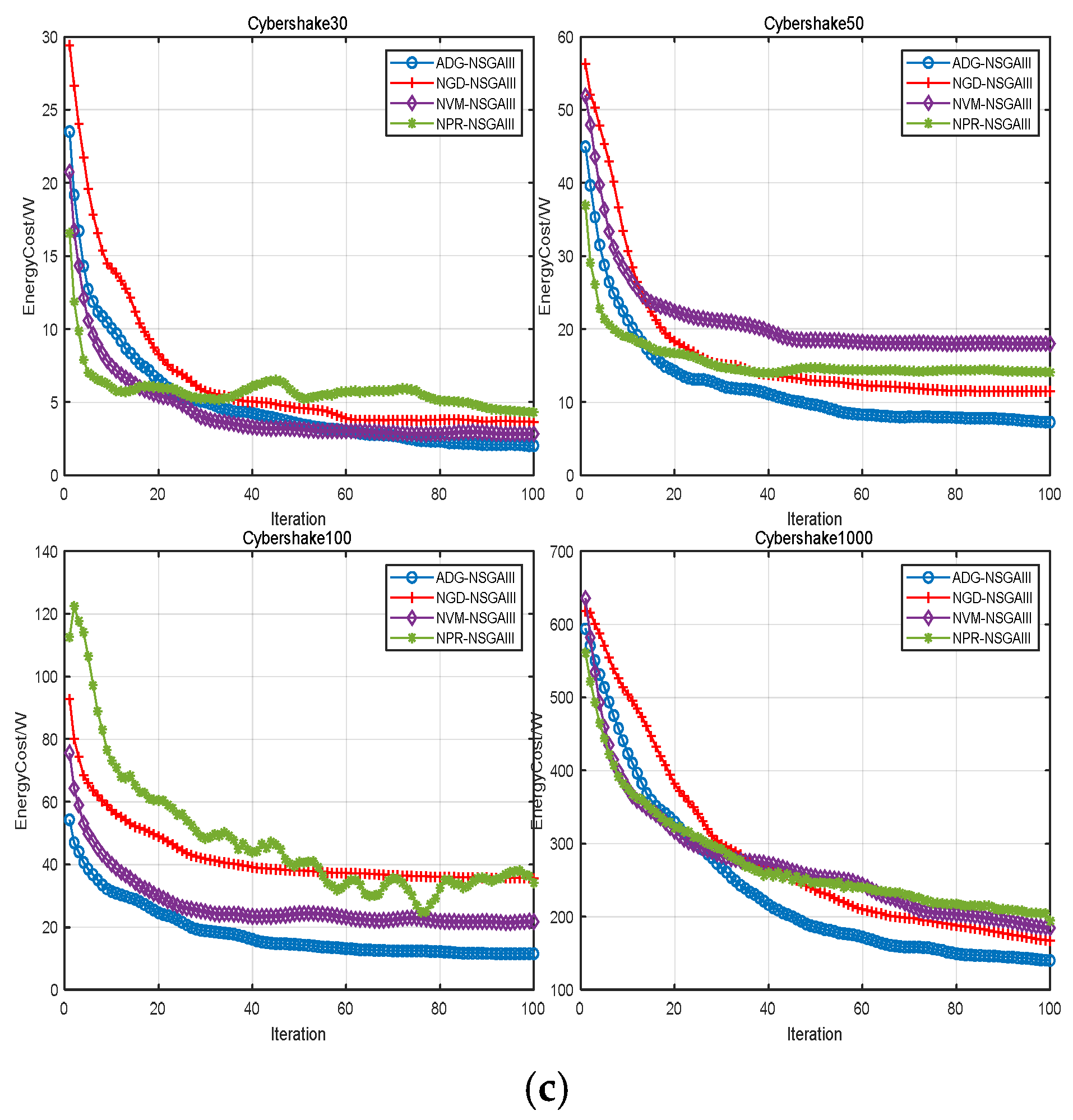
4.2. Ablation Experiment
- (1)
- NGD-NSGAIII: A comparison method without the dynamic grouping mechanism;
- (2)
- NRP-NSGAIII: A comparison method without the intra-group task priority ranking;
- (3)
- NVM-NSGAIII: A comparison method without the task mapping strategy for offspring generation;
- (4)
- ADG-NSGAIII: The complete algorithm proposed in this paper.
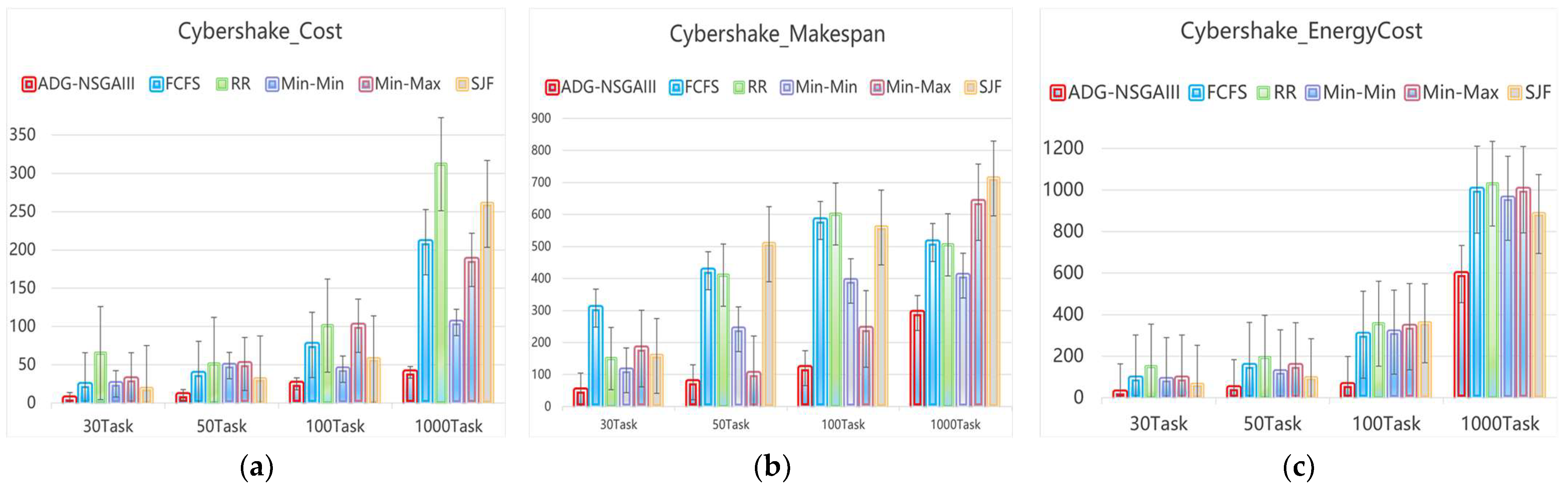
4.3. Algorithm Comparison Experiment
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Deb, M.; Choudhury, A. Hybrid cloud: A new paradigm in cloud computing. In Machine Learning Techniques and Analytics for Cloud Security; Wiley: Hoboken, NJ, USA, 2021; pp. 1–23. [Google Scholar]
- Al-Dhuraibi, Y.; Paraiso, F.; Djarallah, N.; Merle, P. Elasticity in cloud computing: State of the art and research challenges. IEEE Trans Serv. Comput. 2017, 11, 430–447. [Google Scholar] [CrossRef]
- Baldan, F.J.; Ramirez-Gallego, S.; Bergmeir, C.; Herrera, F.; Benitez, J.M. A forecasting methodology for workload forecasting in cloud systems. IEEE Trans Cloud Comput. 2016, 6, 929–941. [Google Scholar] [CrossRef]
- Bindu, G.B.; Ramani, K.; Bindu, C.S. Optimized resource scheduling using the meta heuristic algorithm in cloud computing. IAENG Int. J. Comput. Sci. 2020, 47, 360–366. [Google Scholar]
- Adhikari, M.; Amgoth, T.; Srirama, S.N. A survey on scheduling strategies for workflows in cloud environment and emerging trends. ACM Comput. Surv. (CSUR) 2019, 52, 1–36. [Google Scholar] [CrossRef]
- Song, Y.; Xin, R.; Chen, P.; Zhang, R.; Chen, J.; Zhao, Z. Identifying performance anomalies in fluctuating cloud environments: A robust correlative-GNN-based explainable approach. Future Gener. Comput. Syst. 2023, 145, 77–86. [Google Scholar] [CrossRef]
- Xia, Y.; Luo, X.; Jin, T.; Li, J.; Xing, L. A tri-chromosome-based evolutionary algorithm for energy-efficient workflow scheduling in clouds. Swarm Evol. Comput. 2024, 91, 101751. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.M.; Da Fonseca, V.G. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Chen, W.; Deelman, E. Workflowsim: A toolkit for simulating scientific workflows in distributed environments. In Proceedings of the 2012 IEEE 8th International Conference on E-Science, Chicago, IL, USA, 8–12 October 2012; pp. 1–8. [Google Scholar]
- Maechling, P.; Deelman, E.; Zhao, L.; Graves, R.; Mehta, G.; Gupta, N.; Mehringer, J.; Kesselman, C.; Callaghan, S.; Okaya, D.; et al. SCEC CyberShake workflows—Automating probabilistic seismic hazard analysis calculations. In Workflows for e-Science: Scientific Workflows for Grids; Springer: Berlin/Heidelberg, Germany, 2007; pp. 143–163. [Google Scholar]
- Li, H.; Ruan, J.; Durbin, R. Mapping short DNA sequencing reads and calling variants using mapping quality scores. Genome Res. 2008, 18, 1851–1858. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.A.; Brady, P.R.; Dietz, A.; Cao, J.; Johnson, B.; McNabb, J. A case study on the use of workflow technologies for scientific analysis: Gravitational wave data analysis. In Workflows for e-Science: Scientific Workflows for Grids; Springer: Berlin/Heidelberg, Germany, 2007; pp. 39–59. [Google Scholar]
- Berriman, G.B.; Deelman, E.; Good, J.C.; Jacob, J.C.; Katz, D.S.; Kesselman, C.; Laity, A.C.; Prince, T.A.; Singh, G.; Su, M.H. Montage: A grid-enabled engine for delivering custom science-grade mosaics on demand. In Proceedings of the Optimizing Scientific Return for Astronomy Through Information Technologies, Glasgow, UK, 24–25 June 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5493, pp. 221–232. [Google Scholar]
- Livny, J.; Teonadi, H.; Livny, M.; Waldor, M.K. High-throughput, kingdom-wide prediction and annotation of bacterial non-coding RNAs. PLoS ONE 2008, 3, e3197. [Google Scholar] [CrossRef]
- Saeedi, S.; Khorsand, R.; Bidgoli, S.G.; Ramezanpour, M. Improved many-objective particle swarm optimization algorithm for scientific workflow scheduling in cloud computing. Comput. Ind. Eng. 2020, 147, 106649. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Cheng, R.; Jin, Y.; Olhofer, M.; Sendhoff, B. A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Trans Evol. Comput. 2016, 20, 773–791. [Google Scholar] [CrossRef]
- Tian, Y.; Cheng, R.; Zhang, X.; Jin, Y. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum]. IEEE Comput. Intell. Mag. 2017, 12, 73–87. [Google Scholar] [CrossRef]
- Siahaan, A.P.U. Comparison analysis of CPU scheduling: FCFS, SJF and Round Robin. Int. J. Eng. Dev. Res. 2016, 4, 124–132. [Google Scholar]
- Mustapha, S.M.F.D.S.; Gupta, P. Fault aware task scheduling in cloud using min-min and DBSCAN. Internet Things Cyber-Phys. Syst. 2024, 4, 68–76. [Google Scholar] [CrossRef]
- Mishra, S.K.; Sahoo, B.; Parida, P.P. Load balancing in cloud computing: A big picture. J. King Saud Univ.-Comput. Inf. Sci. 2020, 32, 149–158. [Google Scholar] [CrossRef]


| Types | Mips (MB/s) | CPUs | PerCost ($) | Bandwidth (MB) |
|---|---|---|---|---|
| EC2.S | 512 | 1 | 0.043 | 512 |
| EC2.M | 1024 | 1 | 0.086 | 768 |
| EC2.L | 2048 | 2 | 0.174 | 1280 |
| EC2.XL | 2048 | 4 | 0.350 | 2560 |
| Alibaba Cloud.S | 1024 | 2 | 0.047 | 1280 |
| Alibaba Cloud.M | 1024 | 2 | 0.351 | 1280 |
| Alibaba Cloud.L | 2048 | 4 | 0.050 | 2048 |
| Alibaba Cloud.XL | 5120 | 8 | 0.257 | 2048 |
| Azure.S | 768 | 1 | 0.096 | 1024 |
| Azure.M | 1280 | 2 | 0.192 | 2048 |
| Azure.L | 2560 | 4 | 0.383 | 1640 |
| Azure.XL | 3072 | 8 | 0.766 | 3072 |
| Algorithm | I_MaOPSO +/−/≈ | NSGAII +/−/≈ | NSGAIII +/−/≈ | RVEA +/−/≈ |
|---|---|---|---|---|
| 20 Workflows | 4/9/7 | 2/10/8 | 3/13/4 | 1/11/8 |
| CyberShake | n | NSGAII | NSGAIII | RVEA |
|---|---|---|---|---|
| With ADG | 30 | 9.1860 × 10−1 | 9.2081 × 10−1 | 8.2873 × 10−1 |
| 50 | 9.2981 × 10−1 | 9.3005 × 10−1 | 8.6430 × 10−1 | |
| 100 | 7.8492 × 10−1 | 8.6712 × 10−1 | 8.2984 × 10−1 | |
| 1000 | 7.3192 × 10−1 | 7.7946 × 10−1 | 5.5573 × 10−1 | |
| Without ADG | 30 | 8.4348 × 10−1 | 8.4719 × 10−1 | 9.1223 × 10−1 |
| 50 | 8.7973 × 10−1 | 8.7298 × 10−1 | 9.1858 × 10−1 | |
| 100 | 7.8538 × 10−1 | 7.8348 × 10−1 | 7.6878 × 10−1 | |
| 1000 | 6.3113 × 10−1 | 6.1608 × 10−1 | 4.4648 × 10−1 |
| CyberShake | n | NSGAII | NSGAIII | RVEA |
|---|---|---|---|---|
| WithADG | 30 | 3.8 s | 4.7 s | 4.3 s |
| 50 | 6.6 s | 10.0 s | 11.2 s | |
| 100 | 14.3 s | 30.5 s | 23.5 s | |
| 1000 | 386.2 s | 2949.2 s | 1322.6 s | |
| WithOutADG | 30 | 2.1 s | 3.3 s | 3.2 s |
| 50 | 3.6 s | 7.5 s | 7.6 s | |
| 100 | 8.6 s | 25.5 s | 21.1 s | |
| 1000 | 326.3 s | 2898.5 s | 1021.3 s |
| CyberShake | n | NSGAII | NSGAIII | RVEA |
|---|---|---|---|---|
| WithOutADG | 30 | 100 times | - | - |
| 50 | 100 times | 87 times | 86 times | |
| 100 | 100 times | 76 times | - | |
| 1000 | 100 times | 53 times | 93 times | |
| WithADG | 30 | 87 times | 91 times | 88 times |
| 50 | 73 times | 82 times | 80 times | |
| 100 | 52 times | 46 times | 68 times | |
| 1000 | 43 times | 32 times | 57 times |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Zhang, A.; Sun, C.; Ye, Q. An Evolutionary Algorithm for Multi-Objective Workflow Scheduling with Adaptive Dynamic Grouping. Electronics 2025, 14, 2586. https://doi.org/10.3390/electronics14132586
Zhang G, Zhang A, Sun C, Ye Q. An Evolutionary Algorithm for Multi-Objective Workflow Scheduling with Adaptive Dynamic Grouping. Electronics. 2025; 14(13):2586. https://doi.org/10.3390/electronics14132586
Chicago/Turabian StyleZhang, Guochen, Aolong Zhang, Chaoli Sun, and Qing Ye. 2025. "An Evolutionary Algorithm for Multi-Objective Workflow Scheduling with Adaptive Dynamic Grouping" Electronics 14, no. 13: 2586. https://doi.org/10.3390/electronics14132586
APA StyleZhang, G., Zhang, A., Sun, C., & Ye, Q. (2025). An Evolutionary Algorithm for Multi-Objective Workflow Scheduling with Adaptive Dynamic Grouping. Electronics, 14(13), 2586. https://doi.org/10.3390/electronics14132586






