Development of Digital Twin for DC-DC Converters Under Varying Parameter Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Buck Converter Parameters
2.2. Modular Digital Twin Development
3. Simulation Results
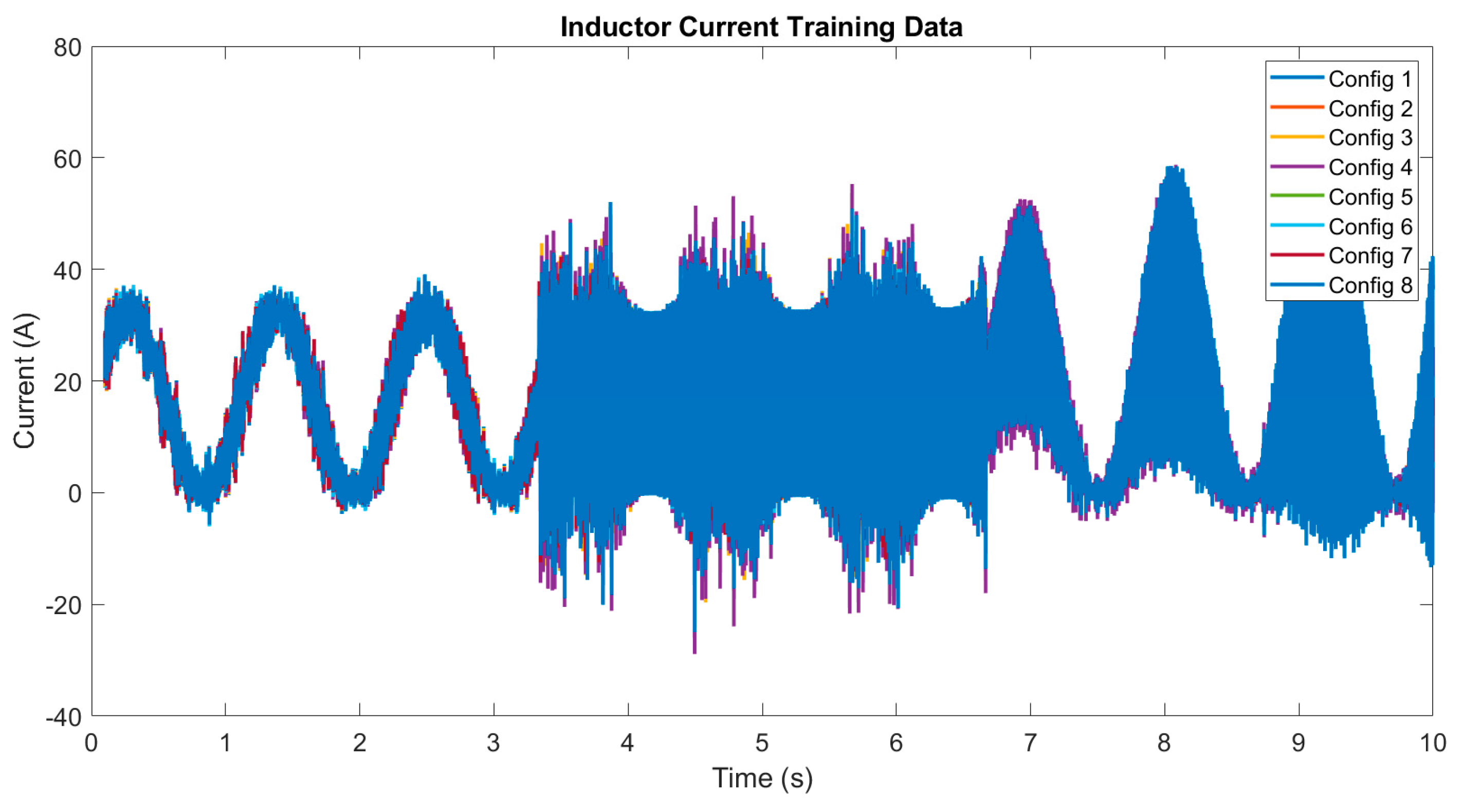
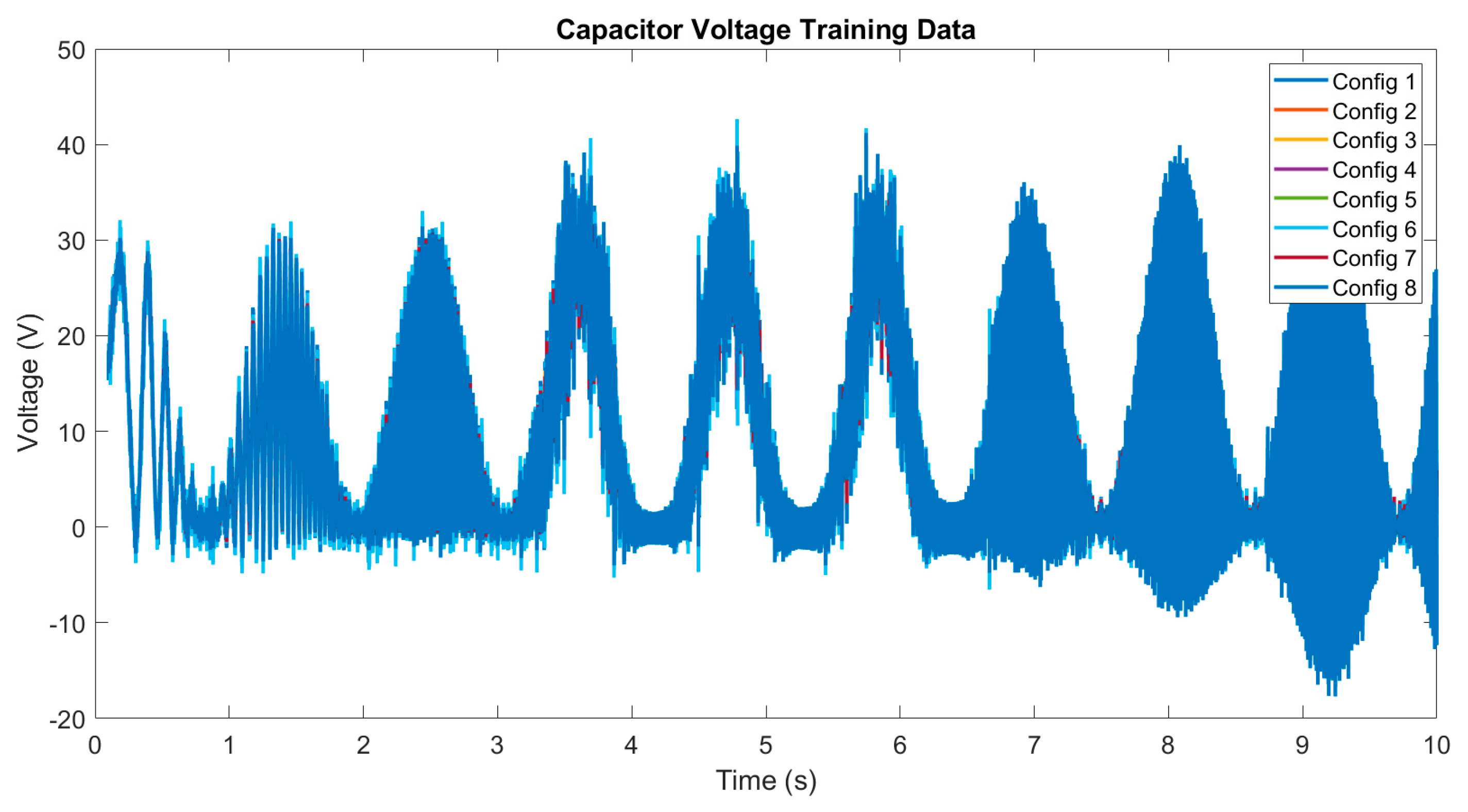
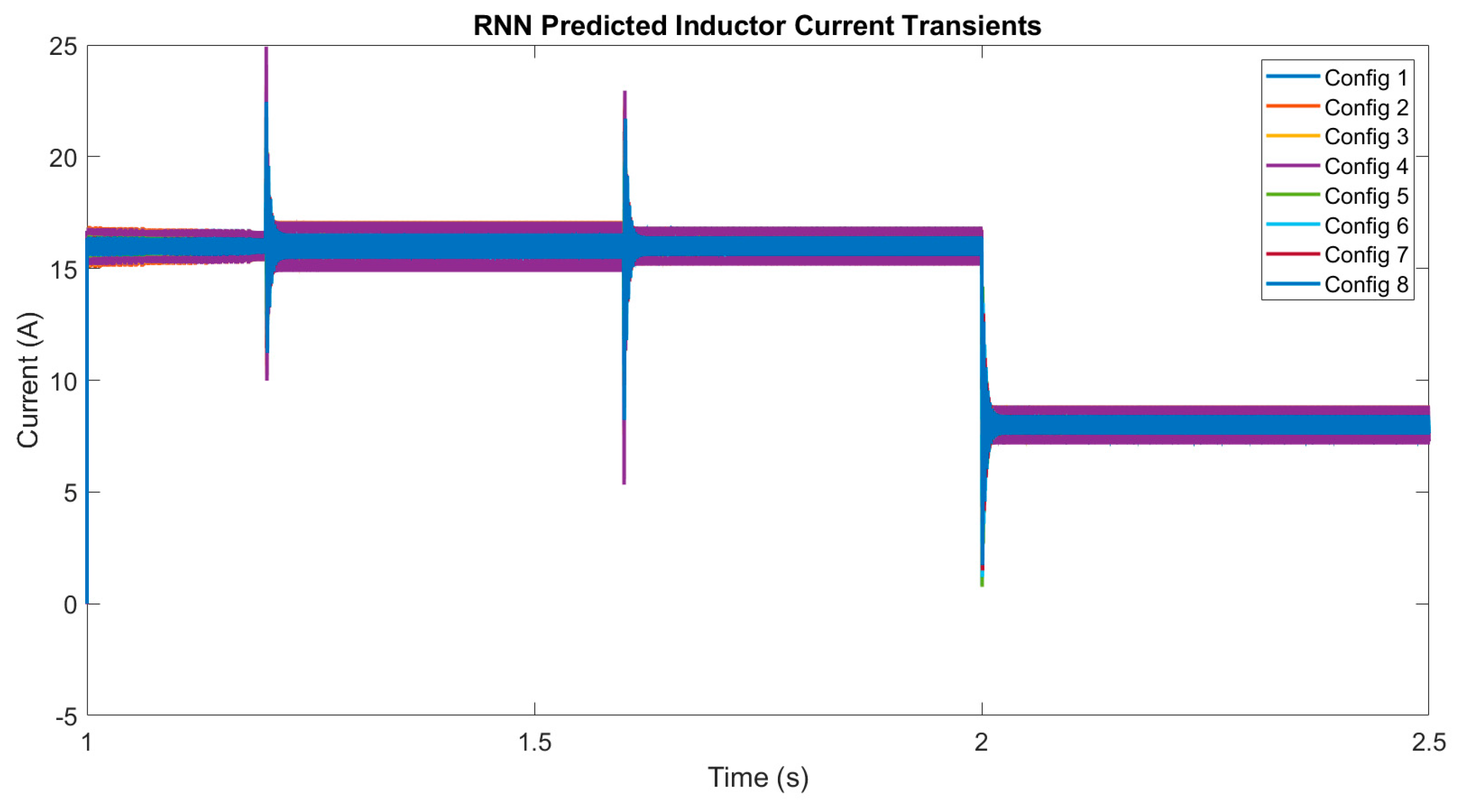
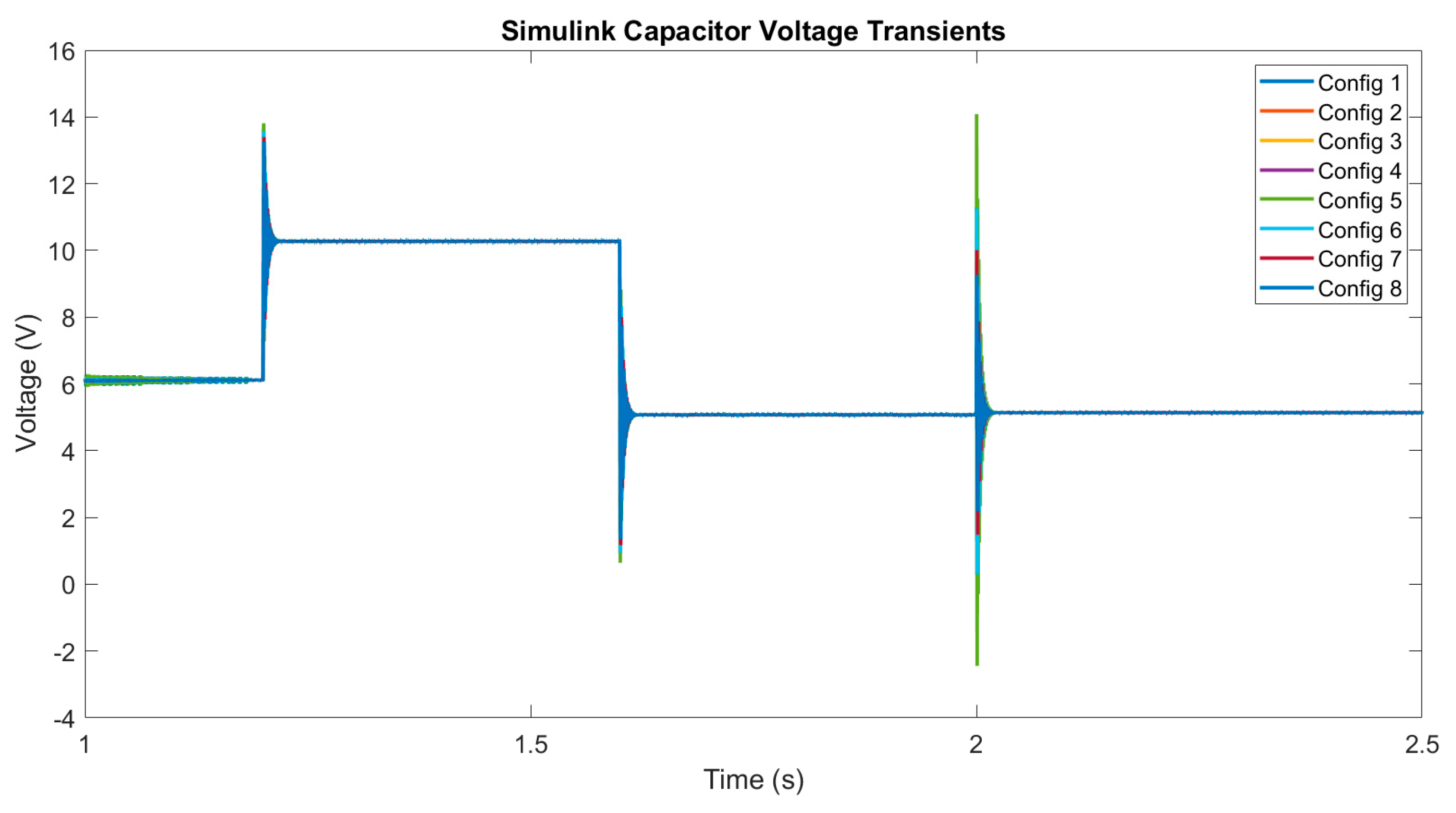
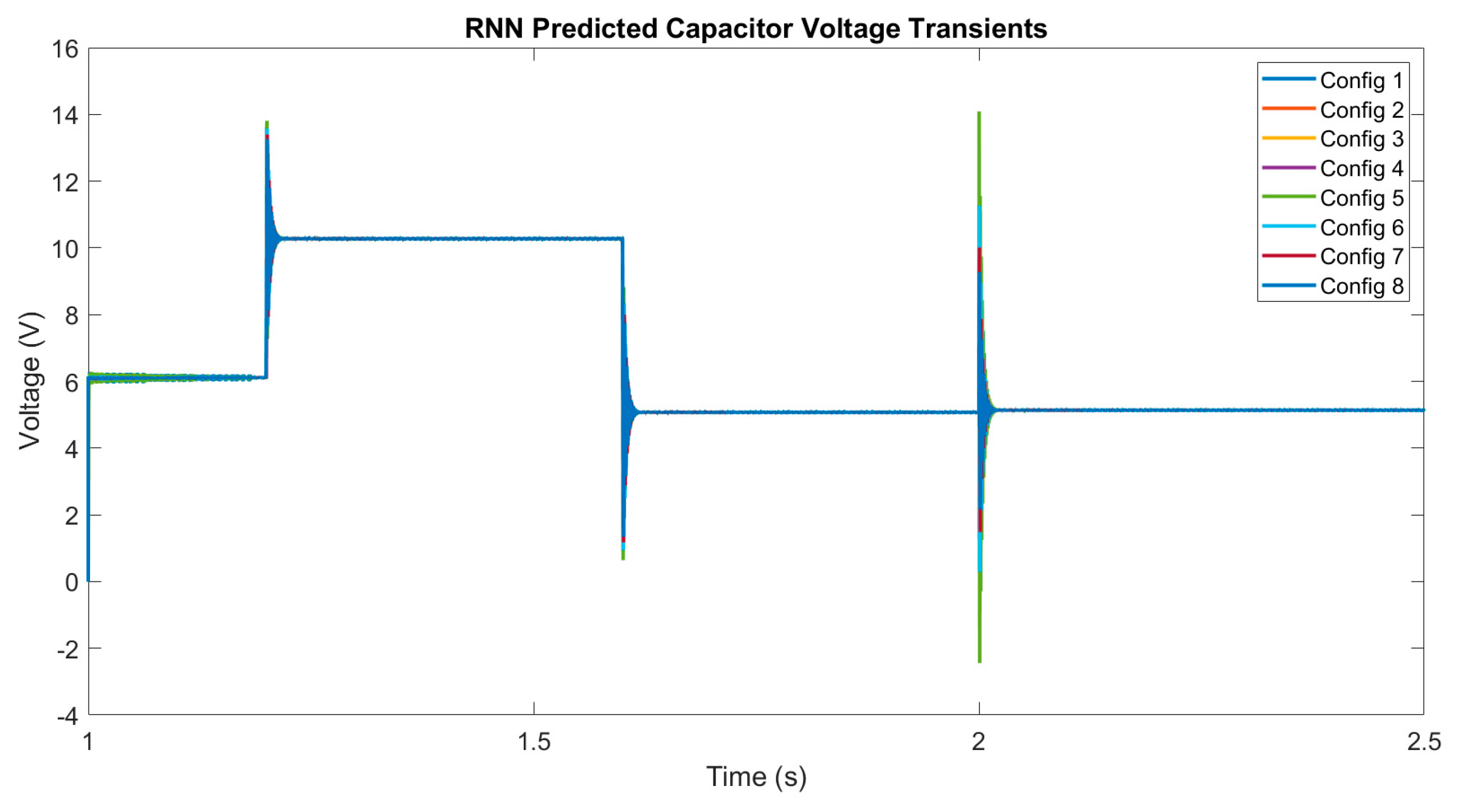
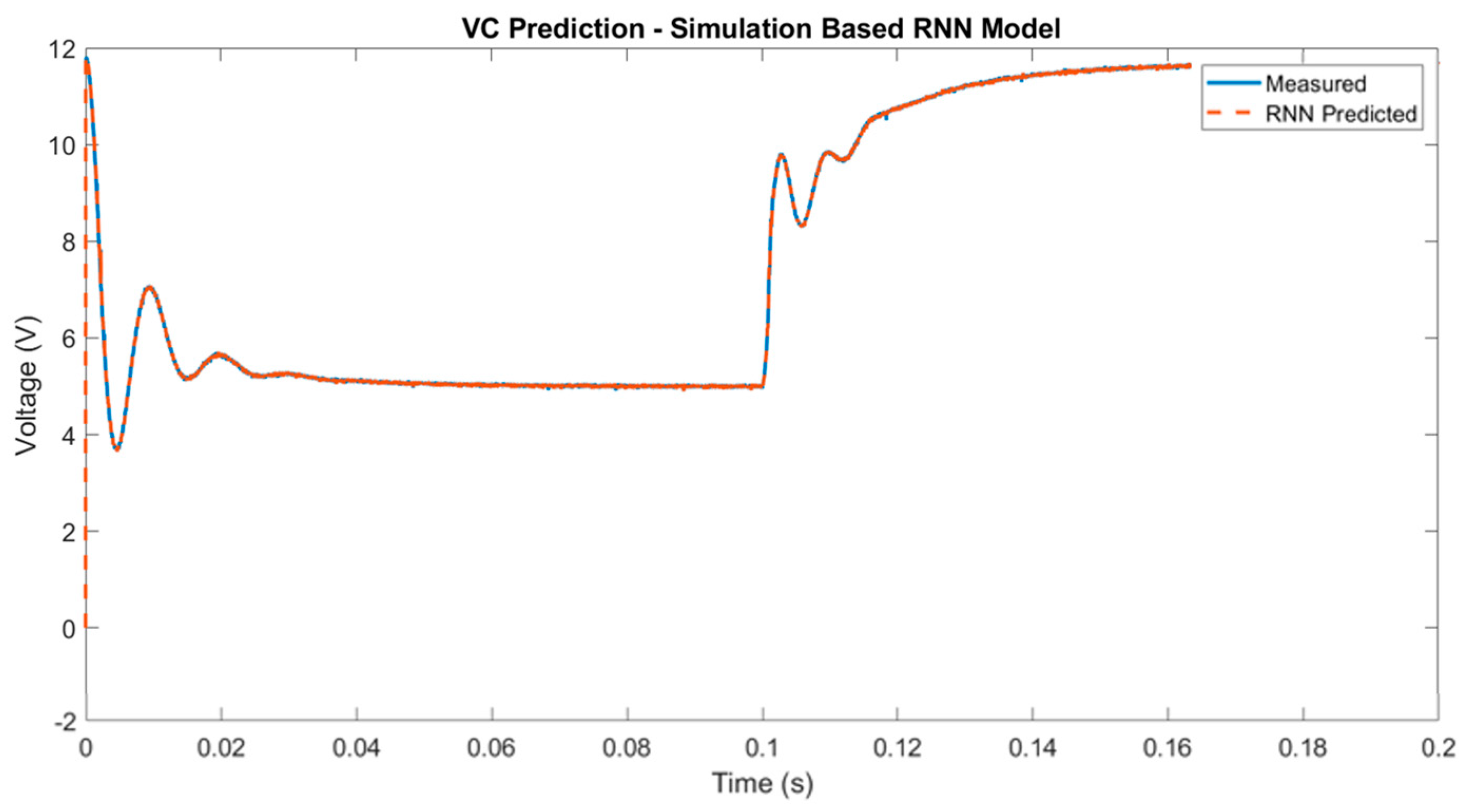
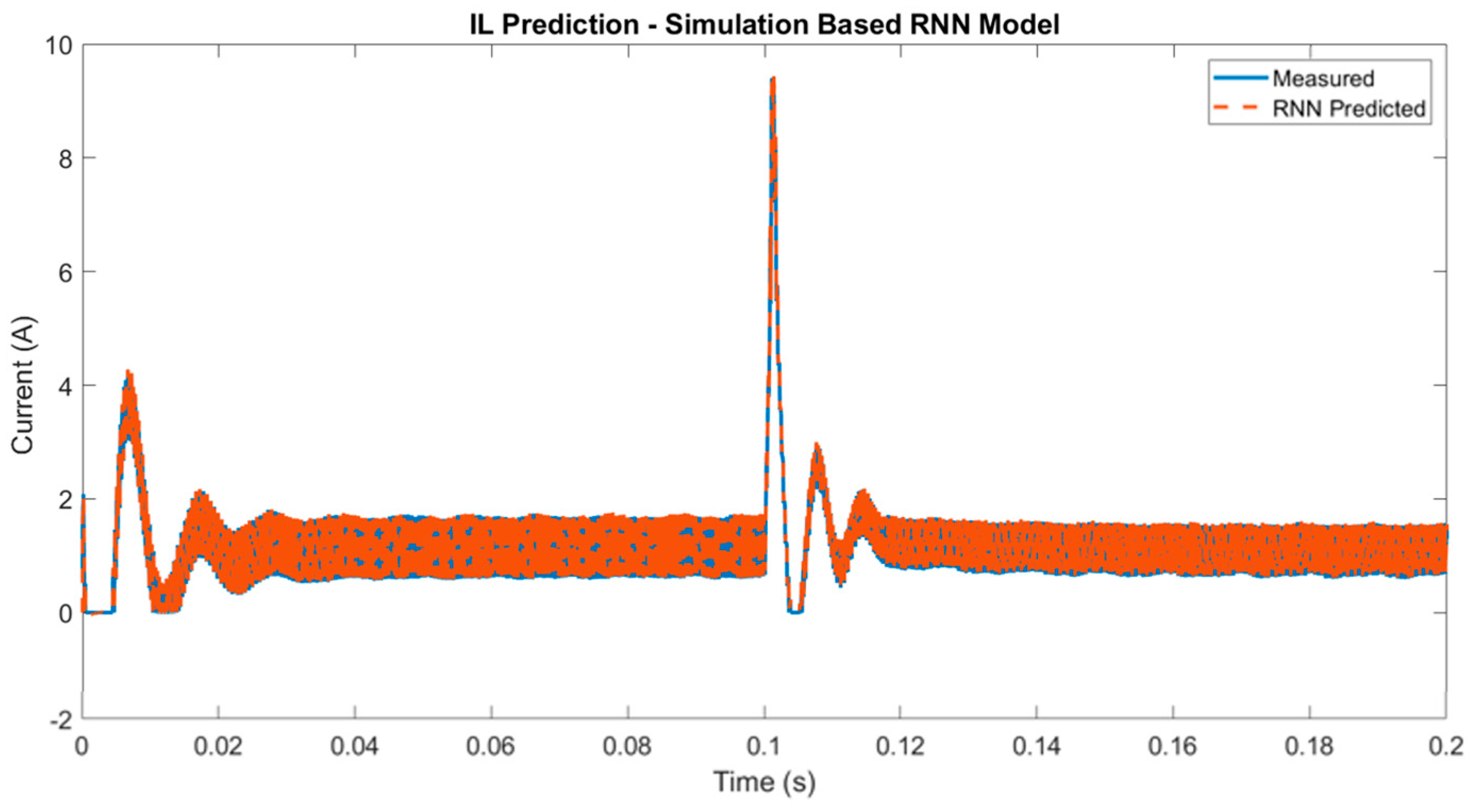
3.1. Digital Twin Testing for Model Trained with Simulated Data
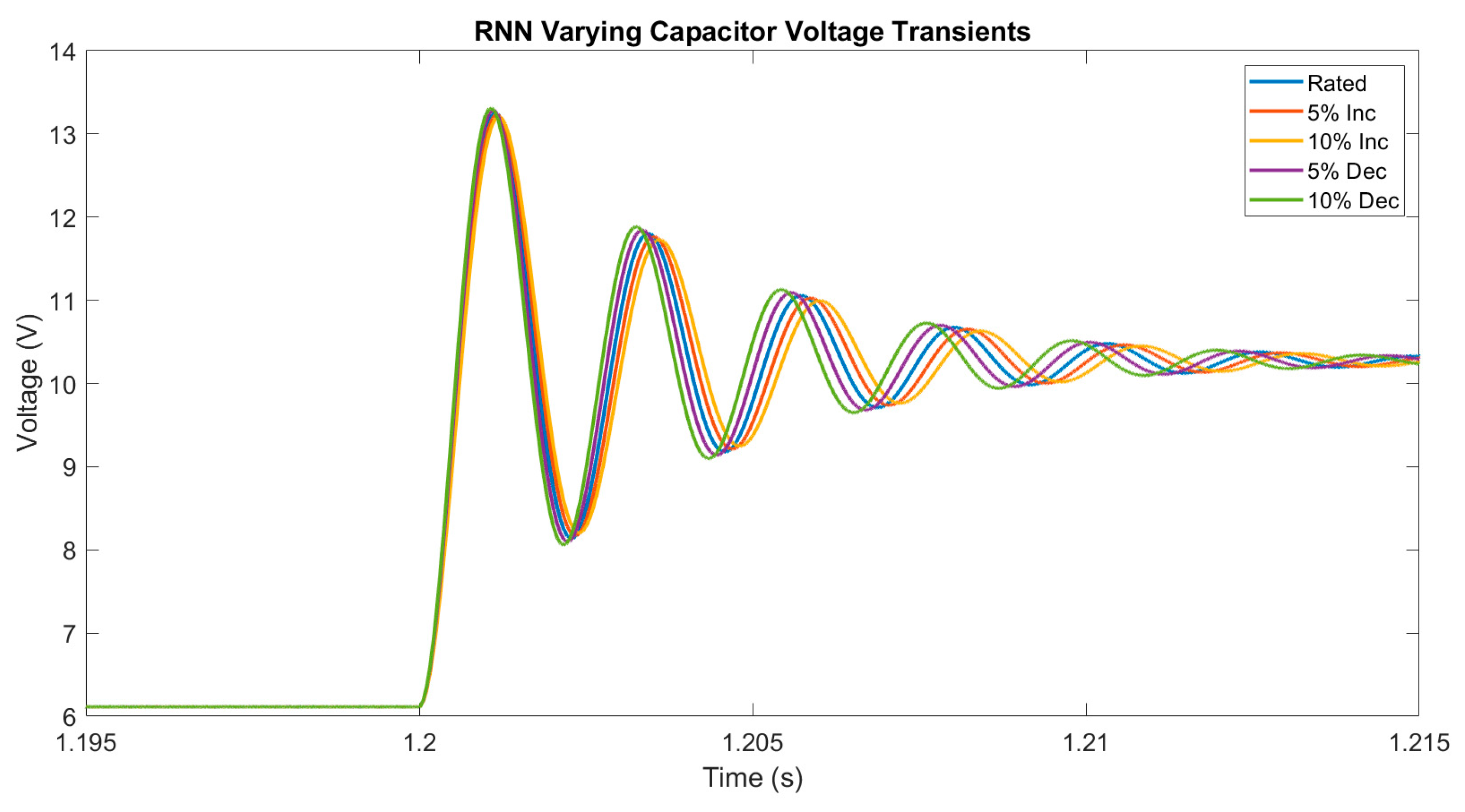
3.2. Model Prediction Accuracy for Small Component Variations
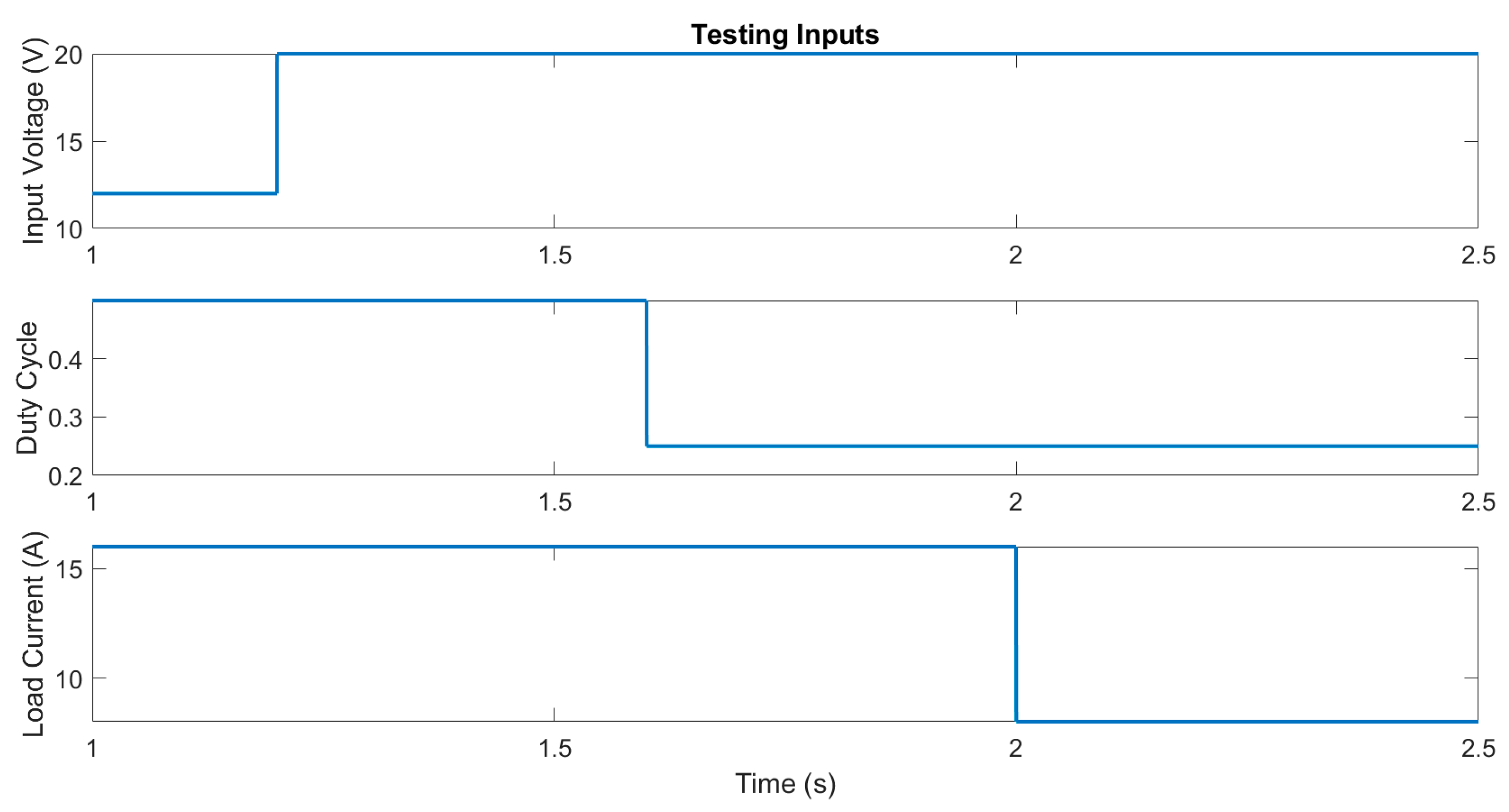
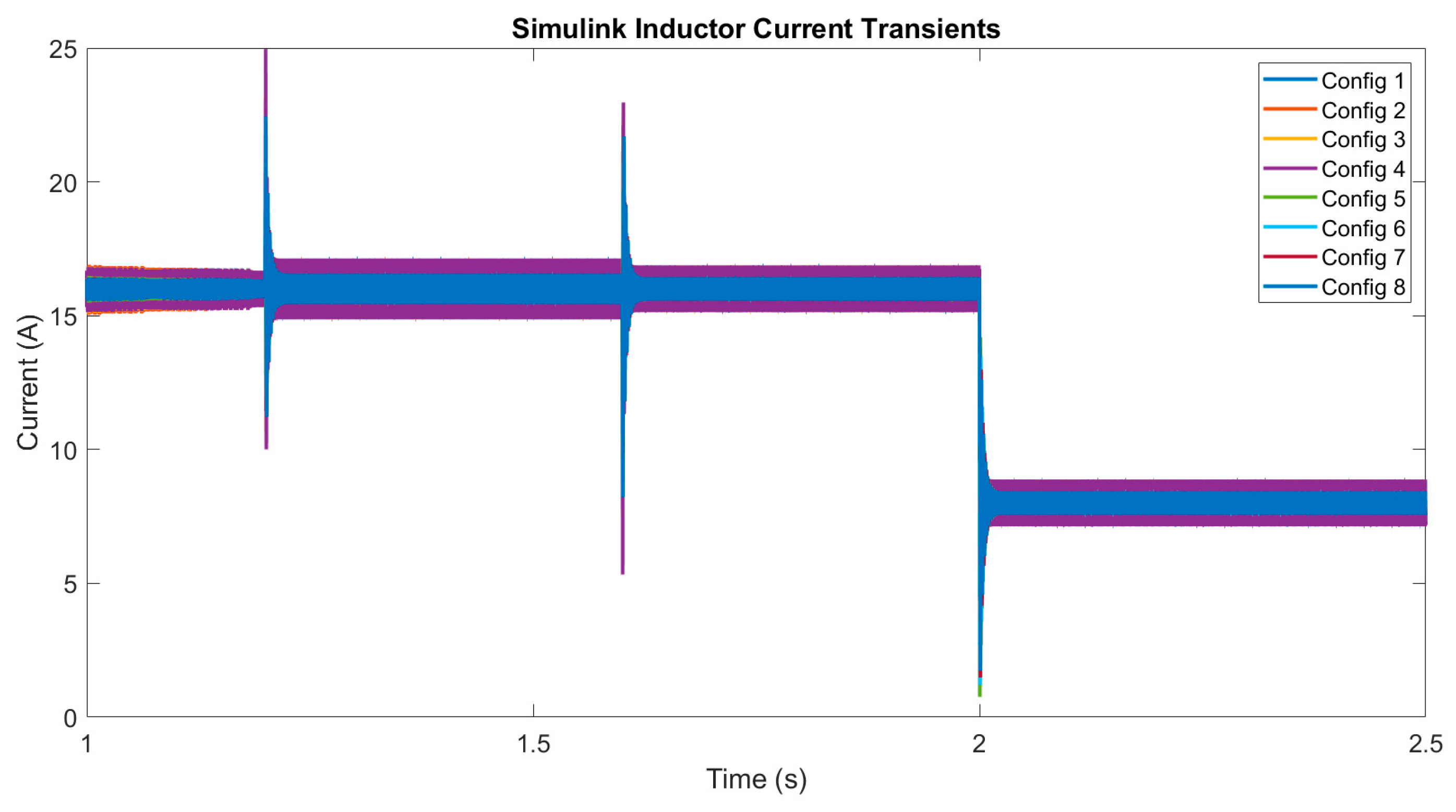
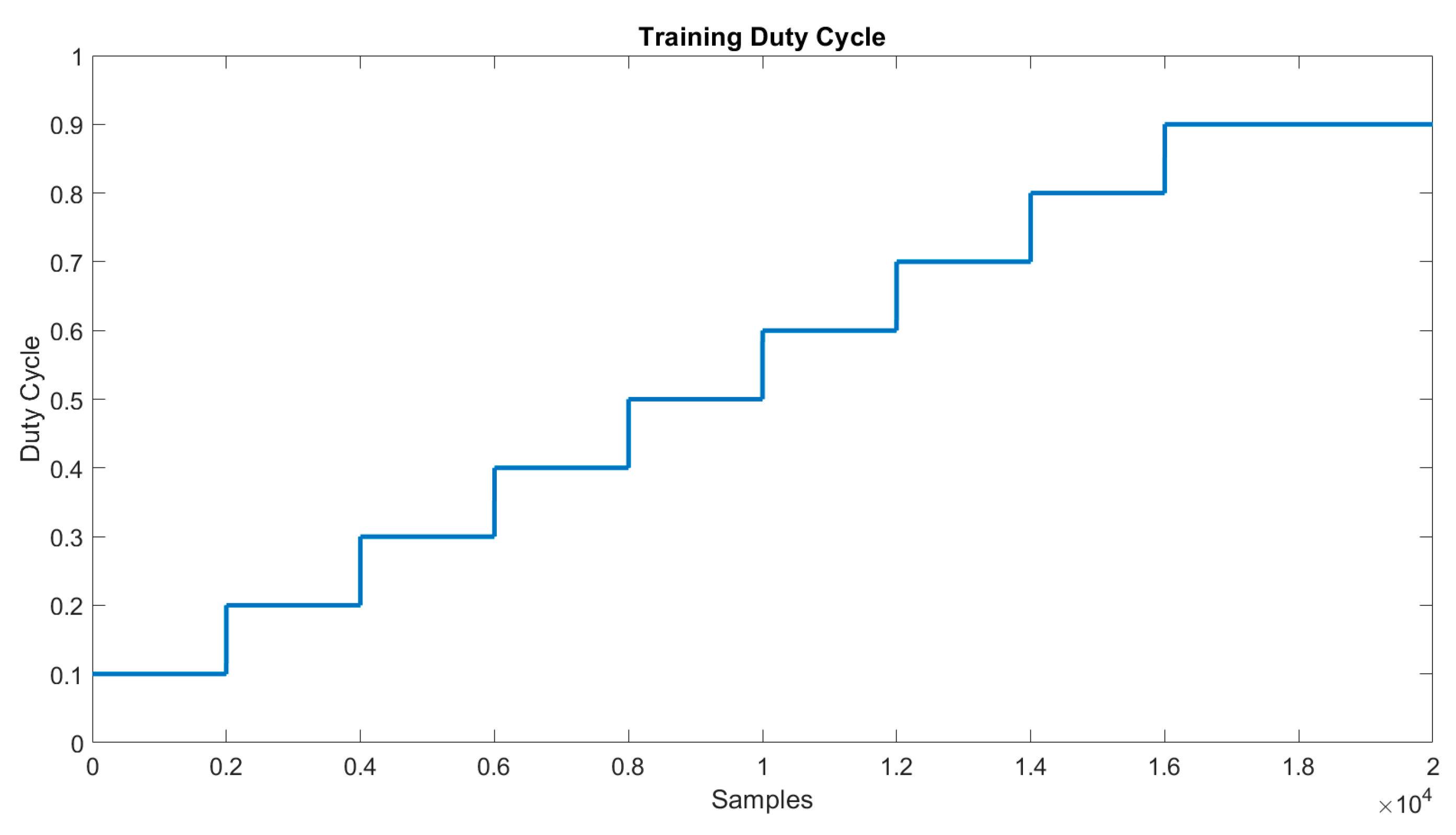
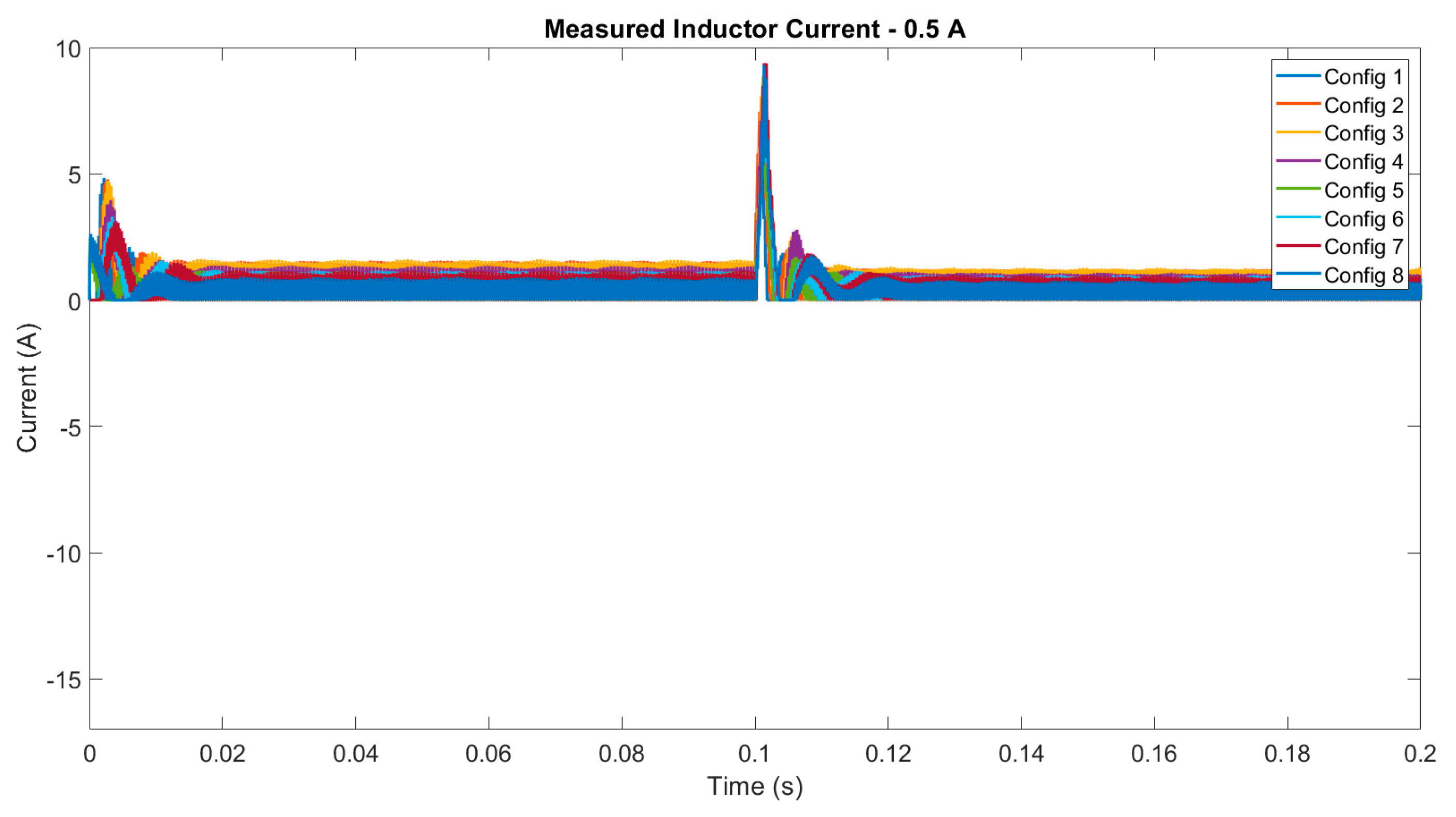
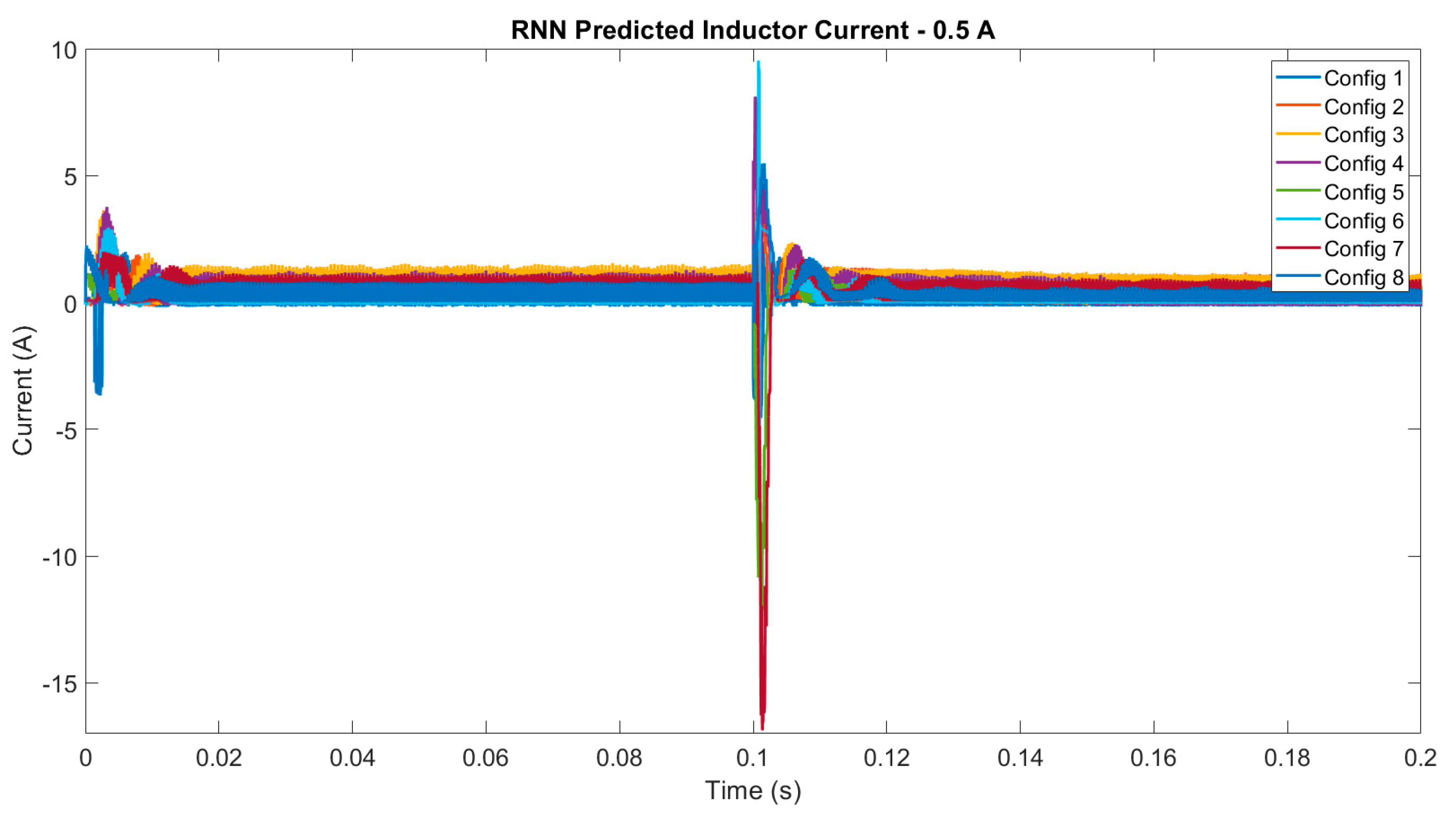
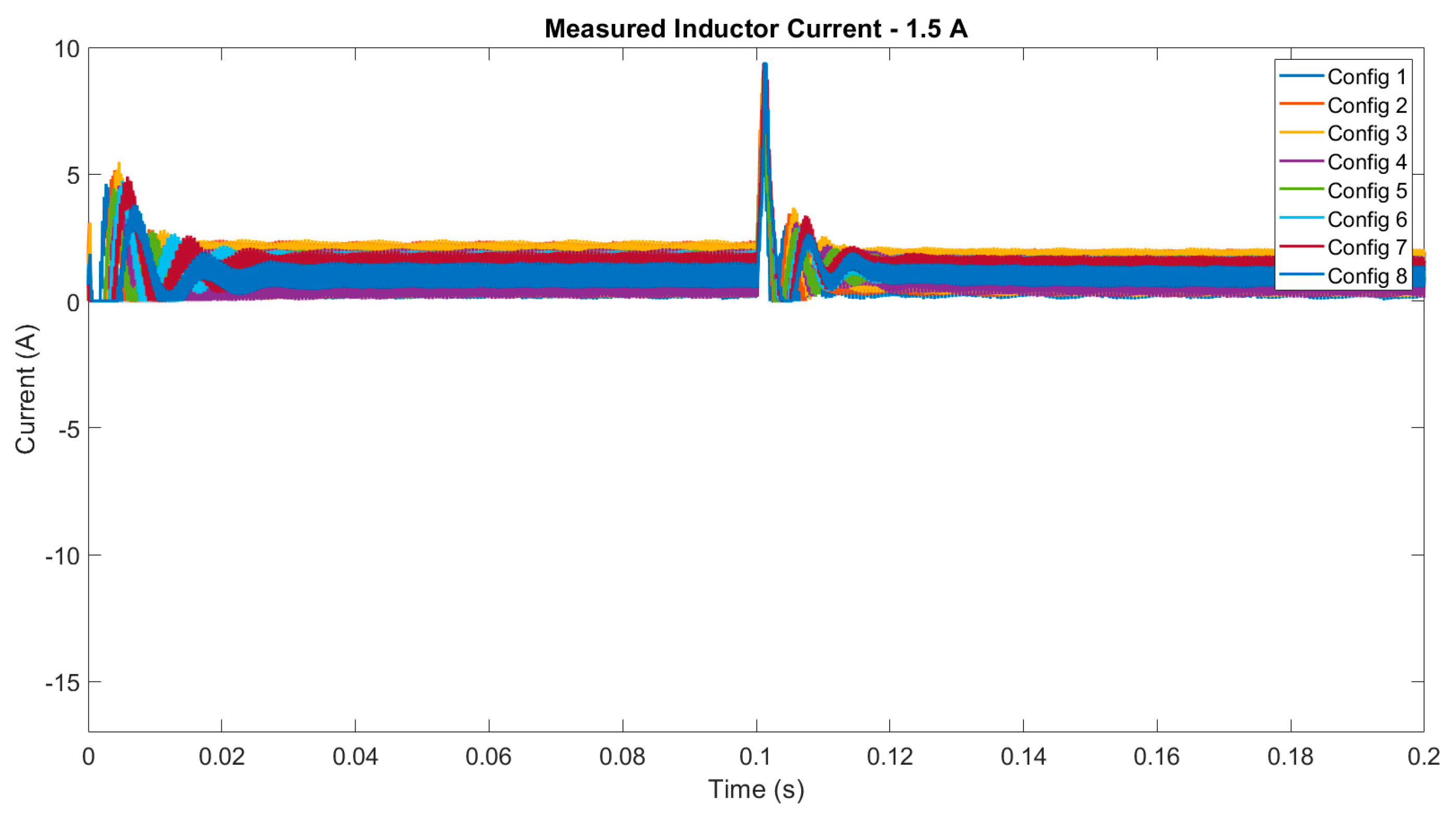
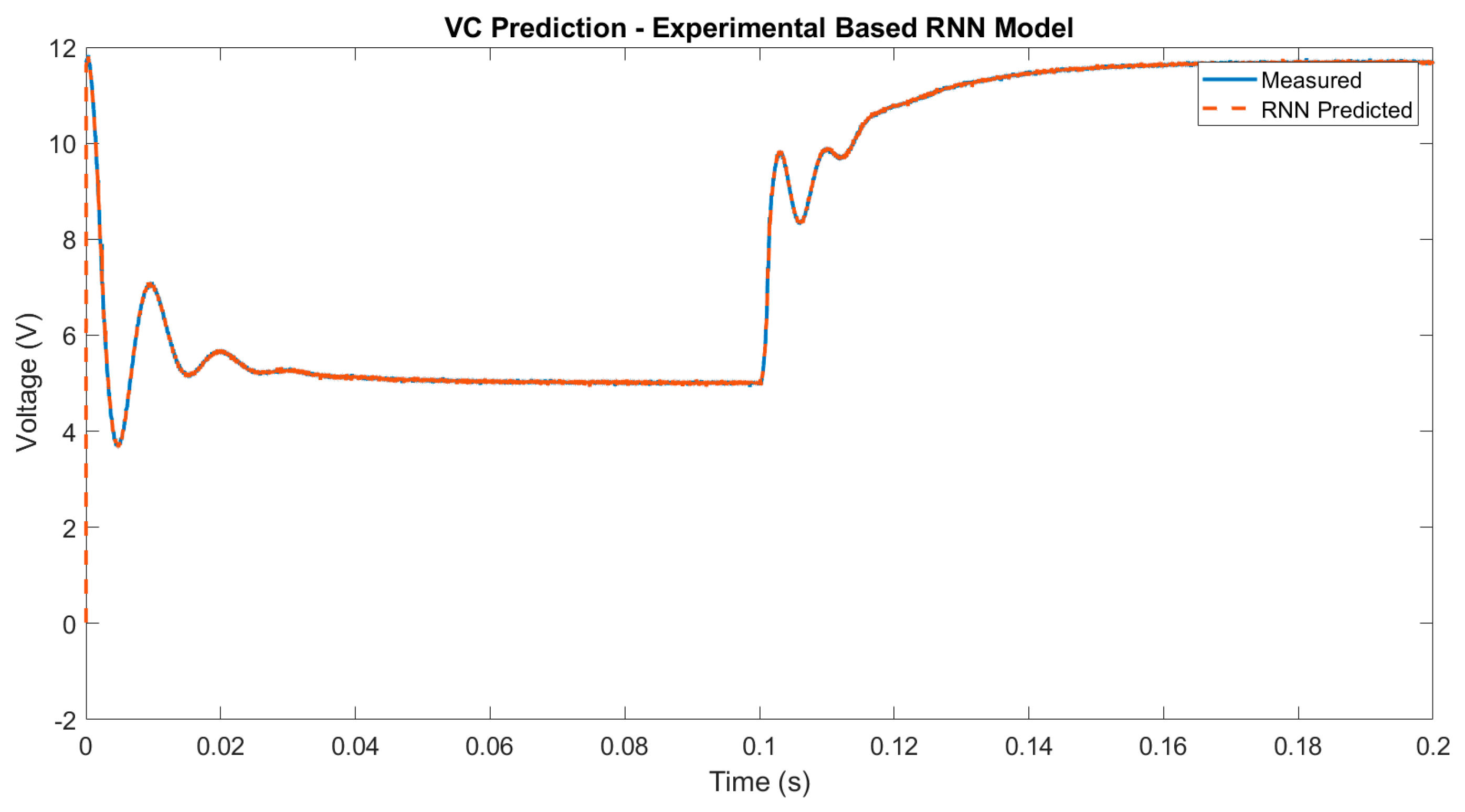
4. Experimental Results
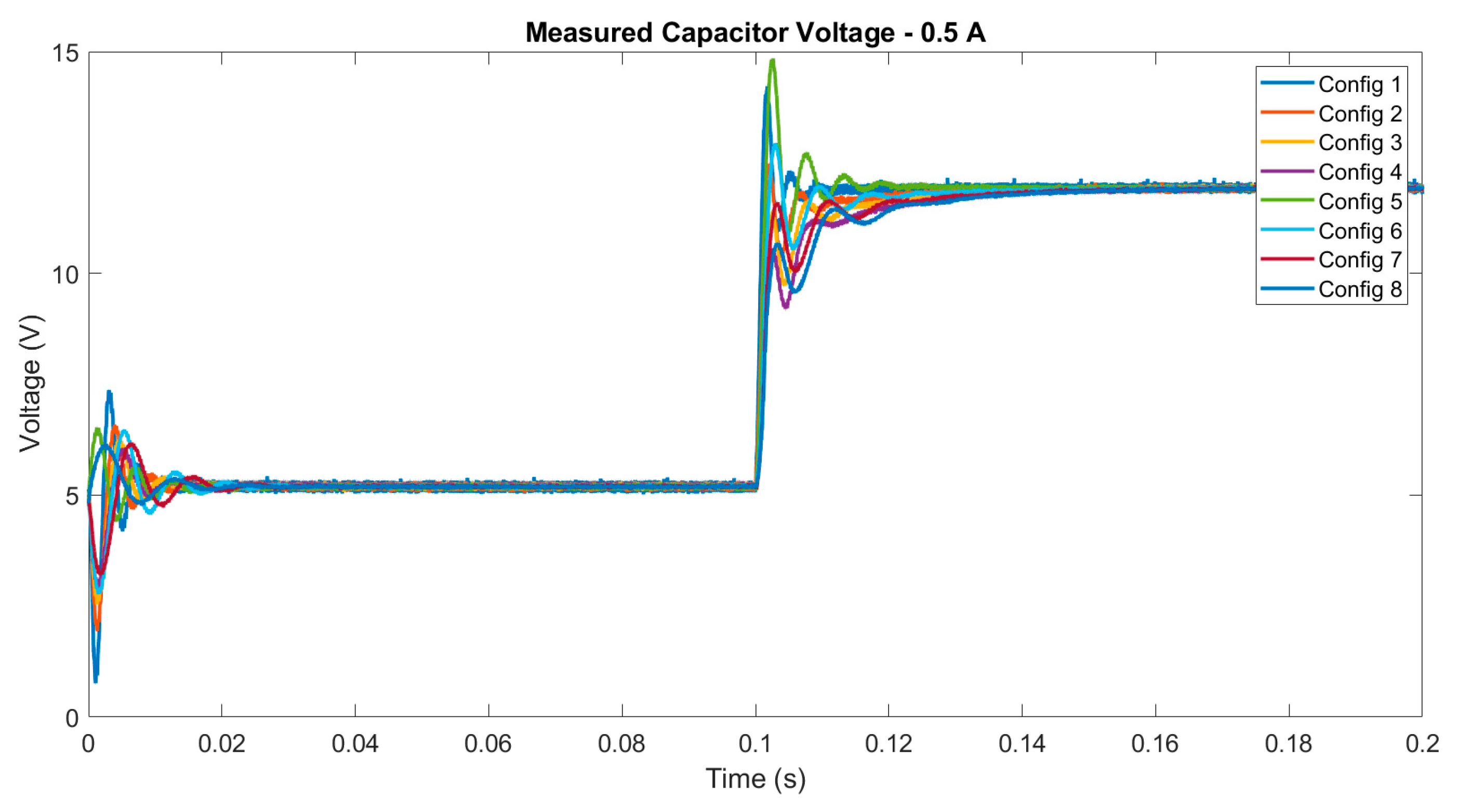
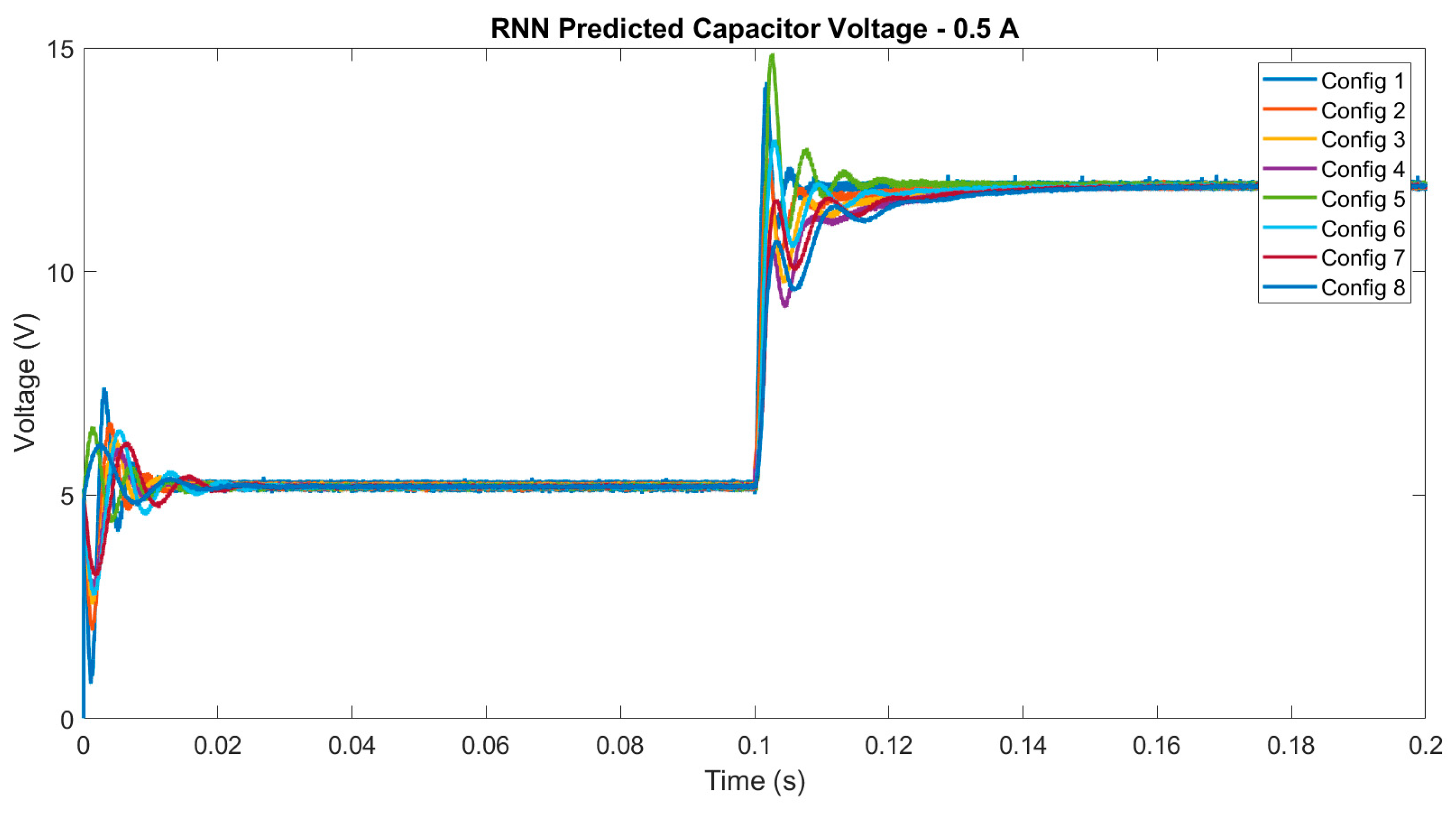
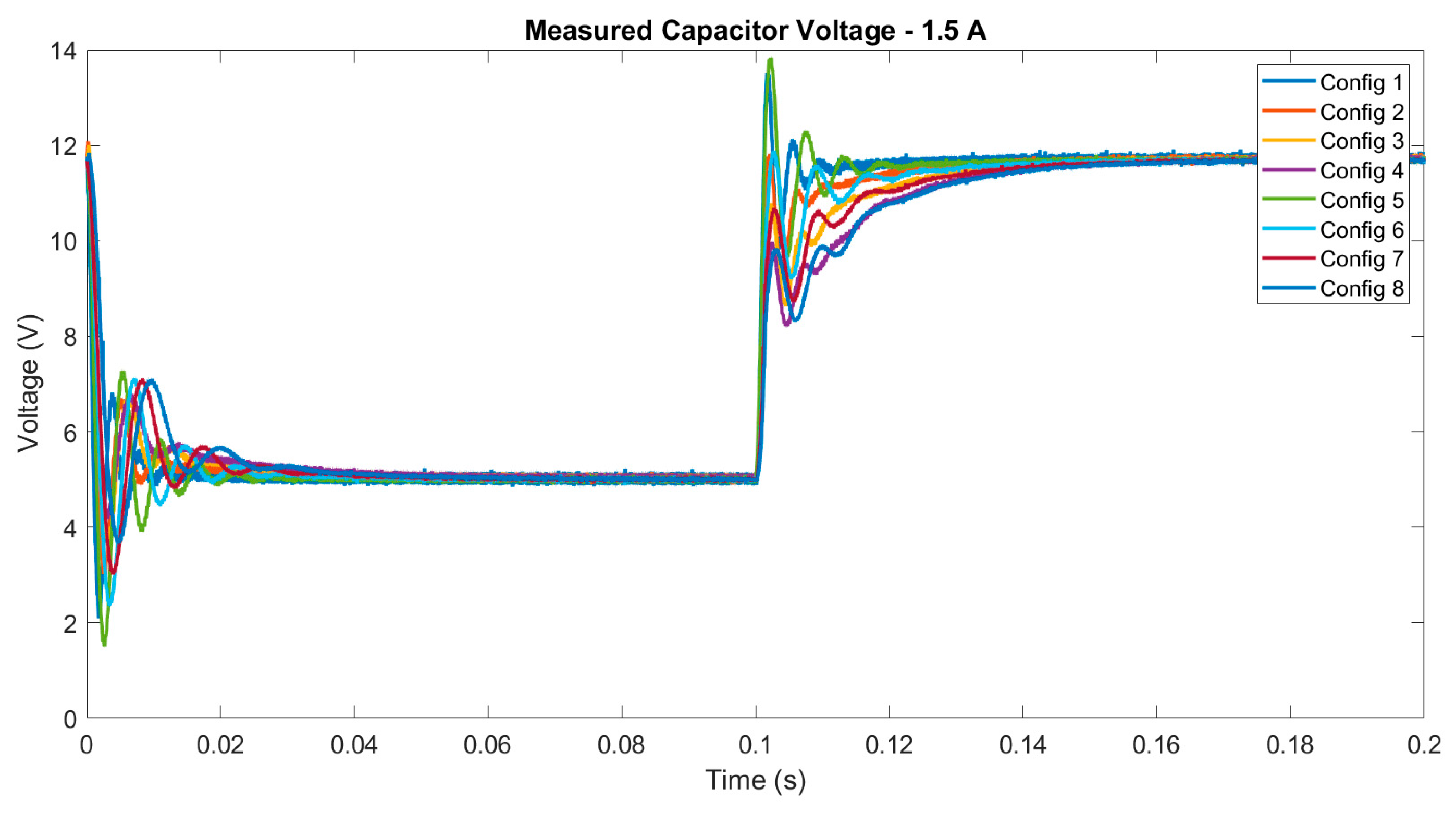
4.1. Digital Twin Testing for Model Trained with Experimental Data
4.2. Digital Twin Trained with Experimental Data Tested on a Physical Converter
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- McCoy, T.J. Electric Ships Past, Present, and Future [Technology Leaders]. IEEE Electrif. Mag. 2015, 3, 4–11. [Google Scholar] [CrossRef]
- Jin, Z.; Sulligoi, G.; Cuzner, R.; Meng, L.; Vasquez, J.C.; Guerrero, J.M. Next-Generation Shipboard DC Power System: Introduction Smart Grid and DC Microgrid Technologies into Maritime Electrical Networks. IEEE Electrif. Mag. 2016, 4, 45–57. [Google Scholar] [CrossRef]
- Al-Falahi, M.D.A.; Tarasiuk, T.; Jayasinghe, S.G.; Jin, Z. AC ship microgrids: Control and power management optimization. Energies 2018, 11, 1458. [Google Scholar] [CrossRef]
- Fang, S.; Wang, Y.; Gou, B.; Xu, Y. Toward Future Green Maritime Transportation: An Overview of Seaport Microgrids and All-Electric Ships. IEEE Trans. Veh. Technol. 2020, 69, 207–219. [Google Scholar] [CrossRef]
- de la Cruz, J.; Wu, Y.; Candelo-Becerra, J.E.; Vásquez, J.C.; Guerrero, J.M. Review of Networked Microgrid Protection: Architectures, Challenges, Solutions, and Future Trends. CSEE J. Power Energy Syst. 2024, 10, 448–467. [Google Scholar]
- Peyghami, S.; Fotuhi-Firuzabad, M.; Blaabjerg, F. Reliability Evaluation in Microgrids with Non-Exponential Failure Rates of Power Units. IEEE Syst. J. 2020, 14, 2861–2872. [Google Scholar] [CrossRef]
- Peyghami, S.; Blaabjerg, F.; Fotuhi-Firuzabad, M. Model-Based Reliability-Centered Design of Power Electronics Dominated Microgrids. In Proceedings of the 2022 17th International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Manchester, UK, 12–15 June 2022; pp. 1–6. [Google Scholar]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An Industry-Based Survey of Reliability in Power Electronic Converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Ma, Z.; Li, Y.; Feng, J.; Fu, N.; Shi, W.; Liang, D. Influence of Power Electronic Devices Failure Rate on Wind Turbine System Reliability. In Proceedings of the 2024 8th International Conference on Green Energy and Applications (ICGEA), Singapore, 14–16 March 2024; pp. 192–195. [Google Scholar]
- Peyghami, S.; Davari, P.; Fotuhi-Firuzabad, M.; Blaabjerg, F. Failure Mode, Effects and Criticality Analysis (FMECA) in Power Electronic-Based Power Systems. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. P.1–P.9. [Google Scholar]
- Li, C.; Spro, O.C.; Fosso, O.B. Lifetime Modelling of Power Electronics for Power Electronic-Based Power System—A Case for Microgrids. In Proceedings of the 2021 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chengdu, China, 18–21 July 2021; pp. 483–488. [Google Scholar]
- Tao, F.; Zhang, H.; Liu, A.; Nee, A.Y.C. Digital Twin in Industry: State-of-the-Art. IEEE Trans. Ind. Inform. 2019, 15, 2405–2415. [Google Scholar] [CrossRef]
- Rajendran, S.; Devi, V.S.K.; Diaz, M. Digital Twin Based Identification of Degradation Parameters of DC-DC Converters Using an Arithmetic Optimization Algorithm. In Proceedings of the 2022 3rd International Conference for Emerging Technology (INCET), Belgaum, India, 27–29 May 2022; pp. 1–5. [Google Scholar]
- Lima, D.M.; Souza, F.A.A.; Morais, E.E.C.; Honório, D.A.; Barreto, L.H.S.C. Proof of Concept of Fault Detection and Identification Framework Applied in Power Converter Based on Digital Twins. In Proceedings of the 2022 Workshop on Communication Networks and Power Systems (WCNPS), Fortaleza, Brazil, 17–18 November 2022; pp. 1–6. [Google Scholar]
- Jessie, B.; Fahimi, B.; Balsara, P. Development of Adaptive Digital Twin for DC-DC Converters Using Artificial Neural Networks. In Proceedings of the 2024 IEEE Transportation Electrification Conference and Expo (ITEC), Chicago, IL, USA, 19–21 June 2024; pp. 1–5. [Google Scholar]
- Ahmeid, M.; Armstrong, M.; Gadoue, S.; Al-Greer, M.; Missailidis, P. Real-Time Parameter Estimation of DC–DC Converters Using a Self-Tuned Kalman Filter. IEEE Trans. Power Electron. 2017, 32, 5666–5674. [Google Scholar] [CrossRef]
- Candan, M.Y.; Ankarali, M.M. Extended Kalman Filter Based State and Parameter Estimation Method for a Buck Converter Operating in a Wide Load Range. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; pp. 3238–3244. [Google Scholar]
- Gaulocher, S.; Papafotiou, G. Explicit Moving Horizon Estimation in DC-DC Converters. In Proceedings of the 2009 European Control Conference (ECC), Budapest, Hungary, 23–26 August 2009; pp. 3945–3950. [Google Scholar]
- Li, Y.; Bohara, B.; Krishnamoorthy, H.S.; Seshadrinath, J. Data-Driven Digital Twins for Monitoring the Health and Performance of Converters. In Proceedings of the 2024 IEEE International Communications Energy Conference (INTELEC), Bengaluru, India, 4–7 August 2024; pp. 1–6. [Google Scholar]
- Rojas-Dueñas, G.; Riba, J.-R.; Moreno-Eguilaz, M. Black-Box Modeling of DC–DC Converters Based on Wavelet Convolutional Neural Networks. IEEE Trans. Instrum. Meas. 2021, 70, 2005609. [Google Scholar] [CrossRef]
- Rojas-Dueñas, G.; Riba, J.-R.; Kahalerras, K.; Moreno-Eguilaz, M.; Kadechkar, A.; Gomez-Pau, A. Black-Box Modelling of a DC-DC Buck Converter Based on a Recurrent Neural Network. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020; pp. 456–461. [Google Scholar]
- Abbas, G.; Nawaz, M.; Kamran, F. Performance Comparison of NARX & RNN-LSTM Neural Networks for LiFePO4 Battery State of Charge Estimation. In Proceedings of the 2019 16th International Bhurban Conference on Applied Sciences and Technology (IBCAST), Islamabad, Pakistan, 8–12 January 2019; pp. 463–468. [Google Scholar]
- Chen, S.; Wang, S.; Wen, P.; Zhao, S. Digital Twin for Degradation Parameters Identification of DC-DC Converters Based on Bayesian Optimization. In Proceedings of the 2021 IEEE International Conference on Prognostics and Health Management (ICPHM), Detroit (Romulus), MI, USA, 7–9 June 2021; pp. 1–9. [Google Scholar]
- Liu, Y.; Qing, X.; Chen, G. One-Cycle Digital Twin-Based Multiparameter Identification of Power Electronic Converters with Simple Implementation and High Accuracy. IEEE Trans. Instrum. Meas. 2024, 73, 3537311. [Google Scholar] [CrossRef]
- Di Nezio, G.; Di Benedetto, M.; Lidozzi, A.; Solero, L. Digital Twin Based Real-Time Analysis of DC-DC Boost Converters. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–7. [Google Scholar]
- Wunderlich, A.; Santi, E. Digital Twin Models of Power Electronic Converters Using Dynamic Neural Networks. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 14–17 June 2021. [Google Scholar]
- Jessie, B.J.; Franzese, P.; Fahimi, B.; Iannuzzi, D. Recurrent Neural Network vs Kalman Filter for Development of Digital Twin of DC-DC Converters. In Proceedings of the 2024 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Naples, Italy, 26–29 November 2024; pp. 1–8. [Google Scholar] [CrossRef]
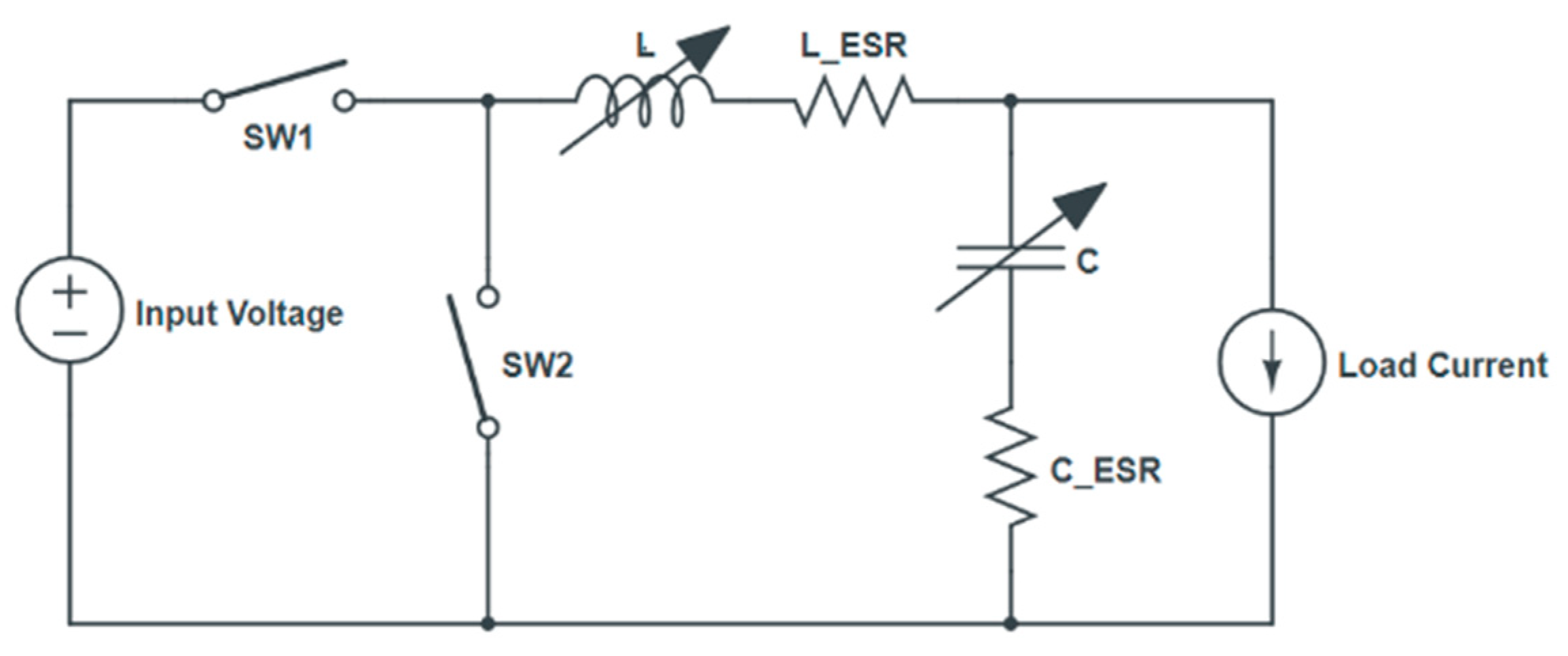
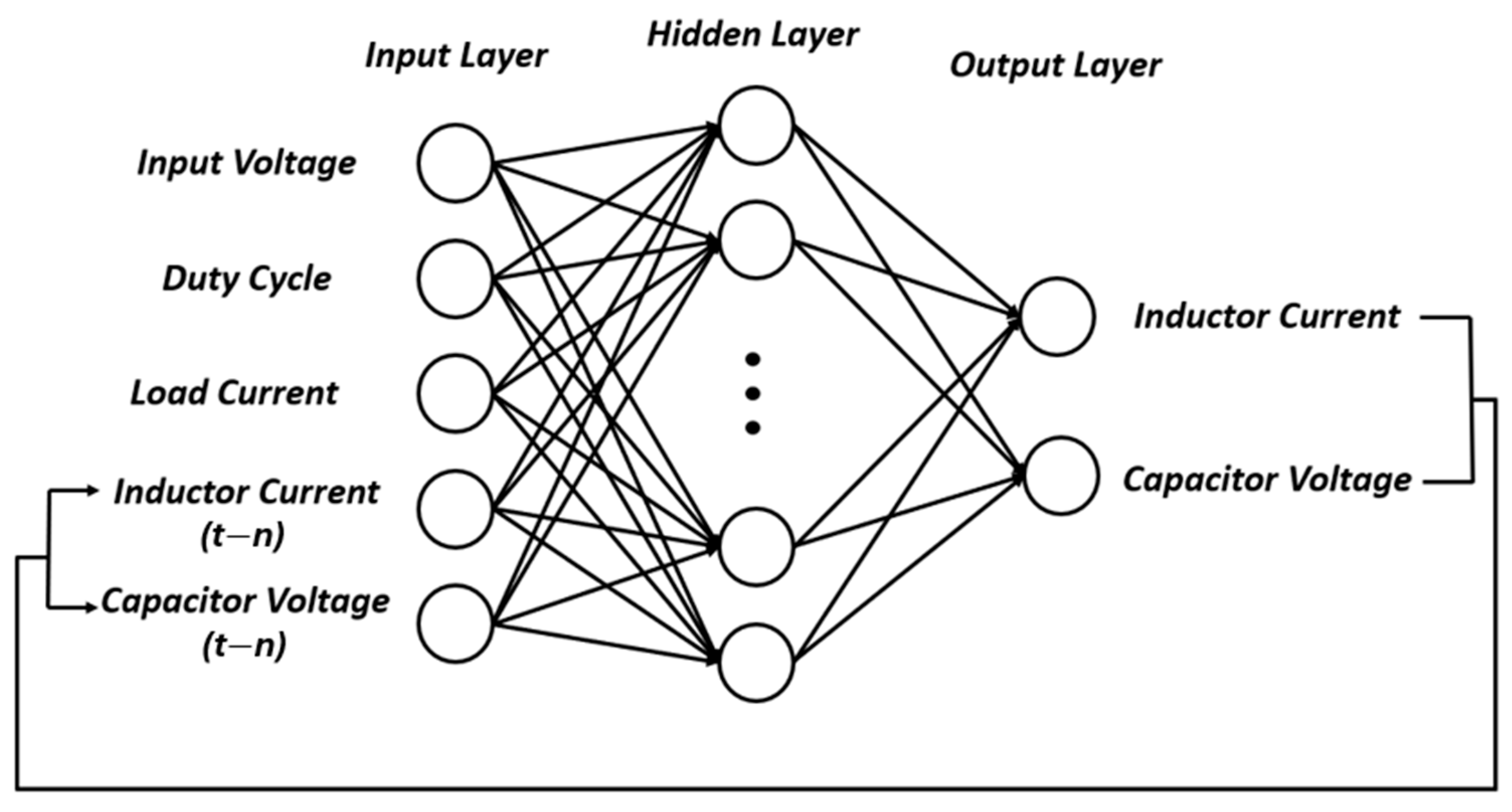

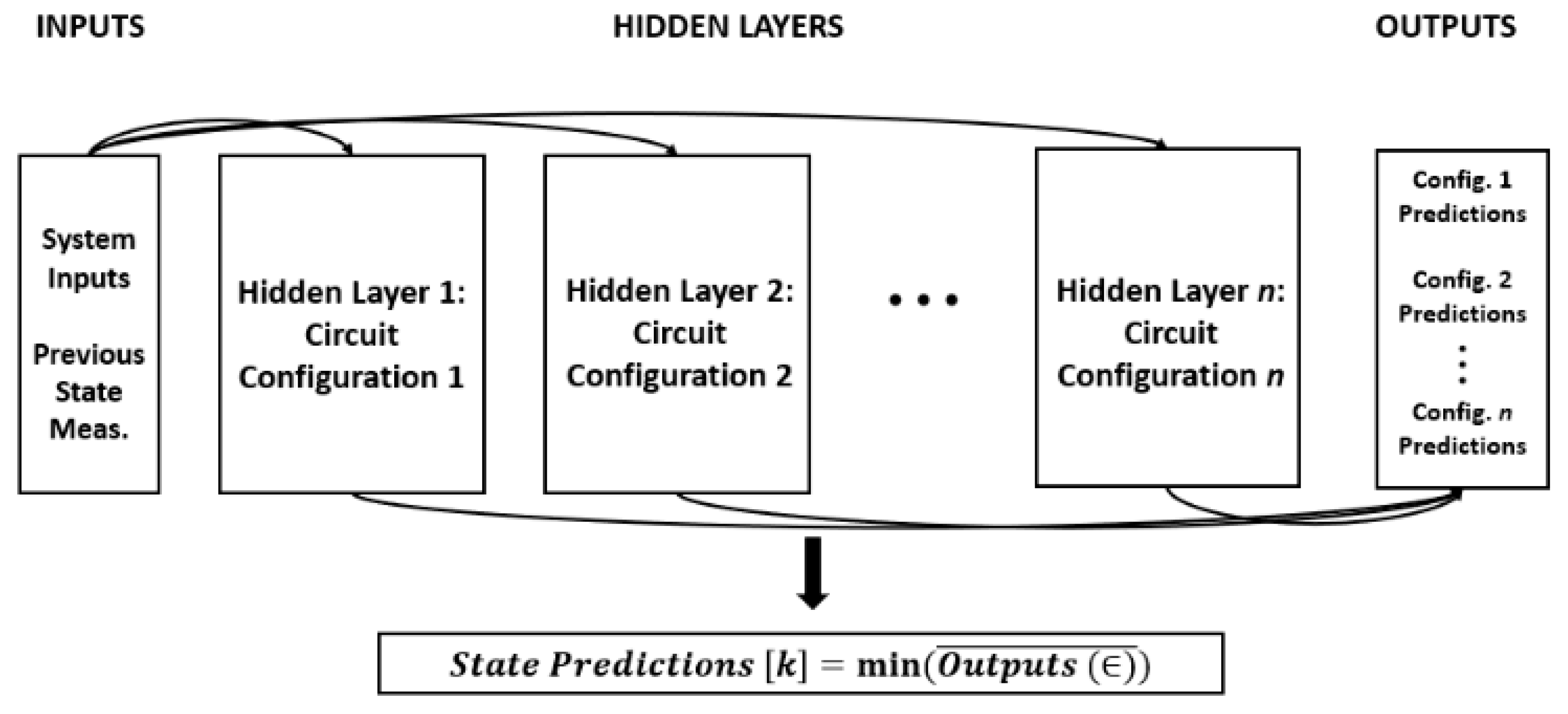
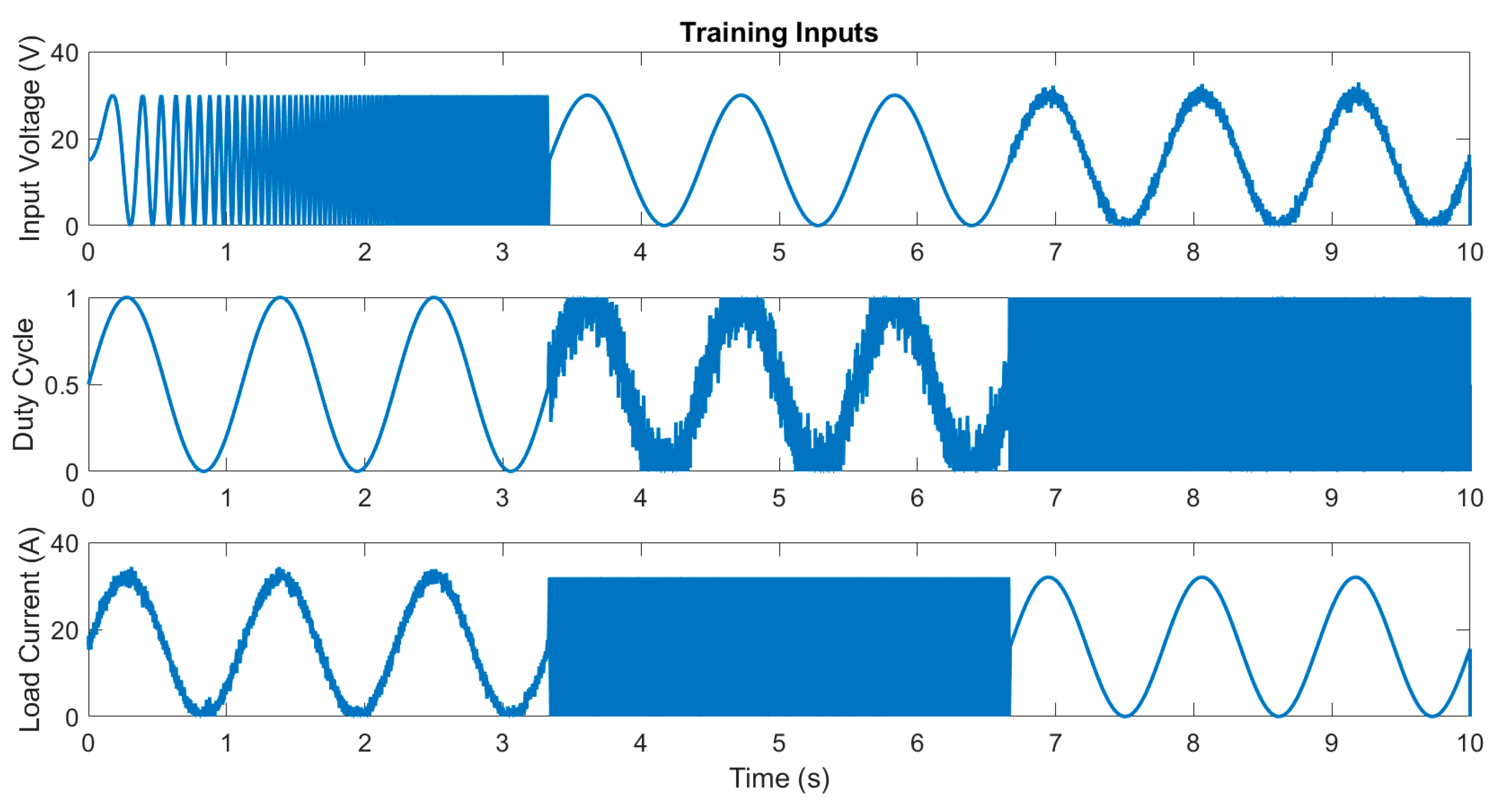





| Buck Converter Circuit Parameters | |
|---|---|
| Inductance | |
| Capacitance | |
| Switch Resistance | |
| Capacitive ESR | |
| Inductive ESR | |
| Buck Converter Configurations | ||
|---|---|---|
| Configuration 1 | Capacitance: | Inductance: |
| Configuration 2 | Capacitance: | Inductance: |
| Configuration 3 | Capacitance: | Inductance: |
| Configuration 4 | Capacitance: | Inductance: |
| Configuration 5 | Capacitance: | Inductance: |
| Configuration 6 | Capacitance: | Inductance: |
| Configuration 7 | Capacitance: | Inductance: |
| Configuration 8 | Capacitance: | Inductance: |
| Inductor Current RNN Prediction Error Mean | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 | Layer 7 | Layer 8 | Scale | ||
| Config 1 | 0.1416 | 0.1608 | 0.1626 | 0.1627 | 0.2674 | 0.2707 | 0.2740 | 0.2761 | 0.0703 | |
| Config 2 | 0.1613 | 0.1407 | 0.1591 | 0.1618 | 0.2520 | 0.2709 | 0.2744 | 0.2766 | 0.0998 | |
| Config 3 | 0.1625 | 0.1584 | 0.1414 | 0.1553 | 0.2675 | 0.2656 | 0.2735 | 0.2765 | 0.1293 | |
| Config 4 | 0.1638 | 0.1623 | 0.1566 | 0.1401 | 0.2705 | 0.2536 | 0.2703 | 0.2758 | 0.1587 | |
| Config 5 | 0.2649 | 0.2508 | 0.2647 | 0.2682 | 0.0709 | 0.1012 | 0.1044 | 0.1070 | 0.1882 | |
| Config 6 | 0.2681 | 0.2697 | 0.2628 | 0.2512 | 0.1013 | 0.0708 | 0.1022 | 0.1074 | 0.2177 | |
| Config 7 | 0.2714 | 0.2731 | 0.2707 | 0.2679 | 0.1049 | 0.1027 | 0.0703 | 0.1008 | 0.2471 | |
| Config 8 | 0.2735 | 0.2753 | 0.2737 | 0.2735 | 0.1071 | 0.1074 | 0.1005 | 0.0707 | 0.2766 | |
| Capacitor Voltage RNN Prediction Error Mean | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 | Layer 7 | Layer 8 | Scale | ||
| Config 1 | 0.0004 | 0.0133 | 0.0125 | 0.0127 | 0.0173 | 0.0156 | 0.0155 | 0.0160 | 0.0003 | |
| Config 2 | 0.0333 | 0.0023 | 0.0176 | 0.0210 | 0.0211 | 0.0334 | 0.0345 | 0.0349 | 0.0073 | |
| Config 3 | 0.0355 | 0.0182 | 0.0022 | 0.0110 | 0.0359 | 0.0231 | 0.0276 | 0.0283 | 0.0143 | |
| Config 4 | 0.0371 | 0.0218 | 0.0116 | 0.0011 | 0.0395 | 0.0160 | 0.0226 | 0.0250 | 0.0213 | |
| Config 5 | 0.0494 | 0.0215 | 0.0351 | 0.0385 | 0.0020 | 0.0430 | 0.0450 | 0.0461 | 0.0283 | |
| Config 6 | 0.0484 | 0.0341 | 0.0237 | 0.0165 | 0.0439 | 0.0006 | 0.0310 | 0.0333 | 0.0354 | |
| Config 7 | 0.0486 | 0.0352 | 0.0280 | 0.0231 | 0.0458 | 0.0313 | 0.0003 | 0.0235 | 0.0424 | |
| Config 8 | 0.0491 | 0.0355 | 0.0288 | 0.0254 | 0.0469 | 0.0336 | 0.0237 | 0.0005 | 0.0494 | |
| RNN Prediction Error for Small Component Variations | |||||
|---|---|---|---|---|---|
| Rated | 5% Increase | 10% Increase | 5% Decrease | 10% Decrease | |
| IL Error Mean (A) | 0.0707 | 0.0673 | 0.0642 | 0.0744 | 0.0786 |
| IL Error Variance (A) | 0.0014 | 0.0013 | 0.0013 | 0.0016 | 0.0017 |
| VC Error Mean (V) | 5.04 × 10−4 | 5.09 × 10−4 | 5.18 × 10−4 | 5.04 × 10−4 | 5.11 × 10−4 |
| VC Error Variance (V) | 4.99 × 10−5 | 4.99 × 10−5 | 4.99 × 10−5 | 4.99 × 10−5 | 4.99 × 10−5 |
| Capacitor Voltage RNN Prediction Error Mean—0.5A Load Current | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 | Layer 7 | Layer 8 | Scale | ||
| Config 1 | 0.0309 | 0.1148 | 0.1819 | 0.2490 | 0.2076 | 0.2098 | 0.2407 | 0.2781 | 0.0228 | |
| Config 2 | 0.1138 | 0.0279 | 0.0899 | 0.1606 | 0.2079 | 0.1508 | 0.1657 | 0.2009 | 0.0593 | |
| Config 3 | 0.1930 | 0.1113 | 0.0256 | 0.0767 | 0.2313 | 0.1177 | 0.1123 | 0.1503 | 0.0957 | |
| Config 4 | 0.2545 | 0.1753 | 0.0932 | 0.0279 | 0.2580 | 0.1292 | 0.0966 | 0.1176 | 0.1322 | |
| Config 5 | 0.1835 | 0.1841 | 0.2259 | 0.2598 | 0.0348 | 0.1793 | 0.2336 | 0.2411 | 0.1687 | |
| Config 6 | 0.2035 | 0.1482 | 0.1195 | 0.1325 | 0.1693 | 0.0234 | 0.1202 | 0.1817 | 0.2052 | |
| Config 7 | 0.2373 | 0.1708 | 0.1178 | 0.0903 | 0.2268 | 0.1163 | 0.0246 | 0.1282 | 0.2417 | |
| Config 8 | 0.2747 | 0.2041 | 0.1556 | 0.1201 | 0.2338 | 0.1831 | 0.1332 | 0.0228 | 0.2781 | |
| Capacitor Voltage RNN Prediction Error Mean—1.5A Load Current | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 | Layer 7 | Layer 8 | Scale | ||
| Config 1 | 0.0316 | 0.1937 | 0.3030 | 0.3732 | 0.2197 | 0.2502 | 0.3298 | 0.4336 | 0.0250 | |
| Config 2 | 0.2085 | 0.0334 | 0.1844 | 0.2638 | 0.1772 | 0.1783 | 0.2253 | 0.3381 | 0.0839 | |
| Config 3 | 0.3037 | 0.1898 | 0.0295 | 0.1234 | 0.2697 | 0.1646 | 0.1446 | 0.2159 | 0.1427 | |
| Config 4 | 0.3768 | 0.2608 | 0.1407 | 0.0317 | 0.3649 | 0.2407 | 0.1656 | 0.1596 | 0.2016 | |
| Config 5 | 0.2093 | 0.1796 | 0.2646 | 0.3615 | 0.0369 | 0.2200 | 0.3242 | 0.4350 | 0.2605 | |
| Config 6 | 0.2523 | 0.1733 | 0.1632 | 0.2317 | 0.2187 | 0.0253 | 0.1693 | 0.3074 | 0.3193 | |
| Config 7 | 0.3372 | 0.2251 | 0.1500 | 0.1655 | 0.3164 | 0.1737 | 0.0268 | 0.1785 | 0.3782 | |
| Config 8 | 0.4371 | 0.3431 | 0.2225 | 0.1540 | 0.4330 | 0.3089 | 0.1767 | 0.0250 | 0.4371 | |
| Inductor Current RNN Prediction Error Mean—0.5A Load Current | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 | Layer 7 | Layer 8 | Scale | ||
| Config 1 | 0.2605 | 0.2228 | 0.2701 | 0.5116 | 0.5793 | 0.5877 | 0.5743 | 0.5772 | 0.1257 | |
| Config 2 | 0.3250 | 0.2235 | 0.2305 | 0.4921 | 0.6243 | 0.5973 | 0.5930 | 0.5973 | 0.2077 | |
| Config 3 | 0.5308 | 0.4658 | 0.2305 | 0.3081 | 0.6997 | 0.5335 | 0.4439 | 0.5290 | 0.2897 | |
| Config 4 | 0.6721 | 0.6125 | 0.4524 | 0.2190 | 0.6149 | 0.3393 | 0.3842 | 0.3208 | 0.3717 | |
| Config 5 | 0.4604 | 0.4215 | 0.5649 | 0.5960 | 0.2771 | 0.4200 | 0.6366 | 0.4245 | 0.4537 | |
| Config 6 | 0.6662 | 0.6180 | 0.6113 | 0.4622 | 0.4149 | 0.2245 | 0.5468 | 0.2644 | 0.5357 | |
| Config 7 | 0.6293 | 0.5953 | 0.4810 | 0.2736 | 0.5524 | 0.3129 | 0.3087 | 0.2651 | 0.6177 | |
| Config 8 | 0.6150 | 0.5899 | 0.5874 | 0.4330 | 0.3856 | 0.1928 | 0.5035 | 0.1257 | 0.6997 | |
| Inductor Current RNN Prediction Error Mean—1.5A Load Current | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 | Layer 7 | Layer 8 | Scale | ||
| Config 1 | 0.2908 | 0.5997 | 0.7520 | 0.5065 | 0.7123 | 0.4781 | 0.4772 | 0.6017 | 0.1555 | |
| Config 2 | 0.8210 | 0.3078 | 0.9155 | 0.8467 | 0.7438 | 0.7230 | 0.6435 | 0.7523 | 0.2641 | |
| Config 3 | 0.6146 | 0.8839 | 0.2992 | 0.3593 | 0.6206 | 0.4176 | 0.7600 | 0.4952 | 0.3727 | |
| Config 4 | 0.2801 | 0.6791 | 0.5723 | 0.2902 | 0.6476 | 0.3411 | 0.5656 | 0.5035 | 0.4812 | |
| Config 5 | 0.6528 | 0.7037 | 0.3110 | 0.4969 | 0.3769 | 0.4333 | 0.6443 | 0.4527 | 0.5898 | |
| Config 6 | 0.4639 | 0.6085 | 0.5577 | 0.4455 | 0.5974 | 0.2700 | 0.4179 | 0.4664 | 0.6984 | |
| Config 7 | 0.6491 | 0.4056 | 0.7517 | 0.6591 | 0.6612 | 0.4838 | 0.3291 | 0.5268 | 0.8069 | |
| Config 8 | 0.4719 | 0.6925 | 0.4301 | 0.3470 | 0.4624 | 0.2651 | 0.5346 | 0.1555 | 0.9155 | |
| Mean State Prediction Error for Simulation-Based Digital Twin Applied to Physical Buck Converter | ||
|---|---|---|
| 0.5 A Load Current | 1.5 A Load Current | |
| Inductor Current | 0.0733 A | 0.0725 A |
| Capacitor Voltage | 0.0211 V | 0.0319 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jessie, B.; Westergaard, T.; Fahimi, B.; Balsara, P. Development of Digital Twin for DC-DC Converters Under Varying Parameter Conditions. Electronics 2025, 14, 2549. https://doi.org/10.3390/electronics14132549
Jessie B, Westergaard T, Fahimi B, Balsara P. Development of Digital Twin for DC-DC Converters Under Varying Parameter Conditions. Electronics. 2025; 14(13):2549. https://doi.org/10.3390/electronics14132549
Chicago/Turabian StyleJessie, Benjamin, Thor Westergaard, Babak Fahimi, and Poras Balsara. 2025. "Development of Digital Twin for DC-DC Converters Under Varying Parameter Conditions" Electronics 14, no. 13: 2549. https://doi.org/10.3390/electronics14132549
APA StyleJessie, B., Westergaard, T., Fahimi, B., & Balsara, P. (2025). Development of Digital Twin for DC-DC Converters Under Varying Parameter Conditions. Electronics, 14(13), 2549. https://doi.org/10.3390/electronics14132549







