Mutual Information-Oriented ISAC Beamforming Design for Large Dimensional Antenna Array
Abstract
1. Introduction
2. System Model
2.1. Signal Model
2.2. Channel Model
2.3. Problem Formulation
3. Problem Reformulation and Proposed Algorithm
3.1. Problem Reformulation
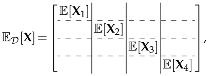
3.2. Proposed PGA Algorithm
| Algorithm 1 PGA algorithm for beamforming matrix design |
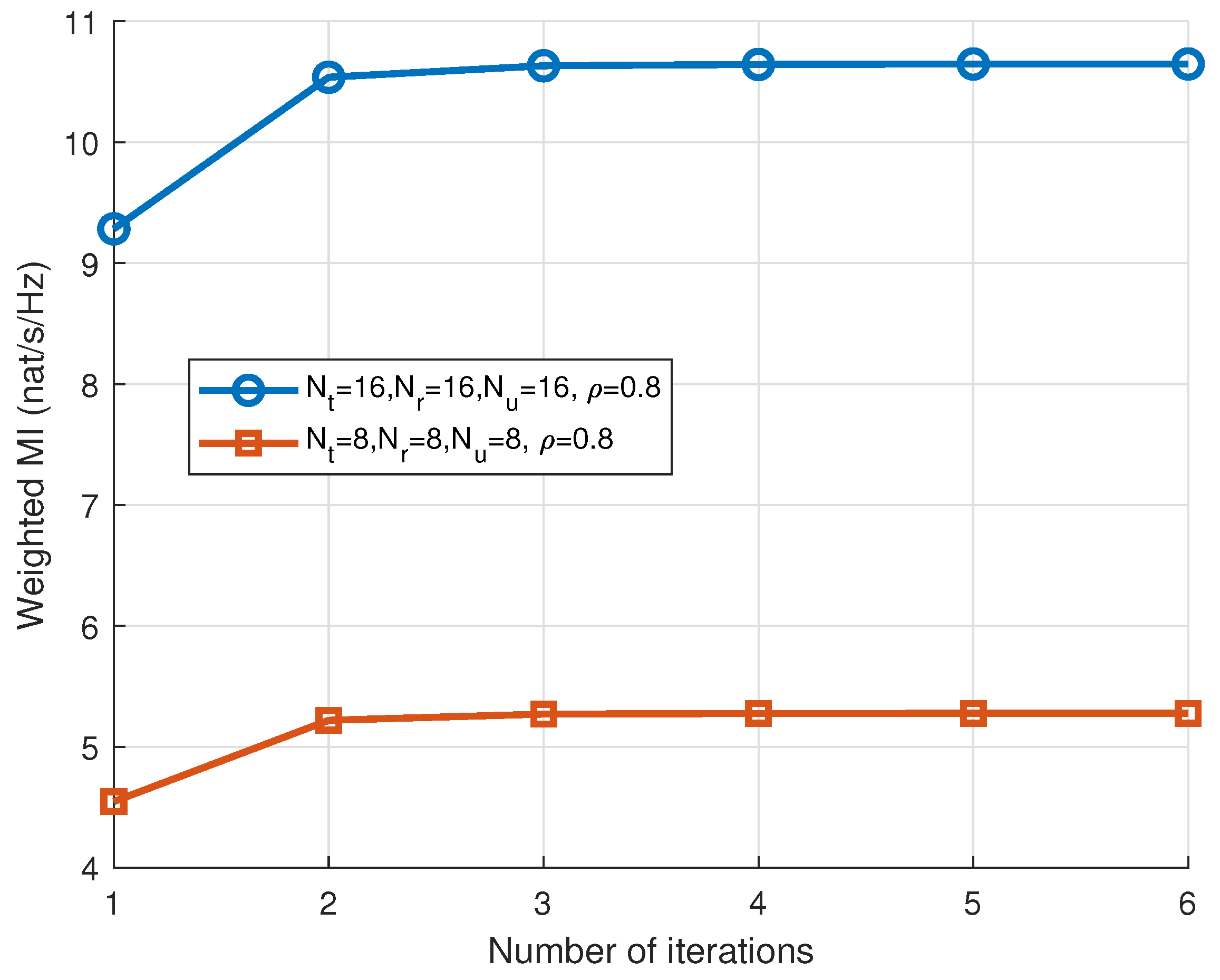
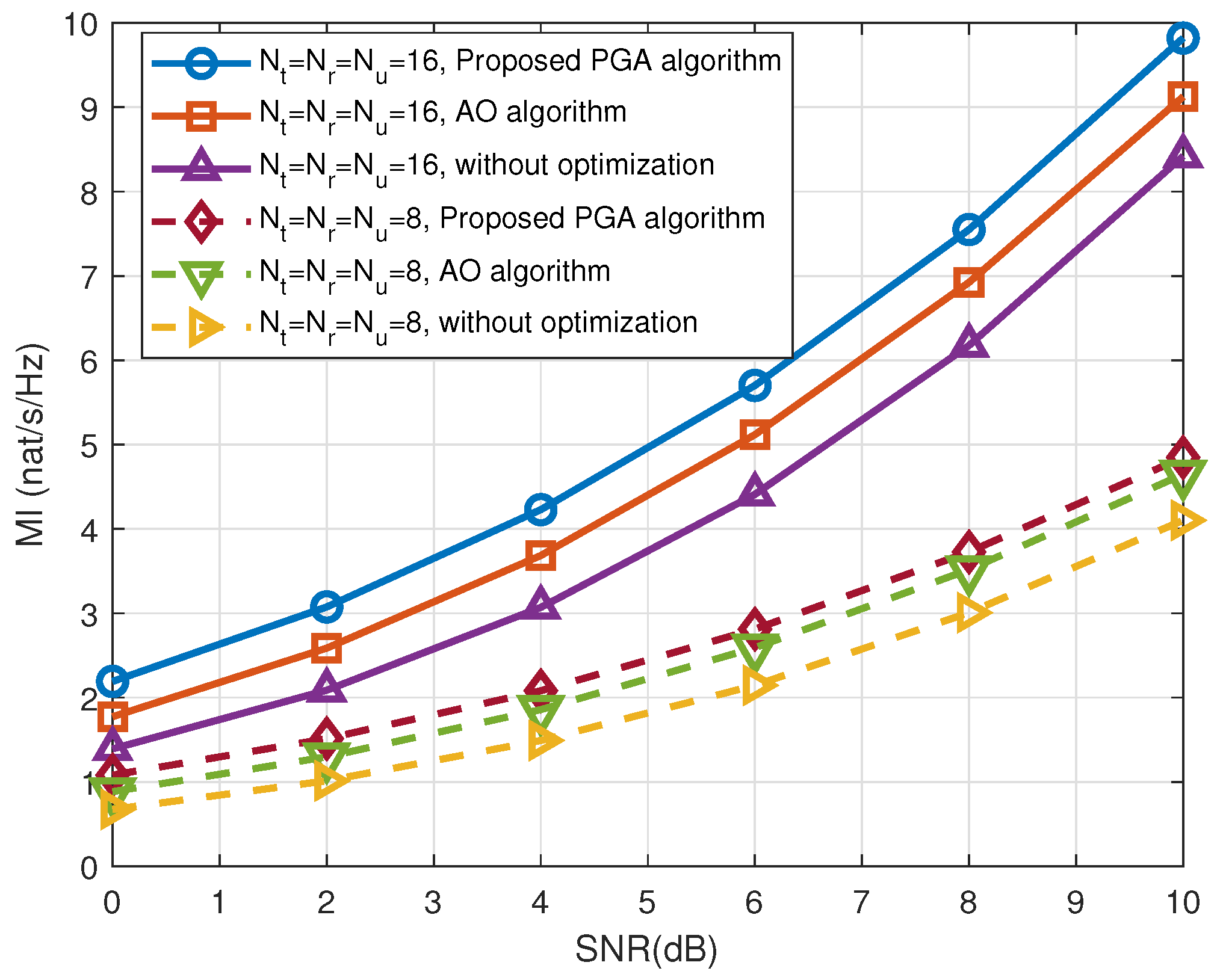
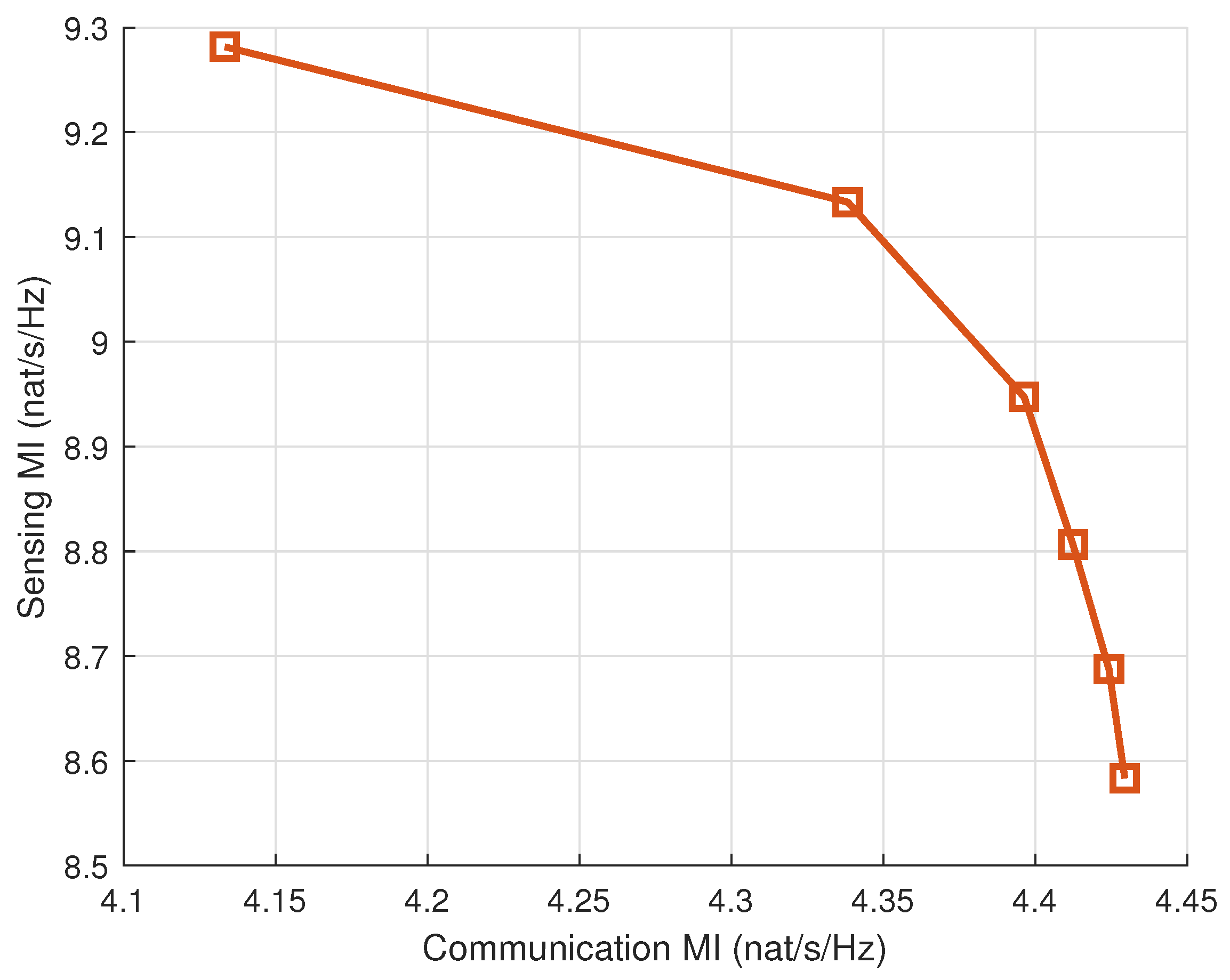
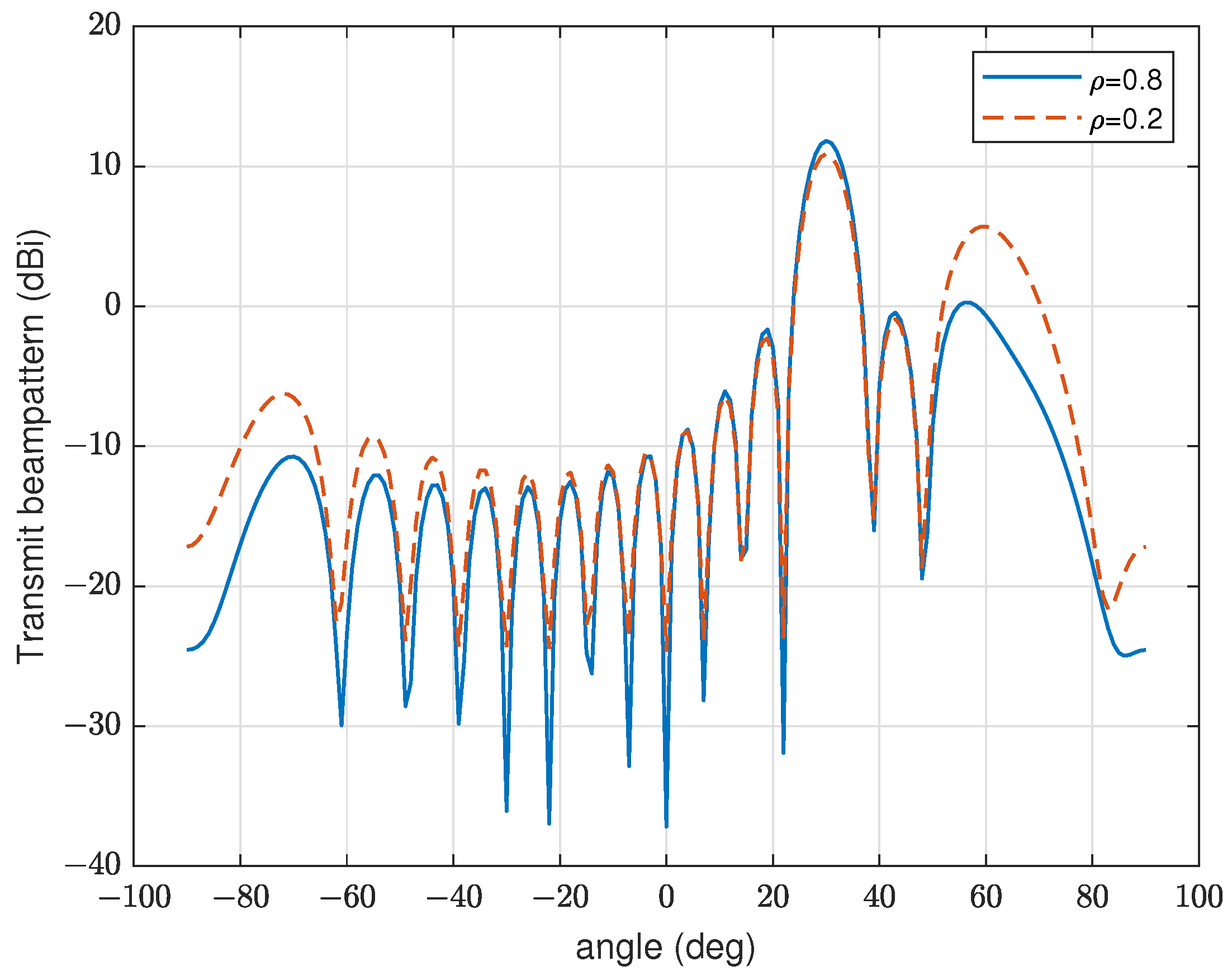
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Parameterized One-Sided Correlation Matrices
Appendix B. Proof of Proposition 2
References
- Zhang, J.A.; Rahman, M.L.; Wu, K.; Huang, X.; Guo, Y.J.; Chen, S.; Yuan, J. Enabling joint communication and radar sensing in mobile networks—A Survey. IEEE Commun. Surv. Tutor. 2022, 24, 306–345. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Li, A.; Sun, H.; Hanzo, L. Mu-MIMO communications with MIMO radar: From co-existence to joint transmission. IEEE Trans. Wirel. Commun. 2018, 7, 2755–2770. [Google Scholar] [CrossRef]
- Liu, F.; Liu, Y.; Li, A.; Eldar, C.M.Y. Cramér-Rao bound optimization for joint radar-communication beamforming. IEEE Trans. Wirel. Commun. 2022, 70, 240–253. [Google Scholar] [CrossRef]
- Liu, R.; Li, M.; Li, Q.; Swindlehurst, A. SNR/CRB-constrained joint beamforming and reflection designs for RIS-ISAC systems. IEEE Trans. Wirel. Commun. 2024, 7, 7456–7470. [Google Scholar] [CrossRef]
- Wang, X.; Fei, Z.; Zhang, J.A.; Xu, J. Partially-connected hybrid beamforming design for integrated sensing and communication systems. IEEE Trans. Commun. 2022, 70, 6648–6660. [Google Scholar] [CrossRef]
- Al-Jarrah, M.; Alsusa, E.; Masouros, C. A unified performance framework for integrated sensing-communications based on KL-divergence. IEEE Trans. Wirel. Commun. 2023, 22, 9390–9411. [Google Scholar] [CrossRef]
- Fei, Z.; Tang, S.; Wang, X. Revealing the Trade-Off in ISAC Systems: The KL Divergence Perspective. IEEE Wirel. Commun. Lett. 2024, 13, 2747–2751. [Google Scholar] [CrossRef]
- Li, J.; Zhou, G.; Gong, T.; Liu, N. A Framework for Mutual Information-Based MIMO Integrated Sensing and Communication Beamforming Design. IEEE Trans. Veh. Technol. 2024, 73, 8352–8366. [Google Scholar] [CrossRef]
- Piao, J.; Wei, Z.; Yuan, X.; Yang, X.; Wu, H.; Feng, Z. Mutual Information Metrics for Uplink MIMO-OFDM Integrated Sensing and Communication System. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 7387–7392. [Google Scholar]
- Huang, X.; Zhang, J.; Xia, W.; Cai, S.; Fan, F.; Yuen, C. Statistical CSI Assisted Beamforming for Co-Existence of MIMO Radar and MIMO Communication System. IEEE Trans. Veh. Technol. 2025. [CrossRef]
- Weichselberger, W.; Herdin, M.; Ozcelik, H.; Bonek, E. A stochastic MIMO channel model with joint correlation of both link ends. IEEE Trans. Wirel. Commun. 2006, 5, 90–100. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Zhang, J.A.; Di Renzo, M.; Quek, T.Q. Joint beamforming for RIS-assisted integrated sensing and communication systems. IEEE Trans. Commun. 2024, 72, 2232–2246. [Google Scholar] [CrossRef]
- Tulino, A.M.; Verdu, S. Random matrix theory and wireless communications. Found. Trends Commun. Inf. Theory 2004, 1, 1–18. [Google Scholar] [CrossRef]
- Hoydis, J.; Couillet, R.; Debbah, M. Asymptotic analysis of double-scattering channels. In Proceedings of the 2011 Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 6–9 November 2011; pp. 1935–1939. [Google Scholar]
- Silverstein, J.W. Strong convergence of the empirical distribution of eigenvalues of large dimensional random matrices. J. Multivar. Anal. 1995, 55, 331–339. [Google Scholar] [CrossRef]
- Belinschi, S.T.; Mai, T.; Speicher, R. Analytic subordination theory of operator-valued free additive convolution and the solution of a general random matrix problem. J. Reine Angew. Math. (Crelles J.) 2017, 2017, 21–53. [Google Scholar] [CrossRef]
- Muller, R.R. On the asymptotic eigenvalue distribution of concatenated vector-valued fading channels. IEEE Trans. Inf. Theory 2002, 48, 2086–2091. [Google Scholar] [CrossRef]
- Zheng, Z.; Wang, S.; Fei, Z.; Sun, Z.; Yuan, J. On the mutual information of multi-RIS assisted MIMO: From operator-valued free probability aspect. IEEE Trans. Commun. 2023, 71, 6952–6966. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Z.; Fei, Z.; Wang, X.; Guo, J. Analysis and Optimization of Multi-RIS-Assisted Dual-Functional Radar-Communication Systems via Free Probability Theory. In Proceedings of the GLOBECOM 2023—2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 6505–6510. [Google Scholar]
- Behdad, Z.; Demir, Ö.; Sung, K.; Björnson, E.; Cavdar, C. Multi-Static Target Detection and Power Allocation for Integrated Sensing and Communication in Cell-Free Massive MIMO. IEEE Trans. Wirel. Commun. 2024, 23, 11580–11596. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Z.; Fei, Z.; Guo, J.; Yuan, J.; Sun, Z. Toward Ergodic Sum Rate Maximization of Multiple-RIS-Assisted MIMO Multiple Access Channels Over Generic Rician Fading. IEEE Trans. Wirel. Commun. 2024, 23, 9613–9628. [Google Scholar] [CrossRef]
- Horn, R.; Johnson, C. Matrix Analysis; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]



| Closed-form expressions | 0.08 s | 0.63 s |
| Monte Carlo simulation | 5.53 s | 22.12 s |
| Proposed PGA algorithm | 0.54 s | 1.41 s |
| AO algorithm [19] | 7.88 s | 98.76 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Cheng, Y.; Wang, S.; Wang, X.; Zheng, Z.; Fei, Z. Mutual Information-Oriented ISAC Beamforming Design for Large Dimensional Antenna Array. Electronics 2025, 14, 2515. https://doi.org/10.3390/electronics14132515
Xu S, Cheng Y, Wang S, Wang X, Zheng Z, Fei Z. Mutual Information-Oriented ISAC Beamforming Design for Large Dimensional Antenna Array. Electronics. 2025; 14(13):2515. https://doi.org/10.3390/electronics14132515
Chicago/Turabian StyleXu, Shanfeng, Yanshuo Cheng, Siqiang Wang, Xinyi Wang, Zhong Zheng, and Zesong Fei. 2025. "Mutual Information-Oriented ISAC Beamforming Design for Large Dimensional Antenna Array" Electronics 14, no. 13: 2515. https://doi.org/10.3390/electronics14132515
APA StyleXu, S., Cheng, Y., Wang, S., Wang, X., Zheng, Z., & Fei, Z. (2025). Mutual Information-Oriented ISAC Beamforming Design for Large Dimensional Antenna Array. Electronics, 14(13), 2515. https://doi.org/10.3390/electronics14132515






