An Efficient Sparse Synthetic Aperture Radar Imaging Method Based on L1-Norm and Total Variation Regularization
Abstract
:1. Introduction
2. Imaging Mode
2.1. Sparse SAR Imaging Model
2.2. TV Regularized Sparse SAR Imaging Model
3. A Composite Regularization Framework for Sparse SAR Imaging Based on L1 and TV Norms
3.1. L1-TV Regularized Sparse Reconstruction Process
3.2. Construction of an Imaging Operator and an Echo Simulation Operator Based on Approximate Observation
3.3. Establishing a Sparse SAR Imaging Model with L1-TV Regularization
4. Performance Validation of L1-TV Regularized Sparse SAR Imaging Algorithm
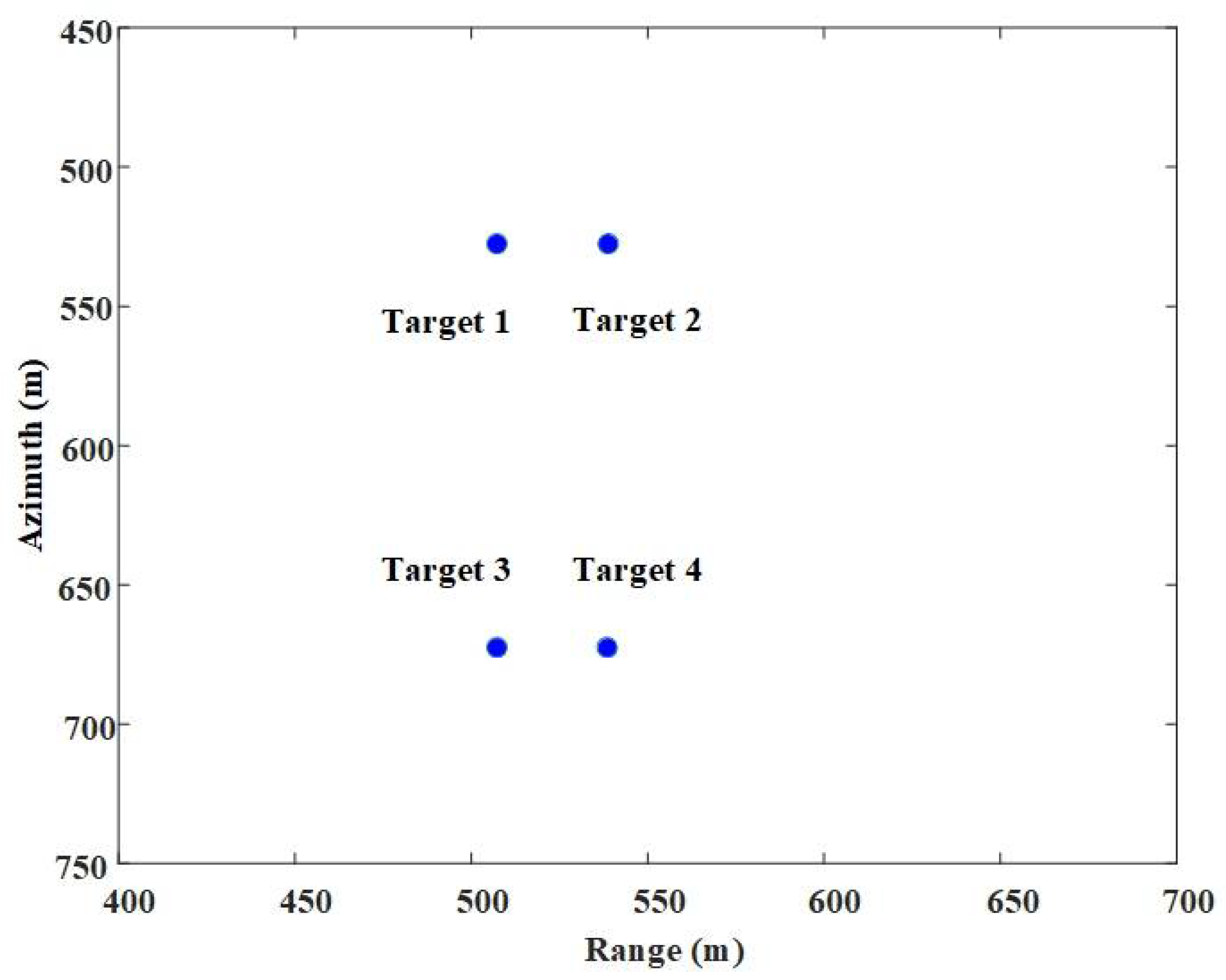
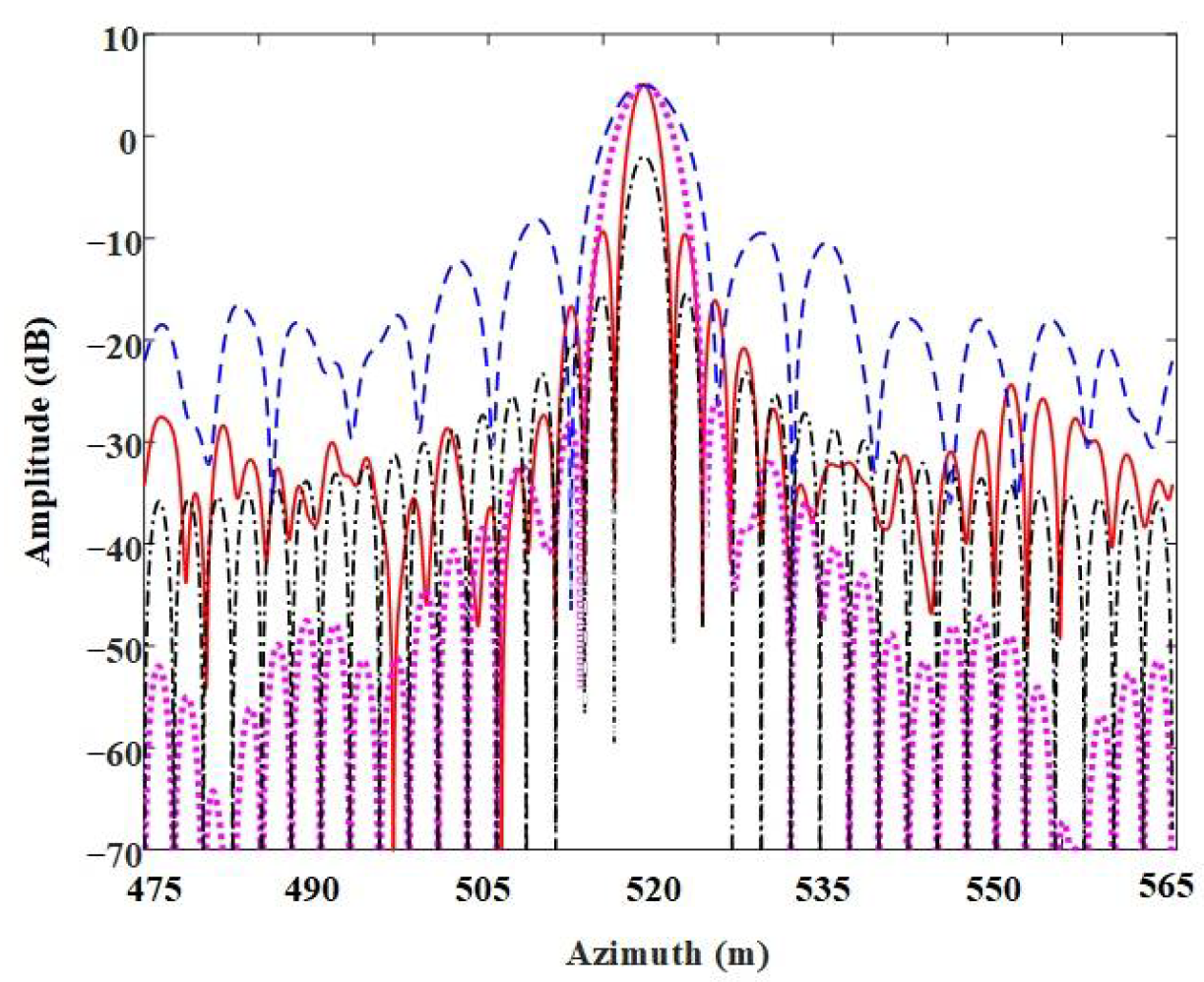
4.1. Point Target Simulation Experiment
4.2. Point Target Simulation Experiment Under Missing Data Condition
4.3. Imaging Experiment of Measured Data
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cumming, I.G.; Wong, F.H. Digital processing of synthetic aperture radar data. Artech House 2005, 1, 108–110. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Herman, M.; Strohmer, T. Compressed sensing radar. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 1509–1512. [Google Scholar]
- Liang, Y. Research on Time Series SAR Image Denoising Algorithm Based on Sparse Representation. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2024. [Google Scholar] [CrossRef]
- Chen, Y.; Jia, H.; Sun, Y.; Wen, J. High-Resolution Radar Range Profile Reconstruction Based on a Parametric Orthogonal Matching Pursuit Algorithm. J. Aerosp. Early Warn. Res. 2024, 38, 313–317. [Google Scholar]
- Hu, Y.; Gao, L.; Zhu, Y.; Sun, Z.; Guo, Z.; Ren, X. Sparse Diagnosis Method for Sudden Faults in Aero-Engine Gas Path Based on Improved Orthogonal Matching Pursuit. Propuls. Technol. 2024, in press. [Google Scholar]
- Hu, S.W.; Lin, G.X.; Hsieh, S.H.; Lu, C.S. Performance Analysis of Joint-Sparse Recovery from Multiple Measurement Vectors via Convex Optimization: Which Prior Information is Better? IEEE Access 2018, 6, 3739–3754. [Google Scholar] [CrossRef]
- Wu, G.; Luo, S. Adaptive fixed-point iterative shrinkage/thresholding algorithm for MR imaging reconstruction using compressed sensing. Magn. Reson. Imaging 2014, 32, 372–378. [Google Scholar] [CrossRef]
- Farhangkhah, N.; Samadi, S.; Khosravi, M.R.; Mohseni, R. Overcomplete pre-learned dictionary for incomplete data SAR imaging towards pervasive aerial and satellite vision. Wirel. Netw. 2024, 30, 3989–4001. [Google Scholar] [CrossRef]
- Du, W.; Hu, Y.; Sun, Y. Image Super-Resolution Reconstruction Method Based on Residual Dictionary Learning. J. Beijing Univ. Technol. 2017, 43, 43–48. [Google Scholar]
- Gao, Z.; Zhao, C.; Huang, P.; Xu, W.; Tan, W. Sparse Recovery STAP Algorithm Based on Adaptive Dictionary Correction. Signal Process. 2024, 40, 492–502. [Google Scholar] [CrossRef]
- Li, Y.; He, J.; Zhou, Y.; Hu, J.; Zhang, L. Sparse Denoising Method for Microseismic Signals in Mines Based on Adaptive Laplace Wavelet Dictionary. Energy Environ. Prot. 2024, 46, 69–76. [Google Scholar] [CrossRef]
- Luan, F.; Yang, F.; Cai, R.; Yang, C. Low-Sampling-Rate CT Reconstruction Based on Dual-Dictionary Adaptive Learning Algorithm. J. Northeast Univ. (Nat. Sci.) 2022, 43, 1709–1716. [Google Scholar]
- Wang, J.; Wang, Q.; Zheng, Y. Electrical Impedance Tomography Reconstruction Algorithm Based on L1 Regularization and Projection Method. In Proceedings of the 33rd Annual Conference of Tianjin Society of Biomedical Engineering, Tianjin, China, 10–11 June 2013; p. 1. [Google Scholar]
- Dong, X.; Zhang, Y. SAR Image Reconstruction from Undersampled Raw Data Using Maximum A Posteriori Estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1651–1664. [Google Scholar] [CrossRef]
- Güven, H.E.; Güngör, A.; Çetin, M. An Augmented Lagrangian Method for Complex-Valued Compressed SAR Imaging. IEEE Trans. Comput. Imaging 2016, 2, 235–250. [Google Scholar] [CrossRef]
- Gao, Z.; Sun, S.; Huang, P.; Qi, Y.; Xu, W. Improved L1/2 Threshold Iterative High-Resolution SAR Imaging Algorithm. J. Radars 2023, 12, 1044–1055. [Google Scholar]
- Chen, M.; Mi, D.; He, P.; Deng, L.; Wei, B. A CT Reconstruction Algorithm Based on L1/2 Regularization. Comput. Math. Methods Med. 2014, 2014, 862910. [Google Scholar] [CrossRef]
- Gao, Z.; Li, X.; Huang, P.; Xu, W.; Tan, W. Sparse Microwave Imaging Algorithm Based on L1/2 Threshold Iteration and an Approximate Observation Operator. Electronics 2023, 12, 4574. [Google Scholar] [CrossRef]
- Zeng, J.; Xu, Z.; Zhang, B.; Hong, W.; Wu, Y. Accelerated L1/2 regularization based SAR imaging via BCR and reduced Newton skills. Signal Process. 2013, 93, 1831–1844. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, Z.; Liu, B.; Zhang, L. Moving Target Detection Based on L1/2-TV Regularized RPCA. Comput. Simul. 2024, 41, 258–263, 428. [Google Scholar]
- Liu, Z.; Xu, Y.; Dong, F. L1-L2 Spatial Adaptive Regularization Method for Electrical Tomography. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 3346–3351. [Google Scholar]
- Liu, M.; Xu, Z.; Chen, T.; Zhang, B.; Wu, Y. Low-Oversampling Staggered SAR Imaging Method Based on L1&TV Regularization. Syst. Eng. Electron. Technol. 2023, 45, 2718–2726.24. [Google Scholar]
- Li, M.; Cai, G.; Bi, S.; Zhang, X. Improved TV Image Denoising over Inverse Gradient. Symmetry 2023, 15, 678. [Google Scholar] [CrossRef]
- Fang, J.; Xu, Z.; Zhang, B.; Hong, W.; Wu, Y. Fast Compressed Sensing SAR Imaging Based on Approximated Observation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 352–363. [Google Scholar] [CrossRef]
- Liu, M.; Pan, J.; Zhu, J.; Chen, Z.; Zhang, B.; Wu, Y. A Sparse SAR Imaging Method for Low-Oversampled Staggered Mode via Compound Regularization. Remote Sens. 2024, 16, 1459. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR processing using chirp scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Xu, Z.; Chang, X.; Xu, F.; Zhang, H. L1/2 Regularization: A Thresholding Representation Theory and a Fast Solver. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1013–1027. [Google Scholar] [CrossRef]
- Duan, L.; Sun, S.; Zhang, J.; Xu, Z. Deblurring Turbulent Images via Maximizing L1 Regularization. Symmetry 2021, 13, 1414. [Google Scholar] [CrossRef]








| Input: | Two-Dimensional Echo Data Y, Iteration Step Parameter δ, The Maximum Iteration Number tmax, Error Parameter ε, Image Size N, Noise Variance σ, Lagrange Multipliers ξ1 and ξ2. |
|---|---|
| Initialization: | |
| Iteration: | |
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. | |
| 10. | |
| End while | |
| Output: | Image sparse reconstruction |
| Parameter | Numerical Value |
|---|---|
| Effective speed of radar platform (m/s) | 150 |
| Scene center slant distance (km) | 10 |
| Doppler bandwidth (MHz) | 7.967 |
| Distance sampling rate (MHz) | 60 |
| Azimuth sampling rate (Hz) | 200 |
| Operating frequency (GHz) | 5.3 |
| Algorithm | PSLR (dB) | ISLR (dB) | IRW (m) |
|---|---|---|---|
| Chirp-scaling algorithm | −13.2764 | −10.1794 | 1.6641 |
| L1/2 regularization algorithm | −13.1921 | −10.2622 | 1.6503 |
| L1&TV algorithm | −25.9566 | −18.8973 | 1.6592 |
| Proposed algorithm | −26.3846 | −23.1482 | 1.6979 |
| Algorithm | Time Consumption(s) | Computational Complexity | Number of Iterations |
|---|---|---|---|
| Chirp-scaling algorithm | 0.915 | O(MN.log(MN)) | 1 |
| L1/2 regularization algorithm | 29.134 | O(T.log(MN)2) | 300 |
| L1&TV algorithm | 21.919 | O(T.log(MN)2) | 10 |
| Proposed algorithm | 8.913 | O(T. log(MN)2) | 4 |
| Algorithm | PSLR (dB) | ISLR (dB) | IRW (m) |
|---|---|---|---|
| Chirp-scaling algorithm | −12.9965 | −9.4812 | 1.4323 |
| L1/2 regularization algorithm | −11.2364 | −9.9881 | 1.4670 |
| L1&TV algorithm | −22.2001 | −16.2028 | 1.5702 |
| Proposed algorithm | −22.6146 | −18.8973 | 1.5065 |
| Parameter | Numerical Value |
|---|---|
| Operating frequency (GHz) | 5.3 |
| Emission pulse width (MHz) | 30.111 |
| Radar emission wavelength (m) | 5.6 × 10−6 |
| Radar effective rate (m/s) | 7062 |
| Distance frequency modulation (MHz/s) | 73,150 |
| Azimuth frequency modulation (Hz/s) | 1755 |
| Distance sampling rate (MHz) | 3.2317 |
| Pulse repetition frequency (Hz) | 1257 |
| Algorithm | PSLR (dB) | ISLR (dB) | IRW (m) |
|---|---|---|---|
| Chirp-scaling algorithm | −10.08 | −11.03 | 2.28 |
| L1/2 regularization algorithm | −10.91 | −11.24 | 2.26 |
| L1&TV algorithm | −17.84 | −18.00 | 1.89 |
| Proposed algorithm | −18.55 | −18.42 | 1.86 |
| Algorithm | PSLR (dB) | ISLR (dB) | IRW (m) |
|---|---|---|---|
| Chirp-scaling algorithm | −0.22 | −11.00 | 16.85 |
| L1/2 regularization algorithm | −1.29 | −9.70 | 9.28 |
| L1&TV algorithm | −10.33 | −11.55 | 2.39 |
| Proposed algorithm | −11.24 | −18.55 | 2.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Ma, H.; Huang, P.; Xu, W.; Tan, W.; Wu, Z. An Efficient Sparse Synthetic Aperture Radar Imaging Method Based on L1-Norm and Total Variation Regularization. Electronics 2025, 14, 2508. https://doi.org/10.3390/electronics14132508
Gao Z, Ma H, Huang P, Xu W, Tan W, Wu Z. An Efficient Sparse Synthetic Aperture Radar Imaging Method Based on L1-Norm and Total Variation Regularization. Electronics. 2025; 14(13):2508. https://doi.org/10.3390/electronics14132508
Chicago/Turabian StyleGao, Zhiqi, Huiying Ma, Pingping Huang, Wei Xu, Weixian Tan, and Zhixia Wu. 2025. "An Efficient Sparse Synthetic Aperture Radar Imaging Method Based on L1-Norm and Total Variation Regularization" Electronics 14, no. 13: 2508. https://doi.org/10.3390/electronics14132508
APA StyleGao, Z., Ma, H., Huang, P., Xu, W., Tan, W., & Wu, Z. (2025). An Efficient Sparse Synthetic Aperture Radar Imaging Method Based on L1-Norm and Total Variation Regularization. Electronics, 14(13), 2508. https://doi.org/10.3390/electronics14132508






