A Node-Degree Power-Law Distribution-Based Honey Badger Algorithm for Global and Engineering Optimization
Abstract
1. Introduction
- This study innovatively incorporates a PDD structure to model the interaction topology of the HBA population, where individuals exchange information exclusively with their connected neighbours. This design better simulates complex real-world network interactions, enhancing algorithm adaptability.
- Three interaction strategies are proposed: (i) PDDHBA-R, which employs roulette selection to randomly choose neighbours for information exchange, increasing the population diversity and exploration capability; (ii) PDDHBA-B, which strategically selects the most promising neighbour to accelerate convergence; and (iii) PDDHBA-H, a hybrid approach that divides the population into elite and non-elite groups and applies different interaction mechanisms to effectively balance exploration and exploitation.
- The comparative experiments demonstrate that PDDHBA-H significantly outperforms other HBA variants and mainstream metaheuristic algorithms in terms of optimization performance, population diversity, and convergence efficiency, highlighting its effectiveness in balancing exploration and exploitation.
2. Honey Badger Algorithm
Numerical Expression of the HBA
| Algorithm 1: Pseudocode of the HBA |
 |
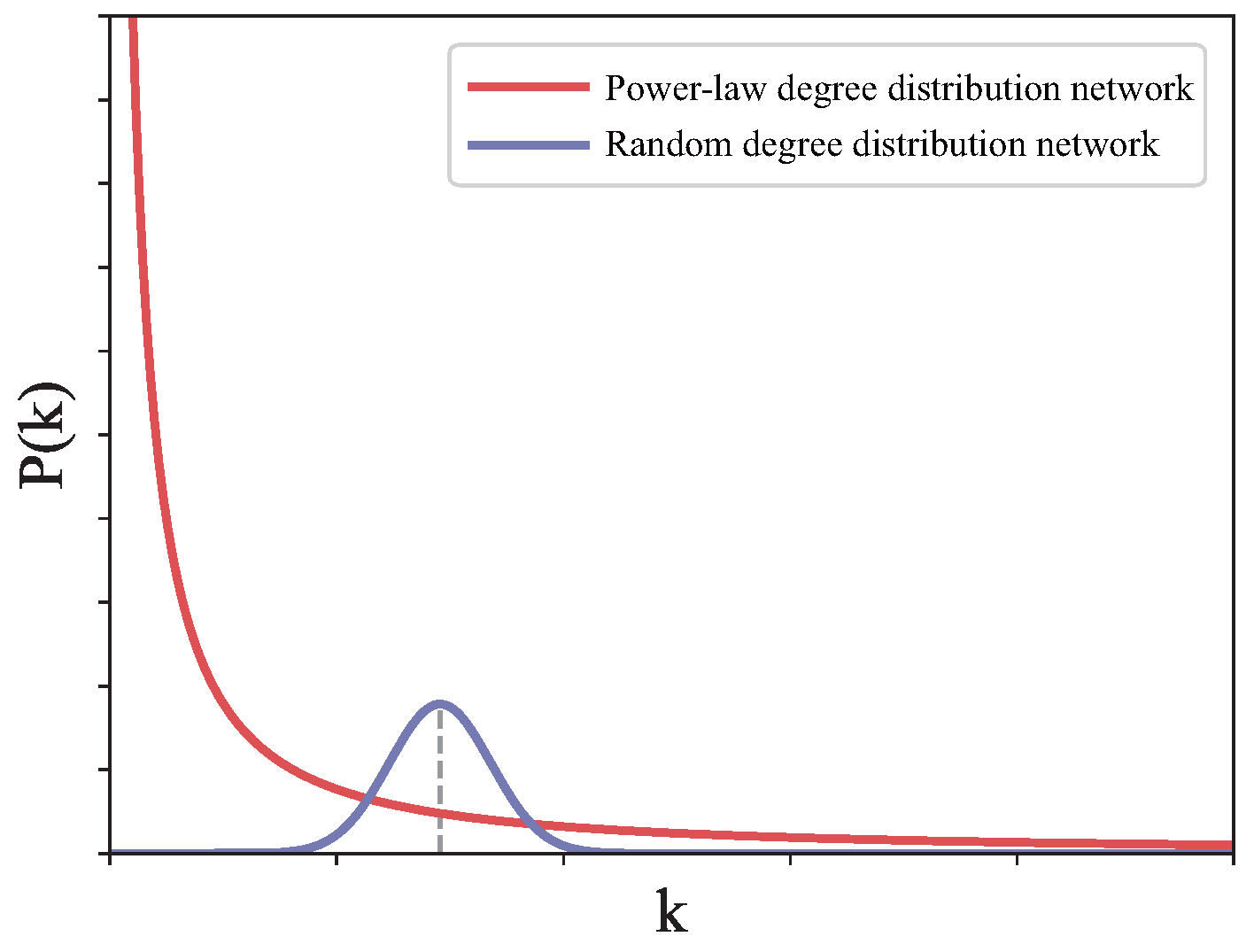
3. Barabási–Albert (BA) Model
4. Power-Law Degree Distribution Topology-Based HBAs
4.1. Motivation
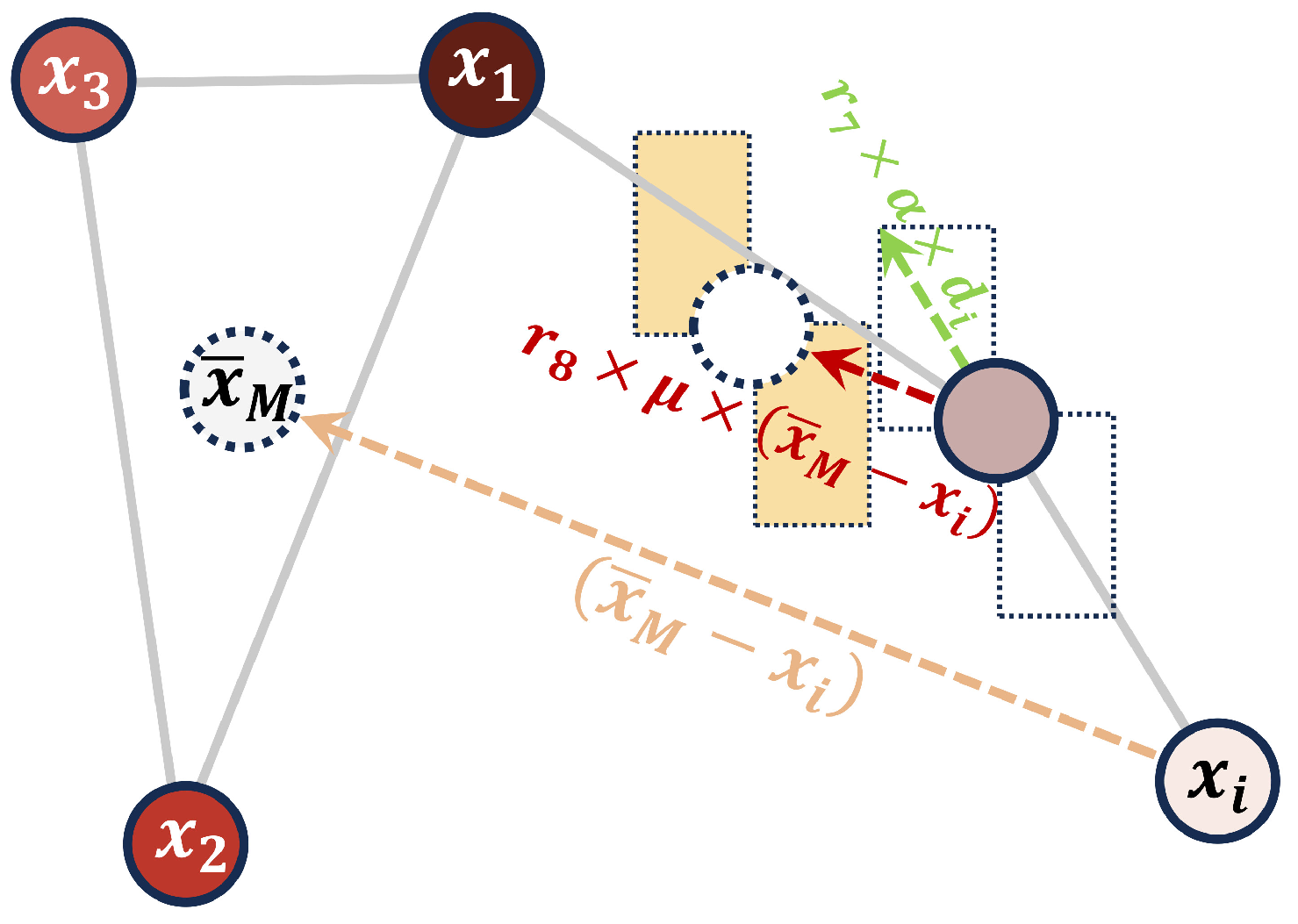
4.2. Random-Neighbour-Based Strategy: PDDHBA-R
4.3. Best-Neighbour-Based Strategy: PDDHBA-B
4.4. Hybrid Strategy: PDDHBA-H
| Algorithm 2: Pseudocode of PDDHBA-H |
 |
5. Experimental Study
5.1. Benchmark Functions and Experimental Setup
5.2. Performance Evaluation Metrics
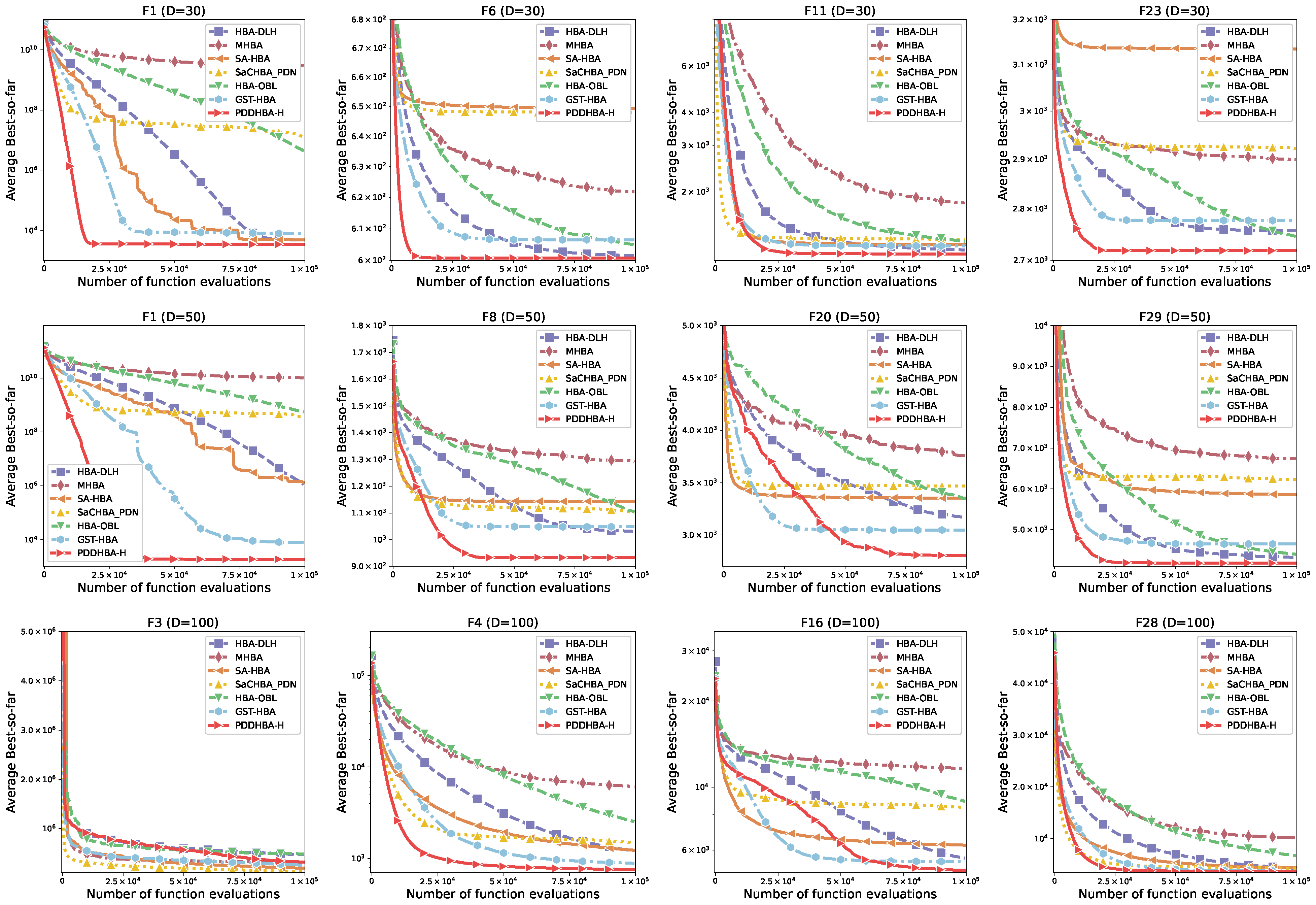
5.3. Comparison of Experimental Results
6. Discussion
6.1. Parameter Sensitivity
6.2. Computational Complexity
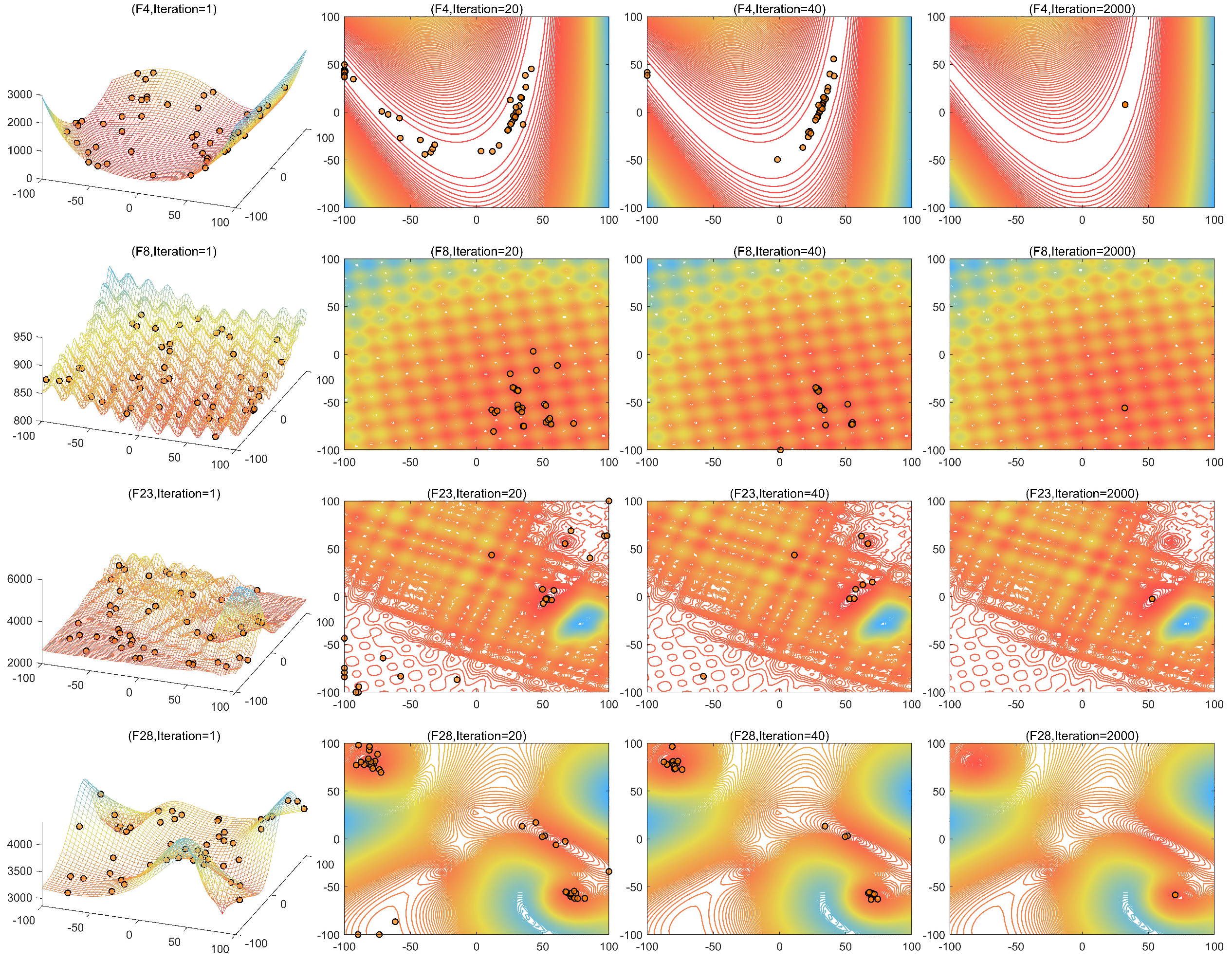
6.3. Search History, Diversity, and Exploration–Exploitation Analysis
6.3.1. Search History Analysis
6.3.2. Diversity Analysis
6.3.3. Exploration and Exploitation Analysis
6.4. Real-World Optimization Problems (Part 1)
6.5. Real-World Optimization Problems (Part 2)
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rao, S.S. Engineering Optimization: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Simon, D. Evolutionary Optimization Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Murty, K.G. Optimization for Decision Making: Linear and Quadratic Models; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Yang, X.-S. Optimization and metaheuristic algorithms in engineering, Metaheuristics in water. Geotech. Transp. Eng. 2013, 1, 23. [Google Scholar]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A survey on new generation metaheuristic algorithms. Comput. Ind. Eng. 2019, 137, 106040. [Google Scholar] [CrossRef]
- Rajwar, K.; Deep, K.; Das, S. An exhaustive review of the metaheuristic algorithms for search and optimization: Taxonomy, applications, and open challenges. Artif. Intell. Rev. 2023, 56, 13187–13257. [Google Scholar] [CrossRef] [PubMed]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. Metaheuristic research: A comprehensive survey. Artif. Intell. Rev. 2019, 52, 2191–2233. [Google Scholar] [CrossRef]
- Hansen, N.; Arnold, D.V.; Auger, A. Evolution Strategies. In Springer Handbook of Computational Intelligence; Kacprzyk, J., Pedrycz, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 871–898. [Google Scholar]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Das, S.; Ponnuthurai, N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2010, 15, 4–31. [Google Scholar] [CrossRef]
- Wang, D.; Dapei, T.; Lei, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (abc) algorithm. J. Of Global Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Aarts, E.; Korst, J.; Michiels, W. Simulated Annealing. In Search Methodologies: Introductory Tutorials in Optimization and Decision Support Techniques; Glover, F., Kochenberger, G.A., Eds.; Springer: Boston, MA, USA, 2005; pp. 187–210. [Google Scholar]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. Gsa: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Oladejo, S.O.; Ekwe, S.O.; Mirjalili, S. The hiking optimization algorithm: A novel human-based metaheuristic approach. Knowl.-Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Wang, X.; Xu, J.; Huang, C. Fans optimizer: A human-inspired optimizer for mechanical design problems optimization. Expert Syst. Appl. 2023, 228, 120242. [Google Scholar] [CrossRef]
- Tang, J.; Liu, G.; Pan, Q. A review on representative swarm intelligence algorithms for solving optimization problems: Applications and trends. IEEE/CAA J. Autom. Sin. 2021, 8, 1627–1643. [Google Scholar] [CrossRef]
- Chakraborty, A.; Kar, A.K. Swarm Intelligence: A Review of Algorithms. In Nature-Inspired Computing and Optimization: Theory and Applications; Yang, X.-S., Ed.; Springer: Cham, Switzerland, 2017; pp. 475–494. [Google Scholar]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey badger algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Düzenli, T.; Onay, F.K.; Aydemir, S.B. Improved honey badger algorithms for parameter extraction in photovoltaic models. Optik 2022, 268, 169731. [Google Scholar] [CrossRef]
- Adegboye, O.R.; Feda, A.K.; Ishaya, M.M.; Agyekum, E.B.; Kim, K.-C.; Mbasso, W.F.; Kamel, S. Antenna s-parameter optimization based on golden sine mechanism based honey badger algorithm with tent chaos. Heliyon 2023, 9, e21596. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, J.; Wei, G. Sachba_pdn: Modified honey badger algorithm with multi-strategy for uav path planning. Expert Syst. Appl. 2023, 223, 119941. [Google Scholar] [CrossRef]
- Asha, A.; Arunachalam, R.; Poonguzhali, I.; Urooj, S.; Alelyani, S. Optimized rnn-based performance prediction of iot and wsn-oriented smart city application using improved honey badger algorithm. Measurement 2023, 210, 112505. [Google Scholar] [CrossRef]
- Nassef, A.M.; Houssein, E.H.; Helmy, B.E.-d.; Rezk, H. Modified honey badger algorithm based global mppt for triple-junction solar photovoltaic system under partial shading condition and global optimization. Energy 2022, 254, 124363. [Google Scholar] [CrossRef]
- Abasi, A.K.; Aloqaily, M.; Guizani, M. Optimization of cnn using modified honey badger algorithm for sleep apnea detection. Expert Syst. Appl. 2023, 229, 120484. [Google Scholar] [CrossRef]
- Lynn, N.; Ali, M.Z.; Suganthan, P.N. Population topologies for particle swarm optimization and differential evolution. Swarm Evol. Comput. 2018, 39, 24–35. [Google Scholar] [CrossRef]
- Payne, J.L.; Giacobini, M.; Moore, J.H. Complex and dynamic population structures: Synthesis, open questions, and future directions. Soft Comput. 2013, 17, 1109–1120. [Google Scholar] [CrossRef]
- Gong, Y.-J.; Zhang, J. Small-world particle swarm optimization with topology adaptation. In Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, Amsterdam, The Netherlands, 6–10 July 2013; pp. 25–32. [Google Scholar]
- Ni, Q.; Yin, X.; Tian, K.; Zhai, Y. Particle swarm optimization with dynamic random population topology strategies for a generalized portfolio selection problem. Nat. Comput. 2017, 16, 31–44. [Google Scholar] [CrossRef]
- Huang, Y.; Lai, L.; Wu, H. Neighbourhood-based small-world network differential evolution with novelty search strategy. Int. J.-Bio-Inspired Comput. 2023, 22, 65–76. [Google Scholar] [CrossRef]
- Wang, C.; Xu, R.-Q.; Ma, L.; Zhao, J.; Wang, L.; Xie, N.-G.; Cheong, K.H. An efficient salp swarm algorithm based on scale-free informed followers with self-adaption weight. Appl. Intell. 2023, 53, 1759–1791. [Google Scholar] [CrossRef]
- Ji, J.; Song, S.; Tang, C.; Gao, S.; Tang, Z.; Todo, Y. An artificial bee colony algorithm search guided by scale-free networks. Inf. Sci. 2019, 473, 142–165. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, S.; Zhou, M.; Wang, Y.; Lei, Z.; Zhang, T.; Wang, J. Scale-free network-based differential evolution to solve function optimization and parameter estimation of photovoltaic models. Swarm Evol. 2022, 74, 101142. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Stumpf, M.P.; Wiuf, C. Sampling properties of random graphs: The degree distribution. Phys. Rev. Stat. Nonlinear Soft Matter Phys. 2005, 72, 036118. [Google Scholar] [CrossRef]
- Hofstad, R.V.D. Random Graphs and Complex Networks; Cambridge University Press: Cambridge, UK, 2024; Volume 2. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition on Constrained Real-Parameter Optimization; Technical Report; National University of Defense Technology: Changsha, China; Kyungpook National University: Daegu, Republic of Korea; Nanyang Technological University: Singapore, 2017. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Pereira, D.G.; Afonso, A.; Medeiros, F.M. Overview of friedman’s test and post-hoc analysis. Commun.-Stat.-Simul. Comput. 2015, 44, 2636–2653. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Verma, P.; Sanyal, K.; Srinivsan, D.; Swarup, K. Information exchange based clustered differential evolution for constrained generation-transmission expansion planning. Swarm Evol. Comput. 2019, 44, 863–875. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Cuckoo search via lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Nadimi-Shahraki, M.H.; Zamani, H. Dmde: Diversity-maintained multi-trial vector differential evolution algorithm for non-decomposition large-scale global optimization. Expert Syst. Appl. 2022, 198, 116895. [Google Scholar] [CrossRef]
- Li, K.; Huang, H.; Fu, S.; Ma, C.; Fan, Q.; Zhu, Y. A multi-strategy enhanced northern goshawk optimization algorithm for global optimization and engineering design problems. Comput. Methods Appl. Mech. Eng. 2023, 415, 116199. [Google Scholar] [CrossRef]
- Yu, H.; Qiao, S.; Heidari, A.A.; El-Saleh, A.A.; Bi, C.; Mafarja, M.; Cai, Z.; Chen, H. Laplace crossover and random replacement strategy boosted harris hawks optimization: Performance optimization and analysis. J. Comput. Des. Eng. 2022, 9, 1879–1916. [Google Scholar] [CrossRef]
- Morales-Castañeda, B.; Zaldivar, D.; Cuevas, E.; Fausto, F.; Rodríguez, A. A better balance in metaheuristic algorithms: Does it exist? Swarm Evol. Comput. 2020, 54, 100671. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y. On the exploration and exploitation in popular swarm-based metaheuristic algorithms. Neural Comput. Appl. 2019, 31, 7665–7683. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for CEC 2011 Competition on Testing Evolutionary Algorithms on Real World Optimization Problems; Jadavpur University: Kolkata, India; Nanyang Technological University: Singapore, 2010; pp. 341–359. [Google Scholar]
- Karami, H.; Anaraki, M.V.; Farzin, S.; Mirjalili, S. Flow direction algorithm (FDA): A novel optimization approach for solving optimization problems. Comput. Ind. Eng. 2021, 156, 107224. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. A new optimization method based on COOT bird natural life model. Expert Syst. Appl. 2021, 183, 115352. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]














| Function | HBA | PDDHBA-B | PDDHBA-R | PDDHBA-H |
|---|---|---|---|---|
| (D = 30) | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| F1 | ||||
| F3 | ||||
| F4 | ||||
| F5 | ||||
| F6 | ||||
| F7 | ||||
| F8 | ||||
| F9 | ||||
| F10 | ||||
| F11 | ||||
| F12 | ||||
| F13 | ||||
| F14 | ||||
| F15 | ||||
| F16 | ||||
| F17 | ||||
| F18 | ||||
| F19 | ||||
| F20 | ||||
| F21 | ||||
| F22 | ||||
| F23 | ||||
| F24 | ||||
| F25 | ||||
| F26 | ||||
| F27 | ||||
| F28 | ||||
| F29 | ||||
| F30 | ||||
| w/t/l | 19/9/1 | 12/17/0 | 8/20/1 | N/A |
| Ranking | 4 | 3 | 2 | 1 |
| Function | HBA | PDDHBA-B | PDDHBA-R | PDDHBA-H |
|---|---|---|---|---|
| (D = 50) | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| F1 | ||||
| F3 | ||||
| F4 | ||||
| F5 | ||||
| F6 | ||||
| F7 | ||||
| F8 | ||||
| F9 | ||||
| F10 | ||||
| F11 | ||||
| F12 | ||||
| F13 | ||||
| F14 | ||||
| F15 | ||||
| F16 | ||||
| F17 | ||||
| F18 | ||||
| F19 | ||||
| F20 | ||||
| F21 | ||||
| F22 | ||||
| F23 | ||||
| F24 | ||||
| F25 | ||||
| F26 | ||||
| F27 | ||||
| F28 | ||||
| F29 | ||||
| F30 | ||||
| w/t/l | 20/7/2 | 15/14/0 | 8/19/2 | N/A |
| Ranking | 4 | 3 | 2 | 1 |
| Function | HBA | PDDHBA-B | PDDHBA-R | PDDHBA-H |
|---|---|---|---|---|
| (D = 100) | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| F1 | ||||
| F3 | ||||
| F4 | ||||
| F5 | ||||
| F6 | ||||
| F7 | ||||
| F8 | ||||
| F9 | ||||
| F10 | ||||
| F11 | ||||
| F12 | ||||
| F13 | ||||
| F14 | ||||
| F15 | ||||
| F16 | ||||
| F17 | ||||
| F18 | ||||
| F19 | ||||
| F20 | ||||
| F21 | ||||
| F22 | ||||
| F23 | ||||
| F24 | ||||
| F25 | ||||
| F26 | ||||
| F27 | ||||
| F28 | ||||
| F29 | ||||
| F30 | ||||
| w/t/l | 22/5/2 | 12/17/0 | 11/17/1 | N/A |
| Ranking | 4 | 3 | 2 | 1 |
| Function | HBA-DLH | MHBA | SA-HBA | SaCHBA_PDN | HBA-OBL | GST-HBA | PDDHBA-H |
|---|---|---|---|---|---|---|---|
| (D = 30) | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| F1 | |||||||
| F3 | |||||||
| F4 | |||||||
| F5 | |||||||
| F6 | |||||||
| F7 | |||||||
| F8 | |||||||
| F9 | |||||||
| F10 | |||||||
| F11 | |||||||
| F12 | |||||||
| F13 | |||||||
| F14 | |||||||
| F15 | |||||||
| F16 | |||||||
| F17 | |||||||
| F18 | |||||||
| F19 | |||||||
| F20 | |||||||
| F21 | |||||||
| F22 | |||||||
| F23 | |||||||
| F24 | |||||||
| F25 | |||||||
| F26 | |||||||
| F27 | |||||||
| F28 | |||||||
| F29 | |||||||
| F30 | |||||||
| w/t/l | 22/7/0 | 28/1/0 | 21/8/0 | 25/4/0 | 24/5/0 | 18/10/1 | N/A |
| Ranking | 3 | 7 | 6 | 5 | 4 | 2 | 1 |
| Function | HBA-DLH | MHBA | SA-HBA | SaCHBA_PDN | HBA-OBL | GST-HBA | PDDHBA-H |
|---|---|---|---|---|---|---|---|
| (D = 50) | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| F1 | |||||||
| F3 | |||||||
| F4 | |||||||
| F5 | |||||||
| F6 | |||||||
| F7 | |||||||
| F8 | |||||||
| F9 | |||||||
| F10 | |||||||
| F11 | |||||||
| F12 | |||||||
| F13 | |||||||
| F14 | |||||||
| F15 | |||||||
| F16 | |||||||
| F17 | |||||||
| F18 | |||||||
| F19 | |||||||
| F20 | |||||||
| F21 | |||||||
| F22 | |||||||
| F23 | |||||||
| F24 | |||||||
| F25 | |||||||
| F26 | |||||||
| F27 | |||||||
| F28 | |||||||
| F29 | |||||||
| F30 | |||||||
| w/t/l | 26/3/0 | 29/0/0 | 23/5/1 | 28/0/1 | 27/2/0 | 21/6/2 | N/A |
| Ranking | 3 | 7 | 4 | 6 | 5 | 2 | 1 |
| Function | HBA-DLH | MHBA | SA-HBA | SaCHBA_PDN | HBA-OBL | GST-HBA | PDDHBA-H |
|---|---|---|---|---|---|---|---|
| (D = 100) | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| F1 | |||||||
| F3 | |||||||
| F4 | |||||||
| F5 | |||||||
| F6 | |||||||
| F7 | |||||||
| F8 | |||||||
| F9 | |||||||
| F10 | |||||||
| F11 | |||||||
| F12 | |||||||
| F13 | |||||||
| F14 | |||||||
| F15 | |||||||
| F16 | |||||||
| F17 | |||||||
| F18 | |||||||
| F19 | |||||||
| F20 | |||||||
| F21 | |||||||
| F22 | |||||||
| F23 | |||||||
| F24 | |||||||
| F25 | |||||||
| F26 | |||||||
| F27 | |||||||
| F28 | |||||||
| F29 | |||||||
| F30 | |||||||
| w/t/l | 28/1/0 | 28/1/0 | 24/3/2 | 27/1/1 | 29/0/0 | 22/5/2 | N/A |
| Ranking | 3 | 7 | 4 | 5 | 6 | 2 | 1 |
| Algorithm | Parameter Settings |
|---|---|
| PSO [11] | = = 2, w = [0.9, 0.4] |
| DE [46] | CR = 0.9, F = 0.7 |
| GWO [39] | a = [2, 0], A = [−a, a], C = [0, 2] |
| WOA [43] | b = 1, a = [2, 0] |
| SSA [44] | ST = 0.8, SD = 20, = 0.2 |
| DBO [45] | k = = 0.1, b = 0.3, S = 0.5 |
| CSA [47] | = 0.01, = 0.25 |
| Function | PSO | DE | GWO | WOA | SSA | DBO | CSA | PDDHBA-H |
|---|---|---|---|---|---|---|---|---|
| (D = 30) | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| F1 | ||||||||
| F3 | ||||||||
| F4 | ||||||||
| F5 | ||||||||
| F6 | ||||||||
| F7 | ||||||||
| F8 | ||||||||
| F9 | ||||||||
| F10 | ||||||||
| F11 | ||||||||
| F12 | ||||||||
| F13 | ||||||||
| F14 | ||||||||
| F15 | ||||||||
| F16 | ||||||||
| F17 | ||||||||
| F18 | ||||||||
| F19 | ||||||||
| F20 | ||||||||
| F21 | ||||||||
| F22 | ||||||||
| F23 | ||||||||
| F24 | ||||||||
| F25 | ||||||||
| F26 | ||||||||
| F27 | ||||||||
| F28 | ||||||||
| F29 | ||||||||
| F30 | ||||||||
| w/t/l | 23/4/2 | 22/1/6 | 22/6/1 | 29/0/0 | 22/7/0 | 27/2/0 | 17/6/6 | N/A |
| Ranking | 3 | 4 | 5 | 8 | 6 | 7 | 2 | 1 |
| Function | PSO | DE | GWO | WOA | SSA | DBO | CSA | PDDHBA-H |
|---|---|---|---|---|---|---|---|---|
| (D = 50) | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| F1 | ||||||||
| F3 | ||||||||
| F4 | ||||||||
| F5 | ||||||||
| F6 | ||||||||
| F7 | ||||||||
| F8 | ||||||||
| F9 | ||||||||
| F10 | ||||||||
| F11 | ||||||||
| F12 | ||||||||
| F13 | ||||||||
| F14 | ||||||||
| F15 | ||||||||
| F16 | ± | ± | ± | ± | ± | ± | ± | ± |
| F17 | ± | ± | ± | ± | ± | ± | ± | ± |
| F18 | ± | ± | ± | ± | ± | ± | ± | ± |
| F19 | ± | ± | ± | ± | ± | ± | ± | ± |
| F20 | ± | ± | ± | ± | ± | ± | ± | ± |
| F21 | ± | ± | ± | ± | ± | ± | ± | ± |
| F22 | ± | ± | ± | ± | ± | ± | ± | ± |
| F23 | ± | ± | ± | ± | ± | ± | ± | ± |
| F24 | ± | ± | ± | ± | ± | ± | ± | ± |
| F25 | ± | ± | ± | ± | ± | ± | ± | ± |
| F26 | ± | ± | ± | ± | ± | ± | ± | ± |
| F27 | ± | ± | ± | ± | ± | ± | ± | ± |
| F28 | ± | ± | ± | ± | ± | ± | ± | ± |
| F29 | ± | ± | ± | ± | ± | ± | ± | ± |
| F30 | ± | ± | ± | ± | ± | ± | ± | ± |
| w/t/l | 24/3/2 | 24/1/4 | 25/2/2 | 29/0/0 | 21/6/2 | 27/2/0 | 22/5/2 | N/A |
| Ranking | 4.5 | 6 | 4.5 | 8 | 3 | 7 | 2 | 1 |
| Function | PSO | DE | GWO | WOA | SSA | DBO | CSA | PDDHBA-H |
|---|---|---|---|---|---|---|---|---|
| (D = 100) | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| F1 | ||||||||
| F3 | ||||||||
| F4 | ||||||||
| F5 | ||||||||
| F6 | ||||||||
| F7 | ||||||||
| F8 | ||||||||
| F9 | ||||||||
| F10 | ||||||||
| F11 | ||||||||
| F12 | ||||||||
| F13 | ||||||||
| F14 | ||||||||
| F15 | ||||||||
| F16 | ||||||||
| F17 | ||||||||
| F18 | ||||||||
| F19 | ||||||||
| F20 | ||||||||
| F21 | ||||||||
| F22 | ||||||||
| F23 | ||||||||
| F24 | ||||||||
| F25 | ||||||||
| F26 | ||||||||
| F27 | ||||||||
| F28 | ||||||||
| F29 | ||||||||
| F30 | ||||||||
| w/t/l | 27/1/2 | 29/0/0 | 25/1/3 | 29/0/0 | 22/3/4 | 27/2/0 | 29/0/0 | N/A |
| Ranking | 5 | 6 | 3 | 8 | 2 | 7 | 4 | 1 |
| Problem | Description | Constraints | Dimensions |
|---|---|---|---|
| Parameter estimation of frequency-modulated sound waves | Bounds constrained | 6 | |
| Lennard-Jones potential energy minimization problem | Bounds constrained | 30 | |
| Optimization problem for bifunctional catalyst blend | Bounds constrained | 1 | |
| Optimal control of a nonlinear stirred-tank reactor | Unconstrained | 1 | |
| Minimization of the Tersoff potential function | Bounds constrained | 30 | |
| Minimization of the Tersoff potential function | Bounds constrained | 30 | |
| Spread-spectrum radar Polly-phase code design | Bounds constrained | 20 | |
| Transmission network expansion planning problem | Equality/inequality constraints | 7 | |
| Large-scale transmission pricing problem | Linear equality constraints | 126 | |
| Design of circular antenna array | Bounds constrained | 12 | |
| Dynamic economic dispatch | Inequality constraints | 120 | |
| Dynamic economic dispatch | Inequality constraints | 216 | |
| Static economic load dispatch | Inequality constraints | 6 | |
| Static economic load dispatch | Inequality constraints | 13 | |
| Static economic load dispatch | Inequality constraints | 15 | |
| Static economic load dispatch | Inequality constraints | 40 | |
| Static economic load dispatch | Inequality constraints | 140 | |
| Hydrothermal scheduling | Inequality constraints | 96 | |
| Hydrothermal scheduling | Inequality constraints | 96 | |
| Hydrothermal scheduling | Inequality constraints | 96 | |
| Spacecraft trajectory optimization | Bounds constrained | 26 | |
| Spacecraft trajectory optimization | Bounds constrained | 22 |
| HBA-DLH | MHBA | SA-HBA | SaCHBA_PDN | HBA-OBL | GST-HBA | PDDHBA-H | |
|---|---|---|---|---|---|---|---|
| Function | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| w/t/l | 9/11/1 | 20/1/0 | 18/3/0 | 17/3/1 | 17/4/0 | 9/10/2 | N/A |
| Ranking | 3 | 7 | 5 | 6 | 4 | 2 | 1 |
| PSO | DE | GWO | WOA | SSA | DBO | CSA | PDDHBA-H | |
|---|---|---|---|---|---|---|---|---|
| Function | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std | Mean ± Std |
| w/t/l | 8/10/3 | 12/4/5 | 14/4/3 | 19/2/0 | 12/7/2 | 15/6/0 | 11/5/5 | N/A |
| Ranking | 4 | 5 | 2 | 8 | 6 | 7 | 3 | 1 |
| Comparison | Algorithm | No. of Functions | Average Rank | Rank Difference | Critical Difference |
|---|---|---|---|---|---|
| vs. original HBA | PDDHBA-H | 87 | 1.66 | N/A | 0.50 |
| HBA | 3.22 | 1.57 | |||
| PDDHBA-B | 2.77 | 1.11 | |||
| PDDHBA-R | 2.36 | 0.70 | |||
| vs. HBA variants | PDDHBA-H | 108 | 1.42 | N/A | 0.87 |
| HBA-DLH | 3.29 | 1.87 | |||
| MHBA | 6.28 | 4.87 | |||
| SA-HBA | 4.69 | 3.28 | |||
| SaCHBA-PDN | 5.09 | 3.67 | |||
| HBA-OBL | 4.56 | 3.14 | |||
| GST-HBA | 2.68 | 1.26 | |||
| vs. metaheuristics | PDDHBA-H | 108 | 1.80 | N/A | 1.01 |
| PSO | 4.31 | 2.52 | |||
| DE | 4.61 | 2.82 | |||
| GWO | 4.22 | 2.42 | |||
| WOA | 7.13 | 5.33 | |||
| SSA | 4.25 | 2.45 | |||
| DBO | 5.90 | 4.10 | |||
| CSA | 3.78 | 1.99 |
| Problem | Algorithm | Worst | Best | Std | Mean |
|---|---|---|---|---|---|
| PDDHBA-H | |||||
| Welded Beam | HBA | ||||
| MHBA | |||||
| SA-HBA | |||||
| SaCHBA_PDN | |||||
| HBA-OBL | |||||
| GST-HBA | |||||
| HBA-DLH | |||||
| PSO | |||||
| DE | |||||
| GWO | |||||
| WOA | |||||
| SSA | |||||
| DBO | |||||
| CSA | |||||
| PDDHBA-H | |||||
| Speed Reducer | HBA | ||||
| MHBA | |||||
| SA-HBA | |||||
| SaCHBA_PDN | |||||
| HBA-OBL | |||||
| GST-HBA | |||||
| HBA-DLH | |||||
| PSO | |||||
| DE | |||||
| GWO | |||||
| WOA | |||||
| SSA | |||||
| DBO | |||||
| CSA | |||||
| PDDHBA-H | |||||
| Cantilever Beam | HBA | ||||
| MHBA | |||||
| SA-HBA | |||||
| SaCHBA_PDN | |||||
| HBA-OBL | |||||
| GST-HBA | |||||
| HBA-DLH | |||||
| PSO | |||||
| DE | |||||
| GWO | |||||
| WOA | |||||
| SSA | |||||
| DBO | |||||
| CSA | |||||
| PDDHBA-H | |||||
| Pressure Vessel | HBA | ||||
| MHBA | |||||
| SA-HBA | |||||
| SaCHBA_PDN | |||||
| HBA-OBL | |||||
| GST-HBA | |||||
| HBA-DLH | |||||
| PSO | |||||
| DE | |||||
| GWO | |||||
| WOA | |||||
| SSA | |||||
| DBO | |||||
| CSA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Song, Z.; Chen, X.; Ji, J. A Node-Degree Power-Law Distribution-Based Honey Badger Algorithm for Global and Engineering Optimization. Electronics 2025, 14, 2302. https://doi.org/10.3390/electronics14112302
Song S, Song Z, Chen X, Ji J. A Node-Degree Power-Law Distribution-Based Honey Badger Algorithm for Global and Engineering Optimization. Electronics. 2025; 14(11):2302. https://doi.org/10.3390/electronics14112302
Chicago/Turabian StyleSong, Shuangyu, Zhenyu Song, Xingqian Chen, and Junkai Ji. 2025. "A Node-Degree Power-Law Distribution-Based Honey Badger Algorithm for Global and Engineering Optimization" Electronics 14, no. 11: 2302. https://doi.org/10.3390/electronics14112302
APA StyleSong, S., Song, Z., Chen, X., & Ji, J. (2025). A Node-Degree Power-Law Distribution-Based Honey Badger Algorithm for Global and Engineering Optimization. Electronics, 14(11), 2302. https://doi.org/10.3390/electronics14112302






