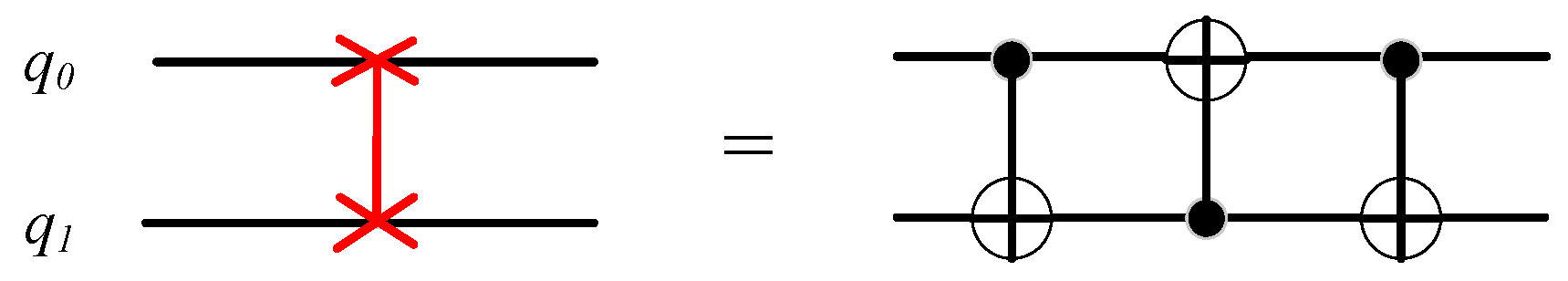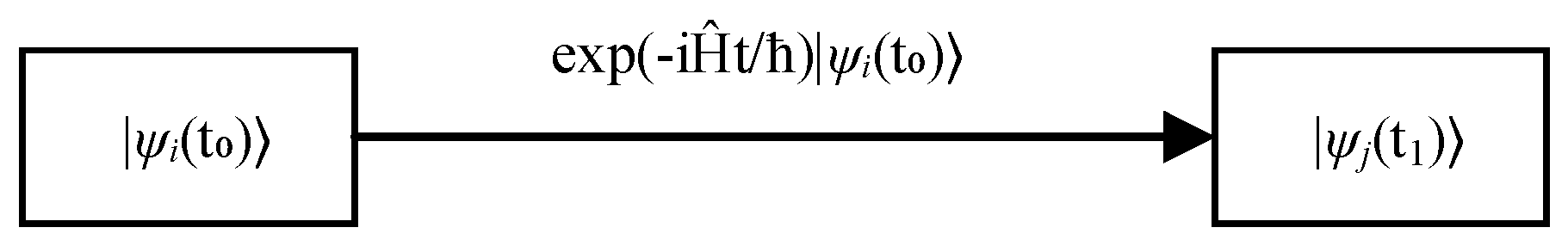In recent years, efforts have been made to improve quantum circuit scheduling algorithms to better adapt to the evolving quantum computing hardware and application requirements. With the continuous advancement and expansion of existing quantum computing hardware, minimizing the number of operations has become a major research focus in quantum circuit scheduling. A two-step method was proposed by Guerreschi [
11], where logical gates are first arranged without considering connections, and routing operations are subsequently added in a way that minimizes overhead. Qmap, a timing and resource-aware mapper, was presented by Lao et al. [
12] to map quantum circuits onto the Surface-17 superconducting processor by addressing hardware constraints, reducing latency and operation overhead via polynomial-complexity scheduling and routing heuristics, and enabling flexibility for different processors through a configuration file. Four general methods were proposed by Alam et al. [
3] to optimize Quantum Approximate Optimization Algorithm (QAOA) circuits through gate reordering. This reordering allows for more quantum gates to be executed in parallel, reduces the number of additional gates required for compiling QAOA circuits, and consequently decreases circuit depth. Four methodologies, including QAIM, IP, IC, and VIC, were proposed by Alam et al. [
13] to optimize QAOA circuits for NISQ processors. By leveraging gate reordering and hardware characteristics, these methods reduce circuit depth and gate count on average, enhance success probability via variation-aware compilation, and introduce the ARG metric to validate compiled circuits on real hardware. Gate model quantum computers are essential for implementing near-term quantum computer architectures and quantum devices. A new qubit mapping scheme, QuCloud+, was proposed by Liu Lei et al. [
14], which improves the fidelity and resource utilization of 2D/3D noisy intermediate-scale quantum (NISQ) computers in both single-task and multi-task programming. By addressing challenges faced by existing mapping schemes, such as crosstalk, the overhead of SWAP operations, and varying device topologies, QuCloud+ enhances the accuracy of quantum computing results and computational efficiency. A multi-qubit lattice surgery scheduling algorithm was proposed by Allyson Silva et al. [
15] to optimize the orchestration of quantum circuits in two-dimensional topological quantum error-correcting codes. This method primarily focuses on the scheduling problem of multi-qubit long-distance operations. The quantum circuit can be transformed into a sequence of only non-Clifford multi-qubit gates by applying simple swapping rules, which significantly reduces the circuit length on the test circuit set. Furthermore, compared to serial execution, the expected execution time of multi-qubit gate circuits is further reduced. CutQC, proposed by Tang et al. [
16], is a scalable hybrid computing approach that integrates classical and quantum computers to facilitate the evaluation of quantum circuits inaccessible to classical simulations or standalone quantum devices. By partitioning large quantum circuits into smaller subcircuits, this method enables their execution on smaller quantum devices, with classical postprocessing used to reconstruct the output of the original circuit. A systematic method for simulating clustered quantum circuits with limited quantum memory was introduced by Tianyi Peng et al. [
17]. Cluster parameters K and d were defined for quantum circuits, with the tensor network of the circuit being decomposed into clusters of, at most, size d, and the number of qubits for quantum communication between clusters being limited to, at most, K. This systematic method reduces the number of qubits and the depth of the circuit, thereby enhancing robustness against relevant noises. A circuit synthesis scheme, proposed by Beatrice Nash et al. [
18], addresses the problem of limited qubit connectivity in NISQ devices. The scheme is designed to optimize quantum circuits to fit the device connectivity, minimize the number of CNOT gates, and improve computational efficiency. Zhao Yun Chen et al. [
19] proposed an optimized classical simulation scheme, which allows a large number of measurement results to be obtained in a short period of time, achieving efficient simulation of multi-qubit quantum circuits. The quantum circuit simulator Qulacs was proposed by Yasunari Suzuki et al. [
20]. It is designed to meet the requirements of quantum computing research and is characterized by high speed and diverse functionalities, providing a powerful tool for quantum computing research. The expressibility and entanglement capabilities of parameterized quantum circuits (PQCs) for hybrid quantum-classical algorithms were explored by Sukin Sim et al. [
21], offering a theoretical foundation and methodologies for the design and selection of appropriate PQCs. The quantum circuit mapping tool MQT QMAP was introduced by Robert Wille et al. [
22], aimed at assisting researchers and developers in efficiently mapping quantum circuits onto practical quantum computing architectures. The circuit compilation problem in distributed quantum computing was studied by Daniele Cuomo et al. [
23], who proposed an optimized compiler framework. By establishing a dynamic network flow model and introducing the concept of quasi-parallelism, the overhead of remote operations was effectively reduced, and compilation efficiency was improved. Moreover, experimental comparisons of different topological structures were conducted, providing valuable insights for the design of distributed quantum computing architectures. The quantum compiler optimization method known as Relaxed Peephole Optimization (RPO) was proposed by Ji Liu et al. [
24]. By utilizing single-qubit state information, this method is designed to simplify quantum circuits, reduce the number of gates, decrease compilation time, and enhance the performance of quantum computing. A quantum circuit compilation framework based on reinforcement learning was introduced by Nils Quetschlich et al. [
25]. In this approach, the quantum circuit compilation process is modeled as a Markov decision process, and reinforcement learning is applied in an effort to address challenges in the development of quantum compilers. The makespan minimization problem in quantum circuit compilation was investigated by Shelvin Chand et al. [
26], who proposed two new heuristic algorithms to address it. One algorithm is a sequential decision-making method based on rollout, where the next operation to be scheduled is determined by the makespan prediction given by a guiding priority rule. The other is a stochastic version of the rollout heuristic, which alternates between rollout and a simple priority rule to explore the search space. SCIM MILQ, a scheduler for quantum tasks in high-performance computing infrastructure, was proposed by Philipp Seitz et al. [
27]. This scheduler combines well-established scheduling techniques with methods unique to quantum computing, such as circuit cutting, and minimizes the makespan while scheduling tasks. Additionally, Pan et al. [
28] review Quantum Secure Direct Communication (QSDC), a quantum communication method that enables direct transmission of secret messages without pre-shared keys by leveraging quantum principles such as entanglement. The paper discusses key protocols, such as the two-step QSDC, DL04 protocol, and measurement-device-independent (MDI) QSDC; experimental advancements, including 100 km fiber transmission; and existing challenges. The role of QSDC in the quantum internet through hybrid architectures is envisioned, with its security foundations in quantum mechanics and practical progress emphasized.
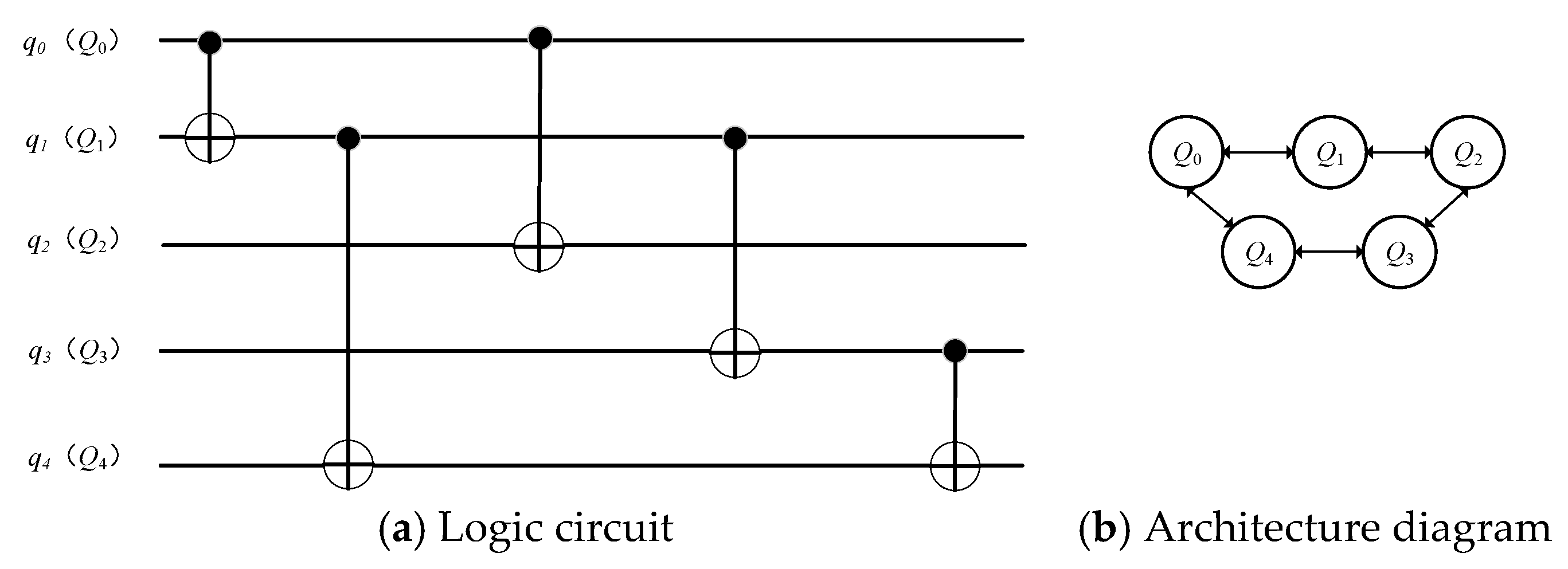
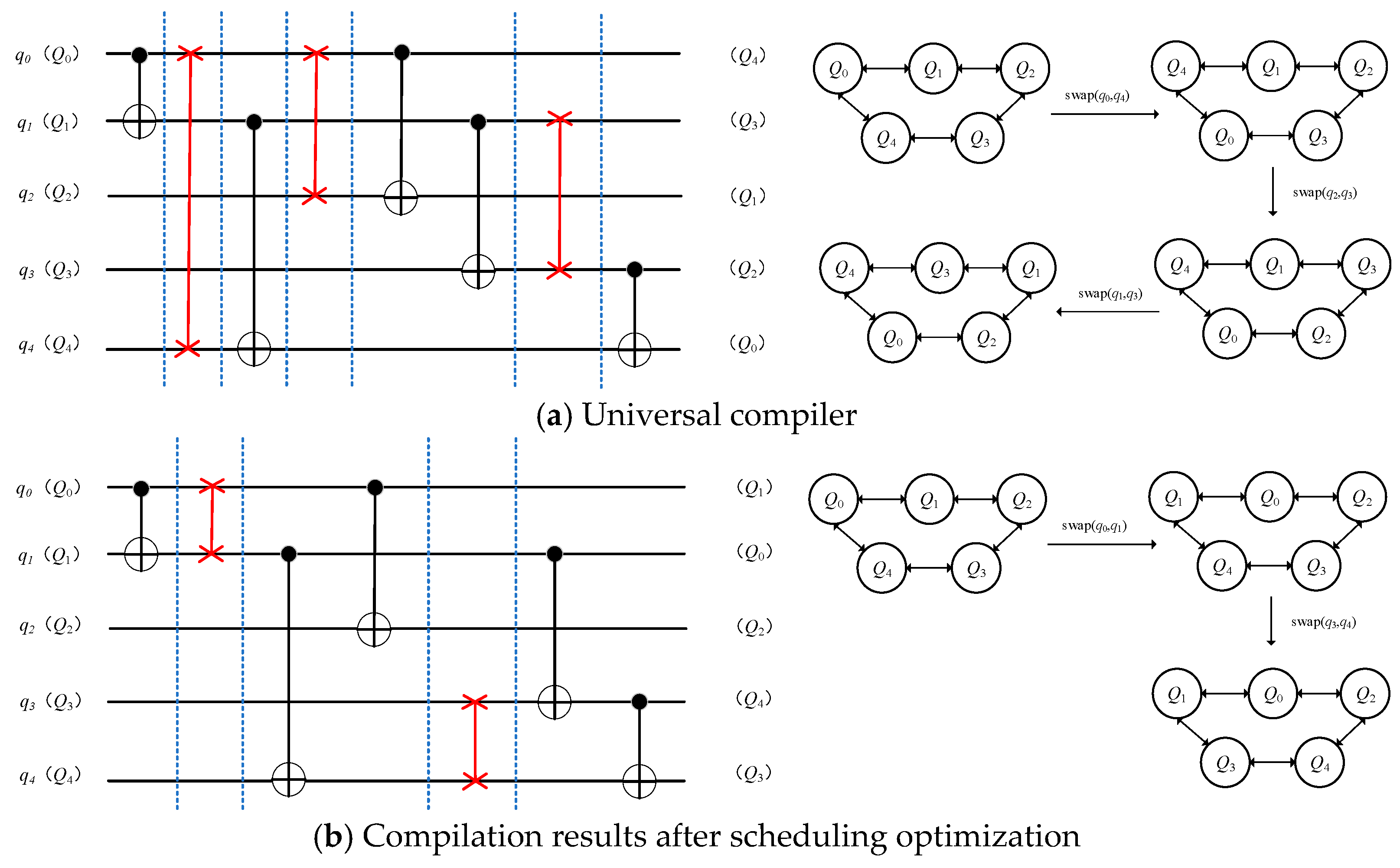
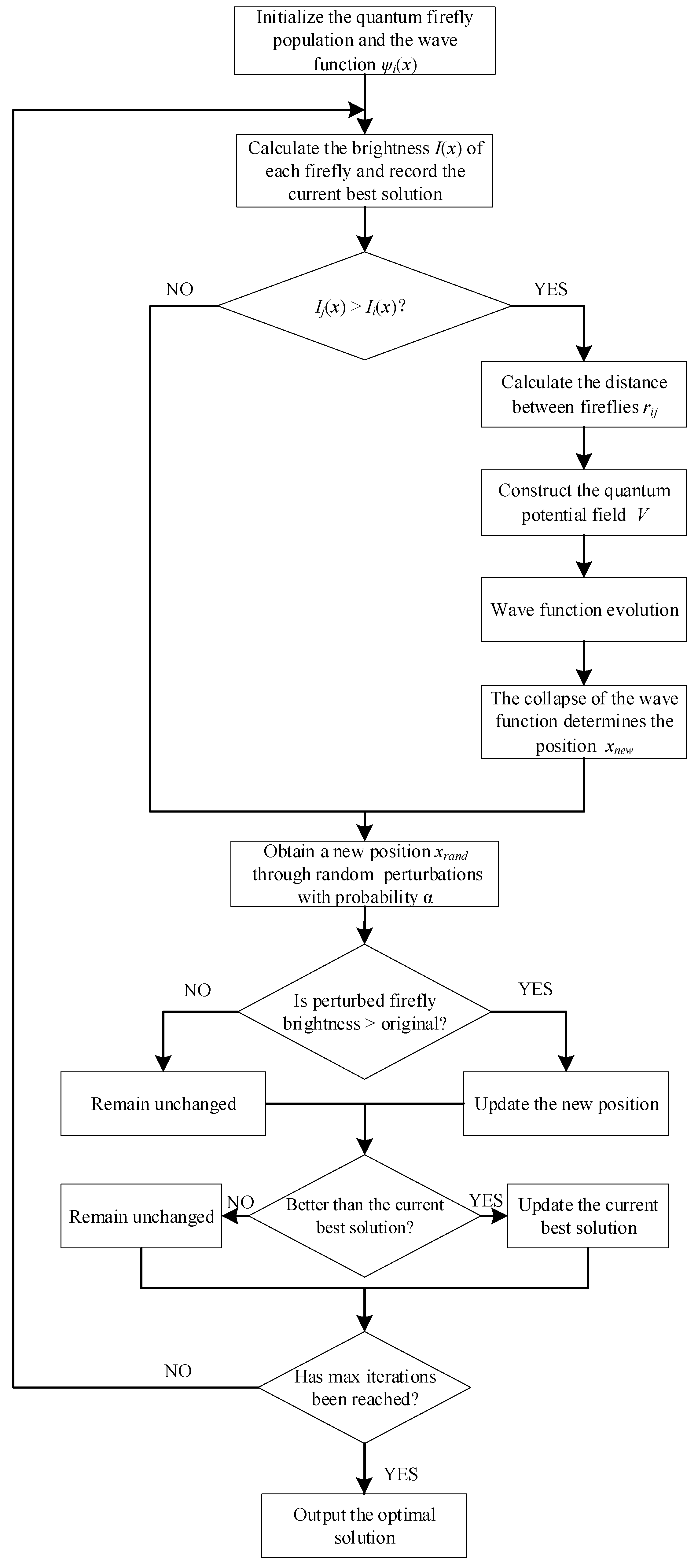
This paper aims to explore the challenges encountered in the quantum circuit scheduling problem. To improve the execution efficiency of quantum circuits, reduce the number of quantum gate operations, and enhance circuit parallelism, the Quantum Firefly Algorithm (QFA) is proposed for optimizing the quantum circuit scheduling method. By combining the wave function evolution in the Quantum Firefly Algorithm with classical search techniques, the structure of the quantum circuit is optimized under the constraints of qubit connection topology and quantum gate dependency relationships. As a result, the circuit depth is reduced, parallelism is improved, and the number of SWAP operations is simultaneously minimized.