Development of High-Quality Cryptographic Constructions Based on Many-Valued Logic Affine Transformations

Abstract

The S-box is a key component of modern ciphers, determining the quality and performance of the cryptographic algorithms in which it is applied. Many constructions for synthesizing high-quality S-boxes have been established, and those based on Galois fields theory—for example, the Nyberg construction applied in the AES cryptographic algorithm—are particularly important. An integral component of the Nyberg construction is the affine transformation, which is used to improve the avalanche and correlation properties of the S-box. In this paper, a new approach is adopted for synthesizing affine transformations for S-boxes based on the quaternary matrices over the Galois field GF(4). We describe four basic structures that serve as the foundation for synthesizing a complete class of 648 affine transformation matrices of order n = 3 and a class of 7776 matrices of order n = 4 and introduce a recurrent structure to facilitate the synthesis of matrices for higher orders. Using these matrices in combination with the Nyberg construction, it is possible to construct bijective S-boxes that outperform the original Nyberg construction and many other known S-boxes in terms of strict avalanche criterion (SAC) and bit independence criterion strict avalanche criterion (BIC SAC) values, while maintaining a maximal level of nonlinearity and good cryptographic properties. We also propose modified GF(4) affine transformations that can be applied to specialized S-boxes which already satisfy the SAC for both component Boolean and 4-functions, as well as the criterion of minimal correlation between input and output, allowing us to enhance their nonlinearity to the value of N_f = 96. We integrate the synthesized S-boxes into the AES algorithm and evaluate their practical performance. The encryption outputs successfully pass the NIST statistical test suite in 96 out of 100 cases, outperforming both the original AES S-box and other reference constructions, confirming the practical strength of the proposed method.

1. Introduction

Cryptographic algorithms are a cornerstone of modern information security systems, with block symmetric ciphers being a particularly notable category. These ciphers are designed to efficiently encrypt large volumes of data and are implemented as hardware modules in nearly all modern processors, including mobile platforms.

The operation of modern ciphers is founded on the encryption principles of diffusion and confusion, introduced by Claude Shannon [1]. A central challenge in designing block symmetric ciphers lies in implementing the concept of confusion, which is achieved through nonlinear components known as S-boxes. S-boxes are critical elements of modern ciphers, significantly influencing their resilience to modern cryptanalysis techniques and often determining the overall performance of cryptographic transformations. Consequently, developing high-quality S-boxes is one of the most crucial tasks in modern cryptography.

Today, a standard set of cryptographic quality criteria is applied to S-boxes, which includes the following basic requirements:

• Nonlinearity;
• Strict avalanche criterion (SAC);
• Bit independence criterion (BIC);
• Linear approximation probability (LAP);
• Differential approximation probability (DAP);
• Correlation independence of output and input vectors of the S-box.

Often, other criteria, such as periods of return to the initial state [2], and sets of criteria that indicate the cryptographic properties of the S-box when it is represented by component functions of many-valued logic are also considered [3].

The first two criteria, implying nonlinearity and the strict avalanche criterion, are the most fundamental for modern S-boxes and thus receive the most attention from researchers. For example, highly nonlinear S-boxes reaching practically maximal values of nonlinearity can be synthesized in Galois fields via the Nyberg construction, which is used in the AES (Rijndael) cryptographic algorithm [4]. After they are generated through the Galois field construction, these cryptographic S-boxes undergo an affine transformation applied to the output binary vectors to enhance their avalanche and correlation properties.

The S-box is a fundamental component of most modern ciphers, playing a crucial role in determining the overall security level of the encryption algorithm. Various methods have been proposed for synthesizing S-boxes with high cryptographic quality.

For example, Zahid et al. [5] utilized trigonometric transformations, where the number of possible S-box designs is limited only by the encryption keys and computational resources, enabling a large design space.

A series of works explored the use of chaotic systems as the basis for S-box generation. Zahid et al. [6] introduced a novel chaotic map combined with nonlinearity tweaking techniques to produce dynamic S-boxes with improved resistance to cryptanalysis. Shakir et al. [7] proposed a hybrid approach that integrates chaotic systems with DNA computing to generate dynamic S-boxes offering a balance of complexity and cryptographic strength. Aydın and Özkaynak [8] developed an automated tool for chaos-driven S-box generation, allowing for enhanced analysis and cryptographic performance. Youssef et al. [9] applied dynamic S-box generation in the context of satellite image encryption, combining hyperchaotic systems with the SVD and RC5 encryption schemes. Zhang et al. [10] proposed a dynamic S-box design based on quantum random walks controlled by hyperchaotic maps, achieving high levels of randomness and cryptographic robustness.

In parallel, evolutionary and heuristic techniques have also gained popularity. Kuznetsov et al. [11] presented an evolutionary approach to S-box synthesis, optimizing nonlinear substitutions using genetic programming principles. Zahid et al. [12] proposed a heuristic evolutionary method for generating dynamic S-boxes with high nonlinearity, demonstrating superior performance over traditional methods. Abdurazzokov [13] described a method for constructing S-boxes by generating non-singular adjacency matrices via genetic algorithms, achieving improved algebraic properties. Finally, Artuğer [14] introduced a construction based on the Josephus problem, providing an innovative deterministic approach for generating strong S-boxes with desirable cryptographic characteristics.

The authors of [15] combined the strengths of genetic algorithms and the theory of dynamic chaos to develop innovative S-boxes with enhanced cryptographic properties.

There is also a more classical but no less effective approach, which consists of using polynomial transformations over the GF(2⁸). In [16], a new approach is proposed, which includes the use of polynomial transformations, dynamic affine transformations, and a permutation technique created by the authors. Similarly, in [17], an algorithm is described for generating S-boxes using the direct product of cyclic groups, achieving high efficiency and enabling the creation of up to 983040 nearly optimal S-boxes, each in just 0.01 s.

Algorithms based on the theory of elliptic curves have also gained popularity. For example, the authors of [18] propose S-box generation methods compatible with existing protocols, offering a high cryptographic strength, dynamism, and increased encryption performance with minimal computational costs. Additionally, in [19], an approach for synthesizing S-boxes designed for lightweight cryptography is outlined, ensuring high adaptability and strong resistance to attacks.

In recent years, artificial intelligence techniques have also been actively applied to the construction of cryptographically strong S-boxes. These approaches typically rely on neural networks, evolutionary algorithms, or swarm intelligence to optimize nonlinearity, avalanche criteria, and resistance to attacks.

Rong et al. [20] proposed an S-box construction algorithm that combines neural networks with genetic algorithms. Their approach trains a neural network to learn optimal transformation structures and then refines them using genetic evolution to improve cryptographic properties. Long and Wang [15] introduced a method based on a discrete chaotic map integrated with an improved artificial bee colony (ABC) algorithm. Their model exploits the global search capabilities of the ABC algorithm to find S-boxes with enhanced nonlinearity and avalanche characteristics. Ahmad and Al-Solami [21] developed an innovative approach using fractional-order Hopfield neural networks to evolve dynamic S-boxes. Their method leverages fractional-order systems’ chaotic dynamics and enhanced convergence properties to generate S-boxes with good nonlinearity and a high level of strict avalanche criterion compliance. Although artificial intelligence methods are still relatively rare in the synthesis of S-boxes, they are increasingly utilized in developing sophisticated attacks. For instance, deep learning models are vulnerable to backdoor attacks that cause targeted misclassification while preserving high accuracy on benign inputs. Lee T. et al. in a recent study [22] demonstrated multi-targeted backdoor attacks in BERT-based models by manipulating trigger word choice and position, achieving success rates of over 95% with minimal accuracy loss on clean data. Such findings underline the growing role of AI in security research and stress the need for S-box constructions to withstand not only classical cryptanalysis but also AI-assisted adversarial techniques.

However, despite the many advantages and wide range of possibilities presented by the above approaches, they also exhibit several persistent limitations, as reported in the literature [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] and confirmed by our comparative analysis:

-

The avalanche properties of most S-boxes are far from ideal;

-

In most cases, the correlation properties of the S-box are flawed;

-

Only small sets of S-boxes with good cryptographic properties can be synthesized using certain methods.

Moreover, the problem of synthesizing optimal S-boxes that simultaneously satisfy all major cryptographic criteria remains unsolved in the general case. Despite notable progress in chaos-based, heuristic, and AI-assisted designs, modern constructions often represent trade-offs between conflicting properties, and no universal solution has yet been established.

These circumstances necessitate the creation of new methods for synthesizing large sets of high-quality S-boxes.

Recently, methods for developing and analyzing cryptographic constructions using many-valued logic functions have gained significant attention in cryptography. They facilitate substantial improvements in the quality of cryptographic constructions, enhancing their correspondence to cryptographic quality criteria.

Modern cryptographic systems demand S-boxes that simultaneously optimize multiple conflicting properties: high nonlinearity, strict avalanche criteria, and low computational overhead. While the existing approaches excel in addressing individual metrics, they often fail to deliver balanced solutions. This paper bridges that gap by introducing a novel integration of the Nyberg construction with optimized GF(4) affine transformations. Our unique approach combines the following: mathematically guaranteed algebraic properties from finite field theory, enhanced four-valued avalanche characteristics that are unattainable in binary systems, and practical implementation efficiency through configurable lookup table (LUT)/arithmetic modes. This trifecta of advantages addresses several critical considerations in cipher design, maintaining theoretical security bounds while enabling real-world deployment across a diverse range of platforms, from hardware security modules to lightweight IoT devices.

In this light, we have to note that S-boxes represent an essential component of any block symmetric cipher, in line with Shannon’s principles of confusion and diffusion. The cryptographic quality of an S-box fundamentally determines the strength and efficiency of the overall cipher. Consequently, improvements in the S-box structure can directly impact the cipher’s performance, potentially allowing for fewer encryption rounds or reducing the complexity of the core transformation. Therefore, developing robust, high-quality S-boxes remains a central objective in modern cryptographic design.

In this paper, we introduce the use of affine transformation matrices over the GF(4) with practically valuable orders $n=3,4$ to enhance the cryptographic properties of S-boxes. We also propose a novel scheme for applying these matrices to S-boxes with optimal avalanche properties, improving their nonlinearity.

The paper presents techniques for synthesizing the complete set of affine transformation matrices over the GF(4) of order $n=3$, as well as constructions for synthesizing a large collection of quaternary affine transformation matrices of order $n=4$. Furthermore, we introduce a recursive construction for generating affine transformation matrices over the GF(4) for arbitrary orders n.

New S-boxes based on the original Nyberg construction are synthesized with the help of matrices of affine transformation over the GF(4), and their cryptographic properties are superior to known analogs. The nonlinearity values of S-boxes corresponding to the SAC and the criterion of the absence of correlation between the output and input vectors increase.

To demonstrate the practical viability of our approach, we embed the proposed S-box into the AES encryption algorithm and conduct extensive testing using the NIST statistical suite. The results show improved randomness and cryptographic robustness compared to the standard AES S-box, confirming the method’s effectiveness for real-world cryptographic applications.

The purpose of this paper is to improve the cryptographic quality of bijective S-boxes by synthesizing affine transformations over GF(4).

The paper is organized as follows:

-

Section 2 describes the fundamental criteria for evaluating the cryptographic quality of S-boxes and introduces the constructions to which the proposed affine transformations are applied, including the Nyberg construction and S-boxes with maximal avalanche characteristics.

-

Section 3 addresses the synthesis of non-binary affine transformation matrices. In this section, we also present our algorithm for applying affine transformations to S-boxes with optimal avalanche properties, ensuring the preservation of these properties while enhancing the S-box nonlinearity.

-

Section 4 focuses on analyzing the cryptographic properties of the constructed S-boxes and provides a discussion of the results obtained.

-

Section 5 concludes the paper with a summary of the research findings.

2. Materials and Methods

The level of implementation of Shannon’s encryption concepts—diffusion and confusion—depends on the quality of the chosen cryptographic transformation. The S-box is the most important component of modern ciphers, allowing them to resist the main types of cryptanalysis attacks, such as linear cryptanalysis, differential cryptanalysis, and correlation cryptanalysis. As such, cryptographic S-boxes receive a great deal of attention from modern researchers. Estimations of the cryptographic quality of S-boxes are currently made with a generally accepted set of cryptographic quality criteria, which assume that the S-box is represented as a set of component Boolean functions $S=\left\{f_i\right\}, i=1,2,\dots ,k,$ where $k$ is the number of outputs/inputs of the S-box.

A component Boolean function $f_i, i=1,2,\dots ,k$ is an individual output bit function of an S-box, where the S-box is represented as a vector of $k$ such functions.

After the S-box has been represented in the form of component Boolean functions, the corresponding cryptographic quality criteria are applied.

• Nonlinearity [23].

The nonlinearity distance of an S-box can be defined as the minimum of the Hamming distance between its component Boolean functions and all codewords of the affine code

$$N_S=\underset{i}{\min }\left\{\mathrm{dist}(f_i,{\phi }_j)\right\}, i=1,\dots ,k, j=1,\dots ,2^{k+1},$$

(1)

where $f_i$ is a component Boolean function; ${\phi }_j$ are the codewords of the affine $A(N,k)$-code; and $\mathrm{dist}(·)$ is the operator for the Hamming distance evaluation.

An alternative way to find the nonlinearity distance of a component Boolean function $f_i$ is to use the Walsh–Hadamard transform

$$N_f=2^{k-1}-{\displaystyle \frac{1}{2}}\max \left\{\left|W(\mathsf{\omega })\right|\right\},$$

(2)

where $W(\mathsf{\omega })$ is the Walsh–Hadamard transform vector of the Boolean function $f_i$ that can be found using the product of its truth table represented as an exponential form $\{0\leftrightarrow 1,1\leftrightarrow -1\}$ on the Walsh–Hadamard matrix

$$W=F{A}_N,$$

(3)

where

$$A_{2^k}=\left[\begin{array}{cc}{H}_{2^{k-1}}& H_{2^{k-1}}\\ H_{2^{k-1}}& -H_{2^{k-1}}\end{array}\right], A_1=1.$$

(4)

As is the case when estimating the nonlinearity distance in the time domain (1), when estimating the nonlinearity distance of component Boolean functions in the Walsh–Hadamard transform domain (2), the total nonlinearity distance of the entire S-box is determined as the minimum of nonlinearity distance among each of the component Boolean functions $N_S=\underset{i}{\min }\{N_{f_i}\}$.

2.

Strict Avalanche Criterion (SAC) [24].

The definition of the strict avalanche criterion of S-boxes is based on the definition of the error propagation criterion. It corresponds to the error propagation criterion [5], which is evaluated using the minimum and maximum values of the weight of the derivatives of the component Boolean functions

$$D_{u}f(x)=f(x)\oplus f(x\oplus u),$$

(5)

along all directions $\forall u\in V_k, wt(u)=1$, where $V_k$ is a linear vector space of vectors of length $k$, and $wt(·)$ is the operator for evaluation of the Hamming weight. The ideal case, in which all derivatives (5) are balanced, i.e., their Hamming weights are equal to $N/2$, means that the component Boolean function corresponds to the strict avalanche criterion, i.e., the probability of changing its output when changing the value of any of its inputs is equal to $0.5$.

3.

Bit Independence Criterion (BIC) [25].

Consider two component Boolean functions $f_a$ and $f_b$ of an S-box for given values $a\ne b, 1\le a,b\le k$. If the new Boolean function $f_a\oplus f_b$, formed as a superposition of these two component Boolean functions, is highly nonlinear and satisfies the SAC, then the S-box is said to satisfy the BIC. Essentially, the BIC evaluates the correlation between the component Boolean functions of the S-box, and in order for an S-box to meet the BIC, its component Boolean functions must be independent of each other.

4.

Linear Approximation Probability (LAP) [26].

The linear approximation probability for an S-box is the probability that its inputs will approach its outputs linearly for a given number of input–output pairs. A weaker S-box will have a higher linear approximation probability due to its greater susceptibility to linear attacks. On the other hand, a lower linear approximation probability indicates a stronger S-box that is more resistant to linear attacks. The following formula can be used to calculate the linear approximation probability:

$$L{P}_S={\displaystyle \frac{\underset{\alpha ,\beta \ne 0}{\max }(\#\{x|0\le x<2^k, \underset{s=1}{\overset{k}{\oplus }}x[s]•\alpha [s]=\underset{t=1}{\overset{k}{\oplus }}S(x)[t]•\beta []\})-2^{k-1}}{2^k}},$$

(6)

where $\alpha ,\beta$ are the input and output masks, respectively, and notation [s] denotes extraction of the s-th bit, while $•$ denotes the bitwise logical AND.

5.

Differential Approximation Probability (DAP) [27].

The differential approximation probability of an S-box estimates the likelihood that a specific input differential of the S-box will result in a particular output differential over a specified number of rounds. This can be used to quantify the likelihood of a certain differential feature occurring within the S-box. To calculate the differential approximation probability, an exhaustive search is typically performed over all possible input and output differentials for a given number of rounds. The occurrences of each differential are counted, and the probability is calculated as the ratio of the occurrences of the desired differential to the total number of input–output pairs tested.

A lower differential approximation probability indicates that the S-box is more resistant to differential cryptanalysis. Such a probability suggests that the S-box does not exhibit any strong differentials, making it more challenging for attackers to exploit these features and break the cipher:

$$DP(\Delta u,\Delta v)={\displaystyle \frac{\left|\{u\in V_k|S(u)\oplus S(u\oplus \Delta u)=\Delta v\}\right|}{2^k}},$$

(7)

where $\Delta u$ and $\Delta v$ are the input and output differentials, respectively.

6.

Correlation independence of output and input vectors of the S-box [28].

To estimate how the S-box corresponds to the correlation independence of output and input vectors, we use the maximum along the absolute values of the correlation coefficients $\max \left\{\left|r_{i,j}\right|\right\}$ of the correlation matrix $R=‖r_{i,j}‖$, which determines the degree of the linear relationship between the output $y$ and input $x$ vectors of the S-box:

$$r_{i,j}=1 - {\displaystyle \frac{{\displaystyle \sum _{m=1}^N(x_{m,i}\oplus y_{m,j})}}{N/2}}, i,j=0,\dots ,k-1$$

(8)

Lower values of $\max \left\{\left|r_{i,j}\right|\right\}$ indicate a higher level of cryptographic quality in the S-box.

One of the new approaches for estimating the cryptographic quality of S-boxes involves using the representation of the S-box not only in the form of component Boolean functions, but also component functions of many-valued logic, as described in [29].

Definition 1 ([29]). 

A function of q-valued logic of $k$ variables is a mapping ${\left\{0,1,2,\dots ,q-1\right\}}^k\to \left\{0,1,2,\dots ,q-1\right\}$.

Many-valued logic functions are more general mathematical objects than Boolean functions. So, for value $q=2$, Definition 1 is the definition of Boolean functions.

Many-valued logic involves expanding the boundaries of awareness and the formal description of the logical connections of the real world. While binary logic is generally accepted, J. Łukasiewicz [30] drew attention to many-valued logic as a means of expressing various shades of information in sentences. After its discovery, famous mathematicians, economists, and philosophers began to implement this strategy and expressed interest in improving the quality of information transfer.

When analyzing a cipher, a cryptanalyst is not limited to the mathematical apparatus of Boolean functions but may use all possible representations of cipher constructions, particularly cryptographic S-boxes. Thus, S-boxes with four inputs of length $N=16$ can be represented by four component Boolean functions or two component 4-functions (see

Table 1. S-box representation using Boolean and many-valued logic functions.

$Q$	4	7	2	14	1	13	8	11	15	12	6	10	5	9	3	0
$f_{20}$	0	1	0	0	1	1	0	1	1	0	0	0	1	1	1	0
$f_{21}$	0	1	1	1	0	0	0	1	1	0	1	1	0	0	1	0
$f_{22}$	1	1	0	1	0	1	0	0	1	1	1	0	1	0	0	0
$f_{23}$	0	0	0	1	0	1	1	1	1	1	0	1	0	1	0	0
$f_{40}$	0	3	2	2	1	1	0	3	3	0	2	2	1	1	3	0
$f_{41}$	1	1	0	3	0	3	2	2	3	3	1	2	1	2	0	0

[29] for an example, which is a simplified illustration for a small S-box).

Similarly, eight-input S-boxes of length $N=256$, which are the de facto standard in modern cryptographic algorithms, can be represented using eight component Boolean functions, four component 4-functions, and two component 16-functions.

On the other hand, ref. [31] introduces a definition of an SAC for q-functions.

Definition 2 ([31]). 

The weight $\varpi (u)$ of a q-valued vector is the number of its nonzero components.

Definition 3 ([31]). 

The derivative of the function $f$ with respect to the direction of the vector u is the function

$$D_{u}f(x)=f(x\underset{q}{\oplus }u)-f(x) (\mathrm{mod}q),$$

(9)

where $\underset{q}{\oplus }$ means the modulo q addition.

Definition 4 ([31]). 

The function of q-valued logic $f(x)$ satisfies the propagation criterion $PC(u)$ with respect to the vector $u\in V_k$ if its derivative in the direction u is a balanced function, i.e., values $0,1,\dots ,q-1$ are taken with equal probabilities: $p(D_{u}f(x)=i(\mathrm{mod}q))={\displaystyle \frac{1}{q}}$ for all $i=0,1,\dots ,q-1$. In other words, $K^0=K^1=\dots =K^{q-1}$, where $K^i$ is the number of sets of variable values for which the derivative takes the value $i$. The function of q-valued logic $f(x)$ satisfies the propagation criterion $PC(k)$ of degree $k$ if it satisfies the propagation criterion $PC(u)$ with respect to all vectors u of weight $1\le \varpi (u)\le k$.

Definition 5 ([31]). 

The function of q-valued logic $f(x)$ satisfies the SAC if it satisfies the propagation criterion $PC(1)$ of degree 1.

In this paper, we not only evaluate the obtained S-boxes using the classical set of criteria for the cryptographic quality of component Boolean functions but also estimate their component 4-functions’ compliance with the SAC, according to the results presented in [31].

We note that the efficient evaluation of cryptographic quality indicators, such as nonlinearity, avalanche properties, and differential uniformity, for large S-boxes is a critical and still unresolved task. In this study, we relied on efficiently written MATLAB version R2023b scripts based on vectorized and bitwise operations, which were sufficient for analyzing 8-bit S-boxes. Nevertheless, the development of general-purpose, scalable tools for evaluating large S-boxes remains an important direction for future research.

While the cryptographic analysis in this manuscript focuses on classical metrics, it is important to note that the effectiveness of modern attacks, such as deep learning-assisted differential attacks or algebraic side-channel vulnerabilities, is often influenced by the same cryptographic properties (e.g., diffusion, confusion) that are evaluated using classical methods. Future work may explore how these modern attacks interact with traditional cryptographic metrics.

Let us consider two S-box constructions that are used as source material in this paper.

One of the most practically applicable is the cryptographic S-box of the Nyberg construction [32], which is used in the AES cryptographic algorithm.

The classical Nyberg construction is based on the multiplicative inversion of the input S-box values in the extended Galois field,

$$y=x^{-1}\mathrm{modd}\left[f\right(z), p], y,x\in GF(2^k),$$

(10)

where $\mathrm{modd}$ denotes the operation of taking an element by double modulo, and $f\left(z\right)$ is the primitive irreducible polynomial. For example, in the AES cryptographic algorithm, the type of primitive irreducible polynomial is fixed as $f(x)=x^8+x^4+x^3+x+1$, while the specific S-box, which is built on the basis of this primitive irreducible polynomial, is presented in

Table 2. S-box based on multiplicative inversion for all 8-bit numbers in GF (2⁸).

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	1	141	246	203	82	123	209	232	79	41	192	176	225	229	199
1	116	180	170	75	153	43	96	95	88	63	253	204	255	64	238	178
2	58	110	90	241	85	77	168	201	193	10	152	21	48	68	162	194
3	44	69	146	108	243	57	102	66	242	53	32	111	119	187	89	25
4	29	254	55	103	45	49	245	105	167	100	171	19	84	37	233	9
5	237	92	5	202	76	36	135	191	24	62	34	240	81	236	97	23
6	22	94	175	211	73	166	54	67	244	71	145	223	51	147	33	59
7	121	183	151	133	16	181	186	60	182	112	208	6	161	250	129	130
8	131	126	127	128	150	115	190	86	155	158	149	217	247	2	185	164
9	222	106	50	109	216	138	132	114	42	20	159	136	249	220	137	154
A	251	124	46	195	143	184	101	72	38	200	18	74	206	231	210	98
B	12	224	31	239	17	117	120	113	165	142	118	61	189	188	134	87
C	11	40	47	163	218	212	228	15	169	39	83	4	27	252	172	230
D	122	7	174	99	197	219	226	234	148	139	196	213	157	248	144	107
E	177	13	214	235	198	14	207	173	8	78	215	227	93	80	30	179
F	91	35	56	52	104	70	3	140	221	156	125	160	205	26	65	28

[32].

Galois fields provide excellent confusion, which is a key property for cryptographic S-boxes. However, the diffusion achieved by Galois field constructions alone can be insufficient. To address this limitation, affine transformations are applied in the S-box design. These affine transformations improve diffusion by spreading the input values more evenly across the output, which enhances the overall cryptographic strength of the S-box. The combination of Galois field-based constructions with affine transformations ensures both strong confusion and adequate diffusion, making the design more resistant to cryptanalytic attacks.

The Nyberg construction further improves the cryptographic quality of the S-box obtained using (10) by applying an affine transformation, which is specified using the following formula:

$$S_i\equiv R{y}_i+C\mathrm{mod}2, i=1,\dots ,N.$$

(11)

In this case, the original AES cryptographic algorithm uses the following form of the affine transformation matrix $R$ and vector $C$:

$$\left(\begin{array}{c}s(0)\\ s(1)\\ s(2)\\ s(3)\\ s(4)\\ s(5)\\ s(6)\\ s(7)\end{array}\right)=\left(\begin{array}{cccccccc}1& 0& 0& 0& 1& 1& 1& 1\\ 1& 1& 0& 0& 0& 1& 1& 1\\ 1& 1& 1& 0& 0& 0& 1& 1\\ 1& 1& 1& 1& 0& 0& 0& 1\\ 1& 1& 1& 1& 1& 0& 0& 0\\ 0& 1& 1& 1& 1& 1& 0& 0\\ 0& 0& 1& 1& 1& 1& 1& 0\\ 0& 0& 0& 1& 1& 1& 1& 1\end{array}\right)\left(\begin{array}{c}y(0)\\ y(1)\\ y(2)\\ y(3)\\ y(4)\\ y(5)\\ y(6)\\ y(7)\end{array}\right)+\left(\begin{array}{c}1\\ 1\\ 0\\ 0\\ 0\\ 1\\ 1\\ 0\end{array}\right)\mathrm{mod}2$$

(12)

Using an affine transformation can improve the cryptographic properties of the S-box. However, according to the research performed in this paper, the cryptographic properties of the S-box can be improved further using non-binary matrices of affine transformation.

The second example of the source material for the S-boxes used in this paper, together with proposed GF(4) affine transformations, are the S-boxes synthesized according to the method outlined in [33]. To comprehensively present this material, we will briefly summarize the key steps of this method.

Step 1. Using Method M1 (Method M1 is a recursive synthesis technique that constructs S-boxes with optimal avalanche properties by combining algebraic filtering, combinatorial optimization, and many-valued logic decomposition) [34], synthesize a set of $J_1=3968$ high-quality S-boxes of length $N=256$, which meet the strict avalanche criterion of component 4-functions and the criterion of maximum avalanche effect of component Boolean functions.

Step 2. Going through the entire set of S-boxes obtained in Step 1, decompose them into component 4-functions. After decomposing the obtained 4-functions into two component Boolean functions, select those in which both component Boolean functions meet the SAC conditions.

Step 3. From the obtained set of 4-functions, it is necessary to select those that are unique.

After duplicates have been removed from this set, obtain 769 suitable functions.

Step 4. Combining the obtained 4-functions by applying theorem [35], generate a set of S-boxes, selecting those that are bijective. The theorem referred to in this context is Kim’s theorem, which facilitates the construction of S-boxes based on component functions. It introduces a property where all linear combinations of the component functions must be balanced. This property helps simplify the process of S-box construction.

After completing Step 4, obtain a set with the cardinality of $J=117,588$ unique S-boxes.

An example S-box is presented in

Table 3. S-box with good avalanche characteristics of Boolean and 4-functions.

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	10	5	26	64	97	177	239	66	167	85	222	251	59	188	220	164
1	25	46	84	30	133	243	86	117	105	226	207	187	128	224	184	15
2	50	104	34	45	199	106	73	153	246	211	143	125	244	140	19	148
3	124	54	49	6	126	93	173	219	231	147	65	202	144	39	168	200
4	70	91	129	75	242	44	131	162	150	31	56	228	253	29	229	120
5	111	149	95	90	48	151	182	198	35	12	248	170	33	249	76	193
6	169	99	110	115	171	138	218	4	16	204	190	55	205	80	213	53
7	119	114	71	189	158	238	24	191	208	130	11	36	100	233	9	209
8	152	194	136	135	109	192	227	51	92	121	37	215	94	38	185	62
9	214	156	155	172	212	247	7	113	77	57	235	96	58	141	2	98
A	160	175	176	234	203	27	69	232	13	255	116	81	145	22	118	14
B	179	132	254	180	47	89	252	223	195	72	101	17	42	74	18	165
C	3	201	196	217	1	32	112	174	186	102	20	157	103	250	127	159
D	221	216	237	23	52	68	178	21	122	40	161	142	206	67	163	123
E	236	241	43	225	88	134	41	8	60	181	146	78	87	183	79	210
F	197	63	245	240	154	61	28	108	137	166	82	0	139	83	230	107

[33], and the values of the main indicators of the cryptographic quality of this S-box are presented further. This S-box belongs to a specific class of S-boxes that can be used in cases where ideal avalanche and correlation properties are of the utmost importance. However, the nonlinearity of this S-box is poor.

The cryptographic properties of this S-box can be improved by using a modified version of the GF(4) affine transformations scheme.

3. Results

The basic idea of the transition to GF(4) affine transformations is to rewrite (11) with respect to the arithmetic of the Galois field GF(4). The arithmetic of the Galois field GF(4) can be constructed only based on one primitive irreducible polynomial $g(x)=x^2+x+1$. We present the multiplication and addition tables of the Galois field $GF(4)$:

$$\begin{array}{cc}+& \begin{array}{cccc}0& 1& 2& 3\end{array}\\ \begin{array}{c}0\\ 1\\ 2\\ 3\end{array}& \overline{)\begin{array}{cccc}0& 1& 2& 3\\ 1& 0& 3& 2\\ 2& 3& 0& 1\\ 3& 2& 1& 0\end{array}}\end{array}, \begin{array}{cc}\times & \begin{array}{cccc}0& 1& 2& 3\end{array}\\ \begin{array}{c}0\\ 1\\ 2\\ 3\end{array}& \overline{)\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 2& 3\\ 0& 2& 3& 1\\ 0& 3& 1& 2\end{array}}\end{array}$$

(13)

Thus, we can rewrite (11) with respect to Galois field $GF(4)$ arithmetic:

$$S_i\equiv R{y}_i+C \mathrm{modd}(g(x),2), i=1,\dots ,N,$$

(14)

where $S_i$ and $y_i$ are represented as vectors consisting of elements of the Galois field GF(4), while $R$ and $C$ are a matrix and a vector over the Galois field GF(4). Note that when using (14) instead of (11) for an S-box of length $N=256$, vectors $S_i$, $y_i$ in the case of representation over the Galois field GF(4) will consist of four elements, instead of eight, as in the case of the Galois field GF(2). 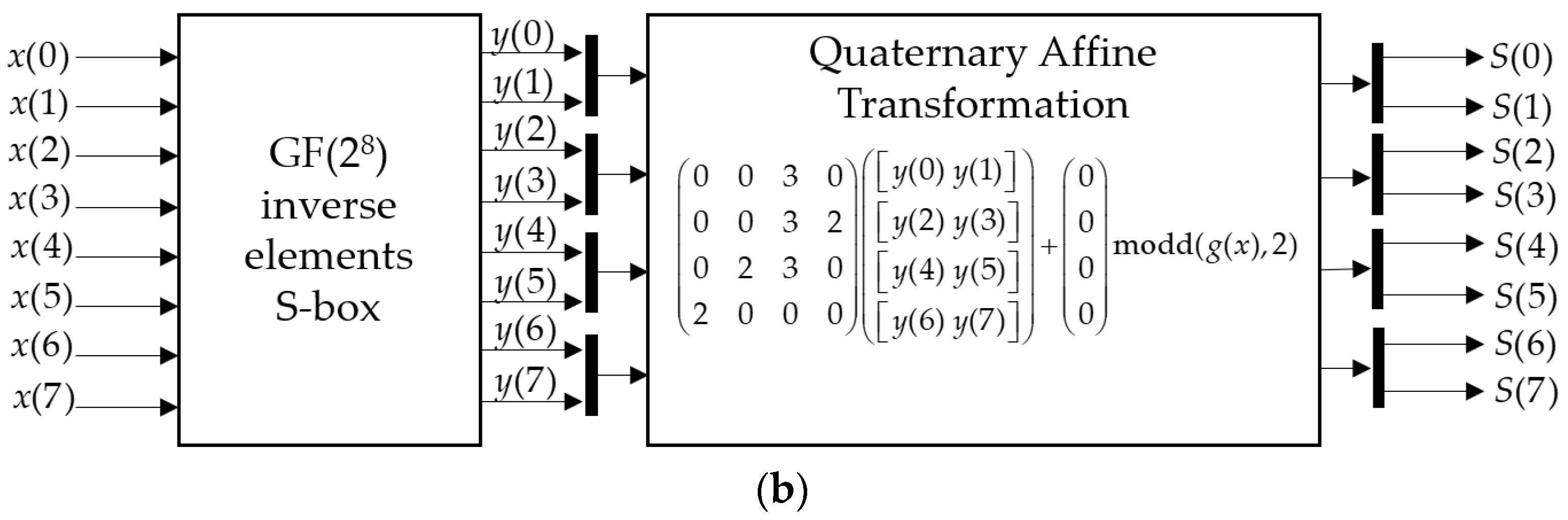Thus, to ensure the operation of the scheme, we need matrices $R$ of the affine transformation of a two-fold smaller order (Figure 1).

For a specific practical application of (14), it is necessary to construct $R$ matrices of the affine transformation that would ensure the bijectivity of the resulting S-box. Below, we present a method for synthesizing such matrices for practically valuable values of their orders $n=3,4$ as well as a recurrent construction for arbitrary n.

3.1. Synthesis of Matrices of GF(4) Affine Transformations of Order $n=3$

The solution to the problem of synthesizing matrices of affine transformation over a Galois field GF(4) of practically important order $n=4$ to ensure the operation of S-boxes of practically valuable length $N=256$ by the exhaustive search method is associated with the enumeration of elements using fairly computationally expensive operations over the Galois field GF(4). Therefore, we propose a regular method for synthesizing these matrices based on matrices of affine transformations of lower order $n=3$.

We have established the synthesis of a complete set of matrices (all possible existing structures) of affine transformation over a Galois field GF(4) that would ensure the bijectivity of the resulting S-boxes can be performed on the basis of four basic constructions:

$$\begin{array}{l}{C}_{3,1}=\left(\begin{array}{ccc}0& 0& x\\ 0& x& 0\\ x& 0& 0\end{array}\right); C_{3,2}=\left(\begin{array}{ccc}0& 0& x_1\\ 0& x& x_1\\ x& 0& x_1\end{array}\right);\\ C_{3,3}=\left(\begin{array}{ccc}{x}_1& 0& 0\\ x_1& x& 0\\ x_1& 0& x\end{array}\right); C_{3,4}=\left(\begin{array}{ccc}0& x_1& 0\\ 0& x_1& x\\ x& x_1& 0\end{array}\right),\end{array}$$

(15)

where in $C_{3,1}$ index 3 means the order $n$ of the matrix, and index 1 means the number of structures.

In this case, the parameter $x\in \{1,2,3\}$ includes all possible combinations of values from the given set, including repetitions.

The value $x_1\in \{1,2,3\}$ always forms a constant column consisting of uncombined values, that is, only 1, or only 2, or only 3 values are possible there. There cannot be any combined values.

Note that each of the structures $C_{3,1},C_{3,2},C_{3,3},C_{3,4}$ allows all possible row permutations, the number of which is $3!$. Thus, we can calculate the cardinality of the affine transformations generated by the structure $C_1$ as $\#C_1=3^3\cdot 3!=162$.

In this case, the cardinality of the sets generated by the matrices $C_2,C_3,C_4$ is defined as $\#C_1=3^3\cdot 3!=162$.

Thus, the total cardinality of the constructed set of affine transformation matrices is $\#C_i=4\cdot 162=648, i=1,2,\dots ,4$. This was confirmed by the exhaustive search method. The four constructions in Construction (15) became the basis for constructing a complete class of affine transformations of order $n=4$, which have the greatest practical significance for synthesizing S-boxes.

S-boxes with a length of 256 represent a versatile and robust solution, making them highly suitable for modern cryptographic systems and practical implementations.

To construct such S-boxes, it is essential to develop new rules within the GF(4), enabling operations and mappings capable of accommodating larger S-box structures. A logical starting point is to build upon existing constructions, particularly those based on (15).

These constructions serve as the basis for generating new transformations, which can be specifically designed to meet the requirements of 256-length S-boxes.

We present a new construction for affine transformations of order $n=4$ based on a matrix $C_{3,1}$:

$$C_{3,1}=\left(\begin{array}{ccc}0& 0& x\\ 0& x& 0\\ x& 0& 0\end{array}\right) \Rightarrow C_{4,1}=\left(\begin{array}{cccc}0& 0& 0& x\\ 0& 0& x& 0\\ 0& x& 0& 0\\ x& 0& 0& 0\end{array}\right).$$

(16)

The structure $C_{4,1}$ can be extended to the case of an arbitrary order of matrices of affine transformation over GF(4), defined by the following recurrent formula:

$$C_{n,1}=\left(\begin{array}{llll}0\hfill & 0\hfill & \dots \hfill & x\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill \\ 0\hfill & x\hfill & \dots \hfill & 0\hfill \\ x\hfill & 0\hfill & \dots \hfill & 0\hfill \end{array}\right)$$

(17)

In this case, the cardinality of the class generated by the construction $C_{n,1}$ is $\#C_{n,1}=3^{n}n!.$ In the case of $n=4$, we have $\#C_{4,1}=3^{n}4!=1944$.

Additionally, matrices of affine transformations over the Galois field GF(4) can be constructed on the basis of constructions $C_{3,2},C_{3,3},C_{3,4}$ by concatenating a column and a row containing all zeros and one element x at the crosshair. In particular, the following matrix can be constructed on the basis of the construction $C_{3,2}$:

$$C_{3,2}=\left(\begin{array}{ccc}0& 0& x_1\\ 0& x& x_1\\ x& 0& x_1\end{array}\right)\Rightarrow C_{4,2}=\left(\begin{array}{cccc}0& 0& 0& x_1\\ 0& 0& x& x_1\\ 0& x& 0& x_1\\ x& 0& 0& 0\end{array}\right).$$

(18)

Based on the construction $C_{3,3}$, the following matrix of the affine transformation of order $n=4$ can be constructed:

$$C_{3,3}=\left(\begin{array}{ccc}{x}_1& 0& 0\\ x_1& x& 0\\ x_1& 0& x\end{array}\right)\Rightarrow C_{4,3}=\left(\begin{array}{cccc}0& x_1& 0& 0\\ 0& x_1& x& 0\\ 0& x_1& 0& x\\ x& 0& 0& 0\end{array}\right).$$

(19)

Based on the construction $C_{3,4}$, we obtain the following matrix:

$$C_{3,4}=\left(\begin{array}{ccc}0& x_1& 0\\ 0& x_1& x\\ x& x_1& 0\end{array}\right)\Rightarrow C_{4,4}=\left(\begin{array}{cccc}0& 0& x_1& 0\\ 0& 0& x_1& x\\ 0& x& x_1& 0\\ x& 0& 0& 0\end{array}\right).$$

(20)

It is clear that the cardinality of the affine transformation matrices that can be constructed on the basis of constructions $C_{4,2},C_{4,3},C_{4,4}$ is $\#C_{4,2}=\#C_{4,3}=\#C_{4,4}=3^3\cdot 4!\cdot 3=1944$.

Thus, the total number of affine transformation matrices over the Galois field $GF(4)$ that are synthesized based on all proposed constructions of order $n=4$ is $\#C_{4,i}=7776$.

As a result, we have constructed new rules for order $n=4$ of the affine transformation matrix, enabling construction of S-boxes with good cryptographic properties of length $N=256$.

3.2. S-Box Synthesis

We use formula (14) to synthesize a cryptographic S-box, applying the following type of GF(4) affine transformation:

$$R=\left(\begin{array}{cccc}0& 0& 3& 0\\ 0& 0& 3& 2\\ 0& 2& 3& 0\\ 2& 0& 0& 0\end{array}\right)$$

(21)

Table 4. S-box based on the Nyberg construction and affine transformation (21).

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0	32	75	137	5	186	194	105	25	58	120	65	199	109	145	173
1	122	59	171	198	191	72	142	50	222	188	205	233	253	130	213	247
2	96	22	238	101	86	10	155	53	97	100	159	212	4	126	255	113
3	164	94	251	38	85	112	66	178	117	216	12	54	106	131	254	124
4	128	221	232	98	132	36	153	250	35	114	139	24	118	208	57	116
5	197	34	220	37	42	240	47	127	92	156	60	69	170	229	174	228
6	196	18	119	89	246	3	200	146	185	110	235	241	20	219	44	64
7	242	43	39	31	8	27	163	172	11	134	73	204	239	33	227	243
8	211	30	62	195	7	150	95	70	143	83	23	61	169	48	179	51
9	209	234	52	6	29	167	63	182	104	244	115	151	49	225	183	175
A	1	46	148	81	123	147	82	214	192	21	56	230	217	161	121	190
B	168	77	176	245	40	90	210	166	19	91	74	140	79	111	15	102
C	68	88	180	223	45	181	177	184	187	224	154	252	76	237	103	129
D	226	236	87	158	157	13	125	41	55	135	189	149	67	17	203	202
E	231	136	133	9	141	152	249	71	84	26	165	93	2	138	144	215
F	206	28	80	248	218	78	16	107	193	99	14	207	201	108	162	160

shows the specific form of the S-box after applying the affine transformation (21) based on the S-box of the Nyberg construction (Table 2).

The cryptographic properties of the obtained S-box, which is given in Table 4, are shown further.

3.3. Proposed Algorithm for Affine Transformation

We have proposed a modified scheme of affine transformation over the Galois field GF(4). When combined with S-boxes [33] that satisfy the SAC for both component Boolean functions and 4-functions, this scheme enables the creation of high-cryptographic-quality S-boxes.

According to our proposed method, the affine transformation of S-boxes is performed as follows:

$${\alpha }_j.S_i={\displaystyle \sum _{u=1}^n{\alpha }_j\times y_i{R}^{\prime }(j,u)}+C\mathrm{mod}4,$$

(22)

where the notation ${\alpha }_j.S_i$ denotes taking the $j$-th quaternary digit of the $i$-th element of the S-box element, while the notation $R^{\prime }(j,k)$ denotes extracting the element with indices $(j,k)$ from the matrix $R^{\prime }$, and $\times$ denotes multiplication in the Galois field following the multiplication table (13). Modified constructions of $C_{4,2},C_{4,3},C_{4,4}$ are used as matrices $R^{\prime }$:

$$\begin{array}{l}{C}_{4,21}=\left(\begin{array}{cccc}x& 0& 0& x_1\\ 0& 0& x& x_1\\ 0& x& 0& x_1\\ 0& 0& 0& 0\end{array}\right); C_{4,22}=\left(\begin{array}{cccc}0& 0& 0& x_1\\ x& 0& x& x_1\\ 0& x& 0& x_1\\ 0& 0& 0& 0\end{array}\right);\\ C_{4,23}=\left(\begin{array}{cccc}0& 0& 0& x_1\\ 0& 0& x& x_1\\ x& x& 0& x_1\\ 0& 0& 0& 0\end{array}\right); C_{4,24}=\left(\begin{array}{cccc}0& 0& 0& x_1\\ 0& 0& x& x_1\\ 0& x& 0& x_1\\ x& 0& 0& 0\end{array}\right);\\ C_{4,31}=\left(\begin{array}{cccc}x& x_1& 0& 0\\ 0& x_1& x& 0\\ 0& x_1& 0& x\\ 0& 0& 0& 0\end{array}\right); C_{4,32}=\left(\begin{array}{cccc}0& x_1& 0& 0\\ x& x_1& x& 0\\ 0& x_1& 0& x\\ 0& 0& 0& 0\end{array}\right);\\ C_{4,33}=\left(\begin{array}{cccc}0& x_1& 0& 0\\ 0& x_1& x& 0\\ x& x_1& 0& x\\ 0& 0& 0& 0\end{array}\right); C_{4,34}=\left(\begin{array}{cccc}0& x_1& 0& 0\\ 0& x_1& x& 0\\ 0& x_1& 0& x\\ x& 0& 0& 0\end{array}\right);\\ C_{4,41}=\left(\begin{array}{cccc}x& 0& x_1& 0\\ 0& 0& x_1& x\\ 0& x& x_1& 0\\ 0& 0& 0& 0\end{array}\right); C_{4,42}=\left(\begin{array}{cccc}0& 0& x_1& 0\\ x& 0& x_1& x\\ 0& x& x_1& 0\\ 0& 0& 0& 0\end{array}\right);\\ C_{4,43}=\left(\begin{array}{cccc}0& 0& x_1& 0\\ 0& 0& x_1& x\\ x& x& x_1& 0\\ 0& 0& 0& 0\end{array}\right); C_{4,44}=\left(\begin{array}{cccc}0& 0& x_1& 0\\ 0& 0& x_1& x\\ 0& x& x_1& 0\\ x& 0& 0& 0\end{array}\right).\end{array}$$

(23)

Our research established that the best-quality results were achieved by matrices constructed based on (23), which do not contain a value of 1 in their composition. Let us consider a specific matrix,

$$R^{\prime }=\left(\begin{array}{cccc}2& 0& 3& 0\\ 0& 0& 3& 2\\ 0& 2& 3& 0\\ 0& 0& 0& 0\end{array}\right),$$

(24)

and then construct a new S-box using (22) and the S-box given in Table 3, which corresponds to the SAC of component Boolean functions and 4-functions. The resulting S-box is presented in

Table 5. S-box satisfying the SAC after an affine transformation.

	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	15	6	47	128	178	210	121	131	245	166	107	93	29	216	104	244
1	46	59	164	43	198	81	167	150	190	115	73	221	192	112	220	9
2	19	188	51	58	69	191	142	238	87	97	201	154	84	200	33	228
3	152	23	18	7	155	170	250	109	117	225	130	79	224	53	252	76
4	135	173	194	141	83	56	193	243	231	41	28	116	90	42	118	156
5	185	230	169	175	16	229	215	71	49	8	92	255	50	94	136	66
6	254	177	187	145	253	207	111	4	32	72	219	21	74	160	102	22
7	149	147	133	218	235	123	44	217	96	195	13	52	180	126	14	98
8	236	67	204	197	186	64	113	17	168	158	54	101	171	55	222	27
9	103	232	237	248	100	85	5	146	138	30	125	176	31	202	3	179
A	240	249	208	127	77	45	134	124	10	89	148	162	226	39	151	11
B	209	196	91	212	57	174	88	105	65	140	182	34	63	143	35	246
C	1	78	68	110	2	48	144	251	223	183	36	234	181	95	153	233
D	106	108	122	37	20	132	211	38	159	60	242	203	75	129	241	157
E	120	82	61	114	172	199	62	12	24	214	227	139	165	213	137	99
F	70	25	86	80	239	26	40	184	206	247	163	0	205	161	119	189

.

In this case, the cryptographic properties of the S-box in Table 5 are shown further.

4. Discussion

4.1. Cryptographic Quality Indicators of the Proposed S-Boxes Compared with the Best-Known Analogs

In

Table 6. S-box quality indicator values.

S-Box	Nonlinearity	SAC	BIC Nonlinearity	BIC SAC	LAP	DAP	$\mathbf{max}\left\{\left|{\mathit{r}}_{\mathit{i},\mathit{j}}\right|\right\}$	SAC of Component 4-Functions
Proposed methods
Nyber construction with GF(4) affine transformation (Table 4)	112	0.5005	112	0.5031	0.0625	0.0156	0.125	0.6250
S-box with affine transformation on GF(4) (Table 5)	96	0.5	77.7143	0.4799	0.5	1	0	0.5
Regular methods
Original Nyberg construction without affine transformation [22]	112	0.5032	112	0.5057	0.0625	0.0156	0.125	0.6484
AES S-box (Nyberg construction with binary affine transformation) [22]	112	0.5049	112	0.5046	0.0625	0.0156	0.125	0.6016
S-box [5]	111.5	0.5059	104.2143	0.5022	0.125	0.0391	0.1406	0.6484
S-box [14]	110.5	0.5107	102.8571	0.4971	0.1328	0.0391	0.1406	0.6719
S-box [16]	111.5	0.5095	103.9286	0.4986	0.125	0.0391	0.1406	0.6562
S-box [18]	106.25	0.5010	103.1429	0.5069	0.1328	0.0469	0.1562	0.625
Special method
S-box [23] (S-box, which satisfies SAC of component Boolean and 4-functions)	80	0.5	83.4286	0.4967	0.5	1	0	0.5
Chaos-based methods
S-box [36]	106	0.4993	104.2143	0.5030	0.125	0.0390	0.1562	0.6797
S-box [37]	107	0.5781	102.93	0.4991	0.1719	0.0469	0.1562	0.6406
AI-based method
S-box [21]	111.25	0.5007	102.5714	0.5034	0.1406	0.0391	0.125	0.6094

, we present the calculated cryptographic quality indicators of the S-boxes synthesized in this paper based on GF(4) affine transformations, as well as the cryptographic characteristics of known analogs. MatLAB was employed to conduct the required computations and simulations, which provided the data presented in Table 6.

An analysis of the data presented in Table 6 indicates that the use of affine transformations over GF(4) leads to a greater improvement in avalanche properties (better correspondence to SAC and BIC SAC) than the use of the classical affine transformation over GF(2). At the same time, the nonlinearity maintains the same high-level characteristic as the Nyberg construction.

The improved avalanche properties achieved through our proposed GF(4) affine transformations significantly enhance the practical security of S-boxes against differential and linear cryptanalysis. While the theoretical bounds for LAP and DAP remain unchanged from the original Nyberg construction, the fundamental security improvements manifest through several important mechanisms.

By optimizing the SAC to achieve near-ideal values (0.5005), our transformations ensure that input changes propagate more uniformly and unpredictably throughout the S-box structure. This disrupts the formation of useful differential characteristics that attackers rely on, effectively increasing the complexity of constructing successful differential trails. The inherent properties of 4-valued logic introduce additional nonlinear interactions between bits, creating more complex input–output relationships that mask linear correlations and reduce the effectiveness of linear approximations.

The practical security implications are substantial. While the worst-case LAP/DAP metrics may appear unchanged in theoretical analysis, in practice, the actual work factor required for successful attacks increases significantly. Attackers face greater difficulty in constructing effective differential trails or linear approximations due to the enhanced diffusion properties and algebraic complexity introduced by the GF(4) operations, which necessitates the use of longer, more complex attack paths with lower success rates.

Furthermore, these security improvements are achieved without compromising other critical cryptographic properties. The transformations maintain maximal nonlinearity (112) while preserving the bijectivity and computational efficiency required for practical implementation. The result is an S-box construction that offers enhanced real-world security against sophisticated cryptanalytic techniques while remaining suitable for deployment in modern cryptographic systems. This combination of strong avalanche properties with maintained theoretical security bounds represents a meaningful advancement in S-box design, particularly for applications where resistance to both theoretical and practical attacks is paramount.

Cryptographic S-boxes [33] are specialized and constructed to correspond as closely as possible to the SAC and to have a low correlation between output and input vectors; however, the original construction has a very small value of nonlinearity (80). Using the matrices of affine transformations over GF(4) proposed in this paper, we were able to increase the nonlinearity of these S-boxes to a value of 96 while maintaining their correspondence to the SAC of both component 4-functions and Boolean functions.

The GF(4) transformation slightly reduces BIC nonlinearity (Table 6), reflecting an intentional trade-off to maximize nonlinearity and SAC, the properties which are most critical for attack resistance. BIC nonlinearity remains cryptographically sufficient, and the enhanced BIC SAC mitigates potential weaknesses by enforcing stricter bit independence.

We show the fine structure of the distribution of derivatives in Figure 2.

Additionally, the proposed mathematical apparatus of affine transformations over the GF(4) significantly expands the assortment of high-quality S-boxes. This apparatus can be applied to other S-box constructions to improve their cryptographic properties and increase the cardinality of the resulting sets of high-quality substitution constructions.

The proposed synthesis method offers a fundamentally different approach compared to existing affine transformation techniques traditionally constructed over GF(2). By employing affine transformations over the quaternary field GF(4), we introduce a framework based on many-valued logic, which substantially broadens the design space and enables more granular control over the resulting cryptographic properties. This approach ensures the preservation of bijectivity and supports the generation of large classes of S-boxes with optimal nonlinear, avalanche, and correlation characteristics. Beyond empirical performance, this construction provides a new theoretical perspective for S-box design, offering formal structure and generalizability not found in previous works.

Notably, our proposed method’s computational complexity of the affine transformation step is lower than that of the classical Nyberg construction. In the AES S-box, the affine transformation involves multiplying each S-box element by an 8×8 matrix over GF(2). In contrast, our approach uses a 4 × 4 matrix over GF(4), effectively reducing the number of operations per element (as the operations over GF(4) are of comparable computational complexity to operations over GF(2) if performed using a lookup table on modern platforms) while maintaining strong cryptographic properties. Furthermore, in practical implementations, S-boxes are typically realized via lookup tables, minimizing the impact of arithmetic operations over the field. Therefore, our method ensures efficient computation and scalability, especially for S-box sizes of up to 256 elements, which are standard in modern cryptographic algorithms.

To contextualize the advantages of our GF(4)-based approach, in

Table 7. Cryptographic properties of S-box design approaches.

Basic Criteria	Classic AES	Chaos-Based [36,37]	Proposed Nyberg + GF(4) Affine Transform	SAC-Optimized	Proposed SAC-Optimized + GF(4) Affine Transform
Nonlinearity	112	106–111.75	112	80	96
SAC	0.5049	0.4993–0.5781	0.5005	0.5	0.5
SAC of component 4-functions	0.6016	0.6094–0.6797	0.6250	0.6250	0.5
BIC Nonlinearity	112	102.93–104.2143	112	83.4286	77.71
$\max \left\{\left|r_{i,j}\right|\right\}$	0.125	0.1250–0.1562	0.125	0	0
Implementation	LUT/GF operations	LUT/Complex	LUT/GF operations	LUT/Complex	LUT/Complex
Algebraic Proofs	Yes	No	Yes	Yes	Yes

, we compare it with two dominant S-box design paradigms: conventional binary-field GF(2) constructions and heuristic methods (e.g., chaos-based or genetic algorithms). Unlike these alternatives, our method combines algebraic guarantees by providing mathematical properties to ensure bijectivity, invertibility, and controlled nonlinearity with the flexibility of 4-valued logic optimization.

Our analysis reveals two significant advancements.

1.

For the Nyberg-based construction, the advancements are as follows:

-

Maximal 112 nonlinearity (matching AES) is maintained;

-

SAC correspondence is improved (from 0.5029 to 0.5005);

-

All algebraic guarantees are preserved.

2.

For the SAC-optimized S-box, the advancements are as follows:

-

A perfect 0.5 SAC is maintained for both Boolean and 4-valued functions;

-

A perfect 0 correlation coefficient between input and output vectors is observed;

-

Nonlinearity is increased by 20% (80→96) compared to the original SAC-optimized construction;

-

A new trade-off occurs: perfect SAC with maintained nonlinearity.

The SAC-optimized variant is particularly valuable for applications requiring strict avalanche criteria, while the Nyberg-based version offers balanced protection. Both demonstrate that GF(4) is able to target specific cryptographic properties without compromising its implementation efficiency.

4.2. Practical Evaluation of Proposed S-Boxes in AES

To validate the practical applicability of the proposed S-boxes, we integrated them into the AES algorithm, replacing the standard Rijndael S-box with our alternative, which was constructed using GF(4) affine transformations (Table 5).

The experiment was performed as follows:

-

The test dataset was composed of 100 randomly selected files, each 1 MB in size.

-

Each file was encrypted using AES with different S-box variants.

-

The encrypted outputs were analyzed using the NIST Statistical Test Suite (SP 800-22) to assess their randomness and cryptographic strength.

-

Success criteria: We counted the number of files that successfully passed all NIST tests, indicating the strong cryptographic quality of the encryption output.

The results are presented in

Table 8. The results of the operation of different S-boxes in the structure of the AES cryptographic algorithm.

S-Box Variant	Files That Passed NIST Tests (Out of 100)
Original AES S-box (Rijndael)	94/100
Proposed S-box (SAC + GF(4) affine transformations)	96/100
Dynamic chaos-based S-box [7]	93/100

.

Our proposed S-box achieved a slightly higher pass rate in the NIST randomness tests compared to the standard AES S-box and other considered constructions. Notably, this improvement was achieved without degrading the encryption performance, as the S-box in our method is precomputed and applied via lookup tables.

Thus, our experiments confirmed that the proposed S-box is not only theoretically robust but also practically effective when embedded into real cryptographic algorithms such as AES.

The potential applications of the proposed GF(4) transforms in various cryptographic systems are as follows. The S-boxes obtained could be deployed in Internet of Things (IoT) encryption systems, where resource constraints demand highly efficient yet secure cryptographic components. Additionally, they could be integrated into block cipher suites for securing data transmission in a variety of protocols. The versatility of the proposed S-box makes it suitable for both constrained and general-purpose cryptographic environments, where high security and efficiency are critical. On resource-constrained platforms, the efficiency of the S-box is determined by its high cryptographic quality. A high-quality S-box provides strong security properties, allowing for the design of simpler ciphers without compromising on security. This makes it particularly suitable for environments where computational resources are limited but robust cryptographic performance is still required. The ability to simplify the overall cipher construction while maintaining security is a key advantage of using S-boxes obtained in this paper in such contexts.

5. Conclusions

Our research yielded several important results.

• We introduced the concept of using GF(4) affine transformations to enhance the cryptographic quality of S-boxes. A complete set of $\#C_i=648, i=1,2,\dots ,4$ affine transformation matrices of order $n=3$ were synthesized based on four basic constructions. A set of $\#C_{4,i}=7776$ matrices of a GF(4) affine transformation of order $n=4$ were synthesized. It was determined that, based on these matrices and the Nyberg construction, it is possible to construct bijective S-boxes for which the SAC and BIC SAC indices are better than those of the original Nyberg construction and many other known analogs, while the nonlinearity still reaches a maximum value.
• A modified GF(4) affine transformation scheme was proposed, which preserves the avalanche properties of the original S-box while improving its nonlinear characteristics. When applied to specialized S-boxes that satisfy the SAC for both component Boolean and 4-functions, as well as the criterion of minimal correlation between input and output, this scheme significantly enhances their nonlinearity. The level of nonlinearity achieved using this approach reached a value of 96, demonstrating a substantial improvement in cryptographic strength.
• In summary, we produced S-boxes based on the Nyberg construction, enhanced through GF(4) affine transformations. These S-boxes exhibited high cryptographic quality and demonstrated strong compliance with the SAC for component Boolean functions, making them particularly suitable for practical use in block symmetric ciphers and other applications requiring robust S-boxes. Our research also yielded specialized S-boxes with high nonlinearity and ideal compliance with cryptographic criteria, including the SAC for component Boolean and 4-functions, as well as correlation independence between the S-box’s input and output vectors.
• The practical effectiveness of the proposed S-boxes was confirmed through integration into the AES algorithm. In our experiments, in which we encrypted 100 files of 1 MB each and tested the outputs with the NIST statistical suite, the AES implementation using our S-box achieved a 96% pass rate, outperforming both the standard AES S-box (94%) and the S-box from [7] (93%). This highlights our method’s applicability in real-world encryption systems.