1. Introduction
As network and multimedia technologies develop rapidly, the quantity of images transmitted over networks has grown explosively. Nonetheless, the characteristic of network openness has made the security of image information an increasingly critical issue. Unlike text data, the high redundancy and strong correlation of pixels in images lead to problems such as slow encryption speeds and low efficiency in traditional encryption methods [
1,
2,
3,
4,
5]. As a result, to ensure the security of image information, many researchers have devoted themselves to the study and development of efficient encryption algorithms tailored to the specific characteristics of images [
6,
7,
8,
9,
10]. Among various algorithms, chaotic maps, because of their remarkable features, including sensitivity to starting parameters, non-periodicity, randomness, and unpredictability, offer high security and ease of implementation for encryption algorithms. Therefore, in the past few years, chaotic-map-based image encryption methods have drawn significant interest [
11,
12,
13].
In 2014, Zhou et al. [
14] put forward an image encryption algorithm which incorporates three chaotic maps: Logistic-Tent, Logistic-Sine, and Tent-Sine. When compared with an individual one-dimensional chaotic map, the sequence produced by combining multiple one-dimensional chaotic maps exhibited greater randomness. However, one-dimensional chaotic maps have various disadvantages, for example, short periods, small key spaces, low security, and suboptimal encryption performance [
15,
16]. In contrast, encryption algorithms built upon chaotic maps with high-dimensionality have garnered widespread attention due to their larger key spaces, strong sensitivity to initial conditions, and higher complexity of generated random sequences [
17,
18,
19,
20]. Nevertheless, image encryption algorithms designed using high-dimensional chaotic maps still face challenges, including insufficient chaotic characteristics, long processing times, and the increasing sophistication of decryption methods targeting chaotic techniques. To mitigate these risks, researchers have sought to introduce new technologies, such as neural networks [
21,
22], deep learning [
23], artificial intelligence [
24], and quantum computing [
25], for the design of more secure, efficient, and flexible encryption algorithms and to address the increasingly complex network environment and advanced attack strategies.
DNA cryptography, as an emerging field, has gradually gained widespread attention. Its origins can be traced back to Adleman’s [
26] exploration of the feasibility of DNA computing, which introduced biological elements into the field of information security. The enormous parallel processing ability, vast storage capacity, and extremely low power consumption of DNA sequences have prompted researchers to leverage DNA technology for the evolution of unique information security systems. Among these, image encryption schemes leveraging chaotic dynamics and DNA-inspired encoding strategies have become the subject of intense scholarly interest. In 2015, Li et al. [
27] created a cryptographic technique for two images that makes use of DNA subsequence operations and chaotic maps. They utilized Lorenz and Chen maps to generate chaotic sequences that were used for image encryption by converting them into DNA matrices based on selected DNA coding rules. In that same year, Wu et al. [
28] introduced an encryption technique for color images utilizing DNA-based sequences and multiple optimized one-dimensional chaotic maps. This scheme achieved encryption through DNA operations and random shuffling. However, the use of a single DNA encoding and operation rule strategy, or relying solely on low-dimensional chaotic maps for encryption, often leads to security vulnerabilities in the encryption structure and results in lower complexity. In 2021, Cun et al. [
29] combined a new chaotic map boasting a elevated Lyapunov exponent and improved dynamic behavior with dynamic DNA encoding, enhancing the application prospects of dynamic DNA encoding within the scope of image encryption.
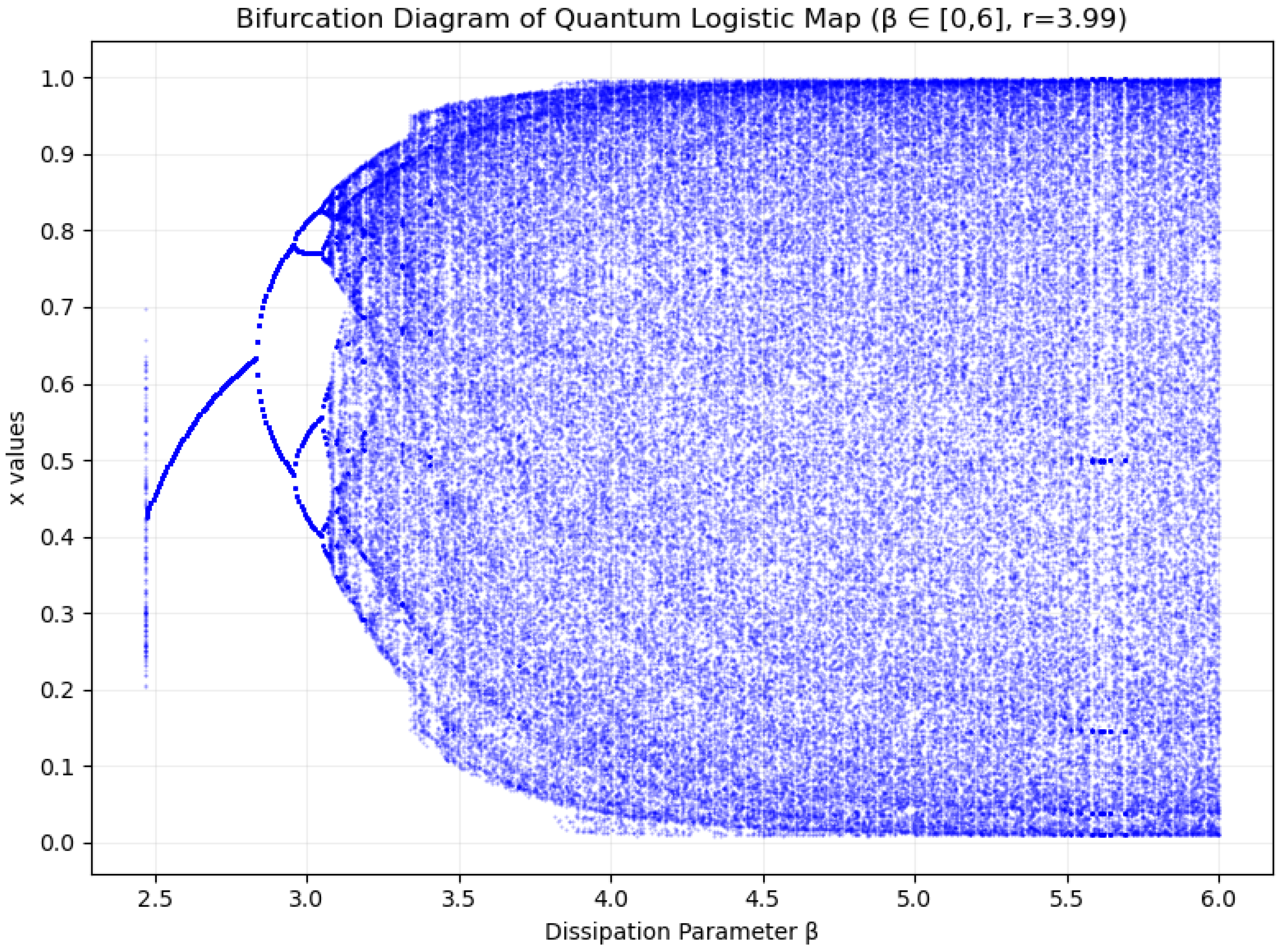
In recent years, quantum algorithms [
30,
31] have drawn extensive attention in the communication and processing domains. Compared with classical algorithms, they possess remarkable advantages regarding speed and security aspects. Notably, quantum chaos has shown great potential in the image processing field. The so-called quantum chaos is essentially the quantization of classical chaotic maps. In general, quantum maps fall into two categories: one involves the quantization of nonautonomous maps featuring a periodic time dependence, while the other concerns the quantization of abstract dynamical maps [
32]. Akhshani et al. [
32] were the first to propose an image encryption framework incorporating principles of a higher-complexity quantum chaotic map. They utilized the remarkable sensitivity of quantum chaos to subtle differences in starting conditions and regulatory parameters, thereby augmenting the security of the algorithm. Subsequently, Zhang et al. [
33] combined quantum chaos, a Lorenz chaotic map, and DNA encoding, leveraging the outstanding randomness and high sensitivity of quantum chaos to achieve significant breakthroughs in the field of image encryption.
Meanwhile, Yin et al. [
34] constructed a quantum communication network, successfully achieving quantum entanglement distribution and digital signature experiments, breaking through the fault-tolerance limit, and opening up a new path for the development of quantum networks. Cao et al. [
35] introduced a high-efficiency quantum-based digital signature scheme, built an integrated security network, and facilitated the realization of cryptographic security goals. These research results provided crucial references for this paper’s research on the use of chaotic maps and DNA coding in encrypting images. They are of great significance in promoting the integration and optimization of technologies, and are helpful for further exploring the innovative development direction of image encryption technologies.
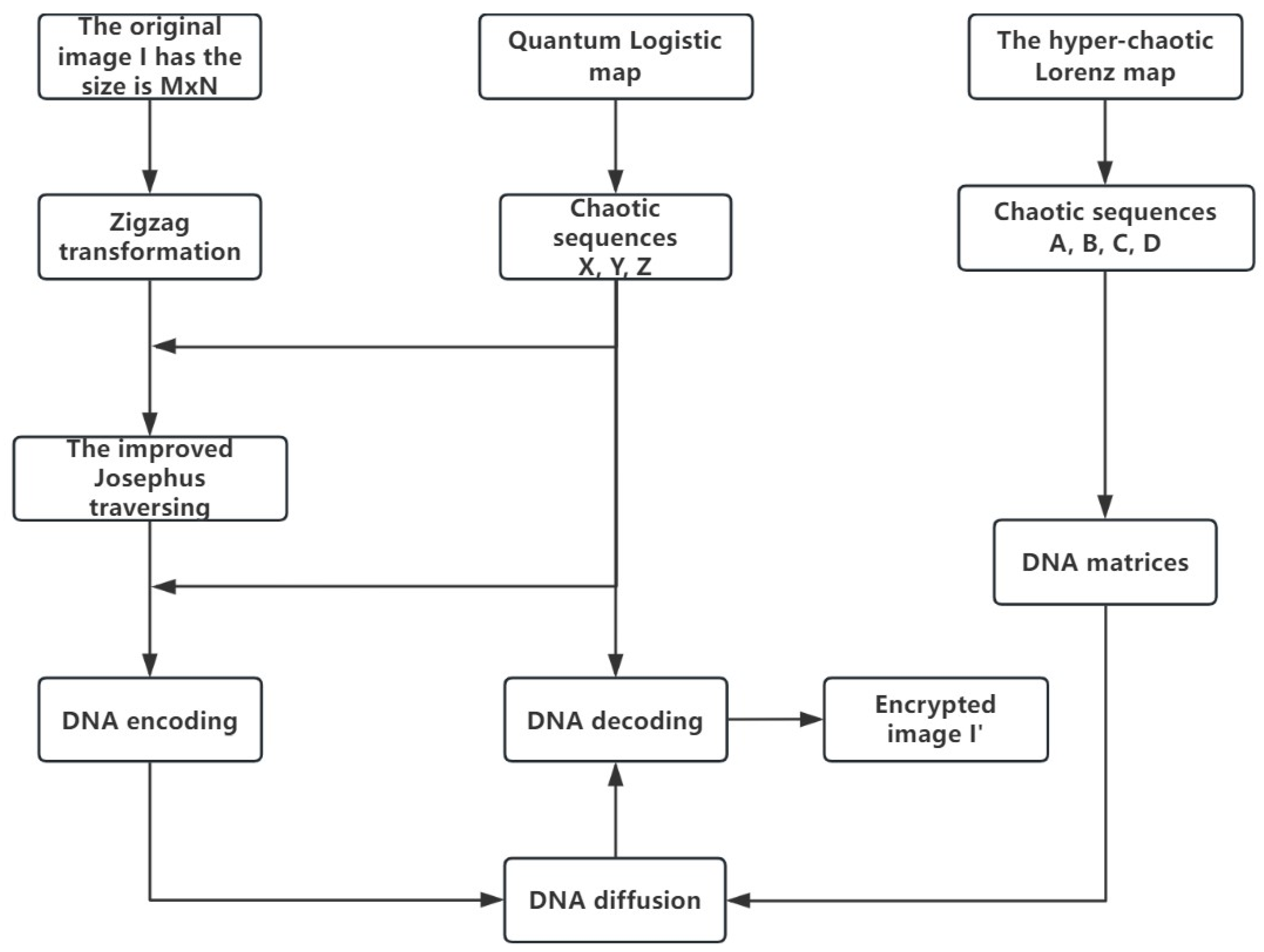
Our study presents an improved image cryptography scheme designed to bolster security by leveraging a quantum Logistic map’s natural randomness, a hyper-chaotic Lorenz map’s intricate dynamical properties, and a biologically inspired DNA dynamic encoding approach. By merging these cutting-edge techniques, the proposed scheme not only amplifies the algorithm’s unpredictability and sophistication but also significantly enhances the robustness of the encrypted outputs against potential breaches. This innovative fusion positions this solution as a highly reliable and efficient option for safeguarding digital images.
The following outlines the paper’s structure. In
Section 2, we detail the chaotic maps adopted in the encryption scheme.
Section 3 presents the DNA coding and operations.
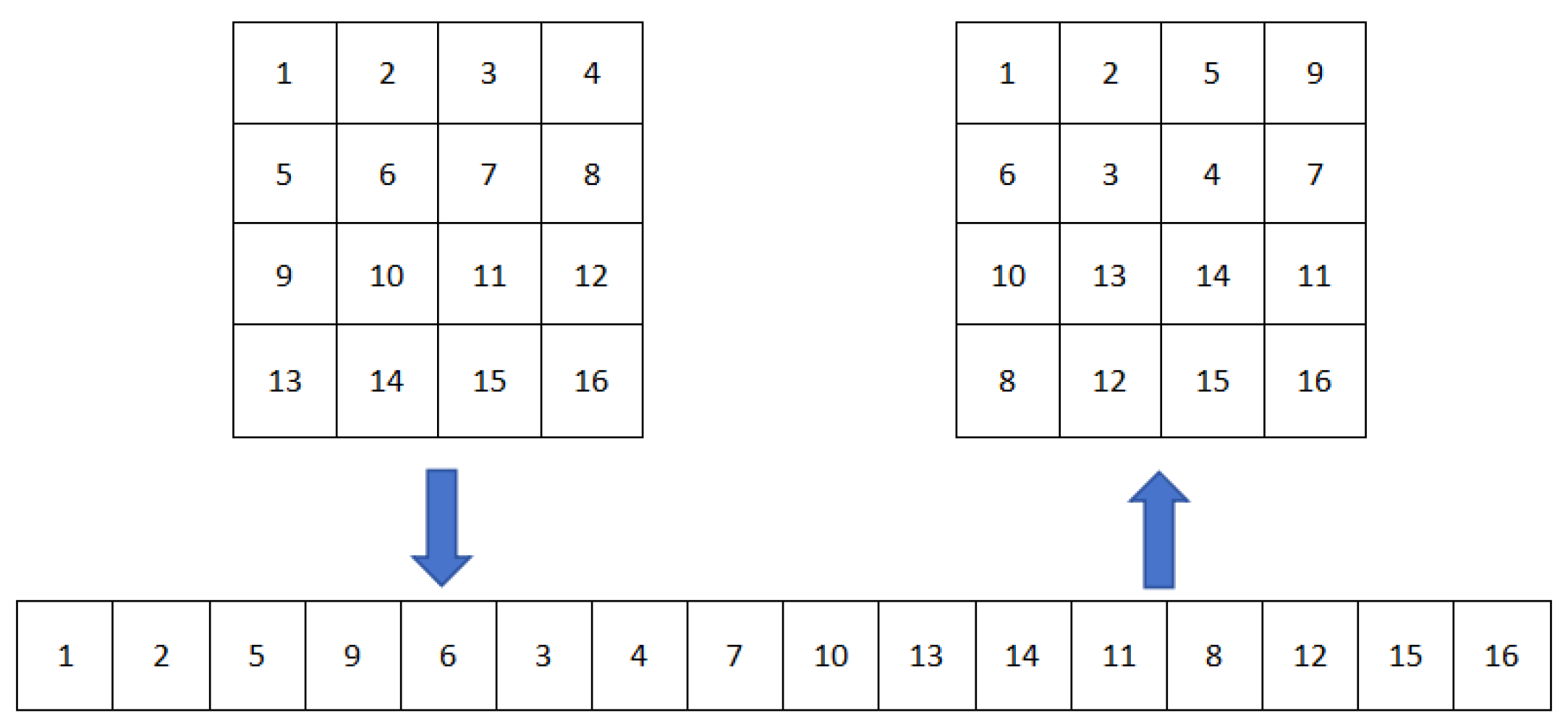
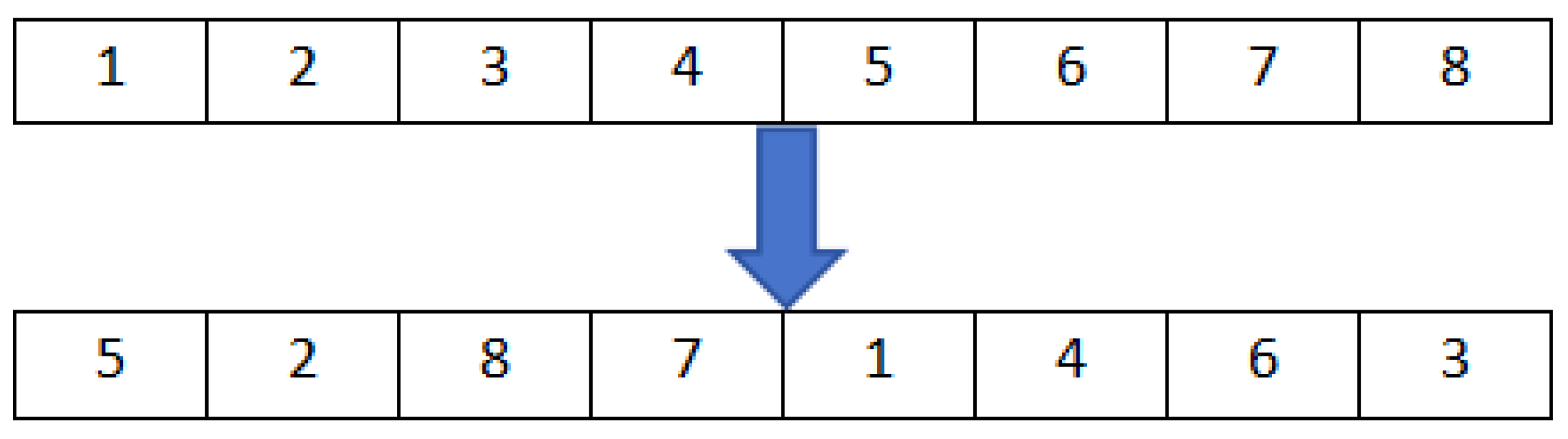
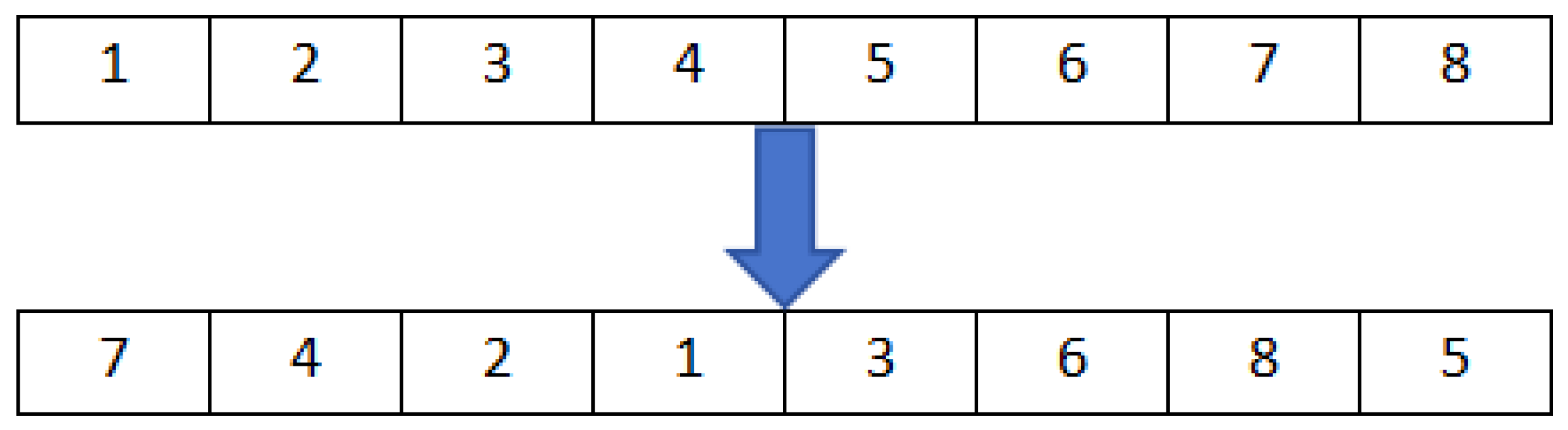
Section 4 discusses Zigzag transformation and Josephus traversing.
Section 5 elaborates on the encryption theory and implementation stages of our proposed algorithm. In
Section 6, we conducted experimental simulations and performed comprehensive security analyses on the algorithm. Furthermore, we contrast our findings with prior algorithms.
Section 7 offers the conclusions and future prospects.
3. DNA Coding and Operations
DNA coding refers to the composition of genes on a DNA molecule and how these genes are transcribed into RNA and translated into proteins. In 1994, Dr. Adleman from the University of California, USA, published a seminal paper in the journal Science exploring the possibilities of molecular biocomputational methods for DNA. He successfully solved a Hamiltonian path problem with seven vertices using biochemical methods, which demonstrated the feasibility of using DNA for specific computational purposes [
26]. This study sparked interest in DNA-based molecular computing, and many of the advantageous properties of DNA, such as its high parallelism, vast storage capacity, high operational efficiency, and low energy consumption, were gradually recognized. In recent years, this field has garnered increasing attention from scholars, with DNA computing models and algorithms showing immense potential in fields such as bioinformatics, computer science, and biomedical research. Furthermore, DNA computing continues to attract the attention of both the academic and industrial communities worldwide. With advancements in technology and the development of theory, researchers have increasingly explored the combination of DNA computing and intelligent computational approaches like genetic algorithms, neural networks, fuzzy systems, and chaotic maps, providing new ideas and solutions for tackling complex problems [
40,
41,
42].
3.1. DNA Coding
As the hereditary material in living cells, DNA adopts a double-helical structure, mainly situated in the nucleus and mitochondria. Its genetic units, genes, are composed of four deoxynucleotide bases: Adenine (A), Cytosine (C), Guanine (G), and Thymine (T). The double-helix structure of DNA is formed by two complementary strands coiled around each other, with hydrogen bonds between the base pairs linking them. The base pairing rule is that Adenine (A) bonds with thymine (T) via two hydrogen bonds, whereas guanine (G) links to cytosine (C) with three. These deoxynucleotides form the encoding sequence of DNA according to the nucleotide pairing principle.
The nucleotide pairing principle in DNA is conceptually similar to binary complement rules, such as 0 and 1, 00 and 11, 01 and 10 being complementary pairs. If we assign a 2-bit binary code to each base, four bases (A, T, C, G) can be encoded into four binary numbers (00, 01, 10, 11), resulting in 24 possible binary combinations. However, to comply with the base pairing principles of DNA sequences, only eight of these combinations are valid, as shown in
Table 1.
To further extend the pairing principles of DNA sequences, we now explore how these principles are applied to image encoding. In this study, 8-bit grayscale images are employed, where the pixel intensity values fall within the interval [0, 255]. Here, 0 symbolizes the darkest shade, 255 represents the brightest white, and the intermediate values represent various degrees of gray. In this manner, a decimal pixel value can be converted into an 8-bit binary code indicating its grayscale level. For instance, the pixel value of 210 has a binary representation of “11010010”. According to encoding Rule 1 listed in
Table 1, its corresponding DNA sequence is “AGTC". Alternatively, if Rule 8 is used for encoding, the DNA sequence obtained would be “CTGA”. This demonstrates that the DNA sequence obtained depends on the chosen encoding rule. Similarly, in the decoding process, only the correct encoding rule can successfully decode the sequence. If mismatches between encoding and decoding rules occur, this will lead to failure in obtaining the accurate pixel value. For example, decoding the DNA sequence “AGTC” generated by Rule 1 using Rule 1 will yield the original binary sequence “11101010”. However, if a different encoding rule, such as Rule 8, is applied to interpret the identical DNA strand “AGTC”, the resulting binary sequence “10000111” will differ from the original binary sequence “11010010”. Therefore, maintaining consistency between encoding and decoding rules is a prerequisite for accurate reconstruction of the original image.
3.2. DNA Operations
As DNA computing progresses, scholars have put forward DNA-based arithmetic operations including addition, subtraction, and XOR. However, unlike traditional binary arithmetic, each DNA encoding rule corresponds to a specific DNA operation result. That is, the eight different DNA encoding rules are associated with eight different sets of DNA addition and subtraction rules. In this study, Rule 1 from
Table 1 is selected for the operations, and the DNA addition, subtraction, and XOR rules are separately illustrated in
Table 2,
Table 3 and
Table 4.
As seen in
Table 2,
Table 3 and
Table 4, once the DNA encoding rule has been determined, its corresponding operation results are also fixed. Moreover, the addition and subtraction results for a given DNA encoding rule are uniquely determined. In our encryption work, we employ DNA dynamic technology for DNA encoding, addition, and XOR operations, to achieve pixel diffusion in images, thus improving the algorithm’s level of complication and protection.
6. Experimental Simulation and Safety Analysis
6.1. Experimental Simulation
The proposed algorithm was simulated in a Python 3.13.3 (64-bit) environment. When conducting the experiments,
(Peppers) and
(Cameraman) grayscale images were selected as the original images. The initial values for the quantum Logistic map were
,
and
, with parameters
and
. The initial parameter values for the hyper-chaotic Lorenz map were
,
,
, and
.
Figure 6 displays the original and encrypted images. Clearly, the encrypted image bears no visual resemblance to the original and provides no insight into its content. Therefore, the algorithm effectively encrypted the image and ensured robust safeguarding of its original data.
6.2. Key Space Analysis
To safeguard digital images effectively, a robust encryption method must feature an extensive key space capable of withstanding brute-force attempts. As a rule of thumb, the encryption key’s complexity should meet or exceed a threshold to provide adequate protection. In our encryption algorithm, the quantum Logistic map and the hyper-chaotic Lorenz map serve as the core components for image encryption. The entire encryption operation relies on the following keys:
- (1)
Parameters of the quantum Logistic map: , r, and initial values , , .
- (2)
Initial values of the hyper-chaotic Lorenz map: , , , and .
where the parameters and initial values ranges for the quantum Logistic map are as follows:
,
and
,
,
. Given that a quantum Logistic map demonstrates an extraordinary sensitivity to parameters and initial values (with a sensitivity of
) [
33], the key space for the quantum Logistic map can be ascertained using the subsequent approach: the parameter key space
, the initial value key spaces
,
. Therefore, the total key space for the quantum Logistic map is
. Similarly, since the precision of the initial values in the hyper-chaotic Lorenz map is
, the key space for the hyper-chaotic Lorenz map is
.
Following the preceding examination, the encryption algorithm’s total key space is . The enormous size of this key space provides robust protection against brute-force cracking attempts, validating the encryption method’s exceptional security credentials and its reliable defense against such adversarial intrusion strategies.
6.3. Key Sensitivity Analysis
A well-performing image encryption method hinges on a key that is sensitive—tiny alterations in the key must generate a unique decrypted image, ensuring security. In this particular approach, the key encompasses parameters and initial conditions for both the quantum Logistic map and the hyper-chaotic Lorenz map. To assess how responsive the quantum Logistic map is to perturbations to its initial state, we carried out a detailed examination, using the iconic
Peppers image as a benchmark to verify its sensitivity. Under the initial parameters of
,
and
, the system-produced encrypted image is depicted in
Figure 7a, and when decrypted with the same parameters, the original image was perfectly restored, as in
Figure 7b. During the experiment, it was found that when a minute perturbation of
or
was applied to the initial values (
,
and
), the system exhibited significant sensitivity. Firstly, the encrypted result in
Figure 7c exhibits visually distinguishable differences compared to the standard encrypted image
Figure 7a. Secondly, although the deviation in the key was minimal, decryption using the perturbed parameters failed to fully restore the original image, see
Figure 7d. This phenomenon reveals the unique dynamical characteristics of the quantum Logistic map: the system exhibits a high degree of sensitivity to initial conditions, where even minute differences in parameters are exponentially amplified through iterative operations, ultimately leading to a complete alteration of the output sequence. The experimental results indicate that the quantum Logistic map demonstrated superior performance in terms of parameter sensitivity, thereby providing a theoretical basis for the development of high-security image encryption systems.
6.4. Crop Attack Analysis
The rise of digital imagery in vital sectors like cyber security, healthcare, and military messaging has highlighted the necessity for robust image encryption algorithms for resilience against interference. In real-world scenarios, encrypted images face numerous attack tactics, with crop attacks being a prevalent risk. To systematically assess the algorithm’s resilience to these attacks, this study designed a tiered testing scheme. We simulated crop attack scenarios by artificially setting three progressive levels of data corruption: mild (
data removal), moderate (
removal), and severe (
removal), as illustrated in
Figure 8. The visual information shows encrypted images subjected to progressive cropping (
Figure 8a–c) alongside their reconstructed counterparts (
Figure 8d–f). Remarkably, even when half the encrypted data were deliberately discarded (
Figure 8f), the decryption process successfully preserved the fundamental structure and key visual elements of the source image. This phenomenon not only fully demonstrates the remarkable robustness of the proposed algorithm, but also provides crucial support for the practical application of the algorithm in unreliable channels.
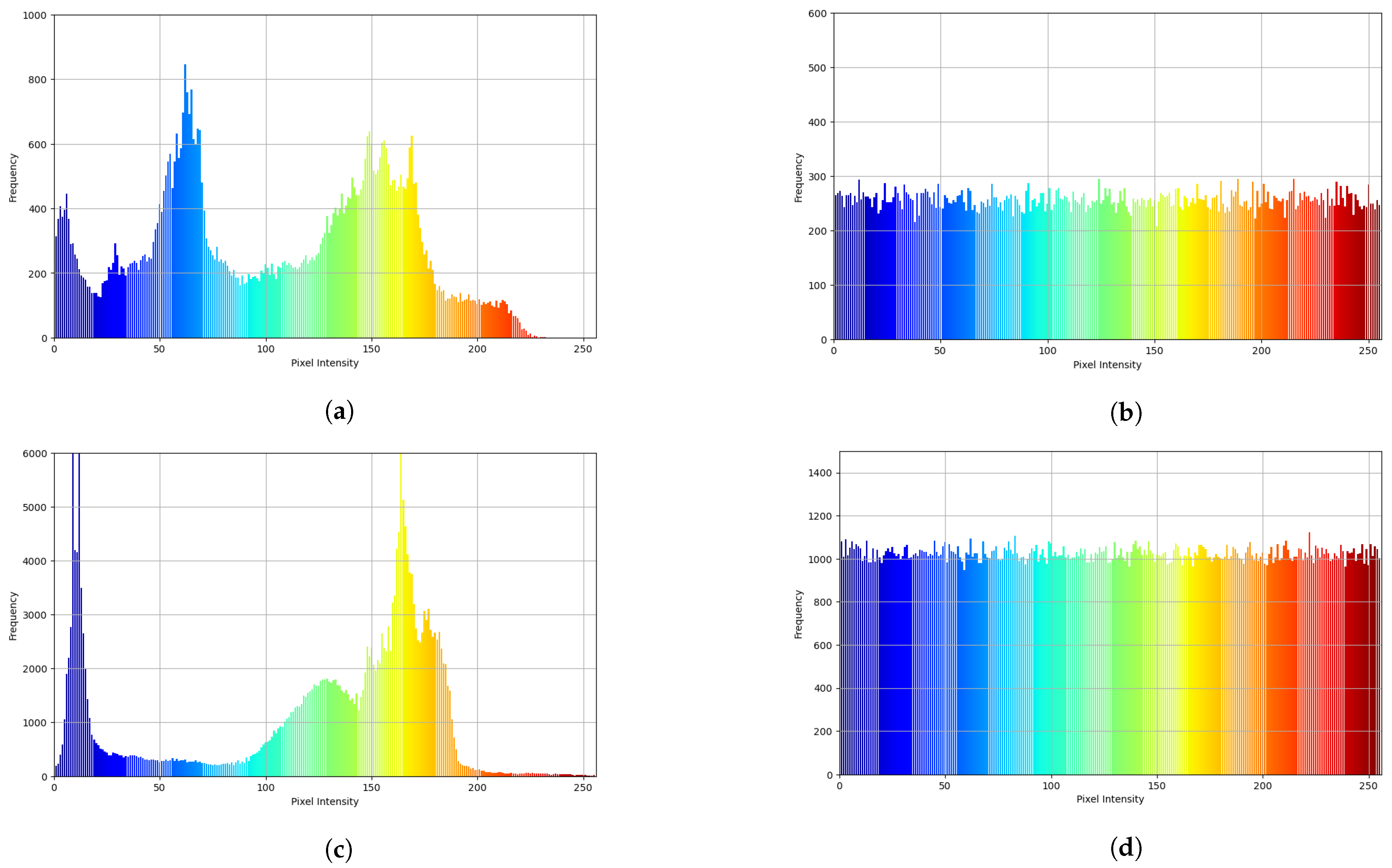
6.5. Histogram Analysis
An image histogram essentially captures the statistical spread of pixel values across an image. Generally manifested as a graphical plot with 256 discrete bins, where each bin corresponds to a unique grayscale value within the range of 0–255, and the magnitude of each bin’s height precisely measures the prevalence of that grayscale level in the image. By carefully analyzing the histogram, one gains a clear understanding of how grayscale values are distributed throughout the image. In the context of encryption algorithms, a high-quality algorithm should yield an encrypted image with a pixel value distribution that is as evenly dispersed as possible, as this directly correlates with enhanced encryption performance. In the present study, we conducted a detailed examination and comprehensive comparison of the histograms for both the original and encrypted versions of the Peppers and Cameraman images, as depicted in
Figure 9.
The analysis showed that the grayscale distributions of the original Peppers and Cameraman images exhibited multiple peaks and valleys, showing distinct statistical characteristics. Conversely, the corresponding encrypted images had a grayscale distribution that was more concentrated, without obvious patterns or regularities, and lacking clear statistical features. This outcome demonstrated that the encryption operation had reliably scrambled and concealed the original image data. Thus, the suggested algorithm can robustly withstand statistical assault and exhibits strong security features.
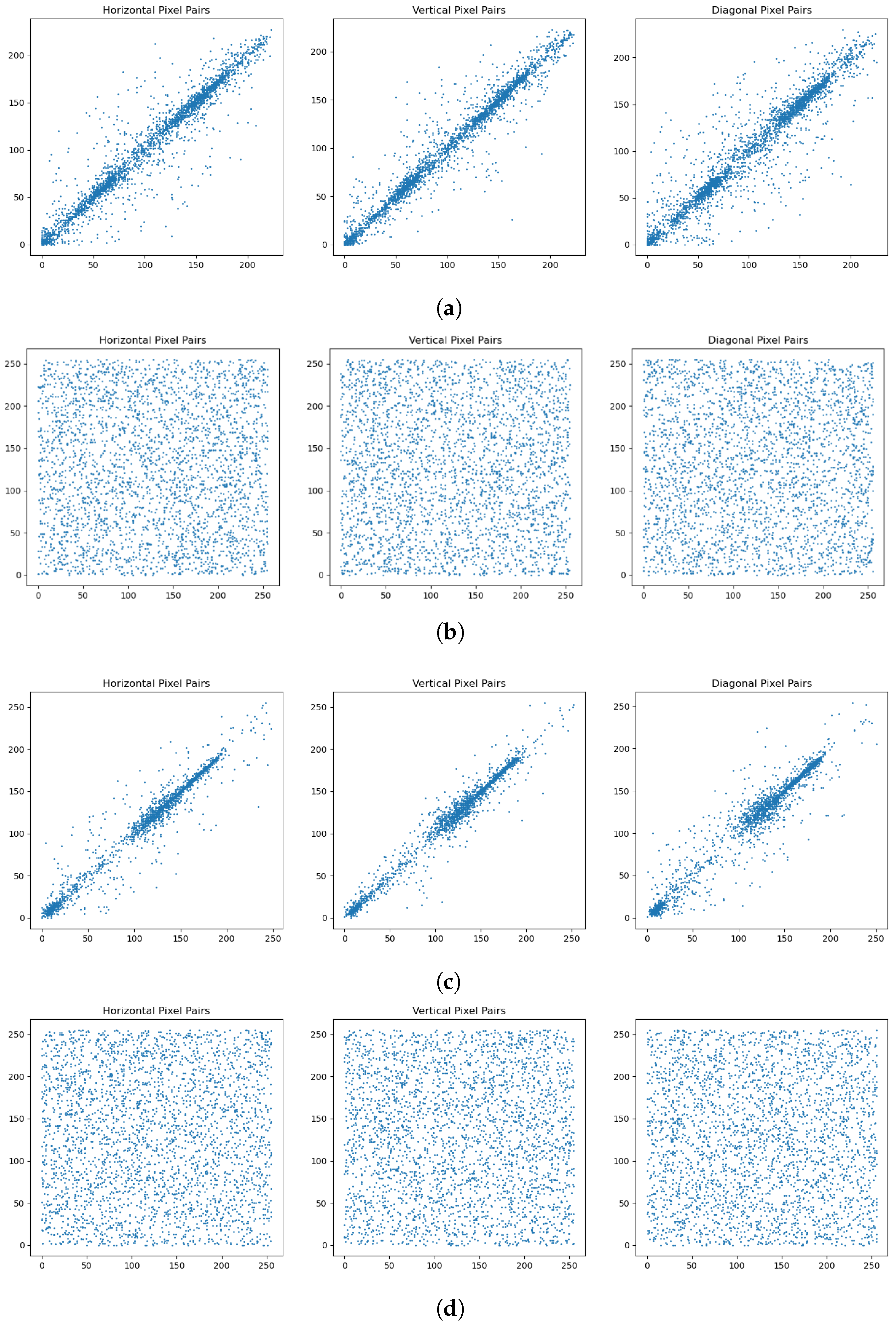
6.6. Adjacent Pixel Correlation Analysis
In image processing and computer vision, analyzing the correlation between neighboring pixels is a fundamental technique for evaluating the alignment of grayscale or color values. This relationship is quantified using the correlation coefficient r, a statistical metric that measures the intensity and direction of the linear association between two variables. The value of r ranges from to 1: 1 denotes a perfect positive correlation, where an increase in one variable is accompanied by a proportional increase in the other; indicates a perfect negative correlation, where one variable decreases proportionally as the other increases; and 0 signifies no linear relationship between the variables. The strength of the correlation is reflected in the magnitude of , where higher absolute values indicate stronger associations. Conventionally, variables are considered highly correlated when falls within the interval [0.7, 1].
In our work, we arbitrarily picked 3000 corresponding pixel pairs from both the original and the ciphered images, and constructed two sequences
and
based on their corresponding grayscale values [
46]. The mathematical expressions for determining the covariance and variance values are given as follows:
The coefficient of association between neighboring pixels [
33] can be determined by applying the formula below:
Following this, we analyzed the pixel correlation for 3000 random adjacent pairs in the original and encrypted images across the horizontal, vertical, and diagonal axes. To thoroughly examine these correlations,
Figure 10 illustrates the correlation patterns between neighboring pixels along three axes for both the Peppers and Cameraman images, comparing their original and encrypted states. Additionally,
Table 5 provides a quantitative comparison of these encrypted image correlations against the results documented in Refs. [
33,
44,
45].
Figure 10 illustrates the significant difference in pixel correlation between the original and encrypted images. The original image exhibits a positive correlation among pixel grayscale values in the horizontal, vertical, and diagonal orientations, with pronounced correlations. On the contrary, the encrypted image shows nearly zero correlation between adjacent pixels in these three directions, indicating that the original image’s pixel coherence has been disrupted. The encrypted image, therefore, exhibits no significant correlation in any direction. An examination of the correlation metrics presented in
Table 5 indicates that for the Peppers image, our encryption algorithm yielded lower correlation values in both the horizontal and vertical directions. Similarly, for the Cameraman image, our encryption approach reduced the horizontal and diagonal correlation. These findings confirm that the proposed algorithm effectively mitigated correlation analysis, impeding attackers from extracting meaningful information from adjacent pixels and thereby bolstering the security and efficacy of the image encryption.
6.7. Information Entropy Analysis
Information entropy quantifies information uncertainty. In information theory, it measures a random variable’s unpredictability. Higher entropy values denote greater uncertainty and more information. Conversely, lower entropy indicates less uncertainty and a lower information content. An ideal and completely random image has an information entropy of 8. Therefore, an image whose entropy value approaches the ideal 8 has more randomly distributed pixel values, thereby offering greater protection against attacks. The information entropy formula for images [
47] is defined as
In our analysis, as depicted in
Table 6, we present the information entropy metrics for images that were encrypted using the methodologies outlined in Refs. [
33,
45] and our newly proposed technique. The total number of grayscale levels, denoted as
L, was fixed at 256 for this investigation.
As tabulated in
Table 6, the entropy metrics for images secured by the methods detailed in Refs. [
33,
45] and our suggested algorithm are presented.
Evidently, compared with the original, the encrypted version demonstrated entropy levels that aligned more closely with the ideal theoretical value, indicating a near-random distribution, with minimal discernible patterns. Our findings reveal that the encryption method employed here achieved a superior entropy performance relative to the techniques referenced in Refs. [
33,
45], as it more accurately approximated the expected disorder characteristics of a securely encrypted image. Specifically, the method exhibited a more uniform pixel distribution, making it significantly more resistant to entropy-based attacks.
6.8. Differential Attack Analysis
A differential attack is a cryptanalytic method designed to assess the robustness of encryption systems. This approach examines how minor modifications to input data, such as altering a single pixel, can produce measurable variations in the encrypted output. By analyzing these discrepancies, cryptographers can evaluate the vulnerability of cryptographic algorithms to such targeted manipulations. Specifically, a differential attack measures how much the encrypted data changes when the encryption key is slightly modified. In our work, we used NPCR and UACI to measure the resilience of the algorithm against differential attacks.
NPCR (Number of Pixels Change Rate) measures encrypted image sensitivity and encryption process efficacy relative to the original images. It measures the proportion of differing pixel values at matching locations across two images (typically the original and encrypted image, or two encrypted images using different keys). An NPCR value close to the ideal
indicates high key sensitivity and strong differential-attack resistance, thereby indicating a higher-security encryption algorithm. The NPCR [
45] computation formula is given below:
UACI (Unified Average Changing Intensity) is utilized to gauge the dissimilarity between the encrypted and original images and assess the encryption’s effectiveness. It primarily measures the average change intensity of pixel values, reflecting the extent of detail variation between the encrypted image and the original one. The ideal UACI value is
, and the nearer an obtained value is to this standard, the greater the key sensitivity and the better the resistance against differential attacks, signifying a more secure encryption method. The following equation outlines the UACI calculation method [
45]:
According to the established formula,
M represents the total rows, while
N corresponds to the columns in the image. The pixel intensities at coordinates
are designated as
for the original image and
for its encrypted counterpart. The difference metric
is 0 when
and
share identical values; conversely, it assumes a value of 1 whenever a discrepancy exists between them.
In our research, we performed a differential attack analysis on the chosen Peppers and Cameraman images.
Table 7 presents the NPCR and UACI metrics for the encrypted images, together with the relevant results from Refs. [
33,
45]. Evidently, the NPCR values obtained by our encryption method are closer to 8, indicating that the algorithm exhibited excellent encryption performance and practical applicability.
6.9. Key Stream Correlation Analysis
When assessing encryption security, we should focus on the independence of chaotic sequences from plaintext to resist chosen plaintext attacks, for which the Pearson correlation coefficient and
p-value serve as critical analytical indicators. The Pearson correlation coefficient assesses the intensity and direction of the linear association between any two variables, with its detailed definition and formula provided in
Section 6.6 (Equation (
7)). The
p-value is an indicator used for testing the significance of the correlation. The
p-value quantifies how likely we are to obtain the observed correlation coefficient, or a more extreme value, when assuming no actual relationship exists between the variables (the null hypothesis). In statistics, researchers typically compare this
p-value against a predetermined significance threshold, commonly set at 0.05. If the
p-value falls below this cutoff, we conclude that the correlation is statistically significant, suggesting the observed relationship probably is not just random noise. On the other hand, a
p-value above 0.05 implies the correlation lacks significance, meaning any apparent connection between the variables likely stems from chance rather than a genuine linear association. When assessing whether chaotic sequences remain independent of plaintext in encryption systems, a
p-value exceeding 0.05 supports an algorithm’s security by indicating no meaningful correlation between the sequences and the original data. However, if the
p-value is less than 0.05, this warrants closer attention, as it may indicate potential risks in the encryption algorithm, necessitating further improvement. In the following, we calculate the Pearson correlation coefficients and corresponding
p-values for chaotic sequences (
X,
Y,
Z,
A,
B,
C,
D) against the pixel values of the
Peppers image as an example. The results are presented in
Table 8.
Table 8 presents the correlation analysis results between seven chaotic sequences and the pixel values of the plaintext image, including Pearson correlation coefficients,
p-values, and the actual lengths of the sequences. The Pearson correlation coefficients for all sequences are extremely low, indicating that the chaotic sequences exhibit almost no linear correlation with the plaintext, making it difficult for attackers to extract sequence information through linear analysis. The
p-value analysis showed that, except for the X sequence (
), which has a significant correlation, the
p-values of the remaining sequences all exceed 0.05, indicating that their correlations are not statistically significant. Overall, most chaotic sequences contribute to encryption security. However, the case of the X sequence suggests that there is still room for optimization in our algorithm, to improve its resistance to chosen plaintext attacks.
6.10. Computational Complexity Analysis
In evaluating the practical application potential of encryption algorithms, computational complexity is a crucial metric. It not only directly affects the algorithm’s computational efficiency in different computing environments but also determines whether the algorithm is suited for resource-constrained devices and scenarios with stringent real-time requirements. By conducting a detailed complexity assessment of the crucial phase in the encoding and decoding procedures, it is possible to gain a clear understanding of an algorithm’s performance bottlenecks, providing a solid theoretical foundation for optimizing the algorithm and its rational application in real-world scenarios. Taking the encryption process as an example, the computational complexity of our method can be broken down into these key steps:
Step 1 Chaotic sequence generation
- (1)
Quantum Logistic map: generates three sequences of lengths N, N, . The theoretical complexity is , with dominating (since the Z sequence is the longest), thus approximating to .
- (2)
The hyper-chaotic Lorenz map: generates four sequences of lengths , , , , with a complexity of ).
Step 2 Image scrambling
- (1)
Zigzag transformation: single matrix traversal, with complexity .
- (2)
Improved Josephus traversing: by precomputing the step size parameter (Equation (
4)), the complexity is reduced from
to
.
Step 3 DNA dynamic diffusion
Encoding/Computation: each pixel is converted into four bases, with complexity . Thus, the total complexity is
Our encryption algorithm, through optimized design and theoretical analysis, achieves linear computational complexity , enhancing execution efficiency, while ensuring security. Although there is room for further improvement for the current study, this result provides the possibility of the algorithm’s application in real-time scenarios. In the future, we will continue to optimize the algorithm’s performance and explore more efficient technological solutions.
7. Conclusions and Outlook
In the context of modern information security and innovation in image encryption techniques, our paper proposes an image encryption algorithm that integrates multidimensional chaos theory with DNA encoding characteristics. The algorithm ingeniously melds the intricate dynamic attributes of a 3D quantum Logistic map, the erratic nature of a 4D hyper-chaotic Lorenz map, and the inherent efficiency of DNA coding, thereby heralding substantial breakthroughs in image encryption technology. Extensive simulations and theoretical scrutiny confirmed the algorithm’s prowess across various parameters such as key space capacity, statistical characteristics, differential behavior, and resistance to standard attacks. This renders the algorithm a robust and viable option, positioning it as a novel, high-efficiency approach to securing visual data.
The key contributions of our study are presented below:
- (i)
The image encryption algorithm incorporates a hybrid approach, merging a quantum Logistic map with a complex four-dimensional hyper-chaotic Lorenz system.
- (ii)
By integrating these chaotic systems with DNA-based techniques, the method facilitates real-time DNA encoding and decoding, while employing both additive and XOR cryptographic operations throughout the encryption process.
- (iii)
In the image scrambling process, two different scrambling methods, namely Zigzag transformation and the improved Josephus traversing, are combined. These two distinct scrambling techniques effectively disperse the pixel positions, resulting in a strong scrambling effect.
In the coming years, image encryption algorithms are expected to evolve towards higher security levels, greater diversification of encryption methods, improved computational efficiency, reduced resource consumption, and broader application areas. This progression will gradually establish a more comprehensive and innovative information protection framework. These advancements are set to have a profound impact on the global information security landscape, enhancing data privacy protection and laying a solid foundation for the robust and sustainable development of the information society.