Research on Offloading and Resource Allocation for MEC with Energy Harvesting Based on Deep Reinforcement Learning
Abstract
1. Introduction
- We design an MEC network system based on energy harvesting, adopting nonlinear energy harvesting techniques. This system focuses on the study of wireless and computing resource allocation as well as offloading decision optimization in multi-user and multiple MEC server computing scenarios. Users can choose among local computing, offloading computing, and task discarding modes. The main problem is formulated as minimizing the total cost composed of the energy consumption, delay, and task discarding cost. Meanwhile, we jointly optimize bandwidth allocation, power allocation, computing resources, local CPU frequency, and energy harvesting.
- Due to the time-varying nature of the user’s energy collection in this EH-enabled MEC system, a Lyapunov-based architecture is employed to design a Lyapunov penalty plus offset function. This leads to the formation of a problem that aims to minimize the total cost by weighting the delay, energy consumption, and task discard cost.
- Subsequently, we propose MDP decisions, design action and state, determine reward functions, and propose a Q-learning approach to solve the problem of resource and offload allocation optimization.
- To solve the problem of large Q-matrix data, the A3C method is further proposed, and the A3C-based algorithm is designed.
2. Related Work
2.1. Computational Offloading and Resource Allocation Study
2.2. Energy Harvesting-Driven MEC Systems
2.3. Reinforcement Learning in MEC
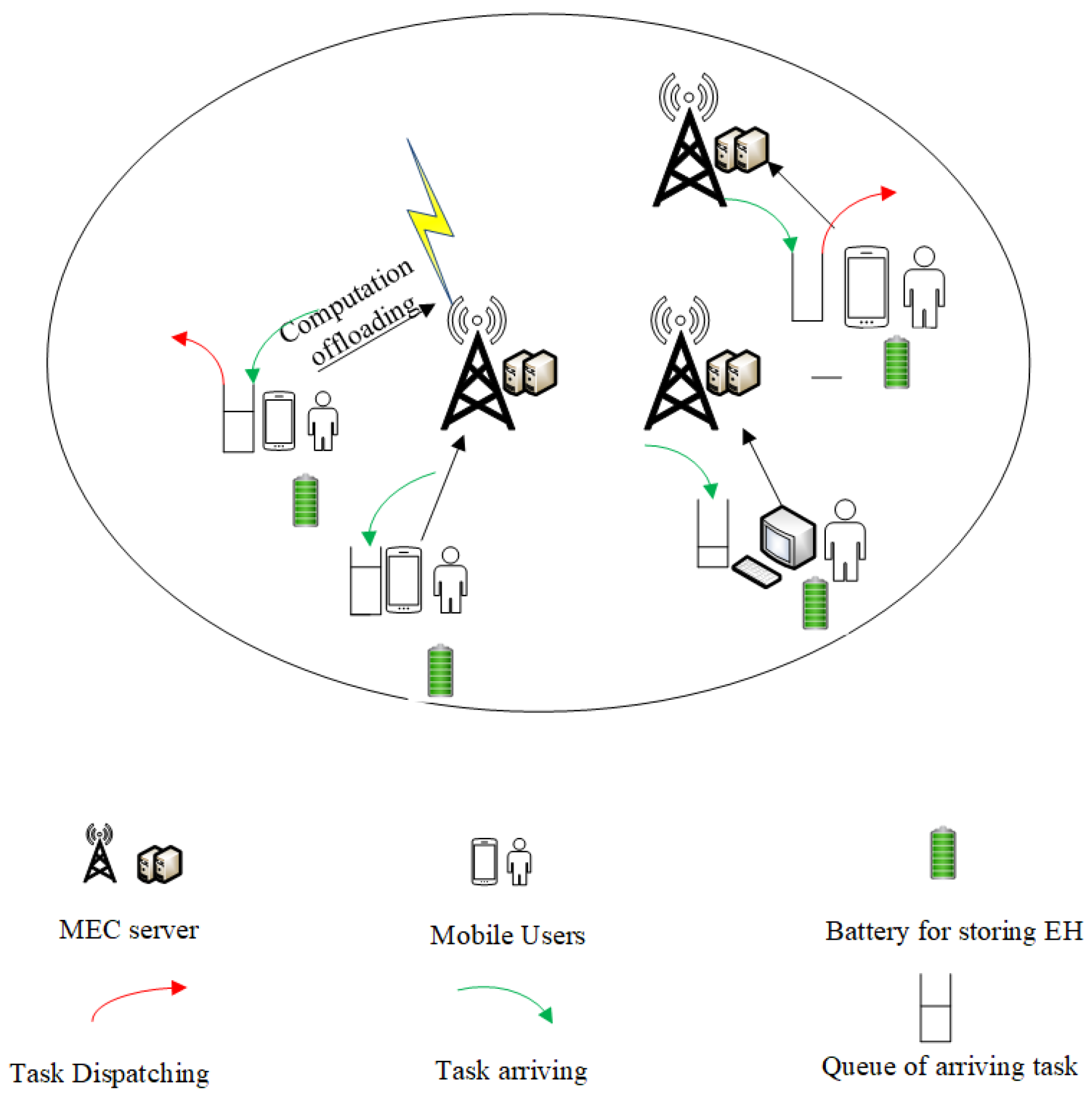
3. System Model
3.1. Computing Model
3.1.1. Local Computation
3.1.2. MEC Server Computation
3.2. Communication Model
3.3. Task Drop Model
3.4. Energy Harvesting Model
4. Problem Formulation
5. Problem Solution
5.1. MDP Framework
- State: In current time slot t, we define the state of the system as , including the channel gains between MDs and MBSs. We formulate a four-tuple to represent the system. The available MEC server computing resources are denoted as ; the data size of each arrival task, ; channel interference received between the MD and MBS, ; and the harvested energy, . Thus, we describe the vector of state system at time slot t as
- Action: Each agent needs to independently adopt actions based on the current state and time slot t, the action is defined as , which includes computational resource allocation, wireless resource allocation, offloading decision schemes, and energy harvesting, i.e., the available computing resource capacity of the MD, the computational resource allocation of MEC server , the transmission power of MD , the bandwidth allocation between MD i and MBS m, , and computation offloading decision schemes . Hence, we define the action as a set of tuples:
- Reward: After taking a feasible action, MDs can obtain a corresponding reward for the action taken from the environment based on the current state . In this investigation, we focus on formulating a multiobjective optimization problem between the task completion delay, overall energy consumption, and the cost of task discard. Then, we transform the primal problem into an optimization problem based on the Lyapunov framework by optimizing the upper bound of the Lyapunov drift-plus-penalty function to solve the corresponding resource allocation, energy harvesting, and offloading decision schemes. It is notable that the reward value of each agent should fulfill the constraints so as to guarantee the validity of the computing results. The reward function is shown below:where .
5.2. Q-Learning Algorithm
| Algorithm 1 Computational offloading and resource allocation algorithms based on Q-learning |
|
5.3. A3C Algorithm
| Algorithm 2 Joint optimization of the computation offloading decision, energy harvesting time allocation, and mode selection |
|
5.4. A3C Algorithm Core Parameter Settings and the Training Process
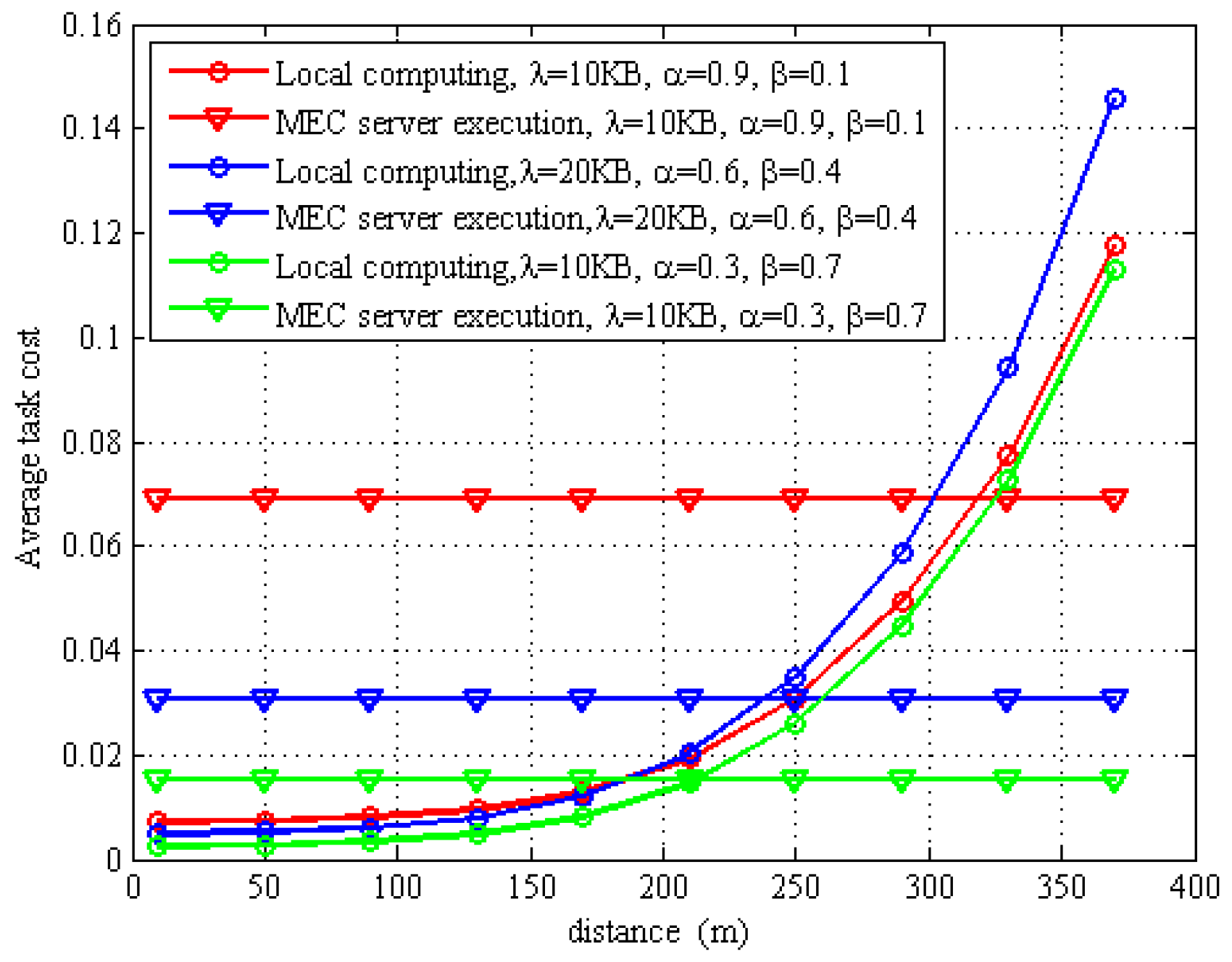
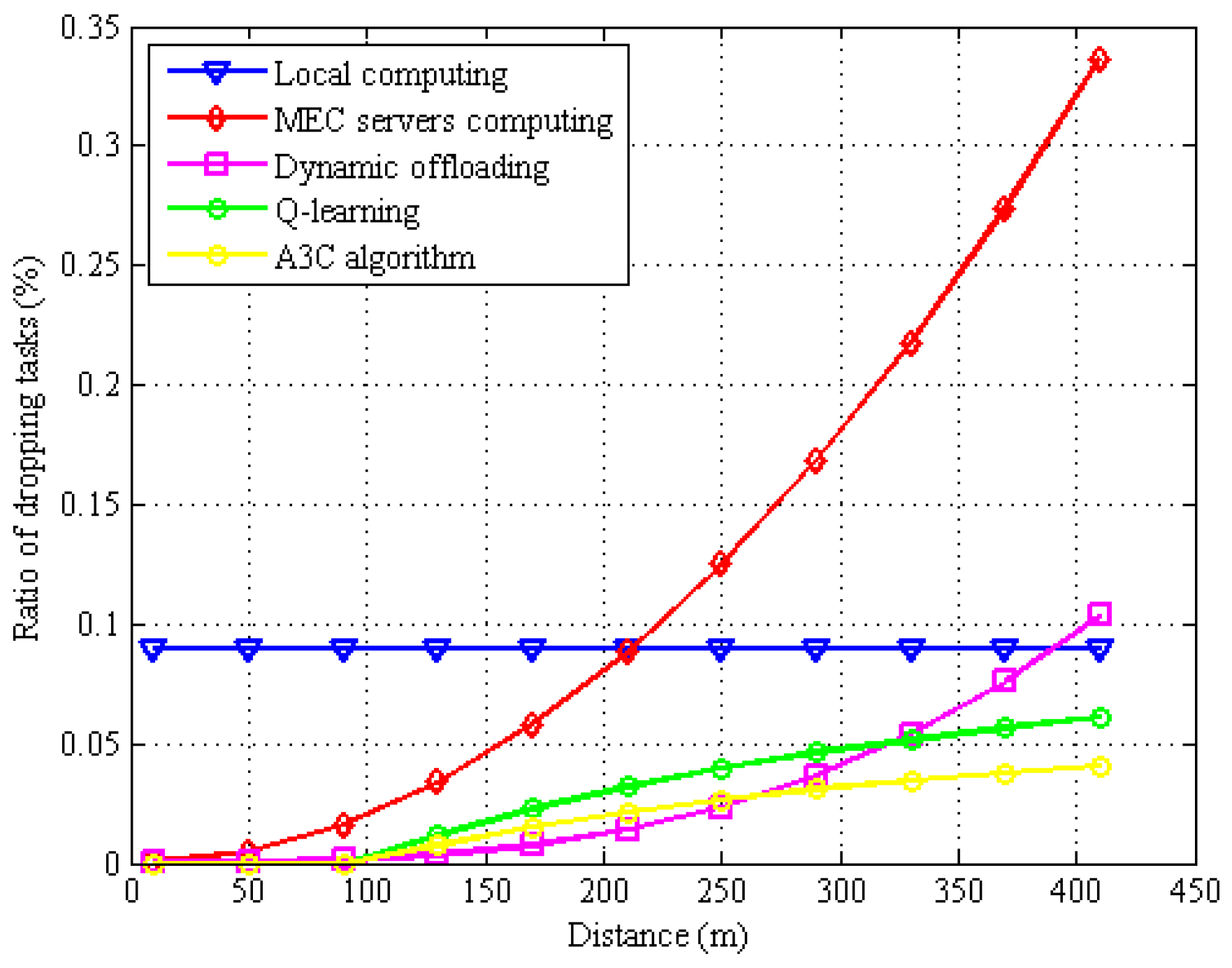
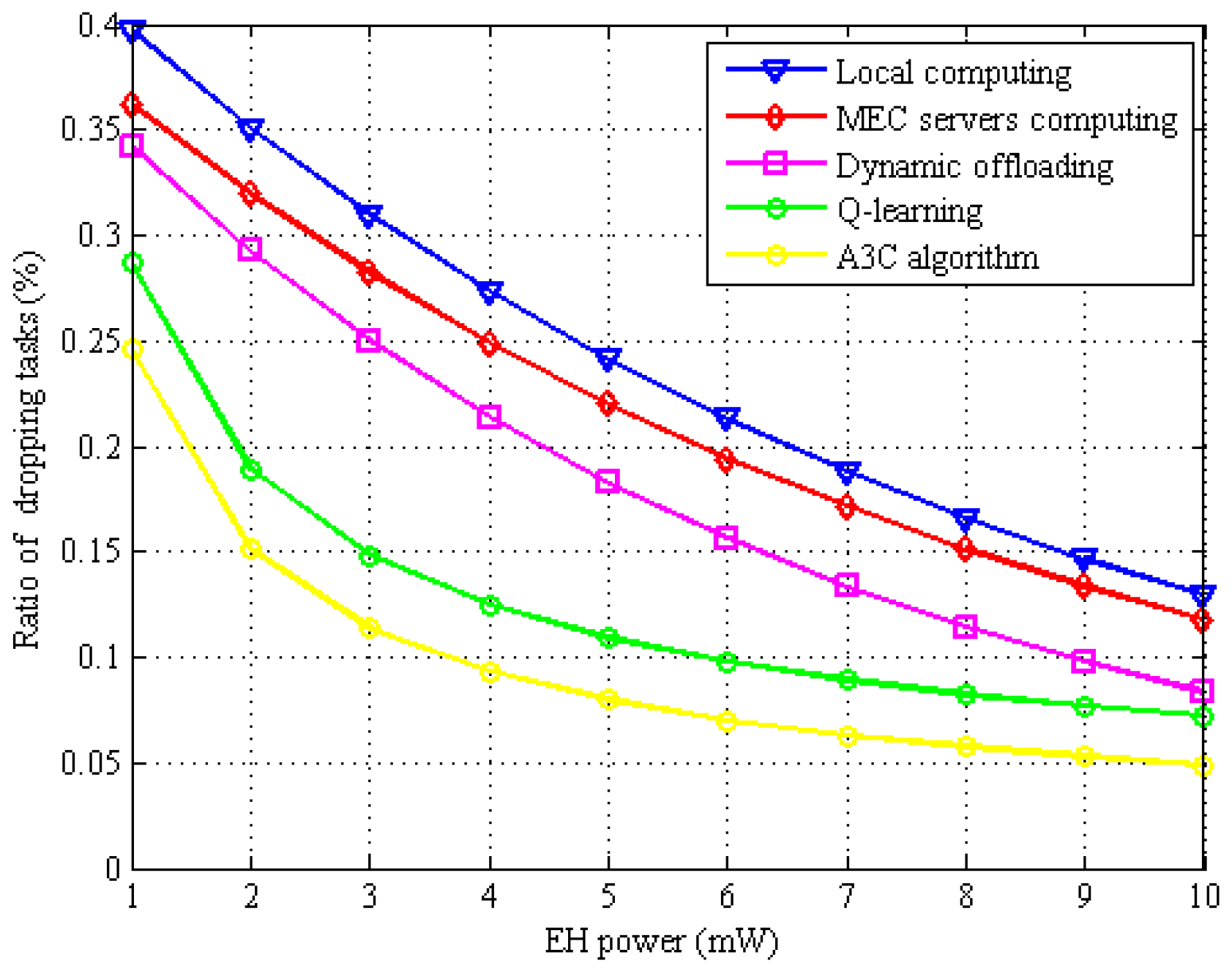
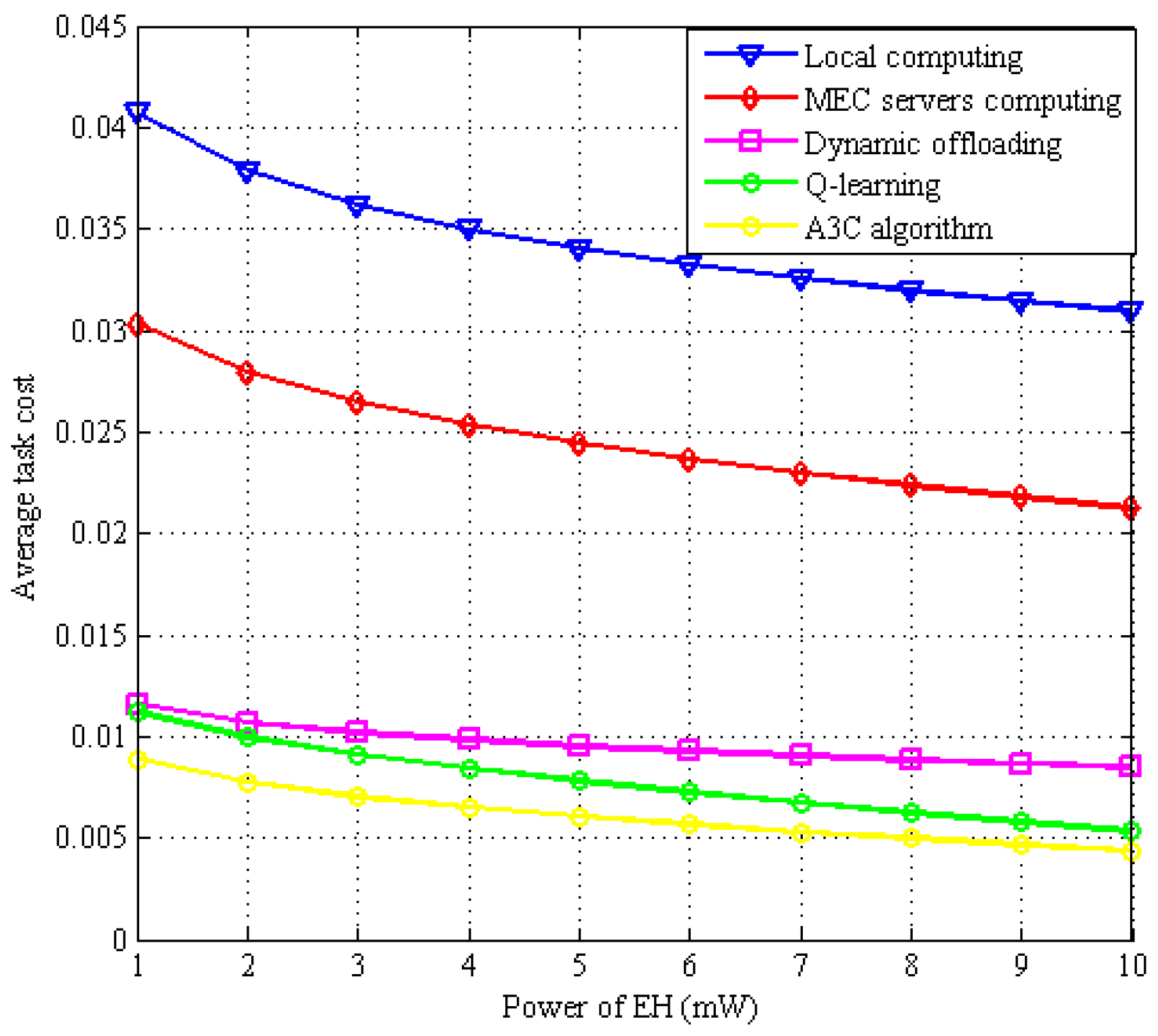
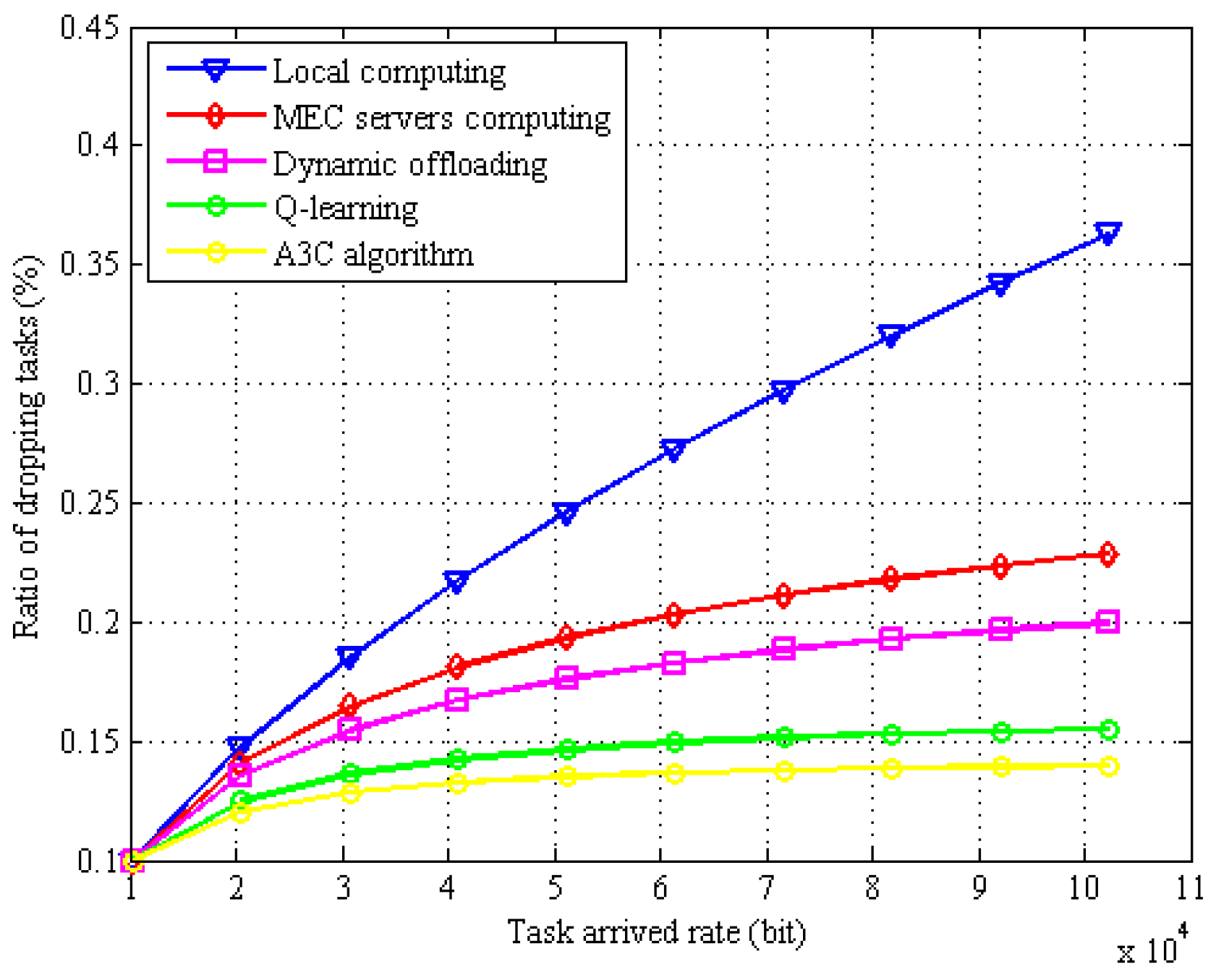
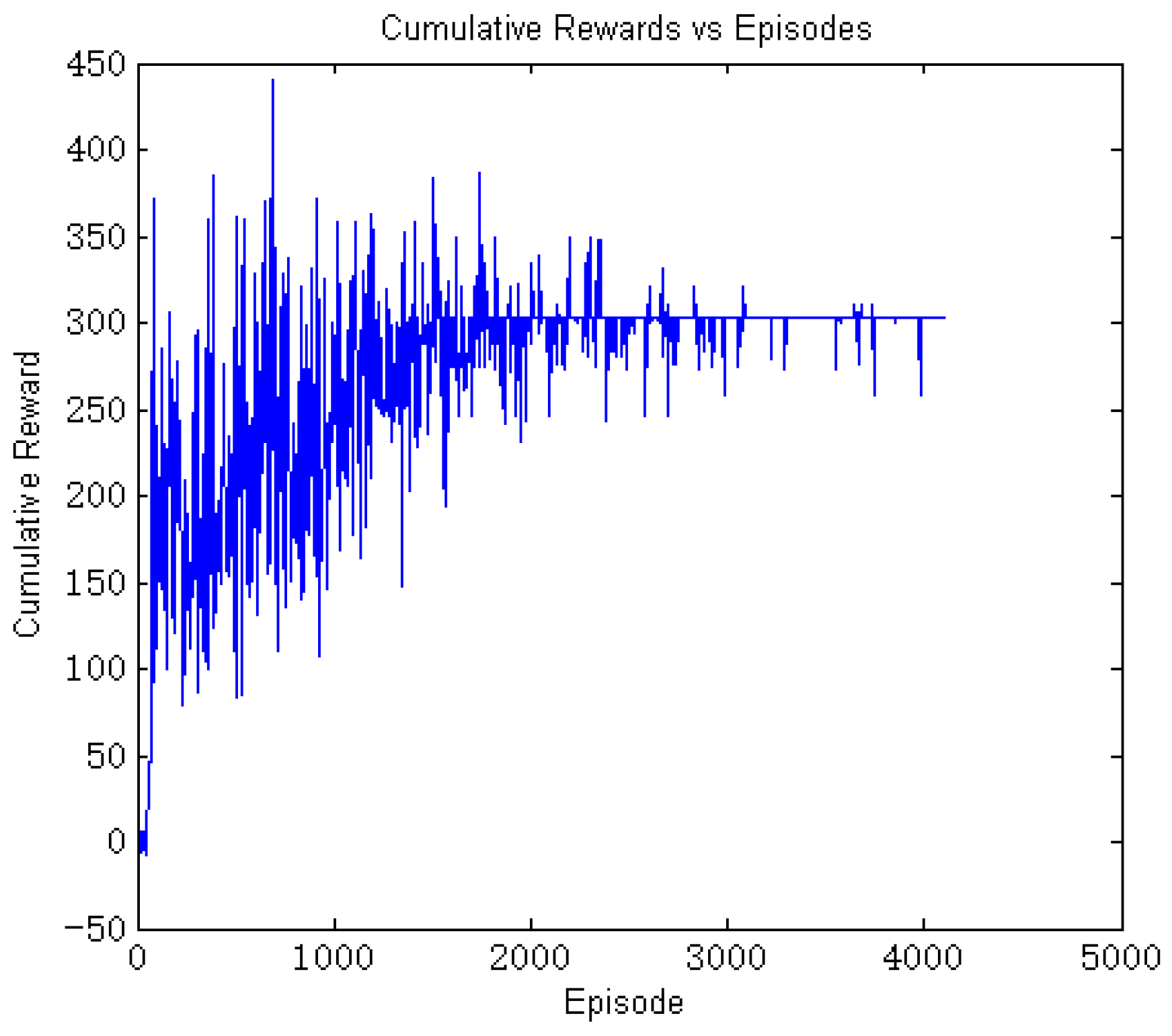
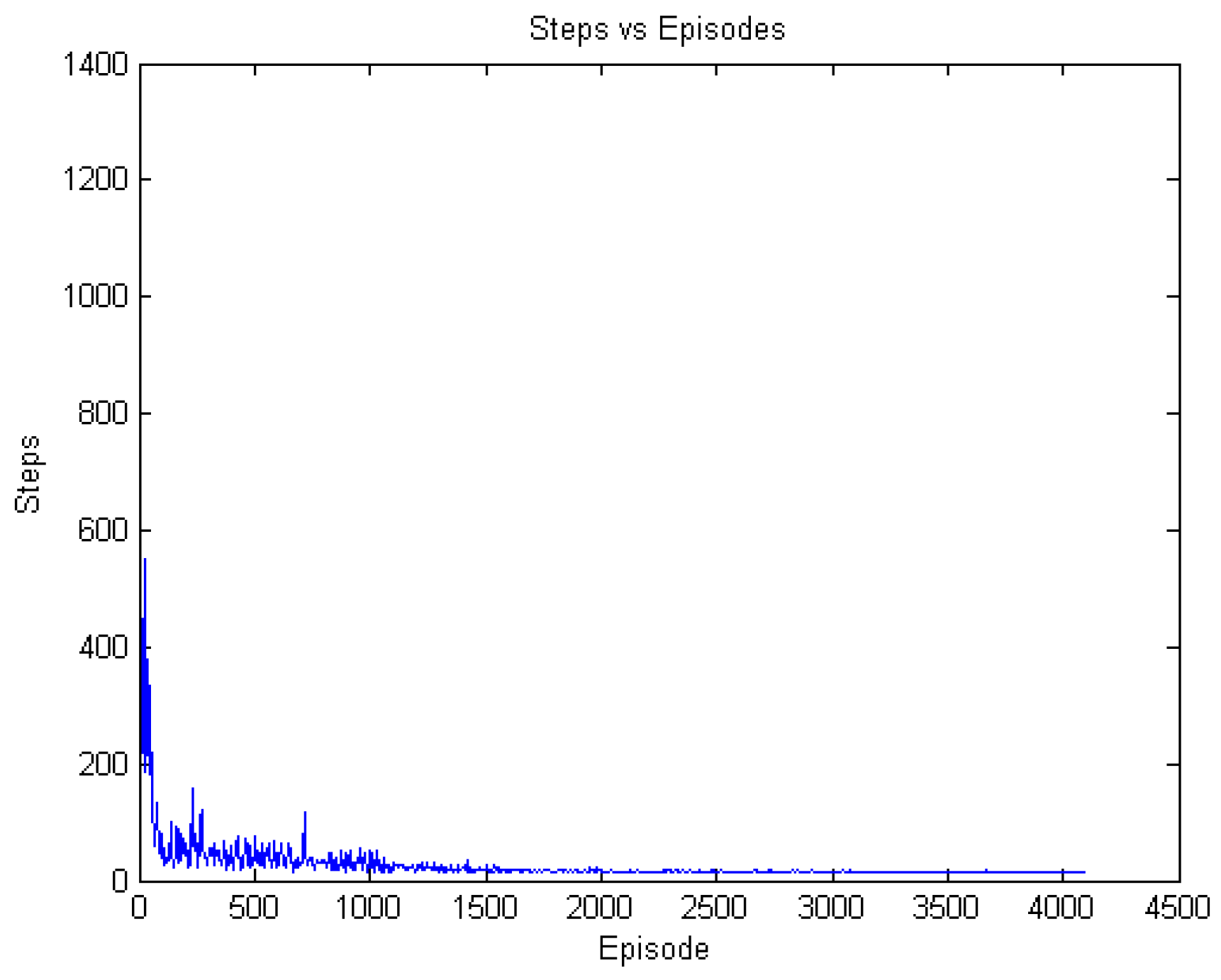
6. Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bebortta, S.; Senapati, D.; Panigrahi, C.; Pati, B. Adaptive Performance Modeling Framework for QoS-Aware Offloading in MEC-Based IIoT Systems. IEEE Internet Things J. 2022, 9, 10162–10171. [Google Scholar] [CrossRef]
- Mach, P.; Becvar, Z. Mobile Edge Computing: A Survey on Architecture and Computation Offloading. IEEE Commun. Surv. Tutor. 2017, 19, 1628–1656. [Google Scholar] [CrossRef]
- Hu, H.; Wang, Q.; Hu, R.; Zhu, Z. Mobility-Aware Offloading and Resource Allocation in a MEC-Enabled IoT Network with Energy Harvesting. IEEE Internet Things J. 2021, 8, 17541–17556. [Google Scholar] [CrossRef]
- Ale, L.; Zhang, N.; Fang, X.; Chen, X.; Wu, S.; Li, L. Delay-Aware and Energy-Efficient Computation Offloading in Mobile-Edge Computing Using Deep Reinforcement Learning. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 881–892. [Google Scholar] [CrossRef]
- Jiao, X.; Chen, Y.; Chen, Y.; Guo, X.; Zhu, W. SIC-Enabled Intelligent Online Task Concurrent Offloading for Wireless Powered MEC. IEEE Internet Things J. 2024, 11, 22684–22696. [Google Scholar] [CrossRef]
- Guo, K.; Gao, R.; Xia, W.; Quek, T. Online Learning Based Computation Offloading in MEC Systems with Communication and Computation Dynamics. IEEE Trans. Commun. 2021, 69, 1147–1162. [Google Scholar] [CrossRef]
- Yang, G.; Hou, L.; He, X.; He, D.; Chan, S.; Guizani, M. Offloading Time Optimization via Markov Decision Process in Mobile-Edge Computing. IEEE Internet Things J. 2021, 8, 2483–2493. [Google Scholar] [CrossRef]
- Khalid, R.; Shah, Z.; Naeem, M.; Ali, A.; Al-Fuqaha, A.; Ejaz, W. Computational Efficiency Maximization for UAV-Assisted MEC Networks with Energy Harvesting in Disaster Scenarios. IEEE Internet Things J. 2024, 11, 9004–9018. [Google Scholar] [CrossRef]
- Liu, L.; Chang, Z.; Guo, X. Socially Aware Dynamic Computation Offloading Scheme for Fog Computing System with Energy Harvesting Devices. IEEE Internet Things J. 2018, 5, 1869–1879. [Google Scholar] [CrossRef]
- Chu, W.; Jia, X.; Yu, Z.; Lui, J.; Lin, Y. Joint Service Caching, Resource Allocation and Task Offloading for MEC-Based Networks: A Multi-Layer Optimization Approach. IEEE Trans. Mob. Comput. 2024, 23, 2958–2975. [Google Scholar] [CrossRef]
- Bi, S.; Ho, C.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Chang, Z.; Wang, Z.; Guo, X.; Yang, C.; Han, Z.; Ristaniemi, T. Distributed Resource Allocation for Energy Efficiency in OFDMA Multicell Networks with Wireless Power Transfer. IEEE J. Sel. Areas Commun. 2019, 37, 345–356. [Google Scholar] [CrossRef]
- Dai, Y.; Zhang, K.; Maharjan, S.; Zhang, Y. Edge Intelligence for Energy-Efficient Computation Offloading and Resource Allocation in 5G Beyond. IEEE Trans. Veh. Technol. 2020, 69, 12175–12186. [Google Scholar] [CrossRef]
- Rodrigues, T.; Suto, K.; Nishiyama, H.; Liu, J.; Kato, N. Machine Learning Meets Computation and Communication Control in Evolving Edge and Cloud: Challenges and Future Perspective. IEEE Commun. Surv. Tutor. 2020, 22, 38–67. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, R.; Lai, S.; Fan, L.; Lei, X.; Karagiannidis, G. Distributed Machine Learning for Multiuser Mobile Edge Computing Systems. IEEE J. Sel. Top. Signal Process. 2022, 16, 460–473. [Google Scholar] [CrossRef]
- Zhou, H.; Jiang, K.; Liu, X.; Li, X.; Leung, V. Deep Reinforcement Learning for Energy-Efficient Computation Offloading in Mobile-Edge Computing. IEEE Internet Things J. 2022, 9, 1517–1530. [Google Scholar] [CrossRef]
- Jiang, F.; Dong, L.; Wang, K.; Yang, K.; Pan, C. Distributed Resource Scheduling for Large-Scale MEC Systems: A Multiagent Ensemble Deep Reinforcement Learning with Imitation Acceleration. IEEE Internet Things J. 2022, 9, 6597–6610. [Google Scholar] [CrossRef]
- Liu, T.; Ni, S.; Li, X.; Zhu, Y.; Kong, L.; Yang, Y. Deep Reinforcement Learning Based Approach for Online Service Placement and Computation Resource Allocation in Edge Computing. IEEE Trans. Mob. Comput. 2023, 22, 3870–3881. [Google Scholar] [CrossRef]
- Zhao, Z.; Shi, J.; Li, Z.; Si, J.; Xiao, P.; Tafazolli, R. Multiobjective Resource Allocation for mmWave MEC Offloading Under Competition of Communication and Computing Tasks. IEEE Internet Things J. 2022, 9, 8707–8719. [Google Scholar] [CrossRef]
- Malik, R.; Vu, M. Energy-Efficient Joint Wireless Charging and Computation Offloading in MEC Systems. IEEE J. Sel. Top. Signal Process. 2021, 15, 1110–1126. [Google Scholar] [CrossRef]
- Saleem, U.; Liu, Y.; Jangsher, S.; Li, Y.; Jiang, T. Mobility-Aware Joint Task Scheduling and Resource Allocation for Cooperative Mobile Edge Computing. IEEE Trans. Wirel. Commun. 2021, 20, 360–374. [Google Scholar] [CrossRef]
- Hu, H.; Song, W.; Wang, Q.; Hu, R.; Zhu, H. Energy Efficiency and Delay Tradeoff in an MEC-Enabled Mobile IoT Network. IEEE Internet Things J. 2022, 9, 15942–15956. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, F.; Chen, X.; Wu, Y. Efficient Multi-Vehicle Task Offloading for Mobile Edge Computing in 6G Networks. IEEE Trans. Veh. Technol. 2022, 71, 4584–4595. [Google Scholar] [CrossRef]
- Yin, L.; Guo, S.; Jiang, Q. Joint Task Allocation and Computation Offloading in Mobile Edge Computing with Energy Harvesting. IEEE Internet Things J. 2024, 11, 38441–38454. [Google Scholar] [CrossRef]
- Gu, Q.; Jian, Y.; Wang, G.; Fan, R.; Jiang, H.; Zhong, Z. Mobile Edge Computing via Wireless Power Transfer Over Multiple Fading Blocks: An Optimal Stopping Approach. IEEE Trans. Veh. Technol. 2020, 69, 10348–10361. [Google Scholar] [CrossRef]
- Guo, M.; Wang, W.; Huang, X.; Chen, Y.; Zhang, L.; Chen, L. Lyapunov-Based Partial Computation Offloading for Multiple Mobile Devices Enabled by Harvested Energy in MEC. IEEE Internet Things J. 2022, 9, 9025–9035. [Google Scholar] [CrossRef]
- Yan, J.; Bi, S.; Zhang, Y.J.A. Offloading and Resource Allocation with General Task Graph in Mobile Edge Computing: A Deep Reinforcement Learning Approach. IEEE Trans. Wirel. Commun. 2020, 19, 5404–5419. [Google Scholar] [CrossRef]
- Liu, L.; Feng, J.; Pei, Q.; Chen, C.; Dong, M. Blockchain-Enabled Secure Data Sharing Scheme in Mobile-Edge Computing: An Asynchronous Advantage Actor–Critic Learning Approach. IEEE Internet Things J. 2021, 8, 2342–2353. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Z.; Zhang, Y.; Wu, Y.; Chen, X.; Zhao, L. Deep Reinforcement Learning-Based Dynamic Resource Management for Mobile Edge Computing in Industrial Internet of Things. IEEE Trans. Ind. Inform. 2021, 17, 4925–4934. [Google Scholar] [CrossRef]
- Tuong, V.; Truong, P.; Nguyen, T.; Noh, W.; Cho, S. Partial Computation Offloading in NOMA-Assisted Mobile-Edge Computing Systems Using Deep Reinforcement Learning. IEEE Internet Things J. 2021, 8, 13196–13208. [Google Scholar] [CrossRef]
- Bi, S.; Huang, L.; Wang, H.; Zhang, Y. Lyapunov-Guided Deep Reinforcement Learning for Stable Online Computation Offloading in Mobile-Edge Computing Networks. IEEE Trans. Wirel. Commun. 2021, 20, 7519–7537. [Google Scholar] [CrossRef]
- Samanta, A.; Chang, Z. Adaptive Service Offloading for Revenue Maximization in Mobile Edge Computing with Delay-Constraint. IEEE Internet Things J. 2019, 6, 3864–3872. [Google Scholar] [CrossRef]
- Chen, J.; Xing, H.; Xiao, Z.; Xu, L.; Tao, T. A DRL Agent for Jointly Optimizing Computation Offloading and Resource Allocation in MEC. IEEE Internet Things J. 2021, 8, 17508–17524. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, J.; Wu, Y.; Gao, J.; Zhao, L. Dynamic Task Offloading and Resource Allocation for NOMA-Aided Mobile Edge Computing: An Energy Efficient Design. IEEE Trans. Serv. Comput. 2024, 17, 1492–1503. [Google Scholar] [CrossRef]
- Li, H.; Chen, Y.; Li, K.; Yang, Y.; Huang, J. Dynamic Energy-Efficient Computation Offloading in NOMA-Enabled Air–Ground-Integrated Edge Computing. IEEE Internet Things J. 2024, 11, 37617–37629. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, J.; Letaief, K. Dynamic Computation Offloading for Mobile-Edge Computing with Energy Harvesting Devices. IEEE J. Sel. Areas Commun. 2016, 34, 3590–3605. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, H.; Zhang, X.; Yuan, D. Joint Service Caching, Communication and Computing Resource Allocation in Collaborative MEC Systems: A DRL-Based Two-Timescale Approach. IEEE Trans. Wirel. Commun. 2024, 23, 15493–15506. [Google Scholar] [CrossRef]
- Watkins, C.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Sun, W.; Zhao, Y.; Ma, W.; Guo, B.; Xu, L.; Duong, T. Accelerating Convergence of Federated Learning in MEC with Dynamic Community. IEEE Trans. Mob. Comput. 2024, 23, 1769–1784. [Google Scholar] [CrossRef]
- Ye, X.; Li, M.; Si, P.; Yang, R.; Wang, Z.; Zhang, Y. Collaborative and Intelligent Resource Optimization for Computing and Caching in IoV with Blockchain and MEC Using A3C Approach. IEEE Trans. Veh. Technol. 2023, 72, 1449–1463. [Google Scholar] [CrossRef]
- Sun, M.; Xu, X.; Han, S.; Zheng, H.; Tao, X.; Zhang, P. Secure Computation Offloading for Device-Collaborative MEC Networks: A DRL-Based Approach. IEEE Trans. Veh. Technol. 2023, 72, 4887–4903. [Google Scholar] [CrossRef]
- Tong, Z.; Cai, J.; Mei, J.; Li, K.; Li, K. Dynamic Energy-Saving Offloading Strategy Guided by Lyapunov Optimization for IoT Devices. IEEE Internet Things J. 2022, 9, 19903–19915. [Google Scholar] [CrossRef]
| Existing Works | Methodology | Optimization Objectives | Experimental Scenarios | Consider Constraints |
|---|---|---|---|---|
| [19] | Multiobjective optimization problem | Achieve maximum revenue and maximum service utilization | For mobile devices with latency and resource constraints | Task delay |
| [20] | Nested algorithm | Minimize the total energy consumption of the system | Compute offload wireless charging | Task delay |
| [21] | Genetic algorithm, heuristic algorithm | Minimize task delay | Mobile perception scene | Delay constraint, power constraint |
| [22] | Lyapunov optimization theory | Minimize the long-term average energy efficiency of the network | A multi-user and multi-server MEC Internet of Things system | Computing resources, power resource constraint |
| [23,24,25,26] | Lyapunov optimization theory | Minimize system cost | Multi-server MEC system | Energy constraint, task queue stability constraint |
| [27] | Deep reinforcement learning framework | Minimize the energy time cost (ETC) of MD | Multi-task MEC system | Delay constraints |
| [28] | A3C Deep Reinforcement Learning algorithm | Minimize the energy consumption of the MEC system and maximize the throughput of the blockchain system | Data sharing in MEC | delay constraints |
| [29] | DDPG | Minimize the long-term average delay of all computing tasks | Dynamic resource management in MEC | Power constraints, energy consumption constraints, computer resource constraints |
| [30] | The ACDQN algorithm of deep reinforcement learning | Minimize the weighted sum of energy consumption and delay | NOMA assists the MEC system | Channel resource constraints |
| [31] | Lyapunov-guided deep reinforcement learning | Maximize the weighted sum calculation rate | Multi-user MEC | offloading decision constraints, resource allocation constraints |
| Notations | Meanings |
|---|---|
| The set of users in the system | |
| The set of mobile devices | |
| The set of MBSs | |
| t | The time slot |
| The length of each time slot | |
| The data size of the arrived computation task | |
| The maximum delay in computing the task completion | |
| The set of computation task offloading decision strategies | |
| Local computing decision | |
| The decision of offloading from MD i to MBS m server process | |
| The decision of computation task discarding | |
| The computation resource allocation of the local computation of MD i | |
| The computation resource allocation of MBS server m for MD i | |
| The bandwidth allocation between MD i and MBS m | |
| The power allocation of MD i for task offloading | |
| The harvested energy of MD i in time slot t | |
| The battery capacity of MD i in time slot t | |
| The weighting parameter of energy consumption | |
| The weighting parameter of the delay of task completion | |
| The weighting parameter of the cost of task discarding | |
| Channel gains between MDs and MBSs | |
| F | Available MEC server computing resources |
| The data size of the arrived computation task | |
| Channel interference between MDs and MBSs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Mi, J.; Guo, C.; Fu, Q.; Tang, W.; Luo, W.; Zhu, Q. Research on Offloading and Resource Allocation for MEC with Energy Harvesting Based on Deep Reinforcement Learning. Electronics 2025, 14, 1911. https://doi.org/10.3390/electronics14101911
Chen J, Mi J, Guo C, Fu Q, Tang W, Luo W, Zhu Q. Research on Offloading and Resource Allocation for MEC with Energy Harvesting Based on Deep Reinforcement Learning. Electronics. 2025; 14(10):1911. https://doi.org/10.3390/electronics14101911
Chicago/Turabian StyleChen, Jun, Junyu Mi, Chen Guo, Qing Fu, Weidong Tang, Wenlang Luo, and Qing Zhu. 2025. "Research on Offloading and Resource Allocation for MEC with Energy Harvesting Based on Deep Reinforcement Learning" Electronics 14, no. 10: 1911. https://doi.org/10.3390/electronics14101911
APA StyleChen, J., Mi, J., Guo, C., Fu, Q., Tang, W., Luo, W., & Zhu, Q. (2025). Research on Offloading and Resource Allocation for MEC with Energy Harvesting Based on Deep Reinforcement Learning. Electronics, 14(10), 1911. https://doi.org/10.3390/electronics14101911






