Local-Global Representation Enhancement for Multi-View Graph Clustering
Abstract
1. Introduction
- A new multi-view graph clustering algorithm via local-global representation enhancement is proposed. LGMGC enhances the local and global representations to obtain a more suitable representation for clustering.
- A simple and effective graph encoder that enhances the low-frequency signals to obtain a smoother representation is proposed.
- Comprehensive experimentation on three benchmark datasets illustrates the excellent performance of the proposed algorithm in comparison to existing deep graph clustering algorithms.
2. Related Work
2.1. Graph Clustering Based on Consensus Graph Learning
2.2. Graph Clustering Based on Representation Learning
3. Proposed Algorithm
3.1. Notation and Preliminaries
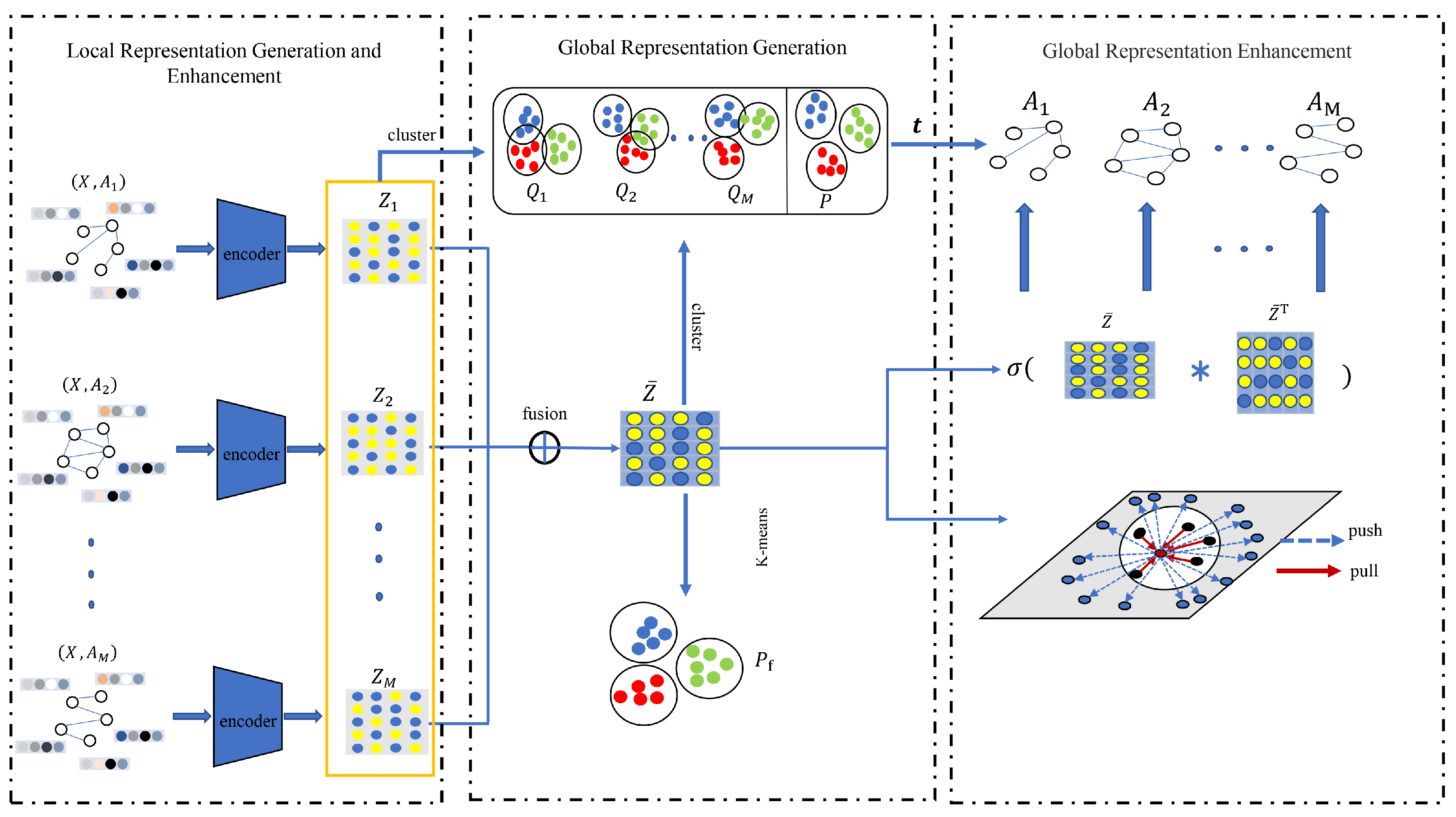
3.2. Framework of Multi-View Graph Clustering via Local-Global Representation Enhancement
3.3. Local Representation Generation and Enhancement
3.4. Global Representation Generation
3.5. Global Representation Enhancement
| Algorithm 1 LGMGC |
|
4. Experiments
4.1. Datasets
4.2. Baseline Algorithms and Evaluation Metrics
- (1)
- GAE is a single view algorithm that uses graph autoencoders to generate embedded representations. this algorithm is applied to each graph view and the best results are reported.
- (2)
- LINE is a single view graph clustering algorithm applied to large-scale graph data. this algorithm is applied to each graph view and the best results are reported.
- (3)
- PMNE projects multi-view graph in to a representative vector space.
- (4)
- RMSC is a multi-view clustering algorithm designed to address noise in input data.
- (5)
- SwMC implements clustering multi-view data while learning weights of each view.
- (6)
- O2MAC learns node embedding by reconstructing entire view with the most information-rich information view.
- (7)
- MvAGC is a multi-view graph clustering algorithm that performs graph filtering to achieve multi-view attributed graph clustering.
- (8)
- MAGC is a multi-view graph clustering method using node attributes and exploring higher-order graph structure information.
- (9)
- LMGEC uses a simple linear model to simultaneously accomplish clustering and representation learning.
4.3. Parameter Settings
4.4. Experimental Results of Different Algorithms
5. Ablation Study
5.1. Effect of Multi-View Learning
5.2. Effect of Reconstruction Loss
5.3. Effect of Neighborhood Contrastive Loss
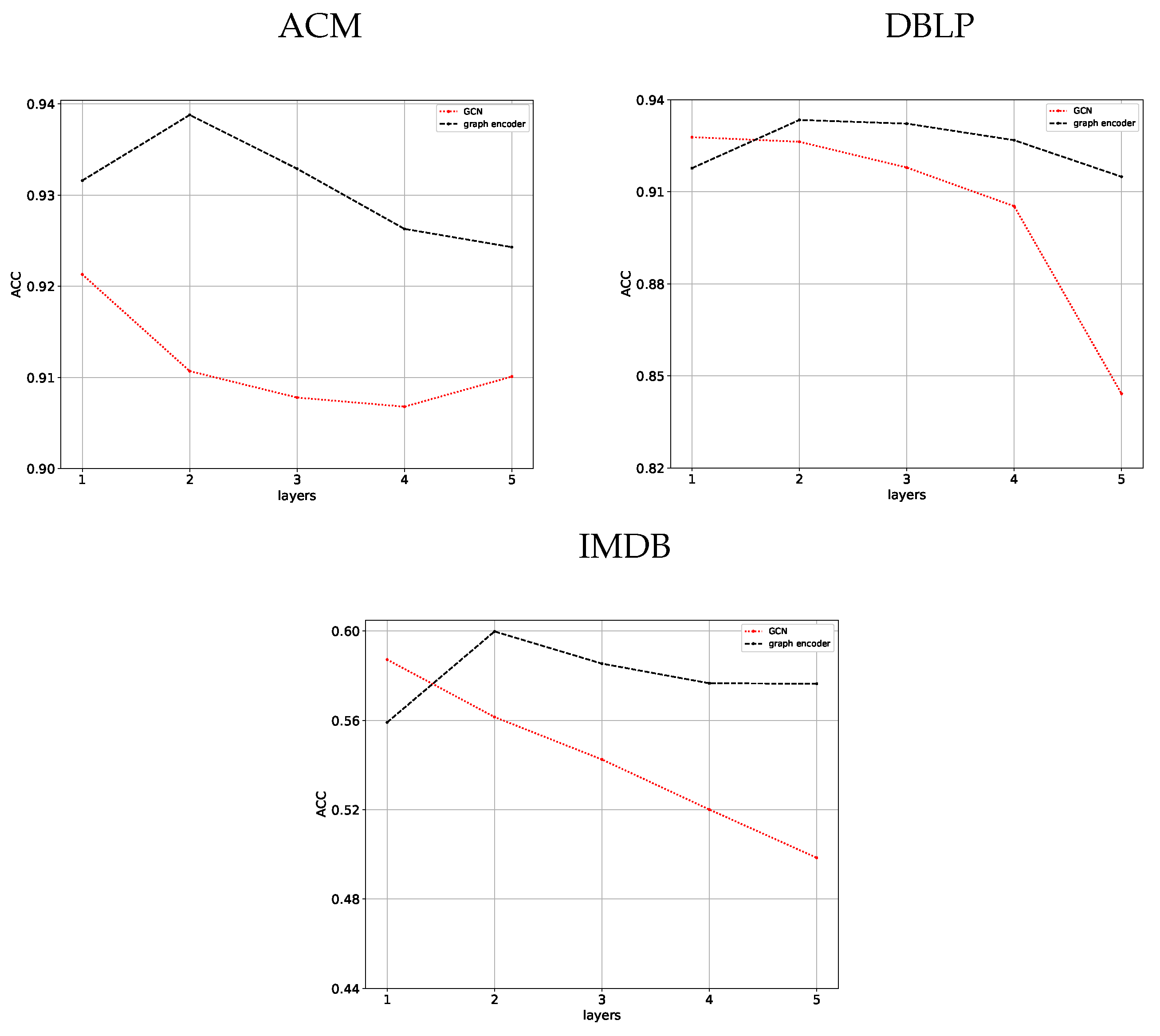
5.4. Effect of Graph Encoder
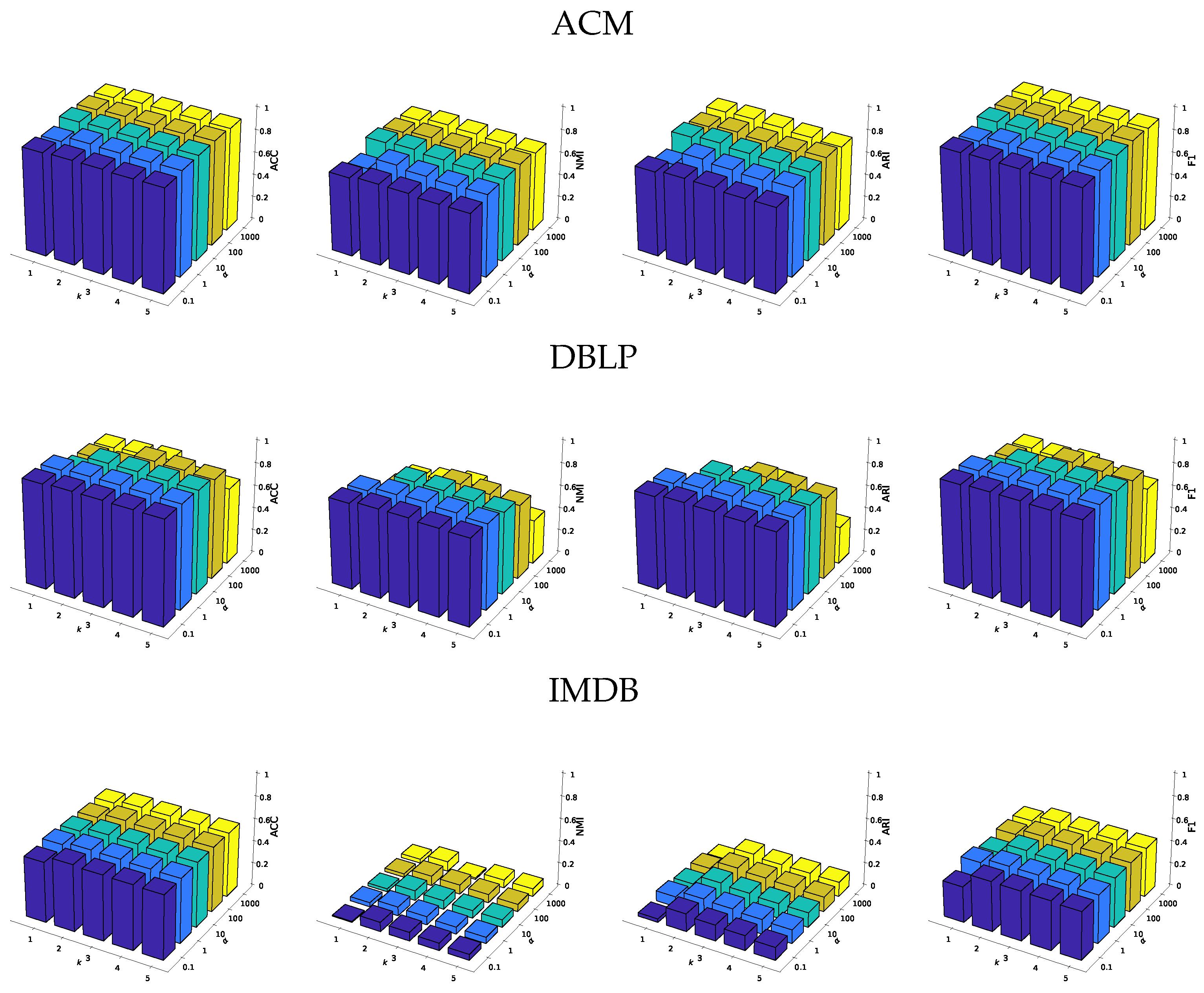
5.5. Parameter Analysis
6. Discussion
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, H.; Wang, J.; Duan, R.; Yan, C. DCOM-GNN: A Deep Clustering Optimization Method for Graph Neural Networks. Knowl.-Based Syst. 2023, 279, 110961. [Google Scholar] [CrossRef]
- Hu, D.; Feng, D.; Xie, Y. EGC: A novel event-oriented graph clustering framework for social media text. Inf. Process. Manag. 2022, 59, 103059. [Google Scholar] [CrossRef]
- Yu, J.; Jia, A.L. MLGAL: Multi-level Label Graph Adaptive Learning for node clustering in the attributed graph. Knowl.-Based Syst. 2023, 278, 110876. [Google Scholar] [CrossRef]
- Guo, Y.; Zang, Z.; Gao, H.; Xu, X.; Wang, R.; Liu, L.; Li, J. Unsupervised social event detection via hybrid graph contrastive learning and reinforced incremental clustering. Knowl.-Based Syst. 2024, 284, 111225. [Google Scholar] [CrossRef]
- Guo, H.; Zhou, Z.; Zhao, D.; Gaaloul, W. EGNN: Energy-efficient anomaly detection for IoT multivariate time series data using graph neural network. Future Gener. Comput. Syst. 2024, 151, 45–56. [Google Scholar] [CrossRef]
- Zhao, S.; Zheng, Y.; Li, J.; Zhang, X.; Tang, C.; Tan, Z. Pure kernel graph fusion tensor subspace clustering under non-negative matrix factorization framework. Inf. Process. Manag. 2024, 61, 103603. [Google Scholar] [CrossRef]
- Li, X.; Sun, L.; Ling, M.; Peng, Y. A survey of graph neural network based recommendation in social networks. Neural Comput. 2023, 549, 126441. [Google Scholar] [CrossRef]
- Mohamed, H.A.; Pilutti, D.; James, S.; Del Bue, A.; Pelillo, M.; Vascon, S. Locality-aware subgraphs for inductive link prediction in knowledge graphs. Pattern Recognit. Lett 2023, 167, 90–97. [Google Scholar] [CrossRef]
- Liao, H.; Hu, J.; Li, T.; Du, S.; Peng, B. Deep linear graph attention model for attributed graph clustering. Knowl.-Based Syst. 2022, 246, 108665. [Google Scholar] [CrossRef]
- Berahmand, K.; Nasiri, E.; Pir mohammadiani, R.; Li, Y. Spectral clustering on protein-protein interaction networks via constructing affinity matrix using attributed graph embedding. Comput. Biol. Med. 2021, 138, 104933. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Xu, Q.; Fang, J.; Tang, R.; Du, P. Bipartite graph-based community-to-community matching in local energy market considering socially networked prosumers. Appl. Energy 2024, 353, 122245. [Google Scholar] [CrossRef]
- Hu, Z.; Deng, J.; Han, J.; Yuan, K. Review on application of graph neural network in traffic prediction. J. Traffic Transp. Eng. 2023, 23, 39–61. [Google Scholar]
- Liu, L.; Kang, Z.; Ruan, J.; He, X. Multilayer graph contrastive clustering network. Inf. Sci 2022, 613, 256–267. [Google Scholar] [CrossRef]
- Wang, R.; Li, L.; Tao, X.; Wang, P.; Liu, P. Contrastive and attentive graph learning for multi-view clustering. Inf. Process. Manag. 2022, 59, 102967. [Google Scholar] [CrossRef]
- Lin, Z.; Kang, Z. Graph Filter-based Multi-view Attributed Graph Clustering. In Proceedings of the IJCAI, Virtual, 19–27 August 2021; pp. 2723–2729. [Google Scholar]
- Pan, E.; Kang, Z. Multi-view contrastive graph clustering. In Proceedings of the NeurIPS, Virtual, 6–14 December 2021; pp. 2148–2159. [Google Scholar]
- Fan, S.; Wang, X.; Shi, C.; Lu, E.; Lin, K.; Wang, B. One2Multi graph autoencoder for multi-view graph clustering. In Proceedings of the WWW’20, Taipei, China, 20–24 April 2020; pp. 3070–3076. [Google Scholar]
- Cai, E.; Huang, J.; Huang, B.; Xu, S.; Zhu, J. Grae: Graph recurrent autoencoder for multi-view graph clustering. In Proceedings of the ACAI, Sanya, China, 22–24 December 2021; pp. 1–9. [Google Scholar]
- Liang, J.; Liu, X.; Bai, L.; Cao, F.; Wang, D. Incomplete multi-view clustering via local and global co-regularization. Sci. China Inf. Sci. 2022, 65, 152105. [Google Scholar] [CrossRef]
- Nie, F.; Li, J.; Li, X. Self-weighted multiview clustering with multiple graphs. In Proceedings of the 26th IJCAI, Melbourne, Australia, 19–25 August 2017; pp. 2564–2570. [Google Scholar]
- Lin, Z.; Kang, Z.; Zhang, L.; Tian, L. Multi-view Attributed Graph Clustering. IEEE Trans. Knowl. Data Eng. 2023, 35, 1872–1880. [Google Scholar] [CrossRef]
- Liu, W.; Chen, P.; Yeung, S. Principled Multilayer Network Embedding. In Proceedings of the ICDM, New Orleans, LA, USA, 18–21 November 2017; pp. 134–141. [Google Scholar]
- Xia, R.; Pan, Y.; Du, L. Robust Multi-view Spectral Clustering via Low-rank and Sparse Decomposition. In Proceedings of the AAAI, Québec City, QC, Canada, 27–31 July 2014; pp. 2149–2155. [Google Scholar]
- Fettal, C.; Labiod, L.; Nadif, M. Simultaneous Linear Multi-View Attributed Graph Representation Learning and Clustering. In Proceedings of the WSDM, Singapore, 27 February–3 March 2023; pp. 303–311. [Google Scholar]
- Kipf, T.; Welling, M. Variational Graph Auto-Encoders. arXiv 2016, arXiv:1611.07308. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, Y.; Yan, J.; Mei, Q. LINE: Large-scale Information Network Embedding. In Proceedings of the ICONIP, San Diego, CA, USA, 7–9 May 2015; pp. 1067–1077. [Google Scholar]
- Xia, W.; Wang, S.; Yang, M.; Gao, Q.; Han, J.; Gao, X. Multi-view graph embedding clustering network: Joint self-supervision and block diagonal representation. Neural Netw. 2022, 145, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Wang, Q.; Tao, Z.; Xie, D.; Gao, Q. Multi-view attribute graph convolution networks for clustering. In Proceedings of the IJCAI, Virtual, 19–27 August 2021; pp. 2973–2979. [Google Scholar]
| Datasets | Nodes | Edges | Features | Clusters |
|---|---|---|---|---|
| ACM | 3025 | Co-Subject (29,281) | 1830 | 3 |
| Co-Author (2,210,761) | ||||
| DBLP | 4057 | Co-Author (11,113) | 334 | 4 |
| Co-Conference (6,776,335) | ||||
| Co-Term (5,000,495) | ||||
| IMDB | 4780 | Co-Actor (98,010) | 1232 | 3 |
| Co-Director (21,018) |
| Algorithms | GAE | LINE | PMNE | RMSC | SwMC | O2MAC | MvAGC | MAGC | LMGEC | LGMGC | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ACM | ACC | 0.8216 | 0.6479 | 0.6936 | 0.6315 | 0.3831 | 0.9042 | 0.8975 | 0.8806 | 0.9302 | 0.9388 |
| NMI | 0.4914 | 0.3941 | 0.4648 | 0.3973 | 0.0838 | 0.6923 | 0.6735 | 0.6180 | 0.7513 | 0.7735 | |
| ARI | 0.5444 | 0.3433 | 0.4302 | 0.3312 | 0.0187 | 0.7394 | 0.7212 | 0.6808 | 0.8031 | 0.8263 | |
| F1 | 0.8225 | 0.6594 | 0.6955 | 0.5746 | 0.4709 | 0.9053 | 0.8986 | 0.8835 | 0.9311 | 0.9382 | |
| DBLP | ACC | 0.8859 | 0.8689 | 0.7925 | 0.8994 | 0.6538 | 0.9074 | 0.9277 | 0.9282 | 0.9285 | 0.9334 |
| NMI | 0.6825 | 0.6676 | 0.5914 | 0.7111 | 0.3760 | 0.7287 | 0.7727 | 0.7768 | 0.7739 | 0.7860 | |
| ARI | 0.7410 | 0.6988 | 0.5265 | 0.7647 | 0.3800 | 0.7780 | 0.8276 | 0.8267 | 0.8284 | 0.8394 | |
| F1 | 0.8743 | 0.8564 | 0.7966 | 0.8248 | 0.5602 | 0.9013 | 0.9225 | 0.9237 | 0.9241 | 0.9289 | |
| IMDB | ACC | 0.4298 | 0.4268 | 0.4958 | 0.2702 | 0.2617 | 0.4502 | 0.5633 | 0.6125 | 0.5893 | 0.5998 |
| NMI | 0.0402 | 0.0031 | 0.0359 | 0.0054 | 0.0056 | 0.0421 | 0.0317 | 0.1167 | 0.0632 | 0.0913 | |
| ARI | 0.0473 | −0.0090 | 0.0366 | 0.0018 | 0.0004 | 0.0564 | 0.0940 | 0.1806 | 0.1294 | 0.1710 | |
| F1 | 0.4062 | 0.2870 | 0.3906 | 0.3775 | 0.3714 | 0.1459 | 0.3783 | 0.4551 | 0.4267 | 0.4565 | |
| Datasets | V1 | V2 | V3 | ALL | |
|---|---|---|---|---|---|
| ACM | ACC | 0.9197 | 0.7230 | - | 0.9388 |
| NMI | 0.7185 | 0.5155 | - | 0.7735 | |
| ARI | 0.7765 | 0.4719 | - | 0.8263 | |
| F1 | 0.9198 | 0.7101 | 0.9382 | ||
| DBLP | ACC | 0.6621 | 0.6717 | 0.9247 | 0.9334 |
| NMI | 0.3743 | 0.3349 | 0.7782 | 0.7860 | |
| ARI | 0.2649 | 0.3125 | 0.8329 | 0.8394 | |
| F1 | 0.6695 | 0.6724 | 0.9197 | 0.9289 | |
| IMDB | ACC | 0.5730 | 0.5787 | - | 0.5998 |
| NMI | 0.0640 | 0.0811 | - | 0.0913 | |
| ARI | 0.1196 | 0.1518 | - | 0.1710 | |
| F1 | 0.4298 | 0.4504 | - | 0.4565 |
| Datasets | LGMGC w/o | LGMGC | |
|---|---|---|---|
| ACM | ACC | 0.9233 | 0.9388 |
| NMI | 0.7349 | 0.7735 | |
| ARI | 0.7854 | 0.8263 | |
| F1 | 0.9241 | 0.9382 | |
| DBLP | ACC | 0.7678 | 0.9334 |
| NMI | 0.5124 | 0.7860 | |
| ARI | 0.5198 | 0.8394 | |
| F1 | 0.7432 | 0.9289 | |
| IMDB | ACC | 0.5852 | 0.5998 |
| NMI | 0.0754 | 0.0913 | |
| ARI | 0.1389 | 0.1710 | |
| F1 | 0.4473 | 0.4565 |
| Datasets | LGMGC w/o | LGMGC | |
|---|---|---|---|
| ACM | ACC | 0.9111 | 0.9388 |
| NMI | 0.7070 | 0.7735 | |
| ARI | 0.7552 | 0.8263 | |
| F1 | 0.9123 | 0.9382 | |
| DBLP | ACC | 0.9232 | 0.9334 |
| NMI | 0.7774 | 0.7860 | |
| ARI | 0.8293 | 0.8394 | |
| F1 | 0.9185 | 0.9289 | |
| IMDB | ACC | 0.5345 | 0.5998 |
| NMI | 0.0044 | 0.0913 | |
| ARI | 0.0188 | 0.1710 | |
| F1 | 0.2916 | 0.4565 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Hou, Z.; Wang, J. Local-Global Representation Enhancement for Multi-View Graph Clustering. Electronics 2024, 13, 1788. https://doi.org/10.3390/electronics13091788
Zhao X, Hou Z, Wang J. Local-Global Representation Enhancement for Multi-View Graph Clustering. Electronics. 2024; 13(9):1788. https://doi.org/10.3390/electronics13091788
Chicago/Turabian StyleZhao, Xingwang, Zhedong Hou, and Jie Wang. 2024. "Local-Global Representation Enhancement for Multi-View Graph Clustering" Electronics 13, no. 9: 1788. https://doi.org/10.3390/electronics13091788
APA StyleZhao, X., Hou, Z., & Wang, J. (2024). Local-Global Representation Enhancement for Multi-View Graph Clustering. Electronics, 13(9), 1788. https://doi.org/10.3390/electronics13091788






