Synchronous Control of High-Speed Train Lift Wing Angle of Attack Drive System Based on Chaotic Particle Swarm Optimization and Linear Auto-Disturbance Resistant Controller
Abstract
1. Introduction
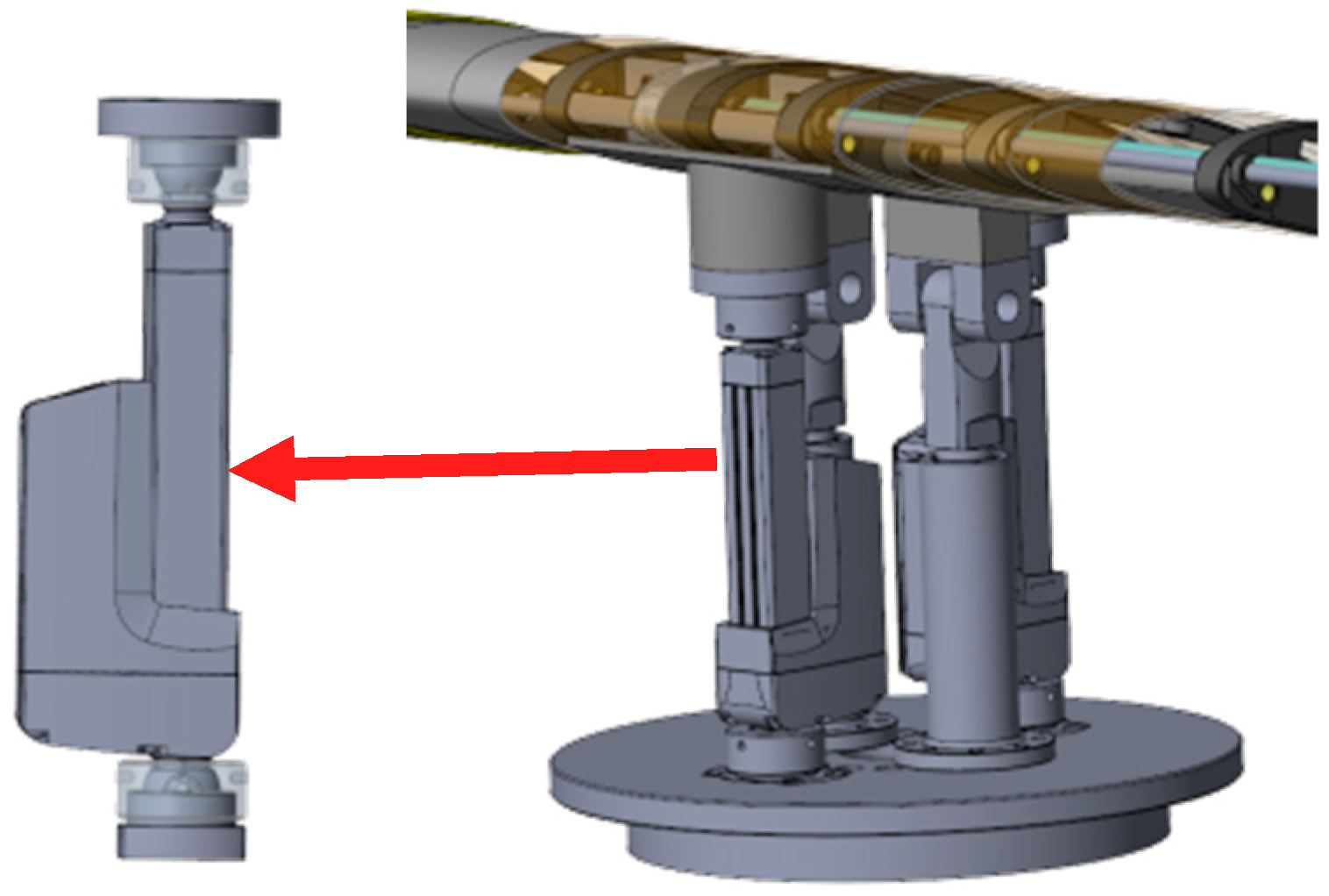
2. Design of the Lifting Wing Angle of Attack Conversion Device
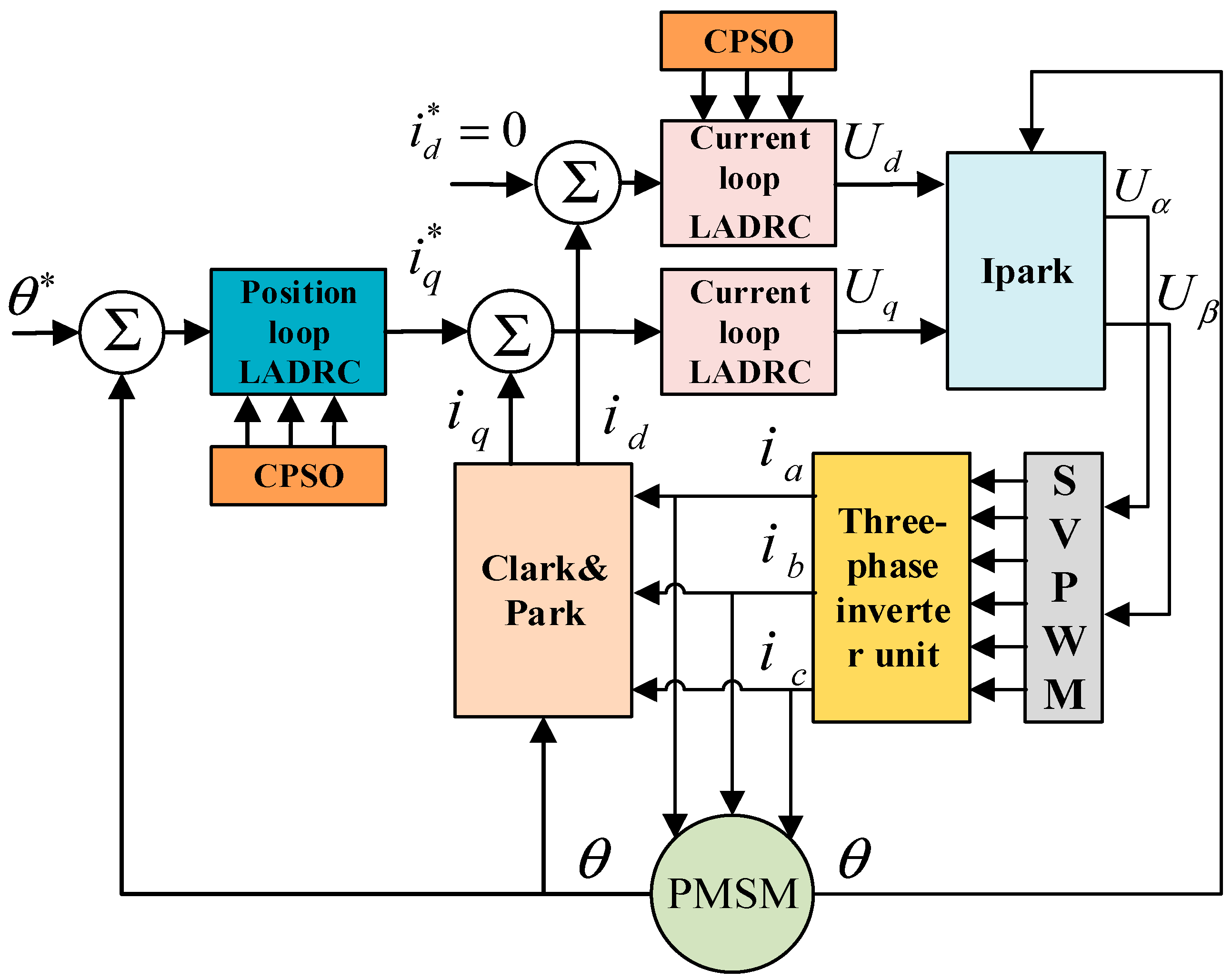
3. Control System Modeling
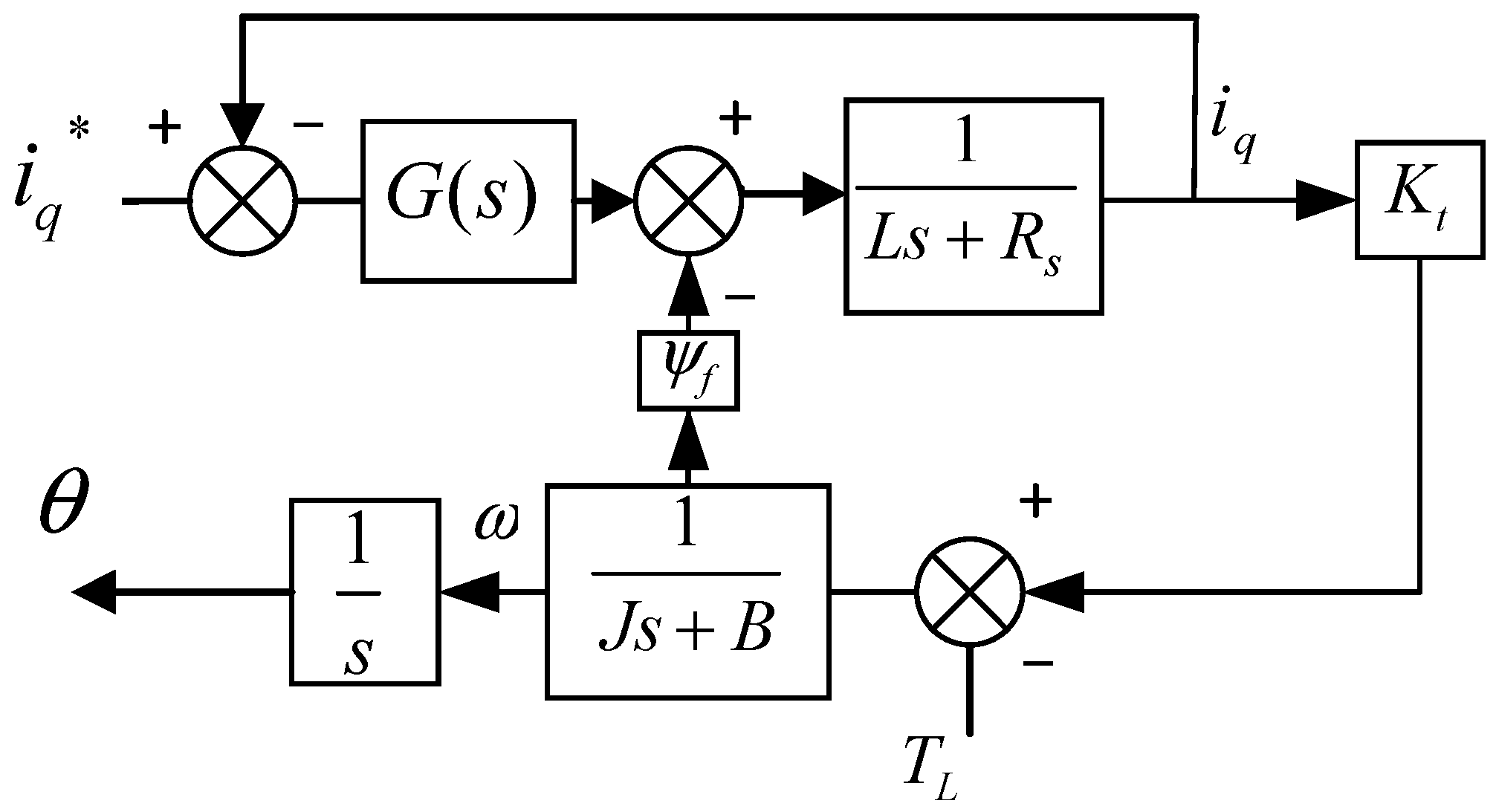
3.1. Permanent Magnet Synchronous Motor Modeling
3.2. Electric Actuator Modeling
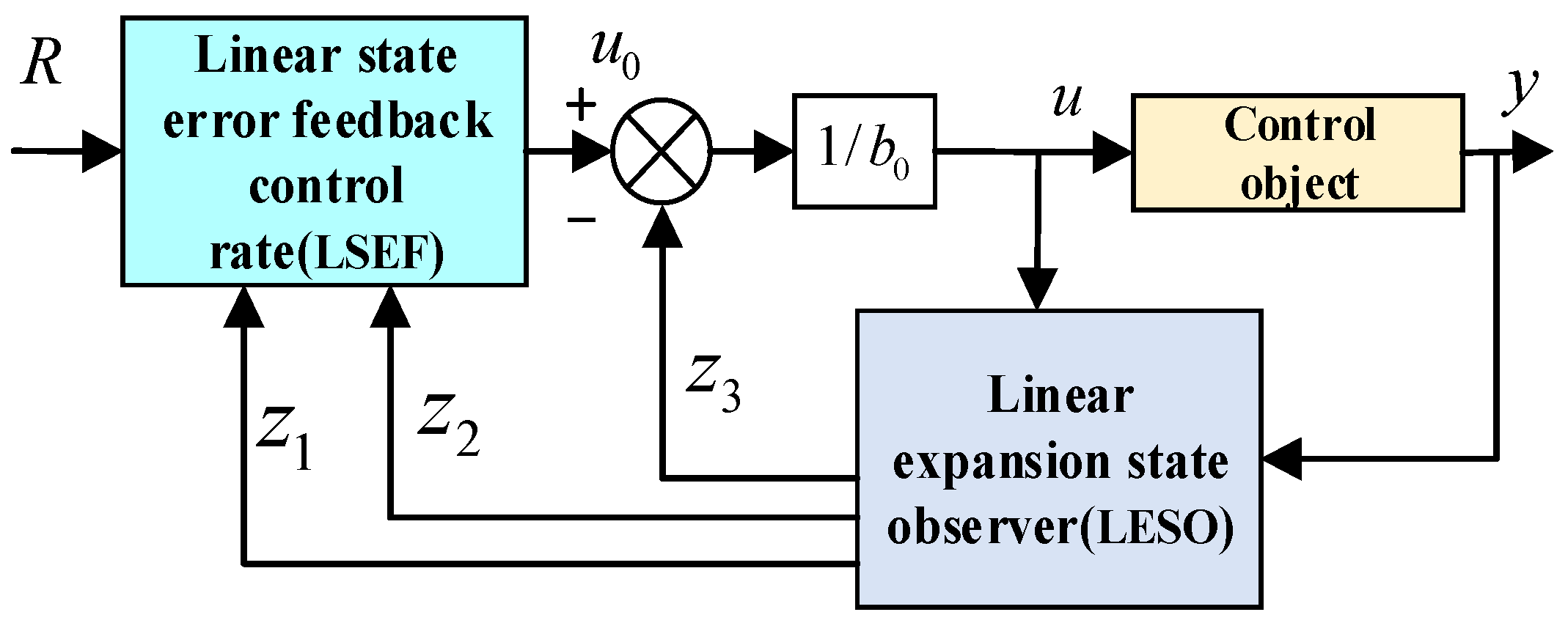
3.3. Linear Auto-Disturbance Resistive Control
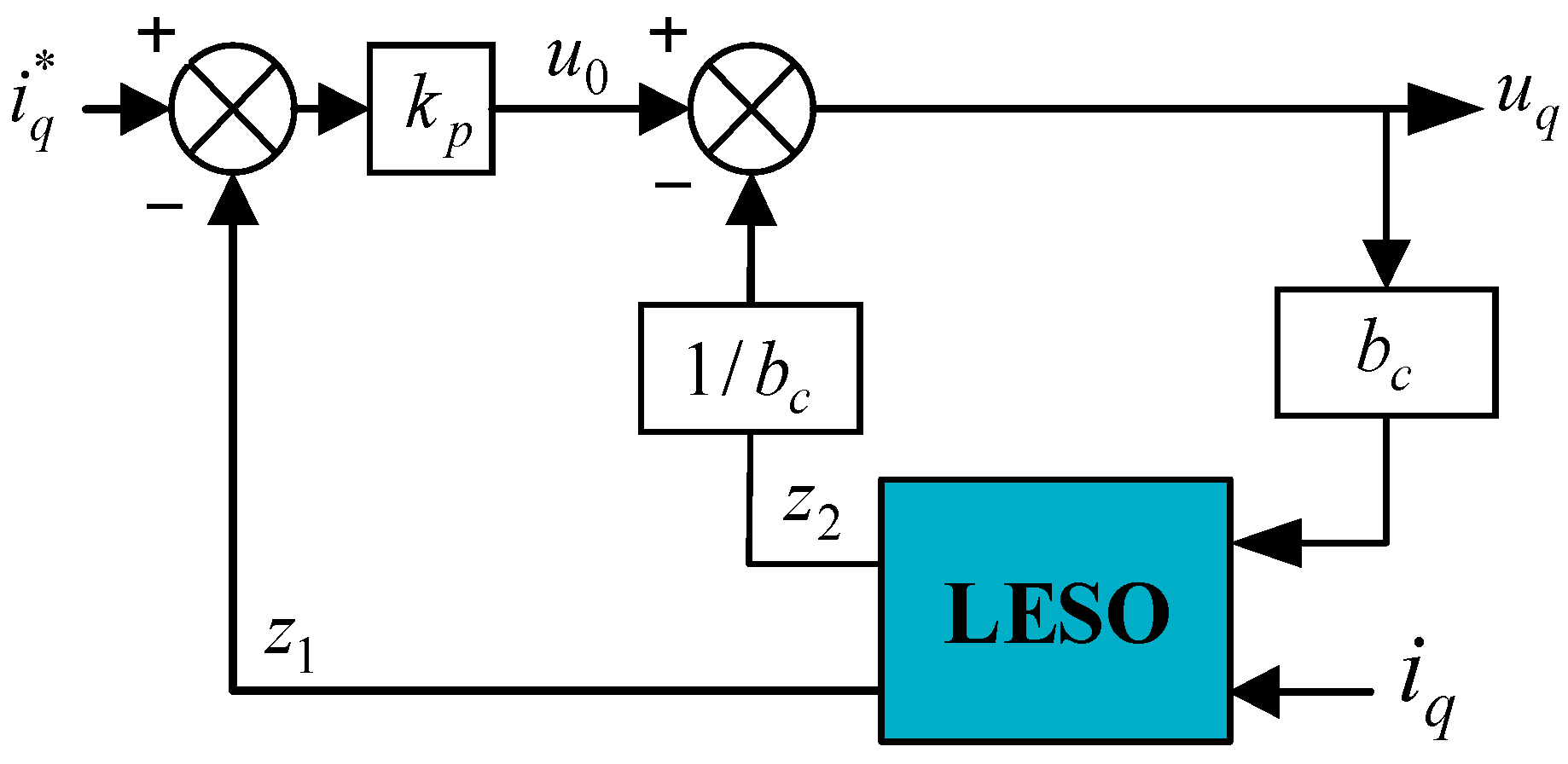
3.3.1. Current Loop Controller Design
3.3.2. Position Loop Controller Design
3.3.3. ADRC Parameter Tuning
3.4. Chaotic Particle Swarm Optimization Algorithm
3.4.1. Particle Swarm Optimization Algorithm Fundamentals
3.4.2. Improvement of the Algorithm
- (1)
- Randomly generate an n-dimensional vector, , according to Equation (32) to get N vectors .When µ is set to µ = 4 in Equation (32), the system becomes completely chaotic.
- (2)
- Ensure each component of Z is within the range of values for the corresponding variable.
- (3)
- Calculate the fitness value of the particle swarm and then select the M solutions with the better performance as the initial solutions from the N initial populations. Additionally, M initial velocities are randomly generated.
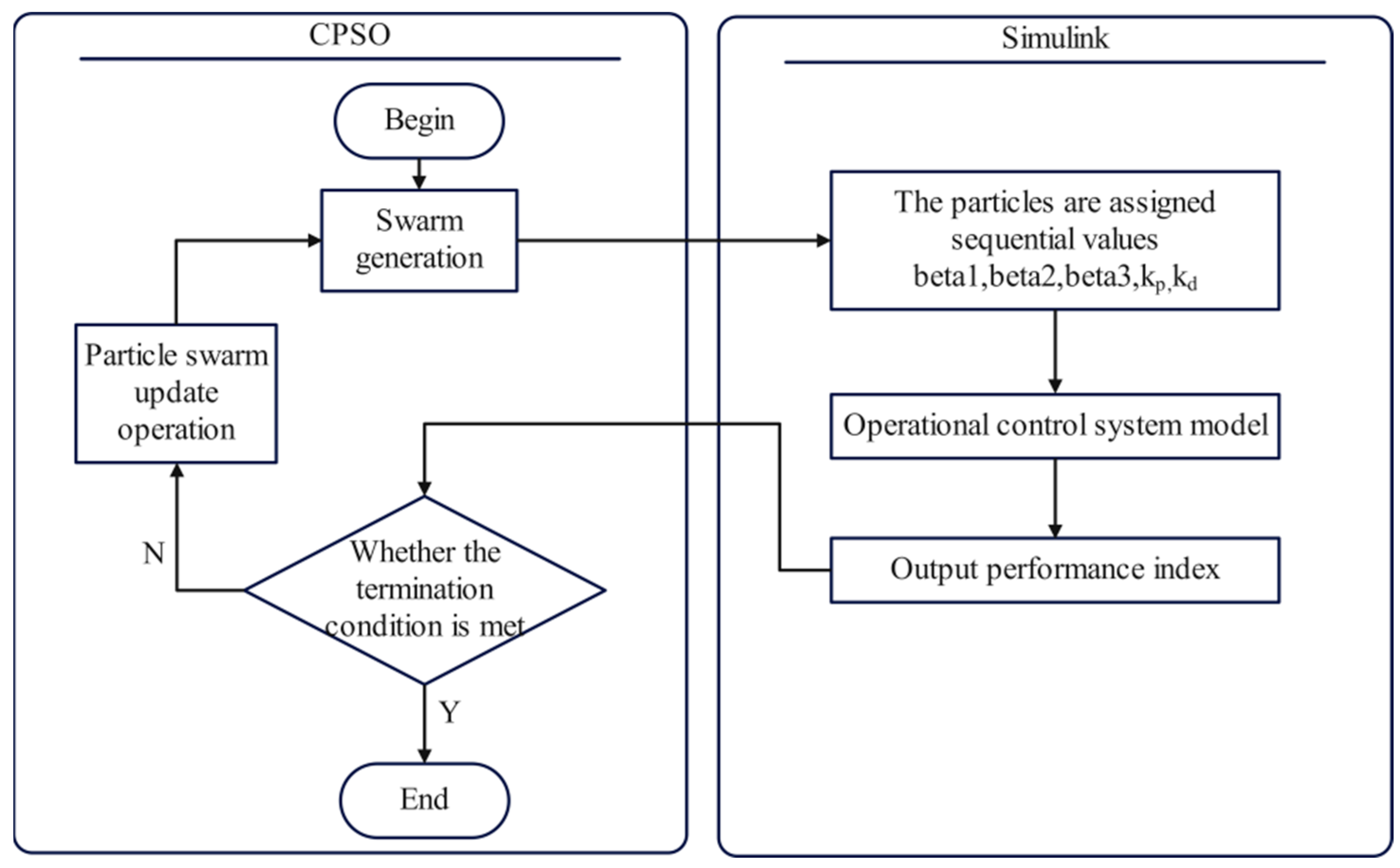
3.4.3. Optimization of ADRC Parameters Using CPSO
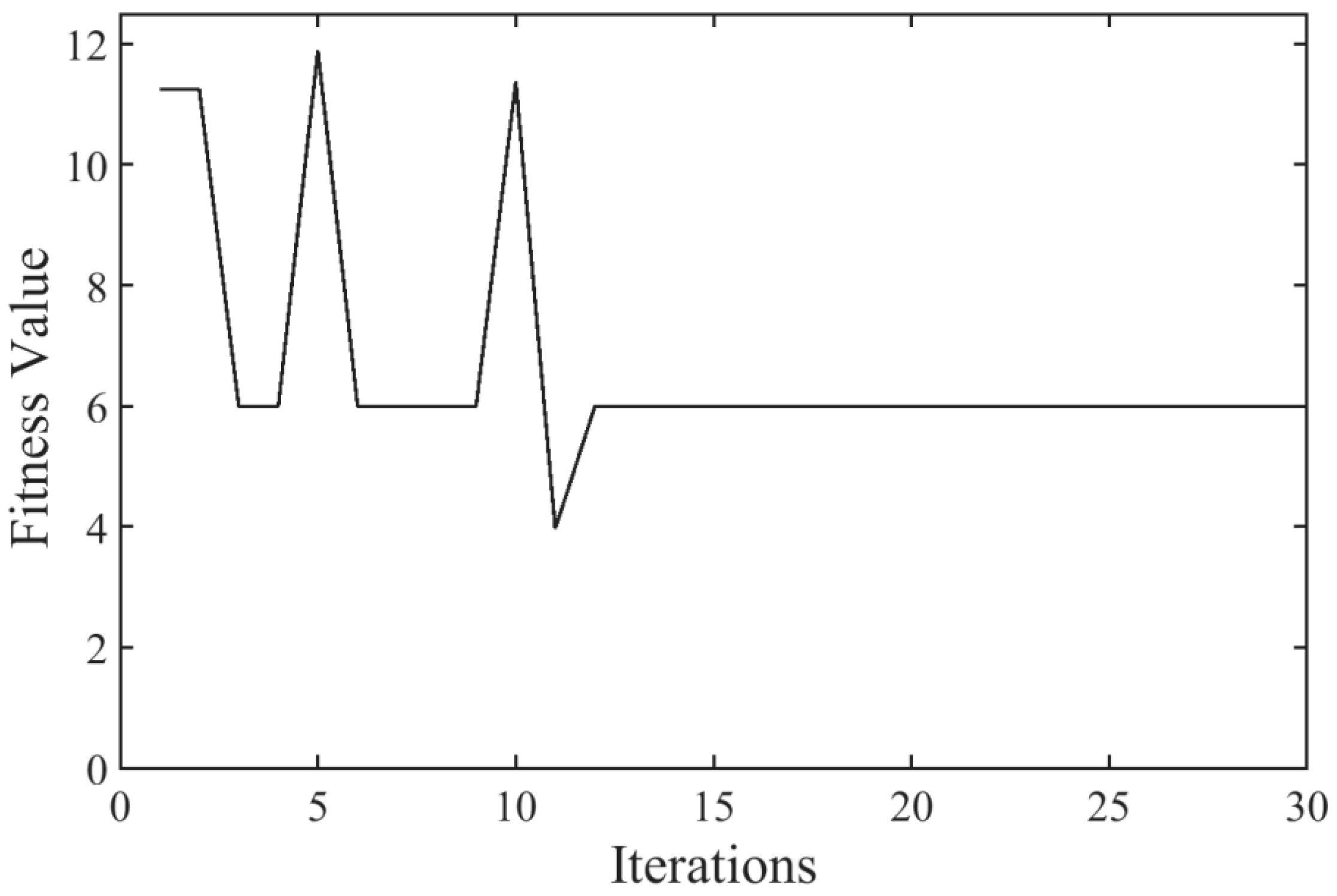
3.4.4. Simulation Study of CPSO Algorithm Optimization
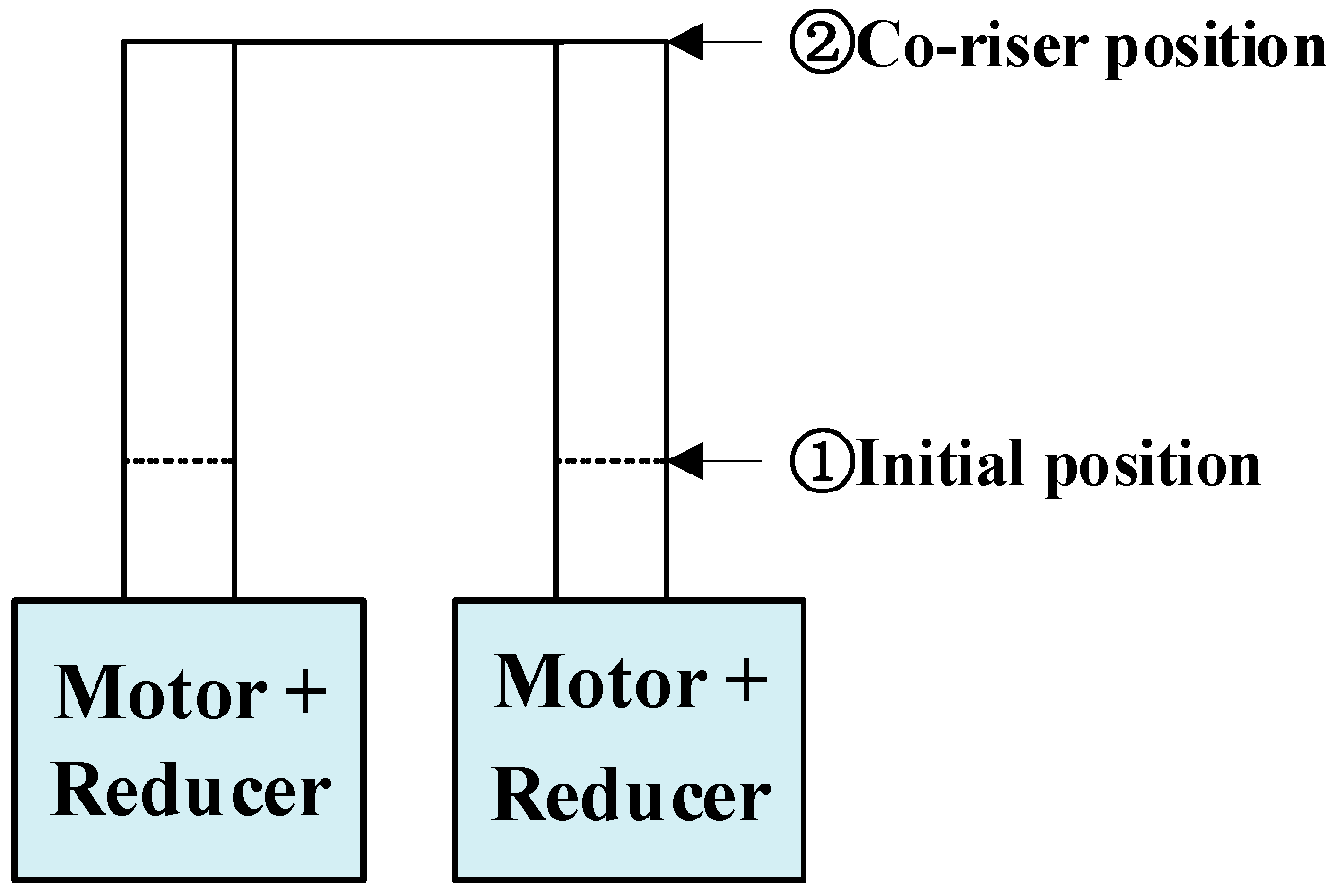
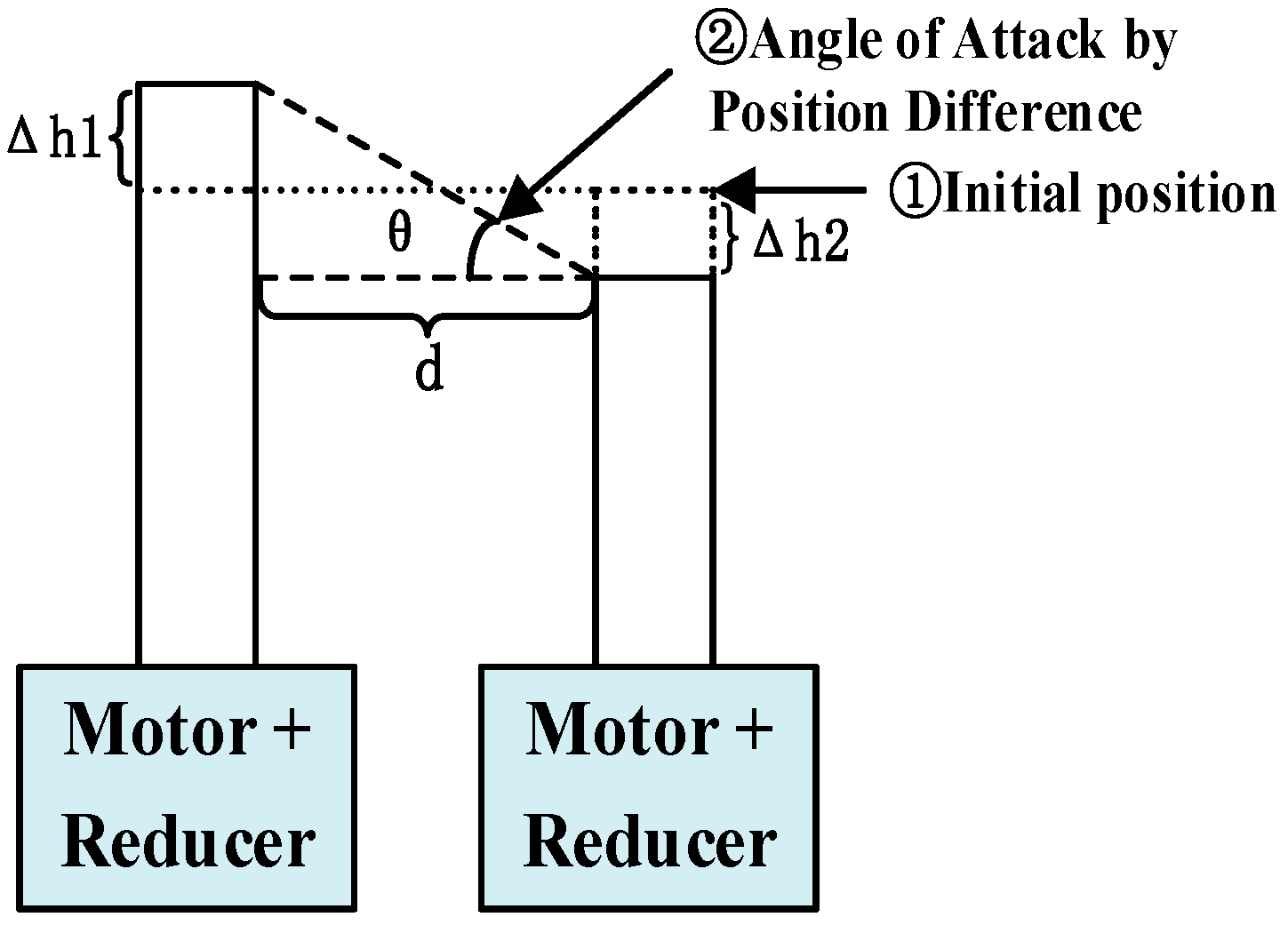
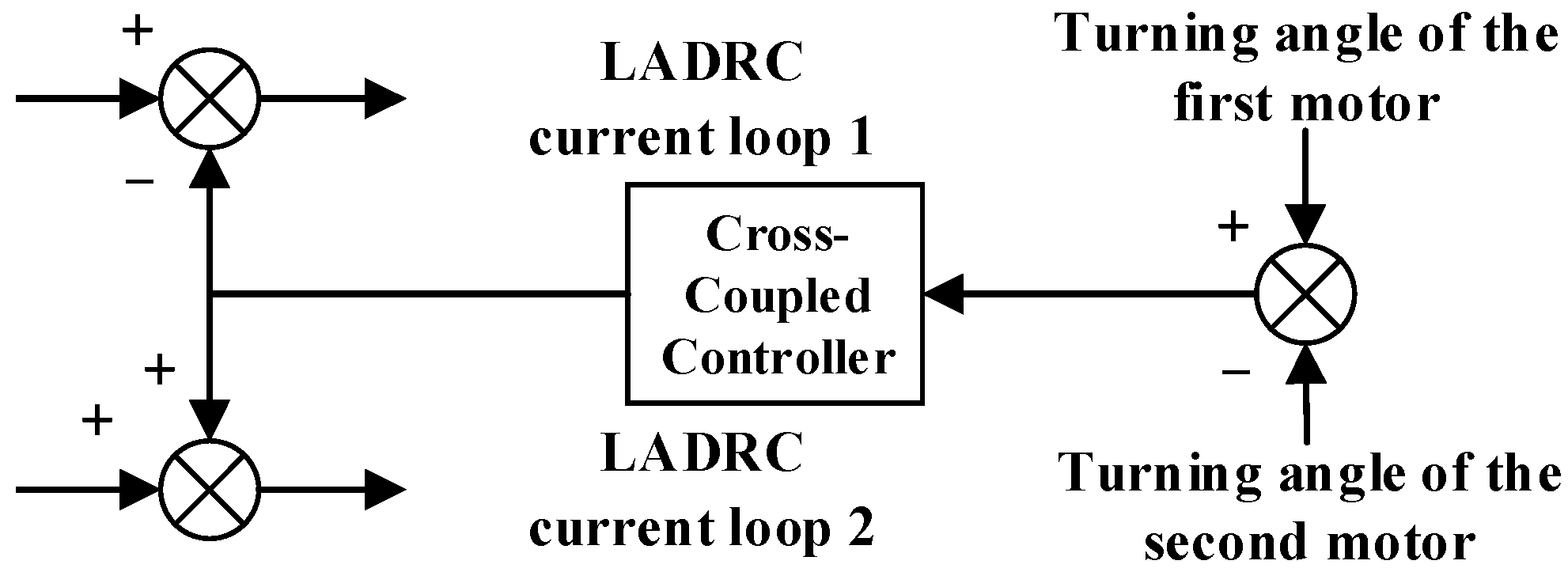
3.5. Cross-Coupling Control of Dual Motors
4. Simulation Studies and Experimental Verification
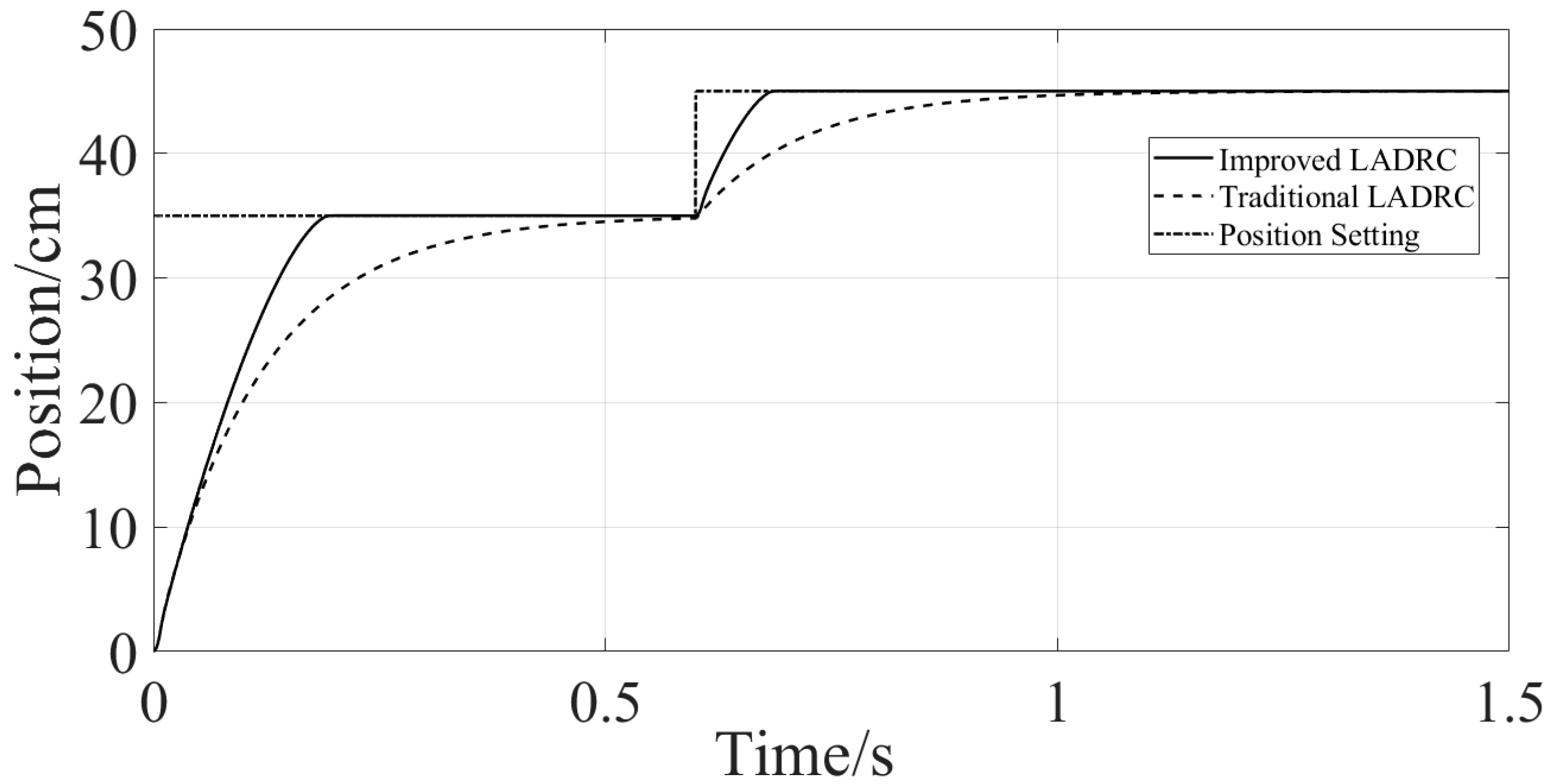
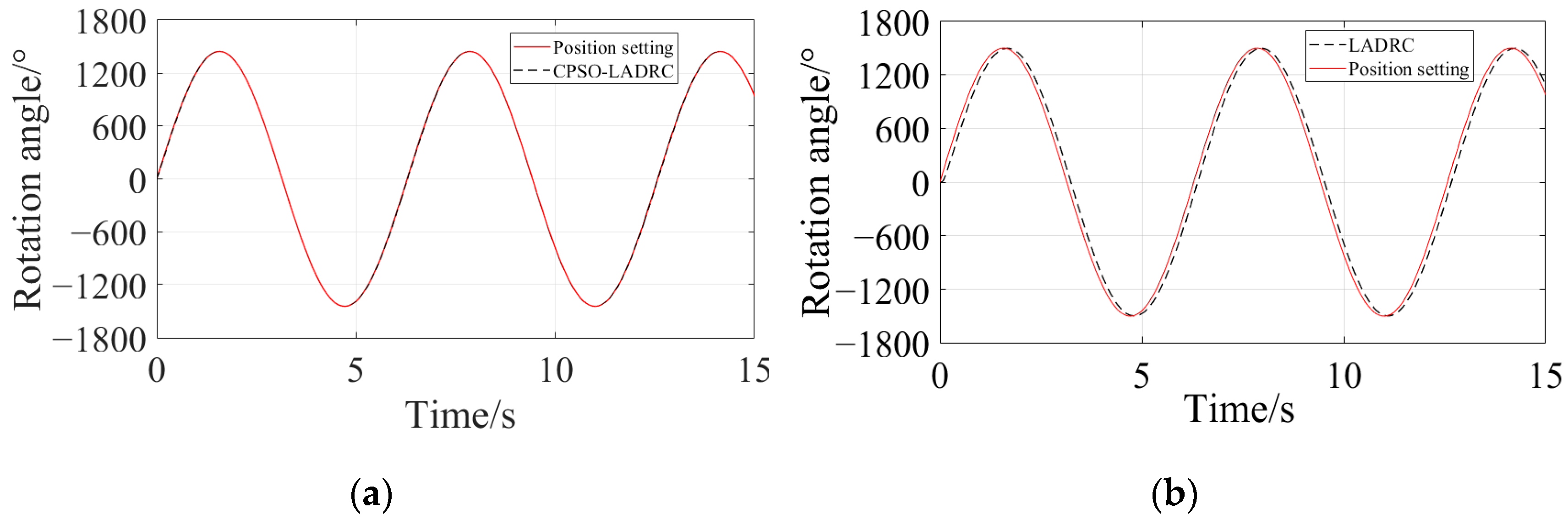
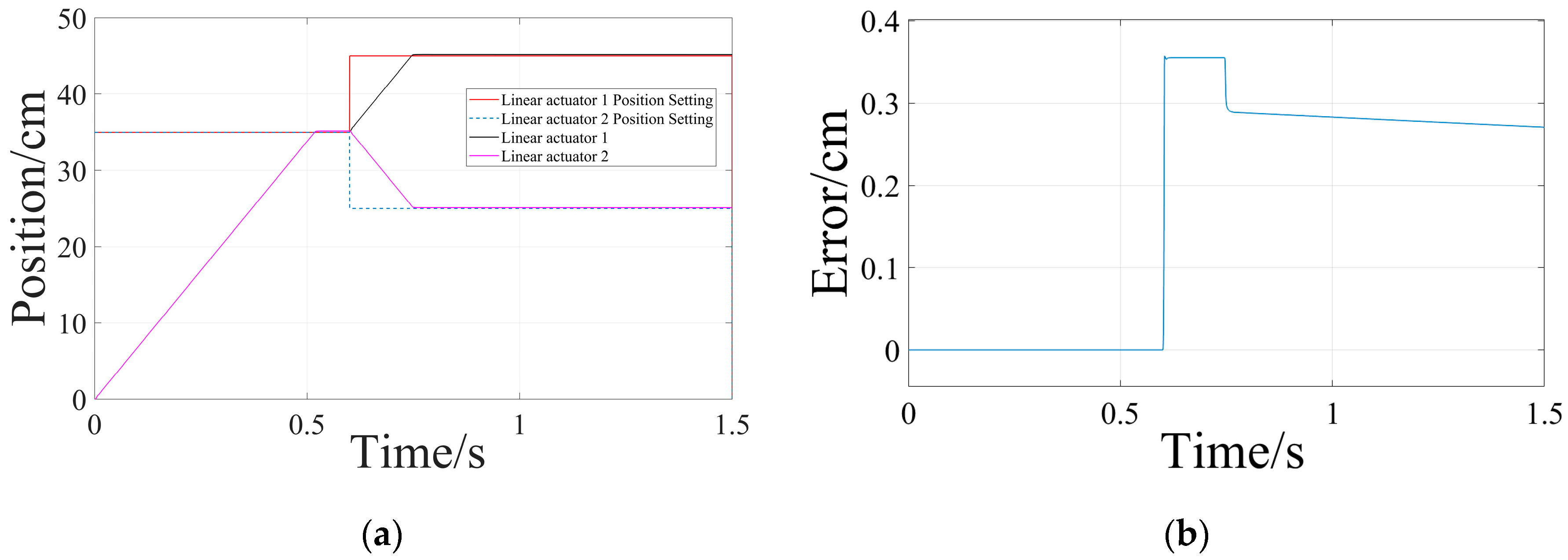
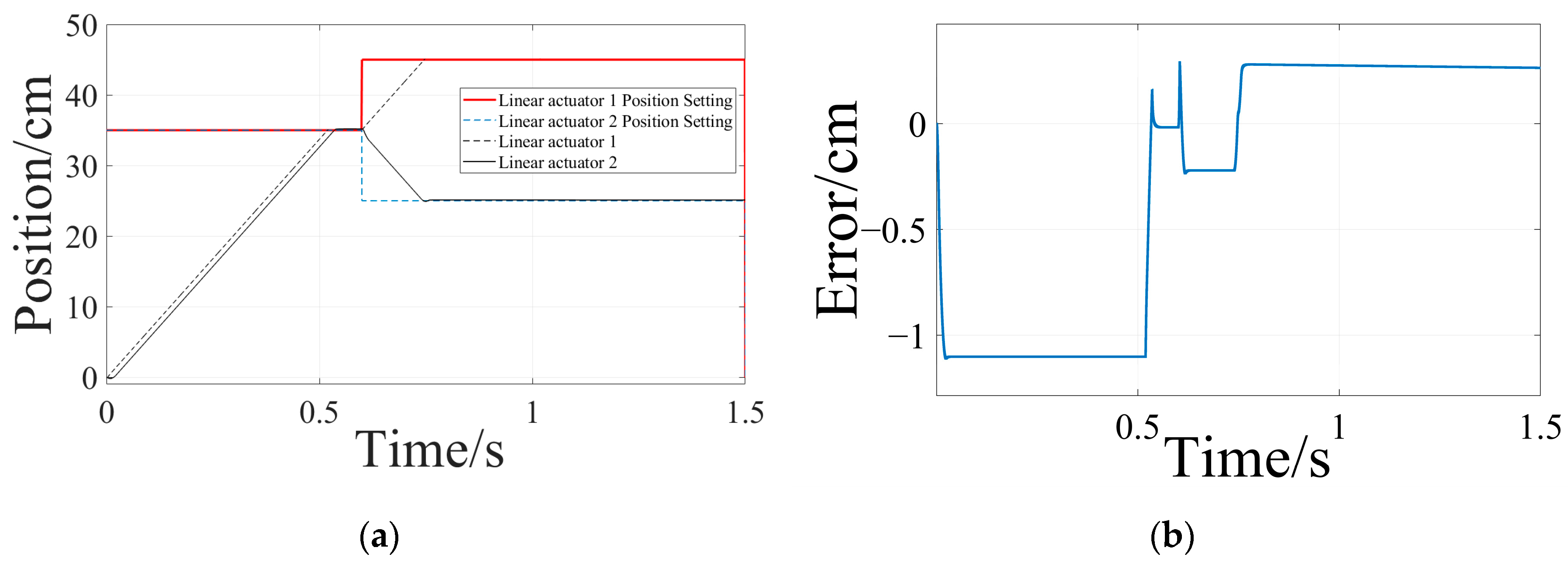
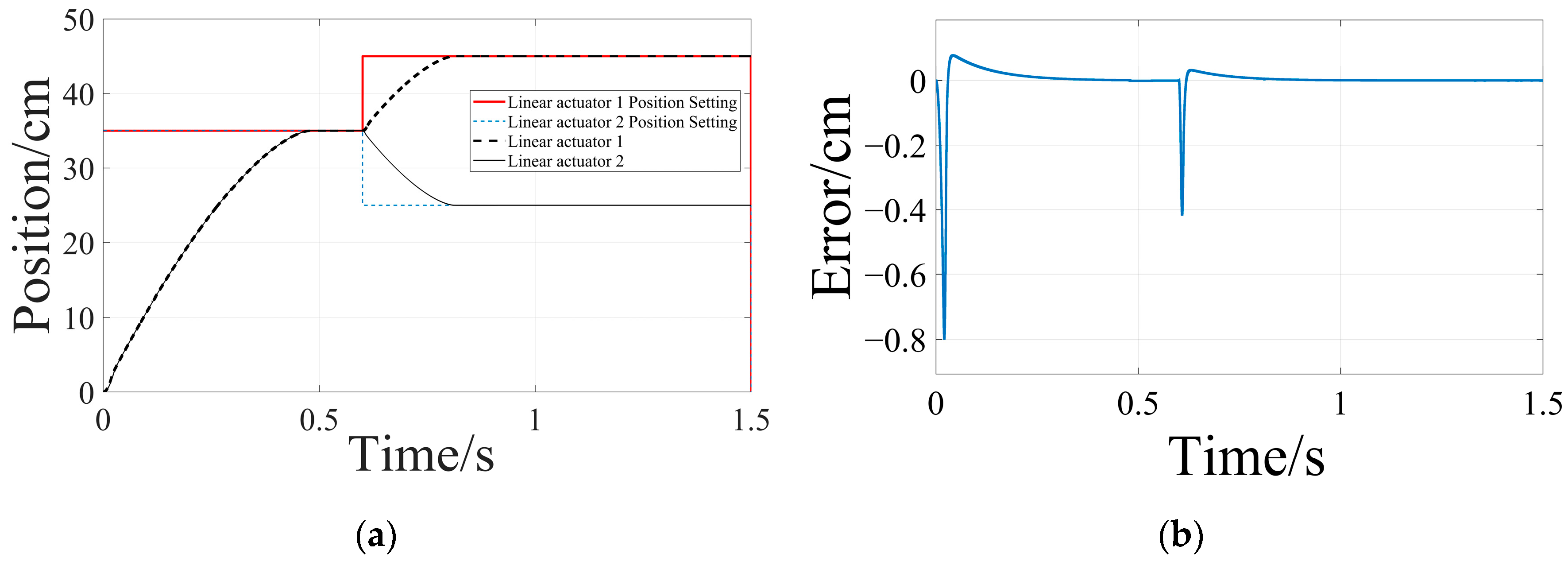
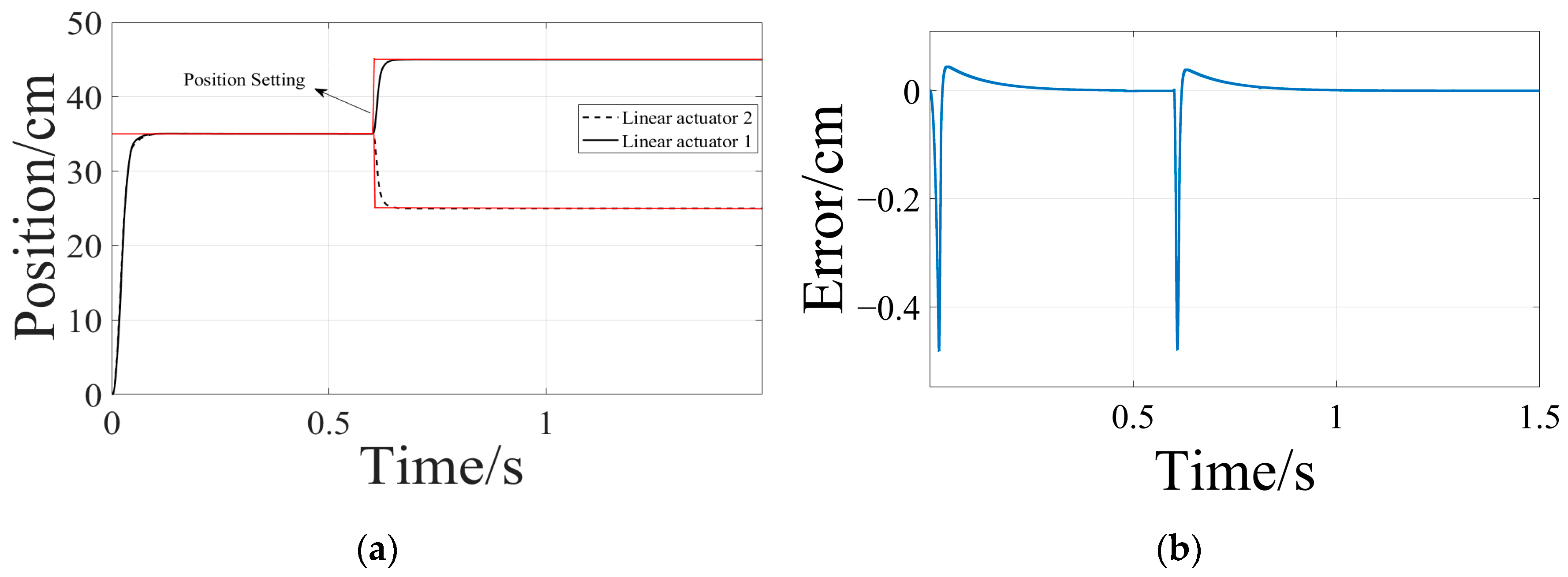
4.1. Simulation Studies
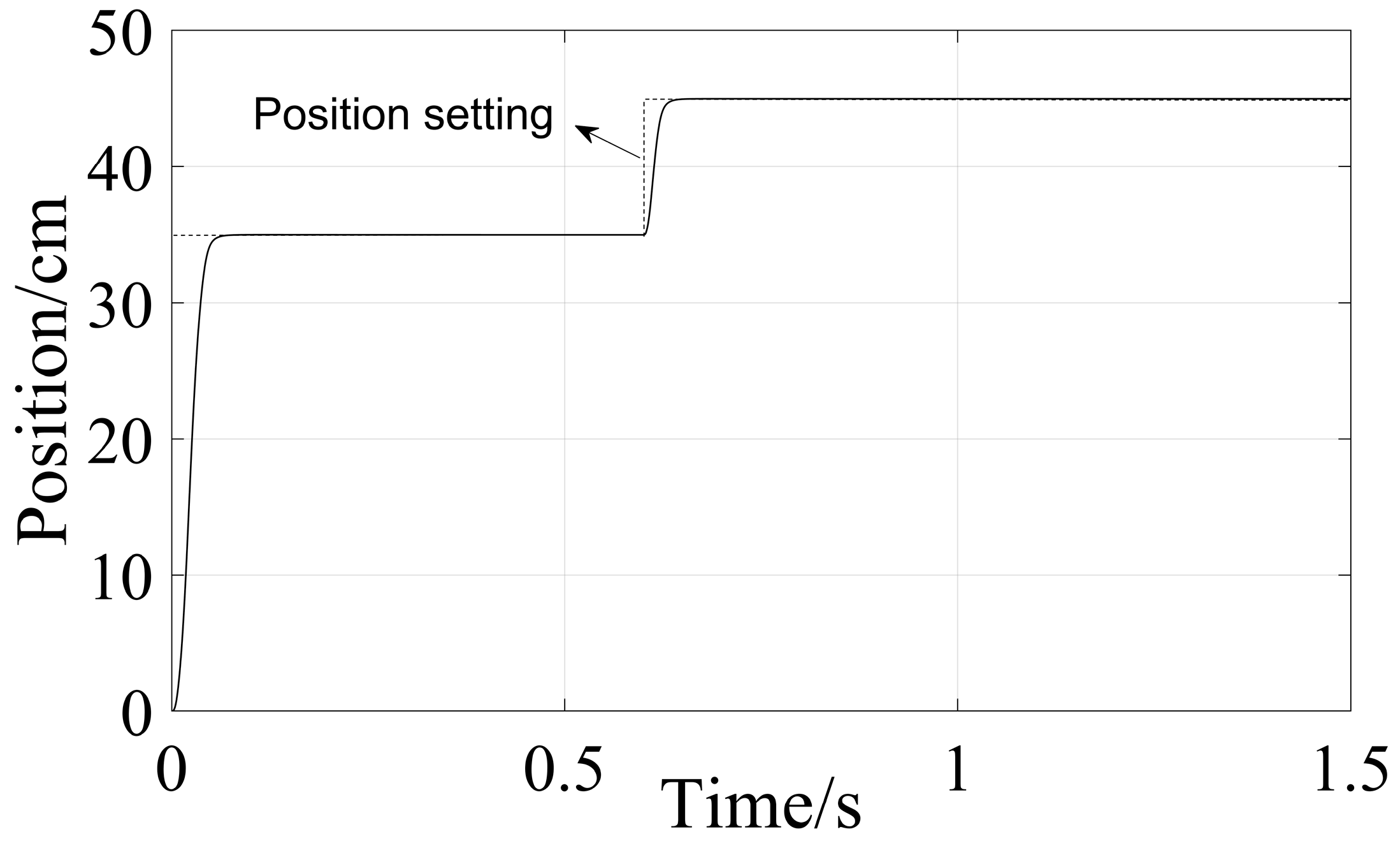
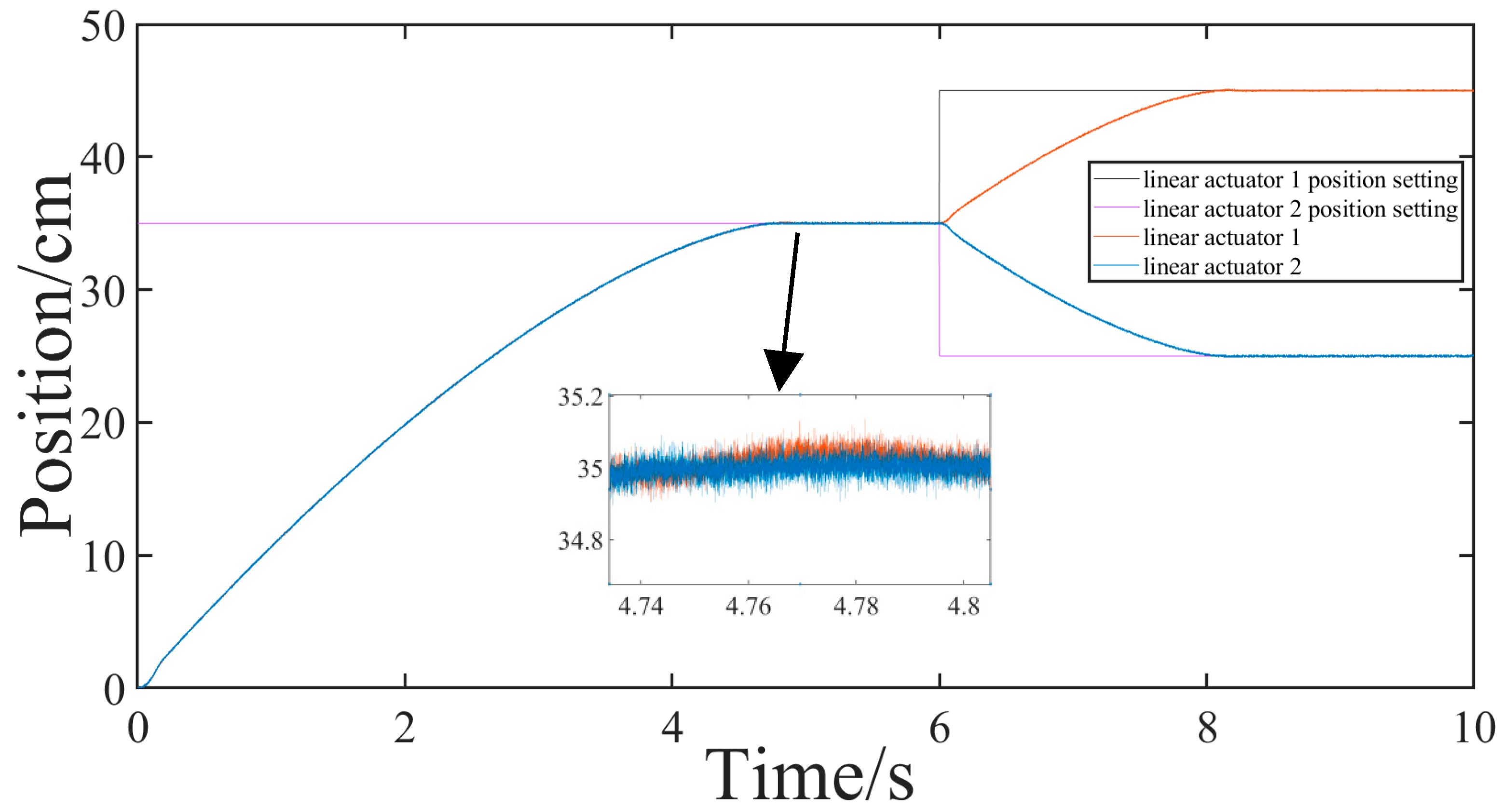
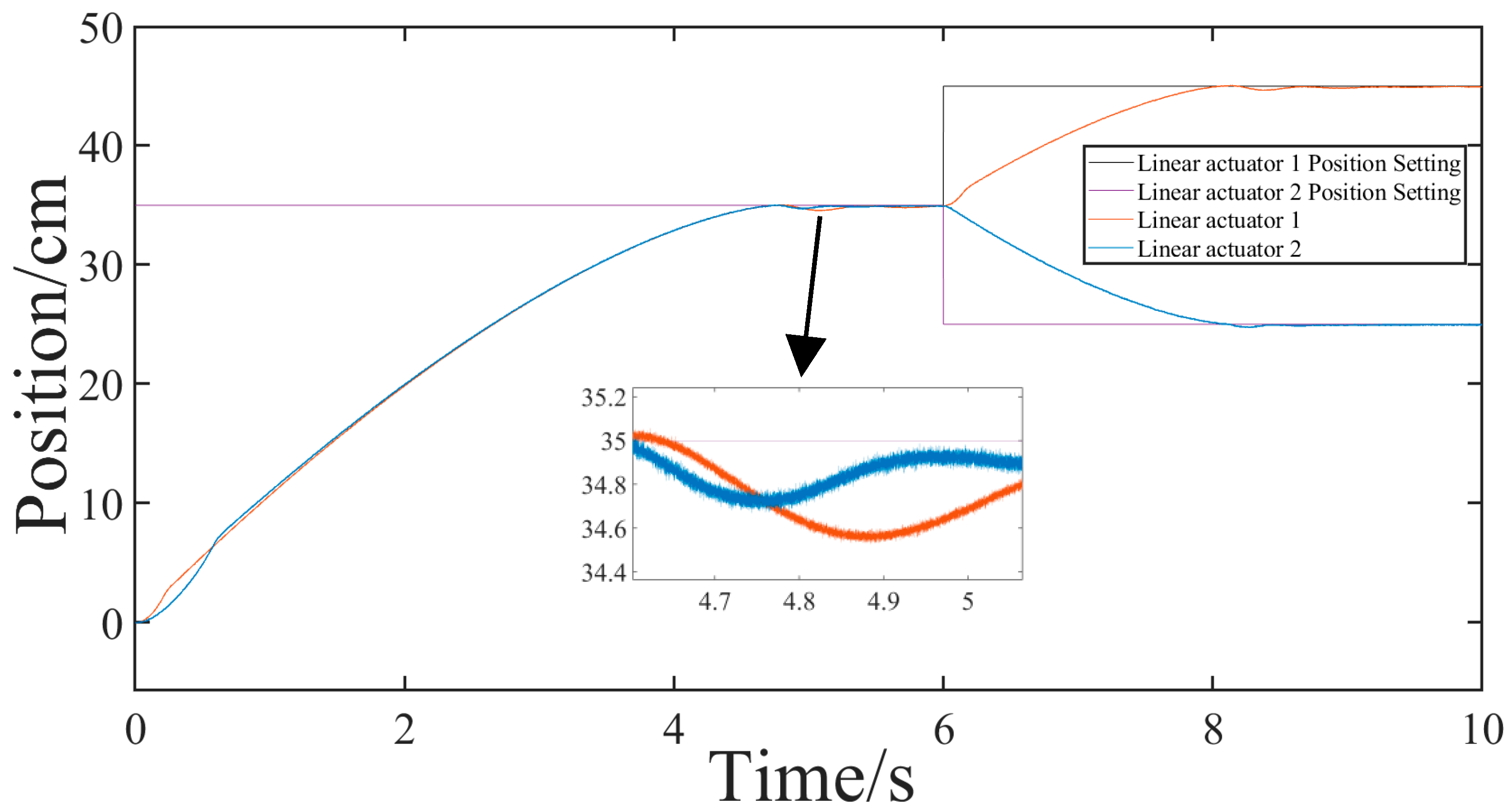
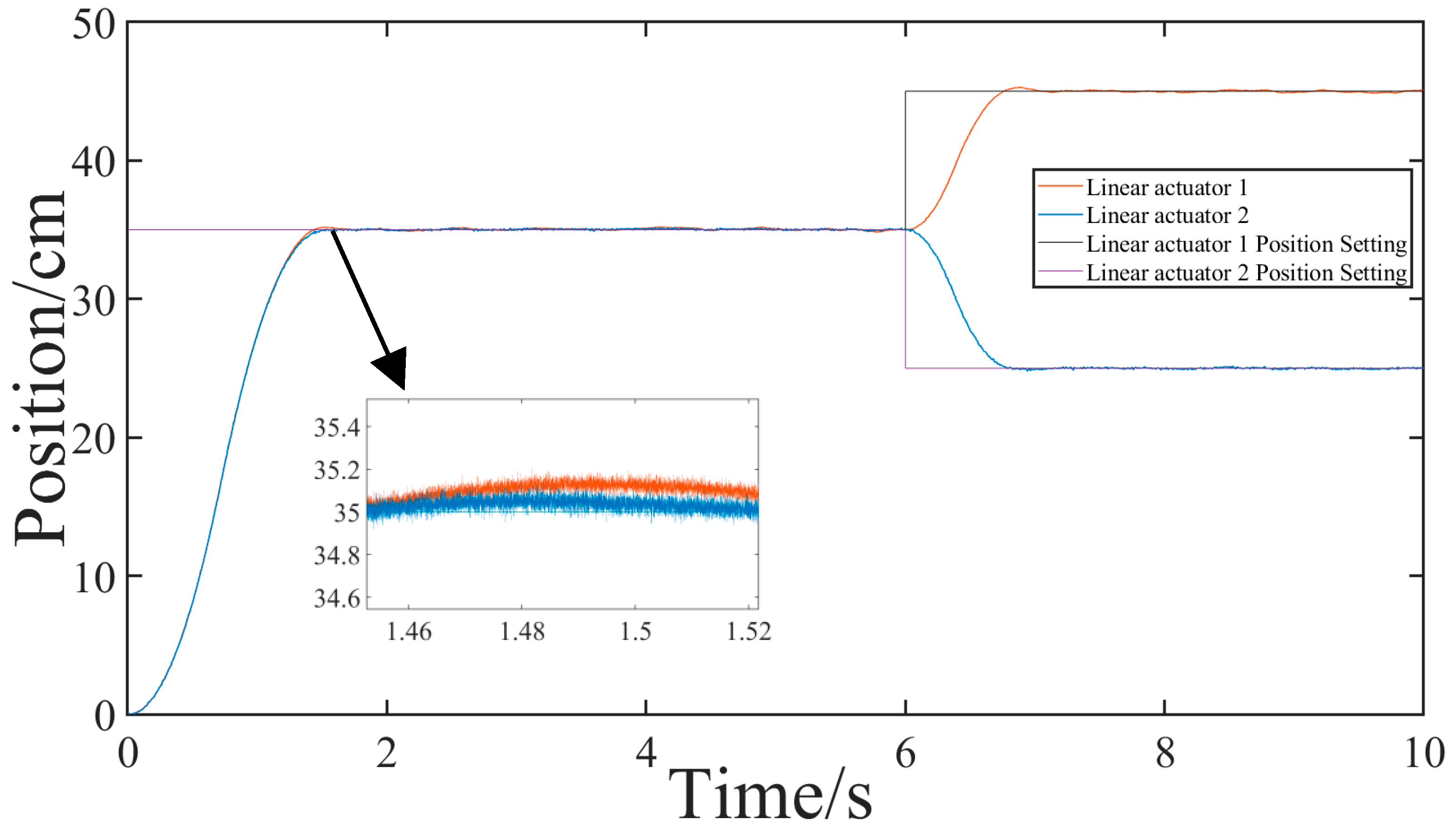
4.2. Experimental Verification
5. Discussion
- (1)
- A more refined adaptive parameter tuning method. Although CPSO exhibits a significant optimization effect, the exploration of more intelligent parameter tuning methods represents an important area for improvement. For example, integrating neural networks for parameter tuning could potentially enhance performance.
- (2)
- Enhanced synchronous loop control. While the ADRC has yielded excellent results, our experiments indicate that even under ADRC control, the motor does not completely utilize its dynamic performance potential. Exploring methods to further enhance the motor’s capabilities emerges as a valuable research direction.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, C.; Hu, H.; Yang, R. Series synchronization control of multi-servo motors. Electr. Autom. 2001, 23, 21–22. [Google Scholar]
- Lorenz, R.D.; Schmidt, P.B. Synchronized motion control for process automation. In Proceedings of the Conference Record of the IEEE Industry Applications Society Annual Meeting, San Diego, CA, USA, 1–5 October 1989; pp. 1693–1698. [Google Scholar]
- Payette, K. The virtual shaft control algorithm for synchronized motion control. In Proceedings of the 1998 American Control Conference. ACC (IEEE Cat. No.98CH36207), Philadelphia, PA, USA, 26 June 1998; Volume 5, pp. 3008–3012. [Google Scholar]
- Han, J. From PID technology to “self-disturbance control” technology. Control Eng. 2002, 9, 13–18. [Google Scholar]
- Thor, M.; Kulvicius, T.; Manoonpong, P. Generic Neural Locomotion Control Framework for Legged Robots. IEEE Trans. Neural. Netw. Learn. Syst. 2021, 32, 4013–4025. [Google Scholar] [CrossRef] [PubMed]
- Makarem, S.; Delibas, B.; Koc, B. Data-Driven Tuning of PID Controlled Piezoelectric Ultrasonic Motor. Actuators 2021, 10, 148. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Farsizadeh, H.; Khooban, M.H. A Novel Nonlinear Deep Reinforcement Learning Controller for DC–DC Power Buck Converters. IEEE Trans. Ind. Electron. 2021, 68, 6849–6858. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, S.; Hu, J.; Huang, D. A Novel Active Disturbance Rejection Control of PMSM Based on Deep Reinforcement Learning for More Electric Aircraft. IEEE Trans. Energy Convers. 2023, 38, 1461–1470. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, S.; Liu, Y. Research on multi-motor synchronous control system based on second-order LADRC. Mach. Tool Hydraul. Pressure 2021, 49, 104–106+172. [Google Scholar]
- Tian, M.; Wang, B.; Yu, Y.; Dong, Q.; Xu, D. Adaptive Active Disturbance Rejection Control for Uncertain Current Ripples Suppression of PMSM Drives. IEEE Trans. Ind. Electron. 2024, 71, 2320–2331. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Suleimenov, K.; Nguyen, B.H.; Vo-Duy, T.; Ta, M.C.; Do, T.D. Dynamical Delay Unification of Disturbance Observation Techniques for PMSM Drives Control. IEEE/ASME Trans. Mechatron. 2022, 27, 5560–5571. [Google Scholar] [CrossRef]
- Wang, C.; Yan, J.; Heng, P.; Shan, L.; Zhou, X. Enhanced LADRC for Permanent Magnet Synchronous Motor with Compensation Function Observer. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3424–3434. [Google Scholar] [CrossRef]
- Liu, X.; Chen, R.; Bai, S. Automatic disturbance rejection control of permanent magnet synchronous motor based on particle swarm optimization. J. North China Univ. Technol 2021, 43, 97–103. [Google Scholar]
- Fang, Q.; Zhou, Y.; Ma, S.; Zhang, C.; Wang, Y.; Huangfu, H. Electromechanical Actuator Servo Control Technology Based on Active Disturbance Rejection Control. Electronics 2023, 12, 1934. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Zhong, Y.; Gao, J. Based on self-corrected self immunity control A multi-motor cooperative system. Modul. Mach. Tool Autom. Manuf. Tech. 2021, 63, 77–81. [Google Scholar]
- Zhang, Y.; Guan, Z.; Wang, T.; Du, P.; Meng, Y. Multi-motor synchronous control based on self disturbance resistance control technology. Electr. Autom. 2017, 39, 9–11+68. [Google Scholar]
- He, Z.; Yu, H. Ring-coupled multiple-motor coordinated sliding mode control based on self-immunity and observer. Micromotor 2021, 54, 48–55. [Google Scholar]
- Abdalla, M.A.; Yang, G.; Huang, C. Performance comparison active disturbance rejection control tuned by particle swarm optimization technique and gravitational search algorithm based load frequency control. In Proceedings of the 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online, 2–3 July 2020; pp. 2128–2134. [Google Scholar]
- Yin, Z.; Du, C.; Liu, J.; Sun, X.; Zhong, Y. Research on Autodisturbance-Rejection Control of Induction Motors Based on an Ant Colony Optimization Algorithm. IEEE Trans. Ind. Electron. 2018, 65, 3077–3094. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, S.; Hu, J.; Huang, D. Multiscenarios Parameter Optimization Method for Active Disturbance Rejection Control of PMSM Based on Deep Reinforcement Learning. IEEE Trans. Ind. Electron. 2023, 70, 10957–10968. [Google Scholar] [CrossRef]
- Pang, H. Research on a New Active Disturbance Rejection Control Algorithm. Control Eng. China 2020, 27, 728–732. [Google Scholar]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Zhiqiang, G.; Shaohua, H.; Fangjun, J. A novel motion control design approach based on active disturbance rejection. In Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No.01CH37228), Orlando, FL, USA, 4–7 December 2001; Volume 5, pp. 4877–4882. [Google Scholar]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Li, J.; Xia, Y.; Qi, X.; Gao, Z. On the Necessity, Scheme, and Basis of the Linear–Nonlinear Switching in Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2017, 64, 1425–1435. [Google Scholar] [CrossRef]
- Yang, J.; Ma, M.; Che, H.; Xu, D.; Guo, Q. Multi-objective adaptive chaotic particle swarm optimization algorithm. Control Decis. 2015, 30, 2168–2174. [Google Scholar]
- Yu, X.; Zhu, L. Dynamic parameter setting and application of active disturbance rejection controller. J. North China Electr. Power Univ. 2005, 32, 9–13. [Google Scholar]










| Traditional LADRC | Improved LADRC | |
|---|---|---|
| First response time in place /s | 0.58 | 0.21 |
| Second response time in place /s | 1.24 | 0.74 |
| First overshoot in place /% | 0.01 | 0.03 |
| Second overshoot in place /% | 0.02 | 0.04 |
| First steady-state error in place /cm | 0.02 | 0.01 |
| Second steady-state error in place /cm | 0.01 | 0.01 |
| Parameter Name | Value |
|---|---|
| DC side voltage /V | 24 |
| Rated torque /N·m | 0.2 |
| Rated Power /KW | 0.064 |
| Back electromotive force | 4.3 |
| Rated speed /rpm | 3000 |
| Stator resistor /Ω | 0.12 |
| d-axis inductance /mH | 0.59 |
| q-axis inductance /mH | 0.59 |
| Permanent magnet chain /Wb | 0.0175 |
| Moment of inertia J/(kg·m2) | 0.00019 |
| Polar logarithm P | 4 |
| Algorithm | ||||||||
|---|---|---|---|---|---|---|---|---|
| LADRC | 227.79 | 17,296.09 | 437,764.16 | 499.97 | 51.32 | 996.24 | 248,123.53 | 1794.21 |
| CPSO-LADRC | 321.63 | 14,258.64 | 512,253.36 | 587.58 | 54.34 | 1254.36 | 386,543.48 | 2165.22 |
| LADRC | CPSO-LADRC | |
|---|---|---|
| Sine wave | 50.3° | 1.8° |
| Triangular wave | 98.2° | 2.3° |
| PI | LADRC | CPSO-LADRC | ||
|---|---|---|---|---|
| No-load | Maximum synchronization error | 0.357 cm | 0.002 cm | 0.008 cm |
| Maximum first response time in place | 0.522 s | 0.480 s | 0.081 s | |
| Maximum second response time in place | 0.751 s | 0.814 s | 0.701 s | |
| Maximum first overshoot in place | 0.481% | 0.005% | 0.004% | |
| Maximum second overshoot in place | 0.403% | 0.006% | 0.003% | |
| Asymmetric load | Maximum synchronization error | 1.153 cm | 0.793 cm | 0.482 cm |
| Maximum first response time in place | 0.535 s | 0.471 s | 0.073 s | |
| Maximum second response time in place | 0.746 s | 0.803 s | 0.698 s | |
| Maximum first overshoot in place | 0.486% | 0.007% | 0.006% | |
| Maximum second overshoot in place | 0.356% | 0.005% | 0.003% |
| PI | LADRC | CPSO-LADRC | ||
|---|---|---|---|---|
| No-load | Maximum synchronization error | 0.36 cm | 0.14 cm | 0.13 cm |
| Maximum first response time in place | 5.21 s | 4.75 s | 1.45 s | |
| Maximum second response time in place | 7.42 s | 8.09 s | 6.86 s | |
| Maximum first overshoot in place | 0.66% | 0.22% | 0.29% | |
| Maximum second overshoot in place | 0.51% | 0.31% | 0.21% | |
| Asymmetric load | Maximum synchronization error | 0.72 cm | 1.27 cm | 0.27 cm |
| Maximum first response time in place | 5.32 s | 4.61 s | 1.44 s | |
| Maximum second response time in place | 7.44 s | 8.01 s | 6.75 s | |
| Maximum first overshoot in place | 1.66% | 1.34% | 0.54% | |
| Maximum second overshoot in place | 1.29% | 0.82% | 0.64% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S.; Liu, X.; Wang, C. Synchronous Control of High-Speed Train Lift Wing Angle of Attack Drive System Based on Chaotic Particle Swarm Optimization and Linear Auto-Disturbance Resistant Controller. Electronics 2024, 13, 1448. https://doi.org/10.3390/electronics13081448
Cheng S, Liu X, Wang C. Synchronous Control of High-Speed Train Lift Wing Angle of Attack Drive System Based on Chaotic Particle Swarm Optimization and Linear Auto-Disturbance Resistant Controller. Electronics. 2024; 13(8):1448. https://doi.org/10.3390/electronics13081448
Chicago/Turabian StyleCheng, Shu, Xuan Liu, and Chengqiang Wang. 2024. "Synchronous Control of High-Speed Train Lift Wing Angle of Attack Drive System Based on Chaotic Particle Swarm Optimization and Linear Auto-Disturbance Resistant Controller" Electronics 13, no. 8: 1448. https://doi.org/10.3390/electronics13081448
APA StyleCheng, S., Liu, X., & Wang, C. (2024). Synchronous Control of High-Speed Train Lift Wing Angle of Attack Drive System Based on Chaotic Particle Swarm Optimization and Linear Auto-Disturbance Resistant Controller. Electronics, 13(8), 1448. https://doi.org/10.3390/electronics13081448





