A Data Augmentation Method for Side-Channel Attacks on Cryptographic Integrated Circuits
Abstract
1. Introduction
- We introduced a cycle-consistent GAN model suitable for generating one-dimensional electromagnetic signals, enabling an effective augmentation of small-sample data.
- We proposed an evaluation criterion for the data augmentation effect on side-channel electromagnetic signals, utilizing the Kolmogorov–Smirnov test to characterize the original and generated data. This criterion serves as the evaluation standard for our network model and work.
- We established a side-channel attack model and validated it using existing data, evaluating the impact of the generated information on the overall experimental results.
2. Related Work
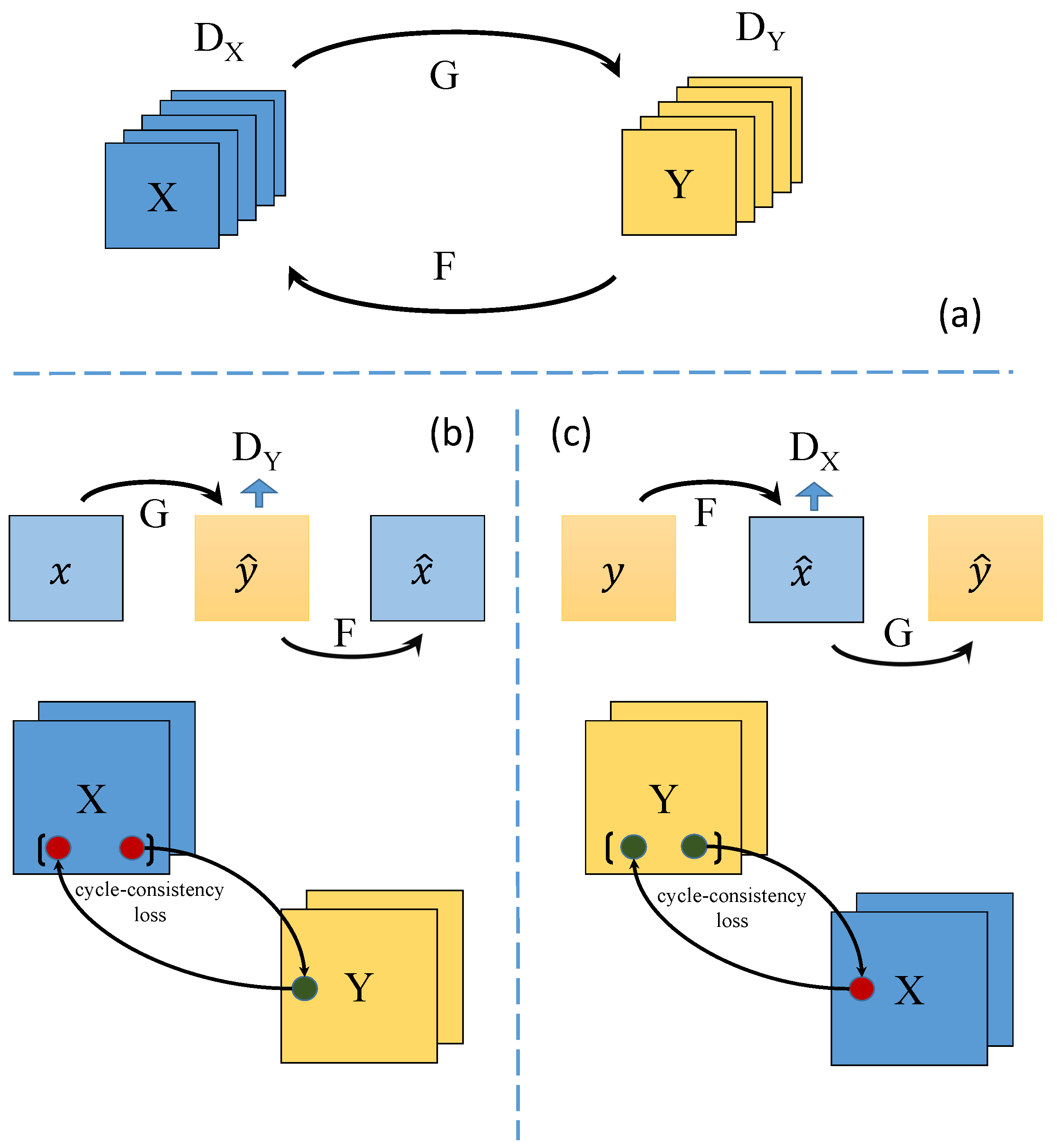
3. Overview of the Framework
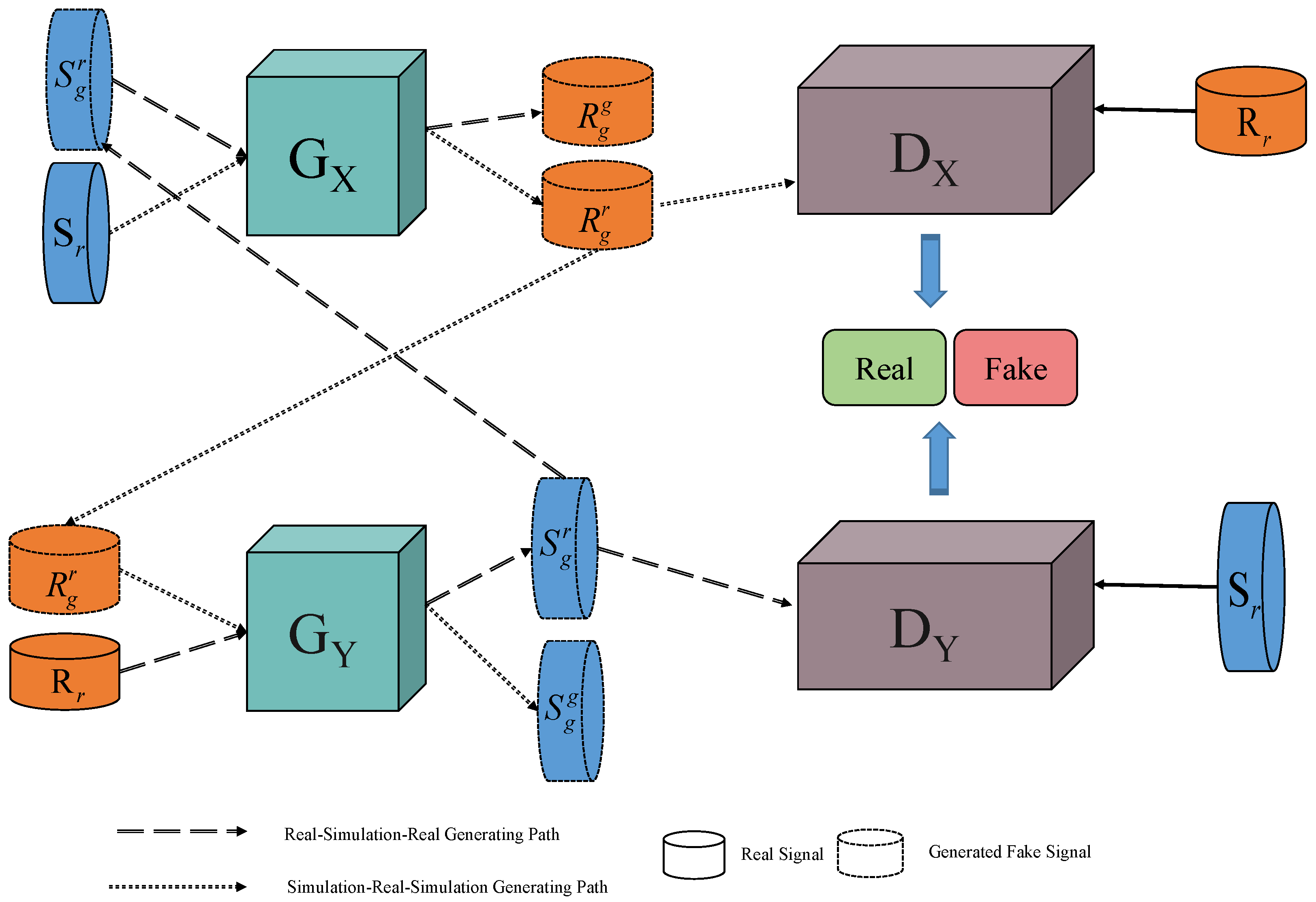
4. EME-CycleGAN
4.1. Basic Structure
4.2. EME-CycleGAN
5. Data Augmentation Consistency Analysis
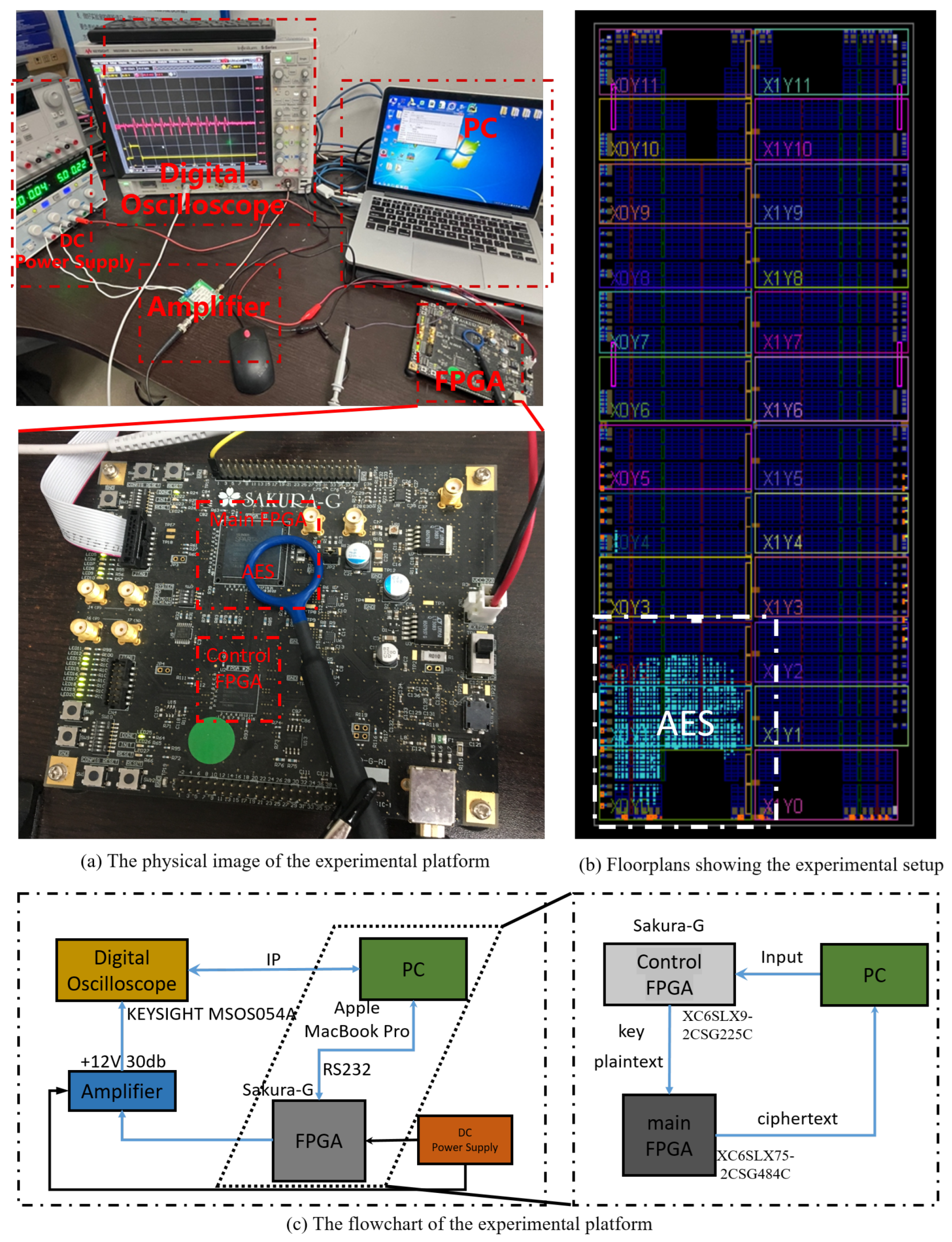
5.1. Real Data Acquisition
- First, the PC sent the plaintext and key required for the encryption algorithm to the FPGA.
- Next, the FPGA executed the AES-128 encryption algorithm, while the side-channel detection device collected the side-channel leakage signals from the proximity of the chip.
- Then, the side-channel detection device transmitted the collected leakage signals to the oscilloscope, which displayed and saved the signals.
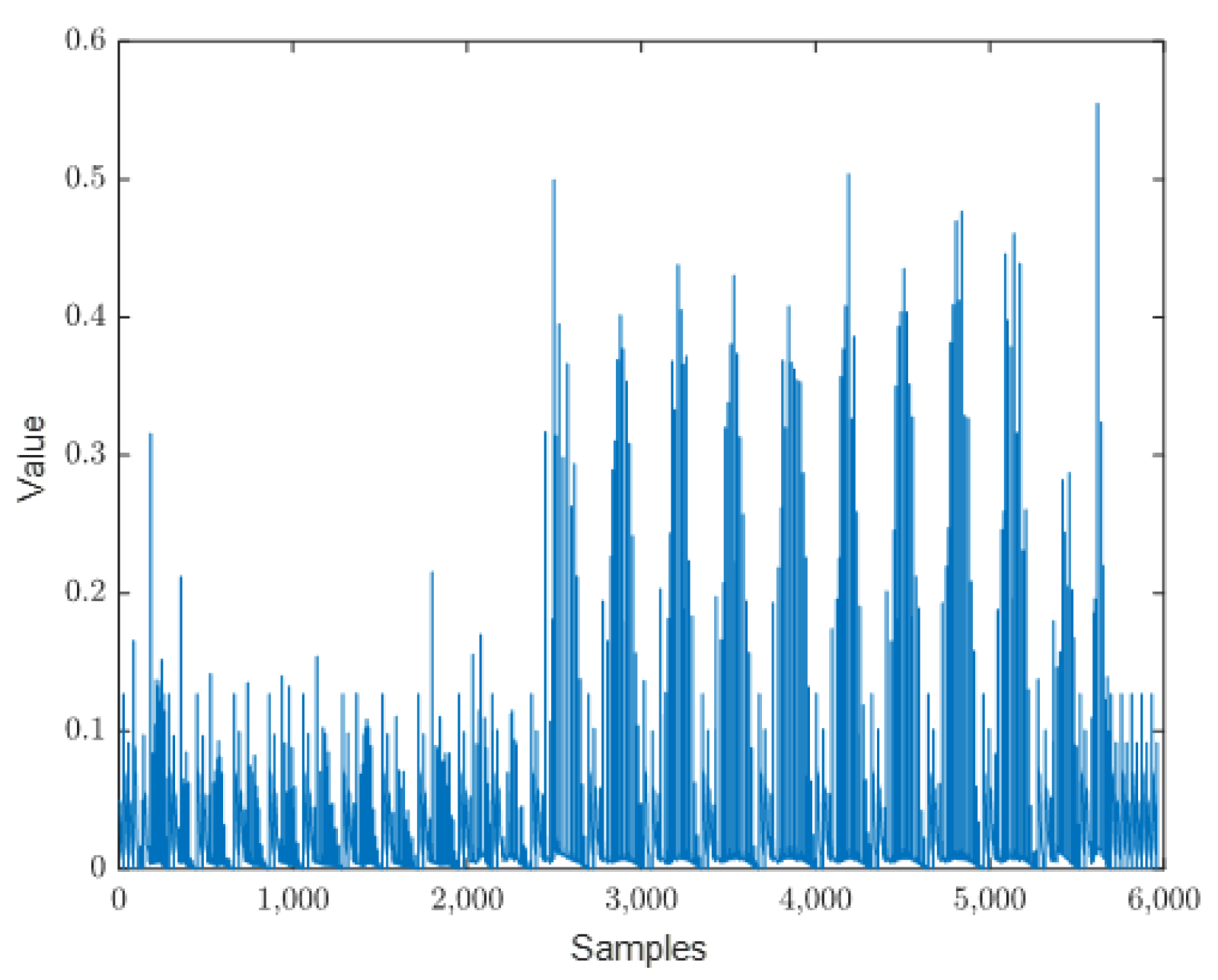
- Finally, the oscilloscope sent the signals back to the PC, and the PC once again sent the plaintext and key to the FPGA, repeating the process to collect a large amount of required side-channel leakage information. The resulting raw electromagnetic leakage waveform of the complete AES encryption process is shown in Figure 5.
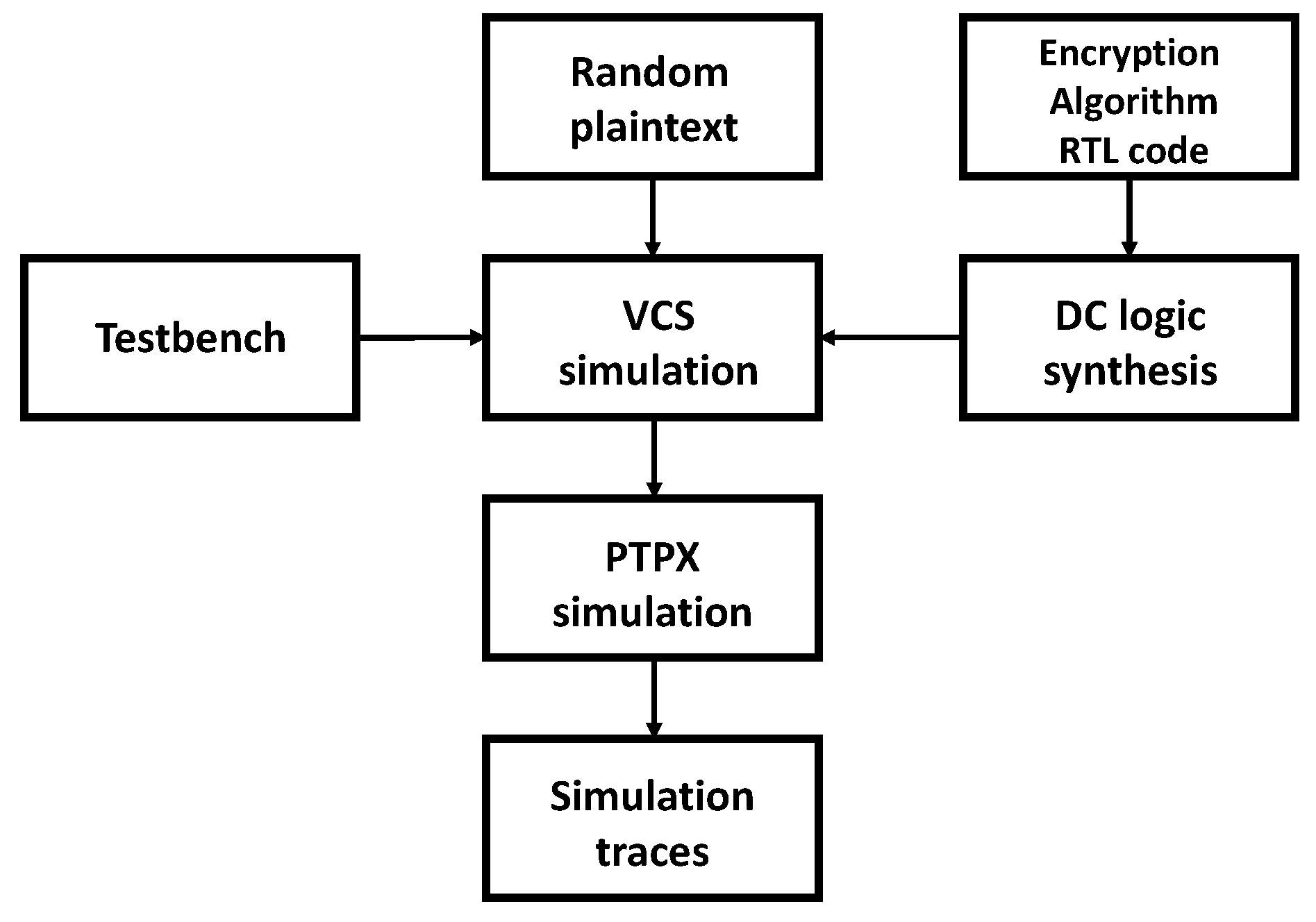
5.2. Simulation Data Acquisition
- First, we set the desired random plaintext for the encryption algorithm and ran the DC software, which read the Synopsys technology library files and RTL code of the encryption algorithm. The software performed logic synthesis to generate the gate-level netlist file;
- Next, using the VCS tool, we read the gate-level netlist file, Verilog technology library files, and functional test files. After simulation, the tool generated a value change dump (VCD) file;
- Then, the PTPX read the VCD file, technology library files, and gate-level netlist file to perform power calculations. The tool outputted a power accumulation file;
- Finally, using MATLAB Version 2020 software, we read the power accumulation file and parsed it into the desired simulation waveform data. The resulting power leakage waveform of the complete AES encryption process, obtained through the above steps, is shown in Figure 7.
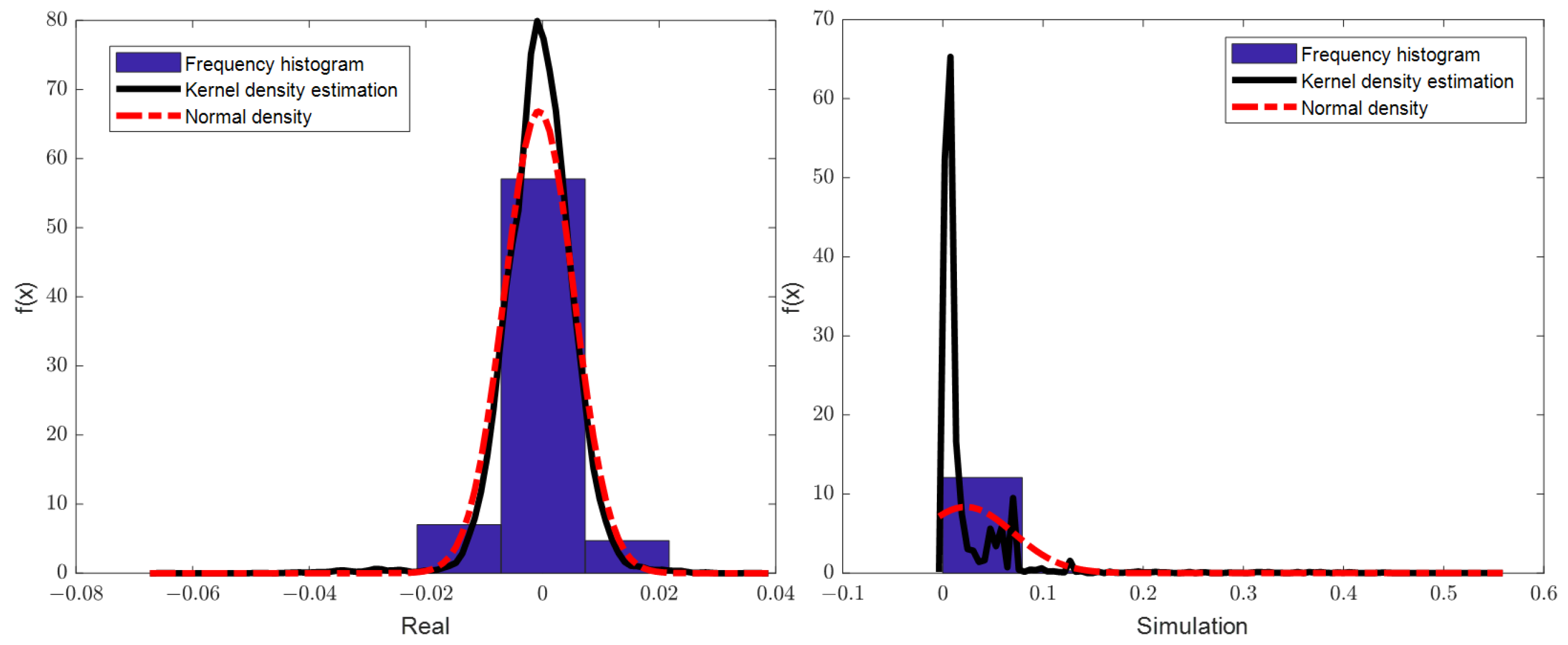
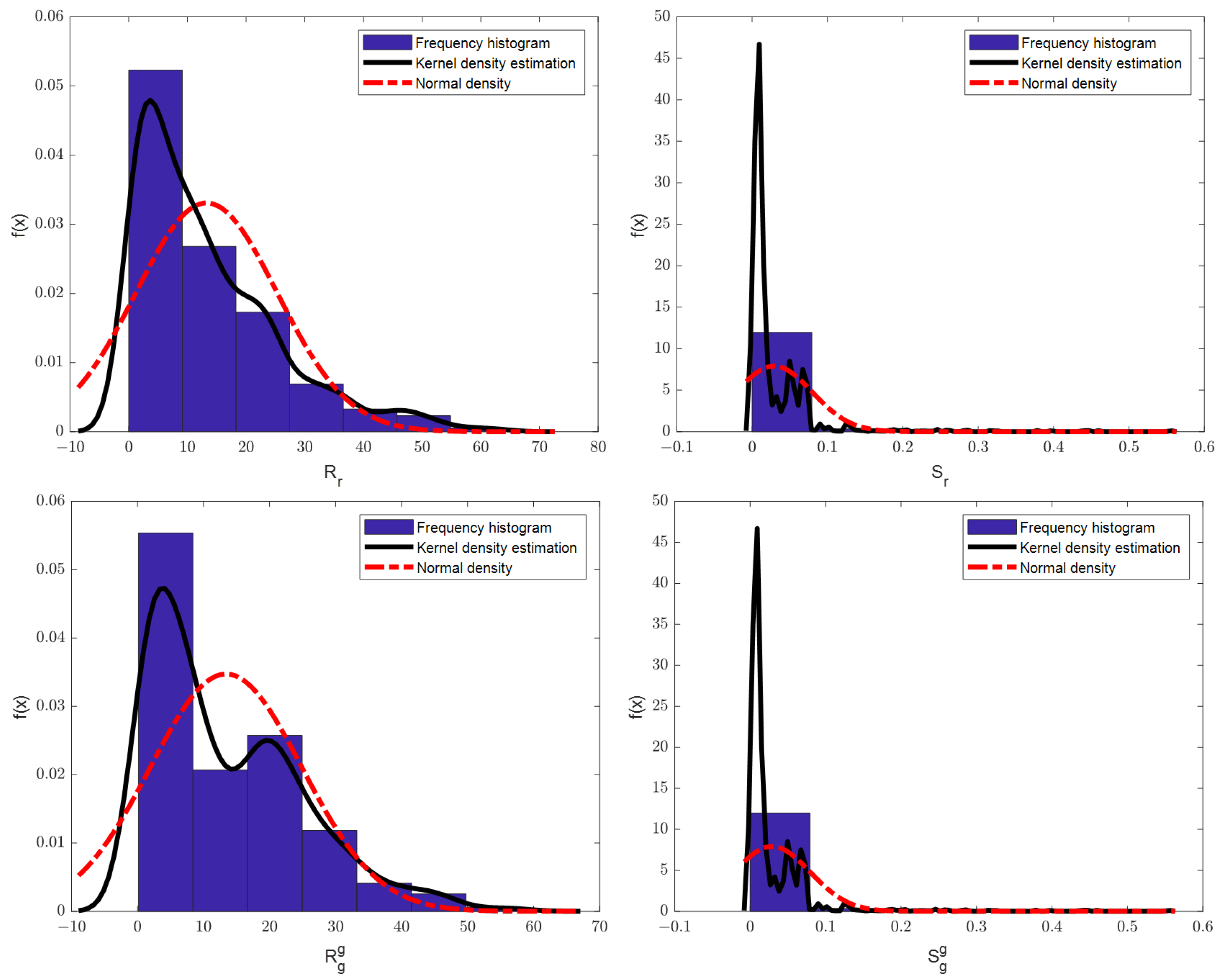
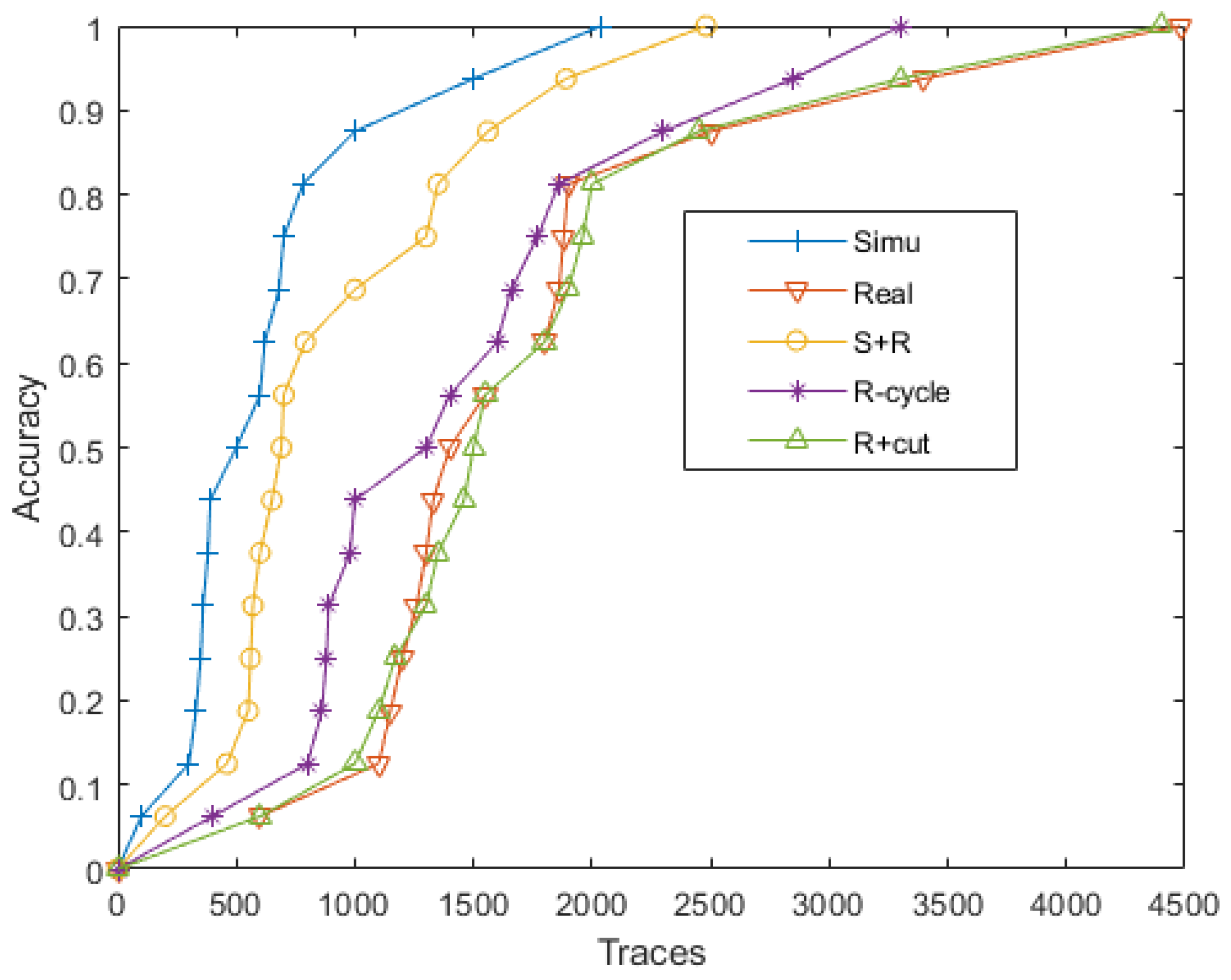
5.3. Kolmogorov–Smirnov Test Method
6. Correlation Power Analysis
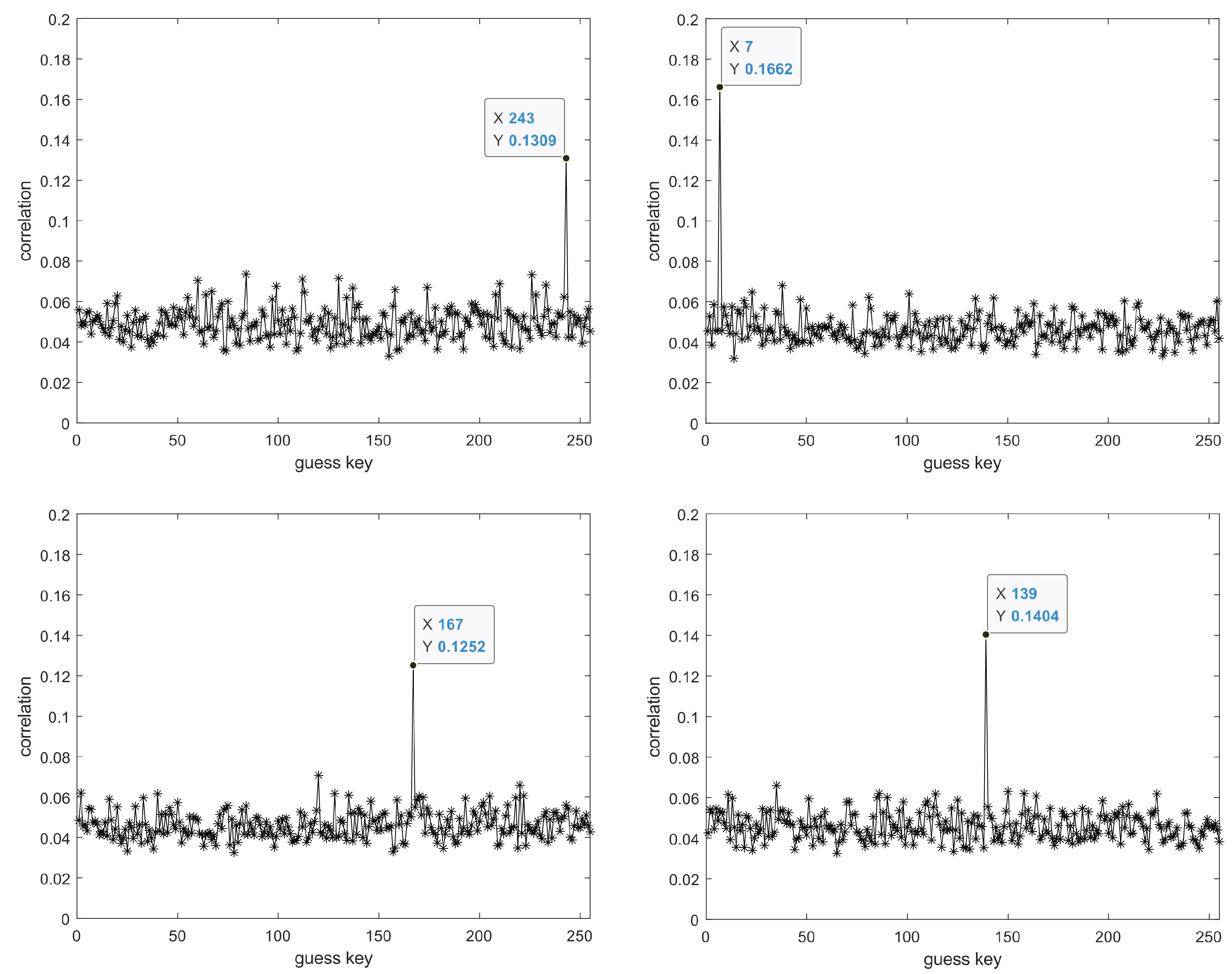
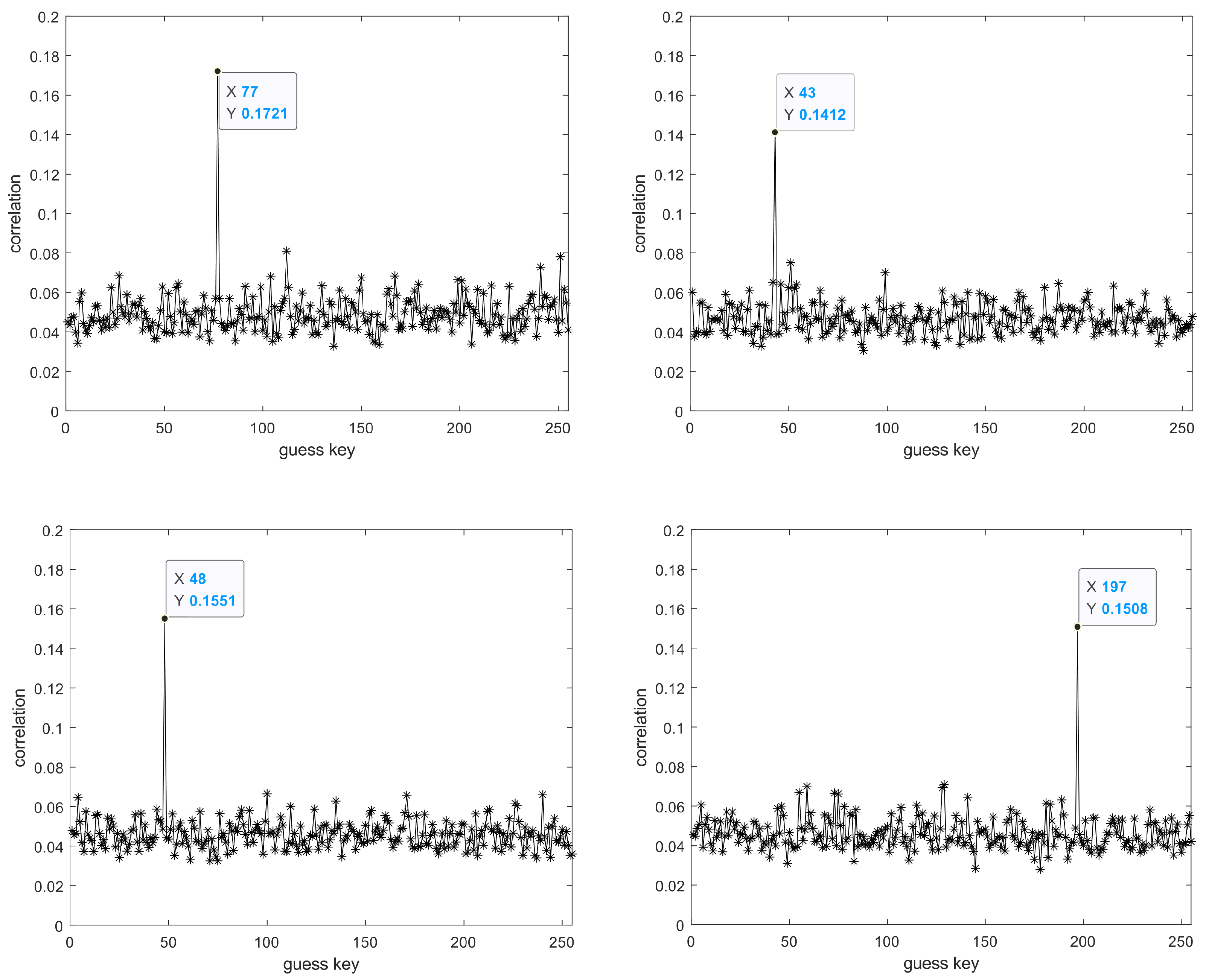
- Select an appropriate intermediate value that satisfies the function for the encryption algorithm of the target device, where d is the non-constant data known to the attacker, and is the target key that the attacker intends to attack, which is usually a small part of the cryptographic algorithm’s key. In this paper, the attack point is located at the last round of the encryption algorithm, hence the choice of d as the ciphertext.
- On the side-channel information collection platform, perform M times encryption operations on the encryption chip using random plaintext and a fixed key. Each data of encryption operation d is denoted as , where represents the encryption and the corresponding electromagnetic leakage signal t is denoted as with each leakage signal interest point being N. Therefore, the electromagnetic leakage signal matrix T generated by encryption is obtained, where
- Calculate the hypothetical intermediate values Z of the encryption algorithm. Based on the target key of the attack in the encryption algorithm, set , where K represents the number of values after enumerating . According to the recorded in the encryption operation and the hypothetical key vector , we obtain the intermediate value matrix Z:where .
- Map the intermediate values Z to the hypothetical electromagnetic leakage matrix H according to the side-channel leakage model. In this paper, we chose the Hamming distance model; therefore,represents the Hamming distance of the two transition results, is the value before calculating the intermediate value, ⊕ represents the XOR operation, a is the proportionality coefficient of the side-channel signal, and b represents other side-channel leakages and noise unrelated to the cryptographic algorithm.
- Conduct a correlation statistical analysis between the hypothetical electromagnetic leakage matrix H and the actual electromagnetic emission leakage matrix T. Compare the Pearson correlation coefficient for the hypothetical corresponding to each guessed key and the actual electromagnetic leakage emission signal to obtain the correlation matrix R. The guessed key corresponding to the maximum value in the matrix R is the final attack result.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Joy Persial, G.; Prabhu, M.; Shanmugalakshmi, R. Side channel attack-survey. Int. J. Adv. Sci. Res. Rev. 2011, 1, 54–57. [Google Scholar]
- Lerman, L.; Bontempi, G.; Ben Taieb, S.; Markowitch, O. A Time Series Approach for Profiling Attack. In Security, Privacy, and Applied Cryptography Engineering; Hutchison, D., Kanade, T., Kittler, J., Kleinberg, J.M., Mattern, F., Mitchell, J.C., Naor, M., Nierstrasz, O., Pandu Rangan, C., Steffen, B., et al., Eds.; Series Title: Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8204, pp. 75–94. [Google Scholar] [CrossRef]
- Aljuffri, A.; Zwalua, M.; Reinbrecht, C.R.W.; Hamdioui, S.; Taouil, M. Applying thermal side-channel attacks on asymmetric cryptography. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, 29, 1930–1942. [Google Scholar] [CrossRef]
- Kocher, P.C. Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems. In Proceedings of the Advances in Cryptology—CRYPTO’96: 16th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 1996; Proceedings 16. Springer: Berlin/Heidelberg, Germany, 1996; pp. 104–113. [Google Scholar]
- Paschali, M.; Simson, W.; Roy, A.G.; Göbl, R.; Wachinger, C.; Navab, N. Manifold exploring data augmentation with geometric transformations for increased performance and robustness. In Proceedings of the Information Processing in Medical Imaging: 26th International Conference, IPMI 2019, Hong Kong, China, 2–7 June 2019; Proceedings 26. Springer: Berlin/Heidelberg, Germany, 2019; pp. 517–529. [Google Scholar]
- de la Rosa, F.L.; Gómez-Sirvent, J.L.; Sánchez-Reolid, R.; Morales, R.; Fernández-Caballero, A. Geometric transformation-based data augmentation on defect classification of segmented images of semiconductor materials using a ResNet50 convolutional neural network. Expert Syst. Appl. 2022, 206, 117731. [Google Scholar] [CrossRef]
- Maharana, K.; Mondal, S.; Nemade, B. A review: Data pre-processing and data augmentation techniques. Glob. Transitions Proc. 2022, 3, 91–99. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27, 2672–2680. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Wang, K.; Gou, C.; Duan, Y.; Lin, Y.; Zheng, X.; Wang, F.Y. Generative adversarial networks: Introduction and outlook. IEEE/CAA J. Autom. Sin. 2017, 4, 588–598. [Google Scholar] [CrossRef]
- Gui, J.; Sun, Z.; Wen, Y.; Tao, D.; Ye, J. A review on generative adversarial networks: Algorithms, theory, and applications. IEEE Trans. Knowl. Data Eng. 2021, 35, 3313–3332. [Google Scholar] [CrossRef]
- Hammami, M.; Friboulet, D.; Kéchichian, R. Cycle GAN-based data augmentation for multi-organ detection in CT images via Yolo. In Proceedings of the 2020 IEEE international conference on image processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 390–393. [Google Scholar]
- Rashid, H.; Tanveer, M.A.; Khan, H.A. Skin lesion classification using GAN based data augmentation. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 916–919. [Google Scholar]
- Bissoto, A.; Valle, E.; Avila, S. Gan-based data augmentation and anonymization for skin-lesion analysis: A critical review. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 1847–1856. [Google Scholar]
- Zhu, X.; Liu, Y.; Li, J.; Wan, T.; Qin, Z. Emotion Classification with Data Augmentation Using Generative Adversarial Networks. In Advances in Knowledge Discovery and Data Mining; Series Title: Lecture Notes in Computer Science; Phung, D., Tseng, V.S., Webb, G.I., Ho, B., Ganji, M., Rashidi, L., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 10939, pp. 349–360. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, Y.; Qin, Z.; Li, J. Data Augmentation in Emotion Classification Using Generative Adversarial Networks. arXiv 2017, arXiv:1711.00648. [Google Scholar]
- Frid-Adar, M.; Klang, E.; Amitai, M.; Goldberger, J.; Greenspan, H. Synthetic data augmentation using GAN for improved liver lesion classification. In Proceedings of the 2018 IEEE 15th international symposium on biomedical imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 289–293. [Google Scholar]
- Huang, S.W.; Lin, C.T.; Chen, S.P.; Wu, Y.Y.; Hsu, P.H.; Lai, S.H. Auggan: Cross domain adaptation with gan-based data augmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 8–14 September 2018; pp. 718–731. [Google Scholar]
- Mariani, G.; Scheidegger, F.; Istrate, R.; Bekas, C.; Malossi, C. BAGAN: Data Augmentation with Balancing GAN. arXiv 2018, arXiv:1803.09655. [Google Scholar]
- Yang, H.; Zhou, Y. Ida-gan: A novel imbalanced data augmentation gan. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8299–8305. [Google Scholar]
- Jiangsha, A.; Tian, L.; Bai, L.; Zhang, J. Data augmentation by a CycleGAN-based extra-supervised model for nondestructive testing. Meas. Sci. Technol. 2022, 33, 045017. [Google Scholar] [CrossRef]
- Sandfort, V.; Yan, K.; Pickhardt, P.J.; Summers, R.M. Data augmentation using generative adversarial networks (CycleGAN) to improve generalizability in CT segmentation tasks. Sci. Rep. 2019, 9, 16884. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Qi, C.; Xu, G. Semi-supervised attention-guided cyclegan for data augmentation on medical images. In Proceedings of the 2019 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), San Diego, CA, USA, 18–21 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 563–568. [Google Scholar]
- Park, M.; Tran, D.Q.; Jung, D.; Park, S. Wildfire-detection method using DenseNet and CycleGAN data augmentation-based remote camera imagery. Remote Sens. 2020, 12, 3715. [Google Scholar] [CrossRef]
- Cap, Q.H.; Uga, H.; Kagiwada, S.; Iyatomi, H. Leafgan: An effective data augmentation method for practical plant disease diagnosis. IEEE Trans. Autom. Sci. Eng. 2020, 19, 1258–1267. [Google Scholar] [CrossRef]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-To-Image Translation Using Cycle-Consistent Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Cagli, E.; Dumas, C.; Prouff, E. Convolutional Neural Networks with Data Augmentation Against Jitter-Based Countermeasures: Profiling Attacks without Pre-processing. In Cryptographic Hardware and Embedded Systems—CHES 2017; Series Title: Lecture Notes in Computer Science; Fischer, W., Homma, N., Eds.; Springer International Publishing: Cham, Switzerland, 2017; Volume 10529, pp. 45–68. [Google Scholar] [CrossRef]
- Advanced ASIC Chip Synthesis Using Synopsys® Design CompilerTM Physical CompilerTM and PrimeTime®: Chapter 4; Kluwer Academic Publishers: Boston, MA, USA, 2002. [CrossRef]
- Fasano, G.; Franceschini, A. A multidimensional version of the Kolmogorov-Smirnov test. Mon. Not. R. Astron. Soc. 1987, 225, 155–170. [Google Scholar] [CrossRef]


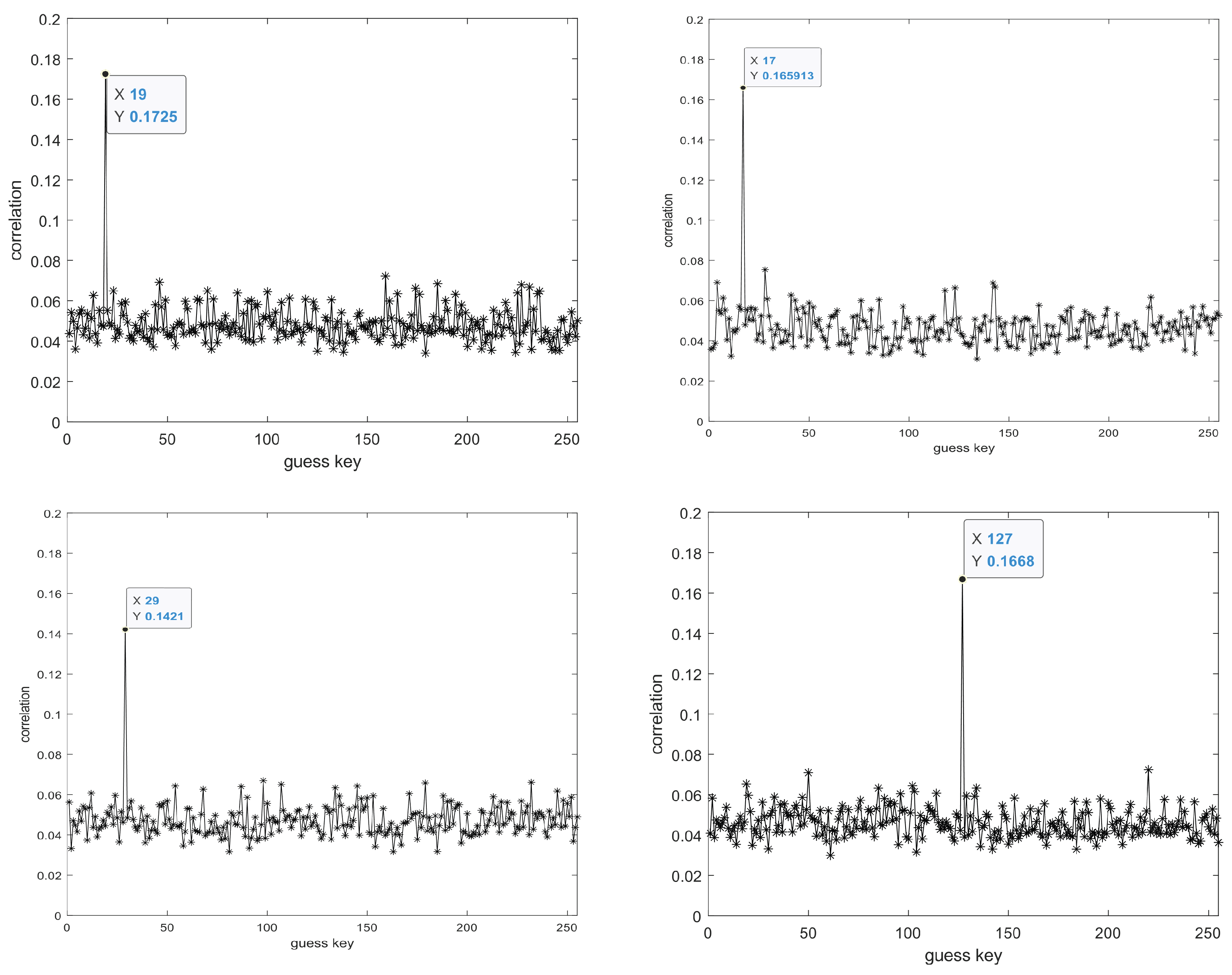

| Byte1 | Byte2 | Byte3 | Byte4 | Byte5 | Byte6 | Byte7 | Byte8 | |
| hex | 13 | 11 | 1d | 7f | e3 | 94 | 4a | 17 |
| dec | 19 | 17 | 29 | 127 | 227 | 148 | 74 | 23 |
| Byte9 | Byte10 | Byte11 | Byte12 | Byte13 | Byte14 | Byte15 | Byte16 | |
| hex | f3 | 07 | a7 | 8b | 4d | 2b | 30 | c5 |
| dec | 243 | 7 | 167 | 139 | 77 | 43 | 48 | 197 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, X.; Zhang, H.; Xu, J.; Fang, X.; Ning, W.; Wang, Y.; Hosen, M.S. A Data Augmentation Method for Side-Channel Attacks on Cryptographic Integrated Circuits. Electronics 2024, 13, 1348. https://doi.org/10.3390/electronics13071348
Cui X, Zhang H, Xu J, Fang X, Ning W, Wang Y, Hosen MS. A Data Augmentation Method for Side-Channel Attacks on Cryptographic Integrated Circuits. Electronics. 2024; 13(7):1348. https://doi.org/10.3390/electronics13071348
Chicago/Turabian StyleCui, Xiaotong, Hongxin Zhang, Jun Xu, Xing Fang, Wenxu Ning, Yuanzhen Wang, and Md Sabbir Hosen. 2024. "A Data Augmentation Method for Side-Channel Attacks on Cryptographic Integrated Circuits" Electronics 13, no. 7: 1348. https://doi.org/10.3390/electronics13071348
APA StyleCui, X., Zhang, H., Xu, J., Fang, X., Ning, W., Wang, Y., & Hosen, M. S. (2024). A Data Augmentation Method for Side-Channel Attacks on Cryptographic Integrated Circuits. Electronics, 13(7), 1348. https://doi.org/10.3390/electronics13071348








