Enhancing Anomaly Detection for Cultural Heritage via Long Short-Term Memory with Attention Mechanism
Abstract
1. Introduction
- (1)
- We propose a novel algorithm for early warning of anomalies in ancient buildings by combining environmental factors with the building structure to improve prediction accuracy.
- (2)
- We introduce the seasonal, trend, shapelet, and mixed anomalies to increase the positive and negative samples of the datasets.
- (3)
- We incorporate the attention mechanism into the domain of ancient buildings and combine it with LSTM architecture to more effectively extract the inherent characteristics of monitoring data, particularly temporal dependencies, enhancing model prediction accuracy. To our knowledge, this investigation is one of the initial endeavors that delve into the augmentation of anomaly data and the application of attention mechanisms in the context of anomaly warning tasks for ancient buildings.
- (4)
- We propose a novel threshold extraction method based on extreme value theory and recurrence interval calculation, which reduces reliance on prior knowledge and allows for the extraction of different warning threshold intervals automatically.
- (5)
- We implement and deploy the anomaly warning program, making it applicable and providing guidelines for conserving cultural heritages in other locations.
2. Materials and Methods
2.1. Experimental Data Acquisition
2.1.1. Experimental Data
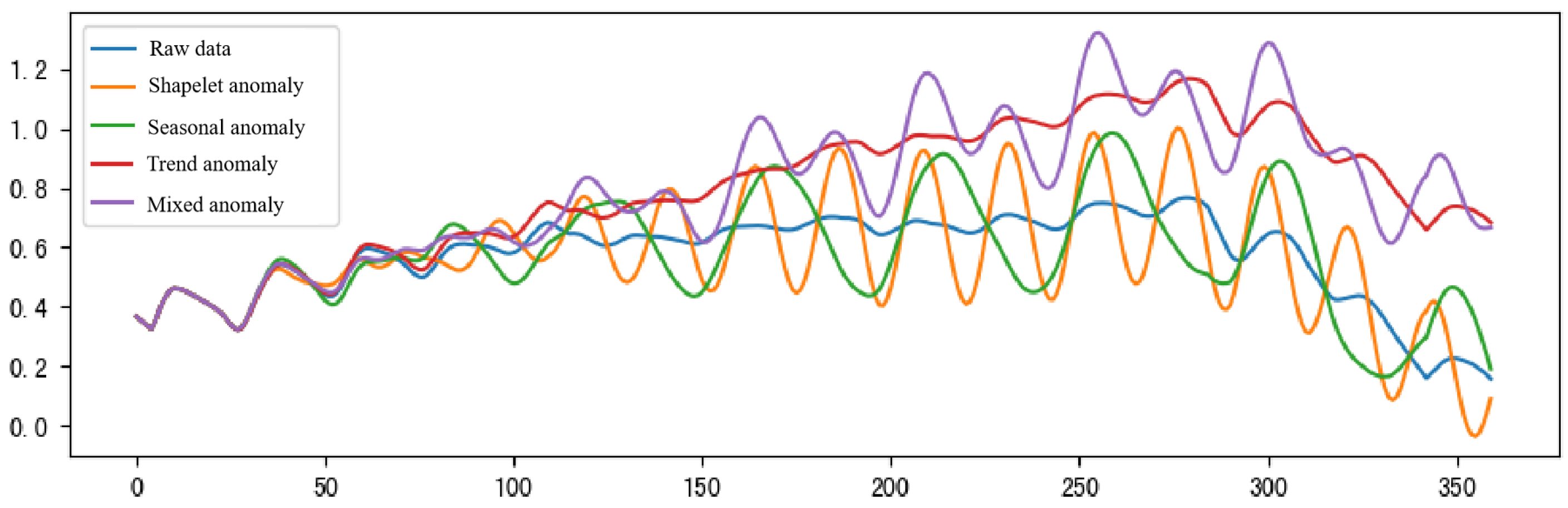
2.1.2. Anomalous Data Synthesis
- (1)
- Add seasonal anomalies. As shown in Equations (1) and (2), the seasonal anomaly is introduced by adding the original series to the series of other periods.where is the original building sequence. is the incremental sequence. l is the sequence length, and is the anomaly period. is the sine function; g is the transition function to model the process of sequence correlation change caused by adding anomalies, and a is half of l. is used to adjust the effect of anomalies on the original sequence, and is random noise.
- (2)
- Add trend anomalies. The trend anomaly is applied by summing the original series with a monotonically increasing or decreasing series, as shown in Equation (3).where is used to moderate the effect of the outliers.
- (3)
- Add shapelet anomalies. The shapelet anomaly is introduced by adding the original sequence to another sequence with the same period, as shown in Equation (4).where is a sine function, is the period of the original sequence. is used to regulate the effect of shapelet anomaly on the original series.
- (4)
- Add mixed anomalies. The mixture of seasonal, trend, and shapelet anomalies is introduced simultaneously, as shown in Equation (5).
- (1)
- For the sample with code i mod 4==0, a shapelet anomaly is introduced.
- (2)
- For the sample with code i mod 4==1, a seasonal anomaly is introduced.
- (3)
- For samples with code i mod 4==2, a trend anomaly is introduced.
- (4)
- For the sample with code i mod 4==3, a mixed anomaly is introduced.
2.2. The Attention Mechanism
- Data input. A linear transformation can map the input sequence to Query, Key, and Value.
- Calculate the correlation. The correlation between the Key and Query is calculated and normalized, and the attention distribution of critical values is obtained using the softmax function.
- Weighted summation. According to the attention distribution calculated in step 2, the corresponding Value is weighted and summed to obtain the output.
2.3. Long Short-Term Memory Network (LSTM)
2.4. The LSTM-Attention Framework
- Cut the displacement and environmental data. In this paper, the displacement and the environmental data are cut to the same size as the sliding window. As shown in the blue dashed box part of the figure, the different colored origin points represent different time series. The sliding window size is W × D, W is the period of the sliding window, and D is the time series dimension. The sliding window moves along the time axis, and the data set in the red box part is obtained after cutting. The small black box is the recent displacement data used as the training set label.
- Extract global time features. LSTM has an excellent performance in long sequence tasks, which is well-suited for cultural heritage where data often exhibits temporal dependencies. This paper uses LSTM to extract the time series features in the window, capture and learn from the temporal patterns, and output the hidden state values to prepare for the subsequent calculation of the weights of each hidden in the self-attention layer, enabling it to discern anomalous behavior over time.
- Extract dependencies of time series. The attention mechanism enhances the LSTM model’s ability to focus on relevant information within the input sequences. This is particularly beneficial for anomaly detection tasks where subtle deviations from normal behavior need to be identified. Reasonable allocation of attention weights can effectively improve the reconstruction ability of the model. The self-attention allocates more weight to the key parts that affect the output more, which can improve the model’s interpretability. The sequence of hidden state values in LSTM contains the environment sequence and the ancient building sequence. Actually, calculating the weight matrix is extracting the dependencies between the time sequences, thereby improving the accuracy of anomaly detection.
- Reconstruct the recent displacement data. Extract the association between features and map them to the output, which will reconstruct the recent displacement data.
2.5. Model Anomaly Threshold Extraction
| Algorithm 1: Threshold extraction. |
Input: : Prediction error set N: Recurrence period G: Extreme value distribution function 1. // Test Gumbel extreme value distribution 2. // Test Weibull extreme value distribution 3. // Test Frechet extreme value distribution 4. // Select the distribution function based on the 5. // Fitting the distribution 6. // Calculate the cumulative probability density distribution 7. // Calculate the probability of the extreme events 8. // Calculate the threshold value based on the inverse function of 9. return Output: |
2.6. Model Performance Criteria
3. Results
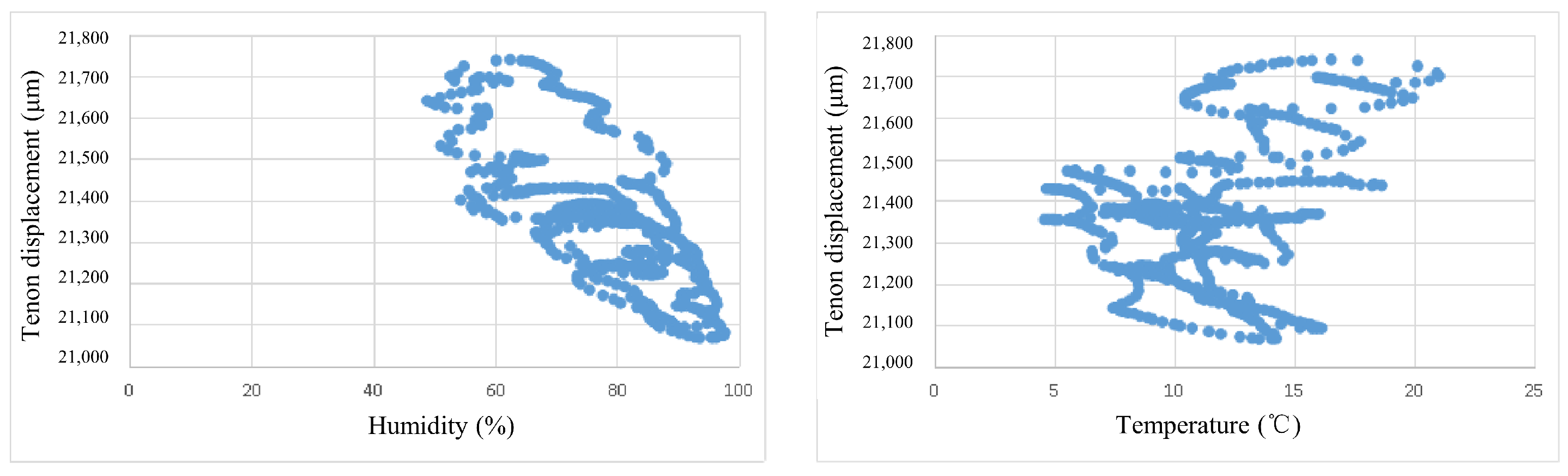
3.1. Risk Source Selection
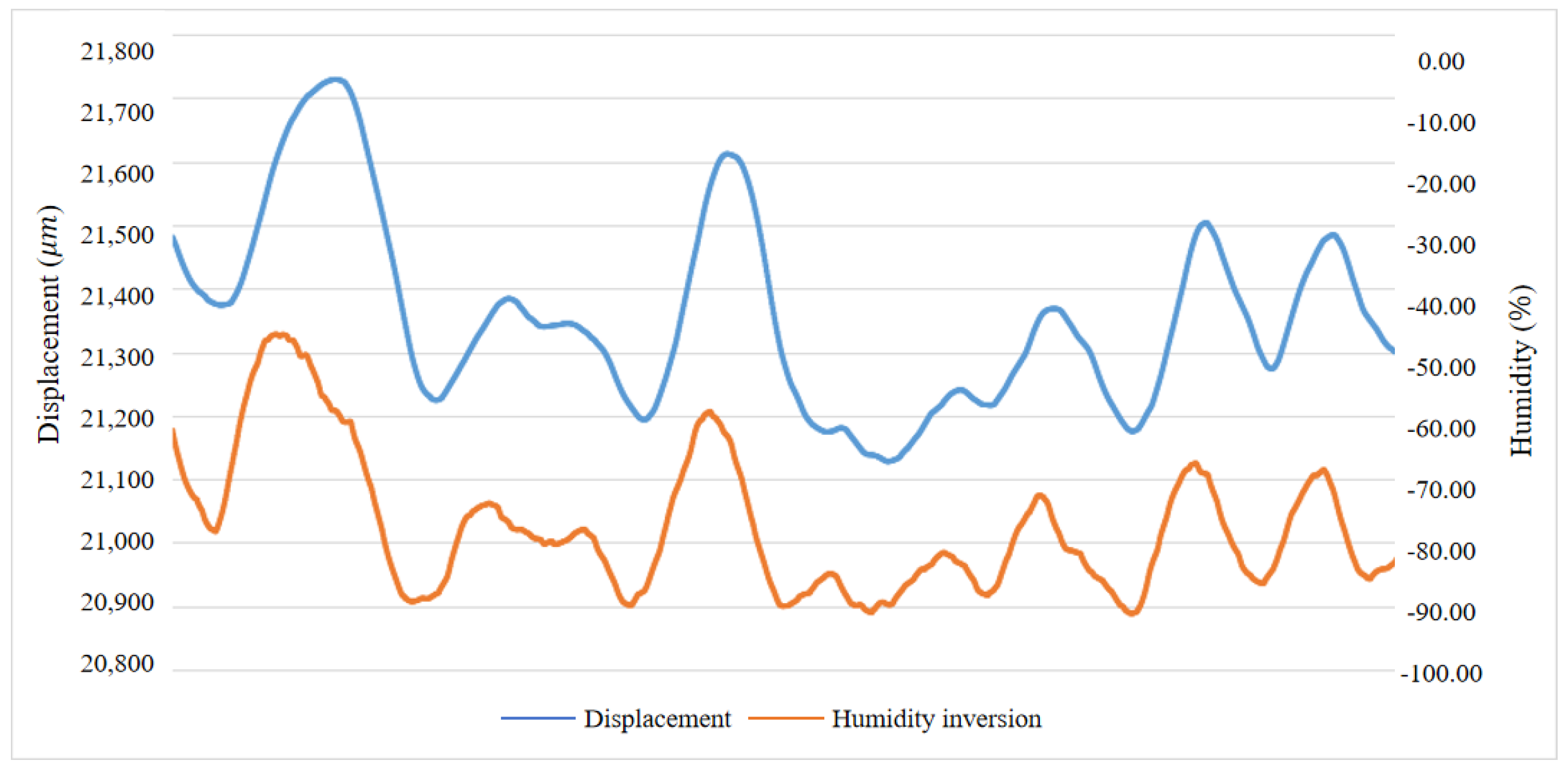
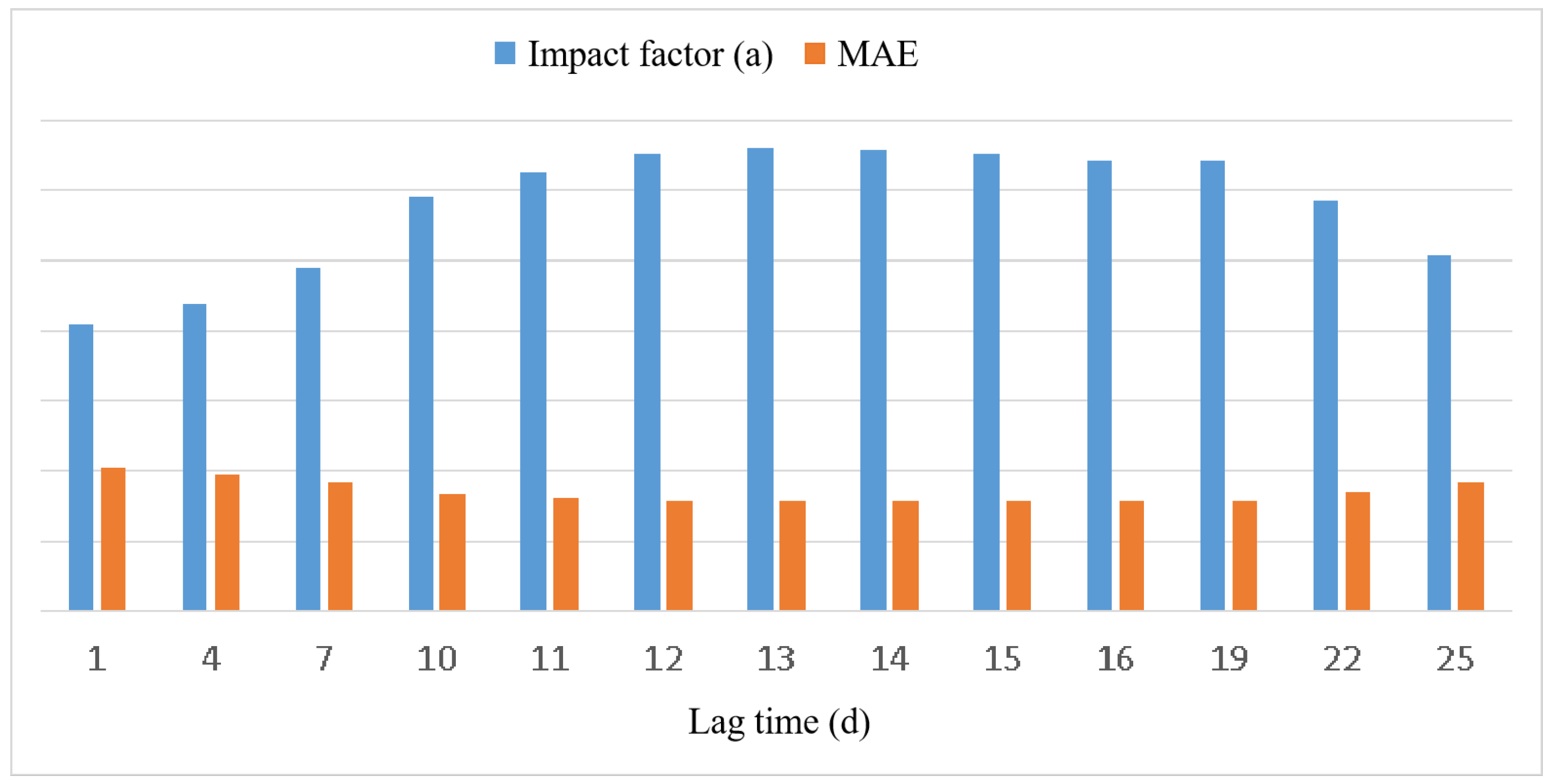
3.2. Hysteresis Analysis
3.3. Parameter Sensitivity Analysis
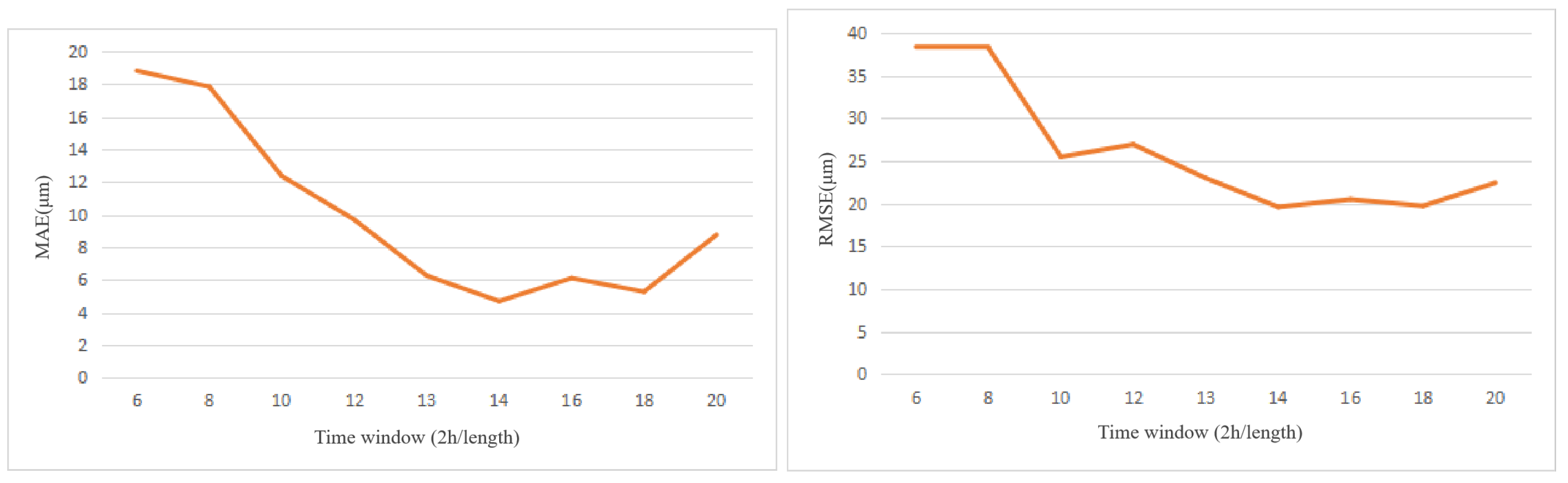
3.3.1. Parameter Sensitivity of Time Window and Reconstruction Step
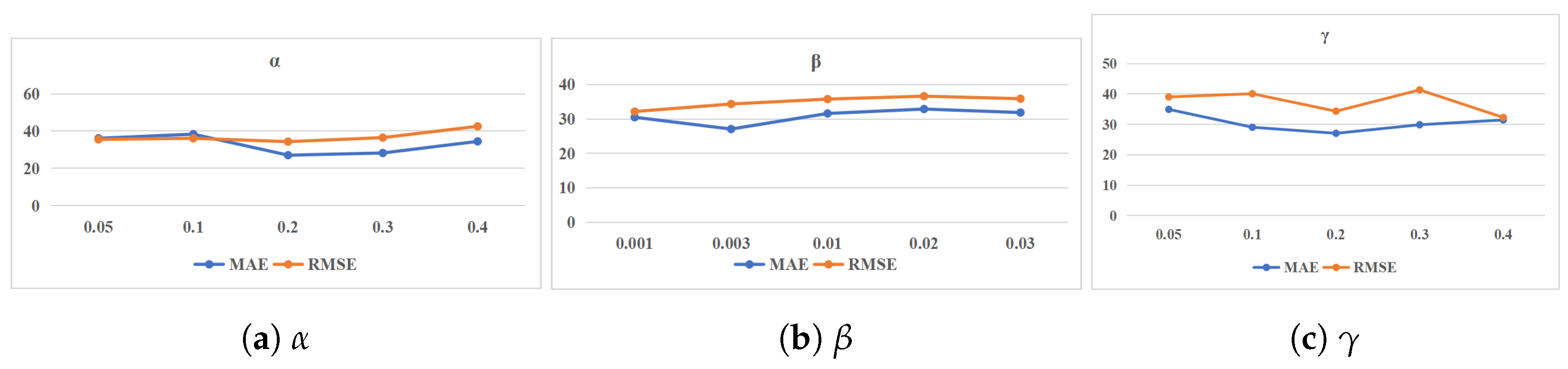
3.3.2. Parameter Sensitivity of Data Synthesis
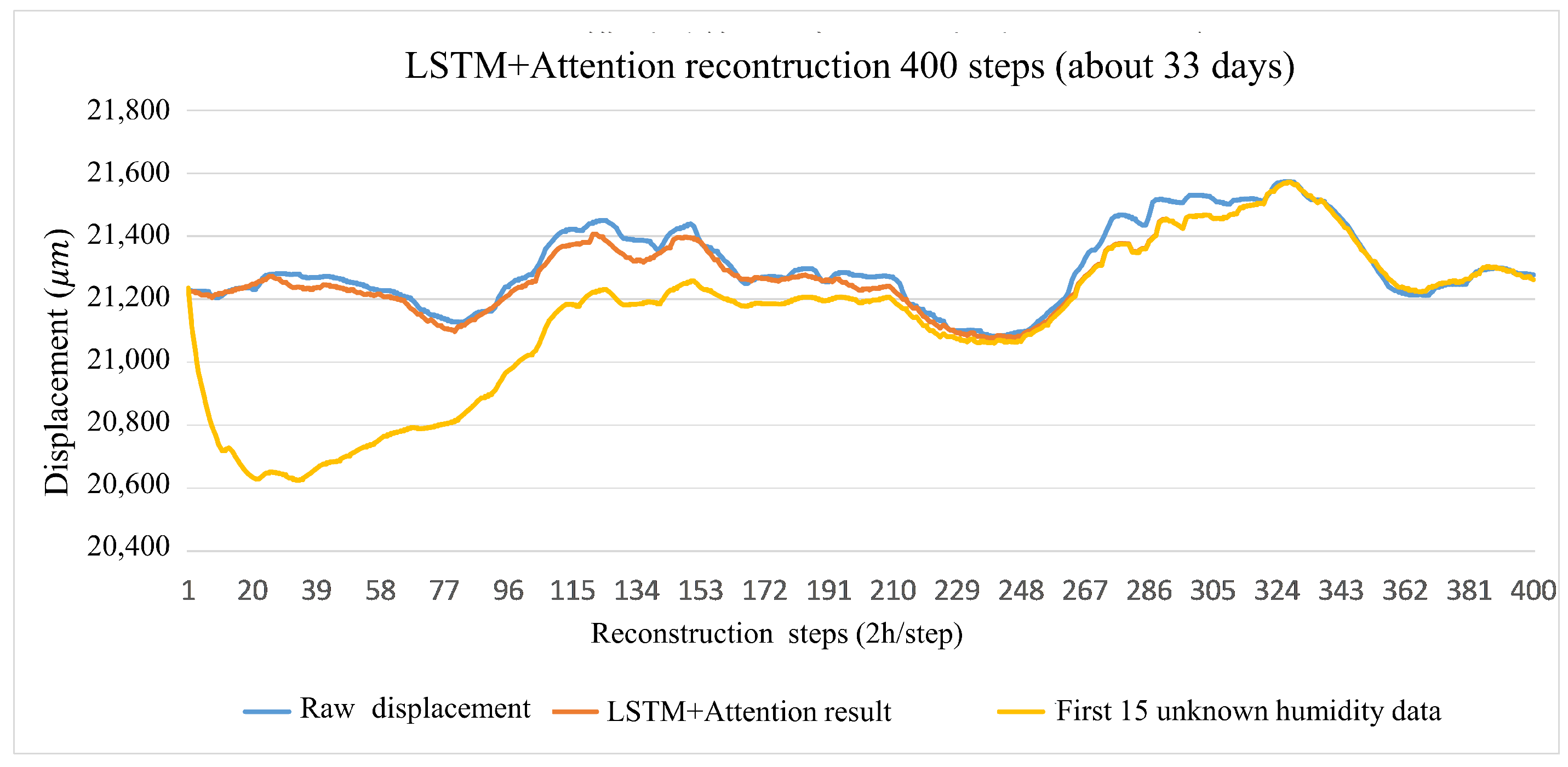
3.4. Validity Analysis
3.5. Necessity Analysis of External Factors
3.6. Ablation Study
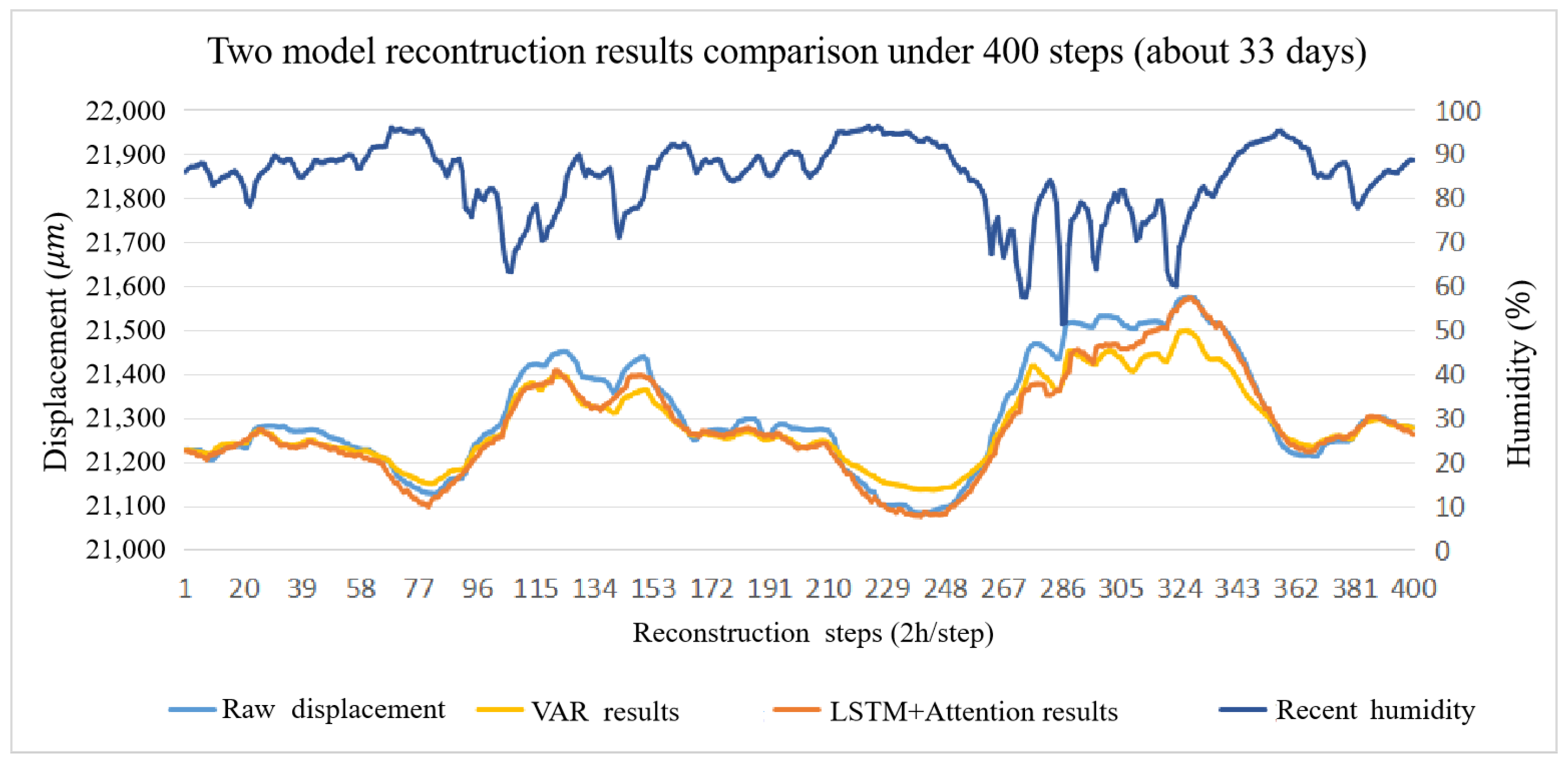
3.7. Model Comparison
3.8. Analysis of Anomaly Warning Indicators
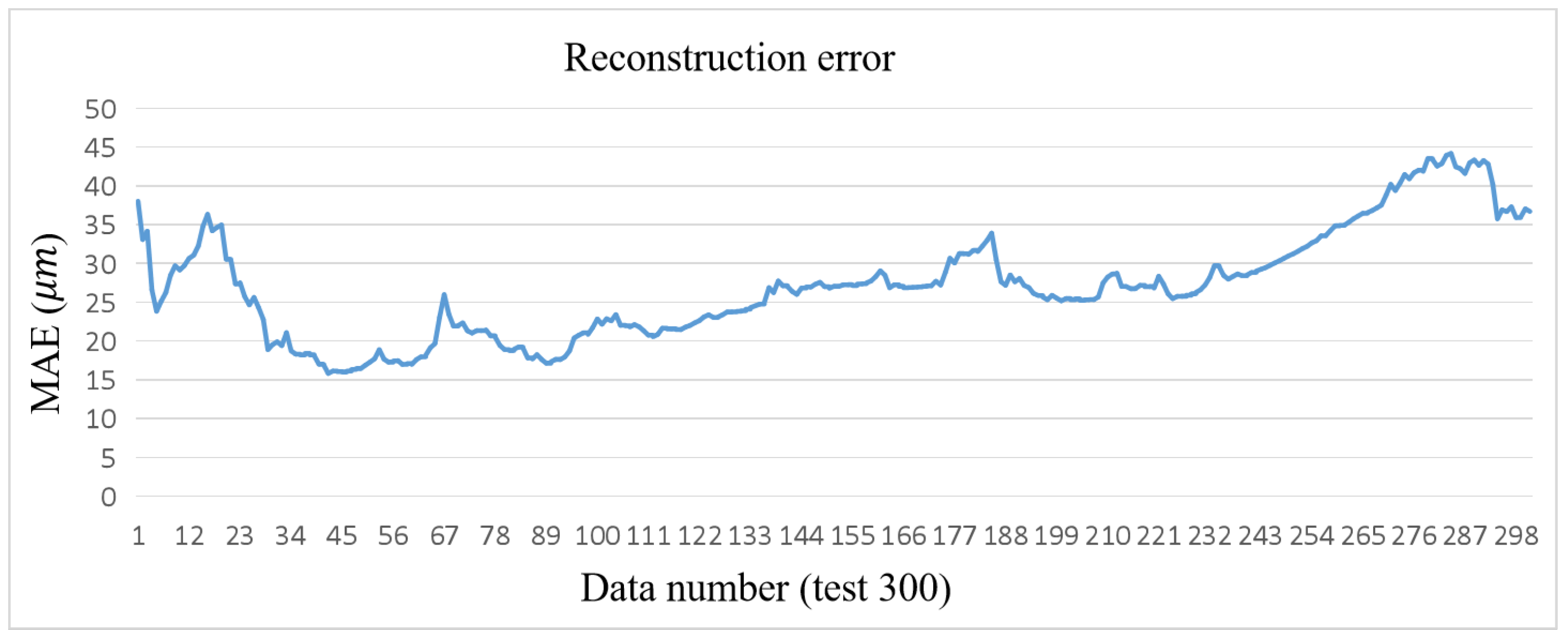
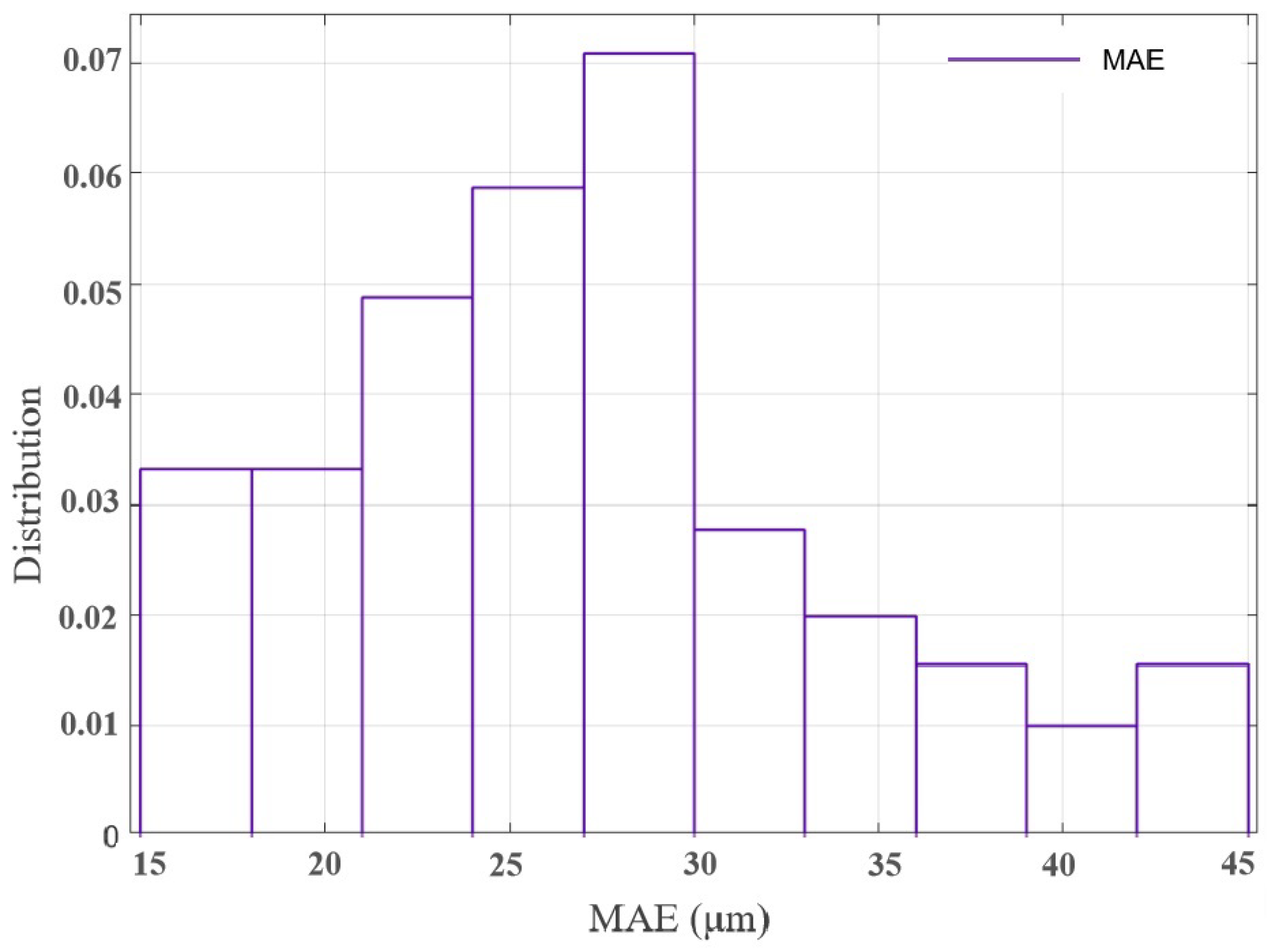
- Probabilistic statistics on MAE. The distribution probability of the error of the test set can be seen in Figure 17, which mainly focuses on the range of 25–30 μm, for which a cumulative probability model is fitted.
- Extract the anomaly warning threshold from the probabilistic model based on the extreme recurrence intervals. Table 9 presents the anomaly warning thresholds of the LSTM-Attention model for 400 steps of reconstruction errors, considering recurrence intervals of one and five years.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qu, J.J.; Cheng, G.D.; Zhang, K.C.; Wang, J.C.; Zu, R.P.; Fang, H.Y. An experimental study of the mechanisms of freeze/thaw and wind erosion of ancient adobe buildings in northwest China. Bull. Eng. Geol. Environ. 2007, 66, 153–159. [Google Scholar] [CrossRef]
- Betti, M.; Galano, L.; Vignoli, A. Finite element modelling for seismic assessment of historic masonry buildings. Earthquakes and Their Impact on Society; Springer: Cham, Switzerland, 2016; pp. 377–415. [Google Scholar]
- Ereiz, S.; Duvnjak, I.; Damjanović, D.; Bartolac, M. Analysis of seismic action on the tie rod system in historic buildings using finite element model updating. Buildings 2021, 11, 453. [Google Scholar] [CrossRef]
- Liu, S.; Wang, R.; Yu, J.; Peng, X.; Cai, Y.; Tu, B. Effectiveness of the anti-erosion of an MICP coating on the surfaces of ancient clay roof tiles. Constr. Build. Mater. 2020, 243, 118202. [Google Scholar] [CrossRef]
- Xin, Z.; Ke, D.; Zhang, H.; Yu, Y.; Liu, F. Non-destructive evaluating the density and mechanical properties of ancient timber members based on machine learning approach. Constr. Build. Mater. 2022, 341, 127855. [Google Scholar] [CrossRef]
- Tao, S. Protection and repair technology of ancient building walls based on big data. In Civil Engineering and Urban Research; CRC Press: Boca Raton, FL, USA, 2023; Volume 1, pp. 311–317. [Google Scholar]
- Akcaozoglu, S.; Yavascan, E.E.; Gokce, M.V. Deterioration and Conservation Problems of Historical Fountains in Cappadocia-Niğde. Fresenius Environ. Bull. 2020, 29, 2338–2343. [Google Scholar]
- Hatır, M.E.; İnce, İ.; Korkanç, M. Intelligent detection of deterioration in cultural stone heritage. J. Build. Eng. 2021, 44, 102690. [Google Scholar] [CrossRef]
- Severcan, M.H.; Yavaşcan, E.E.; Akçaözoğlu, S.; Akçaözoğlu, K. Investigation of material deterioration and seismic behavior of Fertek and Hançerli Churches in Cappadocia Region. Niğde Ömer Halisdemir Üniversitesi Mühendislik Bilim. Derg. 2022, 11, 1042–1052. [Google Scholar]
- Liu, X.; Koestler, R.J.; Warscheid, T.; Katayama, Y.; Gu, J.D. Microbial deterioration and sustainable conservation of stone monuments and buildings. Nat. Sustain. 2020, 3, 991–1004. [Google Scholar] [CrossRef]
- Fanti, R.; Gigli, G.; Tapete, D.; Mugnai, F.; Casagli, N. Monitoring and modelling slope instability in cultural heritage sites. In Landslide Science and Practice; Volume 6: Risk Assessment, Management and Mitigation; Springer: Berlin/Heidelberg, Germany, 2013; pp. 467–473. [Google Scholar]
- Holickỳ, M.; Sỳkora, M. Assessment of flooding risk to cultural heritage in historic sites. J. Perform. Constr. Facil. 2010, 24, 432–438. [Google Scholar] [CrossRef]
- Staley, D.M.; Negri, J.A.; Kean, J.W.; Laber, J.L.; Tillery, A.C.; Youberg, A.M. Prediction of spatially explicit rainfall intensity–duration thresholds for post-fire debris-flow generation in the western United States. Geomorphology 2017, 278, 149–162. [Google Scholar] [CrossRef]
- Liang, H.; Zou, J.; Khan, M.J.; Jinxuan, H. An sand plug of fracturing intelligent early warning model embedded in remote monitoring system. IEEE Access 2019, 7, 47944–47954. [Google Scholar] [CrossRef]
- Gigli, G.; Fanti, R.; Canuti, P.; Casagli, N. Integration of advanced monitoring and numerical modeling techniques for the complete risk scenario analysis of rockslides: The case of Mt. Beni (Florence, Italy). Eng. Geol. 2011, 120, 48–59. [Google Scholar] [CrossRef]
- Xie, P.; Zhou, A.; Chai, B. The application of long short-term memory (LSTM) method on displacement prediction of multifactor induced landslides. IEEE Access 2019, 7, 54305–54311. [Google Scholar] [CrossRef]
- Fan, L.; Li, J.; Pan, Y.; Wang, S.; Yan, C.; Yao, D. Research and application of smart grid early warning decision platform based on big data analysis. In Proceedings of the 2019 4th International Conference on Intelligent Green Building and Smart Grid (IGBSG), Hubei, China, 6–9 September 2019; pp. 645–648. [Google Scholar]
- Zhu, X.; Jin, X.; Jia, D.; Sun, N.; Wang, P. Application of data mining in an intelligent early warning system for rock bursts. Processes 2019, 7, 55. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, D.; Zhang, X.; Yuan, Z.; Cheng, X. Learning graph structures with transformer for multivariate time-series anomaly detection in IoT. IEEE Internet Things J. 2021, 9, 9179–9189. [Google Scholar] [CrossRef]
- Shah, G.; Tiwari, A. Anomaly detection in iiot: A case study using machine learning. In Proceedings of the ACM India Joint International Conference on Data Science and Management of Data, Goa, India, 11–13 January 2018; pp. 295–300. [Google Scholar]
- Feng, X.; Song, D.; Chen, Y.; Chen, Z.; Ni, J.; Chen, H. Convolutional transformer based dual discriminator generative adversarial networks for video anomaly detection. In Proceedings of the 29th ACM International Conference on Multimedia, Virtual Event, China, 20–24 October 2021; pp. 5546–5554. [Google Scholar]
- Bhuvaneshwari, P.; Rao, A.N.; Robinson, Y.H.; Thippeswamy, M. Sentiment analysis for user reviews using Bi-LSTM self-attention based CNN model. Multimed. Tools Appl. 2022, 81, 12405–12419. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Lang, J.; Jiang, Y.; An, L.; Zou, P.; Xu, Y.; Gao, S.; Lin, J.; Fan, C.; et al. Hybrid multimodal feature extraction, mining and fusion for sentiment analysis. In Proceedings of the 3rd International on Multimodal Sentiment Analysis Workshop and Challenge, Lisboa, Portugal, 10 October 2022; pp. 81–88. [Google Scholar]
- Fan, Z.; Hu, G.; Sun, X.; Wang, G.; Dong, J.; Su, C. Self-attention neural architecture search for semantic image segmentation. Knowl.-Based Syst. 2022, 239, 107968. [Google Scholar] [CrossRef]
- Li, K.; Qian, Z.; Han, Y.; Eric, I.; Chang, C.; Wei, B.; Lai, M.; Liao, J.; Fan, Y.; Xu, Y. Weakly supervised histopathology image segmentation with self-attention. Med. Image Anal. 2023, 86, 102791. [Google Scholar] [CrossRef]
- Fan, Z.; Liu, Z.; Wang, Y.; Wang, A.; Nazari, Z.; Zheng, L.; Peng, H.; Yu, P.S. Sequential recommendation via stochastic self-attention. In Proceedings of the ACM Web Conference 2022, Virtual Event, Lyon, France, 25–29 April 2022; pp. 2036–2047. [Google Scholar]
- Zhang, Y.; Yang, B.; Liu, H.; Li, D. A time-aware self-attention based neural network model for sequential recommendation. Appl. Soft Comput. 2023, 133, 109894. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence; Association for the Advancement of Artificial Intelligence: Washington, DC, USA, 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Chen, M.; Peng, H.; Fu, J.; Ling, H. Autoformer: Searching transformers for visual recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 12270–12280. [Google Scholar]
- Hu, Y.; Xiao, F. Network self attention for forecasting time series. Appl. Soft Comput. 2022, 124, 109092. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Chang, T.A.; Bergen, B.K. Word acquisition in neural language models. Trans. Assoc. Comput. Linguist. 2022, 10, 1–16. [Google Scholar] [CrossRef]
- Oota, S.R.; Alexandre, F.; Hinaut, X. Long-term plausibility of language models and neural dynamics during narrative listening. In Proceedings of the Annual Meeting of the Cognitive Science Society; Cognitive Science Society: Seattle, WA, USA, 2022; Volume 44. [Google Scholar]
- Kumar, R.; Kumar, P.; Kumar, Y. Three stage fusion for effective time series forecasting using Bi-LSTM-ARIMA and improved DE-ABC algorithm. Neural Comput. Appl. 2022, 34, 18421–18437. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Liang, J.; Liu, L. DAFA-BiLSTM: Deep Autoregression Feature Augmented Bidirectional LSTM network for time series prediction. Neural Netw. 2023, 157, 240–256. [Google Scholar] [CrossRef] [PubMed]
- Bhaskar, S.; Thasleema, T. LSTM model for visual speech recognition through facial expressions. Multimed. Tools Appl. 2023, 82, 5455–5472. [Google Scholar] [CrossRef]
- Premalatha, S.; Kumar, V.; Jagini, N.P.; Reddy, G.V.S. Development of vanilla LSTM based stuttered speech recognition system using bald eagle search algorithm. Signal, Image Video Process. 2023, 17, 4077–4086. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, L.; Sun, X.; Wang, B. A hybrid XGBoost-ISSA-LSTM model for accurate short-term and long-term dissolved oxygen prediction in ponds. Environ. Sci. Pollut. Res. 2022, 29, 18142–18159. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; Kong, D.; Han, H.; Zhao, Y. EA-LSTM: Evolutionary attention-based LSTM for time series prediction. Knowl.-Based Syst. 2019, 181, 104785. [Google Scholar] [CrossRef]
- Liu, X.; Shi, R.; Hui, Q.; Xu, S.; Wang, S.; Na, R.; Sun, Y.; Ding, W.; Zheng, D.; Chen, X. TCACNet: Temporal and channel attention convolutional network for motor imagery classification of EEG-based BCI. Inf. Process. Manag. 2022, 59, 103001. [Google Scholar] [CrossRef]
- Kim, H.; Kim, S.; Shin, H.; Heo, J.H. Appropriate Model Selection Methods for Nonstationary Generalized Extreme Value Models. J. Hydrol. 2017, 547, 557–574. [Google Scholar] [CrossRef]
- Martins, E.; Stedinger, J. Generalized Maximum Likelihood GEV Quantile Estimators for Hydrologic Data. Water Resour. Res. 2000, 36, 737–744. [Google Scholar] [CrossRef]
- Chikobvu, D.; Chifurira, R. Modelling of extreme minimum rainfall using generalised extreme value distribution for Zimbabwe. South Afr. J. Sci. 2015, 111, 1–8. [Google Scholar] [CrossRef]
- Calabrese, R.; Giudici, P. Estimating bank default with generalised extreme value regression models. J. Oper. Res. Soc. 2015, 66, 1783–1792. [Google Scholar] [CrossRef]
- Rocco, M. Extreme Value Theory for Finance: A Survey. J. Econ. Surv. 2012, 28. [Google Scholar] [CrossRef]
- Johansen, S. Modelling of cointegration in the vector autoregressive model. Econ. Model. 2000, 17, 359–373. [Google Scholar] [CrossRef]
- Box, G.E.; Pierce, D.A. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Zhao, C.; Chang, X.; Xie, T.; Fujita, H.; Wu, J. Unsupervised anomaly detection based method of risk evaluation for road traffic accident. Appl. Intell. 2023, 53, 369–384. [Google Scholar] [CrossRef]
- Tayarani-N, M.H.; Yao, X.; Xu, H. Meta-heuristic algorithms in car engine design: A literature survey. IEEE Trans. Evol. Comput. 2014, 19, 609–629. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2022, 38, 3025–3056. [Google Scholar] [CrossRef]







| Time | Displacement (μm) | Temperature (°C) | Humidity (%) |
|---|---|---|---|
| 00:00:00 | 21,321.5 | 25.438 | 98.175 |
| 02:00:00 | 21,320 | 25.661 | 97.938 |
| 04:00:00 | 21,318.5 | 25.967 | 97.228 |
| 06:00:00 | 21,316.75 | 26.282 | 96.248 |
| ⋮ | ⋮ | ⋮ | ⋮ |
| 20:00:00 | 21,311.5 | 23.173 | 96.108 |
| 22:00:00 | 21,308.25 | 22.870 | 95.871 |
| Parameter | Value |
|---|---|
| 0.2 | |
| 0.005 | |
| 0.2 | |
| 24 | |
| 48 |
| Reference | |||
|---|---|---|---|
| Positive | Negative | ||
| Prediction | Positive | TP (True Positive) | FP (False Positive) |
| Negative | FN (False Negative) | TN (True Negative) | |
| Metrics | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|---|
| MAE | 36.139 | 38.361 | 27.06 | 28.237 | 34.475 |
| RMSE | 35.549 | 36.134 | 34.328 | 36.497 | 42.573 |
| Metrics | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|---|
| MAE | 34.931 | 29.048 | 27.06 | 29.873 | 31.462 |
| RMSE | 39.027 | 40.084 | 34.328 | 41.349 | 32.274 |
| Metrics | 0.001 | 0.005 | 0.01 | 0.02 | 0.03 |
|---|---|---|---|---|---|
| MAE | 30.478 | 27.06 | 31.578 | 32.862 | 31.847 |
| RMSE | 32.138 | 34.328 | 35.745 | 36.597 | 35.864 |
| Evaluation Metrics | Without Attention Mechanism | With Attention Mechanism |
|---|---|---|
| MAE | 39.570 | 27.023 |
| 37.391 | 27.293 | |
| 39.114 | 26.863 | |
| RMSE | 52.530 | 37.239 |
| 46.472 | 34.933 | |
| 49.668 | 35.287 |
| Model | MAE | RMSE |
|---|---|---|
| ARIMA | 56.182 | 62.056 |
| VAR | 38.950 | 44.721 |
| CNN | 51.337 | 57.865 |
| LSTM | 38.692 | 47.751 |
| LSTM-Attention | 27.060 | 34.328 |
| Recurrence Interval | MAE |
|---|---|
| One year | 70.3789 |
| Five years | 75.1033 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Dong, Y.; Shan, Z.; Meng, X.; He, Y.; Jia, P.; Lu, D. Enhancing Anomaly Detection for Cultural Heritage via Long Short-Term Memory with Attention Mechanism. Electronics 2024, 13, 1254. https://doi.org/10.3390/electronics13071254
Wu Y, Dong Y, Shan Z, Meng X, He Y, Jia P, Lu D. Enhancing Anomaly Detection for Cultural Heritage via Long Short-Term Memory with Attention Mechanism. Electronics. 2024; 13(7):1254. https://doi.org/10.3390/electronics13071254
Chicago/Turabian StyleWu, Yuhan, Yabo Dong, Zeyang Shan, Xiyu Meng, Yang He, Ping Jia, and Dongming Lu. 2024. "Enhancing Anomaly Detection for Cultural Heritage via Long Short-Term Memory with Attention Mechanism" Electronics 13, no. 7: 1254. https://doi.org/10.3390/electronics13071254
APA StyleWu, Y., Dong, Y., Shan, Z., Meng, X., He, Y., Jia, P., & Lu, D. (2024). Enhancing Anomaly Detection for Cultural Heritage via Long Short-Term Memory with Attention Mechanism. Electronics, 13(7), 1254. https://doi.org/10.3390/electronics13071254






