Fast Decision-Tree-Based Series Partitioning and Mode Prediction Termination Algorithm for H.266/VVC

Abstract

With the advancement of network technology, multimedia videos have emerged as a crucial channel for individuals to access external information, owing to their realistic and intuitive effects. In the presence of high frame rate and high dynamic range videos, the coding efficiency of high-efficiency video coding (HEVC) falls short of meeting the storage and transmission demands of the video content. Therefore, versatile video coding (VVC) introduces a nested quadtree plus multi-type tree (QTMT) segmentation structure based on the HEVC standard, while also expanding the intra-prediction modes from 35 to 67. While the new technology introduced by VVC has enhanced compression performance, it concurrently introduces a higher level of computational complexity. To enhance coding efficiency and diminish computational complexity, this paper explores two key aspects: coding unit (CU) partition decision-making and intra-frame mode selection. Firstly, to address the flexible partitioning structure of QTMT, we propose a decision-tree-based series partitioning decision algorithm for partitioning decisions. Through concatenating the quadtree (QT) partition division decision with the multi-type tree (MT) division decision, a strategy is implemented to determine whether to skip the MT division decision based on texture characteristics. If the MT partition decision is used, four decision tree classifiers are used to judge different partition types. Secondly, for intra-frame mode selection, this paper proposes an ensemble-learning-based algorithm for mode prediction termination. Through the reordering of complete candidate modes and the assessment of prediction accuracy, the termination of redundant candidate modes is accomplished. Experimental results show that compared with the VVC test model (VTM), the algorithm proposed in this paper achieves an average time saving of 54.74%, while the BDBR only increases by 1.61%.

1. Introduction

As network technology undergoes iterative upgrades and multimedia technology advances, there is an increasing demand for higher quality and resolution in video content. This demand is particularly evident in applications such as telemedicine, remote business negotiations, and online course education, especially during the prevention and control of COVID-19. As per the Ericsson Mobility Report of November 2021, video traffic has emerged as the dominant force in mobile data traffic, constituting up to 69%. This proportion is anticipated to escalate further to 79% by 2027 [1]. Ultra-high definition (UHD), high dynamic range (HDR), and virtual reality (VR) stand out among various video formats for their realistic perceived quality and immersive visual experiences. However, due to their high resolution, dynamic range, and expanded color spectrum, these videos generate a substantial amount of data. Consequently, they impose heightened demands on storage space and transmission bandwidth, presenting significant challenges for achieving real-time interaction. The high-efficiency video coding (HEVC) standard may encounter limitations in meeting the escalating demands of the video market in the future [2]. To address the evolving requirements of video coding applications, the Joint Video Expert Team (JVET) develop the next generation of video coding standards. Versatile video coding (VVC) was officially released in July 2020 [3]. In evaluating new coding standards, the JVET team initially introduced the joint exploration model (JEM). Within JEM, intra-frame prediction and frame partitioning schemes are implemented to provide pixel flexibility for selecting appropriate block sizes, alongside the introduction of a new quadtree nested binary tree partitioning scheme. Implementing the new scheme, the JEM test model demonstrated a 5% improvement in coding efficiency under a random-access configuration [4]. While delving into video coding, the JVET group introduced the VVC test model (VTM). As the latest coding standard, VVC incorporates several innovative coding techniques, including the quadtree plus multi-type tree (QTMT) structure, multiple-reference line (MRL), intra sub-partitions (ISPs), and multiple transform selection (MTS). The implementation of these techniques has resulted in a significant enhancement in the coding efficiency of VVC, achieving an overall 50% reduction in bit rate compared to HEVC [5]. However, the complexity of VVC also experiences a substantial increase. Under full all-frame configuration conditions, the encoding complexity of VVC exceeds that of HEVC by more than 18 times [6]. Figure 1 illustrates the entire rate-distortion (RD) optimization process for VVC intra-frame coding and HEVC intra-frame coding. The new process introduced by VVC intra-frame coding is indicated by a green module. While the high coding gain achieved by VVC is evident, it comes at the expense of increased complexity, posing challenges in meeting the market demand for high real-time performance. Therefore, our objective is to significantly reduce the coding complexity of VVC while preserving the desired coding efficiency and quality.

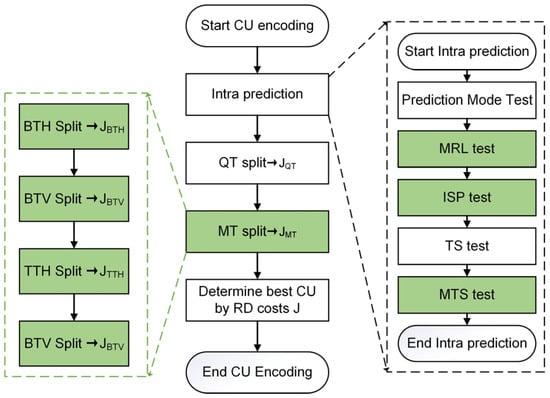
Figure 1. Differences in Rate-Distortion Optimization between VVC intra-frame coding and HEVC intra-frame coding.

As a next-generation video coding standard, VVC continues the block-based coding approach employed by its predecessor, HEVC. In HEVC, a flexible quadtree (QT) partition, is utilized to enhance coding efficiency. The HEVC standard partitions each frame of the image into coding tree units (CTUs) and employs QT technology to further sub-divide the CTU into coding units (CUs) of various sizes. Typically, the CTU size is set to 64, with the minimum CU size being 8. The coding tree units are coded in a depth-first order, employing a Z-scan-like approach. Due to the quadtree division, the shape of a CU can only be adjusted to a square. Consequently, the width and height of a CU should be either 64, 32, 16, or 8 at the same time. On the other hand, the CTU can be further divided into a CU, a prediction unit (PU), and a transformation unit (TU). The prediction unit serves as the fundamental unit for HEVC predictions and comprises a chrominance block, two luminance blocks, and associated syntax elements. The transformation unit and prediction unit are at the same point and can be one or more smaller transformation unit combinations. The difference between the two is that the transformation unit can recursively continue segmentation, while the prediction unit can only perform one segmentation. However, in VVC, partitioning is not confined to the symmetry of the CU, and the concepts of PU and TU from HEVC are abandoned. To better accommodate diverse texture features, VVC introduces the QTMT structure in the CU unit division process. The structure includes six division results: horizontal binary tree (HBT), vertical binary tree (VBT), horizontal ternary tree (HTT), vertical ternary tree (VTT), quaternary tree (QT), and no division. In VVC, the size of the CTU is 128 × 128. Initially, the CTU undergoes quadtree division, followed by binary tree or ternary tree partitioning on all leaf nodes of the quadtree, as illustrated in Figure 2. In order to better illustrate the different partitioning methods of different coding blocks, Figure 3 shows that different CU textures lead to differences in the resulting CU partitions. To streamline the CTU process, multitree partitioning is exclusively applied to quadtree leaf nodes, and quadtree partitioning is prohibited following multitree partitioning. According to statistical analysis, within the VTM, the multi-type tree (MT) division structure constitutes 90% of the coding time [7]. Therefore, the most necessary part of improving VVC is to find an efficient CTU partitioning method.

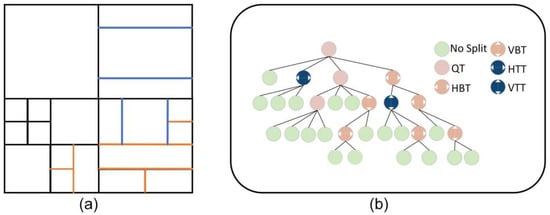
Figure 2. Representation of QTMT partition. (a) Black line inside CU represents quadtree (QT), orange line represents binary tree (BT), and blue line represents ternary tree (TT); (b) VBT and HBT represent Vertical Binary Tree and Horizontal Binary Tree, VTT and HTT represent Vertical Ternary Tree and Horizontal Ternary Tree.

Figure 3. Example of the relationship between CU texture and CU partition.

To enhance the prediction accuracy of various textures and maximize the potential for removing intra-frame redundant information, VVC employs 67 prediction modes in intra-frame prediction. These modes include 65 angle prediction modes, DC modes, and planar modes. Additionally, affine motion compensated prediction (AMCP) is utilized in inter-frame prediction. Compared with the 35 prediction modes included in HEVC, VVC provides richer prediction possibilities and more accurate prediction directions. On the other hand, to alleviate the computational burden of the mode selection process, VVC divides the rough mode selection (RMD) process into two steps. The initial step involves conducting Hadamard cost calculations for the 35 modes in HEVC, selecting N modes with the lowest cost as candidate modes. In the subsequent step, a search is conducted for ±1 adjacent prediction modes from the N modes selected in the first step. The Hadamard cost is then calculated, and the candidate list is updated. Based on different perspectives and methods, a large number of scholars have conducted research on reducing the computational complexity of intra-frame prediction. From the perspective of optimizing the division of CU units, Tang et al. [8] utilized the original information retained by the pooling layer and a shape adaptive CNN network to determine whether CU should be partitioned, thereby reducing the computational complexity of RD calculations. In the context of mode decision, Zhang et al. [9] introduced an optimization strategy for progressive rough mode search. The method selectively examines and calculates the Hadamard cost of predicted modes in certain frames, aiming to alleviate the increased complexity linked to mode selection computation.

To address the computational complexity challenges posed by the QTMT division structure and mode decision, this paper introduces a fast and efficient intra-frame coding algorithm. The primary contributions of this study are as follows: (1) introduction of a decision-tree-based series partitioning decision algorithm, transforming the single-judgment QTMT division process into a joint decision-making process of QT division and MT division. This approach addresses the MT division as a multiple binary classification problem, achieving high-precision division decisions and efficiently eliminating redundant CU division modes. (2) Introduction of a mode prediction termination algorithm based on ensemble learning. This algorithm involves reordering the complete list of candidate modes based on the probability of being selected as the optimal mode. Subsequently, the prediction accuracy of the current candidate modes is determined during the RDO process, reducing the number of candidate modes for the RDO process and thereby achieving the objective of reducing computational complexity.

The subsequent sections of this paper are outlined below. In Section 2, an extensive review of VVC research is presented, focusing on two key aspects: CU segmentation and mode decision. Section 3 delves into the analysis of CU size distribution and optimal intra-frame mode selection in the VVC standard. The proposed algorithm is detailed in Section 4. Finally, Section 5 and Section 6 provide a comprehensive analysis of the data results and the concluding remarks of the proposed algorithm, respectively.

2. Related Works

In the VTM encoder, with the introduction of 67 intra-frame prediction modes and the QTMT division structure, VVC demonstrates superior compression performance compared to HEVC. The CU partitioning process incorporates MT, leading to increased diversity in the sizes of CU partitions. To accommodate the requirements of various texture structures, the complexity of the division mode decision also increases. The overall division of CTU involves calculations in both top-down and bottom-up directions. During the top-down step, partitioning occurs by traversing the parent CU and applying the partition mode list. The rate-distortion cost is then recorded under each partition mode until the leaf node is reached. In the bottom-up stage, a comparison is made between the rate-distortion costs of the child CU and the parent CU. The division mode with the smallest rate-distortion cost is then selected as the optimal division structure for the current CTU. The implementation of this two-way process has significantly enhanced compression efficiency but has also substantially increased computational complexity. Therefore, there is an urgent need to reduce the coding complexity to enhance the real-time transmission performance of VVC.

Over the years, numerous scholars have conducted extensive research on intra-frame division and prediction within coding standards like H.266/VVC, H.265/HEVC, and H.264/AVC. HEVC, as a predecessor to the current generation video coding standard, encapsulates several innovative processing ideas that can be adapted to VVC. In [10,11,12,13,14], researchers investigated fast selection algorithms for intra-frame prediction, focusing on aspects such as CU size and division depth. The authors of [10] propose a fast coding unit depth decision-making method. It models the quadtree CU depth decision-making process in HEVC as a three-layer binary decision-making problem based on the RD cost. Additionally, a flexible CU depth decision structure is introduced to enable a smooth transition between complexity and code rate performance. In [11], an early decision method based on CU size was proposed using vertical and horizontal texture features. Whether CU is a homogeneous region is determined by using the mean absolute deviation (MAD) with lower computational costs. If it is a homogeneous region, the CU size can be determined in advance. In [12], global and local edge complexity features in horizontal, vertical, and two diagonal directions were employed to determine the division of CUs. The CUs and sub-CUs at each depth are categorized as divided, undivided, and pending through type analysis. In [13], a CU size decision algorithm based on texture complexity is proposed. The algorithm streamlines the process by discarding the need to calculate each CU size individually and focuses solely on the CU sizes determined by the image texture. In [14], a fast depth judgment algorithm for increasing the size of coding blocks is presented. The algorithm achieves a reduction in the number of coding blocks in the frame by enlarging the size of PUs and TUs in CTUs. Additionally, the non-essential depth division of the CU is terminated early based on the statistical results of the gradient information of the CU.

The selection of coding modes is a prominent research area in the realm of HEVC fast coding. The authors of [15] propose an early termination scheme for intra-prediction, terminating the current coding unit mode decision and TU size selection by exploiting changes in coding mode cost. The CU cost is calculated by the Hadamard transform in the coarse mode decision stage. In [16], a predictive unit size decision and mode decision based on the texture complexity of gradient is proposed. The texture complexity and texture direction of large CUs are extracted from four directions by applying an intensity gradient filter, and the PU size of large CUs is inferred based on the characteristics of both. Then, the texture direction feature is utilized to remove modes with low prediction likelihood. In [17], a fast mode decision algorithm is proposed by utilizing statistical RD cost and bit cost. To obtain accurate feature information, the statistical properties of the sequence are first measured, and then these properties are used for fast mode adjudication. The algorithm optimizes the coding process with adaptive mode order and effectively reduces the number of mode decisions. The authors of [18] proposed a mode decision algorithm based on predicting size correlation using spatiotemporal correlation and the correlation between different layers of a quadtree. In [19], a fast mode decision algorithm is proposed using the difference in gradient directions. Before performing intra-frame prediction, the gradient direction of each CU is calculated, and a corresponding gradient mode histogram is generated. Subsequently, the gradient mode histogram is utilized to select a small number of modes for the rough mode decision process detection. The authors of [20] propose an adaptive mode hopping algorithm for mode decision-making. The algorithm adaptively selects the optimal set from three candidates for each prediction unit before mode decision-making by analyzing the statistical properties of adjacent reference samples for intra-prediction.

All the aforementioned studies have focused on intra-frame prediction within the HEVC standard, achieving a commendable balance between coding efficiency and complexity reduction. However, the VVC standard introduces new techniques in division structure and intra-frame modes, rendering the original research methods not directly applicable to VTM. Given the characteristics of the QTMT division structure and the incorporation of 67 intra-frame modes, new perspectives can be explored to reduce the computational complexity associated with these advancements. Regarding the optimization of the QTMT division structure, ref. [21] introduces the concept of employing the support vector machine (SVM) for coding unit size decisions. The approach discriminates the division direction by extracting features like texture contrast and CU entropy. Six SVM classifier models undergo online training for various CU sizes, ultimately predicting CU directions within the QTMT coding structures. In [22], a rapid coding unit division decision algorithm is introduced. The algorithm employs a novel cascade decision-making architecture tailored for QTMT division characteristics. It simultaneously determines the division decisions of QT and MT by considering the texture complexity of CUs and the contextual information of neighboring CUs. In [23], an algorithm for CU classification is introduced, which combines the principles of just noticeable distortion (JND) and SVM models. The algorithm devises a hybrid JND threshold model by considering the distortion sensitivity of visual image regions, facilitating the partitioning of CUs. Based on the partition type, the smooth region remains unclassified, the ordinary region follows the original VVC judgment criterion, and the complex region utilizes the SVM classifier for optimal division. In [24], a swift block division algorithm for intra-frame coding is discussed. The skipping of horizontal or vertical modes and early termination is accomplished through the extraction of edge features using the Canny edge detection operator for coded blocks. In [25], an approach is presented to decrease coding complexity by minimizing redundant QTMT divisions. The method employs CU division types and intra-frame prediction modes as output features, leveraging Bayesian classifiers for vertical segmentation and efficient traversal of horizontal ternary trees. In [26], an algorithm is proposed for rapid decision-making in multi-type tree partitioning using the lightweight neural network (LNN). The algorithm initially identifies explicit VVC features and derived VVC features linked to the encoding parameters of the ternary tree. Subsequently, a decision is made, based on the feature results, to either skip or perform the TT segmentation. In [27], the utilization of variance and gradient features for QTMT division decisions is proposed. In this algorithm, the delineation of the smoothed region is terminated, and the decision on whether to perform QT delineation of a CU is determined using gradient features extracted by the Sobel operator. Ultimately, the variance feature of sub-CU variance is employed for the QTMT division, facilitating single division mode selection. The authors of [28] propose a CU size early termination algorithm. This algorithm uses directional gradients to determine in advance the possibility of binary division or ternary division of the current block in the horizontal or vertical direction to achieve the purpose of skipping redundant division modes.

Fast decision-making in mode selection is also a key approach to reducing the computational complexity of VVC. In [29], an optimization algorithm for intra-frame prediction modes based on texture region features is proposed. It operates under the assumption that the content difference in the direction of the optimal mode is minimal. The texture direction of the CU is then leveraged to eliminate certain predicted modes, simplifying the intra-frame prediction process. In [30], a CU size pruning algorithm based on forward prediction is introduced. This algorithm estimates the sum of absolute transformed difference (SATD) cost for various division directions within a simplified rough selection model. The RD cost of different division directions for the sub-CU is then used as the estimated cost for the current CU. Ultimately, the optimal division direction for the current CU is determined based on the estimated SATD cost and RD cost. In [31], a set of angular prediction modes has been added to the intra-prediction mode to more accurately model angular textures. The authors of [32] introduce an adaptive pruning algorithm aimed at filtering predicted modes. This algorithm suggests eliminating redundant computations associated with intra-block copy (IBC) and intra-sub-partitions (ISPs) using learning classifiers. Additionally, it employs an integrated decision-making mechanism to rank candidate modes, followed by sequential RDO cost calculation. The final step involves utilizing the rate-distortion optimization termination model to determine the mode’s achievement of prediction accuracy.

3. Statistical Analysis

To cater to the demand for high-resolution video, the VVC standard has been introduced, aiming to facilitate the transmission of high-quality video. In contrast to HEVC, VVC incorporates a new QTMT structure and 65 angle predictions to enhance the accuracy of predicting high-resolution video texture content. Nevertheless, the extensive CU size division and coding modes lead to an increased computational complexity for the encoder. To strike a better balance between coding quality and bit rate, it is essential to conduct a detailed analysis of the VTM encoder’s operations and characteristics, enabling the design of an efficient VVC intra-frame fast coding algorithm.

To handle complex texture structures, VVC adopts a more flexible QTMT structure and increases the intra-frame angle prediction modes from 33 to 65. This technological update has greatly improved the efficiency of intra-frame prediction for texture-rich videos. However, the use of QTMT structure makes the division of CUs more flexible. Therefore, when making decisions on the optimal division type at each depth layer, it is not only necessary to determine whether to divide but also to determine the specific division type. However, the method of traversing all modes to select the optimal coding mode based on rate-distortion optimization brings increased computational complexity to the encoder. When VVC determines the optimal coding size and optimal coding mode, each CTU to be coded first initializes the coding depth. Subsequently, 67 intra-frame mode encodings are performed, and different division methods correspond to different division sizes. The divided sub-CUs are subjected to 67 intra-frame codings again until they reach the minimum CU size defined by the test environment. During the entire encoding size decision-making process, the VTM encoder needs to perform 30,805 divisions and 2,063,938 intra-mode predictions. If unnecessary division processes can be skipped after intra-frame prediction, the amount of calculation and coding complexity can be greatly reduced. On the other hand, in order to obtain better-reconstructed video frame quality, greater bit consumption is often incurred. In order to achieve higher encoding time saving and lower bit consumption and achieve a good balance between encoding complexity and encoding performance, this paper deals with it from the perspective of reducing redundant partition calculations of QT and MT and determining mode prediction in advance.

Regarding CTU partitioning, the newly introduced MT partitioning method facilitates the utilization of rectangular CUs. The probability of selecting rectangular CUs as the optimal CU shape significantly rises in response to subtle variations in local texture. However, as the CU shape becomes more flexible, it increases the challenge of coding size prediction. Hence, the analysis of CU division sizes is essential; 65 angular prediction modes and advancements in techniques like MRL have significantly contributed to enhanced coding accuracy. To ensure the encoder can flexibly choose the optimal prediction mode from 67 intra-frame prediction modes in a versatile CU division structure, it is crucial to analyze the factors influencing the distribution of optimal prediction modes.

This article conducts a traversal analysis of the depth characteristics of 26 video sequences and the distribution characteristics of 67 intra-frame modes under public testing conditions. It presents the encoding characteristics of VVC with intuitive data information. The 26 video sequences selected for testing encompass various sequence types, resolutions, bit depths, and frame rates. Table 1 provides an overview of the characteristics of the video sequences used in the experiments.

Table 1. Public test sequence.

Class	Sequence	Resolution	Frame Count	Frame Rate (fps)	Bit Depth
A1	Campfire	3840 × 2160	300	30	10
	FoodMarket4		300	60
	Tango2		294	60
A2	Catrobot	3840 × 2160	300	60	10
	DaylightRoad2		300	60
	ParkRunning3		300	50
B	BQTerrace	1920 × 1080	600	60	8
	BasketballDrive		500	50
	Cactus		500	50
	Kimono		240	24
	ParkScene		240	24
C	BQMall	832 × 480	600	60	8
	BasketballDrill		500	50
	PartyScene		500	50
	RaceHorsesC		300	30
D	BasketballPass	416 × 240	500	50	8
	BlowingBubbles		500	50
	BQSquare		600	60
	RaceHorses		300	30
E	FourPeople	1280 × 720	600	60	8
	Johnny		600	60
	KristenAndSara		600	60
F	BasketballDrillText	832 × 480	500	50	8
	ChinaSpeed	1280 × 720	500	30
	SlideEditing		300	20
	SlideShow		500	20

3.1. Size Distribution Analysis of Coding Units in VVC

For the reliability and feasibility of the experiments, six video sequences with different categories, resolutions, bit depths, and texture characteristics are selected from the specified 26 test video sequences for in-depth analysis. Table 2 provides detailed characteristics of the experimental sequences.

Table 2. CU size analysis experimental sequence information.

Class	Sequence	Resolution	Bit Depth	Content Information
A1	FoodMarket	3840 × 2160	10	Global motion
A2	Catrobot	3840 × 2160	10	Local motion information
B	BasketballDrive	1920 × 1080	8	Global motion and local motion
C	PartyScene	832 × 480	8	High texture complexity
D	RaceHorses	416 × 240	8	Large amplitude motion
E	Johnny	1280 × 720	8	Large background area

In terms of CU size division, depth information is a crucial feature. Due to the adoption of the QTMT structure, various combinations between QT and MT are possible. When a CU adopts an MT partitioning structure, subsequent partitioning of that CU will no longer involve QT partitioning. Based on the recursive partitioning characteristics of CUs, there is a close relationship between CU depth and size. If the depth information of a CU is known, the current size information of that CU can be inferred from the depth information of QT and MT. Therefore, in this paper, the CU depth information is represented in the form of ${\mathrm{Q}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{j}}$, where i denotes the QT division depth and j denotes the MT division depth. In the VTM generic coding environment, the size of the coding tree cell is 128 × 128, the minimum QT coding cell size is 8 × 8, and the maximum MT depth is 3. Therefore, the range of values of i is {0, 1, 2, 3, 4}, and the range of values of j is {0, 1, 2, 3}. Among VTM-10.0, the optimal coding depth is analyzed for the six selected sequences under the conditions of QP of 22, 27, 32, and 37, respectively. The experimental results are shown in Figure 4.

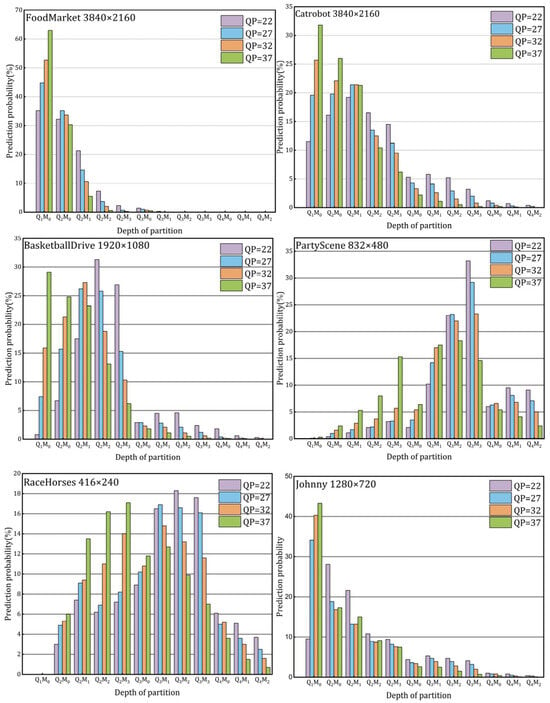
Figure 4. Optimal coding depth analysis of experimental sequences at different QPs.

The figure depicts the probability of choosing various CU partition depths as the optimal depth for each video sequence when encoding with four different QPs. From the perspective of the overall optimal division depth, the vast majority of the test sequence tended to select the small division depths of ${\mathrm{Q}}_1{\mathrm{M}}_0$ and ${\mathrm{Q}}_2{\mathrm{M}}_{\mathrm{j}}$ as the optimal division depths with a prediction probability of 68% or more. Conversely, the probability of selecting the maximum depth ${\mathrm{Q}}_4{\mathrm{M}}_2$ as the optimal coding depth is the lowest among all experimental sequences. Specifically, the figure illustrates a negative correlation between CU division depth and the overall trend of optimal depth selection. Therefore, terminating the QTMT division early is a feasible way to reduce the amount of coding computation. From the perspective of MT optimal division depth, the probability of using only QT division is about 42%. In particular, the probability of only one MT division is 20.2%, which is a large proportion among MT divisions. Therefore, skipping the MT division mode holds a high potential for reducing coding complexity.

3.2. VVC Intra-Frame Mode Analysis

In VTM encoders, a classical three-step intra-frame mode decision method is employed to streamline the complexity of intra-frame mode selection in H.266/VVC. The core of the method is to select the mode with the smallest RDO cost as the optimal prediction mode from the complete mode list (CML), which includes the rough mode decision (RMD) list and the most probable modes (MPM) list. Within the CML, the three modes in the RMD mode list with the smallest Hadamard cost are positioned at the top of the full mode list in ascending order. The remaining candidate modes are then derived from the modes in the MPM list. During the rationality validation of the CML ranking scheme, it was observed that the probability of the same positional candidate mode being selected as the optimal mode varied with the number of candidate modes. Ultimately, the Hadamard cost, MRL prediction information, and spatial coding information of the candidate modes were identified as having a significant impact on the distribution of optimal modes. In order to find a more reasonable order for arranging the candidate modes, three key factors affecting the distribution of optimal modes are analyzed in this section. The selected test sequence information is shown in Table 3.

Table 3. Optimal mode analysis of experimental sequence information.

Class	Sequence	Resolution	Bit Depth	Content Information
A1	Campfire	3840 × 2160	10	The brightness dynamic range is large
A2	Catrobot	3840 × 2160	10	Local motion information
B	Cactus	1920 × 1080	8	Rotating objects
C	BQMall	832 × 480	8	Complex texture content
D	BasketballPass	416 × 240	8	Global and local motion information
E	FourPeople	1280 × 720	8	Simple background

3.2.1. Hadamard Cost of Candidate Models

In the calculation of the probability of a candidate mode being selected as the optimal mode, the Hadamard cost ratio (${\mathrm{H}\mathrm{R}}_{\mathrm{i}}$) of the front and back candidate modes is a crucial influencing factor. The variable ${\mathrm{P}}_{h\left(\mathrm{i}\right)}$ denotes the cumulative probability that the first i candidate modes are selected as the optimal candidate mode and is an overall description of the probability of optimal mode selection. In order to accurately obtain the probability ${\mathrm{P}}_{\mathrm{i}}$ of each candidate mode being selected as the best mode, it is necessary to find the relationship between the Hadamard cost ratio ${\mathrm{H}\mathrm{R}}_{\mathrm{i}}$ and the cumulative probability ${\mathrm{P}}_{h\left(\mathrm{i}\right)}$. ${\mathrm{H}\mathrm{R}}_{\mathrm{i}}$ is calculated as follows:

$${\mathrm{H}\mathrm{R}}_{\mathrm{i}}=\frac{{\mathrm{H}\mathrm{c}}_{\mathrm{i}+1}-{\mathrm{H}\mathrm{c}}_{\mathrm{i}}}{{\mathrm{H}\mathrm{c}}_{\mathrm{i}}}$$

(1)

where ${\mathrm{H}\mathrm{c}}_{\mathrm{i}}$ denotes the Hadamard cost of the ith candidate model. After obtaining ${\mathrm{H}\mathrm{R}}_{\mathrm{i}}$ between the ith and the i + 1th candidate mode by using Equation (1), the value of ${\mathrm{H}\mathrm{R}}_{\mathrm{i}}$ is taken as the total interval and divided into a number of sub-intervals and ${\mathrm{P}}_{h\left(\mathrm{i}\right)}$ is counted for all the samples within the sub-intervals, respectively. Data analysis of the statistical sample information reveals that when the ${\mathrm{H}\mathrm{R}}_{\mathrm{i}}$ of the model is larger, the data of ${\mathrm{P}}_{h\left(\mathrm{i}\right)}$ also tend to increase and there is a clear exponential relationship. Therefore, when there is a large difference between the Hadamard cost of the ith and the i + 1th candidate model, it will make the cumulative probability ${\mathrm{P}}_{h\left(\mathrm{i}\right)}$ of the first i optimal model higher and also proves that there is a strong correlation according to the correlation between ${\mathrm{H}\mathrm{R}}_{\mathrm{i}}$ and ${\mathrm{P}}_{h\left(\mathrm{i}\right)}$.

3.2.2. MRL Forecast Information

In the VVC standard, the reference row of the prediction mode is transformed from a single nearest neighbor reference row in HEVC to multiple reference rows for information multiplexing. Therefore, the difference in the selected reference rows also introduces a certain degree of uncertainty in the selection of the optimal mode. In our experiments, we found that the probability of different candidate modes being selected as the optimal pattern changes when there are differences in the reference rows used. To investigate the impact of variations in reference rows on the distribution of optimal modes, we calculate the probability of optimal modes for all combinations of the CML containing four candidate modes. In the experiments, different combinations of reference rows are applied to the first three candidate modes. When the candidate mode selects the nearest reference row for interpolation prediction, it is represented by “0”. Conversely, when the candidate mode opts for additional reference rows, it is represented by “1”, resulting in a total of 8 combinations. The experimental results, illustrated in Figure 5, reveal a significant impact of different reference row applications on the probability of a candidate mode being selected as the optimal mode.

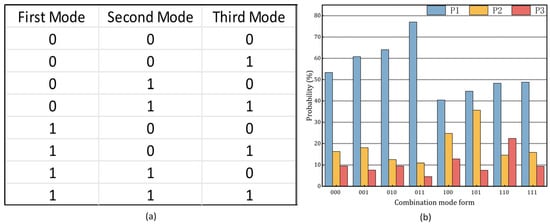
Figure 5. Different combinations of reference rows and corresponding optimal mode distribution results. (a) Combination form of reference lines; (b) Optimal mode distribution probability.

3.2.3. Spatial Coding Information

Higher-resolution videos typically contain more detailed texture content. Specifically, the texture content of neighboring CUs exhibits a high degree of correlation, often leading to similar choices in optimal mode selection. Therefore, the optimal prediction mode information of neighboring CUs can provide information reference for the CUs to be predicted. To assess the strength of the optimal mode correlation between the target CU and its neighboring CUs, an exhaustive mode search is conducted on the test video sequence, and the results are depicted in Figure 6. The experimental results reveal that the probability of the best candidate mode for the current CU being identical to the optimal modes of the left CU and the upper CU is over 30%. This substantiates the significant influence of spatial coding information on optimal mode selection.

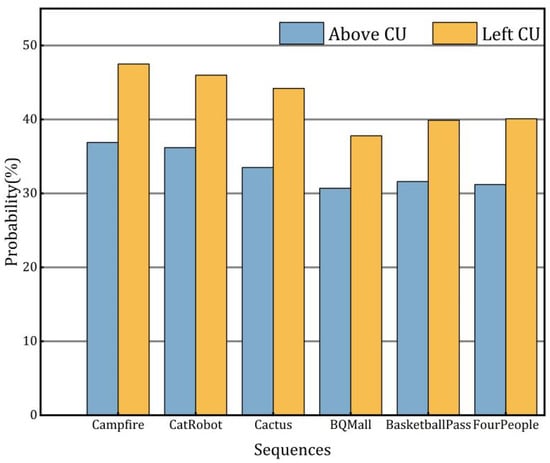
Figure 6. Conditional probability distribution results for the best mode of the current CU and neighboring CU.

4. The Proposed Fast Intra-Coding Algorithm

From a theoretical point of view, the important innovations of VVC are the QTMT division structure and the application of 67 intra-frame prediction modes. Compared with HEVC, it saves about 40% or more of the code rate, but there is also a significant increase in computational complexity. In Section 3, the feasibility and effectiveness of the optimization scheme are verified by the analysis of CU size distribution and intra-frame prediction modes. For the two perspectives of CU division and intra-frame prediction mode selection, we propose an intra-frame coding scheme with a combined approach. The solution includes the decision-tree-based series partitioning decision algorithm (SPD-DT) and the mode prediction termination algorithm based on ensemble learning (PTEL).

4.1. Decision-Tree-Based Series Partitioning Decision Algorithm

In the investigation of CU segmentation, a novel approach involves transforming the CU segmentation decision into a classification problem. The core of the decision lies in selecting the segmentation mode suitable for the current CU texture characteristics from the six available segmentation modes. In [33], a classical CU division decision termination framework is presented, as depicted in Figure 7a. The method uses coding information derived from the current CU depth for intra-frame prediction to decide whether to terminate the division early. If the classifier deems it necessary to continue the division, the candidate division modes are evaluated sequentially until the mode with the least costly rate distortion is identified. In this division decision, performing intra-frame prediction for each decision layer is computationally redundant. As the division process is checked recursively, CU types requiring further division do not need to undergo intra-frame prediction. While terminating the case of five division modes reduces complexity, the improvement in coding efficiency is limited. In [10], the process of CU depth decision-making is modeled as a three-layer binary classification problem. It involves multiple binary classifiers with different parameters, forming a framework for division pattern selection, as illustrated in Figure 7b. The decision method initiates its first level of judgment by determining whether the CU requires division. If division is unnecessary, all division modes are terminated, and the optimal size of the CU is determined. On the other hand, if division is chosen, multiple classifiers are employed to select the candidate division mode with the highest probability. Applying this method reduces computational redundancy in coding unit selection. However, the prediction accuracy is compromised by the “multiple choice” judgment. To address the need for low computational effort and high prediction accuracy in CU segmentation, this paper proposes a decision-making algorithm for tandem segmentation of QT and MT.

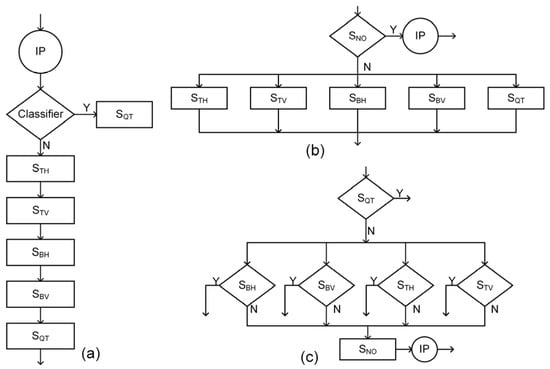
Figure 7. CU partition decision framework. (a) Early termination partitioning framework; (b) Multicategory joint decision-making framework; (c) Proposed series decision-making framework.

The algorithm design is inspired by the sequential properties between QT and MT in the QTMT structure. It transforms the VTM partitioning judgment process into a joint judgment of QT partitioning and MT partitioning. In the QTMT structure, MT division nodes must take over QT leaf nodes. If the MT division is chosen for the CU division, the QT division becomes unavailable for sub-CU partitioning. On the other hand, considering the loss of prediction accuracy caused by the “multiple choice” of classifiers on the MT segmentation judgment, we convert the MT segmentation judgment into multiple binary judgments to achieve high accuracy segmentation prediction. The framework of the decision-making algorithm is depicted in Figure 7c.

The algorithm conducts texture feature extraction for each CU to be encoded, feeding the results into a trained classifier to determine whether it needs to undergo further division into smaller CUs. Among the judgment steps, the QTMT divides the judgment into five different types of binary judgments. Initially, the decision is made on whether to use the QT division for the current CU. If it is determined that the current CU adopts QT partitioning, the screening calculation for the MT division will not be performed at the current depth. If the current CU does not perform QT segmentation, the screening calculation for QT segmentation is not performed and the appropriate segmentation decision is selected from among the four types of MT segmentation. If MT partitioning is selected, the vertical binary tree partitioning adjudicator, horizontal binary tree partitioning adjudicator, vertical ternary tree partitioning adjudicator, and horizontal ternary tree partitioning adjudicator are simultaneously employed to determine the optimal CU partitioning method. If the output results of the five partitioning decisions are all no partitioning, the current CU does not need to be divided more precisely.

In order to realize low-complexity model construction, this study adopts the method of big data offline learning. The division decision model is trained from a large amount of data by machine learning methods. As offline learning is utilized, the classification model does not add encoder loss. Considering the complexity of constructing a segmentation model, this study utilizes multiple classifiers to achieve the segmentation of the QTMT structure, which requires that the complexity of the individual classifiers be as low as possible. Secondly, during CU determination, there may be samples with low classification characterization. To mitigate the loss of RD performance, the classifier needs the ability to handle non-linear problems. Therefore, SVM or decision tree (DT) models are considered in this paper. In the experiments, the test samples exhibit a sufficient number and small feature dimensions. The results indicate that the two machine learning methods show minor differences in prediction accuracy. Regarding computational complexity, DT only requires a “yes or no” judgment during prediction, necessitating minimal computation. In contrast, SVM presents higher difficulty compared to DT. However, DT possesses the ability to capture complex relationships between features. When handling a substantial amount of data, DT can filter feature attributes with strong relevance using information gain. Combining the above analyses, this study ultimately includes DT as the most suitable classifier for CU segmentation decisions.

To ensure the reliability of CU division judgment results, various effective feature attributes need to be selected. Starting from the texture of the overall CU, this article considers CU variance, gradient, contrast, and texture direction. To cope with the flexible division structure of QTMT, this study includes local texture features to cope with the detailed changes in CU. On the other hand, the strong spatial correlation of video content makes the coding information of neighboring CUs an important reference index, including the coding size information of spatially neighboring CUs. To select more effective CU partition features, we conducted information entropy calculation tests on different types of features, selecting features with higher information entropy to demonstrate the effectiveness of the selected features. The higher the information entropy, the more effective the selected features are for the current classification. Finally, the need for comprehensive feature calculation complexity and smaller additional calculations is also one of the considerations for feature selection. We select two major categories comprising 13 coding features with high information gain.

(1)

Texture information

Global texture information: the CU segmentation decision has a strong correlation with the content characteristics of the coded block. In this paper, seven feature points are selected to measure the texture flatness and directionality of the video content. The family of features includes coded block size (${\mathrm{f}}_{\mathrm{C}\mathrm{B}\mathrm{S}}$), maximum gradient magnitude (${\mathrm{f}}_{\mathrm{M}\mathrm{G}\mathrm{M}}$), number of high-gradient pixels (${\mathrm{f}}_{\mathrm{N}\mathrm{H}\mathrm{G}\mathrm{P}}$), horizontal and vertical gradients sum (${\mathrm{f}}_{{\mathrm{G}}_{\mathrm{h}}+{\mathrm{G}}_{\mathrm{v}}}$), average gradient in horizontal direction (${\mathrm{f}}_{\mathrm{A}\mathrm{G}\mathrm{H}}$), average gradient in vertical direction $\left({\mathrm{f}}_{\mathrm{A}\mathrm{G}\mathrm{V}}\right)$, and directionality of texture content (${\mathrm{f}}_{{\mathrm{G}}_h/{\mathrm{G}}_{\mathrm{v}}}$). In particular, the horizontal gradient ${\mathrm{G}}_h$ and vertical gradient ${\mathrm{G}}_{\mathrm{v}}$ of the CU are extracted and computed using the Sobel operator.

$$G_h={\sum }_{i=1}^W{\sum }_{j=1}^{H}A\times \left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]$$

(2)

$$G_{\mathrm{v}}={\sum }_{i=1}^W{\sum }_{j=1}^{H}A\times \left[\begin{array}{ccc}1& 2& 1\\ 0& 0& 0\\ -1& -2& -1\end{array}\right]$$

(3)

where A denotes the luminance matrix of the CU, W is the width of the CU, and H is the height of the CU. The horizontal and vertical gradients and ${\mathrm{f}}_{{\mathrm{G}}_h+{\mathrm{G}}_{\mathrm{v}}}$ are:

$$\begin{array}{l}{f}_{G_h+G_v}={\sum }_{i=0}^{W-1}{\sum }_{j=0}^{H-1}(\left|A_{\left(i,j-1\right)}-A_{\left(i,j+1\right)}\right|\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left|A_{\left(i-1,j\right)}-A_{\left(i+1,j\right)}\right|)\end{array}$$

(4)

where W, H denote the width and height of the CU, respectively. ${\mathrm{A}}_{\left(\mathrm{i},\mathrm{j}\right)}$ denotes the luminance value of the corresponding coordinate of the CU, $1<\mathrm{i}<\mathrm{W},1<\mathrm{j}<\mathrm{H}$.${\mathrm{f}}_{{\mathrm{G}}_h/{\mathrm{G}}_{\mathrm{v}}}$ is used to determine whether there is directionality in the CU texture, calculated as:

$$f_{G_h/G_v}={\sum }_{i=0}^{W-1}{\sum }_{J=0}^{H-1}\frac{\left|A_{\left(i,j-1\right)}-A_{\left(i,j+1\right)}\right|}{\left|A_{\left(i-1,j\right)}-A_{\left(i+1,j\right)}\right|}$$

(5)

${\mathrm{f}}_{\mathrm{M}\mathrm{G}\mathrm{M}}$ and ${\mathrm{f}}_{\mathrm{N}\mathrm{H}\mathrm{G}\mathrm{P}}$ can describe the smoothness and complexity of the texture content, with larger values indicating a higher probability that the coded block will continue to be divided. These features leverage texture information and the high correlation between horizontal and vertical divisions of MT to inform classification decisions.

Local texture information: local texture features provide detailed descriptions of specific texture regions, exerting a significant impact on MT segmentation decisions. This article selects 4 features to describe changes in local texture feature information, including the variance of the upper and lower parts of the CU (${\mathrm{f}}_{\mathrm{U}\mathrm{B}\mathrm{D}}$), the variance of the left and right parts of the CU (${\mathrm{f}}_{\mathrm{L}\mathrm{R}\mathrm{D}}$), the mean value of ${\mathrm{f}}_{\mathrm{U}\mathrm{B}\mathrm{D}}$, and the average value of ${\mathrm{f}}_{\mathrm{L}\mathrm{R}\mathrm{D}}$. In this paper, the method for calculating differences is implemented through the use of local texture variance.

(2)

Adjacent CU encoding information

In order to utilize the information about the size division of neighboring CUs brought about by the strong spatiality of the video, in this paper, ${\mathrm{f}}_{\mathrm{N}\mathrm{Q}\mathrm{T}}$ and ${\mathrm{f}}_{\mathrm{N}\mathrm{Q}\mathrm{T}\mathrm{M}\mathrm{T}}$ are chosen to denote the depth difference between the spatial neighboring CUs and the current CU. Spatially neighboring CUs exist in five different orientations of the current CU: upper right, upper, upper left, left, and lower left. For the representation of depth information, the characterization is borrowed from ${\mathrm{Q}}_{\mathrm{i}}{\mathrm{M}}_{\mathrm{j}}$ in Section 3, where the depth of ${\mathrm{D}}_{\mathrm{Q}\mathrm{T}}$ is i and the depth of ${\mathrm{D}}_{\mathrm{Q}\mathrm{T}\mathrm{M}\mathrm{T}}$ is “i + j”. ${\mathrm{f}}_{\mathrm{N}\mathrm{Q}\mathrm{T}}$ represents the count of occurrences where the ${\mathrm{D}}_{\mathrm{Q}\mathrm{T}}$ of five adjacent CUs exceeds the ${\mathrm{D}}_{\mathrm{Q}\mathrm{T}}$ of the current CU. Similarly, ${\mathrm{f}}_{\mathrm{N}\mathrm{Q}\mathrm{T}\mathrm{M}\mathrm{T}}$ is used to characterize the difference in the number of QTMT depths between the current CU and neighboring CUs. When both eigenvalues are larger, it indicates that the probability of the current CU to continue the division is higher. Conversely, when both eigenvalues are smaller, it indicates that the coding size of the neighboring CUs is larger than that of the current CU, and the probability of the current CU to proceed to terminate the division is higher. Following feature extraction, the data are input into the trained decision tree classifier, initiating the CU joint division decision algorithm. In order to enhance the stability of the model, this paper introduces the method of setting the confidence level to prune the trained decision tree model to avoid overfitting the model. The current CU is determined to be an unknown CU when the confidence level of the leaf nodes of the decision tree is less than 0.9. A traditional full RDO search is performed for unknown CUs to minimize performance loss.

4.2. Mode prediction Termination Algorithm Based on Ensemble Learning

The VVC standard introduces an additional 32 angle prediction modes on top of the 33 angle prediction modes in the HEVC standard, significantly improving video compression efficiency. In order to reduce the computational burden caused by the increase in angle prediction modes, the VTM encoder adopts a three-level optimization strategy (RMD + MPM + RDO). Given that the three-step optimization strategy still necessitates the rate-distortion optimization process based on Lagrange multipliers for all candidate modes, it involves a significant amount of redundant computations. Consequently, this paper introduces a mode prediction termination algorithm based on ensemble learning.

In VVC intra-frame mode analysis, the Hadamard cost of candidate modes, MRL prediction information, and spatial coding information significantly influence the selection of the optimal prediction mode. In order to effectively rank the candidate modes within CML more accurately, these three major categories of features are used as important indicators for integrated decision-making, including a base classifier based on Hadamard cost, a base classifier based on MRL information, a base classifier based on the optimal mode of the upper CU, and a base classifier based on the optimal mode of the left CU. The algorithm proposed in this paper dynamically calculates the probability of the current candidate mode being selected as the optimal mode through four base classifiers. It then reorders the list of candidate modes according to the high probability. Subsequently, RDO cost calculation is performed on the candidate modes in sequence. Finally, the decision tree-based rate-distortion optimization termination model determines whether the selected mode meets the accuracy requirements. If the prediction accuracy requirement is met, the RDO process for the remaining candidate modes will be terminated. If the accuracy requirement is not met, proceed to the next candidate mode judgment in sequence. The algorithm process is shown in Figure 8.

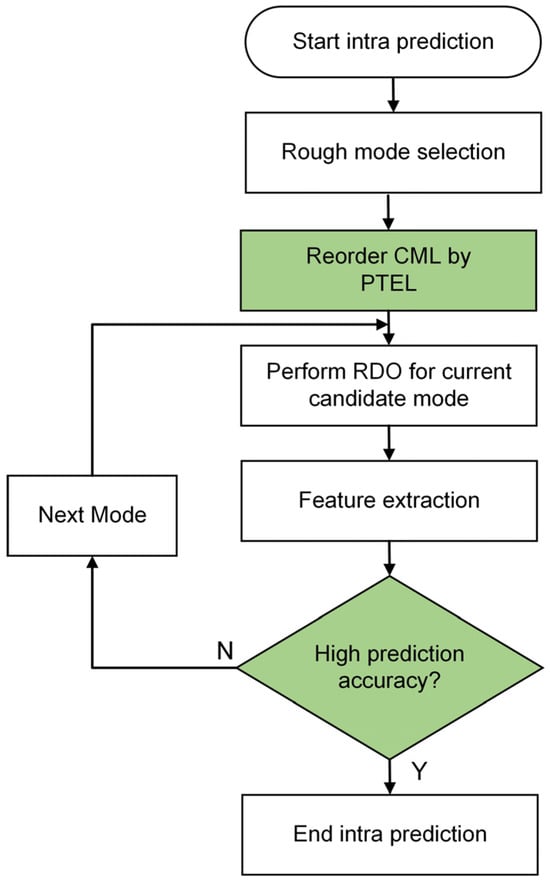
Figure 8. The mode prediction termination framework based on ensemble learning.

The four base classifiers used in this paper have different probability prediction methods. After obtaining the probability information of each classifier, different weights are assigned to dynamically calculate the probability of different candidate modes being selected as the optimal mode. The two base classifiers associated with spatial encoding information select the optimal mode of adjacent CUs as the result of optimal mode selection in predicted CUs. The base classifier for MRL information ${\mathrm{P}}_{\mathrm{i}}$ is obtained by combining results from different reference rows. After obtaining the Hadamard cost of each candidate pattern in CML, the classifier based on Hadamard cost calculates the ${\mathrm{H}\mathrm{R}}_{\mathrm{i}}$ and cumulative probability ${\mathrm{P}}_{h(\mathrm{i})}$ of adjacent candidate modes using Equations (1) and (2), respectively. Ultimately, the ${\mathrm{P}}_{\mathrm{i}}$ of the target candidate mode is the difference between ${\mathrm{P}}_{h(\mathrm{i})}$ and ${\mathrm{P}}_{h(\mathrm{i}-1)}$. For weight calculation, an exhaustive mode search step is conducted on the six selected test sequences to construct a dataset containing the necessary information for the four base classifiers. The overall weight calculation is completed offline and the weight assignments are used directly in the middle of the test.

In the weighting calculation, the number of data samples in which the optimal mode predicted by each base classifier corresponds to the actual optimal mode is the accurate number. The Hadamard cost-based classifier and MRL information-based classifier calculate the probability of being selected as the optimal mode for each candidate mode but cannot obtain the estimated correct number of times. In order to ensure the accuracy of weight calculation, this paper defines the number of correct times, denoted as ${\mathrm{n}}_1$ and ${\mathrm{n}}_2$, as the number of times the base classifier estimates the optimal mode ${\mathrm{P}}_{\mathrm{i}}$ that exceeds 80%. The correct result of the base classifier in spatial coding information is determined by the optimal prediction mode of adjacent CUs. Therefore, the accurate number of base classifiers of this type is obtained by multiplying the total number of samples in the dataset by the average probability. The number of times the base classifier based on the optimal mode of the left CU and the base classifier based on the optimal mode of the upper CU predict correctly is denoted as ${\mathrm{n}}_3$ and ${\mathrm{n}}_4$, respectively. Subsequently, the optimal mode prediction probability model is established based on the maximum likelihood estimation criterion, calculated as follows:

$$\widehat{\mathrm{M}}={\mathrm{a}\mathrm{r}\mathrm{g}}_{\widehat{\mathrm{M}}}^{\mathrm{m}\mathrm{a}\mathrm{x}}\log ({\mathsf{\alpha }}^{{\mathrm{n}}_1}·{\mathsf{\beta }}^{{\mathrm{n}}_2}·{\mathsf{\gamma }}^{{\mathrm{n}}_3}·{\mathsf{\delta }}^{{\mathrm{n}}_4})$$

(6)

where $\mathsf{\alpha }$,$\mathsf{\beta }$,$\mathsf{\gamma }$, and $\mathsf{\delta }$ are the weights of the base classifiers based on Hadamard cost, MRL information, left CU optimal mode, and upper CU optimal mode, respectively, with the sum of the weights equal to 1. For the calculation of the four weight values in the probability model, the expectation maximization (EM) algorithm is used to find the maximum likelihood function. On the other hand, the expectation maximization algorithm can be used to handle parameter estimation of probabilistic models that contain latent variables or incomplete data. Therefore, we select a set of observable samples $\mathrm{x}=({\mathrm{x}}^{(1)},{\mathrm{x}}^{(2)},\dots ,{\mathrm{x}}^{(\mathrm{m})},)$ and a set of unobservable data $\mathrm{z}=({\mathrm{z}}^{(1)},{\mathrm{z}}^{(2)},\dots ,{\mathrm{z}}^{(\mathrm{m})},)$. In the process of finding the maximum the likelihood function, we choose to use Jensen’s inequality to find the lower limit of the likelihood function. Therefore, the maximum likelihood function of the statistical model can be transformed, as shown in Equation (7):

$$\widehat{\mathrm{M}}=\mathrm{a}\mathrm{r}\mathrm{g}{}_{\widehat{\mathrm{M}}}{}^{\mathrm{m}\mathrm{a}\mathrm{x}}\sum _{\mathrm{i}=1}^{\mathrm{m}}{\sum }_{{\mathrm{z}}^{(\mathrm{i})}}{\mathrm{Q}}_{\mathrm{i}}({\mathrm{z}}^{(\mathrm{i})})\log \frac{\mathrm{P}\left({\mathrm{x}}^{(\mathrm{i})},{\mathrm{z}}^{(\mathrm{i})}|\widehat{\mathrm{M}}\right)}{{\mathrm{Q}}_{\mathrm{i}}({\mathrm{z}}^{\mathrm{i}})}$$

(7)

where is ${\mathrm{Q}}_{\mathrm{i}}({\mathrm{z}}^{\mathrm{i}})$ the distribution probability function of unobservable data z, and the calculation formula is as follows:

$${\mathrm{Q}}_{\mathrm{i}}({\mathrm{z}}^{\mathrm{i}})=\frac{\mathrm{P}\left({\mathrm{x}}^{(\mathrm{i})},{\mathrm{z}}^{(\mathrm{i})}|\widehat{\mathrm{M}}\right)}{{\sum }_{{\mathrm{z}}^{\mathrm{i}}}\mathrm{P}\left({\mathrm{x}}^{(\mathrm{i})},{\mathrm{z}}^{(\mathrm{i})}|\widehat{\mathrm{M}}\right)}$$

(8)

Finally, the weights of each base classifier are obtained by taking partial derivatives of each variable. Combining the above calculations, the probability of each candidate mode being selected as the optimal mode is:

$$\left[{\mathrm{P}}_1,{\mathrm{P}}_2,\cdots {\mathrm{P}}_{\mathrm{i}}\right]={\sum }_{\mathrm{n}=1}^4{\mathrm{W}}_{\mathrm{n}}·\left[{{\mathrm{P}}_1}^{\mathrm{n}},{{\mathrm{P}}_2}^{\mathrm{n}},\cdots ,{{\mathrm{P}}_{\mathrm{i}}}^{\mathrm{n}}\right]$$

(9)

where i is the overall number of candidate modes and ${\mathrm{W}}_{\mathrm{n}}$ is the weight of different base classifiers, $\mathrm{n}\in \left(1,2,3,4\right)$.$\left[{{\mathrm{P}}_1}^{\mathrm{n}},{{\mathrm{P}}_2}^{\mathrm{n}},\cdots ,{{\mathrm{P}}_{\mathrm{i}}}^{\mathrm{n}}\right]$ is the probability value that a different mode within the nth base classifier is selected as the optimal mode.

A decision tree model serves as the adjudicator to determine whether the current candidate model meets the accuracy requirements. Since each candidate mode performs the step of RDO before the candidate mode accuracy determination, the features with higher candidate mode coding performance should be selected as the target of feature extraction. The RDO cost ratio between the previous candidate mode and the current candidate mode (${\mathrm{f}}_{\mathrm{R}\mathrm{P}\mathrm{C}}$), the RDO cost ratio between neighboring CUs and to-be-predicted CUs (${\mathrm{f}}_{\mathrm{R}\mathrm{C}\mathrm{N}}$), and the RDO cost ratio between parent CUs and to-be-predicted CUs (${\mathrm{f}}_{\mathrm{R}\mathrm{C}\mathrm{P}}$) are selected as the features for accuracy determination by filtering the high-gain coding features.

4.3. Overall Algorithm

Summarizing the above, the fast encoding algorithm proposed in this paper includes a decision-tree-based series partitioning decision algorithm and a mode prediction termination algorithm based on ensemble learning, which is embedded in VTM to achieve the goal of reducing computational complexity. The general framework diagram for the proposed fast intra-frame coding under the VVC standard is shown in Figure 9. The decision-tree-based series partitioning decision algorithm extracts features from the texture characteristics of video sequence content. When QT partitioning is not performed, MT partitioning is used as the output result. Specifically, the MT partitioning decision consists of four parallel classifiers. This decision architecture reduces the redundant CU size prediction process in the QTMT partitioning structure. The mode prediction termination algorithm based on ensemble learning reorders the complete list of candidate modes according to the probability of each candidate mode being selected as the optimal mode and introduces a decision tree model to audit the prediction accuracy, which overcomes the shortcoming of the VVC criterion that the candidate patterns are ranked by a single Hadamard cost and also realizes the early termination of redundant candidate modes.

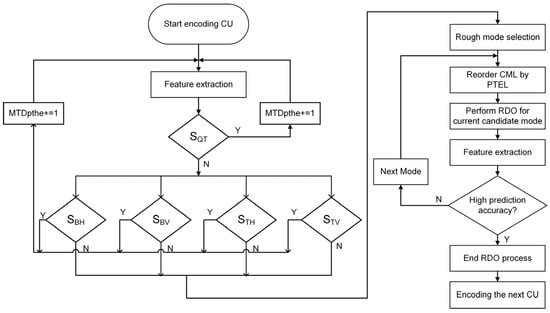
Figure 9. The proposed framework for fast intra-frame coding algorithms.

5. Experimental Results

To effectively demonstrate the performance of the proposed fast intra-frame coding algorithm, we integrate the designed coding scheme into the official reference software VTM 10.0 and test it with 26 officially released video sequences. The experiments in this article were all under the configuration of the VTM general test environment CTC, the QP values were selected as 22, 27, 32, and 37, and the encoding was completed under the All-Intra configuration. The test sequences encompass seven categories with varying resolutions, bit depths, and frame numbers. The specific information for the video sequences is presented in Table 1. The detailed configuration of the performance analysis experiment is outlined in Table 4.

Table 4. Experimental parameter configuration.

Hardware		Software
CPU	Intel(R) Core (TM) i7-11800H (Lenovo, Beijing, China)	Reference software	VTM 10.0
RAM	16 GB	Configuration	All intra
OS	Microsoft Windows 10 64 bit	QP	22,27,32,37

In Section 5.1, the overall experimental performance and the performance of a single algorithm are analyzed. In Section 5.2, the performance of the algorithm proposed in this paper is compared with the experiments of related algorithms. For quality assessment, average time savings (ATS) and Bjøntegaard delta bit rate (BDBR) are used to measure the complexity and bit rate performance of the algorithm. The calculation formula is as follows:

$$\mathrm{A}\mathrm{T}\mathrm{S}(\%)=\frac{{\mathrm{T}}_{\mathrm{V}\mathrm{T}\mathrm{M}}-{\mathrm{T}}_{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{d}}}{{\mathrm{T}}_{\mathrm{V}\mathrm{T}\mathrm{M}}}$$

(10)

where ${\mathrm{T}}_{\mathrm{V}\mathrm{T}\mathrm{M}}$ denotes the original coding time consumption in the VTM encoder and ${\mathrm{T}}_{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{d}}$ denotes the coding time consumption after adding the algorithm in this paper.

$$\mathrm{B}\mathrm{D}\mathrm{B}\mathrm{R}(\%)=\frac{{\mathrm{B}}_{\mathrm{V}\mathrm{T}\mathrm{M}}-{\mathrm{B}}_{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{d}}}{{\mathrm{B}}_{\mathrm{V}\mathrm{T}\mathrm{M}}}$$

(11)

where ${\mathrm{B}}_{\mathrm{V}\mathrm{T}\mathrm{M}}$ denotes the raw bit rate of VTM encoding and ${\mathrm{B}}_{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{d}}$ denotes the raw bit rate consumption after adding the algorithm in this paper.

5.1. Analysis of the Proposed Algorithm

The fast intra-frame coding scheme proposed in this paper includes a decision-tree-based series partitioning decision algorithm and a mode prediction termination algorithm based on ensemble learning. The decision-tree-based series partitioning decision algorithm can skip MT partitioning by concatenating QT partitioning and MT partitioning. The CU that performs MT partitioning adopts a multiclassifier decision form to achieve only one specific mode partitioning at a time. The mode prediction termination algorithm based on ensemble learning involves two steps: reordering candidate modes and determining accuracy. This significantly reduces redundant RDO calculations for candidate modes. Table 5 shows the encoding performance of two single and combination algorithms.

Table 5. Performance comparison of single algorithm and overall algorithm in this paper.

Class	Sequence	SPD-DT		PTEL		Overall
		ATS (%)	BDBR (%)	ATS (%)	BDBR (%)	ATS (%)	BDBR (%)
A1	Campfire	51.31	0.98	14.15	0.12	56.35	1.32
	FoodMarket4	55.63	0.59	12.32	0.10	52.67	1.16
	Tango2	52.32	1.01	12.57	0.13	66.89	2.01
A2	Catrobot	46.37	1.08	14.33	0.51	62.35	1.64
	DaylightRoad2	61.52	0.51	12.58	0.26	63.24	1.58
	ParkRunning3	54.17	0.79	13.46	0.25	58.41	1.65
B	BQTerrace	57.35	2.11	12.64	0.24	56.35	1.56
	BasketballDrive	65.10	2.30	14.92	0.23	59.43	1.86
	Cactus	57.92	1.91	13.13	0.31	62.53	1.71
	Kimono	64.34	1.89	13.55	0.23	66.21	1.53
	ParkScene	58.33	1.35	12.64	0.22	58.42	1.63
C	BQMall	56.36	2.21	12.25	0.33	50.21	1.55
	BasketballDrill	49.58	1.98	12.18	0.27	48.11	1.72
	PartyScene	46.33	0.63	11.97	0.25	49.32	1.31
	RaceHorsesC	49.66	1.22	13.31	0.16	49.23	1.36
D	BasketballPass	47.34	2.42	12.42	0.30	42.13	1.72
	BlowingBubbles	42.35	0.81	11.33	0.23	39.05	1.47
	BQSquare	46.82	0.79	10.25	0.25	44.22	1.36
	RaceHorses	44.21	0.93	13.17	0.24	48.23	1.56
E	FourPeople	58.47	2.81	12.91	0.37	55.88	1.70
	Johnny	9.52	3.35	13.22	0.28	57.69	2.09
	KristenAndSara	59.87	2.48	12.84	0.22	57.46	1.93
Average		51.59	1.55	12.82	0.25	54.74	1.61

From the data in the table, it can be observed that the ATS of the SPD-DT is 51.59%, with only a 1.55% increase in BDBR. This substantial reduction in coding complexity for the test sequences indicates that the proposed algorithm effectively skips redundant divisions in the QTMT structure. In the PTEL, the ATS is 12.82%, with only a 0.25% increase in BDBR. The algorithm achieved time savings of more than 10% for all test sequences, indicating the high stability of the algorithmic model. This also highlights that the proposed algorithm effectively terminates the prediction process of redundant candidate modes, reducing the number of candidate modes for the rate-distortion optimization process. Through the overall analysis of the proposed algorithm, the stability of the BDBR index is weak. From the perspective of the SPD-DT algorithm, the BDBR increase in the DaylightRoad2 sequence under this algorithm is 0.51%, which is the best among all sequences. The BDBR growth of the Johnny sequence under this algorithm is 3.35%, occupying a larger amount of bits. Considering the differences between different sequences, high-resolution sequences have a higher probability of selecting small partition depth CUs, such as CampfireParty and FoodMarket. In order to more intuitively demonstrate the effectiveness of the proposed algorithm in accelerating CU division, we select the “BasketballDrill” sequence for encoding and compare the obtained CU division results with the processing results of VTM10.0, as shown in Figure 10.

Figure 10. Example of comparison of CU partition results. (a) VTM10.0; (b) proposed algorithm.

Furthermore, the overall performance of the proposed scheme is presented in this paper. It achieves a 54.74% decrease in the ATS, with the BDBR increased by only 1.61%, effectively meeting the goal of significantly reducing coding complexity.

5.2. Comparison with Other Algorithms

To further evaluate the performance of the proposed algorithm, this study objectively analyzes and compares it with representative intra-frame coding algorithms: references [27,34,35]. The comparison of algorithm performance is presented in Table 6.

Table 6. Comparison of performance between this algorithm and other algorithms.

Class	Sequence	Chen [27]		Alexandre Tissier [34]		Zhang [35]		Ours
		ATS (%)	BDBR (%)	ATS (%)	BDBR (%)	ATS (%)	BDBR (%)	ATS (%)	BDBR (%)
A1	Campfire	-	-	67.4	2.02	55.92	1.81	56.35	1.32
	FoodMarket4	-	-	67.5	1.4	51.77	1.95	52.67	1.16
	Tango2	-	-	80.9	1.48	65.06	2.07	66.89	2.01
A2	Catrobot	-	-	62.9	2.56	61.22	2.33	62.35	1.64
	DaylightRoad2	-	-	73.7	2.47	61.48	1.77	63.24	1.58
	ParkRunning3	-	-	60.9	0.91	57.88	1.71	58.41	1.65
B	BQTerrace	49.46	1.16	75.1	2.76	54.55	1.50	56.35	1.56
	BasketballDrive	65.34	3.09	76.0	2.51	58.63	1.92	59.43	1.86
	Cactus	55.97	1.74	72.8	2.6	61.26	1.73	62.53	1.71
	Kimono	55.31	1.72	-	-	65.40	1.55	66.21	1.53
	ParkScene	56.36	1.28	-	-	57.94	1.65	58.42	1.63
C	BQMall	56.51	1.79	71.1	3.08	49.5	1.52	50.21	1.55
	BasketballDrill	53.19	1.91	67.7	4.69	47.27	1.79	48.11	1.72
	PartyScene	41.76	0.28	69.3	2.16	48.22	1.18	49.32	1.31
	RaceHorsesC	52.14	0.84	69.2	1.97	48.26	1.35	49.23	1.36
D	BasketballPass	54.15	2.02	67.2	2.86	41.98	1.76	42.13	1.72
	BlowingBubbles	43.97	0.49	64.7	2.37	38.02	1.46	39.05	1.47
	BQSquare	32.35	0.17	70.0	2.43	43.67	1.34	44.22	1.36
	RaceHorses	44.94	0.54	66.5	2.29	47.21	1.76	48.23	1.56
E	FourPeople	62.27	2.55	73.1	3.46	56.81	1.77	55.88	1.70
	Johnny	62.61	3.07	72.9	3.71	57.65	2.30	57.69	2.09
	KristenAndSara	60.83	2.26	71.8	3.32	56.57	1.98	57.46	1.93
Average		52.95	1.56	70.04	2.56	53.92	1.74	54.74	1.61

Compared to the algorithm in [27], the proposed algorithm in this paper achieves a 1.79% reduction in coding complexity but a 0.05% increase in output coding rate. The 0.05% increase in code rate is deemed acceptable considering the 1.79% coding time saving. The algorithm in [34] achieved a 70.04% decrease in coding complexity, which is 15.3% higher than that of the algorithm proposed in this paper. However, in terms of BDBR, that of the algorithm proposed in this paper is 0.95% lower than that of the algorithm in [34]. The increase in bit rate leads to an increase in the size of the video file, which puts a huge burden on storage and transmission. Therefore, the scheme to obtain coding complexity reduction at the expense of bit rate is not desirable. Compared with the algorithm in [35], the algorithm in this paper not only reduces coding complexity by 0.82% but also decreases BDBR by 0.13%, further improving coding performance. A comparison of the coding performance data is presented in Figure 11. Summarizing the above analysis, the proposed fast intra-frame coding algorithm achieves a better compromise between coding complexity and code rate balance, outperforming existing algorithms.

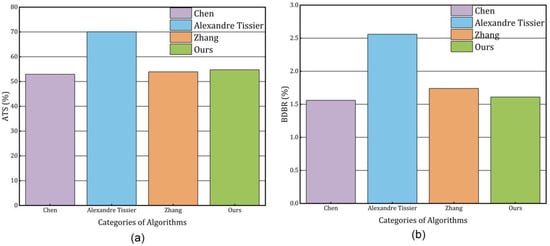
Figure 11. Comparison of average coding performance of the proposed algorithm with different algorithms. (a) Comparison of average time savings; (b) Comparison of BDBR.

6. Conclusions

To achieve greater coding complexity reduction and a smaller bit rate increase, this paper proposes a VVC fast intra-frame coding algorithm, including a decision-tree-based series partitioning decision algorithm and a mode prediction termination algorithm based on ensemble learning. The algorithm idea is to skip MT partitioning in CU partitioning by concatenating QT partitioning judgments and MT partitioning judgments. For CUs that require MT partitioning, multiple classifiers are used to determine a single partitioning pattern separately to avoid redundant CU partitioning. In mode decision-making, the rapid termination of mode selection is achieved by reordering the list of completed candidate modes and incorporating a decision-tree-based model for predicting mode accuracy. The proposed algorithm achieves a 54.74% reduction in coding complexity compared to VTM10.0, with only a 1.61% loss in RD performance. The experimental results demonstrate the effectiveness of the proposed algorithm. Considering the differences between different sequences, high-resolution sequences have a higher probability of selecting small partition depth CUs. Low resolutions often use CU encoding with higher depth. However, in the processing process of this article, there are certain flaws in using a unified method to process high- and low-resolution sequences. In future work, processing sequence differences at different resolutions may lead to better improvements in the optimization of BDBR.