Abstract
The uplink timing synchronization is indispensable for establishing a reliable link between the base station and the user equipment (UE). To tackle this problem, a new random access preamble (RAP) waveform is designed for cellular communication systems operating in high-mobility scenarios for orthogonal time frequency space systems. Meanwhile, we also propose a scheme to detect access UEs and estimate the corresponding round-trip propagation delay (i.e., timing advance (TA)). Concretely, the RAP root sequence consists of chirp sequences in the delay-Doppler domain, and the set of available RAPs is generated by cyclic shifting the root sequence. Then, the cross-correlation in the fractional Fourier domain is carried out to achieve the RAP detection and TA estimation of the access UEs. Exhaustive numerical simulation results corroborate that the proposed scheme has a superior RAP detection and TA estimation performance and exhibits sufficient robustness regarding Doppler shifts and the number of UEs.
1. Introduction
Achieving highly reliable communication in high-mobility and severe multipath delay spread scenarios is an urgent requirement in next-generation wireless communication systems. Recently, orthogonal time frequency space (OTFS) has been a highly promising candidate waveform owing to its remarkable capacity to resist severe delay and Doppler effects [1]. The information symbols are embedded in the delay-Doppler (DD) domain in the OTFS modulation rather than the time–frequency (TF) domain as in orthogonal frequency division multiplexing (OFDM). As a result, the doubly selective fading channel in the TF domain can be transformed into a quasi-static channel and exhibits sparse characteristics in the DD domain, which can effectively overcome the influence of the multipath effect and the Doppler effect.
Several works on OTFS-based multiple access demonstrate the feasibility of OTFS in the uplink of cellular communication systems [2,3,4]. Random access and uplink timing synchronization between the base station (BS) and user equipment (UE) are indispensable for establishing reliable links in competitive access systems.
1.1. Related Work
In cellular systems, the BS detects the access UE through the received random access preamble (RAP) and then estimates their round-trip transmission delay (i.e., timing advance (TA)) to achieve uplink timing synchronization. In fourth-generation (4G) and fifth-generation (5G) systems, the RAP consisting of Zadoff–Chu (ZC) sequences with different cyclic shifts is used to identify different UEs. The UE detection and TA estimation are achieved by detecting the cyclic shift value of the received RAP [5,6,7,8]. However, due to the differences between OTFS and signal-carrier frequency division multiple access (SC-FDMA), the random access procedure in 4G/5G cannot be directly used for OTFS systems. On the other hand, the ZC sequences employed in 4G/5G have limited resistance to severe Doppler effects in higher-mobility scenarios [9]. Therefore, it is necessary to explore the RAP design and random access schemes suitable for OTFS systems. However, there is little prior work on this issue.
To the best of our knowledge, there is only one work on the uplink timing synchronization and random access for OTFS cellular communication systems. Sinha et al. propose an OTFS-based random access scheme, in which a high-power pilot is used as the RAP for each UE in the DD domain, and different UEs are identified by their unique position in the Doppler domain [10]. At the same time, the shift of the delay domain index of the RAP is used to estimate the TA, achieving low complexity and high-precision uplink timing synchronization. However, the number of available RAPs decreases as the Doppler shift increases in high-mobility scenarios, thus increasing the collision probability. Therefore, it is of great significance to explore a better uplink timing synchronization scheme for OTFS systems to promote its application in high-mobility scenarios.
The chirp signal, a typical linear frequency modulation signal, has superior resistance to Doppler shift and can maintain the original signal characteristics in high-mobility scenarios [11]. Some works that employ the chirp signal as the preamble in downlink synchronization have been investigated. Boumard et al. [12] propose a symbol timing offset and carrier frequency offset (CFO) estimation scheme by using matched filtering and the autocorrelation of chirp signals. Moreover, by leveraging the symmetry property of the chirp reference signals, reversed autocorrelators are utilized for time synchronization [13]. In addition, the fractional Fourier transform (FrFT) and Radon–Wigner transform (RWT) of chirp signals exhibit energy concentration properties, which results in a pulse-like waveform [14,15]. For OFDM systems, a joint timing and frequency synchronization scheme by leveraging the FrFT of the chirp preamble is proposed [16]. Furthermore, an RWT-based timing synchronization algorithm for OTFS systems is proposed [17], which achieves excellent performance in downlink communication. However, the utilization of chirp signals for uplink synchronization is quite rare.
1.2. Contributions
Motivated by the aforementioned works, we propose an uplink random access scheme for OTFS-based cellular communication systems based on the cross-correlation of chirp signals in the fractional Fourier domain (FrFD) in this paper. The contributions of this paper are summarized as follows:
- An OTFS-based RAP waveform is designed for cellular communication systems. The RAP consisting of chirp sequences is mapped onto the delay axis in the DD domain, and the set of available RAPs is generated by applying distinct cyclic shifts to a root sequence.
- A novel RAP detection and TA estimation scheme for OTFS systems is proposed. At the BS, the received RAP signals superimposed by multiple UEs are transformed into the DD domain and combined through Doppler diversity. Subsequently, the detection function is obtained by performing a cross-correlation operation in FrFD between the cyclically shifted received sequence and the original root sequence. Finally, the peak of the detection function is utilized to detect the access UEs and estimate the corresponding TAs. Furthermore, we derive the detection threshold according to a specified desired probability of a false alarm. Among them, the Doppler diversity strategy and cross-correlation operation in FrFD are the core innovations of the proposed scheme.
- The performance of the proposed RAP detection and TA estimation scheme is evaluated in static, low-speed, medium-speed, and high-speed scenarios, which proves its robustness to Doppler shifts. In addition, we evaluate the performance when the number of UEs attempting to access simultaneously varied and all exhibit superior performance.
The rest of this article contains the following. The system model and the proposed RAP waveform are shown in Section 2. Section 3 presents the proposed RAP detection and TA estimation scheme and derives the detection threshold. The simulation results are exhibited and analyzed in Section 4. Section 5 is the conclusion.
2. System Model and Random Access Preamble Design
2.1. System Model
The uplink timing synchronization issue in the single-cell multiuser scenario is considered in this paper, where both the UEs and the BS are equipped with single-antenna transceivers for ease of analysis. For the multicell and multiantenna scenario, the proposed scheme will be extended in future works. Before the uplink random access procedure was initiated, the UE completed the downlink synchronization procedure and received the message related to RAP and uplink scheduling information. Then, the UEs can select one of the available RAPs to transmit in the uplink random access physical resource blocks. Since the downlink synchronization was completed, which provides a time reference for the frame header capture of the RAP frame, the information on uplink random access physical resource blocks can be transformed into the DD domain directly for UE detection and TA estimation.
The signal-processing model of OTFS modulation is shown in Figure 1.

Figure 1.
The signal-processing model of OTFS modulation.
Suppose that the number of UEs attempting to access simultaneously is Q, and the RAP transmitted by the q-th UE in the DD domain is . Then, with the inverse symplectic finite Fourier transform (ISFFT), the DD domain RAP is transformed into the TF domain. The RAP in the TF domain is denoted as , which is
where denotes the symbols of the k-th Doppler axis and the l-th delay axis in the DD domain and M and N are the numbers of delay bins and Doppler bins, respectively. Subsequently, the TF domain symbols are transformed into the time domain by the Heisenberg transform, which can be expressed as
where is a rectangular pulse, which is given by
In this case, the Heisenberg transform can be replaced by the inverse fast Fourier transform (IFFT). The time duration of is seconds and the bandwidth is Hz, where T and are the symbol duration and subcarrier spacing of an OTFS frame, respectively.
At the BS, the RAPs of Q users are superimposed after passing through the multipath channel, and the received signal is given by
where L is the number of channel taps and , , and denote the complex channel gain, relative delay, and CFO of the q-th UE at the l-th tap, respectively. denotes the additive white Gaussian noise (AWGN). Subsequently, is transformed into the TF domain by the Wigner transform, which can be given by
where is the same rectangular pulse as the transmitter, in which case the Wigner transform is replaced by a fast Fourier transform (FFT). Then, the TF domain signal is transformed into the DD domain by the symplectic finite Fourier transform (SFFT), i.e.,
Afterward, the received DD domain RAP signal is used to execute the access UE detection and the TA estimation. To avoid multiuser interference (MUI), the symbol duration T and subcarrier spacing must satisfy
where is the maximum propagation delay of the cell and is the maximum Doppler shift.
2.2. Random Access Preamble Design
The RAPs play a vital role in enabling the BS to identify UEs successfully and estimate the corresponding TA accurately. Chirp is a kind of linear frequency modulation signal that is a good choice as the RAP for OTFS in high-mobility scenarios owing to its remarkable correlation properties and resistance to Doppler shift. The continuous time chirp signal is defined as
where denotes the center frequency and denotes the chirp rate. After sampling with period , the discrete time chirp signal with length can be expressed as
where . The signal in (9) is called the root sequence, and other root sequences can be generated by changing or . The set of available RAPs can be generated either by applying cyclic shifts to the same root sequence or by employing cyclic shift sequences of multiple root sequences. Assuming that the cyclic shift offset is , the available RAP is given by
In order to generate as many RAPs as possible, the is set to be as small as possible on the premise of greater than the maximum possible round-trip propagation delay between the UE and BS. The number of available RAPs generated by a root sequence is , where is the round-down operation.
The UE randomly selects one of the available RAPs to initiate random access. Afterward, the RAP composed of a chirp signal is mapped onto the center of the DD plane as shown in Figure 2. Guard bands are set aside for the delay and to Doppler axes to prevent interference with adjacent OTFS frames, respectively. The RAP frame of the q-th UE in the DD domain is
where is the length of the guard band in the delay axis and denotes the round-up operation. In the time domain, guard intervals are added to the head and end of the RAP frames, as shown in Figure 3. At the BS, The RAPs transmitted by different access UEs are superimposed and subsequently transformed into the DD domain. Then, the cross-correlation in the FrFD is executed on the received DD domain superimposed RAP to achieve access UEs detection and corresponding TA estimation.
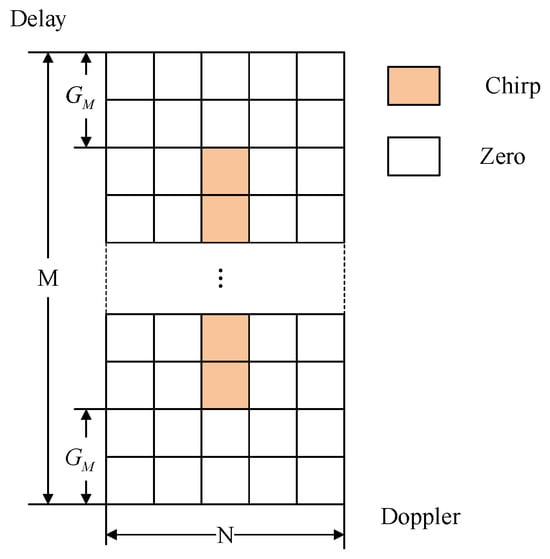
Figure 2.
DD domain form of RAP waveform.
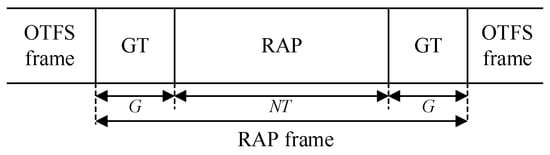
Figure 3.
Time domain form of RAP waveform.
3. Proposed Access UE Detection and TA Estimation Algorithm
The proposed RAP detection and TA estimation mechanism of the OTFS system is similar to that of the 4G/5G systems. The UE randomly selects one RAP from the set of available RAPs to initiate a random access procedure. For each available RAP, the BS detects whether it is contained in the received signal and, if so, estimates the round-trip propagation delay (i.e., TA) between the BS and the UE selecting that RAP. Afterward, the estimated TA is fed back to the UE and used to advance its uplink timing. Therefore, the uplink signals of all UEs can arrive at the BS at the same time.
In high-mobility scenarios, the excellent correlation characteristics of chirp sequences are seriously damaged, and the RAP detection method based on cross-correlation similar to 4G/5G systems is no longer valid. Fortunately, the FrFT of the chirp signal in a specific order exhibits an energy-clustering property, while the FrFT of AWGN in any order does not. Therefore, RAP detection and TA estimation are carried out by cross-correlation in the FrFD in this paper. The FrFT can be seen as a rotation of the signal by any angle in the TF plane. The p-order FrFT of is defined as
where and is the kernel function and is defined as follows
At the BS, the RAPs simultaneously received from different UEs are superimposed together and then transformed into the DD domain. We exploit the Doppler diversity to the received signal to improve the accuracy of RAP detection and TA estimation. Concretely, after calculating the average power of the received signal along the Doppler axis and sorting it from large to small, the associated Doppler axis index is written as , ⋯, . Then, the strongest sequences along the Doppler axis are combined and then cyclically shifted by d samples. Subsequently, the chirp signal is extracted for RAP detection and TA estimation, which can be written as
Afterward, the cross-correlation operation is performed in the FrFD to detect RAPs and estimate TAs. Assume that the optimal rotation angle of the FrFT of the root chirp sequence is (corresponding order is = /(/2)). With order , the FrFT of the root chirp sequence is denoted as , and the FrFT of is denoted as . Therefore, the detection function can be defined as
The access UEs and corresponding TAs can be estimated by the cyclic shift sample in case the amplitude of is larger than the detection threshold . As shown in Figure 4, the detection function exhibits four peaks as the number of simultaneous access UEs is four, and the abscissas of the peaks are the corresponding cyclic shifts . The cyclic shift sample d can be rewritten as , where k is used to detect the RAPs sent by UEs and l is used to estimate the TAs corresponding to these UEs. Therefore, the estimated and TA can be expressed as
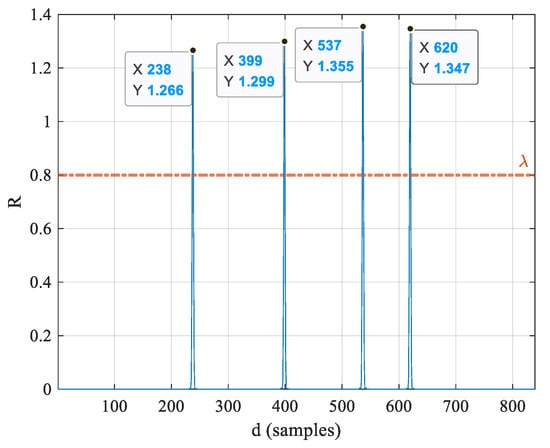
Figure 4.
Magnitude of the proposed detection function R.
For convenience of calculation, the detection function can be reshaped to a two-dimensional matrix of size , which is denoted as . When , the row and column indices are the estimated cyclic shift indices and TA , respectively. It should be noted that for a specific RAP, the estimated TA is determined by the maximum of in that row. In other words, when two or more UEs transmit the same RAP, that is, a collision event occurs, only the UE with the largest received power is detected. Therefore, the estimated and TA can be expressed as
An appropriate detection threshold is crucial to ensure the accuracy of RAP detection and TA estimation, and the minimum detection threshold can be calculated by the desired probability of a false alarm, which is defined as
In order to calculate the , the distribution function of the detection function when the q-th RAP is not transmitted should be calculated. The sampled-type discretization method of FrFT is used to rewrite (12) into discrete form [18], which is expressed as
where the kernel function is rewritten as
where . When the RAP signal is absent in the received signals, i.e., the received signal at the BS contains only noise, the detection function R is denoted as the cross-correlation between the noise and the chirp root sequence in the FrFD. The noise is complex AWGN with zero mean and variance . Then, the FrFT of the noise that is denoted as follows Gaussian distribution with zero mean and variance , where is defined as
In addition, the FrFT of the chirp root sequence is a pulse-like waveform and can be expressed as
Therefore, the detection function can be given by
Given a desired probability of a false alarm , i.e., , the detection threshold is calculated according to (24), which is given by
It is clear that the threshold increases with the increase in the noise variance (i.e., decreasing signal-to-noise ratio (SNR)).
4. Simulation Results
In this section, the proposed RAP detection and TA estimation scheme is simulated through MATLAB. The performance of the proposed scheme is evaluated with regard to the missed detection probability (MDP) of RAP detection and the root mean square error (RMSE) of the TA estimation. To be specific, the MDP is defined as the probability that the q-th UE transmits an RAP but is not detected by the BS. The RMSE of TA estimation is defined as
where K = 100,000 is the times of simulation at each SNR value and and denote the estimated TA and the true TA of the q-th UE, respectively.
A single-cell scenario is considered, and the issue of cell interference is not discussed in this paper. The cell radius is 1500 m, and hence the maximum possible round-trip propagation delay is µs. The BS and each UE are equipped with a single input–single output antenna for the sake of discussion. The 3GPP Extended Vehicular A model (EVA) channel [19] is considered to evaluate the performance of RAP detection and TA estimation. The simulation parameters are listed in Table 1. In this paper, we only consider the RAPs generated from one root sequence, and the case that the set of available RAPs is generated by multiple root sequences will be explored in the future. The desired probability of a false alarm is , and then the threshold can be calculated by (25).

Table 1.
Simulation parameters.
Two other schemes are employed to compare the MDP and RMSE performance of the proposed algorithm. One scheme uses the RAP designed in this paper, and the cross-correlation operation without FrFT is adopted for RAP detection and TA estimation, which is denoted as “Chirp” in simulation figures. With the other, the chirp sequence of the RAP in this paper is replaced by the ZC sequence, and the RAP detection and TA estimation algorithm also uses the cross-correlation without FrFT, which is denoted as “ZC” in the simulation figures. In addition, aiming at the issue of random access and TA estimation in high-mobility scenarios, relevant research on SC-FDMA in satellite communications can be compared, such as ref. [20]. However, it is not included in this paper, mainly due to the following considerations: (1) The essential differences between the SC-FDMA and OTFS make it of limited value to compare them. (2) Ref. [20] studies the random access issue in the satellite communication system, which is characterized by a long propagation delay and low SNR, and it is mainly line of sight propagation, with fewer multiple paths. In addition, although there is a large CFO in the satellite communication system, part of it can be pre-eliminated by ephemeris. However, this paper studies the uplink synchronization problem of high-mobility users in the cellular mobile communication system, which mainly needs to solve the problems of large Doppler frequency shift and multipath propagation, while the propagation delay is relatively small and the SNR is higher than that of satellite communication. (3) Due to different multicarrier waveforms and application scenarios, the frame length, subcarrier spacing, and guard interval of the two systems cannot be uniform, and it is difficult to find a suitable simulation architecture to compare them. Based on the above analysis, we believe that the lack of performance comparisons between the research on SC-FDMA systems and this paper will not damage the integrity and research value of this paper, and can better reflect the logic of this paper.
Figure 5 illustrates the MDP and RMSE performances under different Doppler shifts. The maximum Doppler shifts are set to 0 Hz, 300 Hz, 600 Hz, and 1200 Hz, corresponding to static, low-speed, medium-speed, and high-speed scenarios, respectively. The number of UEs attempting to access simultaneously is . Figure 5a shows the MDP versus SNR performance. The proposed algorithm performance substantially improves as the SNR increases, while the two comparison algorithms show almost the same performance and exhibit a floor effect when the SNR increases. In addition, with the increase in the Doppler shift, the MDP performance of the two comparison algorithms hardly decreases, while that of the proposed method gradually decreases as the Doppler shift increases, with the exception of when it is 0 Hz. When the SNR ≤−5 dB, the MDP performance of the proposed scheme under a Doppler shift of 0 Hz is worse than that under 300 Hz and 600 Hz. The reason is that the same is used for all Doppler shift conditions in the Doppler diversity scheme, which leads to more noise superimposed on the receiving sequence of RAP detection, thus decreasing the performance. It is clear that the proposed algorithm outperforms the comparison algorithms for the SNR >−10 dB and only shows a little gap when the SNR is lower. Figure 5b depicts the RMSE performance of TA estimation. It is evident that the RMSE performance of the proposed scheme exhibits the same trend as the MDP performance. In addition, the RMSE performance of the “ZC” approach is slightly better than that of the “Chirp” approach, and the performance of both approaches decreases with the increase in the Doppler shift and increases with the increase in the SNR. It is obvious that the proposed algorithm outperforms the two comparison approaches in terms of the RMSE. In summary, the proposed algorithm exhibits superior RAP detection and TA estimation performance in harsh environments with a low SNR and high Doppler shift.
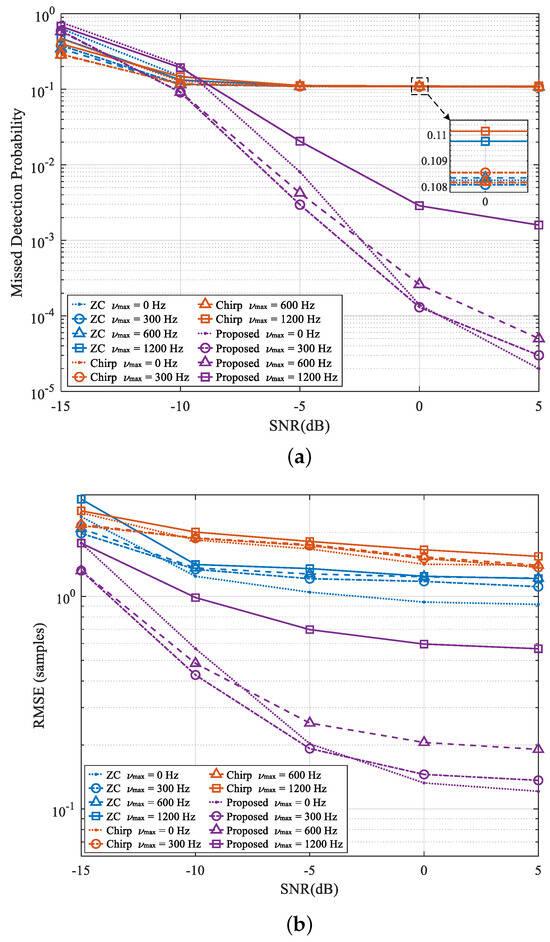
Figure 5.
Performance comparison of the RAP detection and TA estimation scheme for different Doppler shifts. (a) MDP. (b) RMSE.
Figure 6 depicts the performance comparison of the algorithms when the number of UEs attempting to access simultaneously varied. The maximum Doppler shift is equal to 600 Hz and the number of UEs attempting to access simultaneously is . Figure 6a represents the MDP performance versus the SNR for different Qs. The MDP performance of the proposed method gradually improves as the SNR increases. The performance of the two comparison algorithms, however, exhibits a floor effect as the SNR increases. In addition, as the number of UEs increases, inter-user interference and the total noise of the received signal also increase, which deteriorates the detection performance, and thus the MDP performance of the three simulation algorithms degrades. The proposed algorithm outperforms the comparison algorithms for the SNR >−10 dB and only exhibits a small gap for the lower SNR. Figure 6b illustrates the RMSE performance of TA estimation for different Qs. The RMSE performance of the proposed approach increases as the SNR increases and decreases as Q increases. In addition, as the SNR increases, the RMSE performance gap for different Qs becomes smaller and approaches zero. Furthermore, the RMSE performance of the “ZC” approach is slightly better than that of the “Chirp” approach. Meanwhile, the performance of both comparison algorithms decreases with the increase in Q and increases with the increase in the SNR. It is obvious that the proposed algorithm outperforms the two comparison algorithms in terms of the RMSE. In general, the proposed scheme can attain a remarkable performance improvement under multiple access users.
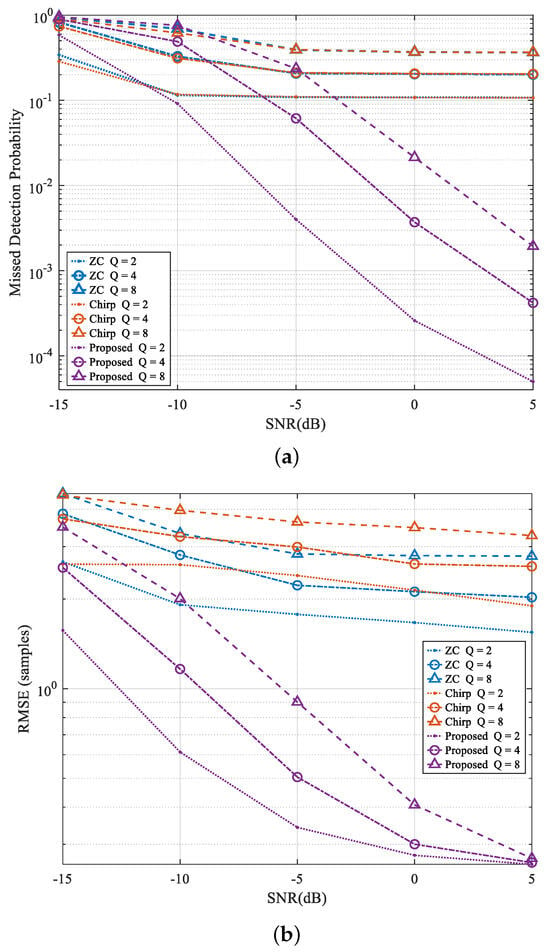
Figure 6.
Performance comparison of the RAP detection and TA estimation scheme for different Qs. (a) MDP. (b) RMSE.
Figure 7 represents the performance comparison between the proposed scheme and the algorithm proposed by Sinha [10]. We observed that the RMSE of the TA estimation in the Sinha algorithm is zero under all simulated conditions, which has an absolute advantage, so only the MDP performance is described here. It is worth mentioning that although the TA estimation performance of the proposed scheme is worse than that of the Sinha algorithm, it can be found from Figure 5 and Figure 6 that the TA estimation error is small and can be eliminated by the guard interval, which can meet the random access requirements. Figure 7a depicts the MDP performance under different Doppler shifts. It can be seen that the proposed scheme outperforms the comparison algorithm when the SNR < 0 dB, while the Sinha algorithm performs better under high SNR conditions. Figure 7b shows the performance under different Qs. When the number of users is small, the proposed scheme maintains a performance gain when the SNR < 0 dB. When the number of users is large (), the MDP performance of the proposed scheme outperforms the Sinha algorithm. The Sinha algorithm has significant advantages in many application scenarios. However, the motivation of the proposed scheme is to solve the bottleneck problem of the Sinha algorithm when the number of UEs increases, rather than replace it completely. Simulation results reveal that the proposed scheme has superior MDP performance under the condition of a low SNR and multiuser access. Therefore, the two algorithms have their advantages and disadvantages in different application scenarios, and we can choose which scheme to use according to the practical scenario.
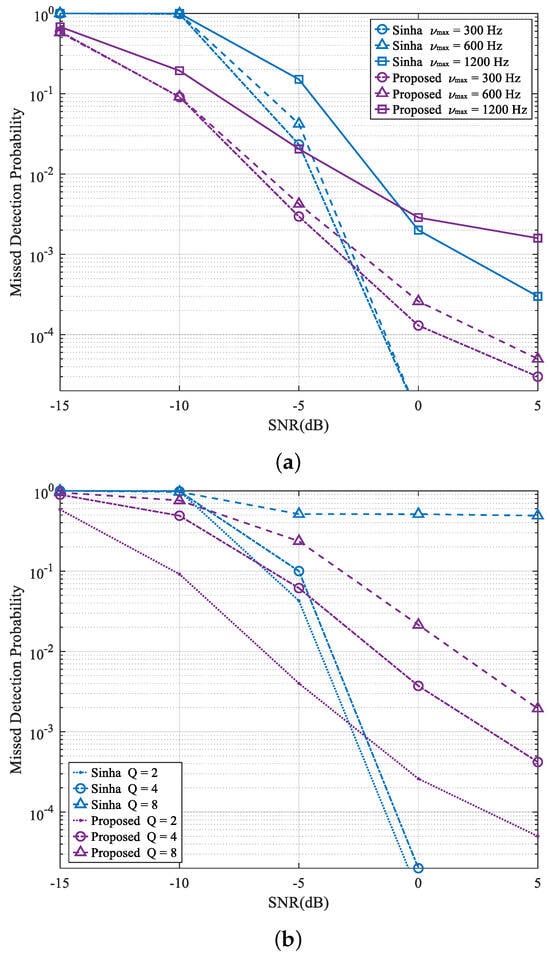
Figure 7.
Comparison of RAP detection performance between the proposed scheme and the Sinha algorithm. (a) Different Doppler conditions. (b) Different Q conditions.
Finally, the complexity of the algorithms is analyzed in terms of the number of complex multiplication operations. The complexity of the proposed scheme depends on the complexity of the FrFT calculation methods. The decomposition discrete algorithm is widely used for FrFT fast calculations [21], which can be realized by FFT, and the complexity is . There are times FrFT that need to be calculated to detect all available RAPs, and the complexity of the proposed scheme is . The complexity of the “ZC” algorithm and “Chirp” algorithm is , and the complexity of the Sinha algorithm is . Therefore, the complexity of the proposed algorithm is higher than other schemes and needs to be further optimized.
In summary, compared with the direct cross-correlation scheme, the cross-correlation operation in the FrFD makes the proposed scheme present with a superior detection performance. Meanwhile, compared with the Sinha algorithm, the proposed scheme exhibits a better RAP detection performance under the condition of a lower SNR and more access users, which is more in line with the requirements of practical scenarios. Therefore, the proposed algorithm is helpful in promoting the application of the OTFS technology in the next-generation communication system in the high-mobility scenarios. However, the FrFT operation for each RAP in the available RAP set leads to high compute complexity, which is an important problem that needs to be solved in future research.
5. Conclusions
A novel RAP detection and TA estimation scheme for the OTFS-based uplink random access process in the cellular communication systems is proposed in this paper. The chirp sequence is utilized as the RAP root sequence, and available RAPs are created by cyclic shifting of the root sequence. Additionally, we designed a scheme to map the RAP to the DD domain resource element. Subsequently, the RAP detection and TA estimation are implemented by cross-correlation in the FrFD. The simulation results demonstrate that the proposed scheme can accomplish a lower MDP of RAP detection and a lower RMSE of TA estimation, even in harsh environments with a high Doppler shift and low SNR. Therefore, the proposed scheme can provide help for the application of OTFS technology in the next communication systems in high-mobility scenarios. In the future, the feasibility of the proposed scheme will be further explored when the available RAPs are generated from multiple different root sequences. Meanwhile, the extension of the proposed scheme in the multicell and multiantenna scenarios will be further studied. Moreover, limited by the complexity of FrFT, the complexity of the proposed RAP detection and TA estimation scheme needs to be further optimized.
Author Contributions
Conceptualization, X.G. and N.Z.; methodology, X.G. and N.Z.; software, X.G.; validation, X.G., Z.C. and C.C.; formal analysis, X.G.; investigation, Z.C.; resources, C.C. and H.W.; data curation, H.W.; writing—original draft preparation, X.G.; writing—review and editing, X.G.; visualization, Z.W.; supervision, Z.W.; project administration, H.W.; funding acquisition, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant U2031208, Grant 61571244, and Grant 12202427.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hadani, R.; Rakib, S.; Tsatsanis, M.; Monk, A.; Goldsmith, A.J.; Molisch, A.F.; Calderbank, R. Orthogonal time frequency space modulation. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Khammammetti, V.; Mohammed, S.K. OTFS-based multiple-access in high Doppler and delay spread wireless channels. IEEE Wirel. Commun. Lett. 2018, 8, 528–531. [Google Scholar] [CrossRef]
- Deka, K.; Thomas, A.; Sharma, S. OTFS-SCMA: A code-domain NOMA approach for orthogonal time frequency space modulation. IEEE Trans. Commun. 2021, 69, 5043–5058. [Google Scholar] [CrossRef]
- Chong, R.; Li, S.; Yuan, J.; Ng, D.W.K. Achievable rate upper-bounds of uplink multiuser OTFS transmissions. IEEE Wirel. Commun. Lett. 2022, 11, 791–795. [Google Scholar] [CrossRef]
- 3GPP TS 36.211; Physical Channels and Modulation (Release 9); Technical Specification Group Radio Access Network. Sophia 3rd Generation Partnership Project: Sophia Antipolis, France, 2010.
- Yu, C.; Xiangming, W.; Wei, Z.; Xinqi, L. Random access algorithm of LTE TDD system based on frequency domain detection. In Proceedings of the 2009 Fifth International Conference on Semantics, Knowledge and Grid, Zhuhai, China, 12–14 October 2009; pp. 346–350. [Google Scholar]
- 3GPP TS 38.211; NR: Physical Channels and Modulation (Release 15). 3rd Generation Partnership Project: Sophia Antipolis, France, 2018.
- Xiong, Q.; Yu, B.; Qian, C.; Li, X.; Sun, C. Random access preamble generation and procedure design for 5G-NR system. In Proceedings of the 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–5. [Google Scholar]
- Chen, F.; Li, X.; Zhang, Y.; Jiang, Y. Design and implementation of initial cell search in 5G NR systems. China Commun. 2020, 17, 38–49. [Google Scholar] [CrossRef]
- Sinha, A.K.; Mohammed, S.K.; Raviteja, P.; Hong, Y.; Viterbo, E. OTFS based random access preamble transmission for high mobility scenarios. IEEE Trans. Veh. Technol. 2020, 69, 15078–15094. [Google Scholar] [CrossRef]
- Zou, J.; Xu, C. Frequency offset tolerant synchronization signal design in NB-IoT. Sensors 2018, 18, 4077. [Google Scholar] [CrossRef] [PubMed]
- Boumard, S.; Mammela, A. Time domain synchronization using Newman chirp training sequences in AWGN channels. In Proceedings of the IEEE International Conference on Communications, Seoul, Repulic of Korea, 16–20 May 2005; Volume 2, pp. 1147–1151. [Google Scholar]
- Boumard, S.; Mammela, A. Robust and accurate frequency and timing synchronization using chirp signals. IEEE Trans. Broadcast. 2009, 55, 115–123. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, B. A Fast Joint Frame Synchronization and Frequency Offset Acquisition Algorithm for OFDM Systems. In Proceedings of the 2008 IEEE Wireless Communications and Networking Conference, Las Vegas, NV, USA, 31 March–3 April 2008; pp. 1267–1272. [Google Scholar]
- Liu, J.; Wei, Y.; Zeng, X.; Lu, J.; Zhang, S.; Wang, M. A novel joint timing/frequency synchronization scheme based on Radon–Wigner transform of LFM signals in CO-OFDM systems. Opt. Commun. 2018, 410, 744–750. [Google Scholar] [CrossRef]
- Tang, X.; Sha, X. Synchronization using chirp training sequences based on fractional fourier transform. In Proceedings of the 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics, Harbin, China, 8–10 June 2010; pp. 1161–1164. [Google Scholar]
- Geng, X.; Chen, Z.; Yang, H.; Liu, Z.; Wu, H. Timing synchronization based on Radon-Wigner transform of chirp signals for OTFS systems. Phys. Commun. 2023, 60, 102161. [Google Scholar] [CrossRef]
- Pei, S.C.; Ding, J.J. Closed-form discrete fractional and affine Fourier transforms. IEEE Trans. Signal Process. 2000, 48, 1338–1353. [Google Scholar]
- 3GPP TS 36.104; Evolved Universal Terrestrial Radio Access (E-UTRA); Base Station (BS) Radio Transmission and Reception (Release 8). 3rd Generation Partnership Project: Sophia Antipolis, France, 2009.
- Zhen, L.; Qin, H.; Song, B.; Ding, R.; Du, X.; Guizani, M. Random access preamble design and detection for mobile satellite communication systems. IEEE J. Sel. Areas Commun. 2018, 36, 280–291. [Google Scholar] [CrossRef]
- Ozaktas, H.M.; Arikan, O.; Kutay, M.A.; Bozdagt, G. Digital computation of the fractional Fourier transform. IEEE Trans. Signal Process. 1996, 44, 2141–2150. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).