Noise-Canceling Channel Estimation Schemes Based on the CIR Length Estimation for IEEE 802.11p/OFDM Systems
Abstract
1. Introduction
2. System Model
2.1. Notations
2.2. OFDM Signal Presentation
3. Proposed NC-CE Schemes
3.1. Initial Step (Long Preamble CE)
3.2. Modified CDP Step
3.2.1. Constructing Data Pilots by LS Method
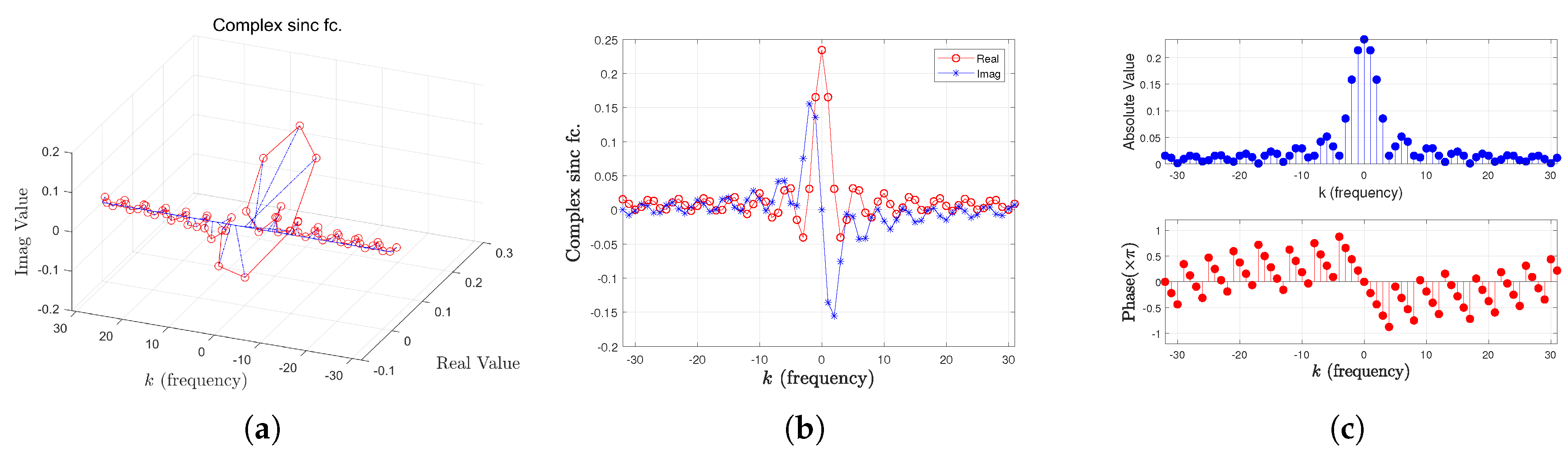
3.2.2. Virtual Subcarrier Filling Step
3.3. Noise-Canceling Step
- : By the IFFT, the CFR can be transformed into the time-domain CIR.
- : Noise cancellation in the time domain is performed by nulling components that exceed the L row in the CIR of .
- : By the FFT, the noise-canceled CIR can be transformed into the CFR.
3.4. Comparison with TDLS Scheme [3]
3.5. Computational Complexity
- : It is observed that is used only once within the data filed (i.e., per packet) and can be pre-defined offline.
- The IFFT/nulling/FFT operation: It can be implemented with very low complexity for a large N. The matrix inversion per the OFDM symbol is not required for 16QAM and 64QAM.
- An interpolation scheme (e.g., TRFI) is not required.
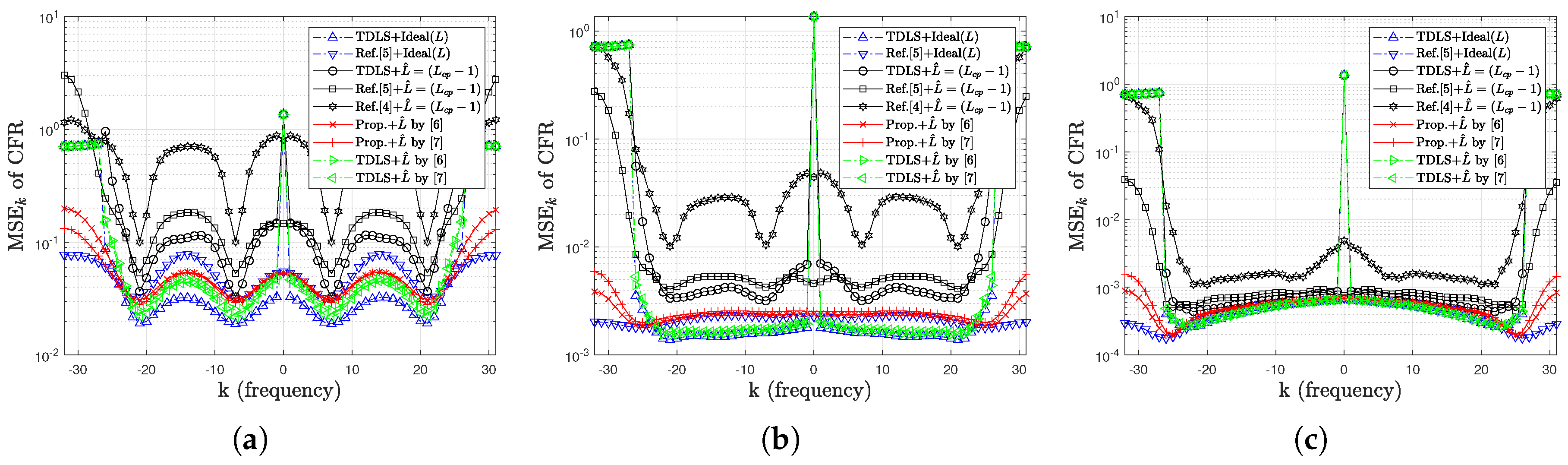
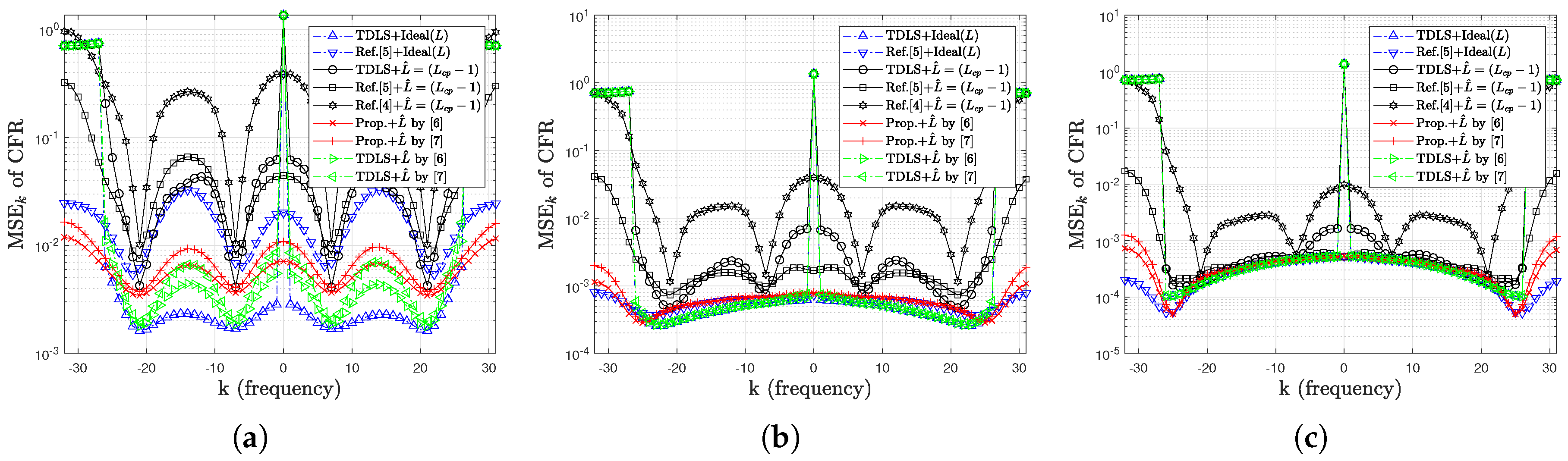
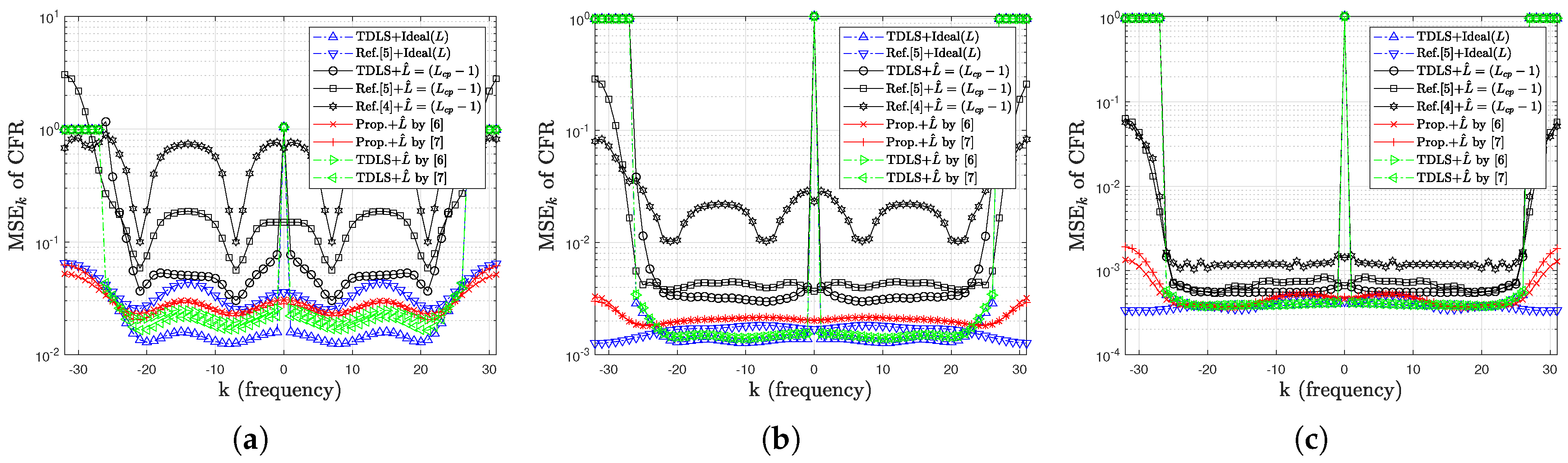
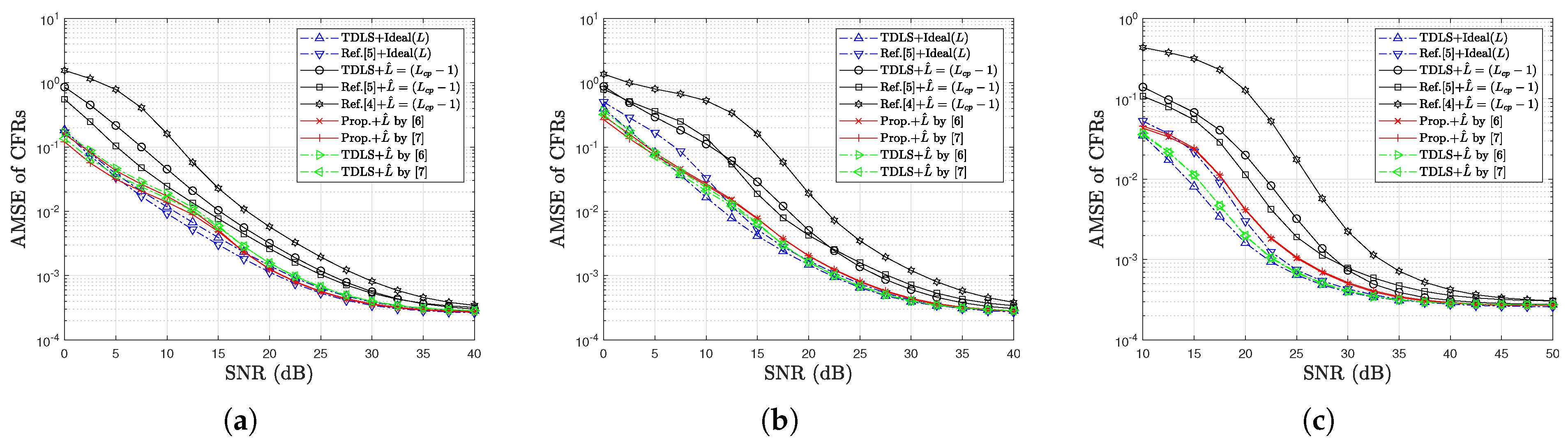
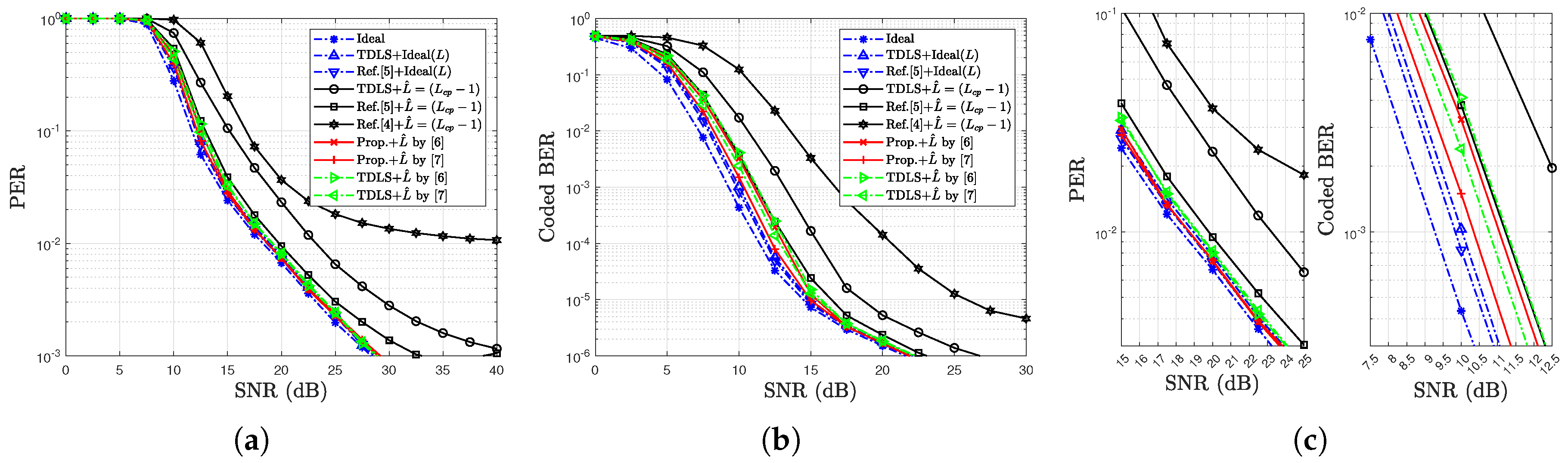
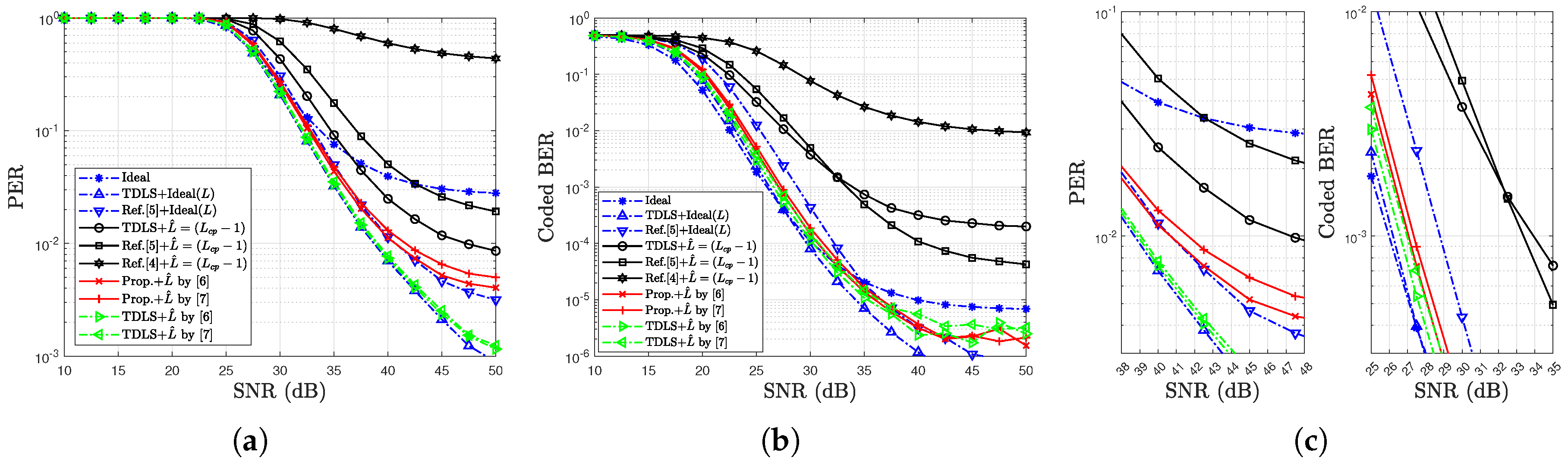
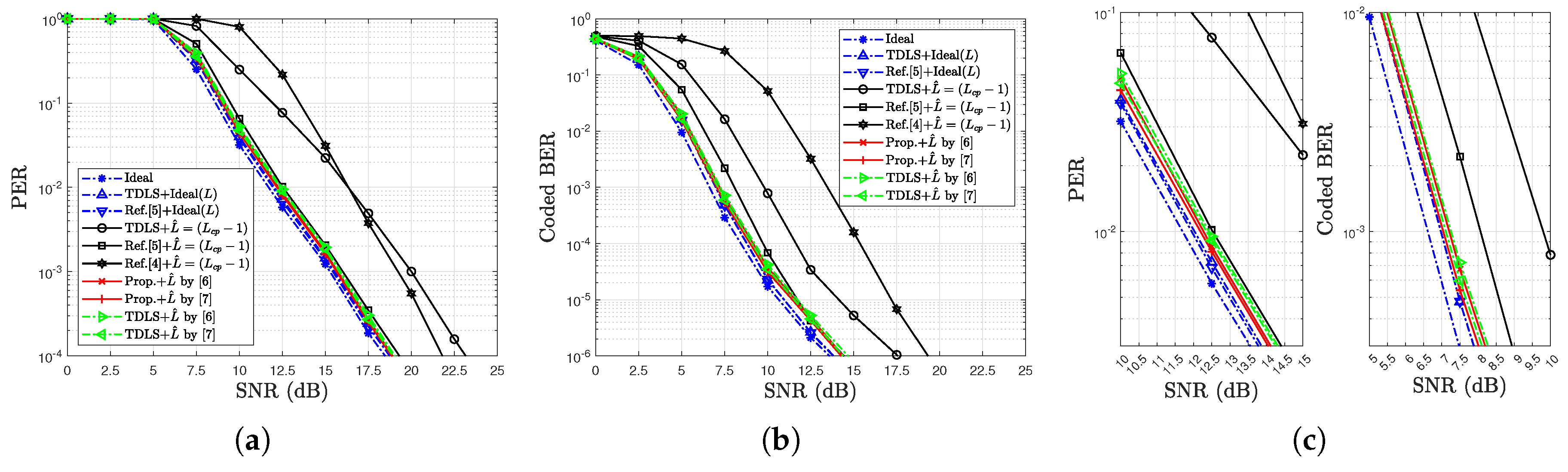
4. Simulation Results
4.1. Simulation Results for MSE
4.2. Simulation Results for Error Rates
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AWGN | additive white Gaussian noise |
| BER | bit error rate |
| CDP | constructed data pilots |
| CFR | channel frequency response |
| CIR | channel impulse response |
| FFT | fast Fourier transform |
| GI | guard interval |
| IFFT | inverse fast Fourier transform |
| ISI | inter-symbol interference |
| MSE | mean square error |
| NC-CE | noise-canceling channel estimation |
| OFDM | orthogonal frequency division multiplexing |
| TRFI | time-domain reliability test and frequency-domain interpolation |
| TDLS | time-domain least square |
| PER | packet error rate |
References
- IEEE Std. 1609.0-2013; IEEE Guide for Wireless Access in Vehicular Environments (WAVE)-Architecture. IEEE: Piscataway, NJ, USA, March 2014.
- Nguyen, V.L.; Hwang, R.H.; Lin, P.C.; Vyas, A. Toward the Age of Intelligent Vehicular Networks for Connected and Autonomous Vehicles in 6G. IEEE Netw. 2022, 3, 44–51. [Google Scholar] [CrossRef]
- Bourdoux, A.; Cappelle, H.; Dejonghe, A. Channel Tracking for Fast Time-Varying Channels in IEEE802.11p Systems. In Proceedings of the 2011 IEEE Global Telecommunications Conference-GLOBECOM 2011, Houston, TX, USA, 5–9 December 2011; pp. 1–6. [Google Scholar]
- Lim, S. A New Channel Estimation Scheme Using Virtual Subcarriers based on Successive Interpolation in IEEE 802.11p WAVE Systems. In Proceedings of the 2021 International Conference on Convergence Content (ICCC 2021), Jeju Island, Republic of Korea, 19–20 December 2021; pp. 441–442. [Google Scholar]
- Han, S.; Park, J.; Song, C. Virtual Subcarrier Aided Channel Estimation Schemes for Tracking Rapid Time Variant Channels in IEEE 802.11p Systems. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Socheleau, F.; Aissa-El-Bey, A.; Houcke, S. Non data-aided SNR estimation of OFDM signals. IEEE Commun. Lett. 2008, 12, 813–815. [Google Scholar] [CrossRef]
- Wang, H.; Lim, S.; Ko, K. Improved Maximum Access Delay Time, Noise Variance, and Power Delay Profile Estimations for OFDM Systems. KSII Trans. Internet Inf. Syst. 2022, 16, 4099–4113. [Google Scholar]
- Eliseev, S.N.; Filimonova, L.N. Channel Estimation of the 802.11p Standard in High-Speed Mobile Environments. In Proceedings of the 2021 Wave Electronics and Its Application in Information and Telecommunication Systems (WECONF), Petersburg, Russia, 31 May–4 June 2021; pp. 1–5. [Google Scholar]
- Miguel, S.; Manuel, G.-M.; Javier, G.; Rafael, M.-M.; Baldomero, C.-P. Analytical Models of the Performance of IEEE 802.11p Vehicle to Vehicle Communications. IEEE Trans. Veh. Technol. 2021, 11, 713–724. [Google Scholar]
- Zhao, Z.; Cheng, X.; Wen, M.; Jiao, B.; Wang, C.X. Channel Estimation Schemes for IEEE 802.11p Standard. IEEE Intell. Transp. Syst. Mag. 2013, 5, 38–49. [Google Scholar] [CrossRef]
- Kim, Y.; Oh, J.; Shin, Y.; Mun, C. Time and frequency domain channel estimation scheme for IEEE 802.11p. In Proceedings of the 17th International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014; pp. 1085–1090. [Google Scholar]
- Lim, S.; Wang, H.; Ko, K. Power-Delay-Profile-Based MMSE Channel Estimations for OFDM Systems. Electronics 2023, 12, 510. [Google Scholar] [CrossRef]
- Kwak, K.; Lee, S.; Kim, J.; Hong, D. A New DFT-Based Channel Estimation Approach for OFDM with Virtual Subcarriers by Leakage Estimation. IEEE Trans. Wirel. Commun. 2008, 7, 2004–2008. [Google Scholar] [CrossRef]
- Kim, K.; Hwang, H.; Choi, K.; Kim, K. Low-Complexity DFT-Based Channel Estimation with Leakage Nulling for OFDM Systems. IEEE Commun. Lett. 2014, 18, 415–418. [Google Scholar] [CrossRef]
- Cho, Y.; Son, H. Enhanced DFT-Based Channel Estimator for Leakage Effect Mitigation in OFDM Systems. IEEE Commun. Lett. 2019, 23, 875–879. [Google Scholar] [CrossRef]
- Park, H. A Low-Complexity Channel Estimation for OFDM Systems Based on CIR Length Adaptation. IEEE Access 2022, 10, 85941–85951. [Google Scholar] [CrossRef]
- Kahn, M. IEEE 802.11 Regulatory SC DSRC Coexistence Tiger Team V2V Radio Channel Models. Doc.: IEEE 802.11-14, February 2014. Available online: https://mentor.ieee.org/802.11/dcn/14/11-14-0259-00-0reg-v2v-radio-channel-models.ppt (accessed on 22 October 2022).








| Comments | Legend | Complexity (MI 1, TRFI) | IFFT/Nulling/FFT | |
|---|---|---|---|---|
| Ideal | L | |||
| Bounds | L | High (O,X) | X | |
| Ref.[5] + Ideal | L | Medium (X,O) | O 2 | |
| [3] | High (O,X) | X | ||
| [5] | Ref.[5] + | Medium (X,O) | O 2 | |
| [4] | Ref.[4] + | Medium (X,O) | X | |
| Proposed | by [6] | by [6] | Low (X,X) | O |
| Methods | by [7] | by [7] | Low (X,X) | O |
| [3,6] | by [6] | by [6] | High (O,X) | X |
| [3,7] | by [7] | by [7] | High (O,X) | X |
| Environment | At PER = 10−2 | At BER = 10−3 | From |
|---|---|---|---|
| Street Crossing NLOS, QPSK | 1.0 dB | 0.9 dB | Figure 11c |
| Street Crossing NLOS, 16QAM | 2.5 dB | 1.8 dB | Figure 12c |
| Street Crossing NLOS, 64QAM | ≫5.5 dB | 6.0 dB | Figure 13c |
| Highway LOS, QPSK | 0.25 dB | 1.0 dB | Figure 14c |
| Highway LOS, 16QAM | 1.3 dB | 1.5 dB | Figure 15c |
| Highway LOS, 64QAM | 2.6 dB | 2.0 dB | Figure 16c |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ko, K.; Wang, H. Noise-Canceling Channel Estimation Schemes Based on the CIR Length Estimation for IEEE 802.11p/OFDM Systems. Electronics 2024, 13, 1110. https://doi.org/10.3390/electronics13061110
Ko K, Wang H. Noise-Canceling Channel Estimation Schemes Based on the CIR Length Estimation for IEEE 802.11p/OFDM Systems. Electronics. 2024; 13(6):1110. https://doi.org/10.3390/electronics13061110
Chicago/Turabian StyleKo, Kyunbyoung, and Hanho Wang. 2024. "Noise-Canceling Channel Estimation Schemes Based on the CIR Length Estimation for IEEE 802.11p/OFDM Systems" Electronics 13, no. 6: 1110. https://doi.org/10.3390/electronics13061110
APA StyleKo, K., & Wang, H. (2024). Noise-Canceling Channel Estimation Schemes Based on the CIR Length Estimation for IEEE 802.11p/OFDM Systems. Electronics, 13(6), 1110. https://doi.org/10.3390/electronics13061110









