Score-Based Black-Box Adversarial Attack on Time Series Using Simulated Annealing Classification and Post-Processing Based Defense
Abstract
1. Introduction
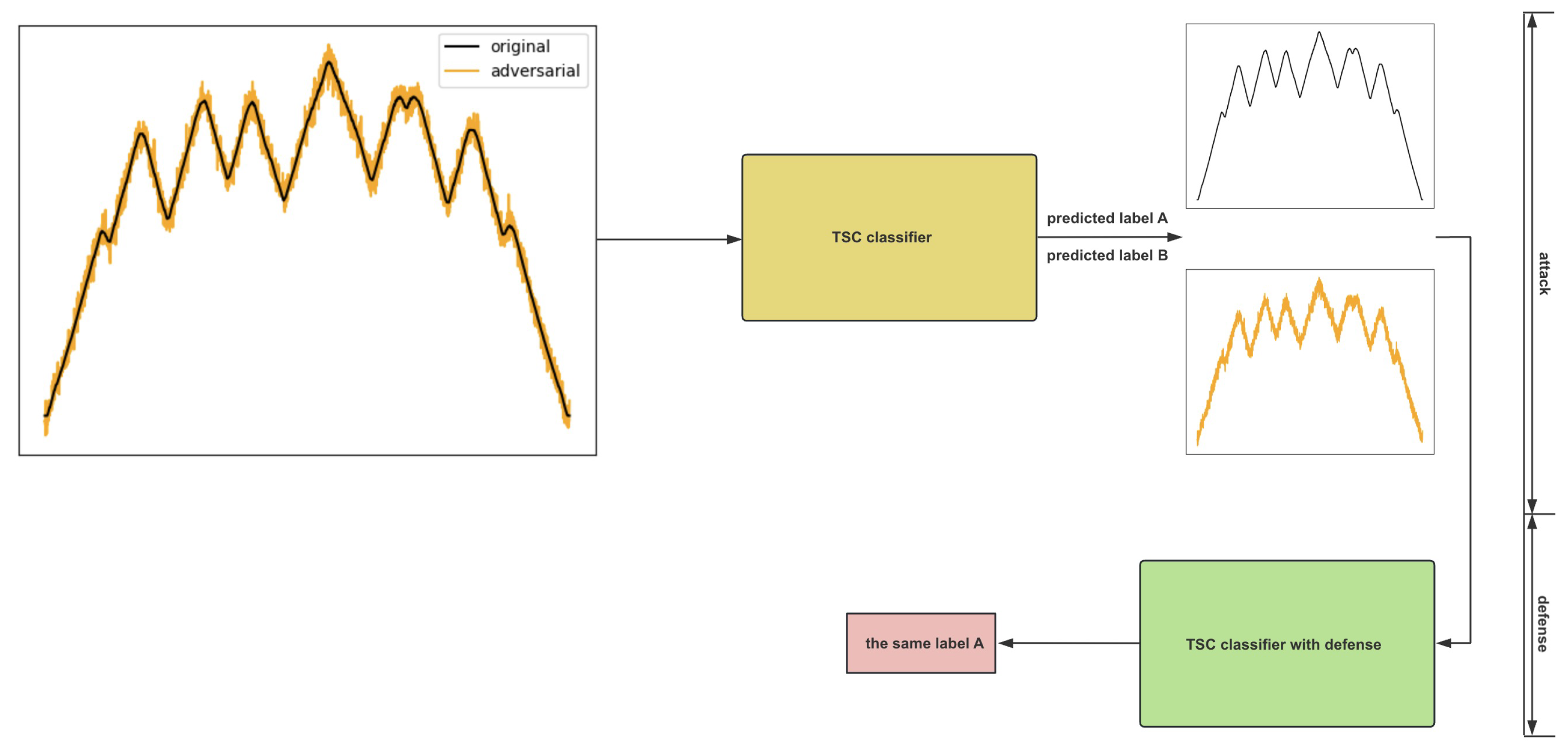
- We propose a more realistic scored-based black-box attack approach on TSC through simulated annealing-based random search algorithm without gradient estimation.
- We propose a post-processing-based defense approach against scored-based black-box attacks on TSC where only output confidence scores are needed. The trend of the loss function is flipped locally while the global trend of the loss function is not changed. Besides, the accuracy of the classifier is not affected.
- We carry out experiments on multiple time series datasets to demonstrate the effectiveness of both the attack and defense approaches.
2. Materials and Methods
2.1. Background
2.2. Methods
2.2.1. Square-Based Attack
| Algorithm 1: Simulated annealing-based adversarial attack |
 |
2.2.2. Post-Processing-Based Defense
| Algorithm 2: Post-processing-based adversarial attack defense |
| Input: confidence scores predicted by classifier P, label K, number of iterations N and hyperparameters period t, and Output: modified confidence score vector 1 /* is the midpoint of the interval */ 2 /* is the constructed loss */ 3 4 5 optimize with loss function for N epochs |
2.3. Experiments
3. Results
4. Discussion
5. Future Research
- Exploring additional random search methods like genetic algorithms as alternatives to simulated annealing for perturbation optimization, and omparing the attack success rates of different methods and analyze their relative advantages and disadvantages.
- The current defense approach has a limitation in that it is not effective against adversarial examples where the starting perturbation already exceeds the range of the constructed loss curve. A potential area of improvement is developing a supplementary post-processing module capable of handling such “immediate” adversarial inputs, which is challenging given only access to confidence scores.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| TSC | Time Series Classification |
| DNN | Deep Neural Network |
| ASR | average success rate |
| DSR | defense success rate |
| AQT | average query times of successful adversarial attacks |
| MQT | median query times of successful adversarial attacks |
References
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar] [CrossRef]
- Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Adversarial Attacks on Deep Neural Networks for Time Series Classification. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Ismail Fawaz, H.; Lucas, B.; Forestier, G.; Pelletier, C.; Schmidt, D.F.; Weber, J.; Webb, G.I.; Idoumghar, L.; Muller, P.A.; Petitjean, F. Inceptiontime: Finding alexnet for time series classification. Data Min. Knowl. Discov. 2020, 34, 1936–1962. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, Y.; Lin, J.; Lu, C.T. Tapnet: Multivariate time series classification with attentional prototypical network. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 6845–6852. [Google Scholar]
- Chen, S.; Huang, Z.; Tao, Q.; Wu, Y.; Xie, C.; Huang, X. Adversarial attack on attackers: Post-process to mitigate black-box score-based query attacks. Adv. Neural Inf. Process. Syst. 2022, 35, 14929–14943. [Google Scholar]
- Li, Y.; Cheng, M.; Hsieh, C.J.; Lee, T.C. A review of adversarial attack and defense for classification methods. Am. Stat. 2022, 76, 329–345. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 99–112. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv 2017, arXiv:1706.06083. [Google Scholar]
- Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 39–57. [Google Scholar]
- Ilyas, A.; Engstrom, L.; Athalye, A.; Lin, J. Black-box adversarial attacks with limited queries and information. In Proceedings of the International Conference on Machine Learning. PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 2137–2146. [Google Scholar]
- Uesato, J.; O’donoghue, B.; Kohli, P.; Oord, A. Adversarial risk and the dangers of evaluating against weak attacks. In Proceedings of the International Conference on Machine Learning. PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 5025–5034. [Google Scholar]
- Ding, D.; Zhang, M.; Feng, F.; Huang, Y.; Jiang, E.; Yang, M. Black-box adversarial attack on time series classification. In Proceedings of the Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 Februray 2023; Volume 37, pp. 7358–7368. [Google Scholar]
- Andriushchenko, M.; Croce, F.; Flammarion, N.; Hein, M. Square attack: A query-efficient black-box adversarial attack via random search. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 484–501. [Google Scholar]
- Tramèr, F.; Kurakin, A.; Papernot, N.; Goodfellow, I.; Boneh, D.; McDaniel, P. Ensemble adversarial training: Attacks and defenses. arXiv 2017, arXiv:1705.07204. [Google Scholar]
- Li, T.; Wu, Y.; Chen, S.; Fang, K.; Huang, X. Subspace adversarial training. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 23–28 August 2022; pp. 13409–13418. [Google Scholar]
- Qin, Z.; Fan, Y.; Zha, H.; Wu, B. Random noise defense against query-based black-box attacks. Adv. Neural Inf. Process. Syst. 2021, 34, 7650–7663. [Google Scholar]
- Salman, H.; Sun, M.; Yang, G.; Kapoor, A.; Kolter, J.Z. Denoised smoothing: A provable defense for pretrained classifiers. Adv. Neural Inf. Process. Syst. 2020, 33, 21945–21957. [Google Scholar]
- Xie, C.; Wang, J.; Zhang, Z.; Ren, Z.; Yuille, A. Mitigating adversarial effects through randomization. arXiv 2017, arXiv:1711.01991. [Google Scholar]
- Liu, X.; Cheng, M.; Zhang, H.; Hsieh, C.J. Towards robust neural networks via random self-ensemble. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 369–385. [Google Scholar]
- Wang, D.; Ju, A.; Shelhamer, E.; Wagner, D.; Darrell, T. Fighting gradients with gradients: Dynamic defenses against adversarial attacks. arXiv 2021, arXiv:2105.08714. [Google Scholar]
- Wu, Y.H.; Yuan, C.H.; Wu, S.H. Adversarial robustness via runtime masking and cleansing. In Proceedings of the International Conference on Machine Learning. PMLR, Miami, FL, USA, 14–17 December 2020; pp. 10399–10409. [Google Scholar]
- Pialla, G.; Ismail Fawaz, H.; Devanne, M.; Weber, J.; Idoumghar, L.; Muller, P.A.; Bergmeir, C.; Schmidt, D.F.; Webb, G.I.; Forestier, G. Time series adversarial attacks: An investigation of smooth perturbations and defense approaches. Int. J. Data Sci. Anal. 2023, 1–11. [Google Scholar] [CrossRef]
- Yang, W.; Yuan, J.; Wang, X.; Zhao, P. TSadv: Black-box adversarial attack on time series with local perturbations. Eng. Appl. Artif. Intell. 2022, 114, 105218. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H. Adversarial Attacks on Time Series. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3309–3320. [Google Scholar] [CrossRef]
- Rathore, P.; Basak, A.; Nistala, S.H.; Runkana, V. Untargeted, Targeted and Universal Adversarial Attacks and Defenses on Time Series. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Chen, Y.; Keogh, E.; Hu, B.; Begum, N.; Bagnall, A.; Mueen, A.; Batista, G. The UCR Time Series Classification Archive. 2015. Available online: www.cs.ucr.edu/~eamonn/time_series_data/ (accessed on 17 January 2024).



| Dataset | TSC Classifier Accuracy | Number of Classes |
|---|---|---|
| UWaveGestureLibraryAll | 95.20% | 8 |
| OSU Leaf | 94.21% | 6 |
| ECG5000 | 94.09% | 5 |
| ChlorineConcentration | 87.66% | 3 |
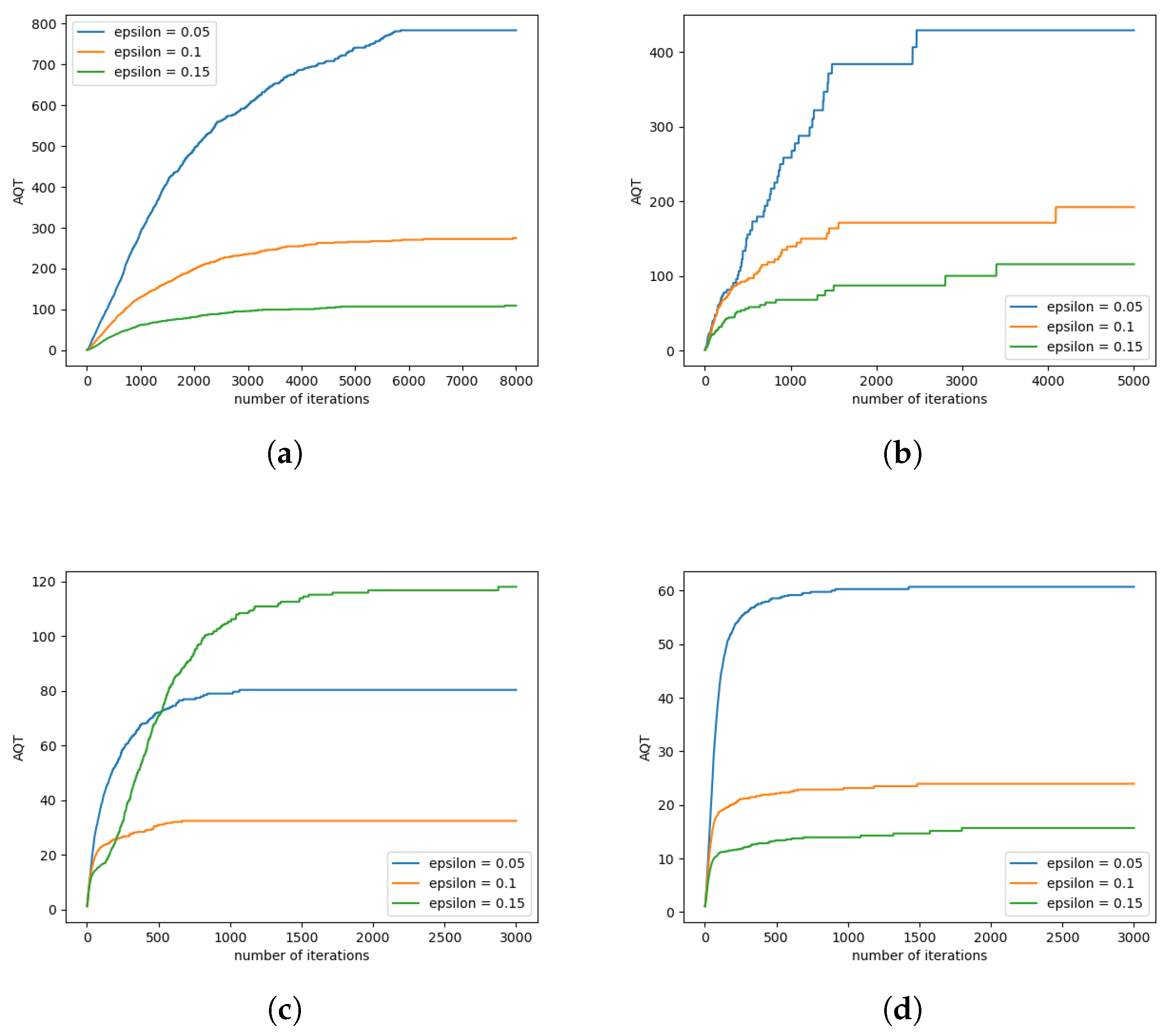
| Dataset | Value | ASR | AQT | MQT | DSR |
|---|---|---|---|---|---|
| UWaveGestureLibraryAll | 0.05 | 59.45% | 781.03 | 403 | 79.46% |
| 0.1 | 94.96% | 277.48 | 17 | 47.94% | |
| 0.15 | 99.91% | 112.20 | 1 | 24.17% | |
| OSU Leaf | 0.05 | 40.27% | 429.33 | 187 | 91.24% |
| 0.1 | 82.74% | 192.35 | 84 | 77.54% | |
| 0.15 | 93.36% | 115.80 | 26 | 57.82% | |
| ECG5000 | 0.05 | 33.75% | 80.34 | 45 | 84.15% |
| 0.1 | 38.36% | 32.45 | 19 | 70.44% | |
| 0.15 | 51.41% | 118.01 | 17 | 62.93% | |
| ChlorineConcentration | 0.05 | 98.28% | 60.70 | 48 | 70.02% |
| 0.1 | 99.13% | 23.94 | 13 | 40.65% | |
| 0.15 | 99.55% | 15.68 | 4 | 26.11% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Luo, Y. Score-Based Black-Box Adversarial Attack on Time Series Using Simulated Annealing Classification and Post-Processing Based Defense. Electronics 2024, 13, 650. https://doi.org/10.3390/electronics13030650
Liu S, Luo Y. Score-Based Black-Box Adversarial Attack on Time Series Using Simulated Annealing Classification and Post-Processing Based Defense. Electronics. 2024; 13(3):650. https://doi.org/10.3390/electronics13030650
Chicago/Turabian StyleLiu, Sichen, and Yuan Luo. 2024. "Score-Based Black-Box Adversarial Attack on Time Series Using Simulated Annealing Classification and Post-Processing Based Defense" Electronics 13, no. 3: 650. https://doi.org/10.3390/electronics13030650
APA StyleLiu, S., & Luo, Y. (2024). Score-Based Black-Box Adversarial Attack on Time Series Using Simulated Annealing Classification and Post-Processing Based Defense. Electronics, 13(3), 650. https://doi.org/10.3390/electronics13030650






