Research on a Deep Ensemble Learning Model for the Ultra-Short-Term Probabilistic Prediction of Wind Power
Abstract
1. Introduction
2. A Model for the Deterministic Prediction of Wind Power Based on Deep Ensemble Learning
2.1. Rank Correlation Coefficient
2.2. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN)
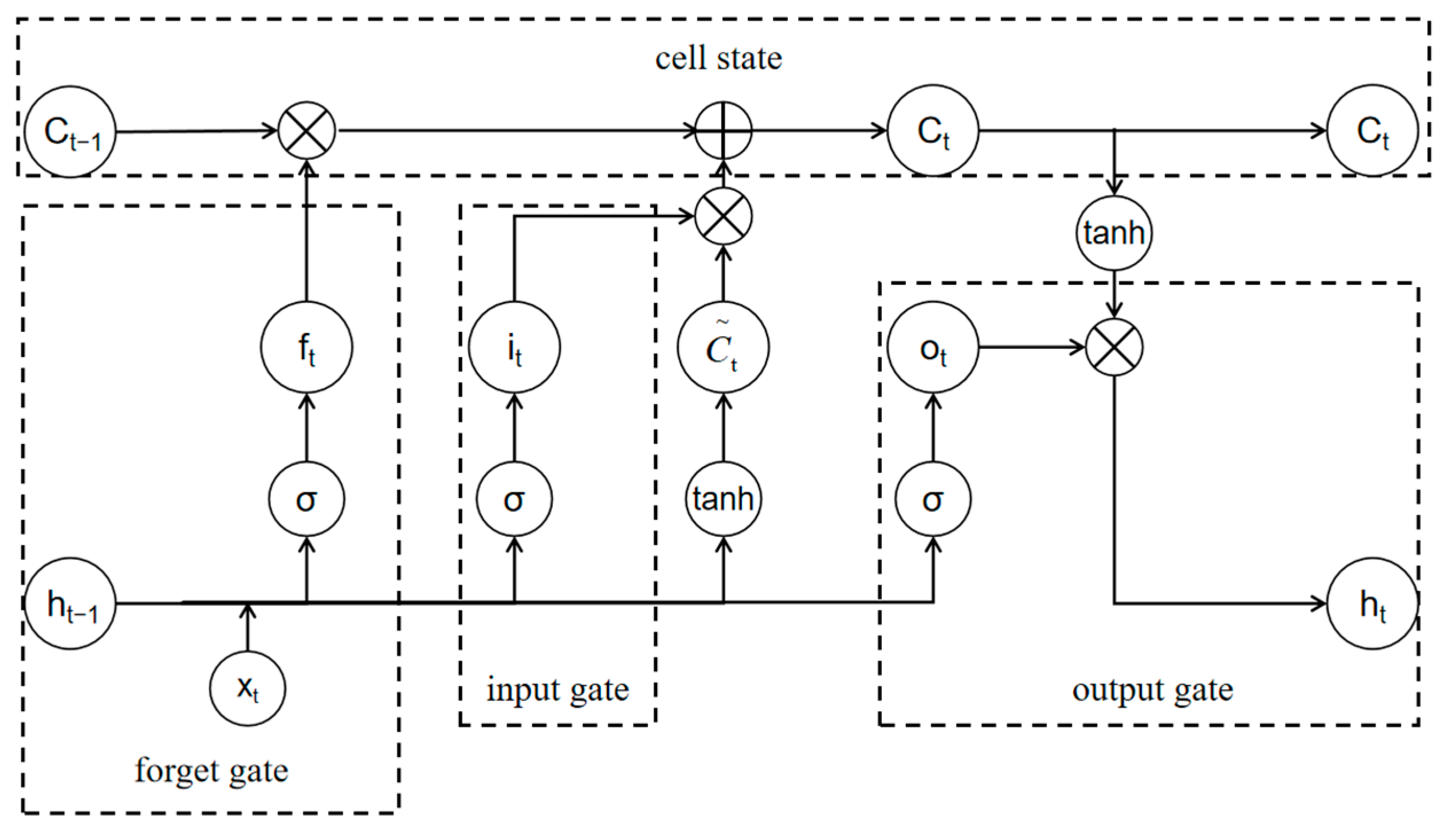
2.3. Convolutional Neural Network (CNN)
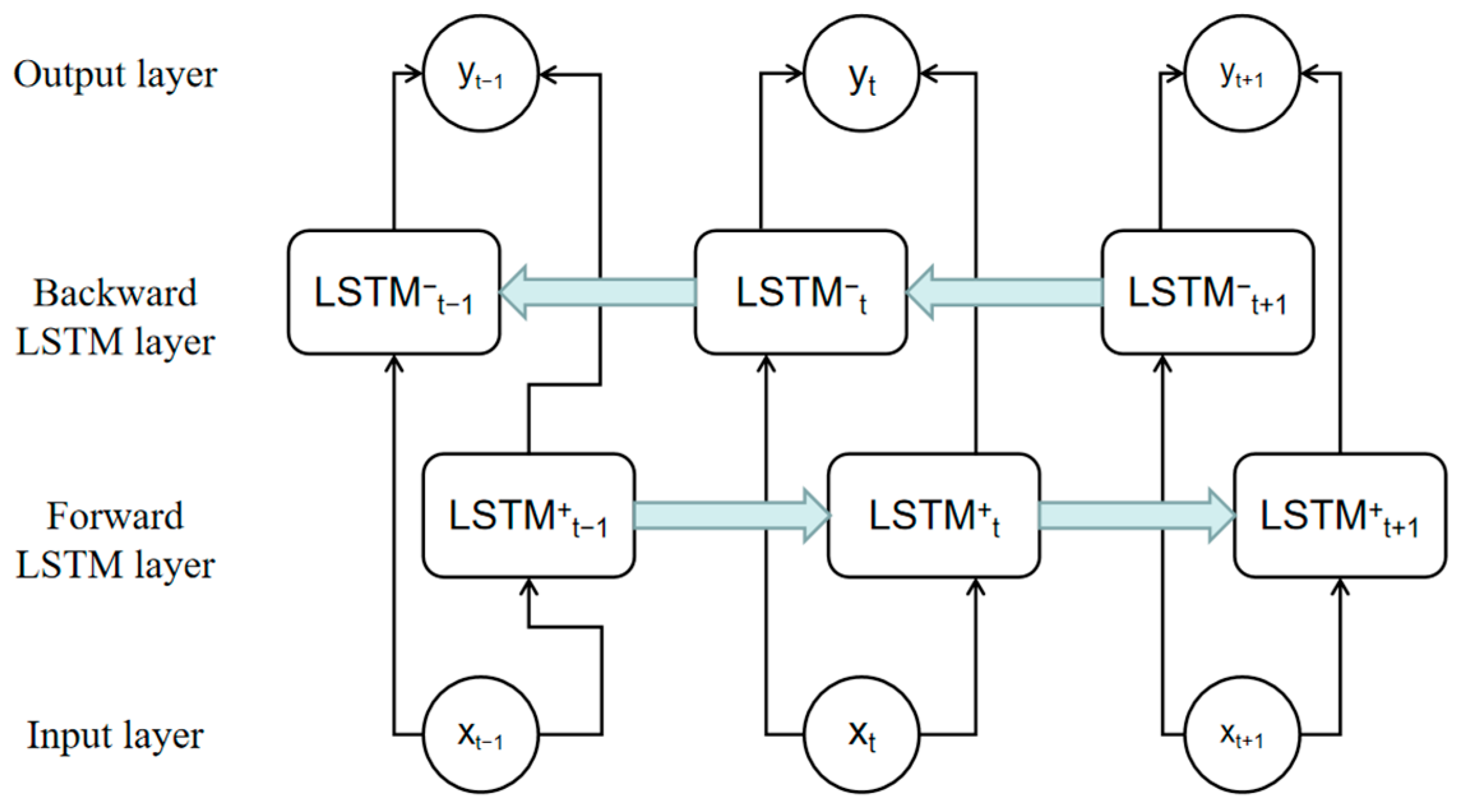
2.4. Bidirectional Long Short-Term Memory (BILSTM)
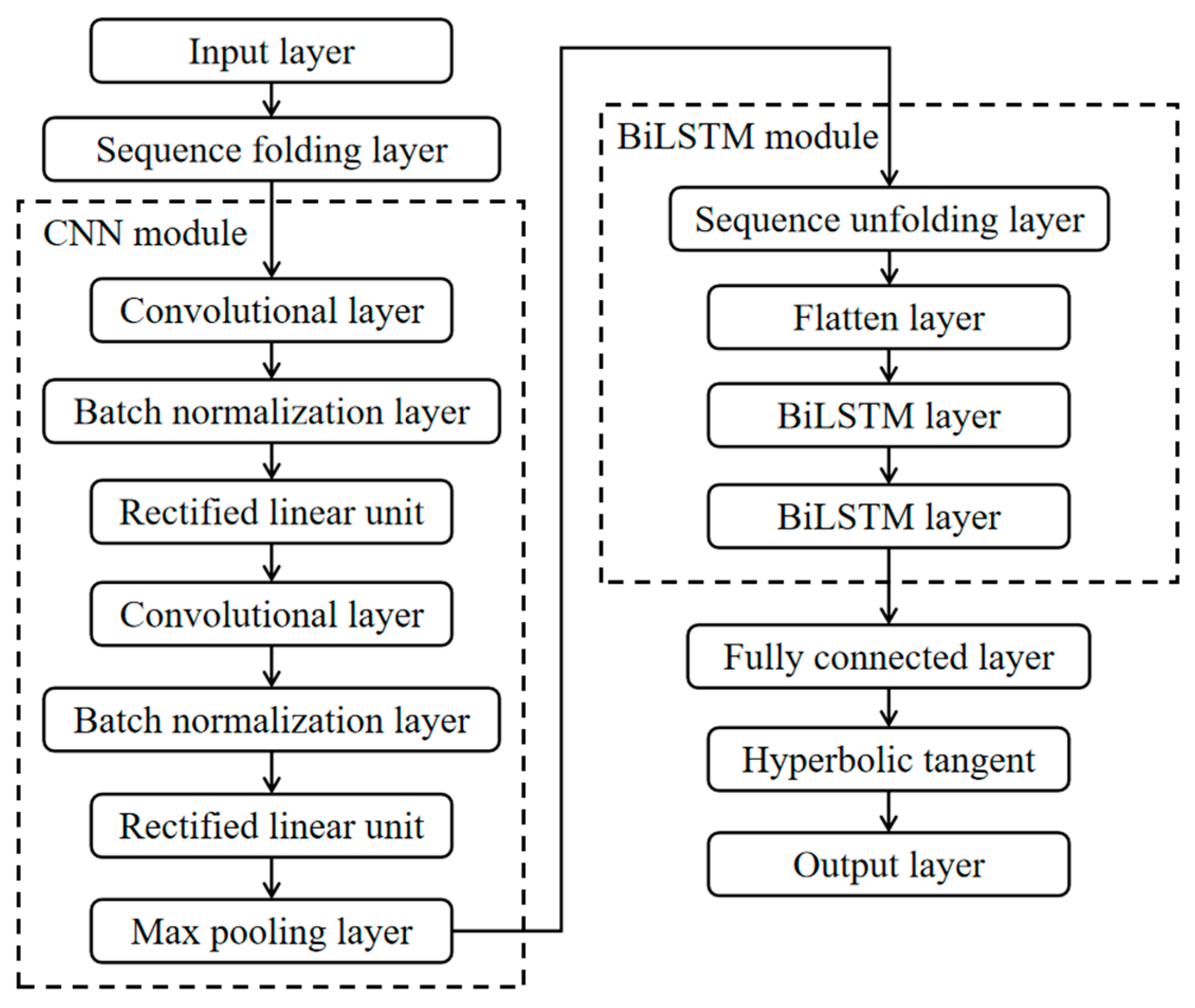
2.5. CNN-BiLSTM Ensemble Model
3. Probabilistic Prediction of Wind Power Based on Nonparametric Estimation
3.1. Kernel Density Estimation
3.2. A Method Based on an Adaptive Bandwidth
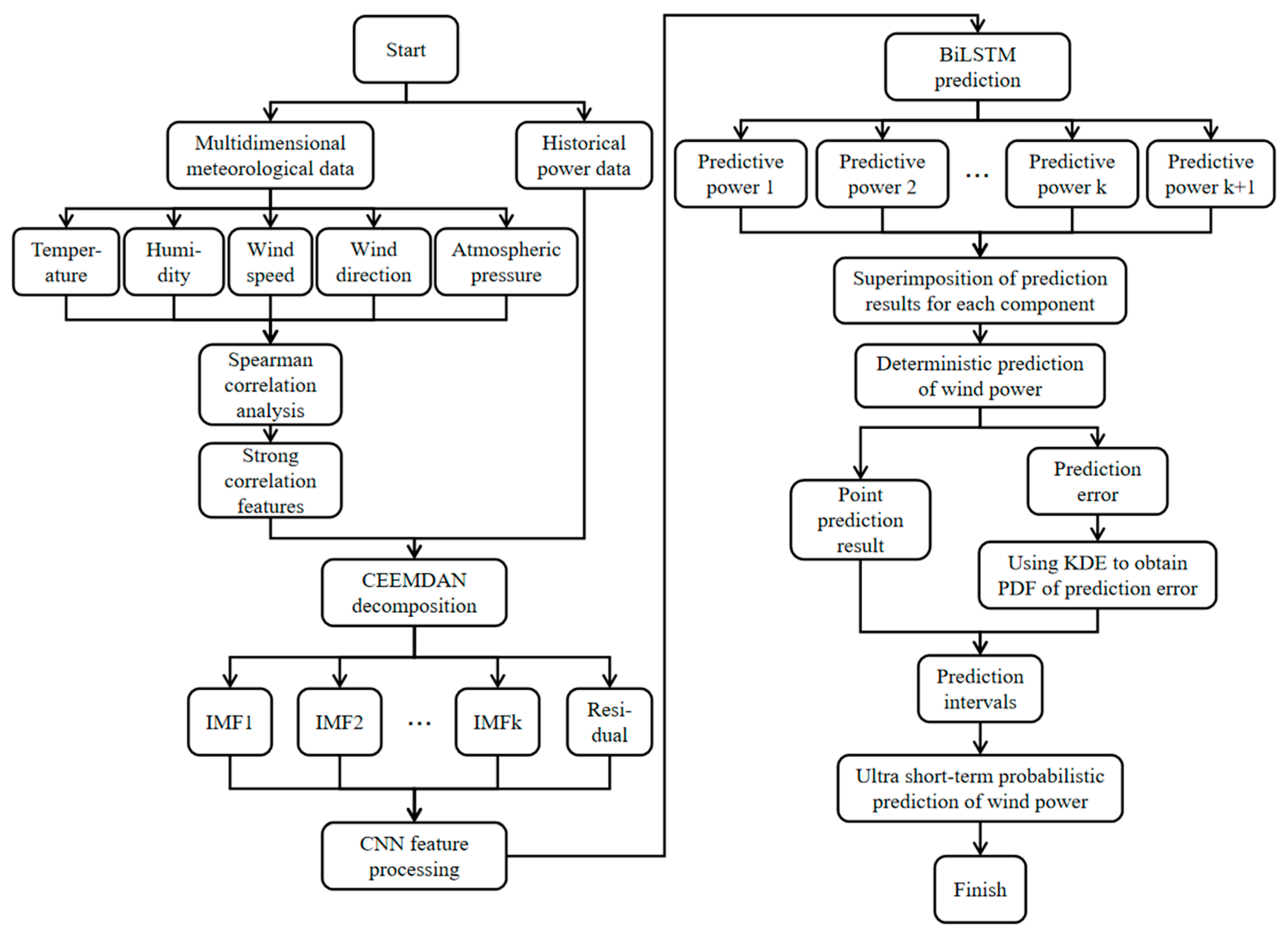
3.3. The Prediction Process of the Proposed Method
3.4. Evaluation Metrics
4. Case Studies
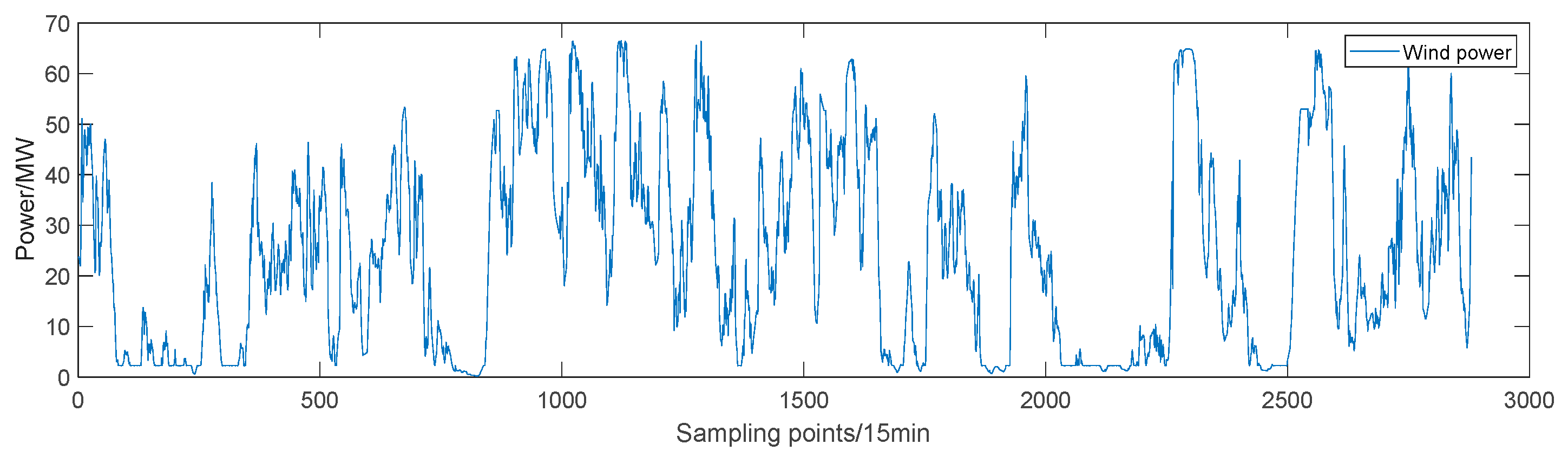
4.1. Dataset Description
4.2. Feature Selection Based on Spearman
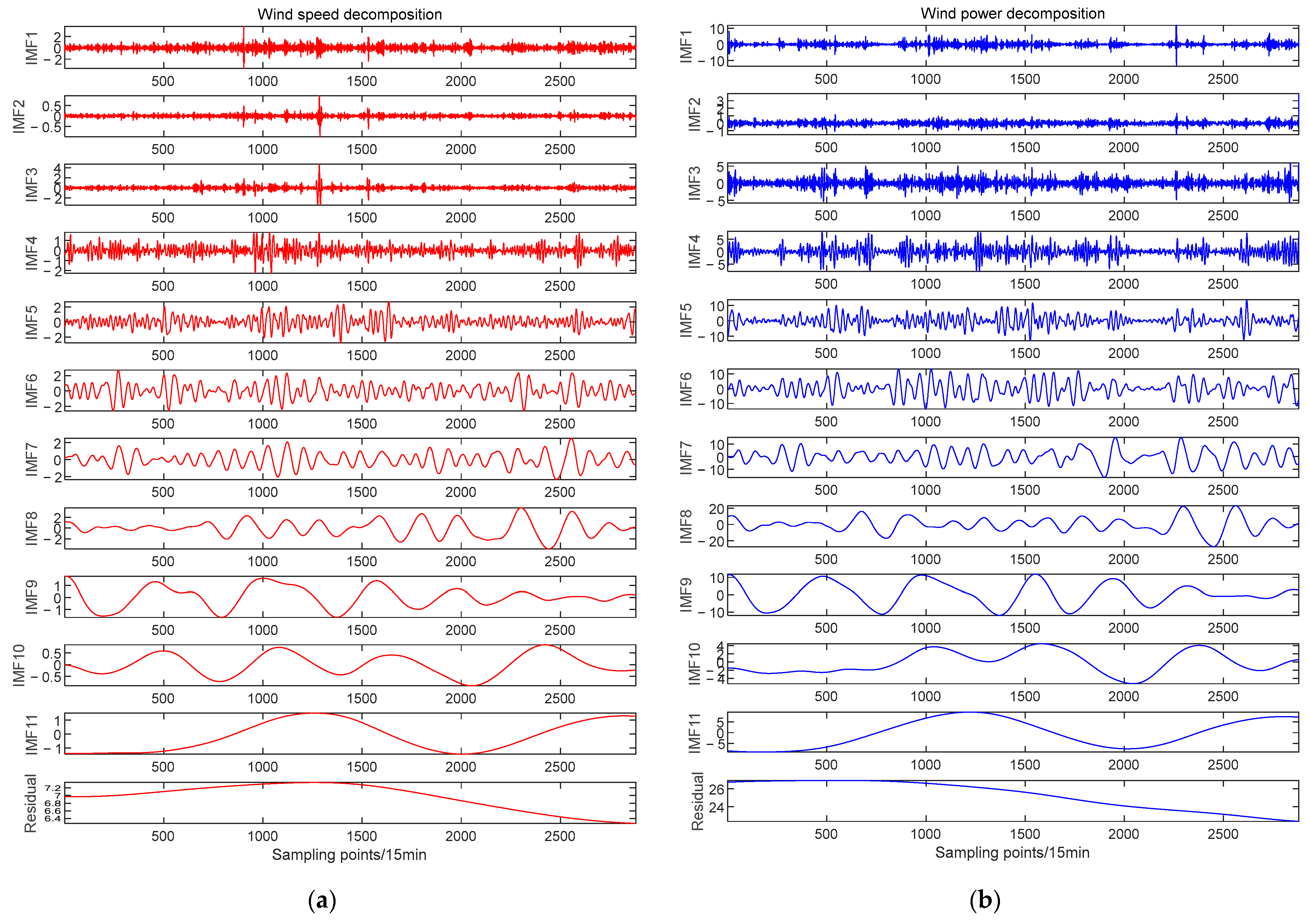
4.3. Time Series Decomposition Based on CEEMDAN
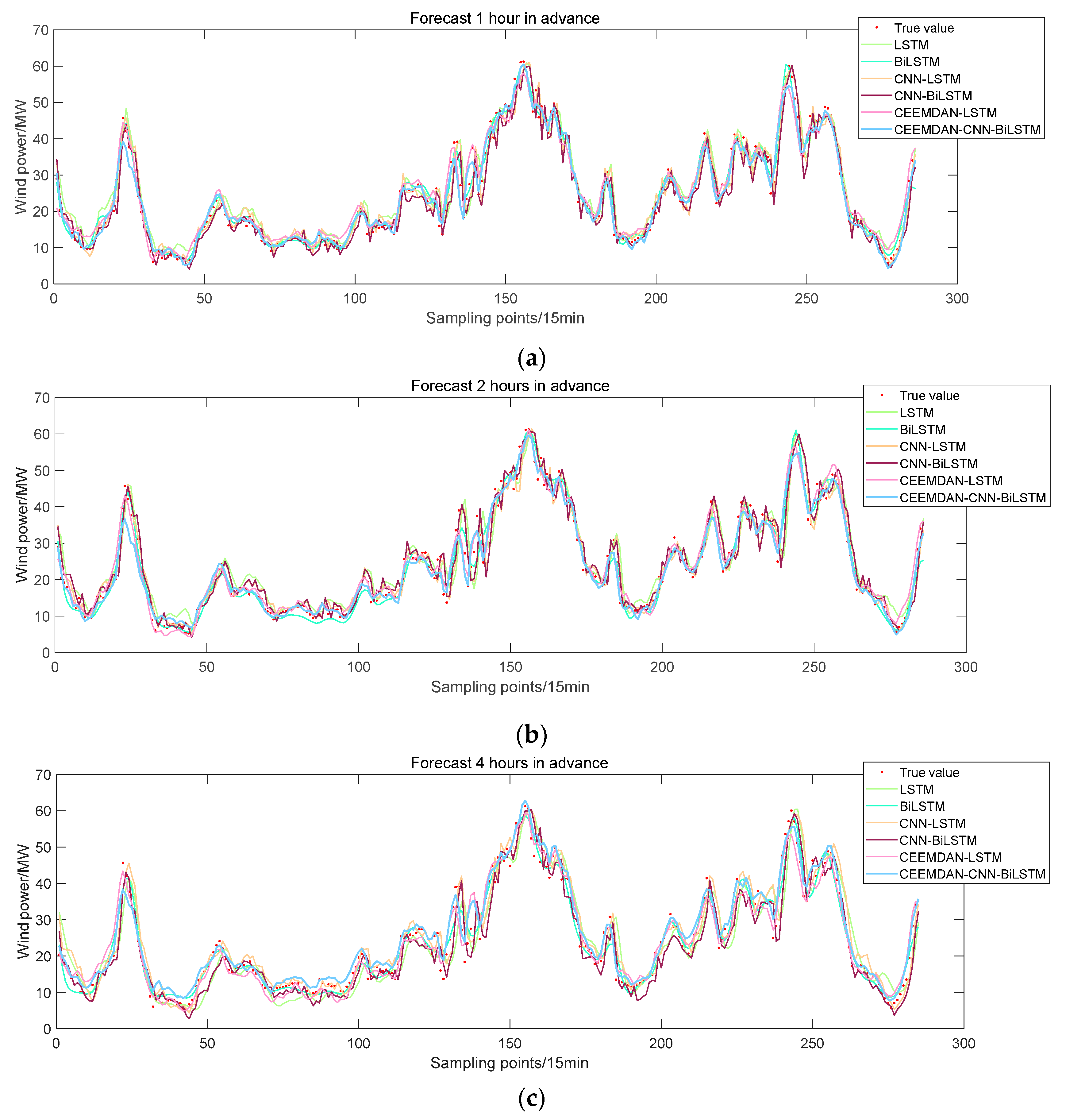
4.4. Analysis of Ultra-Short-Term Deterministic Prediction
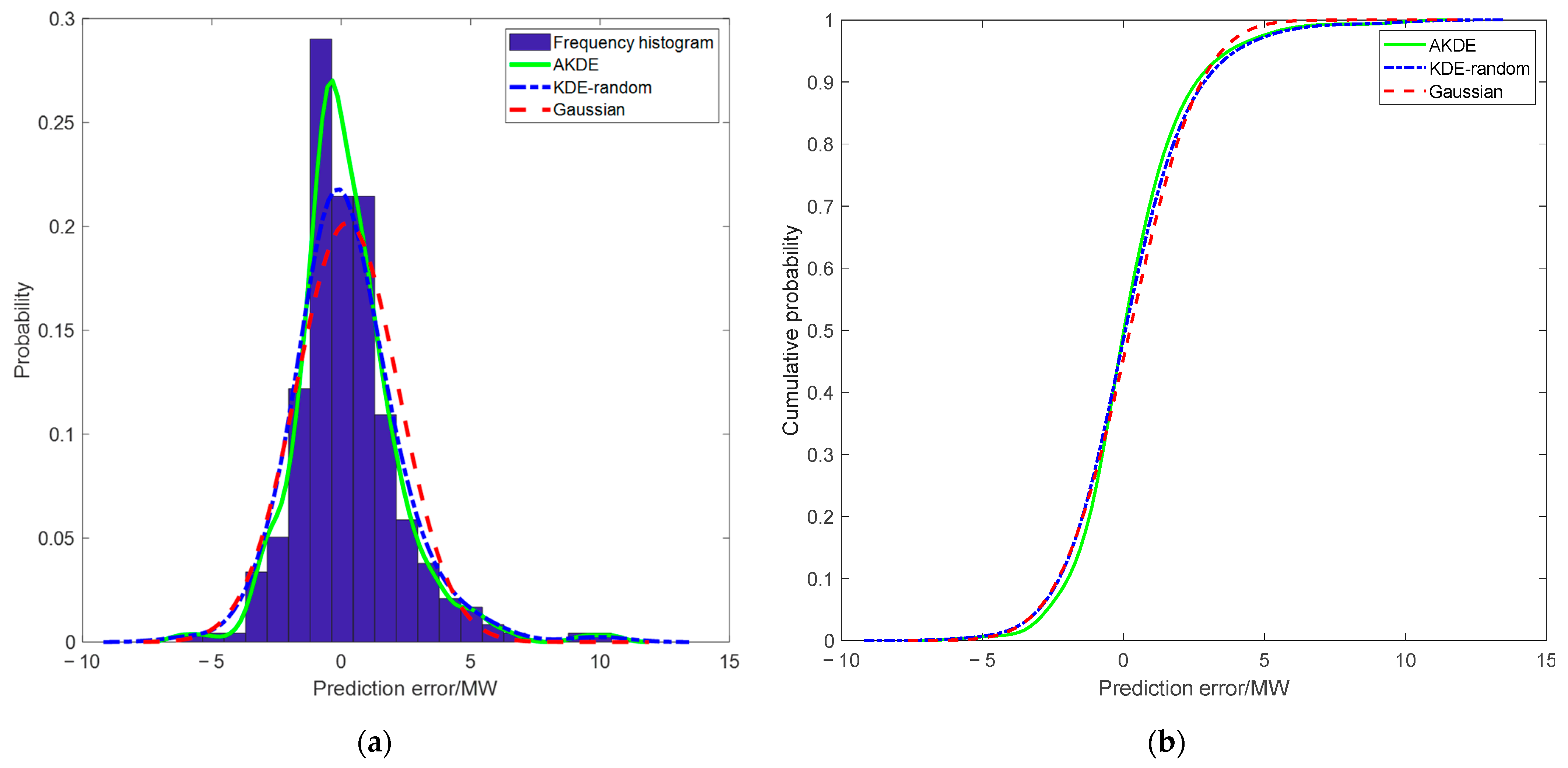
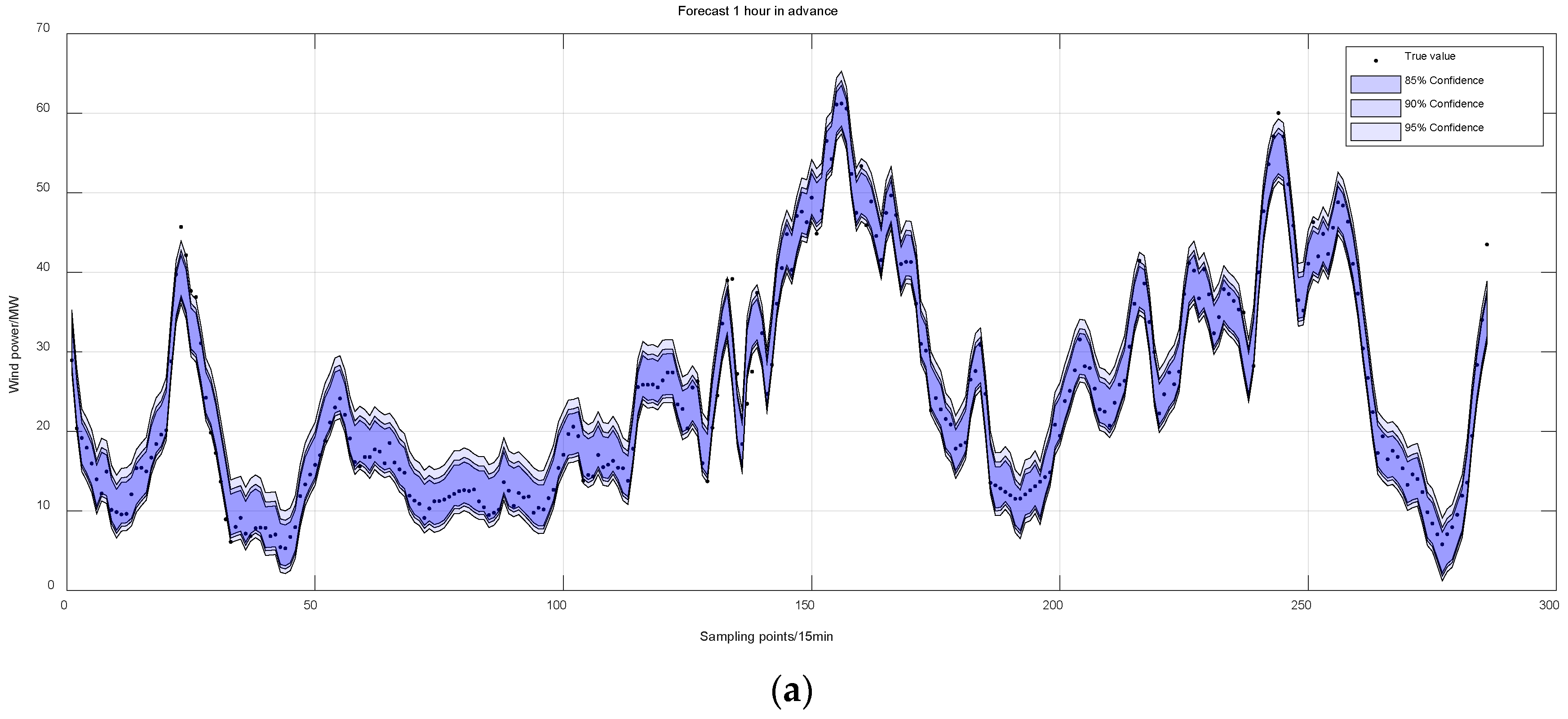
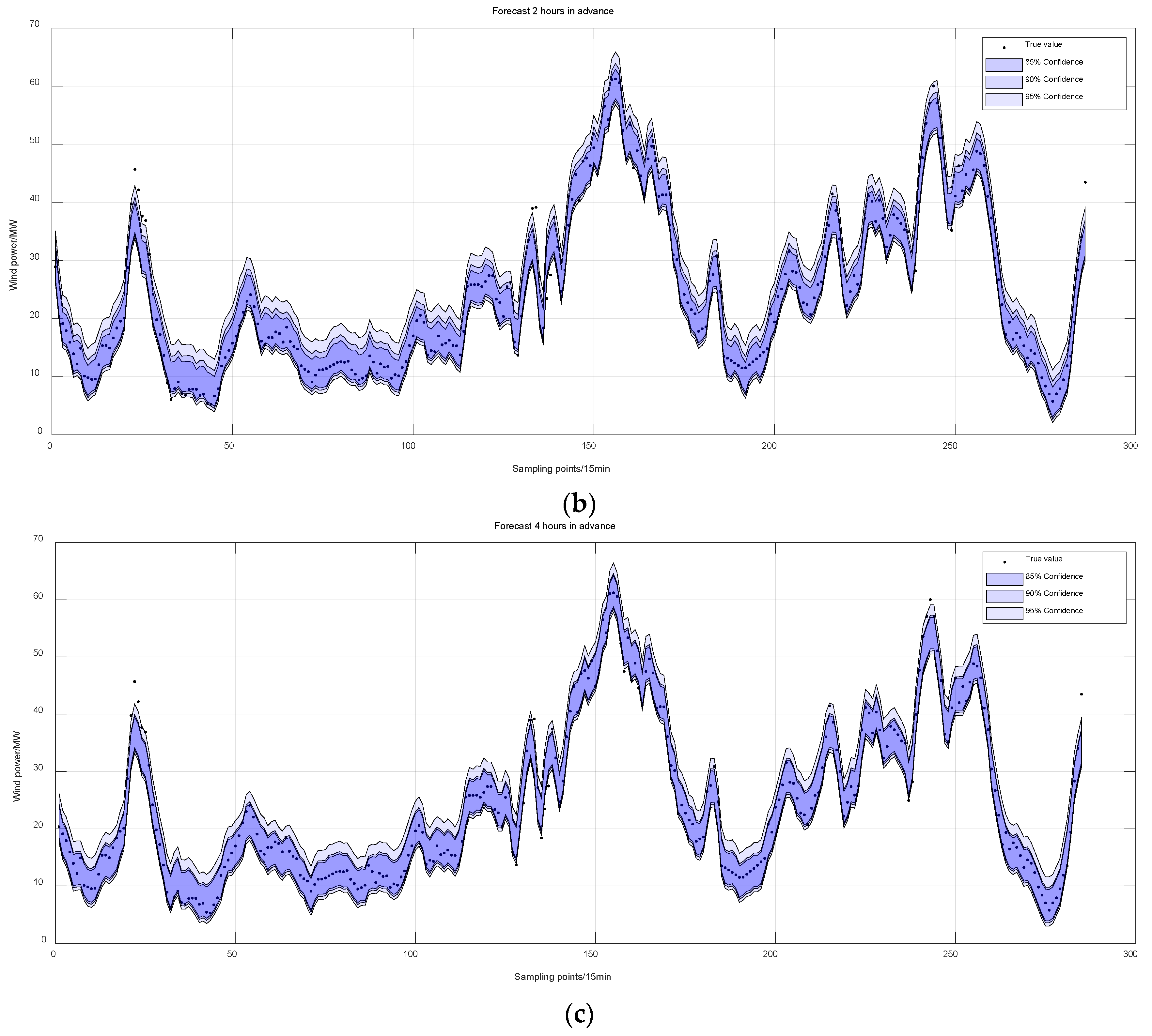
4.5. Analysis of Ultra-Short-Term Probabilistic Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Sun, Y.H.; Wang, S.; Bai, L.Q.; Hou, D.C.; Mahfoud, R.J.; Wang, P. Very short-term probabilistic prediction method for wind speed based on ALASSO-Nonlinear quantile regression and integrated criterion. CSEE J. Power Energy Syst. 2023, 9, 2121–2129. [Google Scholar]
- Zhou, Y.; Sun, Y.H.; Wang, S.; Mahfoud, R.J.; Alhelou, H.H.; Hatziargyriou, N.; Siano, P. Performance improvement of very short-term prediction intervals for regional wind power based on composite conditional nonlinear quantile regression. J. Mod. Power Syst. Clean Energy 2022, 10, 60–70. [Google Scholar] [CrossRef]
- Sun, Y.H.; Zhou, Y.; Wang, S.; Mahfoud, R.M.; Alhelou, H.H.; Sideratos, G.; Hatziargyriou, N.; Siano, P. Nonparametric probabilistic prediction of regional PV outputs based on granule-based clustering and direct optimization programming. J. Mod. Power Syst. Clean Energy 2023, 11, 1450–1461. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y.F.; Huang, Y.T. Wind power ultra-short-term prediction method based on NWP wind speed correction and double clustering division of transitional weather process. Energy 2023, 282, 128947. [Google Scholar] [CrossRef]
- Niu, D.X.; Sun, L.J.; Yu, M.; Wang, K.K. Point and interval forecasting of ultra-short-term wind power based on a data-driven method and hybrid deep learning model. Energy 2022, 254, 124384. [Google Scholar]
- Wan, C.; Song, Y.H. Theories, methodologies and applications of probabilistic forecasting for power systems with renewable energy sources. Autom. Electr. Power Syst. 2021, 45, 2–16. [Google Scholar]
- Yu, G.Z.; Lu, L.; Tang, B.; Wang, S.Y.; Chung, C.Y. Ultra-short-term wind power subsection forecasting method based on extreme weather. IEEE Trans. Power Syst. 2023, 38, 5045–5056. [Google Scholar] [CrossRef]
- Fan, H.J.; Zhen, Z.; Liu, N.; Sun, Y.Q.; Chang, X.Q.; Li, Y.; Wang, F.; Mi, Z.Q. Fluctuation pattern recognition based ultra-short-term wind power probabilistic forecasting method. Energy 2023, 266, 126420. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Revanesh, M.; Huang, C.; Luo, X. Short-term wind speed and power forecasting for smart city power grid with a hybrid machine learning framework. IEEE Internet Things J. 2023, 10, 18754–18765. [Google Scholar] [CrossRef]
- Yang, M.; Zhu, L. Error analysis of photovoltaic power short-term prediction based on non-parametric estimation. Power Syst. Clean Energy 2020, 36, 107–114. [Google Scholar]
- He, Y.Y.; Wang, Y.; Wang, S.; Yao, X. A cooperative ensemble method for multistep wind speed probabilistic forecasting. Chaos Solitons Fractals 2022, 162, 112416. [Google Scholar] [CrossRef]
- Liao, W.; Wang, S.; Bak-Jensen, B.; Pillai, J.R.; Yang, Z.; Liu, K. Ultra-short-term interval prediction of wind power based on graph neural network and improved bootstrap technique. J. Mod. Power Syst. Clean Energy 2023, 11, 1100–1114. [Google Scholar] [CrossRef]
- Wang, S.; Sun, Y.H.; Zhou, Y.; Wang, J.X.; Hou, D.C.; Zhang, L.C. Ultra-short term conditional probability prediction of wind power considering error time dependence. Electr. Power Autom. Equip. 2022, 42, 40–46. [Google Scholar]
- Chen, H.; Xie, L.R.; Xin, B.W.; Bao, H.Y.; Li, J.; Abulizi, M.R. Research on minimum interval of energy storage capacity configuration of tower elevator based on beta distribution. Acta Energ. Sol. Sin. 2021, 42, 454–459. [Google Scholar]
- Zhao, K.N.; Pu, T.J.; Wang, X.Y.; Li, Y. Probabilistic forecasting for photovoltaic power based on improved Bayesian neural network. Power Syst. Technol. 2019, 43, 4377–4386. [Google Scholar]
- Mo, X.J.; Wen, H.T.; Yang, Y.M.; Zhou, H.T.; Chen, S.; Wei, S.Y. A parameter estimation method ofαstable distribution and its application in the statistical modeling of ice-generated noise. Acta Acust. 2023, 48, 319–326. [Google Scholar]
- Sun, R.F.; Zhang, T.; He, Q.; Xu, H.X. Review on key technologies and applications in wind power forecasting. High Volt. Eng. 2021, 47, 1129–1143. [Google Scholar]
- Wang, X.D.; Ju, B.G.; Liu, Y.M.; Zang, T.L. Probability prediction of wind power based on QR-NFGLSTM and kernel density estimation. Acta Energ. Sol. Sin. 2022, 43, 479–485. [Google Scholar]
- Wan, C.; Xu, Z.; Pinson, P.; Dong, Z.Y.; Wong, K.P. Probabilistic forecasting of wind power generation using extreme learning machine. IEEE Trans. Power Syst. 2014, 29, 1033–1044. [Google Scholar] [CrossRef]
- Luo, Y.H.; Wang, X.; Yan, S.J. Risk assessment of photovoltaic distribution network based on adaptive kernel density estimation and cumulant method. Energy Rep. 2022, 8, 1152–1159. [Google Scholar] [CrossRef]
- Yang, M.; Dong, H. Short-term wind power interval prediction based on wind speed of numerical weather prediction and Monte Carlo method. Autom. Electr. Power Syst. 2021, 45, 79–85. [Google Scholar]
- Gao, B.X.; Huang, X.Q.; Shi, J.S.; Tai, Y.H.; Zhang, J. Hourly forecasting of solar irradiance based on CEEMDAN and multi-strategy CNN-LSTM neural networks. Renew. Energy 2020, 162, 1665–1683. [Google Scholar] [CrossRef]
- Hu, C.J.; Zhao, Y.; Jiang, H.; Jiang, M.K.; You, F.C.; Liu, Q. Prediction of ultra-short-term wind power based on CEEMDAN-LSTM-TCN. Energy Rep. 2022, 8, 483–492. [Google Scholar] [CrossRef]
- Yang, X.Y.; Xing, G.T.; Ma, X.; Fu, G. A model of quantile regression with kernel extreme learning machine and wind power interval prediction. Acta Energ. Sol. Sin. 2020, 41, 300–306. [Google Scholar]
- Xiao, B.; Xing, S.H.; Wang, M.C.; Yang. S.L.; Gou, X.K. Prediction method of output power long-term fluctuation characteristic for multiple wind farms after aggregation based on improved KDE method and GA-SVM. Electr. Power Autom. Equip. 2022, 42, 77–84. [Google Scholar]
- Zhou, M.; Wang, B.; Guo, S.D.; Watada, J. Multi-objective prediction intervals for wind power forecast based on deep neural networks. Inf. Sci. 2021, 550, 207–220. [Google Scholar] [CrossRef]
- Wang, K.J.; Qi, X.X.; Liu, H.D. A comparison of day-ahead photovoltaic power forecasting models based on deep learning neural network. Appl. Energy 2019, 251, 113315. [Google Scholar] [CrossRef]
- Wang, S.; Sun, Y.H.; Hou, D.C.; Zhou, Y.; Zhang, W.J. Very short-term adaptive probabilistic forecasting of wind power based on multi-band width kernel density estimation. High Volt. Eng. 2023, 1–10. [Google Scholar] [CrossRef]
- Yang, P.; Lu, L.; Wang, J.B.; Chen, H.C. Analysis of water quality trend in the main stream of the yangtze river based on principal component analysis. Environ. Eng. 2019, 37, 76–80. [Google Scholar]
- Feng, H.F.; Yu, C.S. A novel hybrid model for short-term prediction of PV power based on KS-CEEMDAN-SE-LSTM. Renew. Energy Focus 2023, 47, 100497. [Google Scholar] [CrossRef]
- Hao, H.; Wang, H.L.; Wei, Q. Theory of empirical mode decomposition and its application. Chin. High Technol. Lett. 2016, 26, 67–80. [Google Scholar]
- Zheng, J.D.; Cheng, J.S.; Yang, Y. Modified EEMD algorithm and its applications. J. Vib. Shock. 2013, 32, 21–26+46. [Google Scholar]
- Deng, J.L.; Dong, L.H.; Song, W.; Zhao, X.B.; Liu, T.M.; Pang, Y.T. Processing of seabed polymetallic nodule images based on Sea-thru and Mask R-CNN. Min. Metall. Eng. 2022, 42, 9–13. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Sun, Y.H.; Wang, P.; Zhai, S.W.; Hou, D.C.; Wang, S.; Zhou, Y. Ultra short-term probability prediction of wind power based on LSTM network and condition normal distribution. Wind. Energy 2020, 23, 63–76. [Google Scholar] [CrossRef]
- Zhang, D.D.; Chen, B.; Zhu, H.Y.; Goh, H.H.; Dong, Y.X.; Wu, T. Short-term wind power prediction based on two-layer decomposition and BiTCN-BiLSTM-attention model. Energy 2023, 285, 128762. [Google Scholar] [CrossRef]
- Du, B.G.; Huang, S.; Guo, J.; Tang, H.T.; Wang, L.; Zhou, S.W. Interval forecasting for urban water demand using PSO optimized KDE distribution and LSTM neural networks. Appl. Soft Comput. 2022, 122, 108875. [Google Scholar]
- Yang, X.Y.; Liu, Y.X.; Xing, G.T. Analysis of wind farm participation in the frequency regulation market considering wind power uncertainty. Int. J. Electr. Power Energy Syst. 2021, 130, 106946. [Google Scholar] [CrossRef]
- Xiong, M. Probability interval prediction of short-term wind power based on BP neural network and non-parametric kernel density estimation. J. Beijing Inf. Sci. Technol. Univ. 2020, 35, 51–56. [Google Scholar]
- Dong, W.C.; Sun, H.X.; Tan, J.X.; Li, Z.; Zhang, J.X.; Yang, H.F. Regional wind power probabilistic forecasting based on an improved kernel density estimation, regular vine copulas, and ensemble learning. Energy 2022, 238, 122045. [Google Scholar] [CrossRef]
- Lang, W.M.; Ma, X.J.; Zhou, B.W.; Yang, D.S.; Luo, Y.H.; Liu, L.Q. Wind power probabilistic intervals prediction based on LSTM and nonparametric kernel density estimation. Smart Power 2020, 48, 31–37+103. [Google Scholar]
- Wang, Y.; Xu, H.H.; Zou, R.M.; Zhang, L.J.; Zhang, F. A deep asymmetric laplace neural network for deterministic and probabilistic wind power forecasting. Renew. Energy 2022, 196, 497–517. [Google Scholar] [CrossRef]
- Wang, S.; Sun, Y.H.; Zhang, S.M.; Zhou, Y.; Hou, D.C.; Wang, J.X. Very short-term probabilistic prediction of PV based on multi-period error distribution. Electr. Power Syst. Res. 2023, 214, 108817. [Google Scholar] [CrossRef]
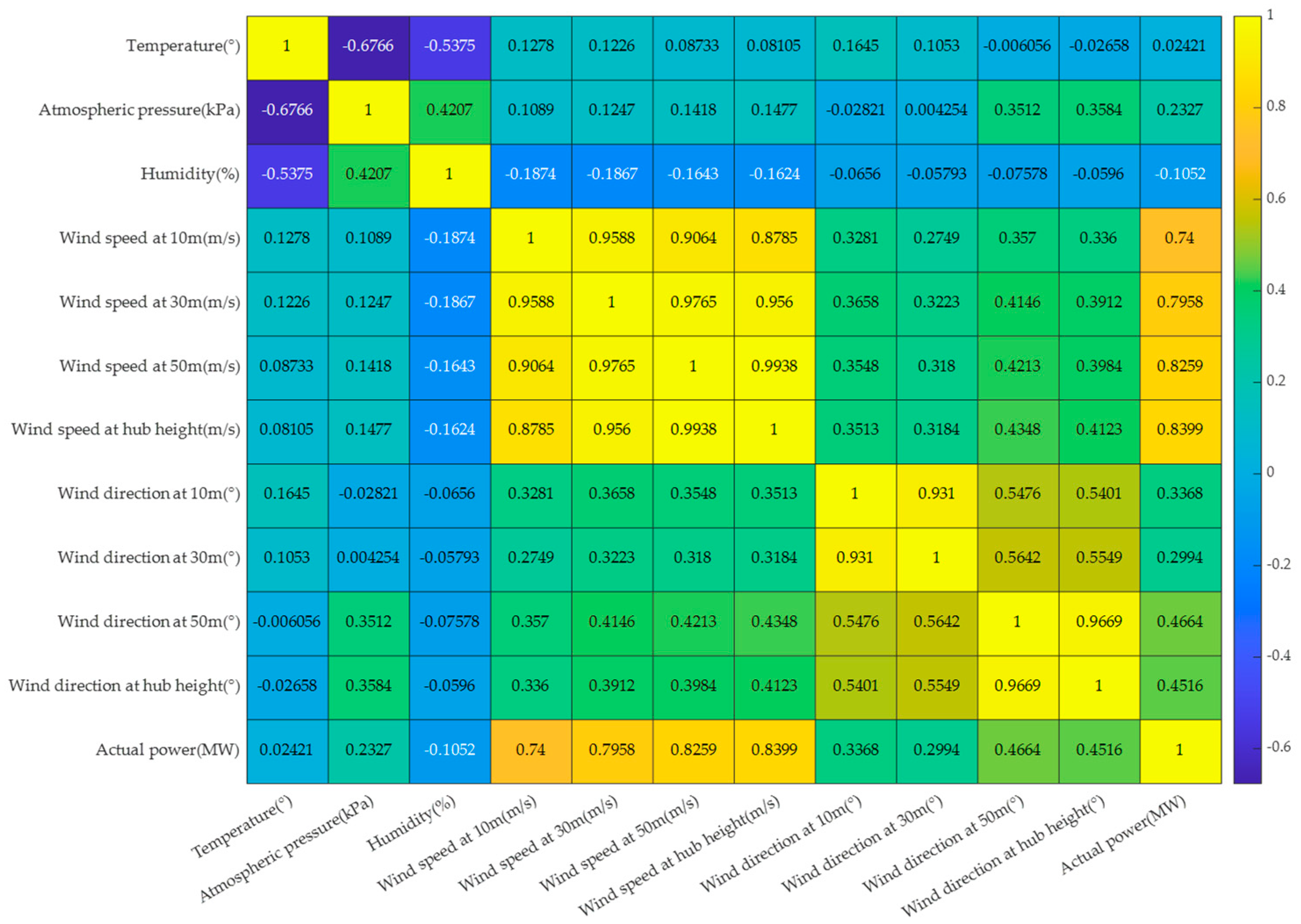
| Correlation Coefficient | Correlation Degree |
|---|---|
| 0.8~1 | Extremely strong correlation |
| 0.6~0.8 | Strong correlation |
| 0.4~0.6 | Moderate intensity correlation |
| 0.2~0.4 | Weak correlation |
| 0~0.2 | Extremely weakly correlated or uncorrelated |
| Dataset | Sample Size | Minimum/MW | Maximum/MW | Average/MW |
|---|---|---|---|---|
| Training set | 2592 | 0.24 | 66.46 | 24.49 |
| Test set | 288 | 5.28 | 61.22 | 24.71 |
| Parameters | CNN | LSTM/BiLSTM |
|---|---|---|
| Optimizer | Adam | |
| Learning rate | 0.005 | |
| Maximum number of iterations | 100 | |
| Number of convolutional layers | 2 | - |
| Number of convolutional kernels | 64 | - |
| Number of hidden layers | - | 2 |
| Number of hidden layer neurons | - | 64 |
| Time Scale | Prediction Model | RMSE/MW | MAE/MW | MAPE/% | R2 |
|---|---|---|---|---|---|
| 1 h | LSTM | 2.6294 | 1.8683 | 9.5981 | 0.9626 |
| BiLSTM | 2.3431 | 1.7705 | 9.3966 | 0.9703 | |
| CNN-LSTM | 2.1619 | 1.4758 | 7.3993 | 0.97472 | |
| CNN-BiLSTM | 2.1996 | 1.4429 | 6.5401 | 0.97383 | |
| CEEMDAN-LSTM | 1.8696 | 1.1178 | 6.2752 | 0.98109 | |
| CEEMDAN-CNN-BiLSTM | 1.2707 | 0.852 | 4.4584 | 0.99126 | |
| 2 h | LSTM | 3.1853 | 2.2832 | 11.8789 | 0.94643 |
| BiLSTM | 2.5297 | 1.848 | 9.0048 | 0.96622 | |
| CNN-LSTM | 2.3982 | 1.7233 | 8.0781 | 0.96964 | |
| CNN-BiLSTM | 2.2047 | 1.644 | 8.09 | 0.97434 | |
| CEEMDAN-LSTM | 2.2283 | 1.1571 | 5.445 | 0.97379 | |
| CEEMDAN-CNN-BiLSTM | 1.5856 | 1.1381 | 5.5868 | 0.98673 | |
| 4 h | LSTM | 4.0624 | 3.1425 | 15.1766 | 0.91595 |
| BiLSTM | 2.883 | 2.1271 | 10.1131 | 0.95767 | |
| CNN-LSTM | 3.2017 | 2.3367 | 10.8311 | 0.94779 | |
| CNN-BiLSTM | 2.9384 | 2.2323 | 10.2973 | 0.95603 | |
| CEEMDAN-LSTM | 2.4764 | 1.3993 | 6.5243 | 0.96877 | |
| CEEMDAN-CNN-BiLSTM | 1.7392 | 1.3449 | 6.3199 | 0.98459 | |
| Average | LSTM | 3.2924 | 2.4313 | 12.2179 | 0.9417 |
| BiLSTM | 2.5853 | 1.9152 | 9.5048 | 0.9647 | |
| CNN-LSTM | 2.5873 | 1.8453 | 8.7695 | 0.9641 | |
| CNN-BiLSTM | 2.4476 | 1.7731 | 8.3091 | 0.9681 | |
| CEEMDAN-LSTM | 2.1914 | 1.2247 | 6.0815 | 0.9746 | |
| CEEMDAN-CNN-BiLSTM | 1.5318 | 1.1117 | 5.455 | 0.9875 |
| Time Scale | Estimation Method | PINC/% | PICP/% | MPIW/MW | IS |
|---|---|---|---|---|---|
| 1 h | Gaussian | 85 | 86.014 | 5.5249 | −2.3811 |
| 90 | 90.5594 | 6.3142 | −1.8079 | ||
| 95 | 95.1049 | 7.4981 | −1.1334 | ||
| KDE-random | 85 | 87.0629 | 5.7148 | −2.3855 | |
| 90 | 91.6084 | 6.6291 | −1.7966 | ||
| 95 | 96.5035 | 8.4578 | −1.1018 | ||
| AKDE | 85 | 84.6154 | 5.1303 | −2.377 | |
| 90 | 88.1119 | 6.1169 | −1.8007 | ||
| 95 | 94.7552 | 7.8927 | −1.088 | ||
| 2 h | Gaussian | 85 | 89.1608 | 5.9117 | −2.6228 |
| 90 | 92.6573 | 6.897 | −2.0389 | ||
| 95 | 94.4056 | 8.0794 | −1.3135 | ||
| KDE-random | 85 | 87.4126 | 5.7459 | −2.5907 | |
| 90 | 92.3077 | 7.1249 | −2.0124 | ||
| 95 | 96.5035 | 9.6531 | −1.2485 | ||
| AKDE | 85 | 84.2657 | 5.1235 | −2.5817 | |
| 90 | 90.9091 | 6.5029 | −1.9969 | ||
| 95 | 95.4545 | 9.0646 | −1.2346 | ||
| 4 h | Gaussian | 85 | 86.6667 | 5.6699 | −2.4258 |
| 90 | 92.2807 | 6.5844 | −1.8604 | ||
| 95 | 94.7368 | 7.8647 | −1.1561 | ||
| KDE-random | 85 | 89.8246 | 5.9759 | −2.4435 | |
| 90 | 93.3333 | 7.043 | −1.8825 | ||
| 95 | 96.8421 | 9.1772 | −1.1458 | ||
| AKDE | 85 | 84.5614 | 5.487 | −2.4169 | |
| 90 | 91.2281 | 6.2186 | −1.8481 | ||
| 95 | 94.7368 | 8.5963 | −1.1342 |
| Prediction Model | PINC/% | PICP/% | MPIW/MW | IS |
|---|---|---|---|---|
| LSTM | 85 | 85.3147 | 10.6719 | −4.5427 |
| 90 | 91.958 | 12.8063 | −3.4158 | |
| 95 | 95.1049 | 16.4635 | −2.0138 | |
| BiLSTM | 85 | 83.2168 | 6.0669 | −2.7684 |
| 90 | 91.6084 | 6.9336 | −2.121 | |
| 95 | 94.4056 | 8.9559 | −1.3755 | |
| CNN-LSTM | 85 | 85.6643 | 10.1444 | −4.4179 |
| 90 | 90.2098 | 12.4575 | −3.3256 | |
| 95 | 95.4545 | 16.1975 | −1.9133 | |
| CNN-BiLSTM | 85 | 84.2657 | 10.7902 | −4.4246 |
| 90 | 90.5594 | 12.8272 | −3.2481 | |
| 95 | 95.4545 | 15.4356 | −1.8937 | |
| CEEMDAN-LSTM | 85 | 83.9161 | 5.6703 | −2.7225 |
| 90 | 90.9091 | 7.0389 | −2.1015 | |
| 95 | 94.7552 | 9.7763 | −1.2905 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Wei, F.; Kuang, K.; Mahfoud, R.J. Research on a Deep Ensemble Learning Model for the Ultra-Short-Term Probabilistic Prediction of Wind Power. Electronics 2024, 13, 475. https://doi.org/10.3390/electronics13030475
Zhou Y, Wei F, Kuang K, Mahfoud RJ. Research on a Deep Ensemble Learning Model for the Ultra-Short-Term Probabilistic Prediction of Wind Power. Electronics. 2024; 13(3):475. https://doi.org/10.3390/electronics13030475
Chicago/Turabian StyleZhou, Yan, Fuzhen Wei, Kaiyang Kuang, and Rabea Jamil Mahfoud. 2024. "Research on a Deep Ensemble Learning Model for the Ultra-Short-Term Probabilistic Prediction of Wind Power" Electronics 13, no. 3: 475. https://doi.org/10.3390/electronics13030475
APA StyleZhou, Y., Wei, F., Kuang, K., & Mahfoud, R. J. (2024). Research on a Deep Ensemble Learning Model for the Ultra-Short-Term Probabilistic Prediction of Wind Power. Electronics, 13(3), 475. https://doi.org/10.3390/electronics13030475






