Underwater Image Enhancement Based on Difference Convolution and Gaussian Degradation URanker Loss Fine-Tuning
Abstract
1. Introduction
- We introduce a difference convolution module into the UIE network. Difference convolution effectively extracts image gradients and edge information, complementing vanilla convolution and thereby enhancing both the detail quality of the enhanced images and the overall performance of the model.
- We introduce a Gaussian degradation-based URanker loss module during the fine-tuning stage. This module guides model convergence by leveraging the URanker score differences between the enhanced results of original and Gaussian-degraded images, which further improves image quality and model generalization.
- Extensive experiments show that our method has better performance on different test datasets compared to other UIE methods.
2. Related Work
2.1. Underwater Image Enhancement
2.2. Difference Convolution
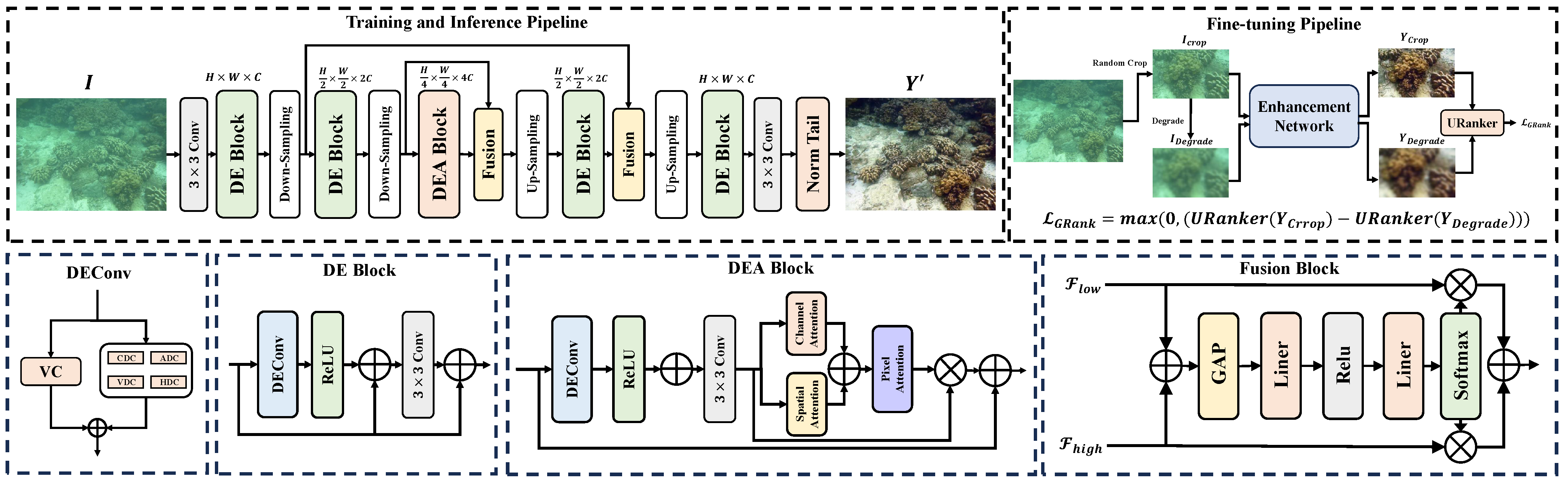
3. Method
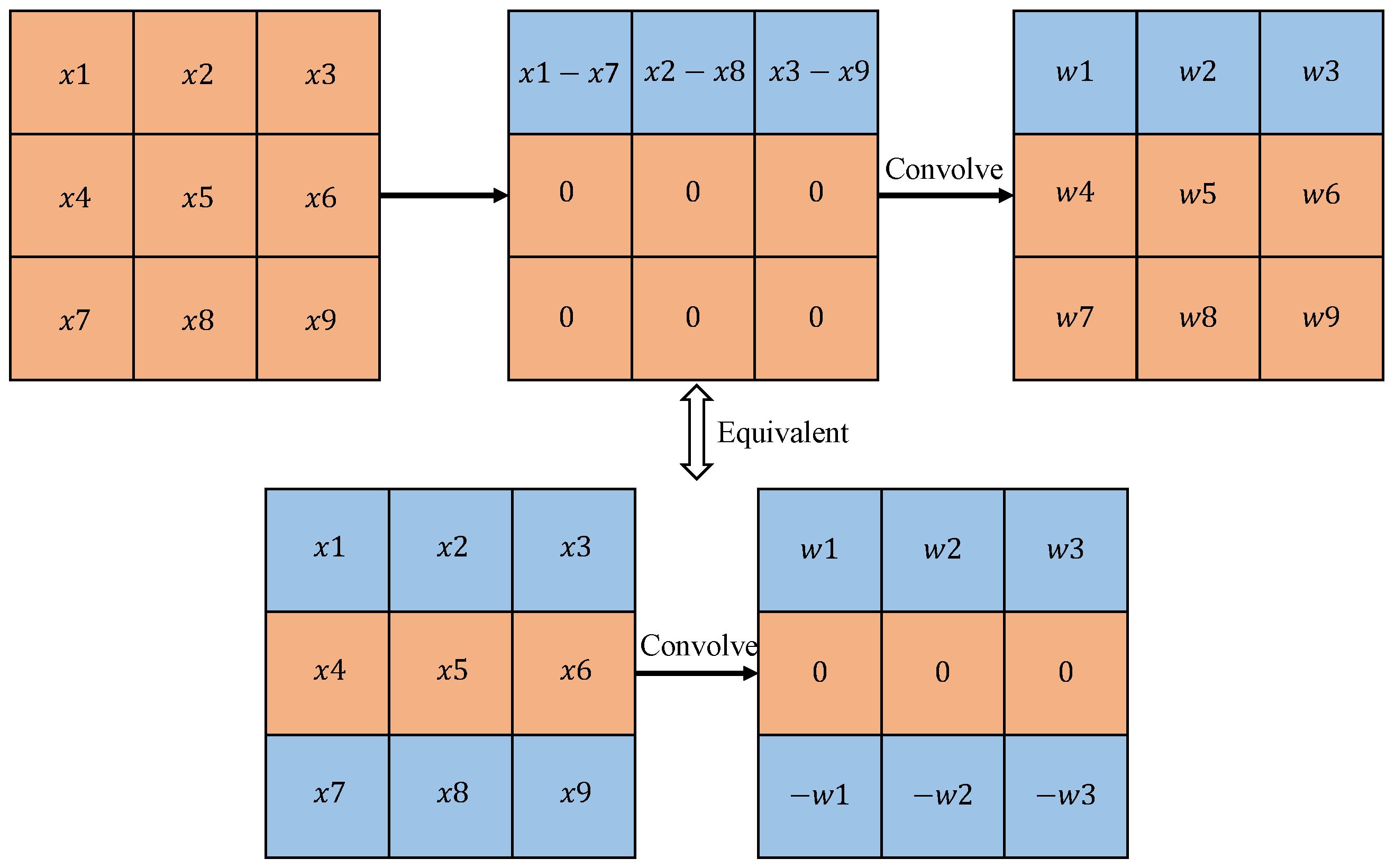
3.1. Difference Convolution Module
3.2. Fusion and Normalization Modules
3.3. Gaussian Degradation-Based URanker Loss Module
3.4. Loss Function
4. Experiment and Analysis
4.1. Datasets and Metrics
4.2. Implementations
4.3. Quantitative Comparisons
4.4. Visual Comparisons
4.5. Application Test
4.6. Ablation Study
4.6.1. Impact of Different Modules on Experimental Results
4.6.2. Impact of Different Convolutions on Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV Navigation and Localization: A Review. IEEE J. Ocean. Eng. 2013, 39, 131–149. [Google Scholar] [CrossRef]
- Cong, R.; Zhang, Y.; Fang, L.; Li, J.; Zhao, Y.; Kwong, S. RRNet: Relational Reasoning Network With Parallel Multiscale Attention for Salient Object Detection in Optical Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5613311. [Google Scholar] [CrossRef]
- Schettini, R.; Corchs, S. Underwater Image Processing: State of the Art of Restoration and Image Enhancement Methods. EURASIP J. Adv. Signal Process. 2010, 2010, 746052. [Google Scholar] [CrossRef]
- Ancuti, C.; Ancuti, C.O.; Haber, T.; Bekaert, P. Enhancing Underwater Images and Videos by Fusion. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 81–88. [Google Scholar]
- Iqbal, K.; Odetayo, M.; James, A.; Salam, R.A.; Talib, A.Z.H. Enhancing the Low Quality Images Using Unsupervised Colour Correction Method. In Proceedings of the 2010 IEEE International Conference on Systems, Man and Cybernetics, Istanbul, Turkey, 10–13 October 2010; pp. 1703–1709. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Single Image Haze Removal Using Dark Channel Prior. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 2341–2353. [Google Scholar] [PubMed]
- Li, C.Y.; Guo, J.C.; Cong, R.M.; Pang, Y.W.; Wang, B. Underwater Image Enhancement by Dehazing with Minimum Information Loss and Histogram Distribution Prior. IEEE Trans. Image Process. 2016, 25, 5664–5677. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Guo, C.; Ren, W.; Cong, R.; Hou, J.; Kwong, S.; Tao, D. An Underwater Image Enhancement Benchmark Dataset and Beyond. IEEE Trans. Image Process. 2019, 29, 4376–4389. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Anwar, S.; Hou, J.; Cong, R.; Guo, C.; Ren, W. Underwater Image Enhancement via Medium Transmission-Guided Multi-Color Space Embedding. IEEE Trans. Image Process. 2021, 30, 4985–5000. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.; Wu, R.; Jin, X.; Han, L.; Zhang, W.; Chai, Z.; Li, C. Underwater Ranker: Learn Which is Better and How to be Better. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; Volume 37, pp. 702–709. [Google Scholar]
- Islam, M.J.; Xia, Y.; Sattar, J. Fast Underwater Image Enhancement for Improved Visual Perception. IEEE Robot. Autom. Lett. 2020, 5, 3227–3234. [Google Scholar] [CrossRef]
- Naik, A.; Swarnakar, A.; Mittal, K. Shallow-UWnet: Compressed Model for Underwater Image Enhancement (Student Abstract). In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 15853–15854. [Google Scholar]
- Chen, Z.; He, Z.; Lu, Z.M. DEA-Net: Single Image Dehazing Based on Detail-Enhanced Convolution and Content-Guided Attention. IEEE Trans. Image Process. 2024, 33, 1002–1015. [Google Scholar] [CrossRef] [PubMed]
- Peng, L.; Zhu, C.; Bian, L. U-Shape Transformer for Underwater Image Enhancement. IEEE Trans. Image Process. 2023, 32, 3066–3079. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. In Computer Vision—ECCV 2016, Proceedings of the 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings Part II 14; Springer: Berlin/Heidelberg, Germany, 2016; pp. 694–711. [Google Scholar]
- Song, Y.; He, Z.; Qian, H.; Du, X. Vision Transformers for Single Image Dehazing. IEEE Trans. Image Process. 2023, 32, 1927–1941. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, W.; Hu, X.; Yang, J. Selective Kernel Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 510–519. [Google Scholar] [CrossRef]
- Drews, P.; Nascimento, E.; Moraes, F.; Botelho, S.; Campos, M. Transmission Estimation in Underwater Single Images. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Sydney, Australia, 2–8 December 2013; pp. 825–830. [Google Scholar]
- Drews, P.L.; Nascimento, E.R.; Botelho, S.S.; Campos, M.F.M. Underwater Depth Estimation and Image Restoration Based on Single Images. IEEE Comput. Graph. Appl. 2016, 36, 24–35. [Google Scholar] [CrossRef] [PubMed]
- Awan, H.S.A.; Mahmood, M.T. Underwater Image Restoration through Color Correction and UW-Net. Electronics 2024, 13, 199. [Google Scholar] [CrossRef]
- Jia, H.; Xiao, Y.; Wang, Q.; Chen, X.; Han, Z.; Tang, Y. Underwater Image Enhancement Network Based on Dual Layers Regression. Electronics 2024, 13, 196. [Google Scholar] [CrossRef]
- Qian, J.; Li, H.; Zhang, B. HA-Net: A Hybrid Algorithm Model for Underwater Image Color Restoration and Texture Enhancement. Electronics 2024, 13, 2623. [Google Scholar] [CrossRef]
- Fu, Z.; Wang, W.; Huang, Y.; Ding, X.; Ma, K.K. Uncertainty Inspired Underwater Image Enhancement. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 465–482. [Google Scholar]
- Yan, H.; Zhang, Z.; Xu, J.; Wang, T.; An, P.; Wang, A.; Duan, Y. UW-CycleGAN: Model-Driven CycleGAN for Underwater Image Restoration. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4207517. [Google Scholar] [CrossRef]
- Chang, S.; Gao, F.; Zhang, Q. Underwater Image Enhancement Method Based on Improved GAN and Physical Model. Electronics 2023, 12, 2882. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, J.; Li, C.; Jiang, Q.; Zhou, M.; Lam, K.M.; Zhang, W.; Fu, X. HCLR-Net: Hybrid Contrastive Learning Regularization with Locally Randomized Perturbation for Underwater Image Enhancement. Int. J. Comput. Vis. 2024, 132, 4132–4156. [Google Scholar] [CrossRef]
- Cong, R.; Yang, W.; Zhang, W.; Li, C.; Guo, C.L.; Huang, Q.; Kwong, S. PUGAN: Physical Model-Guided Underwater Image Enhancement Using GAN With Dual-Discriminators. IEEE Trans. Image Process. 2023, 32, 4472–4485. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution Gray-Scale And Rotation Invariant Texture Classification with Local Binary Patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Juefei-Xu, F.; Boddeti, V.N.; Savvides, M. Local Binary Convolutional Neural Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4284–4293. [Google Scholar] [CrossRef]
- Yu, Z.; Zhao, C.; Wang, Z.; Qin, Y.; Su, Z.; Li, X.; Zhou, F.; Zhao, G. Searching Central Difference Convolutional Networks for Face Anti-spoofing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 5295–5305. [Google Scholar]
- Yu, Z.; Qin, Y.; Zhao, H.; Li, X.; Zhao, G. Dual-Cross Central Difference Network for Face Anti-Spoofing. In Proceedings of the IJCAI International Joint Conference on Artificial Intelligence, Montreal, BC, Canada, 19–27 August 2021. [Google Scholar]
- Su, Z.; Liu, W.; Yu, Z.; Hu, D.; Liao, Q.; Tian, Q.; Pietikäinen, M.; Liu, L. Pixel Difference Networks for Efficient Edge Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 5117–5127. [Google Scholar]
- Wang, Y.; Guo, J.; Gao, H.; Yue, H. UIEC^ 2-Net: CNN-based Underwater Image Enhancement Using Two Color Space. Signal Process. Image Commun. 2021, 96, 116250. [Google Scholar] [CrossRef]
- Wang, C.; Shen, H.Z.; Fan, F.; Shao, M.W.; Yang, C.S.; Luo, J.C.; Deng, L.J. EAA-Net: A novel edge assisted attention network for single image dehazing. Knowl.-Based Syst. 2021, 228, 107279. [Google Scholar] [CrossRef]
- Zhang, H.; Patel, V.M. Densely Connected Pyramid Dehazing Network. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3194–3203. [Google Scholar] [CrossRef]
- Sobel, I.; Feldman, G. A 3 × 3 isotropic gradient operator for image processing. Pattern Classif. Scene Anal. 1973, 1968, 271–272. [Google Scholar]
- Scharr, H. Optimal Operators in Digital Image Processing. Ph.D. Thesis, University of Heidelberg, Heidelberg, Germany, 2000. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Wu, H.; Qu, Y.; Lin, S.; Zhou, J.; Qiao, R.; Zhang, Z.; Xie, Y.; Ma, L. Contrastive Learning for Compact Single Image Dehazing. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 10551–10560. [Google Scholar]
- Li, H.; Li, J.; Wang, W. A Fusion Adversarial Underwater Image Enhancement Network with a Public Test Dataset. arXiv 2019, arXiv:1906.06819. [Google Scholar]
- Akkaynak, D.; Treibitz, T. Sea-thru: A Method for Removing Water from Underwater Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 1682–1691. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 586–595. [Google Scholar]
- Panetta, K.; Gao, C.; Agaian, S. Human-Visual-System-Inspired Underwater Image Quality Measures. IEEE J. Ocean. Eng. 2015, 41, 541–551. [Google Scholar] [CrossRef]
- Yang, M.; Sowmya, A. An Underwater Color Image Quality Evaluation Metric. IEEE Trans. Image Process. 2015, 24, 6062–6071. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.T.; Cosman, P.C. Underwater Image Restoration Based on Image Blurriness and Light Absorption. IEEE Trans. Image Process. 2017, 26, 1579–1594. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhuang, P.; Sun, H.H.; Li, G.; Kwong, S.; Li, C. Underwater Image Enhancement Via Minimal Color Loss and Locally Adaptive Contrast Enhancement. IEEE Trans. Image Process. 2022, 31, 3997–4010. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Islam, M.J.; Wang, R.; Sattar, J. SVAM: Saliency-guided Visual Attention Modeling by Autonomous Underwater Robots. arXiv 2020, arXiv:2011.06252. [Google Scholar]
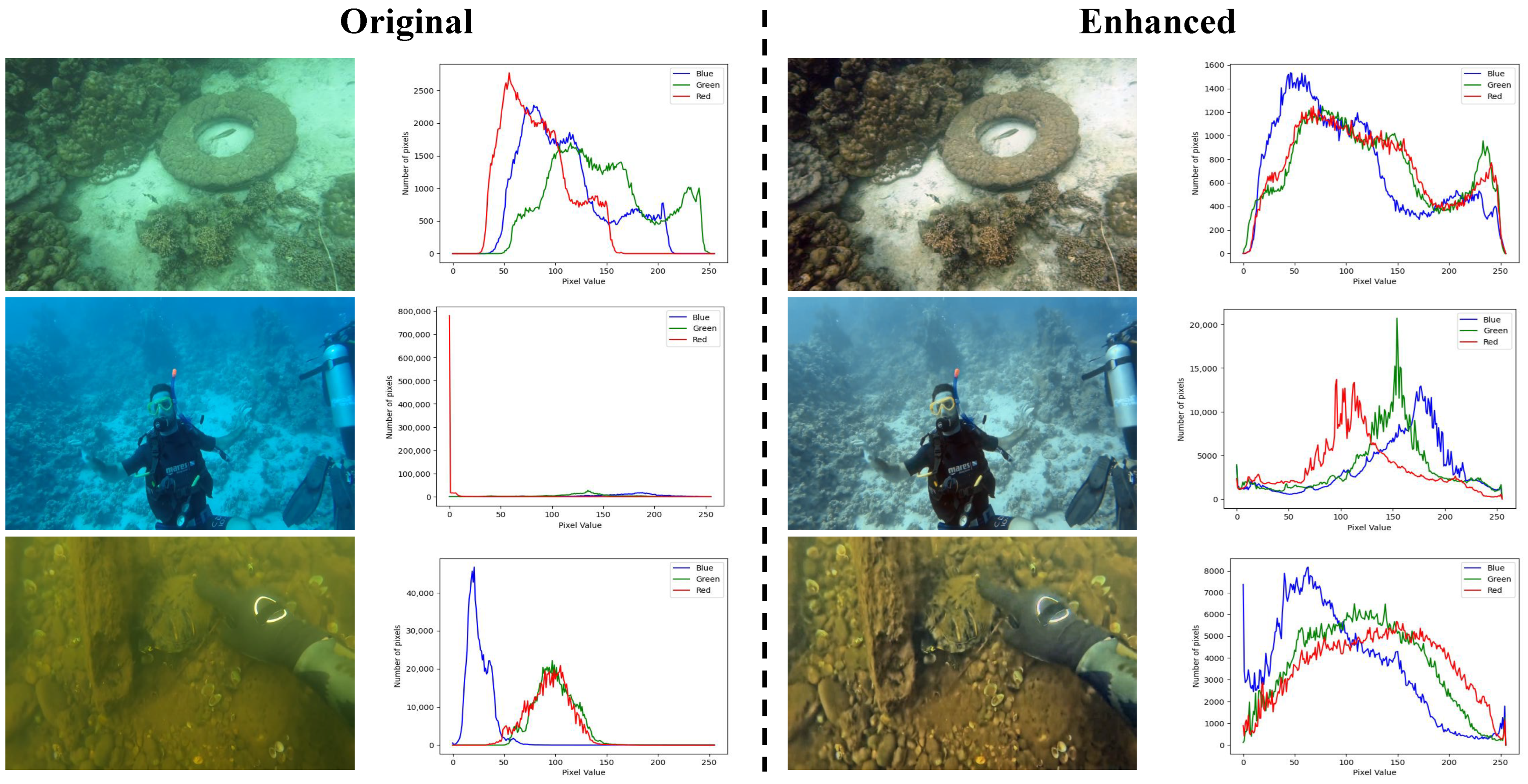









| Method | PSNR ↑ | SSIM ↑ | LPIPS ↓ |
|---|---|---|---|
| UDCP (ICCVW’13) | 10.277 | 0.486 | 0.392 |
| IBLA (TIP’17) | 15.046 | 0.683 | 0.316 |
| WaterNet (TIP’19) | 20.998 | 0.919 | 0.149 |
| FUnIE (RAL’20) | 19.454 | 0.871 | 0.175 |
| Shallow-UWnet (AAAI’21) | 18.120 | 0.721 | 0.289 |
| Ucolor (TIP’21) | 20.730 | 0.900 | 0.165 |
| MLLE (TIP’22) | 18.977 | 0.841 | 0.275 |
| PUIE-Net (ECCV’22) | 21.970 | 0.890 | 0.155 |
| U-shape (TIP’23) | 20.920 | 0.853 | 0.206 |
| PUGAN (TIP’23) | 22.576 | 0.920 | 0.159 |
| NU2Net (AAAI’23, Oral) | 22.669 | 0.924 | 0.154 |
| HCLR-Net (IJCV’24) | 23.667 | 0.932 | 0.136 |
| Ours | 23.436 | 0.935 | 0.125 |
| Method | U45 | SQUID | C60 | |||
|---|---|---|---|---|---|---|
| UCIQE↑ | UIQM↑ | UCIQE↑ | UIQM↑ | UCIQE↑ | UIQM↑ | |
| UDCP (ICCVW’13) | 0.584 | 2.086 | 0.554 | 1.082 | 0.515 | 1.215 |
| IBLA (TIP’17) | 0.579 | 1.672 | 0.466 | 0.866 | 0.564 | 1.893 |
| WaterNet (TIP’19) | 0.582 | 3.295 | 0.571 | 2.518 | 0.566 | 2.653 |
| FUnIE (RAL’20) | 0.599 | 3.398 | 0.532 | 2.746 | 0.570 | 3.258 |
| Shallow-UWnet (AAAI’21) | 0.471 | 3.033 | 0.421 | 2.094 | 0.466 | 2.396 |
| Ucolor (TIP’21) | 0.564 | 3.351 | 0.514 | 2.215 | 0.532 | 2.746 |
| MLLE (TIP’22) | 0.598 | 2.599 | 0.562 | 2.314 | 0.581 | 2.310 |
| PUIE-Net (ECCV’22) | 0.578 | 3.199 | 0.522 | 2.323 | 0.558 | 2.521 |
| U-shape (TIP’23) | 0.553 | 3.248 | 0.528 | 2.256 | 0.534 | 2.783 |
| PUGAN (TIP’23) | 0.599 | 3.395 | 0.566 | 2.399 | 0.612 | 3.001 |
| NU2Net (AAAI’23, Oral) | 0.595 | 3.396 | 0.551 | 2.480 | 0.564 | 2.900 |
| HCLR-Net (IJCV’24) | 0.610 | 3.301 | 0.564 | 2.169 | 0.571 | 2.739 |
| Ours | 0.601 | 3.354 | 0.578 | 2.274 | 0.571 | 2.827 |
| Vanilla Conv | DEConv | Fine-tune | PSNR ↑ | SSIM ↑ |
|---|---|---|---|---|
| ✔ | 23.113 | 0.931 | ||
| ✔ | 23.287 | 0.930 | ||
| ✔ | ✔ | 23.436 | 0.935 |
| Convolution | PSNR ↑ | SSIM ↑ |
|---|---|---|
| Conv | 23.113 | 0.931 |
| Conv + Dilated | 22.976 | 0.921 |
| Conv + Deformable | 23.151 | 0.925 |
| Conv + Diff (ours) | 23.287 | 0.930 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Zeng, Z.; Lao, H.; Zhang, H. Underwater Image Enhancement Based on Difference Convolution and Gaussian Degradation URanker Loss Fine-Tuning. Electronics 2024, 13, 5003. https://doi.org/10.3390/electronics13245003
Cao J, Zeng Z, Lao H, Zhang H. Underwater Image Enhancement Based on Difference Convolution and Gaussian Degradation URanker Loss Fine-Tuning. Electronics. 2024; 13(24):5003. https://doi.org/10.3390/electronics13245003
Chicago/Turabian StyleCao, Jiangzhong, Zekai Zeng, Hanqiang Lao, and Huan Zhang. 2024. "Underwater Image Enhancement Based on Difference Convolution and Gaussian Degradation URanker Loss Fine-Tuning" Electronics 13, no. 24: 5003. https://doi.org/10.3390/electronics13245003
APA StyleCao, J., Zeng, Z., Lao, H., & Zhang, H. (2024). Underwater Image Enhancement Based on Difference Convolution and Gaussian Degradation URanker Loss Fine-Tuning. Electronics, 13(24), 5003. https://doi.org/10.3390/electronics13245003






