Towards Deterministic-Delay Data Delivery Using Multi-Criteria Routing over Satellite Networks

Abstract

The satellite Internet can cover up to 70% of the surface of our planet Earth to provide network services for nearly 3 billion people. As such, it is promising to become the building block of future 6G networks. The satellite Internet is capable of providing uniform communication capacity to every part of the Earth’s surface, due to its uniform and symmetrical constellation structure, while the uneven distribution of ground populations leads to globally uneven traffic delivery requests, incurring a mismatch between the capacity and traffic transmission demands. As such, traditional single-criteria (e.g., shortest delay) routing algorithms can lead to severe network congestion and cannot provision delay-deterministic data delivery. To overcome this bottleneck, we propose a multi-criteria routing and scheduling scheme to redirect time-tolerant data, thus preventing congestion for time-sensitive data, based on the spatiotemporal distribution of data traffic. First, we construct a traffic spatiotemporal distribution model, to indicate the network load status. Next, we model the satellite network multi-criteria routing problem as an integer linear programming one, which is NP-hard and challenging to solve within polynomial time. A novel link weight design based on both the link delay and load is introduced, transforming the mathematical programming problem into a routing optimization problem. The proposed correlation scheduling algorithm fully utilizes idle network link resources, significantly improving network resource utilization and eliminating resource competition between non-time-sensitive and time-sensitive services. Simulation results show that compared with traditional algorithms, the proposed method can increase the throughput of time-sensitive data by up to 20.8% and reduce the packet loss rate of time-sensitive services by up to 76.8%.

1. Introduction

The satellite Internet, with its extensive coverage, is a crucial component of next-generation mobile communication systems, providing network access services to space-based vehicles, airborne aircraft, maritime users, and users in remote terrestrial areas [1,2,3]. Due to the Earth’s rotation and the relative motion between satellites and the Earth, low and medium Earth orbit satellites operate along predetermined orbits, resulting in a uniform distribution of satellite constellations [4]. However, the distribution of ground users, influenced by maritime and geographical factors, is uneven [5,6]. Efficiently utilizing the uniformly distributed satellite communication resources while ensuring the service quality of differentiated services for unevenly distributed users can help reduce satellite network operating costs and enhance user adhesion to the satellite network [7,8]. 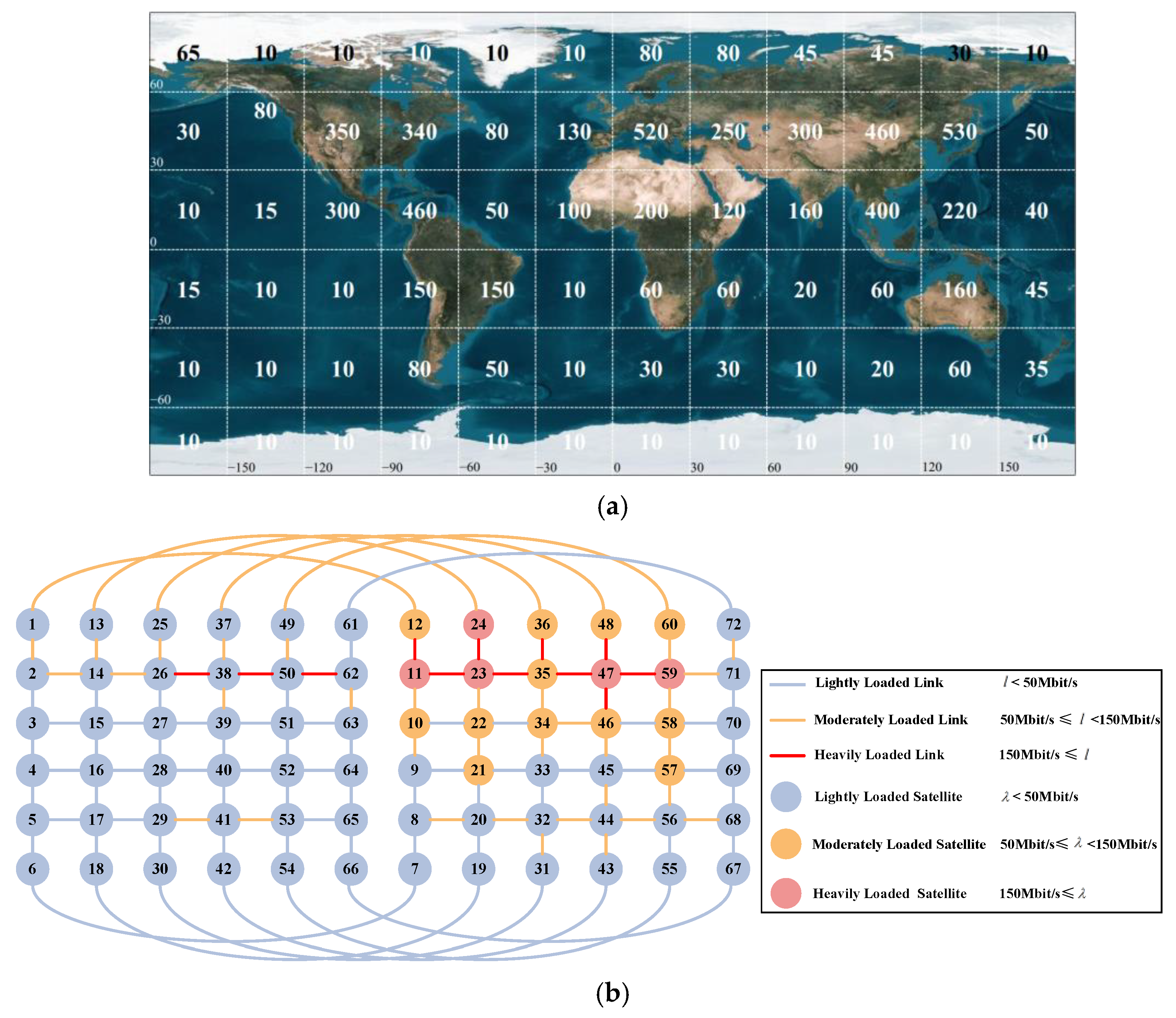The distribution of land-based users influences the traffic load of the satellite Internet, as illustrated in Figure 1a, which presents a static equipment density index map based on data from the literature [9], with longitude on the horizontal axis and latitude on the vertical axis. The ground is divided into 72 regions, with each grid containing a number representing the static communication equipment density index for that region (indicating the communication equipment density in the i-th region). It is assumed that all communication traffic is transmitted via satellite, meaning that the service traffic generated from one grid is routed via satellite to the target grid. The traffic reaching each destination grid is related to the static equipment density index, distance, and time interval between the source node and the destination node. If the satellite network adopts the classic shortest path routing algorithm, the traffic load on inter-satellite links at a given time is as shown in Figure 1b. In this figure, the circles and the numbers on them represent individual satellites, with different circle colors indicating the service load on each satellite: blue, yellow, and red represent low, medium, and high traffic loads, respectively. The lines between circles represent communication links between satellites, where blue, yellow, and red lines represent low, medium, and high link loads, respectively. From Figure 1b, it is evident that unevenly distributed service demand results in significant differences in link loads across the satellite network, with some inter-satellite links becoming bottlenecks that limit the overall capacity of the satellite network.

Figure 1. (a) Static equipment density index and Earth’s regional division; (b) Load distribution of the satellite network under the shortest path algorithm (total daily traffic of 180 T).

To address the issue of network load balancing, scholars have proposed various load balancing methods. Most load balancing methods aim to reduce the probability of bottleneck links with heavy loads by traffic splitting. For example, the widely used Equal-Cost Multi-Path (ECMP) [10] routing mechanism in terrestrial networks establishes multiple paths between any pair of nodes and randomly selects one path for packet forwarding when a packet arrives at an intermediate node, thereby achieving load balancing. However, the randomness in path selection introduces uncertainty in end-to-end delay, and the long link delay in satellite networks exacerbates the challenge of ensuring end-to-end delay. The traffic-light-based intelligent routing (TLR) strategy proposed in the literature [11] marks the congestion level of candidate paths based on the queue length of pending service traffic at neighboring nodes and selects paths with lower congestion levels for packet forwarding. Compared to the ECMP method, the TLR method considers the load of neighboring links, improving local load balancing but neglecting the load of the entire path. The literature [12] introduces an extended localized link state load balancing routing algorithm (LB-ELS), which employs a triggered local congestion notification mechanism and on-demand routing calculation. By assessing the congestion state of all links on each candidate path, it selects the optimal route from a set of candidate paths to mitigate congestion and achieve load balancing. The literature [13] proposes a Distance-based Back-Pressure Routing (DBPR) strategy, which introduces a new metric, destination distance delay, estimated by the Euclidean distance between satellites to predict the propagation delay of packets to the destination. The algorithm dynamically selects non-congested short paths for data transmission by calculating link weights that take into account both queue backlogs and the propagation delay, achieving load balancing by restricting the transmission area. However, due to the lack of a global view, the algorithms proposed in the literature [12,13] face the issue of local optimality [14,15]. The literature [16] proposes a load balancing routing algorithm based on extended link state information, which designs a link congestion notification mechanism. When the queue length at a node reaches or exceeds a threshold, the node is considered congested, and the algorithm recalculates the route to avoid that node. Simultaneously, it computes multiple candidate paths using the K Shortest Paths (KSP) algorithm, allowing a quick switch to other available paths when congestion occurs on the current path. Nevertheless, none of these algorithms considers the impact of service arrival rates during their design.

Considering the impact of historical service arrival rates on the performance of load balancing algorithms, the literature [17] proposed a hybrid traffic detour load balancing routing strategy (HLBR). This approach predicts regions prone to congestion based on the access traffic load in ground areas and calculates detour paths accordingly to achieve load balancing. The literature [18] introduced a multipath search load balancing a routing algorithm based on regional traffic splitting. This algorithm dynamically calculates transition probabilities using link weight factors, steering factors, and node visibility parameters to achieve regional traffic splitting, ensuring that data transmission prioritizes links with a low congestion risk. Additionally, the algorithm calculates the optimal path and alternative paths under delay constraints, effectively addressing dynamic funnel congestion caused by uneven distribution of ground stations. The literature [19] proposed a load balancing routing algorithm based on deep reinforcement learning, where the relationship between traffic information and routing selection is obtained through machine learning. The algorithm uses the link utilization of the entire network and the traffic matrix as input states and designs output actions to select the optimal routing scheme. Feedback on the impact of the chosen route is provided through a reward function, optimizing the network load distribution. However, the methods proposed in the literature [17,18,19] treat time-sensitive and non-time-sensitive services equally, which may result in time-sensitive services choosing longer paths in a satellite network environment, making it difficult to guarantee the QoS requirements for time-sensitive services. The literature [20] proposed a hybrid service-aware routing algorithm based on service scheduling. This algorithm constructs a priority assignment function based on service arrival rates and waiting times, effectively distinguishing and handling services with different QoS requirements. For high-QoS services, the algorithm adopts an intra-orbit priority forwarding strategy, while for low-QoS services, a link-weighted routing algorithm is used. However, this algorithm fails to balance the needs of different services, as it tends to prioritize time-sensitive (high-QoS) services, leaving some low-QoS services without sufficient transmission resources for extended periods, thereby failing to meet their basic service quality requirements.

In summary, given the challenges of existing load balancing methods in simultaneously ensuring load balance and maintaining the service quality of time-sensitive services, this paper proposes a satellite Internet service scheduling algorithm based on the spatiotemporal distribution of service traffic. First, based on the spatiotemporal traffic factor, a shortest-delay path is constructed for time-sensitive services, with bandwidth resources reserved. Second, the load balancing problem for non-time-sensitive services is modeled as an integer linear programming problem, which is NP-hard and difficult to solve within polynomial time. On this basis, a novel link weight based on the link load accumulation factor is designed, transforming the above optimization problem into a routing problem. This allows non-time-sensitive services to fully utilize satellite network resources for data transmission, thereby avoiding contention for resources needed by time-sensitive services. Additionally, a Virtual Private Network (VPN)-based implementation scheme is designed, where VPN updates are triggered periodically, enabling time-based load balancing. This ensures network scalability and supports the deployment of this solution in large-scale networks. The second section of this paper establishes the system model and the spatiotemporal distribution model of service traffic. The third section presents the corresponding mathematical models. The fourth section describes the graph load balancing routing algorithm based on link weight characterization and its implementation. The fifth section provides a simulation of the proposed algorithm. The sixth section discusses the application scenarios and limitations of the proposed algorithm, and the seventh section concludes the paper.

2. System Model

2.1. Constellation Model

This study considers a uniformly distributed low Earth orbit (LEO) satellite network constellation, where all satellite nodes form a set $S=\left\{S_i\right|1\le i\le N\}$. Each satellite in this network is equipped with four full-duplex inter-satellite links, and each satellite can connect with up to four neighboring satellites, including two intra-plane inter-satellite links within the same orbit and two cross-plane inter-satellite links between different orbits [21]. For polar orbit satellites, there are two counter-moving orbits, and the gap formed between these two orbits is known as a cross-seam [22,23]. When satellites move to the cross-seam and high-latitude regions, the relative angular velocity between inter-plane satellites increases significantly, leading to the temporary closure of inter-plane inter-satellite links in these regions [24]. Furthermore, as the LEO satellite network moves periodically along its orbits, the Earth undergoes rotation, resulting in relative motion between satellites and the Earth. This causes the ground area beneath a satellite to change over time. To represent the time-varying topology of the satellite network, this study adopts a snapshot graph model to characterize the time-varying link resources of the satellites. Although the satellite network topology changes over time, within sufficiently small time intervals, the topology remains stable [25,26,27]. Therefore, the time range $T$ can be divided into $N$ adjacent time slots $\{{\tau }_1,\dots .,{\tau }_N\}$, ensuring that within each time slot, the satellite network topology remains unchanged. Based on this time-slot division mechanism, by characterizing the network topology within each time slot $\tau$, the time-varying satellite network snapshot graph model over time $T$ can be represented. The snapshot graph model is represented by $\mathrm{G}=\{{𝒱}_T,{ℰ}_T\}$, where ${𝒱}_T$ is the set of nodes in the snapshot graph, and node $u_{\tau }\in {𝒱}_T$ represents the satellite node $u$ within the time slot $\tau$. ${ℰ}_T$ represents the set of links in the snapshot graph, where link $(u_{\tau },{\mathrm{v}}_{\tau })\in {ℰ}_T$ represents the link between nodes $u_{\tau }$ and $v_{\tau }$ within time slot $\tau$. Additionally, any link $(u_{\tau },{\mathrm{v}}_{\tau })\in {ℰ}_T$ has link attributes $c_{u,v}^{\tau }$, which represent the transmission capacity of that link, measured in bits. Specifically, $c_{u,v}^{\tau }=B_{u,v}^{\tau }\times \left|\tau \right|$, where $B_{u,v}^{\tau }$ is the maximum transmission rate of link $(u_{\tau },{\mathrm{v}}_{\tau })$, and $\left|\tau \right|$ is the duration of the time slot $\tau$. The symbols used in this study are listed in Table 1.

Table 1. Symbol definitions.

Symbol	Symbol Description
$S$	Set of all satellite nodes in the satellite network
$G$	Network topology
${ℰ}_T$	Set of links in the snapshot graph
$B_{u,v}^{\tau }$	Maximum transmission rate of link $(u_{\tau },{\mathrm{v}}_{\tau })$
$R$	Satellite-to-ground traffic demand index
$\rho$	Static equipment density index
$d$	Distance between satellites
$p_{\tau }$	Time traffic ratio
$A$	Total daily traffic
$\lambda$	Average data generation rate of a satellite, in bit/s
${\lambda }_{\tau ,u,v}^{ts}$	Spatiotemporal traffic factor
$C$	Capacity of inter-satellite links
$load$	Load on inter-satellite link
$\mu$	Link load ratio
$Q$	Set of satellite nodes sorted in descending order of traffic arrival rate
$pts$	Path for time-sensitive services
$pnts$	Path for non-time-sensitive services
$\delta$	Link load accumulation factor

2.2. Spatiotemporal Distribution Model of Service Traffic

The distribution of network traffic across the Earth’s surface is closely related to population distribution. Therefore, in densely populated areas such as major cities like Shanghai and New York, network traffic is high, while in sparsely populated regions, such as the Sahara Desert in Africa and the Amazon Rainforest in Brazil, network traffic is low. To characterize the geographical distribution of service traffic, the Earth’s surface can be divided into $K$ regions based on the coverage area of low Earth orbit (LEO) satellites, where each satellite corresponds to a ground region directly beneath it. In fact, the traffic in satellite networks primarily originates from the ground (e.g., mobile Internet traffic) and from the satellites themselves (e.g., remote sensing, navigation, and space experiment data). In this study, we mainly consider satellite-to-ground traffic. The traffic transmission demand index $R$ between satellite $u$ and satellite $v$ is related to the static equipment density index $\rho$ and the distance $d$ between the two satellites. The distance between satellite $u$ and satellite $v$ (in meters) is denoted by $d_{u,v}$. According to the literature [28], when the satellite-to-ground traffic coefficients are $\alpha =0.5$ and $\beta =1.5$, the traffic demand between satellite $u$ and satellite $v$ can be expressed as:

$$R_{u,v}={\displaystyle \frac{{({\rho }_u\ast {\rho }_v)}^{\alpha }}{{d_{u,v}}^{\beta }}}$$

(1)

The distribution of network traffic is influenced not only by geographical location but also by the time of day [18]. It is assumed that users in different regions of the world exhibit similar Internet usage patterns throughout the day, with less network activity at night and more during the daytime. Additionally, the frequency of Internet access varies across different times of the day. According to the literature [29], the trend in network traffic proportions at each hour of the day across global regions is shown in Figure 2. As expected, human network activity is higher during the day than at night, with traffic proportions peaking between 9 AM and 5 PM. At 10 AM, network traffic can account for up to 11% of the total daily traffic, while nighttime traffic is much lower, with an average hourly traffic proportion of around 1%. Based on this time characteristic, a time traffic ratio parameter $p_{\tau }$ can be defined to represent the proportion of traffic during a specific time period $\tau$ relative to the total daily traffic.

Figure 2. Traffic ratio variation.

Therefore, the traffic between any two satellites in the satellite network is related to both time and space. According to the literature [18], the spatiotemporal traffic transmission demand model between any two satellites can be derived from the traffic transmission demand based on the geographical distribution $R_{u,v}$ and the traffic ratio based on the time distribution $p_{\tau }$, expressed as:

$${\lambda }_{\tau ,u,v}={\displaystyle \frac{R_{u,v}}{{\displaystyle {\sum }_{u=1}^N\underset{v\ne j}{{\displaystyle {\sum }_{u=1}^N{R}_{u,v}}}}}}\ast p_{\tau }\ast {\displaystyle \frac{A}{3600}},u\ne v$$

(2)

where $A$ represents the total traffic across the entire network for the whole day, measured in bits. In the service model, the data packets generated per unit time follow a Poisson distribution, and ${\lambda }_{\tau ,u,v}$ represents the amount of traffic transmitted from satellite $u$ to satellite $v$ during the time period $\tau$, measured in bits per second (bit/s). Given the time range $T$ and the snapshot graph $G$, the traffic transmission demand between any two satellites during each time period can be defined as $ℒ=\left\{{\lambda }_{\tau ,u,v}\right|\forall \tau \in T,u,v\in 𝒱\}$. The spatiotemporal traffic factor ${\lambda }_{\tau ,u,v}^{ts}=\omega \times {\lambda }_{\tau ,u,v}$ (where $\omega$ represents the proportion of time-sensitive services within the total traffic), which is used to characterize the time-sensitive traffic demand in each time period.

3. Problem Modeling

Given the above spatiotemporal distribution model for non-time-sensitive services, ensuring the QoS requirements for time-sensitive services requires reducing the probability of conflicts between time-sensitive and non-time-sensitive services and overcoming the dependency of traditional shortest-path routing algorithms on certain optimal paths. Therefore, a routing algorithm can be used to shape network traffic such that non-time-sensitive services are evenly distributed across the network, reducing their occupancy of optimal paths and “making way” for time-sensitive services. To achieve this, given the time range $T$ and the corresponding satellite snapshot graph model $G$, the transmission demand for non-time-sensitive services between each pair of satellites at each specific time interval can be calculated based on the spatiotemporal traffic distribution model. This study aims to minimize the utilization of the most heavily loaded links after satisfying the transmission demands across all satellites within the time range $T=24$ h, thereby achieving evenly distributed load deployment.

Thus, given the snapshot graph model $G$ and the service transmission demand between satellites $ℒ$, we define a decision variable $x(s,d,u,v)$ to represent whether the service from source satellite $s$ to destination satellite $d$ is transmitted through link $(u,v)$. If the service is transmitted, $x(s,d,u,v)=1$; otherwise, $x(s,d,u,v)=0$. Specifically, all decision variables belong to the variable set $𝒳$, and $𝒳=\left\{\mathrm{x}\right(s,d,u,v\left)\right|(\mathrm{u},\mathrm{v})\in ℰ,s,d\in 𝒱\}$. Additionally, we define a continuous variable $\mu \in [0,1]$, representing the utilization ratio of all link capacities. The decision variable set $𝒳$ and $\mu$ must satisfy the following constraints:

Link Capacity Constraint: The total traffic arranged on any link $(\mathrm{u},\mathrm{v})\in ℰ$ should not exceed the maximum data capacity of that link multiplied by a factor $\mu$:

$${\displaystyle \sum _{\mathrm{s},\mathrm{d}\in 𝒱}x(s,d,u,v)}\times {\lambda }_{s,d}\le \mu c_{u,v}$$

(3)

Flow Conservation Constraint: When a node does not serve as a source or destination node, the traffic flowing into node $u$ must equal the traffic flowing out of that node:

$${\displaystyle \sum _{v\in 𝒱}x(s,d,u,v)}={\displaystyle \sum _{v\in 𝒱}x(s,d,u,v)},\forall \mathrm{s},\mathrm{d}\in 𝒱,s,d\ne u$$

(4)

Service Satisfaction Constraint: Assuming that the network’s capacity can meet the transmission demand $ℒ$, for any source–destination pair during a certain time period, a path must be arranged for transmission:

$${\displaystyle \sum _{u\in 𝒱}x(s,d,s,\mathrm{u})}={\displaystyle \sum _{u\in 𝒱}x(s,d,u,d)}=1,\forall s,d\in 𝒱$$

(5)

Therefore, minimizing the load proportion on the most heavily loaded link while satisfying the transmission demands for non-time-sensitive services can be modeled as the following optimization problem:

$$\begin{array}{ll}\mathrm{MC}:& \underset{𝒳,\mu }{\min \mu ,}\\ \mathrm{s}.\mathrm{t}.& \left(3\right), \left(4\right), \left(5\right),\\ & 0\le \mu \le 1\end{array}$$

(6)

In this problem, the decision variables $𝒳$ are integer variables, and $\mu$ is a linear variable, with all constraints being linear. As a result, the problem can be formulated as a mixed-integer linear programming (MILP) problem. It is well known that such problems are difficult to solve in polynomial time and are typical NP-hard problems. Although many commercial mathematical solvers (e.g., CVXPY, Gurobi) support the optimal solution of MILP problems, they still face challenges such as long computation times and high memory requirements. Therefore, the next chapter proposes an efficient solution based on the spatiotemporal distribution model of service traffic.

4. Graph Load Balancing Routing Algorithm Based on Link Weight Characterization and Its Implementation

The MC problem is a mixed-integer linear programming (MILP) problem, which is difficult to solve efficiently. To solve the MC problem effectively, a link weight calculation rule is first designed to dynamically convert the load status and link delay into link weights. Based on this link weight, the efficient solution of the MC problem can be transformed into a shortest path problem. Furthermore, a joint scheduling algorithm for time-sensitive and non-time-sensitive services is proposed, explaining the link weight update rules. This ensures that non-time-sensitive services are evenly distributed across the satellite network while guaranteeing the QoS of time-sensitive services. The algorithm dynamically adjusts link weights in real-time to adapt to changes in the satellite network topology. Given the predictable nature of satellite orbital movements, the algorithm can anticipate changes in network topology and promptly recalculate optimal routes, ensuring continuity in path selection and balanced load distribution. Through this design, the algorithm demonstrates enhanced adaptability and robustness within the frequently changing topological and traffic conditions of satellite networks, significantly improving overall network performance.

4.1. Link Weight Characterization

Existing routing algorithms (e.g., Dijkstra’s algorithm) aim to find the path with the smallest sum of link weights among all paths between source and destination nodes. Therefore, different link weight calculation rules result in different network traffic distributions. For instance, traditional methods typically use a link propagation delay as the link weight, with the network weights remaining fixed over time. This leads to heavy reliance on specific optimal paths for the same network traffic, resulting in a centralized traffic distribution that easily causes network congestion.

To address the need for load balancing in non-time-sensitive services and QoS requirements for time-sensitive services, link weights are calculated for non-time-sensitive services based on the entire network topology and link load, ensuring their even distribution across the network. Simultaneously, specific link weights are designed for time-sensitive services. The detailed rules are as follows:

Link Weight for Time-Sensitive Services: To achieve the low-latency and high-real-time requirements of delay-sensitive services, link weights are characterized solely based on the propagation delay. This approach ensures that path selection prioritizes the links with the lowest delay, thereby meeting the QoS requirements of delay-sensitive services. Consequently, when computing paths for delay-sensitive services, the link weight for an inter-satellite link $(u,v)$ depends only on the propagation delay between the two satellites, as follows:

$$\cos t_{u,v}^{ts}=T_{u,v}^{pro},u\ne v$$

(7)

where $T_{u,v}^{pro}$ represents the propagation delay of link $(u,v)$, which equals the distance between the two satellites divided by the speed of electromagnetic waves.

Link Weight for Non-Time-Sensitive Services: For non-time-sensitive services, to ensure load balancing across the network, the occupancy of optimal paths should be minimized, taking into account the load conditions of different links during the link weight calculation. Additionally, the “best-effort” nature of the network should be maintained, meaning that when different paths between source and destination nodes have similar load conditions, the path with the shorter delay should be preferred. Therefore, the link weight for non-time-sensitive services is measured using the betweenness centrality and the link load ratio.

The betweenness centrality $J_{u,v}$ represents the importance of link $(u,v)$ in the initial state of the network. It is defined as the ratio of the number of shortest paths passing through link $(u,v)$ to the total number of shortest paths in the network:$J_{u,v}={\displaystyle \sum _{s,d \in V}\frac{{\sigma }_{s,d}^{u,v}}{{\sigma }_{s,d}}}$, where ${\sigma }_{s,d}$ is the number of shortest paths between nodes $s$ and $d$, and ${\sigma }_{s,d}^{u,v}$ is the number of shortest paths between $s$ and $d$ that pass through link $(u,v)$. If nodes $s$ and $d$ are not connected, ${\displaystyle \frac{{\sigma }_{s,d}^{u,v}}{{\sigma }_{s,d}}}=0$.

The link load ratio ${\mu }_{u,v}$ represents the capacity utilization of link $(u,v)$, defined as the ratio of the load on link $(u,v)$ to its capacity: ${\mu }_{u,v}={\displaystyle \frac{loa{d}_{u,v}}{C\times T_{\tau }}}$, where $C$ denotes the capacity of the inter-satellite link, $T_{\tau }$ represents the duration of the corresponding time slot, and $loa{d}_{u,v}$ is the sum of time-sensitive and non-time-sensitive traffic on that link. As the total network load increases, the load difference between various links also increases. Therefore, the median of the network-wide link load ratio ${\mu }_{med}$ is used to represent the central value of the network load. For heavily loaded links, their link cost should be reduced to avoid assigning traffic to them; conversely, for lightly loaded links, their link cost should be increased to maximize their utilization. Thus, the load accumulation factor ${\delta }_{u,v}={\displaystyle \frac{{\mu }_{u,v}-{\mu }_{\min }}{{\mu }_{med}-{\mu }_{\min }}}$ can be defined to characterize the influence of the link load on the link weight. The link cost $\cos t_{u,v}^{nts}$ for non-time-sensitive services when calculating paths is:

$$\cos t_{u,v}^{nts}=(1+J_{u,v}+{\delta }_{u,v})\times dela{y}_{u,v}^{nts},u\ne v$$

(8)

Here, $dela{y}_{u,v}^{nts}$ represents the propagation delay between satellite nodes $u$ and $v$. Moreover, considering the potential resource competition between non-time-sensitive services and time-sensitive services, paths are first allocated for time-sensitive services. The remaining link resources are then used to allocate paths for non-time-sensitive services. The initial value of the load ratio $u$ of link $(u,v)$ is ${\mu }_{u,v}^{init}={\displaystyle \frac{loa{d}_{u,v}^{ts}}{C\times T_{\tau }}}={\displaystyle \frac{{\displaystyle \sum _{s,d \in V}{\sigma }_{s,d}^{u,v}}\times {\lambda }_{\tau ,s,d}^{ts}}{C}}$, where ${\sigma }_{s,d}^{ts}$ is the number of shortest paths between satellite $s$ and satellite $d$ that pass through link $(u,v)$, and ${\lambda }_{\tau ,s,d}^{ts}$ represents the spatiotemporal traffic factor between satellite $s$ and satellite $d$ at time $\tau$.

4.2. Routing Algorithm

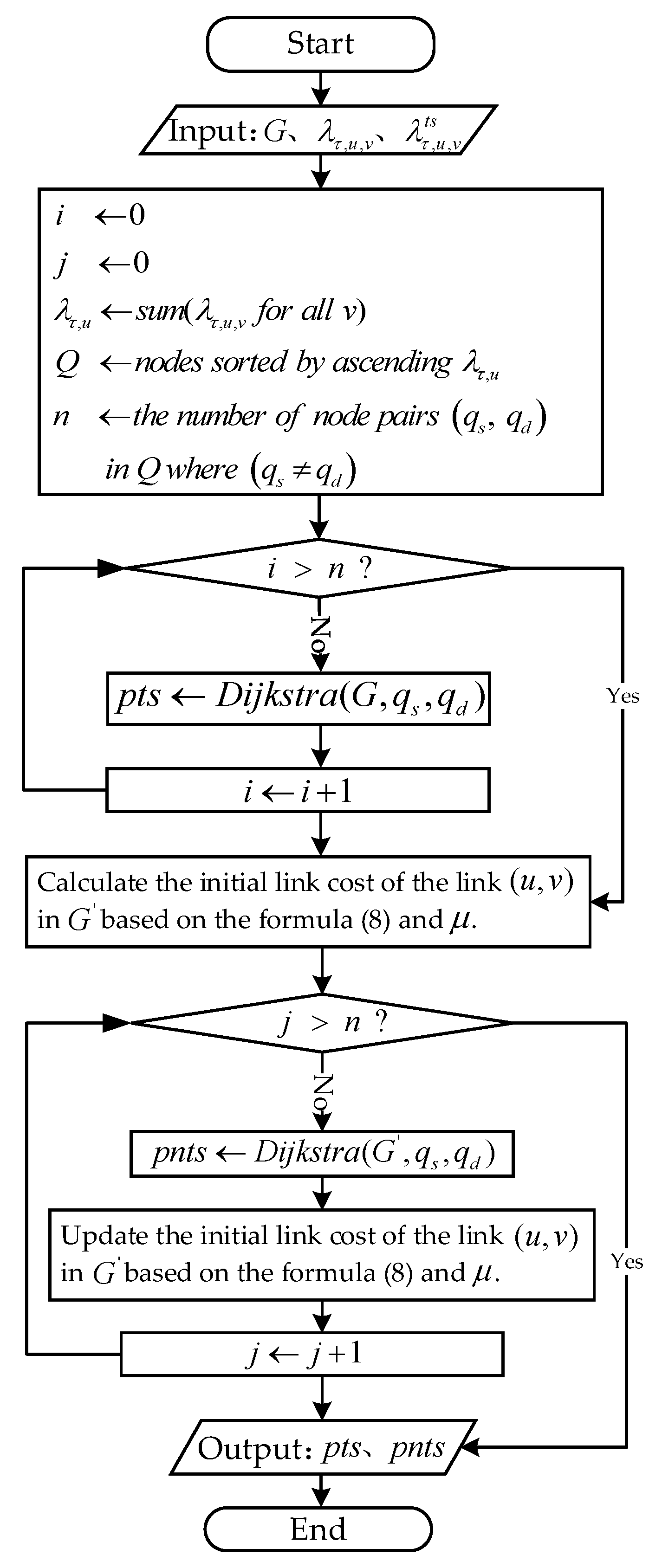
In the satellite Internet service scheduling algorithm based on the spatiotemporal distribution of traffic, the parameter updates of the entire network’s state are related to changes in traffic arrival rates and topology across different time periods. The algorithm calculates two paths for any two satellite nodes in the network: one path for time-sensitive services and another for non-time-sensitive services. The pseudocode is in Algorithm 1:

Algorithm 1 Routing algorithm based on spatiotemporal distribution of traffic

1: Input: 2:  $G=\{{𝒱}_T,{ℰ}_T\}$: Network topology within time range $T$. 3:  ${\lambda }_{\tau ,u,v}$: Traffic arrival rate from satellite $u$ to satellite $v$ at time $\tau$. 4:  ${\lambda }_{\tau ,u,v}^{ts}$: Spatiotemporal traffic factor. 5: Output: 6:  $pts$: Path of time-sensitive service between any two points $s$ and $d$ $(s\ne d)$. 7:  $pnts$: Path of non-time-sensitive service between any two points $s$ and $d$ $(s\ne d)$. 8: //Step 1: Calculate traffic arrival rate for each satellite node. 9:  for each node $u$ in $G$ and each time $\tau$ do 10:     ${\lambda }_{\tau ,u}$ ← sum (${\lambda }_{\tau ,u,v}$ for all $v$). 11:  end for 12: //Step 2: Sort nodes by traffic arrival rate. 13:  $Q$ ← nodes sorted by ascending ${\lambda }_{\tau ,u}$. 14: //Step 3: Calculate time-sensitive service path. 15:  for each pair $(q_s,q_d)$ in $Q$ do 16:    $pts$ ← Dijkstra $(G,q_s,q_d)$. 17:  end for 18:  for each link in $pts$ do 19:    Arrange service on link based on ${\lambda }_{\tau ,u,v}^{ts}$. 20:    Compute traffic proportion $\mu$ on link. 21:  end for 22: //Step 4: Update link cost for non-time-sensitive service. 23:    for each link $(u,v)$ in $G^{\prime }$ do 24:      Calculate the initial link cost of the link $(u,v)$ in $G^{\prime }$ based on the Formula (8) and $\mu$. 25:    end for 26: //Step 5: Calculate non-time-sensitive service path. 27:    for each pair $(q_s,q_d)$ in $Q$ do 28:      $pnts$ ← Dijkstra $(G^{\prime },q_s,q_d)$. 29:      for each link in $pnts$ do 30:        Arrange service on link based on ${\lambda }_{\tau ,u,v}$. 31:        Update $\mu$ and ${\mu }_{med}$. 32:        Update link cost in $G^{\prime }$ according to the Formula (8). 33:      end for 34:    end for

Figure 3 illustrates the flowchart of the routing algorithm based on the spatiotemporal distribution of traffic. In the input variables of the pseudocode for the above algorithm, the initial value of $G=\{{𝒱}_T,{ℰ}_T\}$ represents the network topology corresponding to the current snapshot period $T$, with link weights set to the propagation delay. The initial value of ${\lambda }_{\tau ,u,v}$ is given by Equation (2), while the initial value of ${\lambda }_{\tau ,u,v}^{ts}$ is the product of ${\lambda }_{\tau ,u,v}$ and the time-sensitive traffic proportion $\omega$. In the execution of the satellite Internet service scheduling algorithm based on the spatiotemporal distribution of traffic, there are five main steps: (1) Calculate the total traffic arrival rate for each node; (2) Use the bubble sort algorithm to sort the satellite nodes in ascending order based on their traffic arrival rates, then compute paths in subsequent steps following this order to prioritize the calculation of paths for low-traffic nodes; (3) In the initial network topology, use the shortest path algorithm to compute low-latency paths for time-sensitive services to meet real-time requirements; (4) Calculate the betweenness centrality of the network edges $J$ and the median of the link load ratio ${\mu }_{med}$, then update the link cost in the network topology according to Section 4.1; (5) In the updated network topology, use the shortest path algorithm to calculate paths for non-time-sensitive services, selecting paths with lower loads for these services.

Figure 3. Flowchart of the routing algorithm based on spatiotemporal distribution of traffic.

Assuming there are $n$ nodes and $m$ edges in the network, the average time complexity of the sort algorithm in Step 2 is $O(n^2)$. In Step 3, each satellite node needs to calculate the time-sensitive service paths from itself to all other nodes using the shortest path algorithm, requiring a total of $n(n-1)$ calculations with a time complexity of $O(n\log n)$ for each calculation, leading to a total complexity of approximately $O(n^3\log n)$ for Step 3. In Step 4, the time complexity for calculating the betweenness centrality $J$ using the Girvan–Newman (GN) algorithm is $O(mn)$ [30], and the time complexity for calculating the median of the link load ratio ${\mu }_{med}$ using the SELECT algorithm is $O(m)$ [31]. The calculation of link load ratios is required each time a path is computed for non-time-sensitive services, resulting in a time complexity of $O(m{n}^2+mn)$ for Step 4. Step 5 is similar to Step 4, with a complexity of $O(n^3\log n)$. Therefore, the time complexity of the satellite internet traffic scheduling algorithm based on the spatiotemporal distribution of traffic is approximately $O(n^3\log n+m{n}^2+mn)$. Once the service arrival type is determined, if it is time-sensitive, the traffic is forwarded according to the time-sensitive service path; if it is non-time-sensitive, it is forwarded according to the non-time-sensitive service path.

4.3. Implementation Scheme Based on Virtual Private Network (VPN)

In the satellite Internet, the source ground station transmits encrypted data via a VPN [32] to the satellite, which is then responsible for transmitting the data to the destination ground station connected to a private network. SRv6 can function as the underlying tunneling technology for the VPN, enabling efficient data transmission from the source node to the destination node via SRv6 tunnels. The segment routing (SR) mechanism in SRv6 provides essential functions for time-sensitive traffic transmission, including path segmentation, service priority control, and network slicing. These functions collectively ensure low-latency and highly reliable transmission of time-sensitive traffic, meeting quality of service (QoS) requirements in satellite networks. To implement a VPN-based satellite internet transmission scheme, the following five SRv6 application configurations and VPN update strategies are proposed to meet the QoS requirements of time-sensitive services:

(1) Optimization of Path Segmentation and SID Sequence Configuration: The SRv6 path control mechanism relies on Segment Identifiers (SIDs), where each SID represents a node in the network or a specific forwarding action. The SRv6 SID (Segment Identifier) packet format typically consists of three parts: Locator, Function, and Arguments [33]. The Locator is used to identify different satellite nodes in the satellite Internet. The Function field includes a specific identifier that distinguishes time-sensitive traffic from other types of traffic. This identifier is used in path generation and path selection to differentiate time-sensitive traffic from other services, creating a dedicated path that meets low-latency requirements. Different SID combinations form Segment Lists, which provide independent path information for time-sensitive and non-time-sensitive traffic and are stored in the Segment Routing Header (SRH) of each packet. By predefining SID sequences for time-sensitive traffic during the path planning phase and specifying the transmission path in the IPv6 header, precise control over the data transmission path can be achieved. The traffic is forwarded sequentially according to the SID list during transmission, bypassing route lookups at intermediate nodes and significantly reducing end-to-end latency for time-sensitive traffic.

(2) Service Priority Configuration Based on Traffic Type: SRv6 supports service priority control based on traffic type. By setting a high-priority identifier in the Traffic Class field of the IPv6 header for time-sensitive packets, and leveraging SRv6’s priority forwarding capability, this type of traffic can receive preferential treatment at network nodes, ensuring low-latency and reliable transmission.

(3) Network Slicing and Traffic Isolation Strategy: The network slicing functionality in SRv6 enables independent path resources to be allocated to different types of data flows, each meeting its specific QoS requirements. By assigning different slice identifiers in the SID sequence for time-sensitive and non-time-sensitive services, independent transmission paths can be created for each service. This effectively prevents resource competition between TS and non-TS traffic, ensuring that time-sensitive data maintain a stable transmission path even under network load fluctuations. Specifically, network slicing isolates the transmission path of time-sensitive traffic from other flows, ensuring it maintains the shortest path transmission even under congestion conditions.

(4) Dynamic Path Selection Mechanism: To further optimize the transmission quality of time-sensitive services, a satellite internet traffic scheduling algorithm based on the spatiotemporal distribution of traffic can be incorporated into the SRv6 protocol. This algorithm enables real-time awareness of load conditions across different paths and dynamically selects the optimal path for data forwarding based on the network load, thereby achieving load balancing and efficient resource utilization.

(5) Time-Based VPN Update Strategy: In the satellite Internet, due to the limited network resources and unstable network connections, VPN updates should be scheduled to minimize any negative impact on network performance and user experience. Different regions can establish update schedules based on network load and traffic usage patterns. Typically, updates are triggered during off-peak periods to avoid affecting network performance. For example, updates can be scheduled during times when user activity is low or the network load is light, such as at night or in the early morning.

5. Algorithm Simulation and Results Analysis

To evaluate the performance of the routing algorithm, network simulations were conducted using MATLAB R2024a, based on a constellation $Wal\ker 72/6/3\pi$ configuration. The algorithm’s performance was compared with the shortest path algorithm and the optimized method in terms of load balancing effectiveness, packet loss rate for time-sensitive services, and throughput of time-sensitive services under different total daily traffic volumes. Additionally, the algorithm’s runtime was simulated under varying numbers of tasks. The simulation was conducted using Xi’an local time as a reference, with the local time set to 15:00 to generate service traffic for each region. The packet size was set to 1000 bits, and the inter-satellite link capacity was configured at 200 Mbit/s. The ratio of time-sensitive to non-time-sensitive services was set at 1:4, and the traffic arrival rate was determined by equation (2). The simulation duration was 30 min, running on hardware with an Intel(R) Core(TM) i7-14700HX 2.10 GHz processor and 32 GB of memory.

Figure 4 shows the network load distribution under the satellite Internet service scheduling algorithm based on the spatiotemporal distribution of traffic. Similar to Figure 1b, the traffic arrival rate and link status of satellites at a given time can be calculated based on the ground population distribution and the relative position of satellites to the ground. In Figure 3, there are 40 lightly loaded links, 13 heavily loaded links, and 59 moderately loaded links. Compared to Figure 1b, which has 62 lightly loaded links, 12 heavily loaded links, and 38 moderately loaded links, the satellite Internet service scheduling algorithm based on the spatiotemporal distribution of traffic results in most network links being in a moderately loaded state, improving link utilization in the network.

Figure 4. Load distribution of the satellite network under the satellite Internet service scheduling algorithm based on spatiotemporal distribution of traffic (total daily traffic of 180 T).

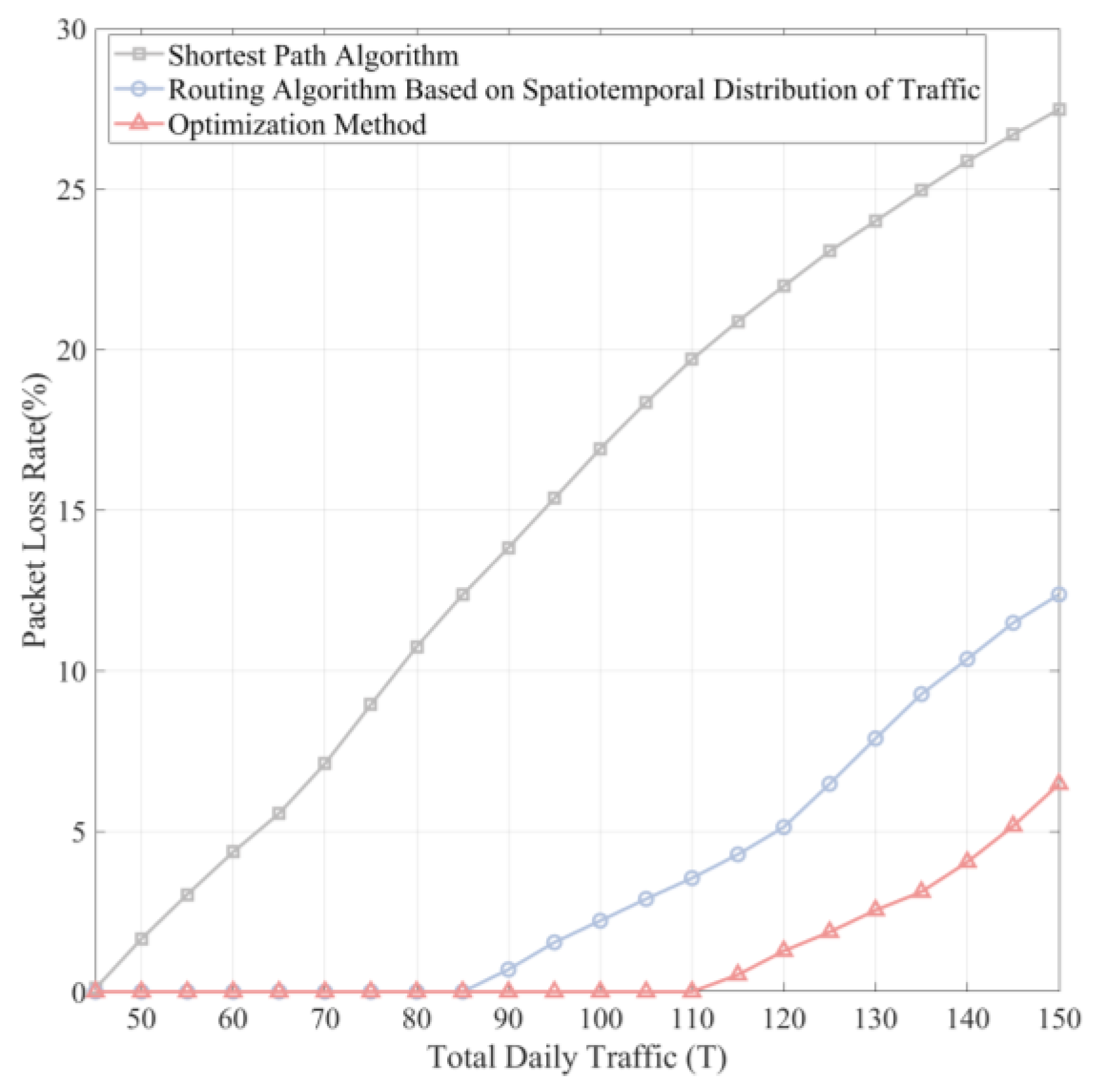
Figure 5 shows the packet loss rate for time-sensitive services under different algorithms. When the network load is light, the packet loss rate for the satellite Internet service scheduling algorithm based on the spatiotemporal distribution of traffic is similar to that of the shortest path algorithm. However, as the network load increases, the packet loss rate for the satellite Internet service scheduling algorithm becomes gradually lower than that of the shortest path algorithm. Specifically, when the network load is 120 Tbit, the packet loss rate for time-sensitive services in the shortest path algorithm is 22%, while it is 5.1% in the satellite Internet service scheduling algorithm based on the spatiotemporal distribution of traffic. The lower packet loss rate of the proposed algorithm is due to its design, where, under high inter-satellite link load conditions, time-sensitive services are transmitted via the shortest path while non-time-sensitive services are routed through less loaded links, even if it means taking a longer path. This strategy fulfills non-time-sensitive service transmission requirements while reserving the remaining bandwidth for time-sensitive services, thereby reducing the contention for transmission resources and lowering the packet loss rate for time-sensitive services. In comparison with the optimized method, when the total daily traffic is less than or equal to 85 Tbit, both the spatiotemporal distribution-based satellite Internet service scheduling algorithm and the optimized method have zero packet loss. However, when the total daily traffic is 150 Tbit, the packet loss rate for the optimized method is 6.47%, while the packet loss rate for the proposed method is 12.37%, showing a performance difference of approximately double.

Figure 5. Packet loss rate comparison for time-sensitive services.

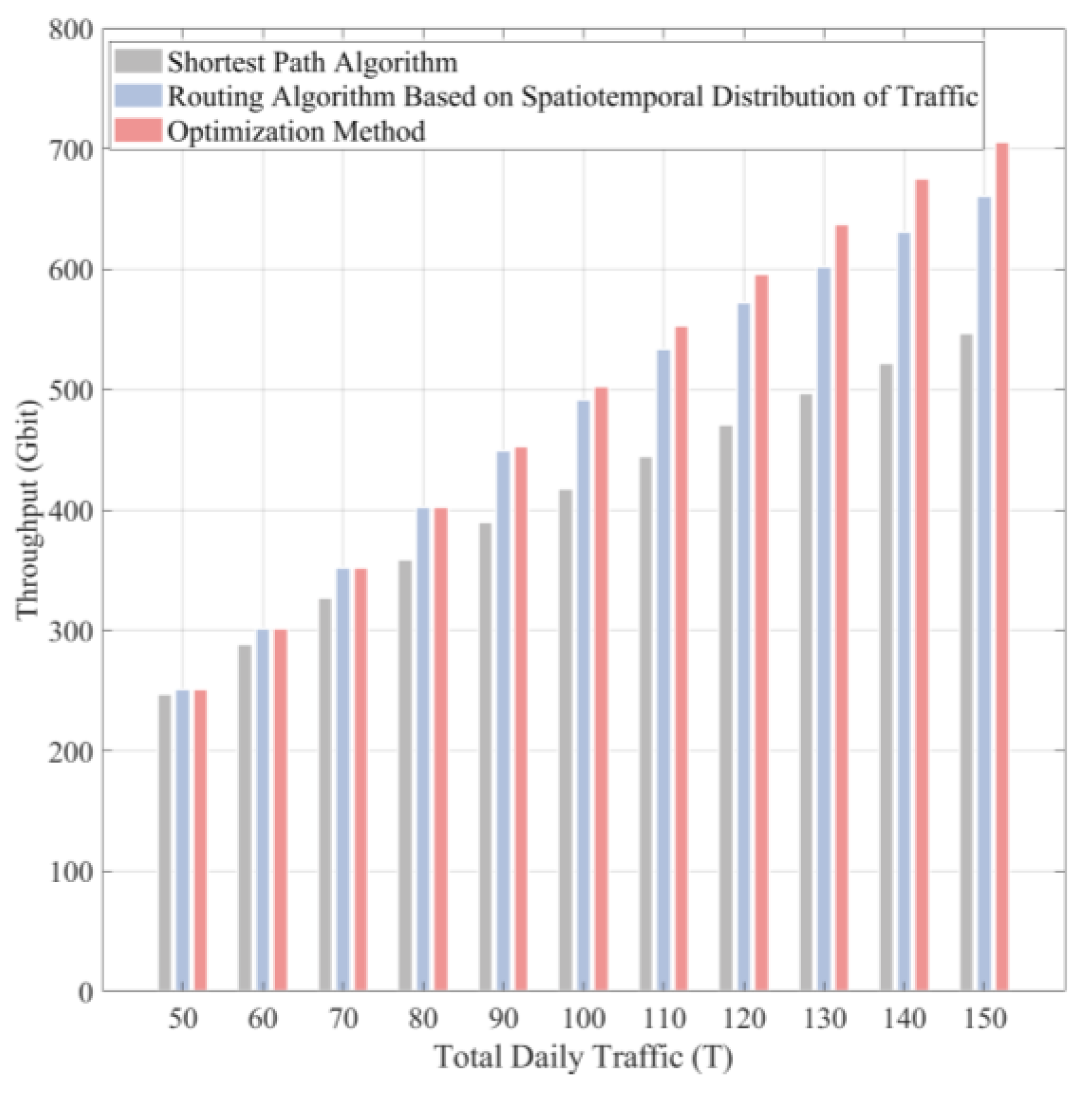
From Figure 6, it can be observed that when the network load is 50 Tbit, the throughput of time-sensitive services in both the traffic distribution-based satellite Internet scheduling algorithm and the shortest path algorithm is nearly identical. This is because, under a low network load, most links are in a light load state. During routing calculations, the link cost in the traffic distribution-based satellite Internet scheduling algorithm is nearly the same as the initial link cost (i.e., the propagation delay between two satellites), resulting in almost identical throughput for both algorithms under a light load. However, as the overall network load increases, the satellite network load becomes increasingly imbalanced. The traffic distribution-based satellite Internet scheduling algorithm adjusts the link costs by balancing the load across the links, distributing non-time-sensitive traffic as evenly as possible across the network. This reduces congestion and utilizes the remaining bandwidth of the links to transmit time-sensitive services, leading to a higher throughput for time-sensitive services compared to the shortest path algorithm. Specifically, when the network load is 150 Tbit, the throughput of the traffic distribution-based satellite Internet scheduling algorithm reaches 661 Gbit, while the throughput of the shortest path algorithm is 547.1 Gbit. In contrast, when the total daily traffic is less than or equal to 90 Tbit, the throughput of time-sensitive services in the traffic distribution-based satellite Internet scheduling algorithm and the optimization method are nearly identical. However, when the total daily traffic reaches 150 Tbit, the optimization method achieves a throughput of 705.56 Gbit, while the throughput of the proposed algorithm is 661.03 Gbit, resulting in a 6.3% difference.

Figure 6. Throughput comparison chart for time-sensitive services.

Table 2 shows the comparison of the time required to calculate the paths for time-sensitive and non-time-sensitive services under two algorithms with different numbers of tasks. As seen in Table 2, the runtime of the optimized method increases sharply as the number of tasks in the network grows. It takes 1640.34 s to plan the paths for 5112 tasks. In contrast, the runtime of the spatiotemporal distribution-based routing algorithm remains relatively stable as the number of tasks increases, requiring only 5.25 s to plan the paths for 5112 tasks. This makes it more suitable for deployment in the highly dynamic environment of the satellite Internet, allowing for real-time online path planning for services.

Table 2. Comparison table of the average runtime of the two algorithms.

	500 Tasks	1000 Tasks	2000 Tasks	3000 Tasks	4000 Tasks	5112 Tasks
Algorithm proposed in the article	0.05 s	0.20 s	0.79 s	1.76 s	3.13 s	5.25 s
Optimization method	2.83 s	40.05 s	63.2 s	87.32 s	165.17 s	1640.34 s

In summary, through simulations comparing the load balancing performance, packet loss rate of time-sensitive services, and throughput of time-sensitive services between the shortest path algorithm and the satellite Internet service scheduling algorithm based on the spatiotemporal distribution of traffic, the effectiveness of the spatiotemporal distribution-based algorithm has been validated. Additionally, simulations provided insights into the differences between the spatiotemporal distribution-based algorithm and the optimized method in terms of time-sensitive service throughput and packet loss rate. The analysis of the runtime trends and the number of network tasks for both methods confirmed the real-time performance of the proposed satellite Internet service scheduling algorithm based on the spatiotemporal distribution of traffic.

6. Discussion

To address the limitations of existing load balancing methods in simultaneously ensuring load balance and meeting the quality of service (QoS) requirements for time-sensitive services, this paper proposes a multi-criteria routing algorithm based on the spatiotemporal distribution of service traffic. By constructing low-latency paths to reserve the bandwidth for time-sensitive services and optimizing link weight assignments, the algorithm ensures the QoS of time-sensitive services while achieving load balancing for non-time-sensitive services. Experimental results demonstrate that the proposed algorithm significantly enhances network resource utilization, increases the throughput of time-sensitive services, and reduces packet loss rates, while maintaining low algorithm complexity and shorter execution times in multi-task environments. Therefore, the algorithm is well suited for scenarios requiring high real-time data processing, such as telemedicine, intelligent transportation, and the Internet of Things (IoT), particularly under high-load conditions, where it prioritizes the transmission of time-sensitive services and optimizes network resource utilization.

However, challenges related to computational resources, storage space, and energy consumption in large-scale satellite network environments may impact the practical deployment of this algorithm. First, dynamic topology management in large-scale networks significantly increases signaling overhead, leading to higher bandwidth consumption and a greater risk of network congestion. The Clustered Multi-Criteria Routing (CMCR) Algorithm proposed in the literature [34] optimizes routing efficiency and load balancing in large-scale LEO constellations through clustering and multi-criteria routing, demonstrating advantages in reducing signaling overhead and computational complexity. In contrast, the algorithm presented in this paper exhibits advantages in global optimization and path flexibility, enabling the assurance of time-sensitive services and overall load balancing under high-load conditions. Nevertheless, further improvements are needed in controlling signaling overhead. Additionally, the limited storage capacity in satellite networks may affect the ability to cache path and link information in large-scale networks, thereby reducing the responsiveness of path optimization. Moreover, the battery capacity of 200–300 watt-hours restricts satellite operations under high-frequency path computation scenarios. Specifically, LEO satellites are typically equipped with low-power processors (e.g., ARM Cortex-A series) and limited memory (500 MB to 1 GB), which may constrain the frequent link weight adjustments required by the algorithm, ultimately affecting the network’s real-time responsiveness. Although this study employs strategies such as time-slot division, lightweight graph-based routing algorithms, and VPN-based implementation schemes to mitigate resource consumption, it has not fully addressed the detailed computation, storage, and energy capabilities of individual satellites, nor has it implemented fine-grained resource scheduling. These limitations highlight areas for future optimization and necessitate further research and refinement in practical deployments.

7. Conclusions

This paper addresses the challenge of balancing load distribution and ensuring the quality of service (QoS) for time-sensitive traffic in satellite networks by proposing a multi-criteria routing algorithm based on the spatiotemporal distribution of service traffic. The algorithm prioritizes low-latency paths for time-sensitive services and optimizes link weight allocation, significantly improving network resource utilization under high-load conditions while maintaining the service quality for both time-sensitive and non-time-sensitive traffic. Experimental results demonstrate that, compared to traditional algorithms, the proposed method increases the throughput of time-sensitive traffic by up to 20.8% and reduces its packet loss rate by up to 76.8%, effectively enhancing overall network resource utilization. Although the performance difference in terms of packet loss rate and throughput for time-sensitive traffic is minor compared to existing optimization methods, the proposed algorithm exhibits significantly reduced path planning time under the same number of tasks, demonstrating superior computational efficiency. Additionally, this study introduces a VPN-based implementation scheme that leverages the flexibility and scalability of the SRv6 protocol, enabling efficient transmission of time-sensitive traffic within the existing network architecture without substantial modifications to the network infrastructure. This approach ensures high-reliability transmission of time-sensitive traffic and optimized resource utilization in satellite Internet environments, making it suitable for large-scale satellite network deployments. Overall, the proposed algorithm provides reliable technical support for real-world applications in large-scale satellite networks and demonstrates strong flexibility and applicability.