Abstract
In industries spanning manufacturing to software development, defect segmentation is essential for maintaining high standards of product quality and reliability. However, traditional segmentation methods often struggle to accurately identify defects due to challenges like noise interference, occlusion, and feature overlap. To solve these problems, we propose a cross-hierarchy feature fusion network based on a composite dual-channel encoder for surface defect segmentation, called CFF-Net. Specifically, in the encoder of CFF-Net, we design a composite dual-channel module (CDCM), which combines standard convolution with dilated convolution and adopts a dual-path parallel structure to enhance the model’s capability in feature extraction. Then, a dilated residual pyramid module (DRPM) is integrated at the junction of the encoder and decoder, which utilizes the expansion convolution of different expansion rates to effectively capture multi-scale context information. In the final output phase, we introduce a cross-hierarchy feature fusion strategy (CFFS) that combines outputs from different layers or stages, thereby improving the robustness and generalization of the network. Finally, we conducted comparative experiments to evaluate CFF-Net against several mainstream segmentation networks across three distinct datasets: a publicly available Crack500 dataset, a self-built Bearing dataset, and another publicly available SD-saliency-900 dataset. The results demonstrated that CFF-Net consistently outperformed competing methods in segmentation tasks. Specifically, in the Crack500 dataset, CFF-Net achieved notable performance metrics, including an Mcc of 73.36%, Dice coefficient of 74.34%, and Jaccard index of 59.53%. For the Bearing dataset, it recorded an Mcc of 76.97%, Dice coefficient of 77.04%, and Jaccard index of 63.28%. Similarly, in the SD-saliency-900 dataset, CFF-Net achieved an Mcc of 84.08%, Dice coefficient of 85.82%, and Jaccard index of 75.67%. These results underscore CFF-Net’s effectiveness and reliability in handling diverse segmentation challenges across different datasets.
1. Introduction
With the continuous progress of industrial technology and the improvement of production requirements, the demand for products in modern society is not only limited to functionality but also puts forward higher standards in terms of quality, shape, appearance, and so on. However, during the manufacturing process, due to the influence of a variety of interfering factors, the surface of the product may produce different degrees of defects, which will not only affect the appearance of the product but also reduce the actual performance of the product. As a result, reliable and efficient surface defect detection has become crucial across multiple industrial sectors, including the textile industry, the steel industry, and semiconductor manufacturing. In each of these fields, the need for consistent and perfect product surfaces has sparked a strong interest among researchers in developing surface defect detection methods. Early surface defect detection mainly adopts manual detection, which not only can easily be affected by subjective factors of detection personnel but also has low detection efficiency and high detection and false detection rates of some types of defects, especially for some defects with small deformations and no obvious distortion. Therefore, researchers are now turning to computer vision technology, leveraging powerful algorithms and high computing capabilities to create advanced, automated surface defect detection methods.
In the early stages of computer vision, defect detection mainly relied on traditional image processing algorithms. For complex environments, these algorithms require frequent parameter tuning, especially under unstable conditions. In addition, they often struggle to handle defects with inconspicuous or irregular contrast, resulting in high false detection rates and limited adaptability. As defect detection needs change, machine learning becomes an advanced solution. This shift has seen the application of simple neural networks, such as single-layer models and multi-layer perceptron, for training and classifying defect features. However, this method requires the pre-extraction of defect areas and is often combined with traditional segmentation techniques to achieve accurate defect detection and classification. Moreover, in open or unpredictable environments, factors such as different lighting conditions, changes in camera angles, and the characteristics of the material being inspected can introduce interference that diminishes the reliability and accuracy of detection. With the emergence of the convolutional neural network (CNN), deep learning technology has shown great potential in image processing tasks, such as face recognition [1,2], object detection [3,4], and semantic segmentation [5,6]. Among them, semantic segmentation has emerged as a valuable approach for industrial quality control, transforming the detection task into the precise delineation of defect versus non-defect areas within an image. Classifying each pixel based on regional defects or normal semantic segmentation is critical to maintaining quality standards in complex and variable environments.
At present, the fully convolutional network (FCN) [7] and U-Net [8] have become foundational architectures due to their efficient model structures, which are well-suited for fast, accurate defect segmentation across various industrial applications. Among them, Shi et al. [9] introduced an advanced segmentation method, which effectively reduces the dependence on large amounts of labeled data by introducing a variety of perturbing cross-pseudo supervision mechanisms. Furthermore, the framework integrates edge pixel-level information to capture detailed edge features that are critical for accurate defect boundary detection. Huang et al. [10] introduced an innovative multi-scale feature integration approach designed to address the limitations of traditional models in extracting local features accurately. Additionally, the model dynamically merges underlying feature information, which strengthens its capability to detect and interpret the diverse. Xu et al. [11] applied a simple linear iterative clustering method to capture essential features of the citrus surface across multiple levels. On this basis, they introduced a cross-fusion transformer module to better transmit and integrate feature information of different scales. Zhang et al. [12] proposed a method to realize real-time detection of production lines by efficiently aggregating multi-scale information from original images and focusing on key feature areas. In this process, the model can dynamically capture and integrate the different scale feature information of the image and effectively improve the detection sensitivity and accuracy of the target defect. Si et al. [13] integrated a local perception module within the encoding network, which significantly enhances the model’s capability to interpret and capture fine-grained regional details and contextual cues. Meanwhile, a spatial detail extraction module was added to fully retain the key spatial detail information. Zhang et al. [14] introduced a context-aware convolution technique aimed at refining the network’s focus on key features, effectively minimizing interference from background noise. Additionally, during the feature fusion process, they developed a specialized module to enhance feature detail, which targets the capture of subtle, complex, and irregular structural details.
Recently, substantial research efforts have focused on analyzing surface defects, particularly in complex and challenging environments. Among them, Lu et al. [15] proposed a sophisticated multi-scale feature enhancement fusion module aimed at improving the quality and integration of deeper feature maps within the backbone network. By enhancing the expressiveness of deeper feature representations and ensuring effective fusion, their approach achieves remarkable accuracy in surface defect detection. Li et al. [16] introduced a novel position attention module designed to enhance the network’s ability to accurately perceive and localize defects within an image. Additionally, they developed a shape detection module incorporating feature difference loss, which plays a crucial role in refining the segmentation process to delineate the precise defect areas. Xiao et al. [17] developed an advanced multilevel receiving field module aimed at achieving a comprehensive perception of surface defects, particularly those that are complex and exhibit significant variability. Song et al. [18] introduced an innovative design by replacing all under-sampled layers in the encoder, with a combination of a spatial attention mechanism and a feedforward neural network. This approach enhances the network’s ability to preserve finer spatial details, which are often lost in traditional under-sampling processes. Luo et al. [19] developed a Gaussian residual attention convolution module aimed at addressing the challenges of distinguishing similar feature defects in low-contrast environments. This approach effectively amplifies key features while suppressing irrelevant or redundant information, improving the accuracy and reliability of defect detection in visually challenging scenarios.
Inspired by the above methods, we propose a cross-hierarchy feature fusion network based on a composite dual-channel encoder for surface defect segmentation. Experimental results on road, bearing, and strip steel defect datasets demonstrate that the proposed CFF-Net network exhibits exceptional segmentation performance. In the Crack500 dataset, our network demonstrated a notable improvement over the U-Net baseline, with an increase of 2.06% in the Mcc, 2.14% in the Dice coefficient, and 2.57% in the Jaccard index. Similarly, in the Bearing dataset, performance gains were observed, with the Mcc improving by 2.70%, the Dice coefficient increasing by 2.74%, and the Jaccard index rising by 3.45%. In the SD-saliency-900 dataset, our network continued to showcase its effectiveness, achieving enhancements of 1.06% in the Mcc, 1.01% in the Dice coefficient, and 1.43% in the Jaccard index. These results demonstrate that the network effectively handles varying defect types and complexities within these datasets, achieving precise segmentation even in challenging scenarios with diverse textures and irregular defect boundaries. The primary contributions of our work can be summarized as follows: (1) In the encoder phase, we introduce a composite dual-channel module that combines standard convolution with dilated convolution in a dual-path parallel configuration, significantly improving the model’s feature extraction capability. (2) To bridge the encoder and decoder, we integrate a dilated residual pyramid module, leveraging convolutions with varied dilation rates to capture multi-scale contextual information. (3) At the output stage, we employ a cross-hierarchy feature fusion strategy, which merges outputs from multiple network layers or stages to obtain edge details. This approach contributes to enhanced segmentation accuracy, particularly in regions with complex boundary structures.
2. Materials and Methods
2.1. Dataset
Crack500 dataset: The Crack500 dataset is specifically crafted to assess the performance of algorithms aimed at detecting cracks in concrete surfaces. It comprises a collection of 500 high-resolution images captured on the pavement of Temple University using mobile phones, as documented in the literature [20]. The images contain a wide variety of crack types, showing variations in size, appearance, and orientation, as well as different lighting conditions and angles. Given the dataset’s relatively modest size and the constraints posed by limited computational resources, each original image has been divided into 16 non-overlapping segments, with a resolution of 256 × 256 pixels. Alongside these segmented images, corresponding ground-truth masks have been created to facilitate accurate model training. This preprocessing step significantly enhances the dataset’s utility, resulting in a total of 1138 training images, 379 validation images, and 379 test images. Figure 1 provides a visual example of some images, and it can be downloaded at [21].

Figure 1.
Visual illustrations of defects on the Crack500 dataset and corresponding annotations.
Bearing dataset: The Bearing dataset is derived from a comprehensive collection of images capturing various defects on bearing surfaces, including abrasion, groove, and scratch defects. Each image in the dataset has been meticulously selected to ensure high quality and relevance. To achieve a precise delineation of these defects, the images were annotated using Labelme 3.16.7 software software, which allows for detailed and accurate marking of the affected areas. Figure 2 visually illustrates the defects present in the dataset, along with their corresponding annotations, providing a clear reference for understanding the nature of the defects. For our study, we utilized a total of 2854 images for training, while 952 images were set for testing and another 952 for validation. The datasets generated and/or analyzed during the current study are not publicly available but may be obtained from the original author upon reasonable request [22].

Figure 2.
Visual illustrations of defects on the Bearing dataset and corresponding annotations.
SD-saliency-900 dataset: To evaluate the performance and robustness of our proposed CFF-Net, we conducted a series of experiments utilizing the SD-saliency-900 dataset [23]. This dataset serves as a challenging public benchmark specifically designed for detecting strip steel defects. It comprises 900 cropped images, each with a resolution of 256 × 256 pixels, covering three distinct defect categories: inclusions, patches, and scratches. Additionally, it offers highly detailed pixel-level ground-truth annotations to ensure precise and reliable evaluation of segmentation performance. Figure 3 illustrates some data samples from the SD-saliency-900 dataset, and it can be downloaded at [24].
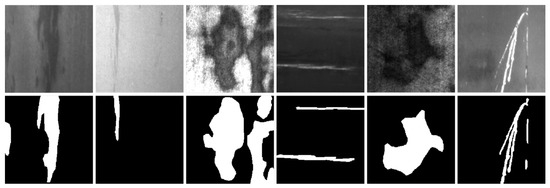
Figure 3.
Visual illustrations of defects on the SD-Saliency-900 dataset and corresponding annotations.
2.2. Overall Architecture of CFF-Net
As shown in Figure 4, the foundational design of our proposed CFF-Net is an encoder–decoder architecture, tailored specifically for the task of surface defect segmentation. Specifically, to begin the segmentation process, a surface defect image with dimensions of 256 × 256 and 3 channels is first input into the model framework. Within the encoder, the composite dual-channel module plays a pivotal role in extracting both global and local features from this input image. By utilizing a dual-channel structure, the CDCM can capture comprehensive spatial and contextual information, ensuring that fine details as well as broader patterns are represented. Then, to enrich the semantic feature representation, a dilated residual pyramid module is incorporated at the bottleneck layer of the network. By leveraging these dilated convolutions, the DRPM can gather feature details across different spatial resolutions, which enhances the model’s ability to understand fine- and coarse-grained patterns. In addition, the DRPM utilizes residual connections to mitigate problems such as disappearing gradients or exploding gradients. Moreover, the DRPM incorporates residual connections, which help stabilize the training process by addressing challenges like vanishing or exploding gradients. The decoder segment incorporates a dual-path structure, which strengthens the model’s ability to capture and merge essential boundary features effectively during the decoding process. This design increases the flexibility of processing and interpreting information, and the system achieves higher accuracy in detecting and retaining boundary details in segmented images. After all operations, the network ends with a 1 × 1 convolution layer, followed by Sigmoid activation, producing the final segmentation graph. The output map has a single channel, where each pixel’s value represents the likelihood of it belonging to the defect region. The following sections will provide a detailed explanation of the proposed module, explaining their structure, functionality, and contributions.
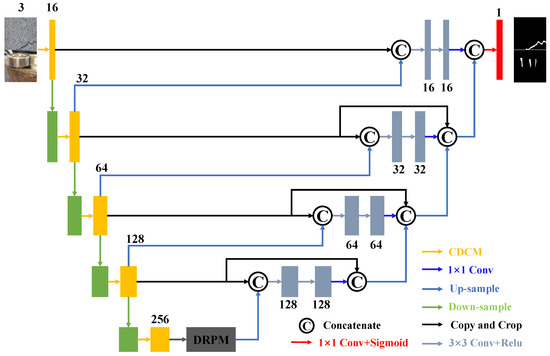
Figure 4.
Overall architecture of CFF-Net.
2.3. Composite Dual-Channel Module
In some special cases, the tiny defects that appear on the surface of the object account for less than 1% of the total pixels of the image, so their size is almost negligible. This extreme smallness presents a major challenge to many algorithms that struggle to distinguish defect areas from the background due to a lack of distinguishable reference points. To address this issue, researchers introduced the selective kernel (SK) method [25], which can automatically adjust its acceptance domain according to the content in the image, thereby maximizing the use of spatial information collected across various scales. Figure 5 illustrates the structural components of the SK module, which leverages its adaptability to achieve notable performance in handling images with a blurred field of view or identifying very small targets. However, it should be noted that the high computational demand associated with the SK module will increase the risk of overfitting in certain applications, which may compromise the model’s consistency and robustness in complex or diverse environments.

Figure 5.
Structure of original selective kernel module.
Inspired by the capabilities of the SK module, we propose a composite dual-channel module, as depicted in Figure 6. Specifically, the input image features are initially fed into a 1 × 1 convolution layer, which is used to size the channel and prepare the input for further processing. Following the initial processing in the CDCM, the feature diverges into two distinct branches. The first path is passed to two sequences of 3 × 3 convolution layers, and after each convolution layer, batch normalization (BN), and ReLU activation are used to normalize and add nonlinearities. This path focuses on extracting fine-grained details from the input, capturing localized information critical for high-resolution defect analysis. The second path is convolved by two expansions with an expansion rate r = 2, which helps capture a larger acceptance field. By using dilated convolutions, this path enhances the module’s capacity to detect larger structures or patterns, essential for analyzing surface defects that might spread over larger regions. After the above two steps, we concatenate the localization details of the first branch with the context information of the second branch. This integration ensures a more complete understanding of both fine and rough features, and it provides a robust feature representation for accurate defect detection. Unlike the SK module, the CDCM incorporates a residual structure that allows the model to retain the basic feature information of the previous layer, thus alleviating problems such as disappearing gradients and preserving low-level details. In addition, CDCM reduces computational complexity and potential overfitting by removing the fully connected layer. Finally, the outputs from the two paths are combined through multiplicative fusion, which effectively enhances the richness and depth of the final feature representation. By doing so, our CDCM achieves a more robust and discriminative feature map, which is especially valuable for tasks requiring precise defect localization and segmentation.

Figure 6.
Structure of composite dual-channel module.
2.4. Dilated Residual Pyramid Module
In practical applications, when a uniform dilation rate is used across continuous convolution layers, many pixels in the receptive field remain unutilized, resulting in voids. To mitigate this issue, varying dilation rates are applied at different convolution layers. This strategy allows for gradual expansion of the acceptance field, which preserves the necessary local details to capture complex image features, as shown in Figure 7. Since traditional convolution and pooling operations tend to lead to the loss of a large number of details in the image, and it is difficult to accurately recover these details with the classical up-sampling technique, the accuracy of semantic segmentation is limited. To address these challenges and push the boundaries of segmentation performance, we developed a dilated residual pyramid module at the bottom of the encoder, as depicted in Figure 8. The DRPM is designed with five separate branches, each dedicated to capturing feature information across various scales. Specifically, the first branch employs two consecutive 3 × 3 convolutions, without any extension, to obtain local information from the input feature map. The second to fourth branches add one dilated convolution (rate = 2), two dilated convolutions (rate = 4, 2), and three dilated convolutions (rate = 6, 4, 2) to two consecutive 3 × 3 convolutions. This design helps identify larger, more complex patterns and enhances semantic understanding. The last branch first performs an average pooling operation on the input feature map, then two 3 × 3 convolutions, followed by an up-sampling of the output using bilinear interpolation to match the size of the original feature map. The feature extraction in each branch can be formulated as follows:
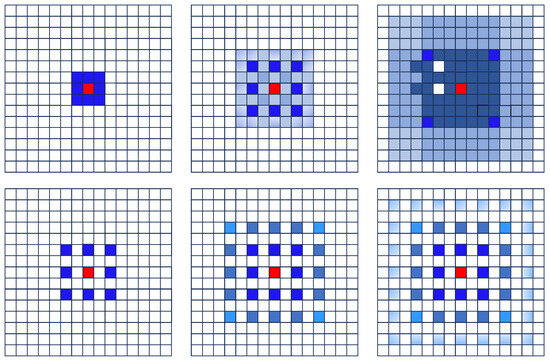
Figure 7.
Comparison experiment of dilatational convolution. The first row: consecutive convolutions with different expansions (rate = 1, 2, 4). The second row: consecutive convolution with the same expansion (rate = 2).
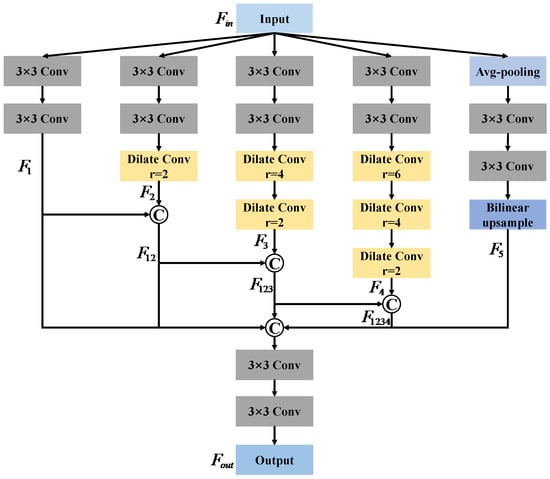
Figure 8.
Structure of dilated residual pyramid module.
Finally, the outputs from each branch are aggregated to form the final output feature map :
Compared to the traditional atrous spatial pyramid pooling (ASPP) module, the DRPM introduces an innovative approach to multi-scale feature fusion. By utilizing a combination of concatenation and summation steps, the DRPM effectively integrates features at different scales while minimizing redundancy. Additionally, it incorporates a hierarchical and iterative feature aggregation mechanism, which progressively refines the multi-scale features to capture intricate patterns and contextual details. By integrating these advancements, DRPM excels at leveraging both local and global contextual information, leading to superior performance in complex tasks like semantic segmentation.
2.5. Cross-Hierarchy Feature Fusion Strategy
The decoding module of the traditional U-Net architecture typically involves an up-sampling operation followed by the integration of feature maps from the encoding path. This design can result in several significant issues. Firstly, the up-sampling process often causes a loss of fine-grained spatial information, which is crucial for accurately segmenting small or intricate objects. Additionally, the integration of feature maps can lead to mismatches in both resolution and semantic information. Therefore, we introduce a cross-hierarchy feature fusion strategy that combines outputs from different layers or stages, as depicted in Figure 1. In contrast to the traditional U-Net architecture, this approach introduces several key differences in its structure and functionality. Firstly, the image features extracted from the last layer of the encoding module are combined with those from the preceding layer through an up-sampling operation. This fusion allows for a more nuanced representation of the features as they transition into the decoding phase. Secondly, the architecture splices the features of the encoding and decoding modules together at the same layer so that spatial information and contextual information are more richly integrated. Lastly, to reduce the overall number of parameters, a 1 × 1 convolution operation is employed within the decoding module. This technique not only helps to reduce computational complexity but also helps to improve feature mapping. Building on the aforementioned enhancements, the cross-hierarchy feature fusion strategy effectively integrates outputs from various layers or phases of the network. This multi-layered approach allows for the consolidation of diverse feature representations, capturing intricate edge details that may be overlooked when relying on single-layer outputs.
2.6. Loss Function
The challenges associated with accurately segmenting small target regions are compounded by various factors, including the diverse nature of surface defect images and the impact of different environmental conditions and shooting angles. These complexities significantly increase the likelihood of class imbalance, making it more difficult for conventional models to perform effectively. Compared to the traditional cross-entropy loss function, Dice [26,27] provides a more powerful optimization mechanism by focusing on the overlap between the predicted and actual regions. Therefore, we choose Dice as the loss criterion, which is calculated as follows:
where is the number of pixels; and represent the actual label and segmentation mask of pixel .
3. Results
3.1. Evaluation Metrics
To rigorously evaluate the performance of our CFF-Net, we have selected three widely recognized metrics that are commonly employed in the field of image segmentation: the Matthews correlation coefficient (Mcc) [28,29], Dice coefficient [30,31], and Jaccard index [32,33]. The formula for these indicators is as follows:
3.2. Parameter Setting
All models were implemented using Python 3, utilizing the Keras framework with TensorFlow as the backend to streamline the development process. The experiments were conducted on a Windows 10 workstation, which is equipped with an NVIDIA Quadro RTX 6000 GPU, providing substantial computational power. All networks were carried out using the Adam optimizer [34,35] with a learning rate set at 0.002, providing an efficient and adaptive approach for weight updates. To balance training speed with hardware capabilities, the model was trained for 200 epochs, with a batch size of 16. Before initiating the training, all input images underwent normalization and were resized to 256 × 256 pixels to maintain a consistent input shape. During the convolutional operations, padding was set to "Same" to preserve the spatial dimensions of the feature maps. To mitigate the risk of overfitting, a dropout rate of 0.2 was employed, meaning 20% of neurons were randomly deactivated during each training iteration. Figure 9 provides the loss and accuracy curves for the validation phases of all methods on three different datasets. These curves demonstrate CFF-Net’s ability to generalize well across distinct datasets and show stable training behavior over time.
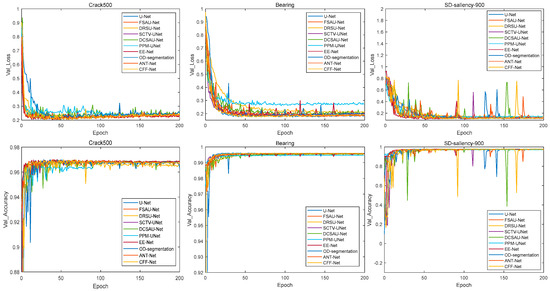
Figure 9.
The loss and accuracy curves for the validation phases of all methods. The first column illustrates the results obtained on the Crack500 dataset, the second column displays the corresponding results for the Bearing dataset, and the last column shows the results for the SD-saliency-900 dataset.
3.3. Comparison Experiments
To demonstrate the superior performance of the proposed CFF-Net network, we began by conducting experiments on the Crack500 dataset. For comparison, we selected several state-of-the-art models developed in recent years, including U-Net [8], FSAU-Net [36], DRSU-Net [37], SCTV-UNet [38], DCSAU-Net [39], PPM-UNet [40], EE-Net [41], OD-segmentation [42], and ANT-Net [43]. In order to ensure accuracy and fairness in the experimental results, all models were trained under the same conditions, including the optimizer, learning rate, batch size, and number of epochs. The quantitative results of these experiments are summarized in Table 1, which details the performance of each model on the Crack500 dataset. The table reveals that, in addition to our proposed CFF-Net, both ANT-Net and DCSAU-Net demonstrate competitive performance. Among them, ANT-Net introduces an innovative clipping technique that combines random clipping with down-sampling, allowing the model to receive different resolutions during training. This approach not only provides varied receptive fields but also reduces image sizes, resulting in more efficient processing. Meanwhile, DCSAU-Net incorporates concepts inspired by the SK network, utilizing a multi-branch CSA block that leverages feature sets from multiple branches in combination with an attention mechanism. Each branch within the CSA block applies a different number of convolutions, enabling it to process varying receptive field sizes and generate comprehensive feature maps. In contrast, the remaining models exhibit weaker segmentation capabilities. This limitation may stem from their reduced effectiveness in handling noise and uneven lighting, which can cause the loss of global features and hinder the networks from learning useful information for accurate segmentation. However, CFF-Net showed the best performance in evaluation indexes, especially the Mcc and Dice, which reached 73.36% and 74.34%, respectively. Although the Jaccard index is only 59.53%, it is still 2.57% higher than the original U-Net. These results underscore the effectiveness of the composite dual-channel module, the dilated residual pyramid module, and the cross-hierarchy feature fusion strategy introduced in CFF-Net, which collectively enhance its ability to accurately segment surface defects.

Table 1.
Comparison experiments on the Crack500 dataset.
As shown in Figure 10, traditional U-Net struggles with images lacking clear features, interpreting both cracks and non-target areas predominantly as background. Similarly, models such as FSAU-Net, DRSU-Net, PPM-UNet, and ANT-UNet attempt to enhance feature analysis by modifying either the encoder structure or the connections within the network. However, these models encounter challenges in accurately identifying subtle cracks and images with minimal light and shadow contrast, particularly in columns 8 and 9. In contrast, models like SCTV-UNet, EE-Net, and OD-segmentation incorporate different types of connections into their architectures to address this issue more effectively. Our proposed CFF-Net combines advantageous elements from each of these models, implementing an adapted encoder structure with additional skip connections to better process the input data. In addition, the DRPM is applied to the output of the encoder, which facilitates a more complete integration of contextual information. In the final output stage, a cross-hierarchy feature fusion strategy is employed to accurately capture edge details. As shown in the last row of Figure 10, CFF-Net is able to process images better than other models, achieving a higher level of detail and recovery in crack detection.

Figure 10.
Visual comparison of different methods on the Crack500 dataset.
To further verify the effectiveness of CFF-Net, we evaluated the bearing dataset using the same metrics as before, and the experimental results are recorded in Table 2. Compared to the Crack500 dataset, all models achieved improved performance on the Bearing dataset. This improvement can be attributed to several factors: the bearing dataset provides twice as many training images, features less shadow and noise interference, and presents clearer visual features, making segmentation tasks less challenging. According to Table 2, CFF-Net achieves Mcc, Dice, and Jaccard values of 76.97%, 77.04%, and 63.28%, respectively, outperforming the other models. These results demonstrate that CFF-Net effectively performs accurate and efficient segmentation on images with surface defects, whether on road cracks or bearing surfaces.

Table 2.
Comparison experiments on the Bearing dataset.
We further visualized the experimental results on the Bearing dataset, as shown in Figure 11, to illustrate the advantages of our proposed CFF-Net. The figure demonstrates that CFF-Net can accurately segment various defects, whether they are road cracks or surface scratches on objects. Compared to other models, CFF-Net’s segmentation results are more closely aligned with the original ground-truth labels. Although certain similar scratches, such as those in columns 8 and 9, are not perfectly differentiated, their overall shapes are still preserved, ensuring minimal impact on the model’s final output. This highlights CFF-Net’s ability to deliver precise segmentation even in challenging cases.

Figure 11.
Visual comparison of different methods on the Bearing dataset.
The performance of CFF-Net was evaluated on the newly incorporated SD-saliency-900 dataset under consistent experimental conditions, with the result summarized in Table 3. From the table, we find that CFF-Net outperformed all other models, achieving top evaluation metrics with Mcc, Dice, and Jaccard values of 84.08%, 85.82%, and 75.67%, respectively. These results demonstrate the proposed model’s ability to effectively detect various types of surface defects with high accuracy. As observed in Table 3, the segmentation targets in the SD-saliency-900 dataset are relatively distinct and minimally influenced by environmental factors such as lighting, allowing all models to achieve their peak performance. Figure 12 further illustrates the superior segmentation capability of CFF-Net, which excels at accurately detecting small defects and maintaining comprehensive coverage for larger defect areas.

Table 3.
Comparison experiments on the SD-saliency-900 dataset.

Figure 12.
Visual comparison of different methods on the SD-saliency-900 dataset.
3.4. Ablation Experiments
In this section, we provide an in-depth analysis of CFF-Net on the Crack500 dataset, in turn adding the CDCM, DRPM, and CFFS to the U-Net framework to evaluate the contribution of each component. After individual tests, we combined two modules at a time and eventually integrated all three modules. The quantitative results are shown in Table 4, while the visual output is shown in Figure 13.

Table 4.
Ablation experiments on the Crack500 dataset.

Figure 13.
Ablation experiments on the Crack500 dataset.
3.4.1. Effect of CDCM
First, the CDCM is applied on its own, replacing two standard convolutions in the U-Net encoder. Table 4 shows a modest improvement across metrics, with the Mcc increasing by 0.078, Dice by 0.078, and Jaccard by 0.094. Visualizations reveal that the CDCM enhances segmentation precision, enabling more detailed feature extraction. This improvement stems from the CDCM’s dual-path parallel structure, which combines standard and dilated convolutions to significantly boost the model’s feature extraction capabilities.
3.4.2. Effect of DRPM
Next, the DRPM is added to the connection between the encoder and decoder for experimentation. With the DRPM incorporated, the model shows improved segmentation performance compared to the original U-Net. This enhancement is due to the hybrid dilated convolution in the DRPM, which effectively expands the receptive field. Visual results indicate that the DRPM not only enhances segmentation for larger, more prominent cracks by making edge structures clearer but also proves effective in identifying smaller, less obvious cracks.
3.4.3. Effect of CFFS
Third, the experimental module is the CFFS, which adds an extra decoding path on the basis of the U-Net framework and integrates each layer decoder step by step. After adding the CFFS, the best results in a single-module experiment are obtained. As seen in the visualizations, the dual decoding paths refine the extracted features and capture edge details more effectively.
3.4.4. Effect of the Combination of Each Module
After the single-module experiment, we advanced to utilizing the modules in pairs. The results displayed in Table 4 indicate that combining the two modules significantly enhances the model’s performance, but there are still some problems. As illustrated in columns 2 and 3 of Figure 13, the CDCM module excels at delineating target regions in images that present considerable segmentation difficulties. In contrast, when the CDCM is paired with the DPRM and the CFFS, the model struggles to accurately identify the object, mistakenly categorizing it as part of the background. To address these shortcomings, we explored the efficacy of integrating all three modules simultaneously. Whether this can be obtained from the data results or from the visual results, such a model effect is the best. As shown in Figure 14, we converted the experimental data into a bar chart, and it can be seen that the performance was significantly improved gradually.
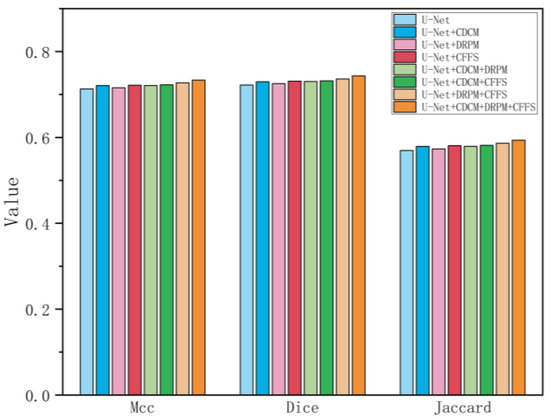
Figure 14.
Bar chart of ablation experiment.
3.5. Computational Efficiency
Analysis of the parameters and computational efficiency of the proposed methods is crucial for comprehensive evaluation. Therefore, we chose parameters and frames per second as evaluation indicators, and the results are shown in Table 5. Notably, the decoder for OD-segmentation integrates a variety of coding features and employs cross-connected local networks. While this design enhances certain aspects of the model, it also leads to an increased number of parameters. Similarly, DCSAU-Net also has a large number of parameters and a longer training time, but the model effect ranks second in the Crack500 comparison experiment. Although other models demonstrate lower computational demands, this reduction often comes at the expense of overall performance. In contrast, our CFF-Net strikes a commendable balance between detection accuracy and computational efficiency, outperforming DCSA-Net in terms of accuracy.

Table 5.
Comparison experiments on the Crack500 dataset.
3.6. Other Comparative Experiments
To fully leverage the capabilities of the CDCM within CFF-Net, we conducted a series of experiments to evaluate its placement within the architecture, as detailed in Table 6. Initially, we integrated the CDCM into the encoder, where it was utilized to process the input features directly. In the subsequent experiment, we repositioned the CDCM to the decoder, enabling it to work with the information generated by the encoder. Lastly, we undertook a more radical approach by eliminating the conventional convolutional layers of the original framework entirely, allowing the CDCM to operate on all feature maps across both the encoder and decoder stages. The results from these experiments clearly indicate that deploying the CDCM within the encoder yields the highest segmentation performance.

Table 6.
Experimental results of the CDCM at different locations on the Crack500 dataset.
To assess the performance differences, we conducted a comparative analysis by substituting the CDCM module in the encoder with the SK module, as outlined in Table 7. The table clearly shows that the CDCM module significantly improves the overall performance of the model.

Table 7.
Comparison experiment between the CDCM and SK on the Crack500 dataset.
3.7. Limitation Analysis of CFF-Net
For a comprehensive evaluation of CFF-Net, we conducted a detailed error case study to determine its limitations when dealing with challenging scenarios. Figure 15 highlights the limitations of CFF-Net on the Crack500 dataset, particularly when dealing with fine, discontinuous cracks embedded within highly textured backgrounds. For instance, in cases where hairline cracks blend with the intricate patterns of concrete textures, the model sometimes misclassifies these cracks as part of the background.

Figure 15.
Examples of poor segmentation on the Crack500 dataset.
Similarly, the Bearing dataset also faces challenges in defect identification. As shown in Figure 16, scratches on the bearing surface are faint and accompanied by glare from uneven lighting. Under such conditions, our method may have difficulty accurately distinguishing between true defects and light reflections, which can lead to the missed detection of scratches or misclassification of reflections as defects.

Figure 16.
Examples of poor segmentation on the Bearing dataset.
In Figure 17, within the SD-saliency-900 dataset, images containing faint scratches or diffuse patches pose challenges, occasionally leading to classification errors or incomplete segmentation. Although our approach integrates multi-scale context information, it sometimes struggles to differentiate subtle defect features from background noise. Furthermore, in scenarios with high background clutter or overlapping defect types, the cross-layer feature fusion strategy can occasionally fail to effectively resolve conflicting information across layers, resulting in boundary inaccuracies.

Figure 17.
Examples of poor segmentation on the SD-saliency-900 dataset.
4. Conclusions
In this paper, we develop a cross-hierarchy feature fusion network based on a composite dual-channel encoder for surface defect segmentation. In the encoder, we moved away from convolution methods and adopted an innovative CDCM structure. This advanced design cleverly integrates expansion convolutional branches with standard convolutional branches, allowing for a deep synergy and efficient utilization of channel information across varying receptive field scales. A key highlight of CFF-Net is the introduction of the DRPM at the junction of the encoder and decoder. Through the fine processing of multiple parallel branches, it not only maintains the integrity of the spatial resolution but also realizes the comprehensive extraction and deep fusion of multi-scale features. In addition, the output section of CFF-Net also innovatively introduces the CFFS. This mechanism adeptly fuses outputs from different layers or stages within the network, enabling the model to effectively capture subtle edge information present in the images. To validate the superior performance of CFF-Net, we specifically selected two surface defect datasets for a comprehensive evaluation. The experimental results demonstrate that CFF-Net achieves remarkable improvements across several evaluation metrics.
Author Contributions
Conceptualization, K.Q. and X.D.; methodology, Y.J.; validation, L.D. and X.J.; writing—original draft preparation, K.Q. and X.D.; writing—review and editing, X.J.; visualization, Y.J.; supervision, L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China, grant number 62102227, Joint Fund of Zhejiang Provincial Natural Science Foundation of China, grant number LTGC23E050001, LTGS23E030001, LZY24E050001, ZCLTGS24E0601, Science and Technology Major Projects of Quzhou, grant number 2023K221.
Data Availability Statement
The Crack500 and SD-saliency-900 are two public datasets, and their links are mentioned in the paper. The Bearing dataset generated and/or analyzed during the current study are not publicly available but may be obtained from the original author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Białek, C.; Matiolański, A.; Grega, M. An efficient approach to face emotion recognition with convolutional neural networks. Electronics 2023, 12, 2707. [Google Scholar] [CrossRef]
- El Alami, A.; Mesbah, A.; Berrahou, N.; Lakhili, Z.; Berrahou, A.; Qjidaa, H. Quaternion discrete orthogonal Hahn moments convolutional neural network for color image classification and face recognition. Multimed. Tools Appl. 2023, 82, 32827–32853. [Google Scholar] [CrossRef]
- García-Aguilar, I.; García-González, J.; Luque-Baena, R.M.; López-Rubio, E. Automated labeling of training data for improved object detection in traffic videos by fine-tuned deep convolutional neural networks. Pattern Recogn. Lett. 2023, 167, 45–52. [Google Scholar] [CrossRef]
- Chen, N.; Feng, Z.; Li, F.; Wang, H.; Yu, R.; Jiang, J.; Tang, L.; Rong, P.; Wang, W. A fully automatic target detection and quantification strategy based on object detection convolutional neural network YOLOv3 for one-step X-ray image grading. Anal. Methods 2023, 15, 164–170. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Ru, J.; Ji, P.; Wu, C. LACTNet: A lightweight real-time semantic segmentation network based on an aggregated convolutional neural network and Transformer. Electronics 2024, 13, 2406. [Google Scholar] [CrossRef]
- Hu, K.; Xie, Z.; Hu, Q. Lightweight convolutional neural networks with context broadcast transformer for real-time semantic segmentation. Image Vision Comput. 2024, 146, 105053. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. 2015, 39, 640–651. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Shi, C.; Wang, K.; Zhang, G.; Li, Z.; Zhu, C. Efficient and accurate semi-supervised semantic segmentation for industrial surface defects. Sci. Rep. 2024, 14, 21874. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Guo, B.; Deng, X.; Guo, W.; Min, X. Trans-DCN: A high-efficiency and adaptive deep network for bridge cable surface defect segmentation. Remote Sens. 2024, 16, 2711. [Google Scholar] [CrossRef]
- Xu, X.; Xu, T.; Li, Z.; Huang, X.; Zhu, Y.; Rao, X. SPMUNet: Semantic segmentation of citrus surface defects driven by superpixel feature. Comput. Electron. Agric. 2024, 224, 109182. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Tian, X.; Tan, J. Data-driven semantic segmentation method for detecting metal surface defects. IEEE Sens. J. 2024, 24, 15676–15689. [Google Scholar] [CrossRef]
- Si, C.; Luo, H.; Han, Y.; Ma, Z. Rail-STrans: A rail surface defect segmentation method based on improved Swin Transformer. Appl. Sci. 2024, 14, 3629. [Google Scholar] [CrossRef]
- Zhang, G.; Lu, Y.; Jiang, X.; Yan, F.; Xu, M. Context-aware adaptive weighted attention network for real-time surface defect segmentation. IEEE Trans. Instrum. Meas. 2024, 73, 5030013. [Google Scholar] [CrossRef]
- Lu, P.; Jing, J.; Huang, Y. MRD-net: An effective CNN-based segmentation network for surface defect detection. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Li, W.; Li, B.; Niu, S.; Wang, Z.; Wang, M.; Niu, T. LSA-Net: Location and shape attention network for automatic surface defect segmentation. J. Manuf. Process. 2023, 99, 65–77. [Google Scholar] [CrossRef]
- Xiao, M.; Yang, B.; Wang, S.; Mo, F.; He, Y.; Gao, Y. GRA-Net: Global receptive attention network for surface defect detection. Knowl. -Based Syst. 2023, 280, 111066. [Google Scholar] [CrossRef]
- Song, Y.; Xia, W.; Li, Y.; Li, H.; Yuan, M.; Zhang, Q. AnomalySeg: Deep learning-based fast anomaly segmentation approach for surface defect detection. Electronics 2024, 13, 284. [Google Scholar] [CrossRef]
- Luo, F.; Cui, Y.; Liao, Y. MVRA-UNet: Multi-view residual attention U-Net for precise defect segmentation on magnetic tile surface. IEEE Access 2023, 11, 135212–135221. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature pyramid and hierarchical boosting network for pavement crack detection. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1525–1535. [Google Scholar] [CrossRef]
- Crack500 Dataset. Available online: https://github.com/guoguolord/CrackDataset (accessed on 20 November 2024).
- Bearing Dateset. Available online: https://m.tb.cn/h.TXXh4Hf?tk=ls6p3Gamn1C (accessed on 20 November 2024).
- Song, G.; Song, K.; Yan, Y. Saliency detection for strip steel surface defects using multiple constraints and improved texture features. Opt. Lasers Eng. 2020, 128, 106000. [Google Scholar] [CrossRef]
- SD-saliency-900 Dataset. Available online: https://gitee.com/dengzhiguang/EDRNet (accessed on 20 November 2024).
- Byra, M.; Jarosik, P.; Szubert, A.; Galperin, M.; Ojeda-Fournier, H.; Olson, L.; O’Boyle, M.; Comstock, C.; Andre, M. Breast mass segmentation in ultrasound with selective kernel U-Net convolutional neural network. Biomed. Signal Process. Control 2020, 61, 102027. [Google Scholar] [CrossRef] [PubMed]
- Luo, H.; Zhou, D.M.; Cheng, Y.J.; Wang, S.Q. MPEDA-Net: A lightweight brain tumor segmentation network using multi-perspective extraction and dense attention. Biomed. Signal Process. Control 2024, 91, 106054. [Google Scholar] [CrossRef]
- Yuan, H.J.; Chen, L.N.; He, X.F. MMUNet: Morphological feature enhancement network for colon cancer segmentation in pathological images. Biomed. Signal Process. Control 2024, 91, 105927. [Google Scholar] [CrossRef]
- Zhang, Q.; Jiang, X.; Huang, X.; Zhou, C. MSR-Net: Multi-scale residual network based on attention mechanism for pituitary adenoma MRI image segmentation. IEEE Access 2024, 12, 119371–119382. [Google Scholar] [CrossRef]
- Nag, S.; Makwana, D.; Mittal, S.; Mohan, C.K. WaferSegClassNet-A light-weight network for classification and segmentation of semiconductor wafer defects. Comput. Ind. 2022, 142, 103720. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Liu, J.Y.; Wang, K.; Zhang, K.; Zhang, G.S.; Liao, X.F.; Yang, G. Global transformer and dual local attention network via deep-shallow hierarchical feature fusion for retinal vessel segmentation. IEEE Trans. Cybern. 2023, 53, 5826–5839. [Google Scholar] [CrossRef] [PubMed]
- Selvaraj, A.; Nithiyaraj, E. CEDRNN: A convolutional encoder-decoder residual neural network for liver tumour segmentation. Neural Process. Lett. 2023, 55, 1605–1624. [Google Scholar] [CrossRef]
- Nham, D.N.; Trinh, M.N.; Nguyen, V.D.; Pham, V.; Tran, T.T. An effcientNet-encoder U-Net joint residual refinement module with Tversky-Kahneman Baroni-Urbani-Buser loss for biomedical image segmentation. Biomed. Signal Process. Control 2023, 83, 104631. [Google Scholar] [CrossRef]
- Yang, C.; Li, B.; Xiao, Q.; Bai, Y.; Li, Y.; Li, Z.; Li, H.; Li, H. LA-Net: Layer attention network for 3D-to-2D retinal vessel segmentation in OCTA images. Phys. Med. Biol. 2024, 69, 045019. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Xie, F.; Qing, W.; Wang, M.; Liu, M.; Sun, D. MGF-net: Multi-channel group fusion enhancing boundary attention for polyp segmentation. Med. Phys. 2024, 51, 407–418. [Google Scholar] [CrossRef] [PubMed]
- Ji, M.M.; Wu, Z.B. Automatic detection and severity analysis of grape black measles disease based on deep learning and fuzzy logic. Comput. Electron. Agric. 2022, 193, 106718. [Google Scholar] [CrossRef]
- Hu, M.; Li, J.; Zhao, Y.; Lu, M.; Li, W. FSAU-Net: A network for extracting buildings from remote sensing imagery using feature self-attention. Int. J. Remote Sens. 2023, 44, 1643–1664. [Google Scholar] [CrossRef]
- Arbane, M.; Khanouche, M.E.; Khodabandelou, G.; Abdelghani, C.; Amirat, Y. DRSU-Net: Depth-residual separable U-Net model for semantic segmentation. In Proceedings of the 2023 International Joint Conference on Neural Networks, Gold Coast, Australia, 18–23 June 2023; pp. 1–6. [Google Scholar]
- Liu, X.; Liu, Y.; Fu, W.; Liu, S. SCTV-UNet: A COVID-19 CT segmentation network based on attention mechanism. Soft Comput. 2023. [Google Scholar] [CrossRef]
- Xu, Q.; Ma, Z.; Na, H.E.; Duan, W. DCSAU-Net: A deeper and more compact split-attention U-Net for medical image segmentation. Comput. Biol. Med. 2023, 154, 106626. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, M.V.S.; Matos, C.E.; Braz Júnior, G.; Cardoso de Paiva, A.; de Almeida, J.D.S.; Costa, G.J.; Bessa, M.L.L.; Freitas Filho, M.P. A PPM-based UNet for Tumour and Kidney segmentation in CT scans. Comput. Method. Biomech. 2023, 11, 1897–1905. [Google Scholar]
- Wang, L.; Shen, M.; Shi, C.; Zhou, Y.; Chen, Y.; Pu, J.; Chen, H. EE-Net: An edge-enhanced deep learning network for jointly identifying corneal micro-layers from optical coherence tomography. Biomed. Signal Process. Control 2022, 71, 103213. [Google Scholar] [CrossRef]
- Wang, L.; Gu, J.; Chen, Y.; Liang, Y.; Zhang, W.; Pu, J.; Chen, H. Automated segmentation of the optic disc from fundus images using an asymmetric deep learning network. Pattern Recogn. 2021, 112, 107810. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Li, T.; Zhang, Q.; Mao, W.; Guan, N.; Tian, M.; Zhuo, C. ANT-UNet: Accurate and noise-tolerant segmentation for pathology image processing. ACM J. Emerg. Tech. Com. 2021, 18, 27. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).