The Study of an Improved Particle Swarm Optimization Algorithm Applied to Economic Dispatch in Microgrids
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
- Regarding model development: Early studies primarily focused on the stability and economic efficiency of grid operations. Reference [5] explored how to improve the economic efficiency of microgrid operations by leveraging the dispatch characteristics of microgrids while also maintaining grid stability. Reference [6] investigated the coordinated dispatch strategy of large grids and natural gas systems to reduce overall operating costs, with the goal of minimizing fuel costs. Reference [7] proposed an analysis model for microgrid operations with the dual objectives of maximizing economic benefits and minimizing emissions. Reference [8] constructed a model from the perspective of coordinated operation across multiple microgrid systems, aiming to minimize economic costs while ensuring system stability. Additionally, since thermal generators are typically present in microgrids, reducing the use of fossil fuels and lowering pollutant emissions have become closely related optimization objectives. To address multi-objective optimization dispatch issues, researchers often introduce penalty functions to transform multi-objective problems into single-objective ones [9,10,11].
- In terms of algorithm optimization: Research has mainly focused on improving global convergence speed and solution accuracy. Particle Swarm Optimization (PSO) is widely applied to solve power system issues due to its simplicity, easy parameter tuning, and robust global search ability. However, PSO has some limitations, such as susceptibility to local optima and a relatively slow convergence speed [12,13,14]. To address these shortcomings, some scholars have proposed new search strategies to improve the algorithm’s global search performance. Additionally, some researchers have combined PSO with other algorithms, as mentioned in references [15,16,17,18], which has also contributed to improving the global search capability of traditional PSO algorithms.
- (1)
- Constructing a dispatch model that includes distributed photovoltaic generation (PV), wind turbines (WT), thermal power generators (DG), and energy storage systems (ESS);
- (2)
- Introducing second-order oscillatory particles and improving the iteration formula of swarm particles to optimize the traditional PSO algorithm;
- (3)
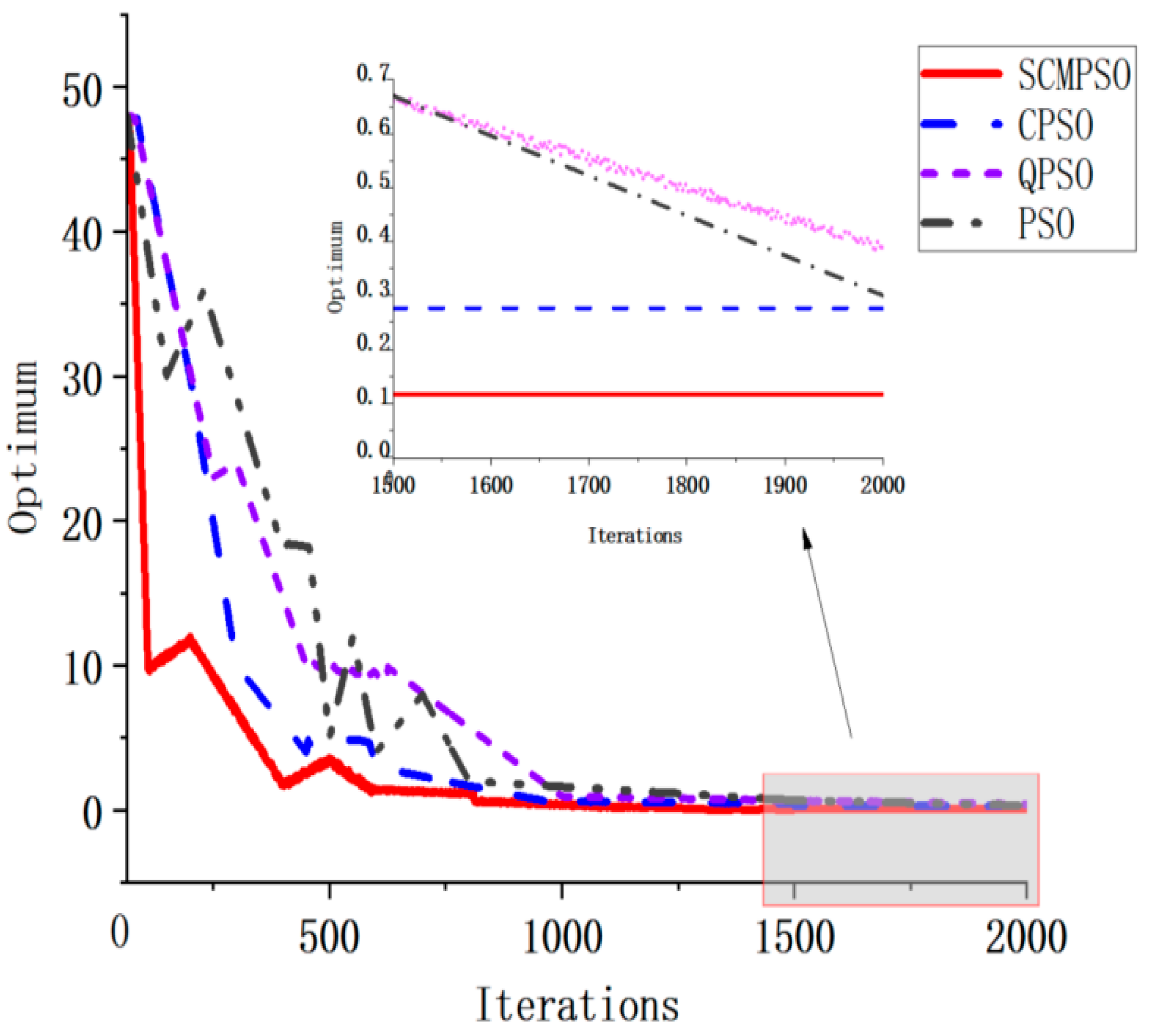
- Conducting a comparative analysis of SCMPSO with traditional PSO, Cooperative Particle Swarm Optimization(CPSO), and Quantum-behaved Particle Swarm Optimization (QPSO) to verify the superiority of SCMPSO in optimization performance.
2. Microgrid Model Construction
2.1. Photovoltaic Model Construction
- PPV: Actual output power of the photovoltaic module;
- Po: Maximum output power under Standard Test Conditions;
- GINC: Actual irradiance (in kW/m2);
- GSTC: Irradiance under reference test conditions, set as 1 kW/m2;
- k: Temperature coefficient of power;
- Tc: Actual operating temperature of the photovoltaic cells;
- To: Set operating temperature, typically 25 °C.
2.2. Establishment of Wind-Power Model
- PWT: Wind turbine output power as a function of wind speed;
- Prated: Rated output of the wind turbine;
- V: Actual wind speed;
- Vi: The minimum wind speed at which the turbine starts generating power;
- Vr: Rated wind speed, which is the wind speed at which the turbine reaches its rated output power;
- Vc: To ensure equipment safety, the maximum wind speed at which the turbine ceases power generation.
2.3. Establishment of Small Thermal Generator Model
- VF(t): Fuel consumption of the thermal generator at time t, measured in liters (L);
- : Actual output power of the thermal generator at time t, expressed in kilowatts (kW);
- PDG(t): Rated output power of the thermal generator at time t, given in kilowatts (kW);
- a1 and a2: Coefficients of the fuel consumption curve, expressed in liters per kilowatt-hour (L/kWh).
2.4. Establishment of Energy Storage Device Model
- : Remaining energy of the storage system at the end of period t;
- : Remaining energy of the storage system at the end of period t−1;
- and : Charging and discharging power of the storage system at period t, measured in kilowatts (kW);
- : Self-discharge rate of the energy storage device;
- and : Charging and discharging efficiency of the storage system, measured as a percentage (%);
- : Rated capacity of the storage system, measured in kilowatt-hours (kWh).
3. Scheduling Model
3.1. Objective Function
- CiOM(t): Operating and maintenance cost of each device at time t;
- CiDG(t): Fuel consumption cost of the thermal generator at time t;
- Cigrid(t): Interaction cost between the microgrid and the main grid at time t;
- KiPV(t), KiWT(t), KiDG(t), and KiESS(t): Operating and maintenance cost coefficients of the photovoltaic system, wind turbine, thermal generator, and energy storage device at time t, respectively;
- PiPV(t), PiWT(t), PiDG(t), and PiESS(t): Power outputs of the photovoltaic system, wind turbine, thermal generator, and energy storage device at time t, respectively;
- CiDG(t): Fuel cost of the thermal generator, where Cr is the fuel price (in CNY/L) and ηiDG is the efficiency of the thermal generator;
- CiDS(t): Depreciation cost of each device, where DSi is the annual depreciation cost of unit i, and Pi*(t) is the output power of unit i at time t. Pi,max is the maximum output power of unit i, a is a constant, and fi is the capacity factor;
- Cigrid(t): Interaction cost between the microgrid and the main grid, where Pci(t) is the amount of electricity purchased from or sold to the main grid at time t, and Cg(t) represents the electricity cost at time t between the main grid and the microgrid.
3.2. Establishment of Constraint Conditions
3.2.1. Power Balance Constraint
3.2.2. Microgrid and Main Grid Interaction Power Constraint
3.2.3. Distributed Power Output Constraint
3.2.4. Pollutant Emission Constraint
3.2.5. Ramp Rate Constraint
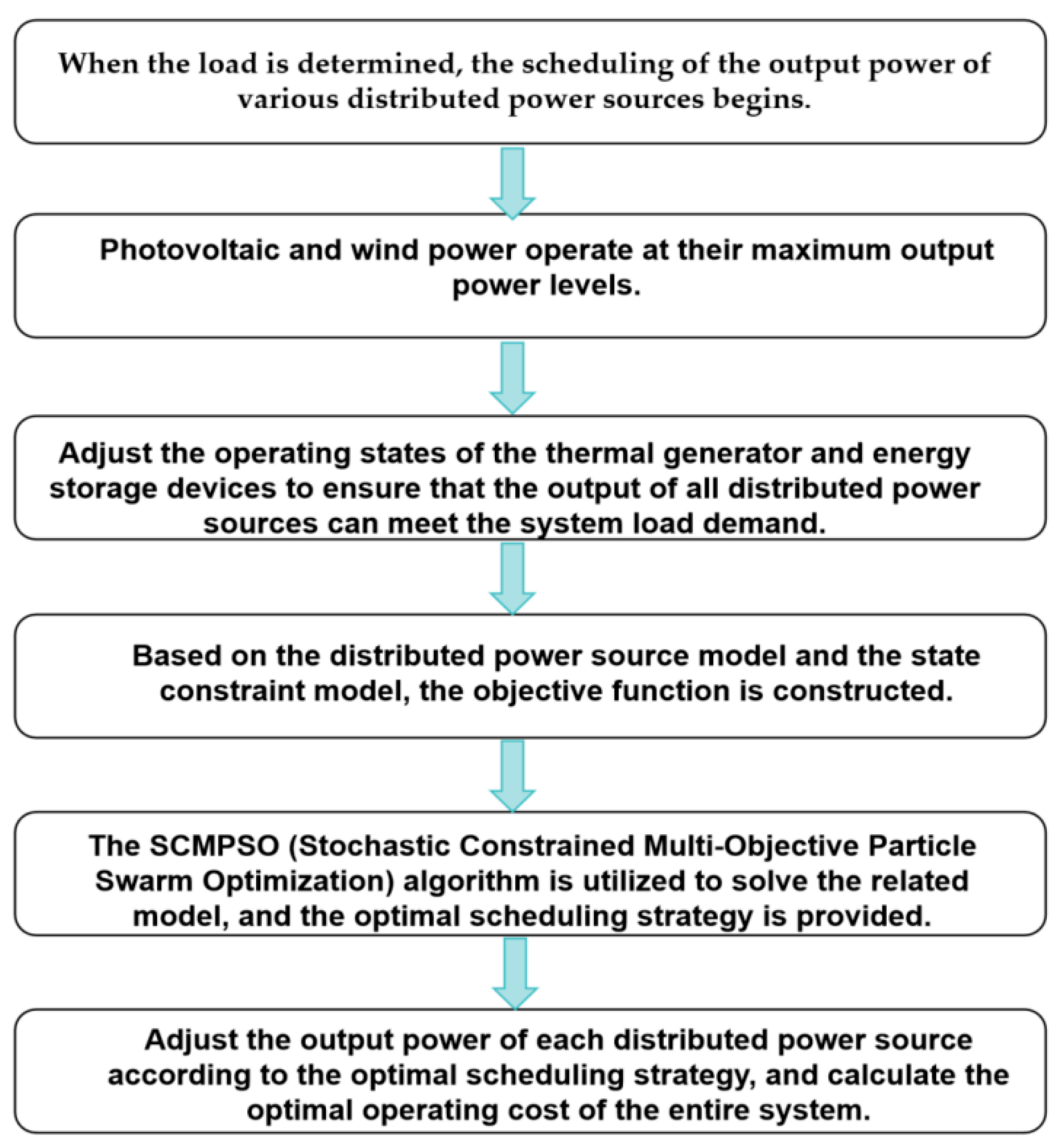
3.3. Scheduling Strategy
- PV and WT: PV generation relies on solar energy, while wind-power generation depends on wind energy. Both are clean energy sources. Although they exhibit significant fluctuations, fully utilizing these resources helps reduce generation costs and avoids environmental pollution.
- Thermal Power Generation: Currently, thermal power remains an indispensable part of China’s power system. Its advantage lies in providing stable electricity that is capable of meeting large load demands. However, the downside of thermal power generation is the significant consumption of fossil fuels and its associated environmental pollution.
- Energy Storage Devices: Energy storage systems have the advantage of fast response times. In microgrid systems, they effectively buffer the impact of PV and wind-power integration on the main grid, ensuring stable system operation.
4. Improved Second-Order Oscillation Particle Swarm Optimization Algorithm
4.1. Traditional Particle Swarm Optimization
4.2. Chaotic Mapping Second-Order Oscillation Particle Swarm Optimization
4.2.1. Chaotic Mapping Population
- Define the chaotic Henon mapping function to produce a D-dimensional vector, where each value within the vector is confined to the range of rand(0.1).
- Map the population positions using the chaotic Henon function.
4.2.2. Adaptive Weight Iteration Improvement
4.2.3. Dynamic Learning Factor Improvement
4.2.4. Improvement in Algorithm Iteration
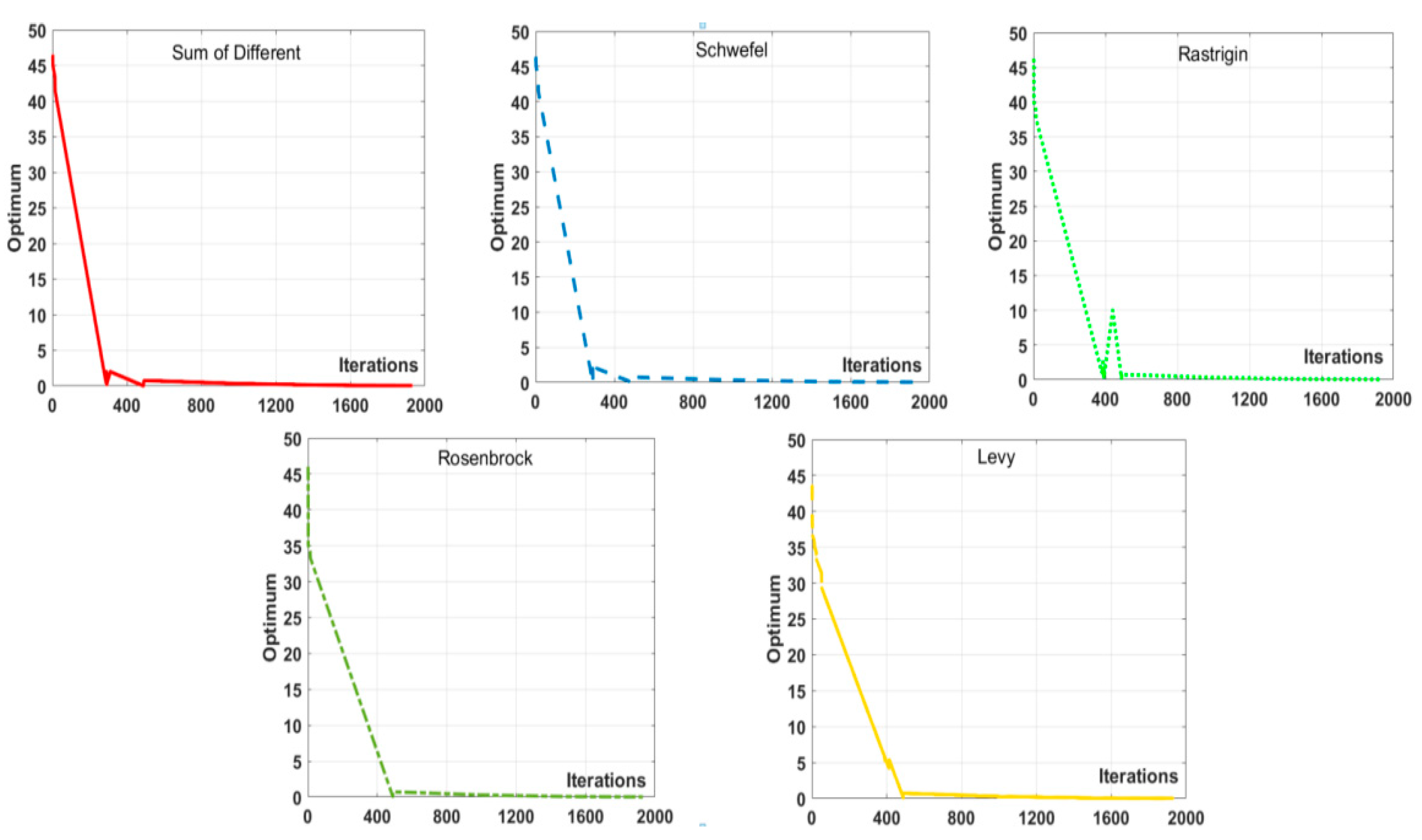
4.2.5. Testing of the Improved Particle Swarm Algorithm
- Sum of Different Powers: This function serves as a tool to evaluate the convergence rate of the enhanced algorithm;
- Schwefel: Used to test the precision of the search conducted by the improved algorithm;
- Rastrigin: Used to test the algorithm’s ability to avoid getting stuck in local minima;
- Rosenbrock: Used to evaluate the performance of the improved algorithm in a multi-dimensional space;
- Levy: Used to test the robustness of the algorithm. The relevant parameters for the benchmark functions are shown in Table 3.
4.3. Model Solution
5. Case Study
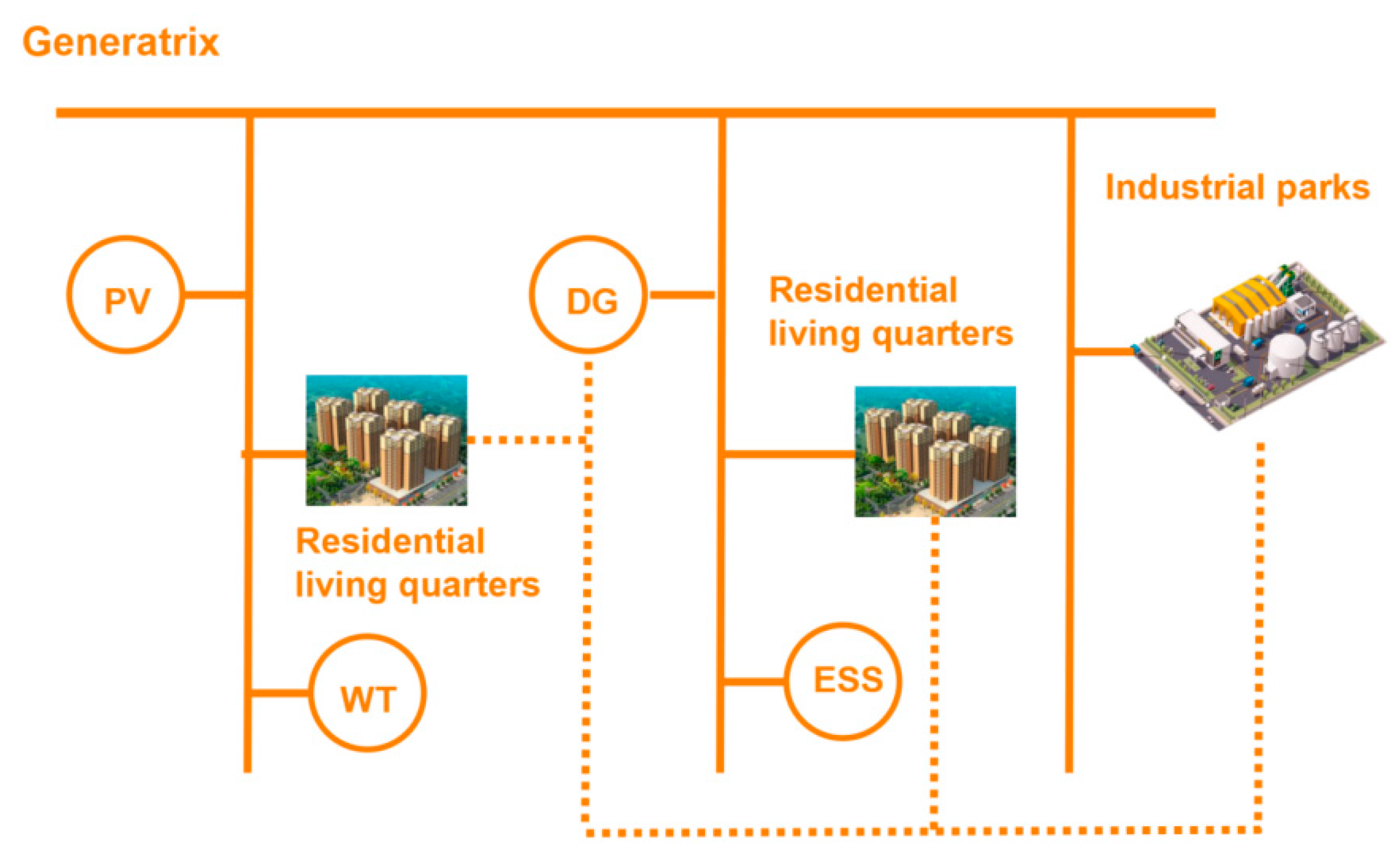
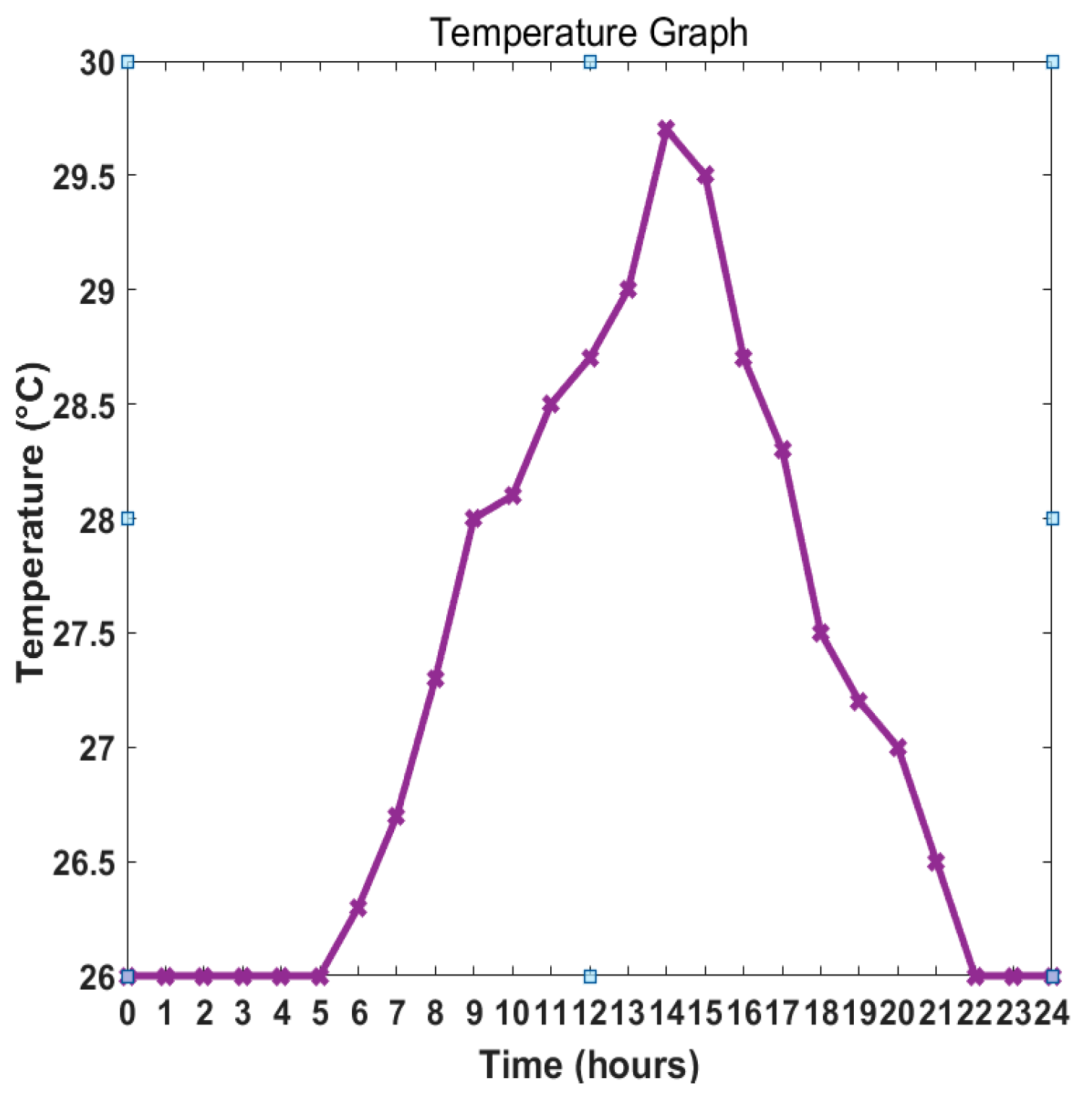
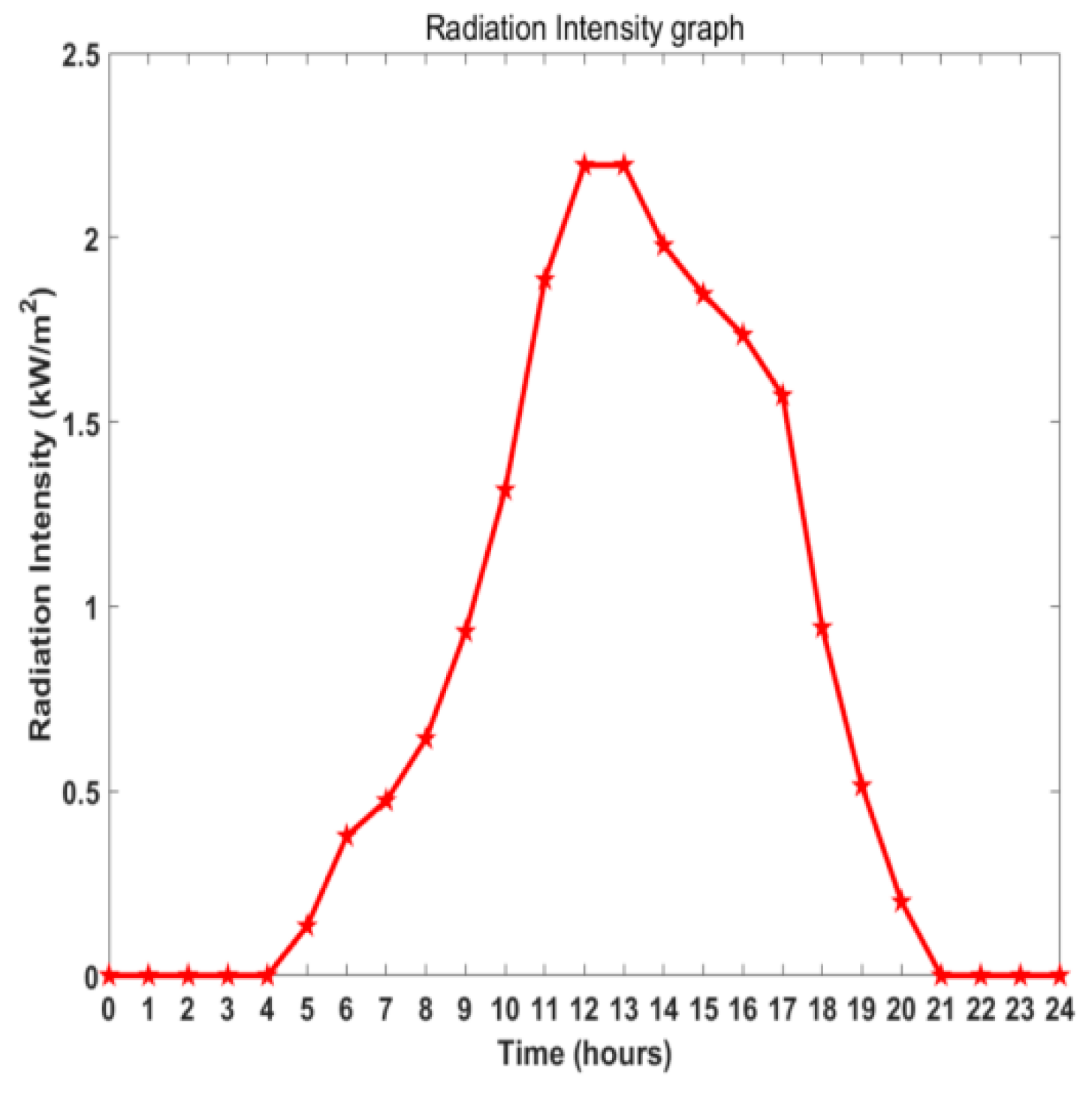
5.1. Case Introduction
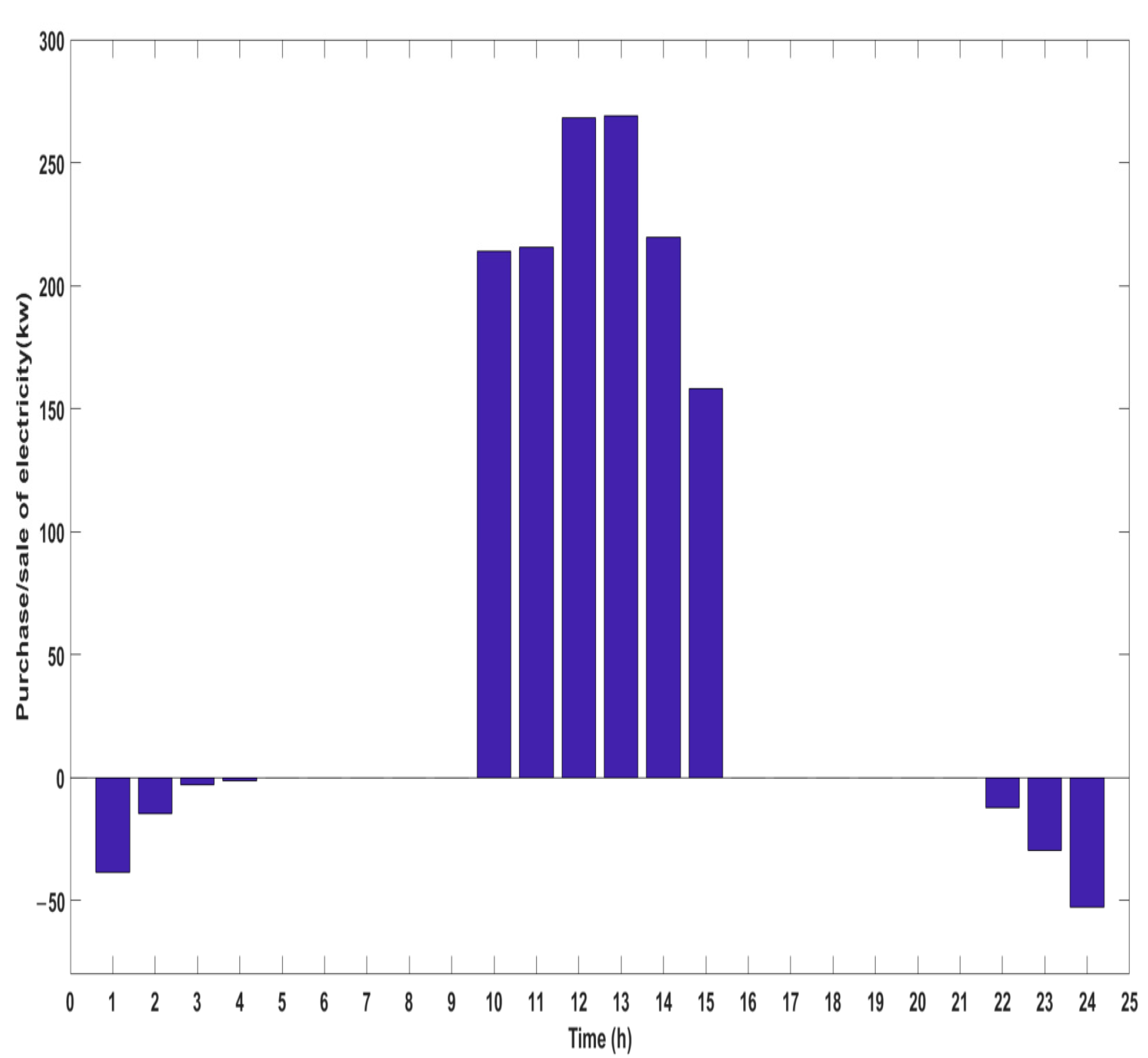
5.2. Simulation Analysis
- Electricity Purchase Period (00:00–04:00, 22:00–24:00)
- 2.
- No Interaction Period between Microgrid and Main Grid (05:00–09:00, 16:00–21:00)
- 3.
- Electricity Sale Period (10:00–15:00)
6. Conclusions
- Typical Summer Dispatch Plan: In a subtropical monsoon climate, such as in a certain region of Jiangsu, China, summer is characterized by heat and abundant sunlight. Based on the scheduling strategy and comprehensive cost considerations, the specific dispatch plan is as follows: distributed photovoltaic (PV) and wind-power generation should be fully utilized as much as possible. On this basis, to ensure a stable system operation, small thermal generators must bear the main power output. Additionally, energy storage devices play a key role in peak shaving and valley filling, as well as improving power quality. This dispatch plan not only guarantees system stability but also increases the utilization of clean energy, reduces environmental pollution, and enhances overall economic efficiency.
- SCMPSO: Compared to the traditional PSO algorithm, the SCMPSO algorithm accelerates the search speed and broadens the search range in the early stages of optimization, while effectively avoiding local optima in the later stages. The reliability and superiority of the SCMPSO algorithm were confirmed through validation with multiple benchmark functions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, Y.; Du, H.; Zou, H.; Zhou, P.; Antunes, C.H.; Neumann, A.; Yeh, S. Fifty years of Energy Policy: A bibliometric overview. Energy Policy 2023, 183, 113769. [Google Scholar] [CrossRef]
- Feng, C.; Liao, X. An overview of “Energy þ Internet” in China. J. Clean. Prod. 2020, 258, 120630. [Google Scholar] [CrossRef]
- Duan, Y.; Zhao, Y.; Hua, J. An initialization-free distributed algorithm for dynamic economic dispatch problemsinmicrogrid: Modeling, optimization and analysis. Sustain. Energy Grids Netw. 2023, 34, 101004. [Google Scholar] [CrossRef]
- Abdelghany, M.B.; Al-Durra, A.; Gao, F. A Coordinated Optimal Operation of a Grid-Connected Wind-Solar Microgrid Incorporating Hybrid Energy Storage Management Systems. IEEE Trans. Sustain. Energy 2024, 15, 39–51. [Google Scholar] [CrossRef]
- Gholami, A.; Shekari, T.; Aminifar, F.; Shahidehpour, M. Microgrid scheduling with uncertainty: The quest for resilience. IEEE Trans. Smart Grid 2016, 7, 2849–2858. [Google Scholar] [CrossRef]
- Correa-Posada, C.M.; Sánchez-Martın, P. Security-constrained optimal power and natural-gas flow. IEEE Trans. Power Syst. 2014, 29, 18–24. [Google Scholar] [CrossRef]
- Sadeghian, H.; Ardehali, M. A novel approach for optimal economic dispatch scheduling of integrated combined heat and power systems for maximum economic profit and minimum environmental emissions based on Benders decomposition. Energy 2016, 102, 10–23. [Google Scholar] [CrossRef]
- Shen, X.; Cao, M.; Zhou, N.; Zhang, L. Research on coordinated optimal scheduling and economic operation of multi-microgrid distribution system. J. Electron. Meas. Instrum. 2016, 30, 568–576. [Google Scholar]
- Yin, L.; Cai, Z. Multimodal multi-objective hierarchical distributed consensus method for multimodal multi-objective economic dispatch of hierarchical distributed power systems. Energy 2024, 295, 130996. [Google Scholar] [CrossRef]
- Rezaei, N.; Ahmadi, A.; Khazali, A.; Aghaei, J. Multi-objective risk-constrained optimal bidding strategy of smart microgrids: An IGDT-based normal boundary intersection approach. IEEE Trans. Ind. Inf. 2018, 15, 1532–1543. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, L.; Wangb, B.; Li, J. Optimizing power systems and microgrids: A novel multi-objective model for energy hubs with innovative algorithmic optimization. Int. J. Hydrogen Energy 2024, 69, 927–943. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, F.; Xu, T.; Zhu, N.; Jonrinaldi. Hierarchical parallel search with automatic parameter configuration for particle swarm optimization. Appl. Soft Comput. J. 2024, 151, 111126. [Google Scholar] [CrossRef]
- Wang, C. The Optimal Operation of Microgrid Based on Improved Particle Swarm Optimization for Combined Cooling, Heating and Power. Master’s Thesis, China University of Mining and Technology, Beijing, China, 2022. [Google Scholar]
- Xiong, G.J.; Shuai, M.H.; Hu, X. Combined heat and power economic emission dispatch using improved bare bone multi-objective particle swarm optimization. Energy 2022, 244, 123108. [Google Scholar] [CrossRef]
- Jakubik, J.; Binding, A.; Feuerriegel, S. Directed particle swarm optimization with Gaussian-process-based function forecasting. Eur. J. Oper. Res. 2021, 295, 157–169. [Google Scholar] [CrossRef]
- Zhao, X.G.; Zhang, Z.Q.; Xie, Y.M.; Meng, J. Economic-environmental dispatch of microgrid based on improved quantum particle swarm optimization. Energy 2020, 195, 117014. [Google Scholar]
- Kacimi, M.A.; Guenounou, O.; Brikh, L.; Yahiaoui, F.; Hadid, N. New mixed-coding PSO algorithm for a self-adaptive and automatic cleaning of Mamdani fuzzy rules. Eng. Appl. Artif. Intell. 2020, 89, 103417. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Zhang, G. CPSO-CNN: An efficient PSO-based algorithm for fine-tuning hyper-parameters of convolutional neural networks. Swarm Evol. Comput. 2019, 49, 114–123. [Google Scholar] [CrossRef]
- Roudbari, F.N.; Ehsani, H.; Amiri, S.R.; Samadani, A.; Shabani, S.; Khodadad, A. Advances in photovoltaic thermal systems: A comprehensive review of CPVT andPVT technologies. Sol. Energy Mater. Sol. Cells 2024, 276, 113070. [Google Scholar] [CrossRef]
- Teferra, D.M.; Ngoo, L.M.; Nyakoe, G.N. Fuzzy-based prediction of solar PV and wind power generation for microgrid modeling using particle swarm optimization. Heliyon 2023, 9, e12802. [Google Scholar] [CrossRef]
- Ding, M.; Wang, B.; Zhao, B.; Chen, Z.N. Configuration optimization of capacity of standalone PV-wind-diesel battery hybrid microgrid. Power Syst. Technol. 2013, 37, 575–581. [Google Scholar]
- Zhang, J.; Su, L.; Chen, Y.; Su, J.; Wnag, L. Energy management of microgrid and its control strategy. Power Syst. Technol. 2011, 35, 24–28. [Google Scholar]
- Liu, J.; Xu, F.; Lin, S.; Cai, H.; Yan, S. A multi-agent-based optimization model for microgrid operation using dynamic guiding chaotic search particle swarm optimization. Energies 2018, 11, 3286. [Google Scholar] [CrossRef]
- Chu, S.-C.; Panb, X.Y.J.-S.; Lin, B.-S.; Lee, Z.-J. Amulti-strategy surrogate-assisted social learning particle swarm optimization for expensive optimization andapplications. Appl. Soft Comput. J. 2024, 162, 11187. [Google Scholar] [CrossRef]
- Priya, G.V.; Ganguly, S. Multi-swarm surrogate model assisted PSO algorithm to minimize distribution network energy losses. Appl. Soft Comput. J. 2024, 159, 111616. [Google Scholar] [CrossRef]
- Tantu, A.T.; Biramo, D.B. Power flow control and reliability improvement through adaptive PSO based network reconfiguration. Heliyon 2024, 10, e36668. [Google Scholar] [CrossRef]






| Category | PV | WT | DG | ESS |
|---|---|---|---|---|
| Lifespan (years) | 25 | 20 | 10 | 10 |
| Installation Cost (RMB/kW) | 5000 | 8000 | 1500 | / |
| Maintenance Cost (RMB/kW) | 50 | 150 | 100 | 50 |
| Depreciation Cost (RMB/year) | 36,000 | 225,000 | 45,000 | / |
| Maximum Output Power (kW) | 10 | 10 | 1000 | 10 |
| Pollutant Type | Treatment Cost (RMB/kg) | DG Emission Factor (g/kWh) | Main Grid Emission Factor (g/kWh) |
|---|---|---|---|
| CO2 | 0.2 | 650 | 870 |
| SO2 | 14.5 | 0.02 | 1.8 |
| NOX | 63.5 | 6.3 | 1.6 |
| Function Name | Dimension | Search Domain | Acceptance | Optimum |
|---|---|---|---|---|
| Sum of Different Powers | 50 | [−10,10]D [−100,100]n[−100,100]n [−100,100]n[−100,100]n | 0.01 | 0 |
| Schwefel | 50 | [−100,100]D | 0.01 | 0 |
| Rastrigin | 50 | [−5,5]D | 0.01 | 0 |
| Rosenbrock | 50 | [−50,5]D | 0.01 | 0 |
| Levy | 50 | [−10,10]D | 0.01 | 0 |
| Time Period | Peak Period 11:00–14:00, 19:00–21:00 | Standard Period 8:00–10:00, 15:00–18:00, 22:00–23:00 | Off-Peak Period 0:00–7:00 |
|---|---|---|---|
| Electricity Purchase Price (RMB/kWh) | 0.83 | 0.49 | 0.17 |
| Electricity Sale Price (RMB/kWh) | 0.65 | 0.38 | 0.13 |
| Time Period | System Load Power/kW | PV/kW | WT/kW | DG/kW | ESS/kW | Interactive Power/kW |
|---|---|---|---|---|---|---|
| 00:00–01:00 | 510.34 | 0 | 1.32 | 425.98 | 45.81 | 38.55 |
| 01:00–02:00 | 480.52 | 0 | 0 | 420.98 | 444.98 | 14.56 |
| 02:00–03:00 | 440.91 | 0 | 0 | 400 | 38.18 | 2.73 |
| 03:00–04:00 | 430.16 | 0 | 0 | 400 | 29.95 | 1.21 |
| 04:00–05:00 | 380.59 | 0 | 0 | 380.59 | 0 | 0 |
| 05:00–06:00 | 385.37 | 70.12 | 1.27 | 313.98 | 0 | 0 |
| 06:00–07:00 | 400.64 | 71.36 | 1.43 | 327.85 | 0 | 0 |
| 07:00–08:00 | 410.69 | 73.59 | 1.75 | 337.3 | −1.95 | 0 |
| 08:00–09:00 | 450.73 | 78.65 | 2.15 | 410.69 | −40.76 | 0 |
| 09:00–10:00 | 650.12 | 82.13 | 4.27 | 500.32 | −150.73 | −214.13 |
| 10:00–11:00 | 680.49 | 83.32 | 2.21 | 510.3 | −130.98 | −215.64 |
| 11:00–12:00 | 720.95 | 87.95 | 1.95 | 520.67 | −157.73 | −268.11 |
| 12:00–13:00 | 700.76 | 90.12 | 1.93 | 520.4 | −180.85 | −269.16 |
| 13:00–14:00 | 650.48 | 91.32 | 1.89 | 530.64 | −193.13 | −219.76 |
| 14:00–15:00 | 630.39 | 93.28 | 1.83 | 547.6 | −170.46 | −158.14 |
| 15:00–16:00 | 600.75 | 91.7 | 1.77 | 547.6 | −40.68 | 0 |
| 16:00–17:00 | 580.13 | 90.12 | 1.74 | 528.95 | −40.68 | 0 |
| 17:00–18:00 | 570.48 | 85.69 | 1.83 | 526.91 | −43.95 | 0 |
| 18:00–19:00 | 550.72 | 79.48 | 1.77 | 427.52 | 41.95 | 0 |
| 19:00–20:00 | 570.09 | 77.95 | 1.74 | 450.22 | 40.18 | 0 |
| 20:00–21:00 | 600.48 | 0 | 1.27 | 555.26 | 43.95 | 0 |
| 21:00–22:00 | 610.87 | 0 | 0 | 550.79 | 47.68 | 12.4 |
| 22:00–23:00 | 615.48 | 0 | 0 | 540.39 | 445.48 | 29.61 |
| 23:00–24:00 | 580.48 | 0 | 0 | 480.37 | 47.35 | 52.76 |
| Types | Types of Costs | Operation and Maintenance Cost/RMB | Fuel Cost/RMB | Depreciation Cost/RMB | Grid Interaction Cost/RMB | Environmental Cost/RMB |
|---|---|---|---|---|---|---|
| SCMPSO | detailed data | 3542.64 | 2865.43 | 712.86 | −642.80 | 95.17 |
| CPSO | detailed data | 3615.72 | 2931.54 | 722.65 | −554.18 | 100.59 |
| QPSO | detailed data | 3684.42 | 2955.17 | 740.43 | −541.75 | 103.05 |
| PSO | detailed data | 3773.59 | 3170.43 | 757.29 | −500.48 | 108.72 |
| Types | CO2 Emissions (KG) | CO2 Treatment Cost/RMB | SO2 Emissions (KG) | SO2 Treatment Cost/RMB | NOX Emissions (KG) | NOX Treatment Cost/RMB | Environmental Cost/RMB |
|---|---|---|---|---|---|---|---|
| SCMPSO | 224.765 | 44.953 | 0.17 | 2.465 | 0.752 | 47.752 | 95.17 |
| CPSO | 247.675 | 49.535 | 0.184 | 2.668 | 0.762 | 48.387 | 100.59 |
| QPSO | 256.0925 | 51.2185 | 0.185 | 2.6825 | 0.774 | 49.149 | 103.05 |
| PSO | 278.075 | 55.615 | 0.194 | 2.813 | 0.792 | 50.292 | 108.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, A.; Lee, S.-K. The Study of an Improved Particle Swarm Optimization Algorithm Applied to Economic Dispatch in Microgrids. Electronics 2024, 13, 4086. https://doi.org/10.3390/electronics13204086
Dong A, Lee S-K. The Study of an Improved Particle Swarm Optimization Algorithm Applied to Economic Dispatch in Microgrids. Electronics. 2024; 13(20):4086. https://doi.org/10.3390/electronics13204086
Chicago/Turabian StyleDong, Ang, and Seon-Keun Lee. 2024. "The Study of an Improved Particle Swarm Optimization Algorithm Applied to Economic Dispatch in Microgrids" Electronics 13, no. 20: 4086. https://doi.org/10.3390/electronics13204086
APA StyleDong, A., & Lee, S.-K. (2024). The Study of an Improved Particle Swarm Optimization Algorithm Applied to Economic Dispatch in Microgrids. Electronics, 13(20), 4086. https://doi.org/10.3390/electronics13204086







