Optimal Placement of HVDC-VSC in AC System Using Self-Adaptive Bonobo Optimizer to Solve Optimal Power Flows: A Case Study of the Algerian Electrical Network
Abstract
1. Introduction
- The optimization problem incorporates the equations for the VSC stations, DC grids, and AC/DC coupling, which are modeling components.
- Optimization variables—the VSC injections of active (P) and reactive (Q) power are control variables in the optimization problem.
- Implementation of the self-adaptive bonobo optimizer (SABO) was made to find the optimal location of the HVDC line in the system to optimize desired objectives
- The proposed algorithm was tested on the IEEE 30 bus and the large-scale Algerian 114-bus electric network; the simulation results were compared with several results of algorithms mentioned in other recent literature in terms of the quality and robustness of the solution.
2. VSC-HVDC Model
- The converter transformer
- The AC filters
- The phase reactor
- The converter.
3. Formulation Problem
3.1. Objective Functions
3.1.1. Minimization of the Total Generation Costs (TGCs)
3.1.2. Minimization of the Total Active Power Transmission Losses (APTLs)
3.2. The Control and State Variables IN Hybrid AC/DC Network
3.2.1. The Control Variables
3.2.2. The State Variables
3.3. Constraints
3.3.1. The Equality Constraint
3.3.2. The Inequality Constraint
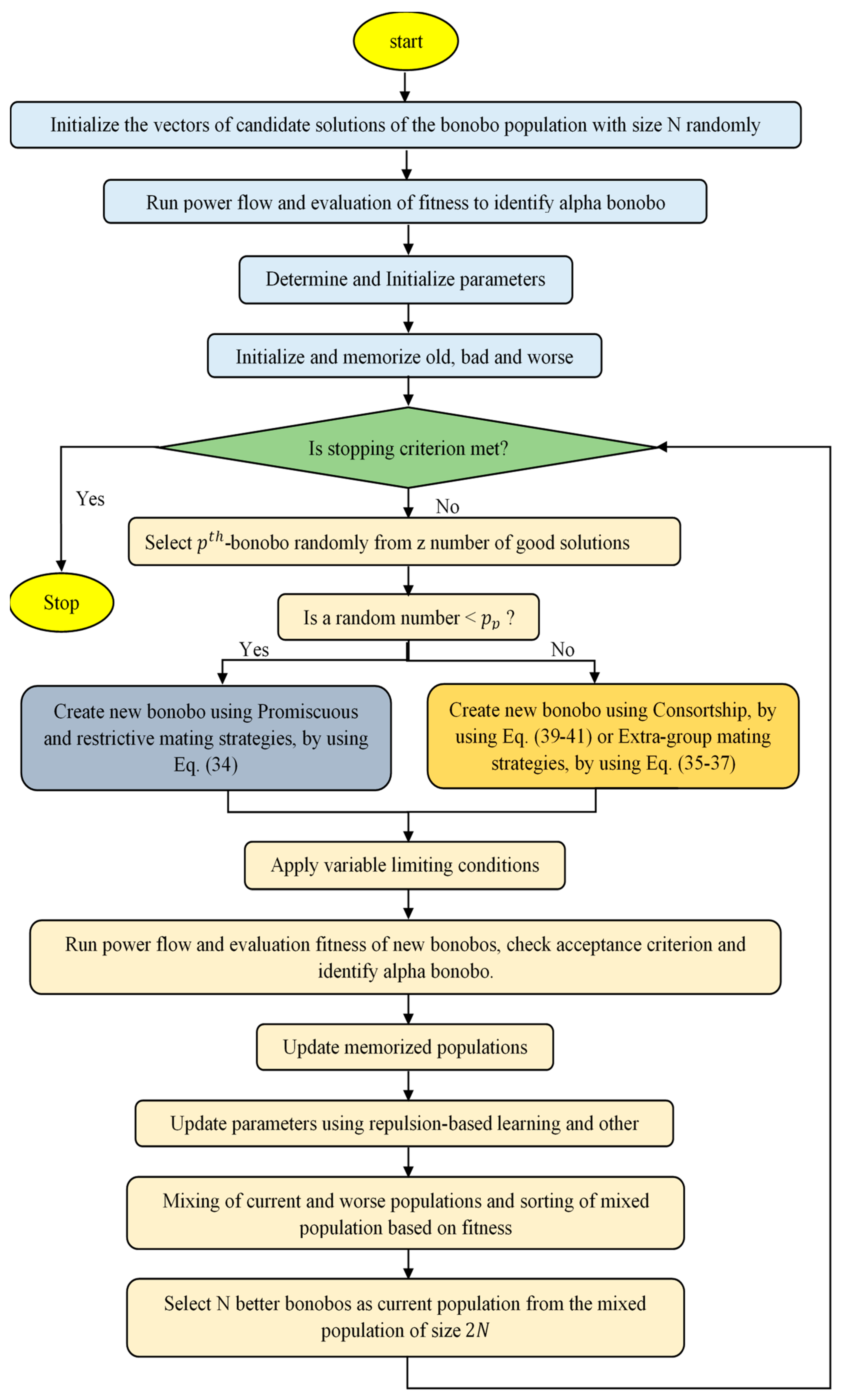
4. Self-Adaptive Bonobo Optimizer (SABO) Algorithm
4.1. The SABO Works
4.2. Using Different Mating Strategies to Create New Bonobos
4.2.1. Mating Strategies: Restrictive and Promiscuous
4.2.2. Extra-Group Mating
4.2.3. Consortship Mating
4.3. Modified Boundary Handling Technique
5. Simulation Results and Discussions
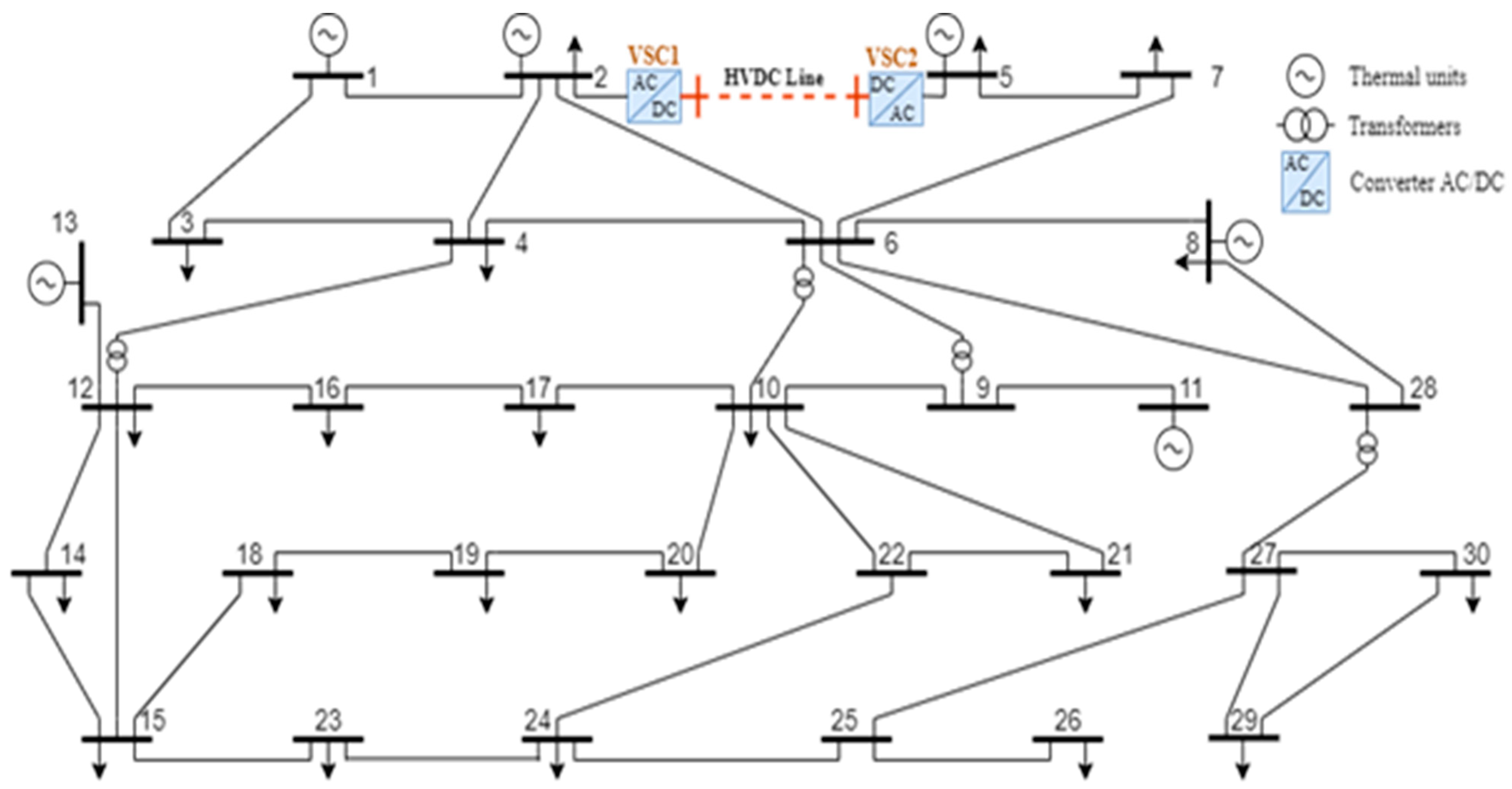
5.1. IEEE 30-Bus System
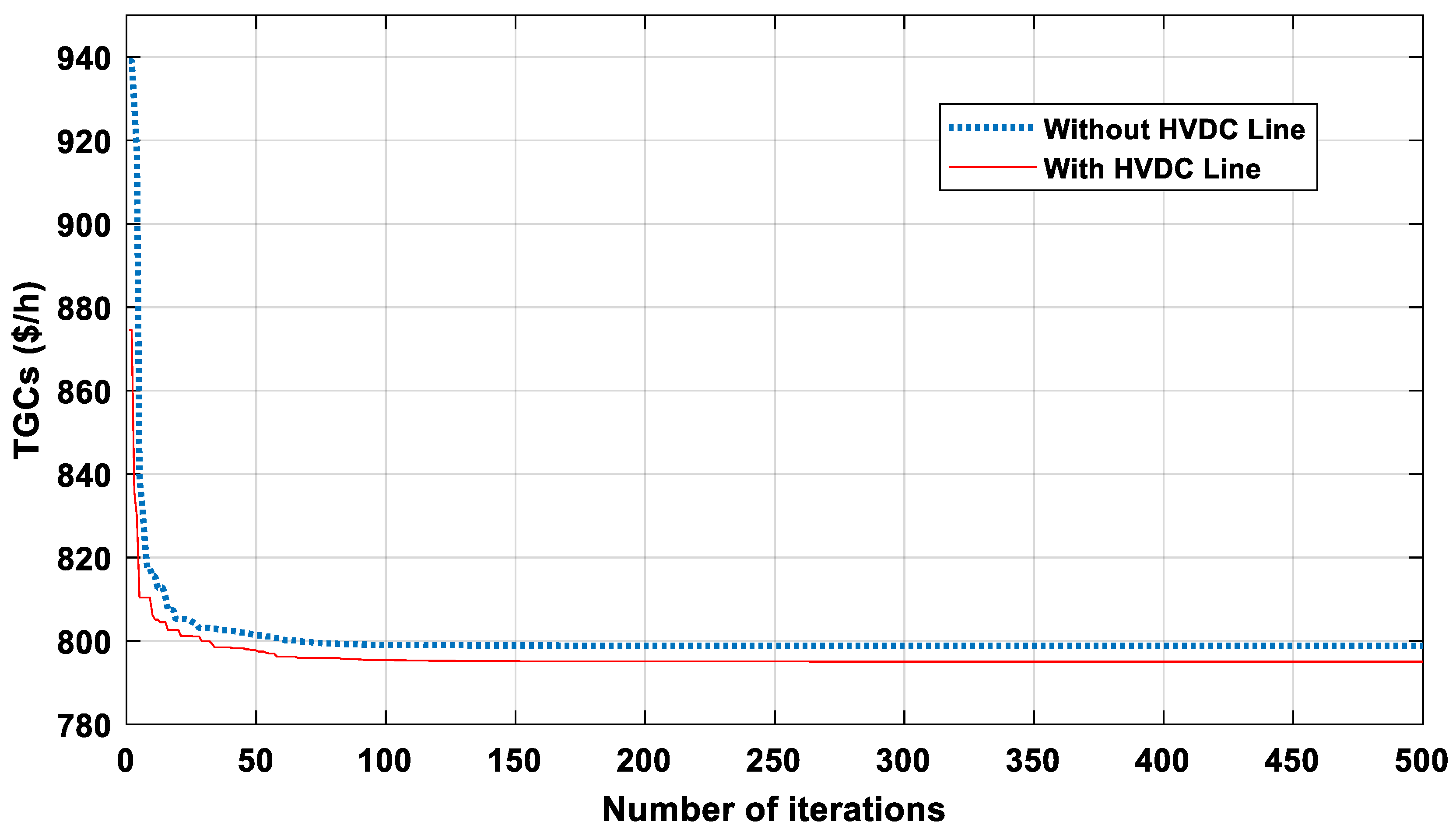
5.1.1. Case-1: Minimization of Total Generation Costs (TGCs)
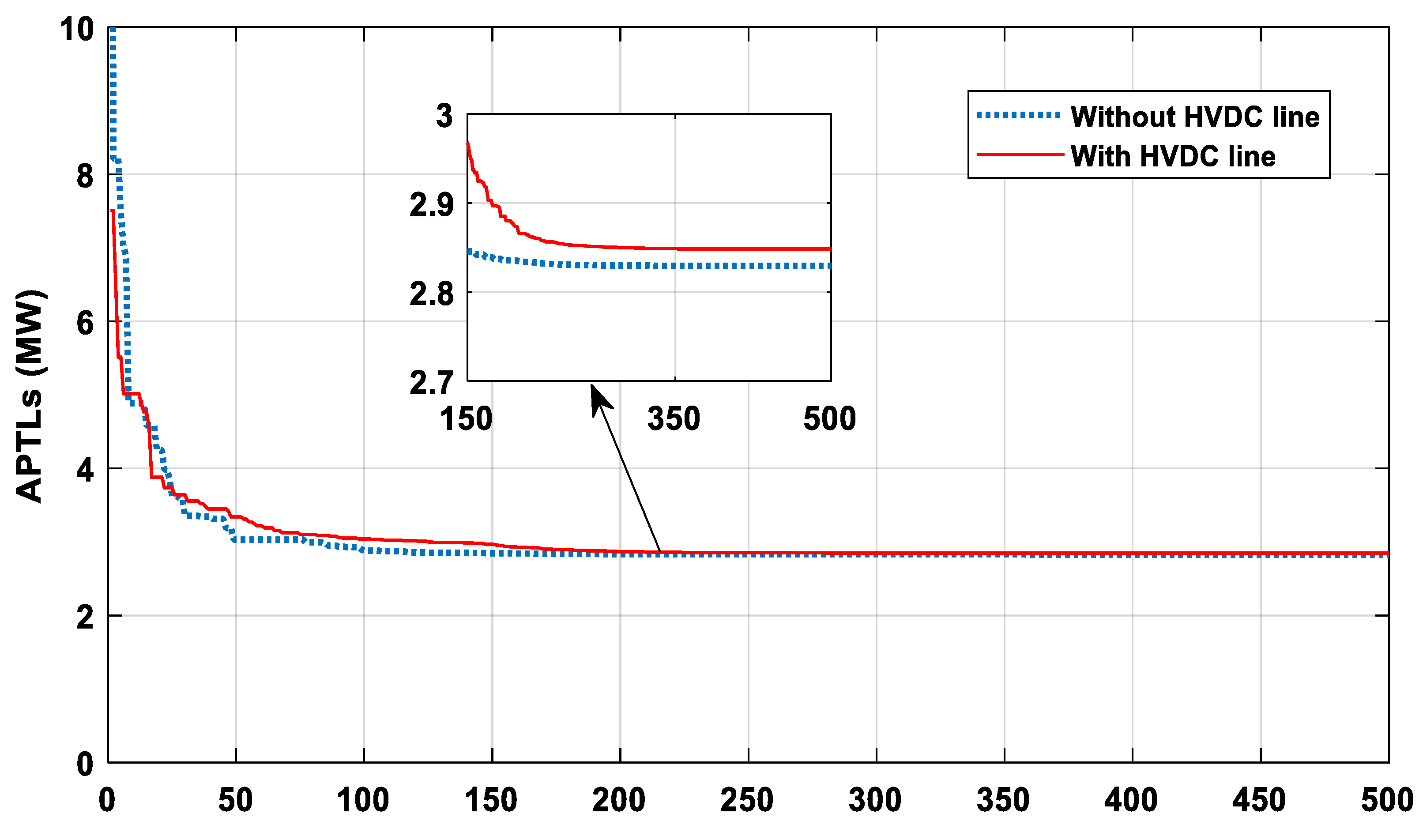
5.1.2. Case-2: Minimization of Total Active Power Transmission Losses (APTLs)
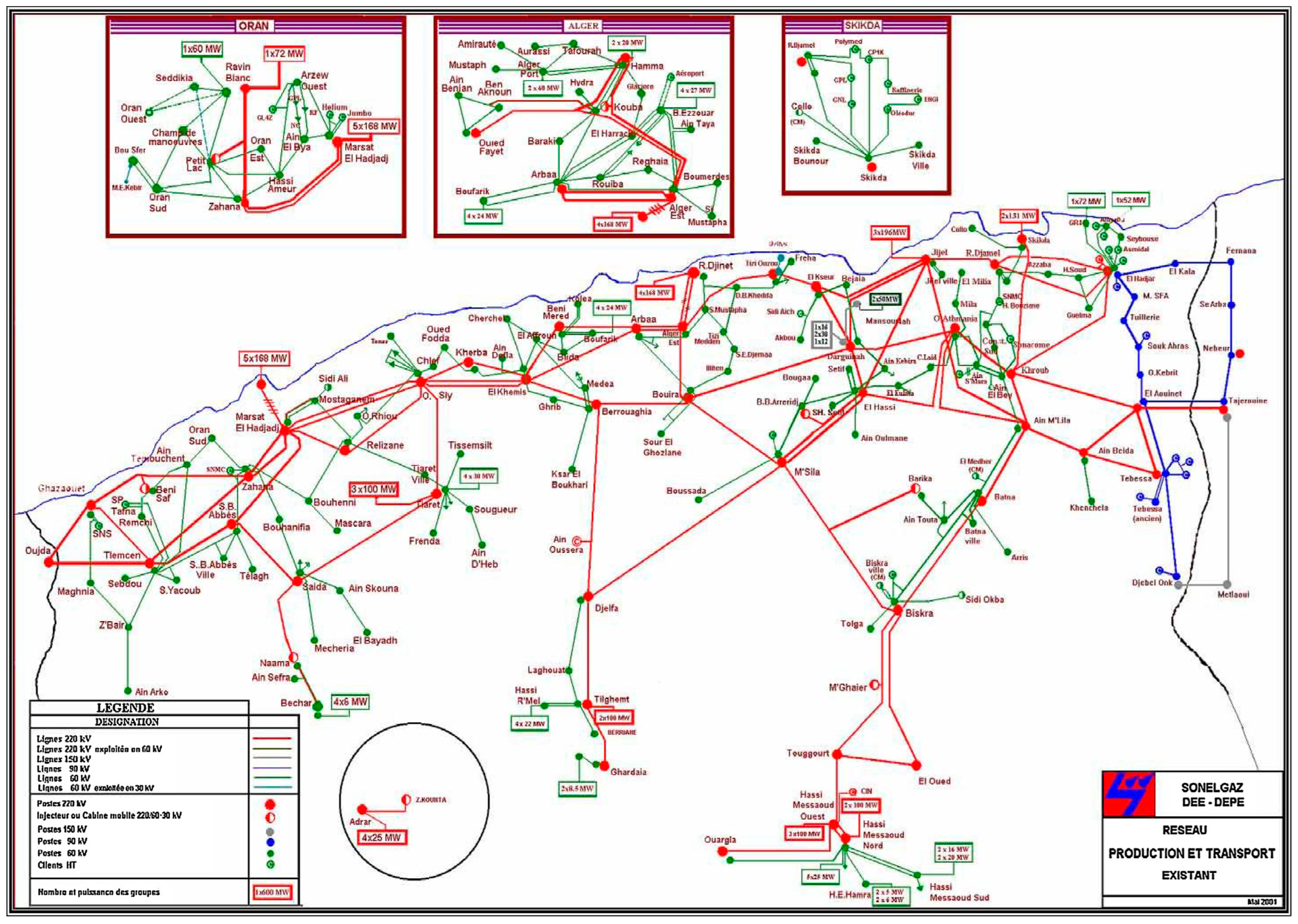
5.2. Large Algerian Electrical Test System DZ114
5.2.1. Case-1: Minimization of Total Generation Costs (TGCs)
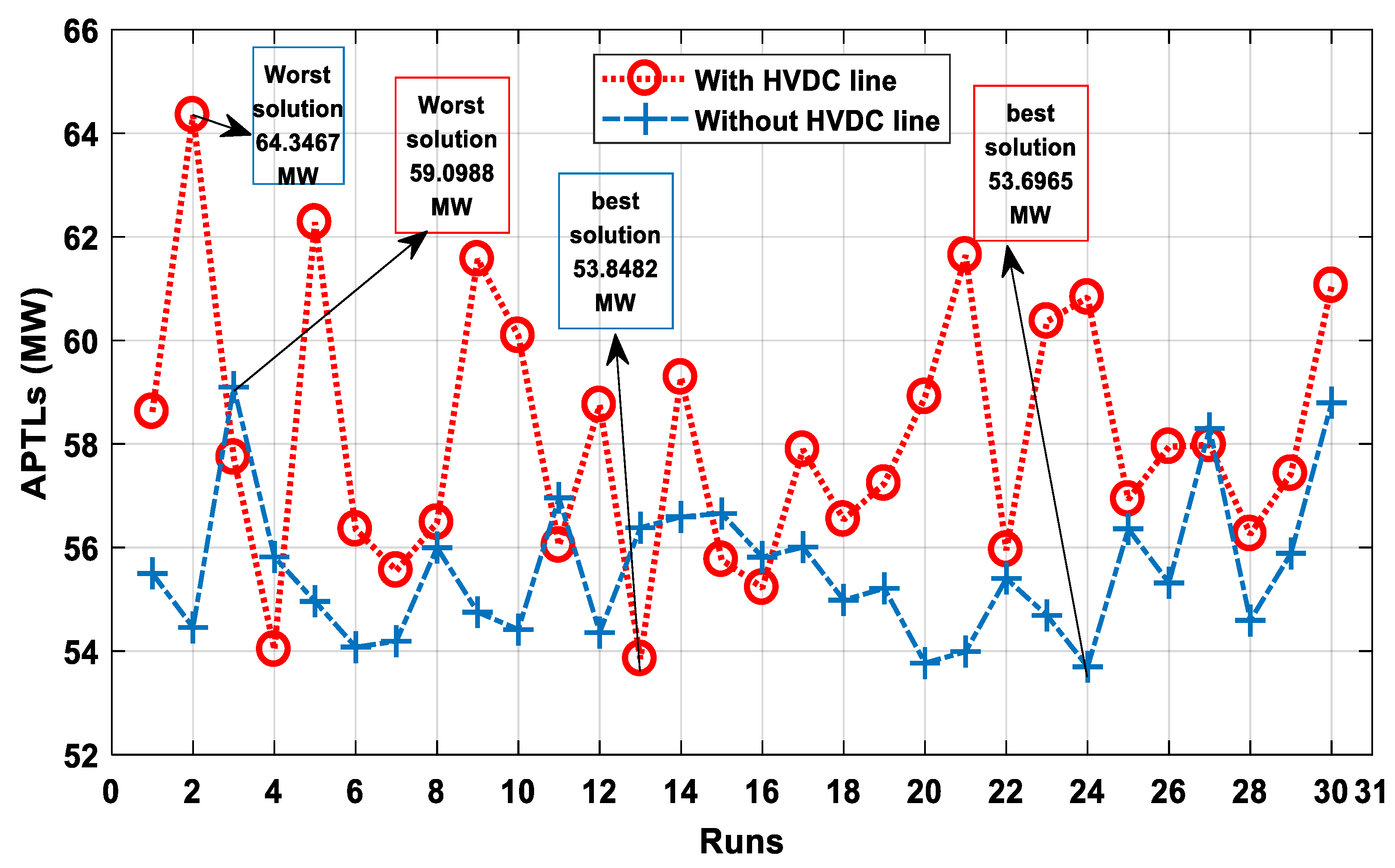
5.2.2. Case-2: Minimization of Total Active Power Transmission Losses (APTLs)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, M.H.; Kamel, S.; Hassan, M.H.; Tostado-Véliz, M.; Zawbaa, H.M. An Improved Wild Horse Optimization Algorithm for Reliability Based Optimal DG Planning of Radial Distribution Networks. Energy Rep. 2022, 8, 582–604. [Google Scholar] [CrossRef]
- Sarhan, S.; Shaheen, A.M.; El-Sehiemy, R.A.; Gafar, M. Enhanced Teaching Learning-Based Algorithm for Fuel Costs and Losses Minimization in AC-DC Systems. Mathematics 2022, 10, 2337. [Google Scholar] [CrossRef]
- Khoa, T.H.; Vasant, P.M.; Singh, M.S.B.; Dieu, V.N. Swarm Based Mean-Variance Mapping Optimization for Convex and Non-Convex Economic Dispatch Problems. Memetic Comput. 2017, 9, 91–108. [Google Scholar] [CrossRef]
- Elattar, E.E.; Shaheen, A.M.; Elsayed, A.M.; El-Sehiemy, R.A. Optimal Power Flow with Emerged Technologies of Voltage Source Converter Stations in Meshed Power Systems. IEEE Access 2020, 8, 166963–166979. [Google Scholar] [CrossRef]
- Zohrizadeh, F.; Josz, C.; Jin, M.; Madani, R.; Lavaei, J.; Sojoudi, S. A Survey on Conic Relaxations of Optimal Power Flow Problem. Eur. J. Oper. Res. 2020, 287, 391–409. [Google Scholar] [CrossRef]
- Mahdad, B. Improvement Optimal Power Flow Solution Considering SVC and TCSC Controllers Using New Partitioned Ant Lion Algorithm. Electr. Eng. 2020, 102, 2655–2672. [Google Scholar] [CrossRef]
- Kouadri, R.; Musirin, I.; Slimani, L.; Bouktir, T.; Othman, M.M. Optimal Power Flow Control Variables Using Slime Mould Algorithm for Generator Fuel Cost and Loss Minimization with Voltage Profile Enhancement Solution. Int. J. Emerg. Trends Eng. Res. 2020, 8, 36–44. [Google Scholar]
- Bouchekara, H.R.E.H.; Abido, M.A.; Boucherma, M. Optimal Power Flow Using Teaching-Learning-Based Optimization Technique. Electr. Power Syst. Res. 2014, 114, 49–59. [Google Scholar] [CrossRef]
- Abd, S.; Kamel, E.S.; El, R.A.; Francisco, S.; Yu, J. Single- and Multi-Objective Optimal Power Flow Frameworks Using Jaya Optimization Technique Respectively. Neural Comput. Appl. 2019, 31, 8787–8806. [Google Scholar]
- Houssein, E.H.; Hassan, M.H.; Mahdy, M.A.; Kamel, S. Development and Application of Equilibrium Optimizer for Optimal Power Flow Calculation of Power System. Appl. Intell. 2023, 53, 7232–7253. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Murtadha, M.; Bo, R.; Sadegh, M.; Mohammed, H.; Alrifaey, M. Optimal Power Flow Using a Hybridization Algorithm of Arithmetic Optimization and Aquila Optimizer. Expert Syst. Appl. 2024, 235, 121212. [Google Scholar] [CrossRef]
- Reviews, S.E.; Version, D.; Reviews, S.E. Review of VSC HVDC Connection for Offshore Wind Power Integration. Renew. Sustain. Energy Rev. 2016, 59, 1405–1414. [Google Scholar]
- Renedo, J.; Asrul, A.; Kazemtabrizi, B.; García-cerrada, A.; Rouco, L.; Zhao, Q.; García-gonzález, J.; De Investigación, I.; Iit, T.; Icai, E.; et al. Electrical Power and Energy Systems a Simplified Algorithm to Solve Optimal Power Flows in Hybrid VSC-Based. Electr. Power Energy Syst. 2019, 110, 781–794. [Google Scholar] [CrossRef]
- Ma, J.; He, F.; Zhao, Z. Line Loss Optimization Based OPF Strategy by Hierarchical Control for DC Microgrid. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition, ECCE 2015, Montreal, QC, Canada, 20–24 September 2015; pp. 6212–6216. [Google Scholar]
- Gabash, A. Review of Battery Storage and Power Electronic Systems in Flexible A-R-OPF Frameworks. Electronics 2023, 12, 3127. [Google Scholar] [CrossRef]
- Sau-bassols, J.; Zhao, Q.; Garc, J. Optimal Power Flow Operation of an Interline Current Flow Controller in an Hybrid AC/DC Meshed Grid. Electr. Power Syst. Res. 2019, 177, 105935. [Google Scholar] [CrossRef]
- Ma, Q.; Wei, W.; Chai, W.; Mei, S. ScienceDirect Solvability Region of AC—DC Power Systems with Volatile Renewable Energy Sources. Energy Rep. 2022, 8, 1463–1472. [Google Scholar] [CrossRef]
- Beerten, J.; Belmans, R. Development of an Open Source Power Flow Software for HVDC Grids and Hybrid AC/DC Systems: MatACDC. IET Gener. Transm. Distrib. 2015, 9, 966–974. [Google Scholar] [CrossRef]
- Fernández-Pérez, J.-C.; Cerezo, F.M.E.; Rodríguez, L.R. Linear Power Flow Algorithm with Losses for Multi-Terminal VSC AC/DC Power Systems. IEEE Trans. Power Syst. 2021, 37, 1739–1749. [Google Scholar] [CrossRef]
- Karami, E.; Gharehpetian, G.B.; Mohammadpour, H.; Khalilinia, A.; Bali, A. Generalised Representation of Multi-Terminal VSC-HVDC Systems for AC—DC Power Flow Studies. IET Energy Syst. Integr. 2020, 2, 50–58. [Google Scholar] [CrossRef]
- E-hawary, M.E.; Ibrahim, S.T. A New Approach to AC-DC Load Flow Analysis. Electr. Power Syst. Res. 1995, 33, 193–200. [Google Scholar] [CrossRef]
- Feng, W.; Member, S.; Tuan, L.A.; Tjernberg, L.B.; Member, S.; Mannikoff, A.; Bergman, A.; Member, S. A New Approach for Bene Fi t Evaluation of Multiterminal VSC—HVDC Using A Proposed Mixed AC/DC Optimal Power Flow. IEEE Trans. Power Deliv. 2014, 29, 432–443. [Google Scholar] [CrossRef]
- Yang, Z.; Member, S.; Zhong, H.; Bose, A.; Fellow, L. Optimal Power Flow in AC–DC Grids with Discrete Control Devices. IEEE Trans. Power Syst. 2017, 33, 8950. [Google Scholar] [CrossRef]
- Using, H.; Lion, A. Optimal Power Flow Solution for Wind Integrated Power in Presence of VSC- Optimal Power Flow Solution for Wind Integrated Power in Presence of VSC-HVDC Using Ant Lion Optimization. Indones. J. Electr. Eng. Comput. Sci. 2018, 12, 625–633. [Google Scholar]
- Pizano-martinez, A.; Fuerte-esquivel, C.R.; Acha, E.; Member, S. Modeling of VSC-Based HVDC Systems for a Newton-Raphson OPF Algorithm. IEEE Trans. Power Syst. 2007, 22, 1794–1803. [Google Scholar] [CrossRef]
- Algorithms, G. Networks for Grid Integration of Offshore Wind Farms Using. Energies 2013, 6, 1–26. [Google Scholar]
- Elsayed, A.M.; Shaheen, A.M.; Alharthi, M.M. Adequate Operation of Hybrid AC / MT-HVDC Power Systems Using an Improved Multi-Objective Marine Predators Optimizer. IEEE Access 2021, 51065–51087. [Google Scholar] [CrossRef]
- Point, S.O. Minimization of Network Power Losses in the AC-DC Hybrid Distribution Network through Network Reconfiguration Using Soft Open Point. Electronics 2021, 10, 326. [Google Scholar] [CrossRef]
- Flow, P.; Grids, V.A.; Baradar, M.; Member, S.; Hesamzadeh, M.R. Second-Order Cone Programming for Optimal. Math. Program. 2003, 95, 3–51. [Google Scholar]
- Ac, H.; Power, D.C.; Hotz, M.; Member, S.; Utschick, W.; Member, S. Hynet: An Optimal Power Flow Framework For hybrid AC/DC power systems. IEEE Trans. Power Syst. 2019, 35, 1036–1047. [Google Scholar]
- Maulik, A.; Das, D. Optimal Power Dispatch Considering Load and Renewable Generation Uncertainties in an AC—DC Hybrid Microgrid. IET Gener. Transm. Distrib. 2019, 13, 1164–1176. [Google Scholar] [CrossRef]
- Lotfjou, A.; Fu, Y.; Shahidehpour, M. Hybrid AC / DC Transmission Expansion Planning. IEEE Trans. Power Deliv. 2012, 27, 1620–1628. [Google Scholar] [CrossRef]
- Zhao, M.; Chen, Z.; Blaabjerg, F. Load Flow Analysis for Variable Speed Offshore Wind Farms. IET Renew. Power Gener. 2009, 3, 120–132. [Google Scholar] [CrossRef]
- Gengyin, L.; Ming, Z.; Member, S.; Jie, H.; Guaagkai, L.; Haifeng, L. Power Flow Calculation of Power Systems Incorporating VSC-HVDC. In Proceedings of the 2004 International Conference on Power System Technology, Singapore, 21–24 November 2004; pp. 21–24. [Google Scholar]
- Beerten, J.; Cole, S.; Belmans, R. Generalized Steady-State VSC MTDC Model for Sequential AC/DC Power Flow Algorithms. IEEE Trans. Power Syst. 2012, 27, 821–829. [Google Scholar] [CrossRef]
- Beerten, J. MatACDC 1.0 User’s Manual. Dep. Electr. Eng. Univ. Leuven 2012, 1–36. [Google Scholar]
- Bouchekara, H.R.E.H.; Chaib, A.E.; Abido, M.A.; El-Sehiemy, R.A. Optimal Power Flow Using an Improved Colliding Bodies Optimization Algorithm. Appl. Soft Comput. J. 2016, 42, 119–131. [Google Scholar] [CrossRef]
- Sayah, S. Modified Differential Evolution Approach for Practical Optimal Reactive Power Dispatch of Hybrid AC−DC Power Systems. Appl. Soft Comput. J. 2018, 73, 591–606. [Google Scholar] [CrossRef]
- Kumar, A.; Saikat, D.; Dilip, S.; Pratihar, K. An Improved Design of Knee Orthosis Using Self–Adaptive Bonobo Optimizer (SaBO). J. Intell. Robot. Syst. 2023, 107, 8. [Google Scholar]
- Das, A.K. A New Bonobo Optimizer (BO) for Realparameter Optimization. In Proceedings of the IEEE Region 10 Symposium (TENSYMP), Kolkata, India, 7–9 June 2019. [Google Scholar]
- Farh, H.M.H.; Al-shamma, A.A.; Al-shaalan, A.M.; Alkuhayli, A. Technical and Economic Evaluation for Off-Grid Hybrid Renewable Energy System Using Novel Bonobo Optimizer. Sustainability 2022, 14, 1533. [Google Scholar] [CrossRef]
- Alsac, O.; Stott, B. Optimal Load Flow with Steady-State Security. IEEE Trans. Power Appar. Syst. 1974, PAS-93, 745–751. [Google Scholar] [CrossRef]
- Ben oualid Medani, K.; Sayah, S.; Bekrar, A. Whale Optimization Algorithm Based Optimal Reactive Power Dispatch: A Case Study of the Algerian Power System. Electr. Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Herbadji, O.; Slimani, L.; Bouktir, T. Optimal Power Flow with Four Conflicting Objective Functions Using Multiobjective Ant Lion Algorithm: A Case Study of the Algerian Electrical Network. Iran. J. Electr. Electron. Eng. 2019, 15, 94–113. [Google Scholar]
- Slimani, L.; Bouktir, T. Optimal Power Flow Solution of the Algerian Electrical Network Using Differential Evolution Algorithm. TELKOMNIKA Indones. J. Electr. Eng. 2012, 10, 199–210. [Google Scholar]
- Mahdad, B.; Srairi, K. Solving Practical Economic Dispatch Using Hybrid GA-DE-PS Method. Int. J. Syst. Assur. Eng. Manag. 2014, 5, 391–398. [Google Scholar] [CrossRef]
- Kouadri, R.; Musirin, I.; Slimani, L.; Bouktir, T. OPF for Large Scale Power System Using Ant Lion Optimization: A Case Study of the Algerian Electrical Network. IAES Int. J. Artif. Intell. 2020, 9, 252–260. [Google Scholar] [CrossRef]



| Control Variables | Limits | Case 1: TGCs (USD/h) | ||||||
|---|---|---|---|---|---|---|---|---|
| Without HVDC | With HVDC | |||||||
| Min | Max | JAYA [9] | SMA [7] | EEO [9] | AO-AOA [11] | SABO | SABO | |
| PG1 | 50 | 200 | 177.0106 | 177.5784 | 176.7345 | 177.0037 | 177.0646 | 178.0241 |
| PG2 | 20 | 80 | 48.6495 | 48.6770 | 48.78826 | 48.5782 | 48.6784 | 49.0698 |
| PG5 | 15 | 50 | 21.2822 | 21.2668 | 21.35174 | 21.3235 | 21.2994 | 20.3217 |
| PG8 | 10 | 35 | 21.0841 | 21.2316 | 21.59308 | 21.0818 | 21.0916 | 20.0680 |
| PG11 | 10 | 30 | 11.9518 | 12.0890 | 11.90222 | 11.9328 | 11.8472 | 11.5181 |
| PG13 | 12 | 40 | 12.0048 | 12.0000 | 12.01063 | 12.0035 | 12.0000 | 12.0000 |
| VG1 | 0.95 | 1.1 | 1.1000 | 1.1000 | 1.081652 | 1.09530 | 1.1000 | 1.1000 |
| VG2 | 0.95 | 1.1 | 1.0882 | 1.0879 | 1.083692 | 1.06812 | 1.0877 | 1.0839 |
| VG5 | 0.95 | 1.1 | 1.0625 | 1.0618 | 1.034161 | 1.05370 | 1.0613 | 1.0780 |
| VG8 | 0.95 | 1.1 | 1.0695 | 1.0701 | 1.040193 | 1.04973 | 1.0690 | 1.0698 |
| VG11 | 0.95 | 1.1 | 1.1000 | 1.1000 | 1.058904 | 1.09511 | 1.1000 | 1.1000 |
| VG13 | 0.95 | 1.1 | 1.1000 | 1.1000 | 1.035318 | 1.04431 | 1.1000 | 1.1000 |
| T11 | 0.9 | 1.1 | 1.0239 | 1.0259 | 0.049801 | 1.04510 | 1.0363 | 1.0448 |
| T12 | 0.9 | 1.1 | 0.9000 | 0.9010 | 0.035215 | 0.91041 | 0.9033 | 0.9000 |
| T15 | 0.9 | 1.1 | 0.9741 | 0.9803 | 0.04999 | 0.96710 | 0.9772 | 0.9824 |
| T36 | 0.9 | 1.1 | 0.9595 | 0.9568 | 0.96527 | 0.9593 | 0.9633 | |
| QC10 | 0 | 5 | 5.000 | 4.3806 | 1.039025 | 4.49630 | 5.0000 | 5.0000 |
| QC12 | 0 | 5 | 4.9197 | 4.7790 | 0.9264 | 3.63150 | 5.0000 | 4.9998 |
| QC15 | 0 | 5 | 5.000 | 4.8272 | 0.963273 | 4.63540 | 5.0000 | 4.9997 |
| QC17 | 0 | 5 | 5.000 | 4.9942 | 0.971492 | 4.88170 | 5.0000 | 5.0000 |
| QC20 | 0 | 5 | 4.9949 | 2.5651 | 0.045018 | 4.20613 | 4.2704 | 4.3136 |
| QC21 | 0 | 5 | 4.9698 | 2.8396 | 0 | 4.97820 | 5.0000 | 5.0000 |
| QC23 | 0 | 5 | 4.9892 | 3.4609 | 0.049426 | 4.95210 | 2.6829 | 2.7305 |
| QC24 | 0 | 5 | 5.000 | 4.9957 | 0.048943 | 4.99160 | 5.0000 | 5.0000 |
| QC29 | 0 | 5 | 2.0948 | 1.1562 | 0.043546 | 2.11586 | 2.2158 | 2.4387 |
| PS1 | −100 | 100 | - | - | - | - | - | −92.09 |
| QS1 | −100 | 100 | - | - | - | - | - | 10.64 |
| PSslack | −100 | 100 | - | - | - | - | - | 90.35 |
| QSslack | −100 | 100 | - | - | - | - | - | 0.00 |
| Optimal location of HVDC line | - | - | - | - | - | Line 5 Bus (2–5) | ||
| TGCs (USD/h) | 798.9386 | 798.9709 | 800.4145 | 800.0239 | 798.8979 | 795.0720 | ||
| (MW) | 8.58378 | 8.5752 | 8.99217 | 8.873080 | 8.5813 | 5.866 | ||
| (MW) | - | - | - | - | - | 1.5257 | ||
| (MW) | - | - | - | - | - | 0.21 | ||
| APTLs (MW)of AC/DC system | - | - | - | - | - | 7.6017 | ||
| The convergence time (second) | - | - | - | - | 63.8806 | 510.717 | ||
| Control Variables | Limits | Case 2: APTLs (MW) | ||||||
|---|---|---|---|---|---|---|---|---|
| Without HVDC | With HVDC | |||||||
| Min | Max | JAYA [9] | SMA [7] | EEO [9] | AO-AOA [11] | SABO | SABO | |
| PG1 | 50 | 200 | 51.5290 | 51.2614 | 51.49013 | 51.4988 | 51.2295 | 51.2490 |
| PG2 | 20 | 80 | 80.000 | 80.0000 | 79.99994 | 80.000 | 80.0000 | 80.0000 |
| PG5 | 15 | 50 | 50.000 | 50.0000 | 49.99974 | 50.000 | 50.0000 | 49.9996 |
| PG8 | 10 | 35 | 35.000 | 34.9999 | 34.99917 | 35.000 | 35.0000 | 35.0000 |
| PG11 | 10 | 30 | 30.000 | 30.0000 | 30.000 | 30.000 | 29.9999 | 29.9999 |
| PG13 | 12 | 40 | 40.000 | 40.0000 | 39.99999 | 40.000 | 40.0000 | 39.9999 |
| VG1 | 0.95 | 1.1 | 1.0500 | 1.1000 | 1.061175 | 1.06193 | 1.1000 | 1.1000 |
| VG2 | 0.95 | 1.1 | 1.0477 | 1.0979 | 1.057169 | 1.05172 | 1.0977 | 1.0962 |
| VG5 | 0.95 | 1.1 | 1.0292 | 1.0793 | 1.037851 | 1.03225 | 1.0799 | 1.0892 |
| VG8 | 0.95 | 1.1 | 1.0364 | 1.0876 | 1.043643 | 1.03964 | 1.0869 | 1.0879 |
| VG11 | 0.95 | 1.1 | 1.0500 | 1.1000 | 1.050452 | 1.05861 | 1.1000 | 1.1000 |
| VG13 | 0.95 | 1.1 | 1.0500 | 1.1000 | 1.051736 | 1.05512 | 1.1000 | 1.1000 |
| T11 | 0.9 | 1.1 | 1.0372 | 1.0331 | 0.049996 | 1.04764 | 1.0630 | 1.0658 |
| T12 | 0.9 | 1.1 | 0.9000 | 0.9193 | 0.029683 | 0.90000 | 0.9038 | 0.9001 |
| T15 | 0.9 | 1.1 | 0.9846 | 0.9870 | 0.05 | 0.98360 | 0.9864 | 0.9887 |
| T36 | 0.9 | 1.1 | 0.9664 | 0.9834 | 0.018962 | 0.96880 | 0.9675 | 0.9739 |
| QC10 | 0 | 5 | 4.3257 | 1.0281 | 1.02419 | 4.52370 | 4.9974 | 4.9949 |
| QC12 | 0 | 5 | 5.000 | 0.2155 | 0.933052 | 0.95180 | 4.9993 | 4.9993 |
| QC15 | 0 | 5 | 5.000 | 4.7108 | 0.990881 | 4.57320 | 4.7827 | 4.8029 |
| QC17 | 0 | 5 | 4.9979 | 2.4109 | 0.973498 | 4.66150 | 5.0000 | 4.9955 |
| QC20 | 0 | 5 | 4.1615 | 4.9982 | 0.049819 | 4.15290 | 3.7924 | 3.9913 |
| QC21 | 0 | 5 | 5.000 | 4.9042 | 0.03386 | 4.22410 | 5.0000 | 4.9995 |
| QC23 | 0 | 5 | 3.3293 | 0.3454 | 0.049166 | 3.11720 | 2.4482 | 2.5848 |
| QC24 | 0 | 5 | 5.000 | 4.9181 | 0.049966 | 4.63050 | 4.9997 | 4.9982 |
| QC29 | 0 | 5 | 1.8872 | 2.8276 | 0.039794 | 2.18670 | 1.9277 | 2.2502 |
| PS1 | −100 | 100 | - | - | - | - | - | −55.64 |
| QS1 | −100 | 100 | - | - | - | - | - | 11.06 |
| PSslack | −100 | 100 | - | - | - | - | - | 54.58 |
| QSslack | −100 | 100 | - | - | - | - | - | 0.00 |
| Optimal location of HVDC line | - | - | - | - | - | Line 5 Bus (2–5) | ||
| TGCs (USD/h) | 967.7316 | 967.0437 | 967.5845 | 967.6703 | 966.9680 | 967.0105 | ||
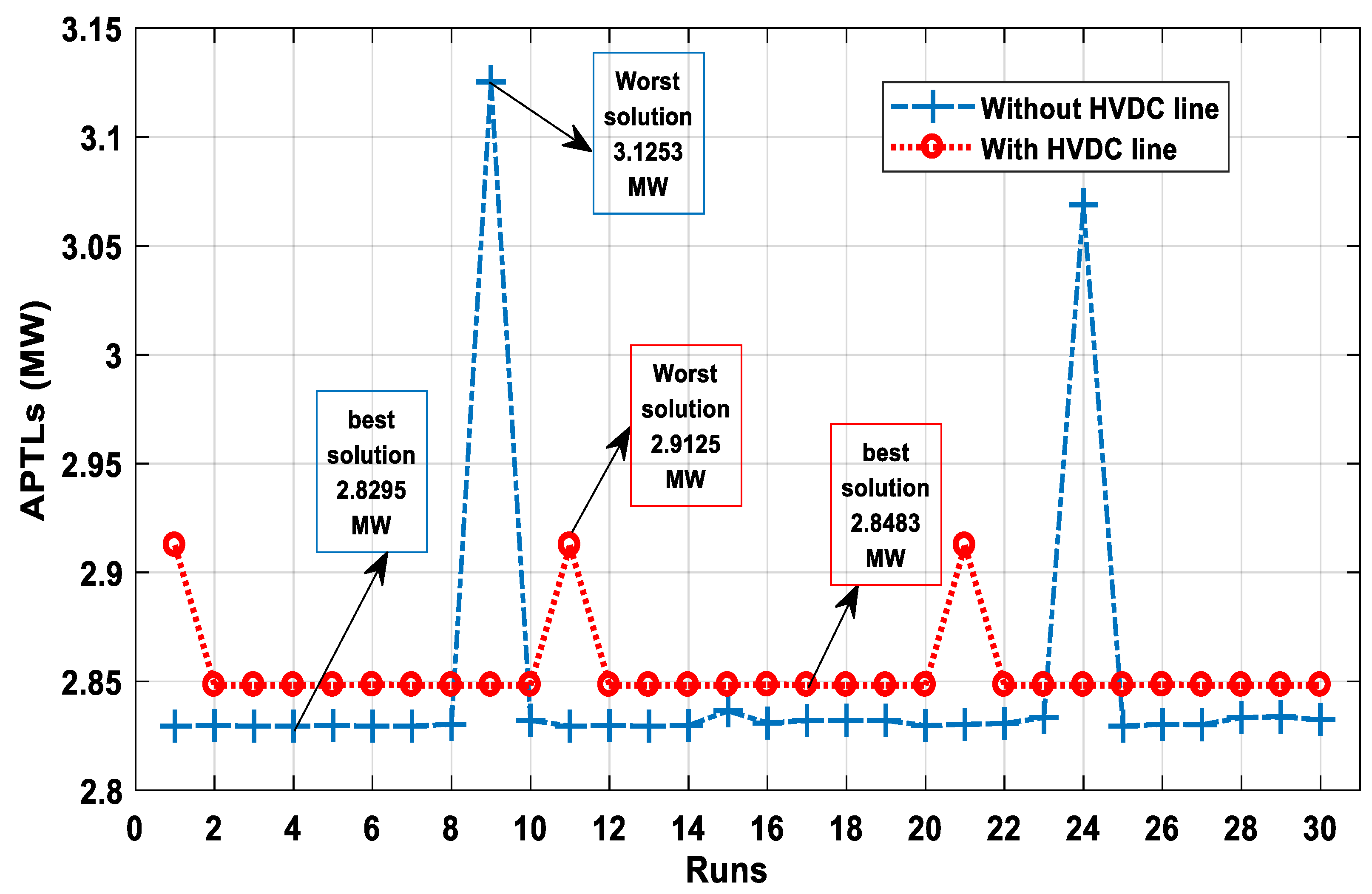
| (MW) | 3.1291 | 2.8612 | 3.088974 | 3.017910 | 2.8295 | 1.781 | ||
| (MW) | - | - | - | - | - | 0.99 | ||
| (MW) | - | - | - | - | - | 0.08 | ||
| APTLs (MW)of AC/DC system | - | - | - | - | - | 2.8483 | ||
| The convergence time (second) | - | - | - | - | 64.533 | 514.580 | ||
| Control Variables | Limits | Case 1: TGCs (USD/h) | Case 2: APTLs (MW) | |||
|---|---|---|---|---|---|---|
| Min | Max | Without HVDC | With HVDC | Without HVDC | With HVDC | |
| PG 4 | 135 | 1350 | 449.1546 | 450.5743 | 502.9009 | 519.8323 |
| PG 5 | 135 | 1350 | 445.4603 | 448.1035 | 506.9725 | 487.2334 |
| PG 11 | 10 | 100 | 99.8786 | 99.9825 | 99.8891 | 99.6393 |
| PG 15 | 30 | 300 | 194.1843 | 193.5099 | 116.9265 | 127.2726 |
| PG 17 | 135 | 1350 | 448.1758 | 447.5191 | 608.1340 | 639.7914 |
| PG 19 | 34.5 | 345 | 195.4801 | 193.2714 | 205.3335 | 150.0935 |
| PG 22 | 34.5 | 345 | 189.3318 | 190.0804 | 131.5792 | 154.8630 |
| PG 52 | 34.5 | 345 | 190.3655 | 186.5989 | 120.8845 | 120.7498 |
| PG 80 | 34.5 | 345 | 195.3247 | 191.6183 | 272.5870 | 254.6253 |
| PG 83 | 30 | 300 | 192.0720 | 192.0580 | 179.0298 | 170.1840 |
| PG 98 | 30 | 300 | 187.2295 | 192.1012 | 251.4170 | 265.6369 |
| PG 100 | 60 | 600 | 599.9521 | 599.9732 | 387.0482 | 391.4905 |
| PG 101 | 20 | 200 | 199.9881 | 199.9941 | 198.5835 | 199.9958 |
| PG 109 | 10 | 100 | 99.8483 | 99.9396 | 99.4402 | 99.4404 |
| PG 111 | 10 | 100 | 99.9404 | 99.9277 | 99.9706 | 100.0000 |
| VG 4 | 0.9 | 1.1 | 1.0545 | 1.0539 | 1.0614 | 1.0804 |
| VG 5 | 0.9 | 1.1 | 1.0471 | 1.0456 | 1.0504 | 1.0736 |
| VG 11 | 0.9 | 1.1 | 1.0489 | 1.0553 | 1.0493 | 1.0674 |
| VG 15 | 0.9 | 1.1 | 1.0563 | 1.0541 | 1.0608 | 1.0799 |
| VG 17 | 0.9 | 1.1 | 1.0561 | 1.0613 | 1.0695 | 1.0813 |
| VG 19 | 0.9 | 1.1 | 1.0012 | 1.0271 | 1.0567 | 1.0386 |
| VG 22 | 0.9 | 1.1 | 1.0053 | 1.0241 | 1.0573 | 1.0499 |
| VG 52 | 0.9 | 1.1 | 1.0326 | 1.0330 | 1.0428 | 1.0568 |
| VG 80 | 0.9 | 1.1 | 1.0375 | 1.0436 | 1.0513 | 1.0266 |
| VG 83 | 0.9 | 1.1 | 1.0747 | 1.0750 | 1.0832 | 1.0548 |
| VG 98 | 0.9 | 1.1 | 1.0634 | 1.0803 | 1.0793 | 1.0759 |
| VG 100 | 0.9 | 1.1 | 1.0819 | 1.0949 | 1.0962 | 1.0788 |
| VG 101 | 0.9 | 1.1 | 1.0617 | 1.0827 | 1.0772 | 1.0776 |
| VG 109 | 0.9 | 1.1 | 1.0718 | 1.0954 | 1.0848 | 1.0947 |
| VG 111 | 0.9 | 1.1 | 1.0268 | 1.0541 | 1.0811 | 1.0489 |
| Control Variables | Limits | Case 1: TGCs (USD/h) | Case 2: APTLs (MW) | |||
|---|---|---|---|---|---|---|
| Min | Max | Without HVDC | With HVDC | Without HVDC | With HVDC | |
| T 160 | 0.9 | 1.1 | 0.9004 | 0.9022 | 0.9006 | 0.9023 |
| T 161 | 0.9 | 1.1 | 0.9231 | 0.9135 | 0.9614 | 0.9438 |
| T 162 | 0.9 | 1.1 | 0.9412 | 0.9156 | 0.9674 | 0.9688 |
| T 163 | 0.9 | 1.1 | 0.9413 | 0.9727 | 0.9605 | 0.9717 |
| T 164 | 0.9 | 1.1 | 0.9726 | 0.9711 | 0.9646 | 0.9558 |
| T 165 | 0.9 | 1.1 | 0.9710 | 0.9844 | 0.9486 | 0.9742 |
| T 166 | 0.9 | 1.1 | 0.9888 | 1.0044 | 1.0013 | 0.9886 |
| T 167 | 0.9 | 1.1 | 0.9552 | 1.0142 | 0.9648 | 1.0145 |
| T 168 | 0.9 | 1.1 | 0.9597 | 0.9922 | 0.9392 | 0.9857 |
| T 169 | 0.9 | 1.1 | 1.0034 | 0.9954 | 0.9605 | 0.9869 |
| T 170 | 0.9 | 1.1 | 1.0331 | 1.0239 | 0.9898 | 1.0063 |
| T 171 | 0.9 | 1.1 | 0.9572 | 0.9324 | 0.9600 | 0.9653 |
| T 172 | 0.9 | 1.1 | 1.0237 | 1.0071 | 0.9561 | 1.0309 |
| T 173 | 0.9 | 1.1 | 0.9824 | 1.0074 | 0.9988 | 0.9989 |
| T 174 | 0.9 | 1.1 | 0.9619 | 1.0076 | 0.9587 | 0.9605 |
| T 175 | 0.9 | 1.1 | 0.9238 | 1.0801 | 1.0198 | 1.0652 |
| Control Variables | Limits | Case 1: TGCs (USD/h) | Case 2: APTLs (MW) | |||
|---|---|---|---|---|---|---|
| Min | Max | Without HVDC | With HVDC | Without HVDC | With HVDC | |
| QC41 | 0 | 25 | 20.3355 | 19.3062 | 22.8674 | 21.9126 |
| QC50 | 0 | 25 | 11.2038 | 12.8306 | 10.1334 | 6.7341 |
| QC55 | 0 | 25 | 16.0482 | 19.4523 | 19.6093 | 22.4936 |
| QC66 | 0 | 25 | 23.8080 | 23.9402 | 22.2982 | 23.7515 |
| QC67 | 0 | 25 | 16.3570 | 2.3715 | 17.9964 | 12.8060 |
| QC77 | 0 | 25 | 11.5375 | 5.5738 | 6.6413 | 6.9476 |
| QC93 | 0 | 25 | 24.6758 | 21.9619 | 24.5343 | 24.7118 |
| PS1 | −100 | 100 | - | −18.4787 | −15.0939 | |
| QS1 | −100 | 100 | - | 29.3269 | - | 21.8249 |
| PSslack | −100 | 100 | - | 17.85 | - | 14.49 |
| QSslack | −100 | 100 | - | 6.97 | - | −6.27 |
| Control Variables | Limits | Case 1: TGCs (USD/h) | Case 2: APTLs (MW) | |||
|---|---|---|---|---|---|---|
| Min | Max | Without HVDC | With HVDC | Without HVDC | With HVDC | |
| Optimal location of HVDC line | - | Line 99 Bus 73–67 | - | Line 99 Bus 73–67 | ||
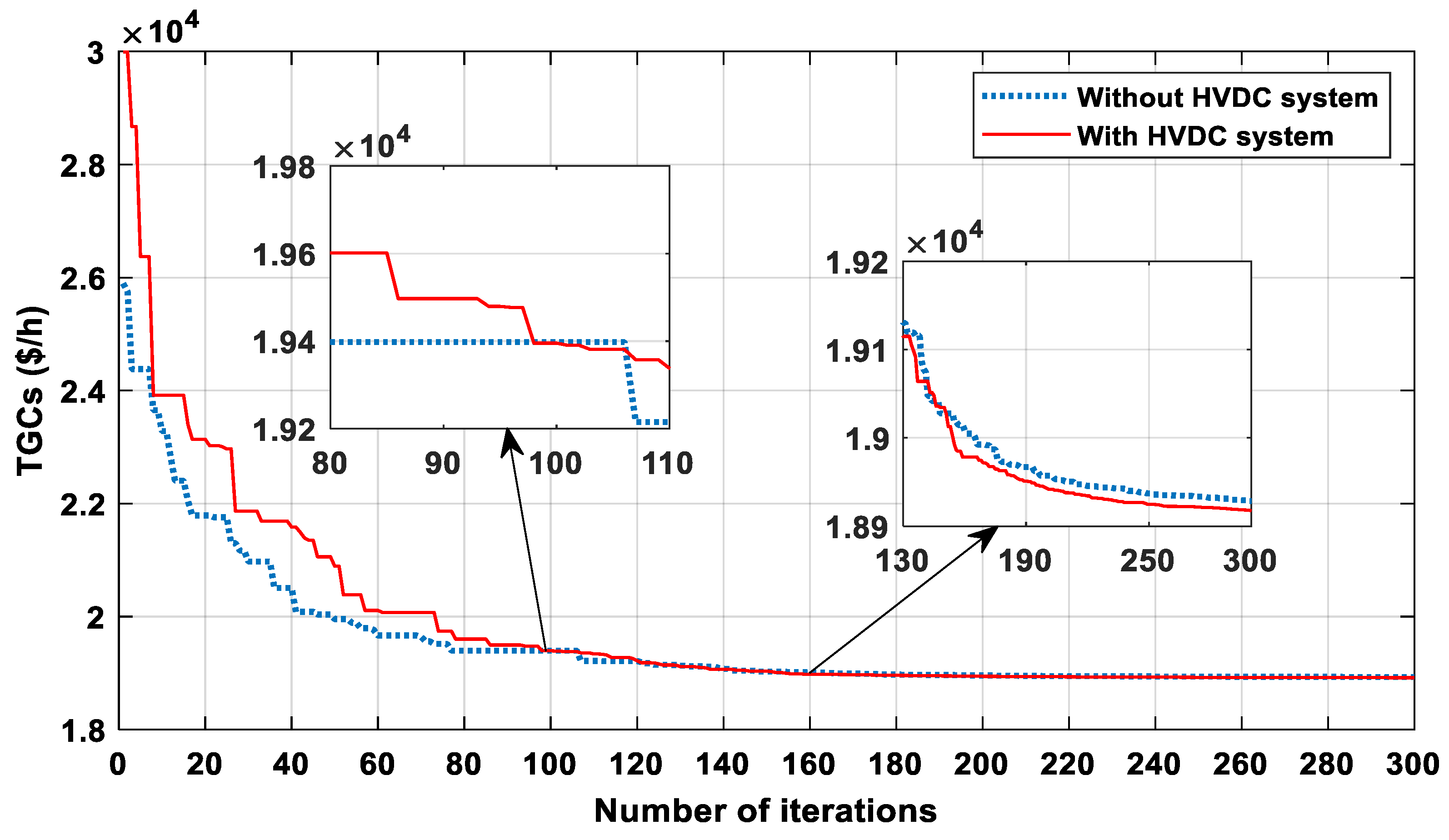
| TGCs (USD/h) | 18,928,4612 | 18,917.4349 | 20,468.7419 | 20,498.3401 | ||
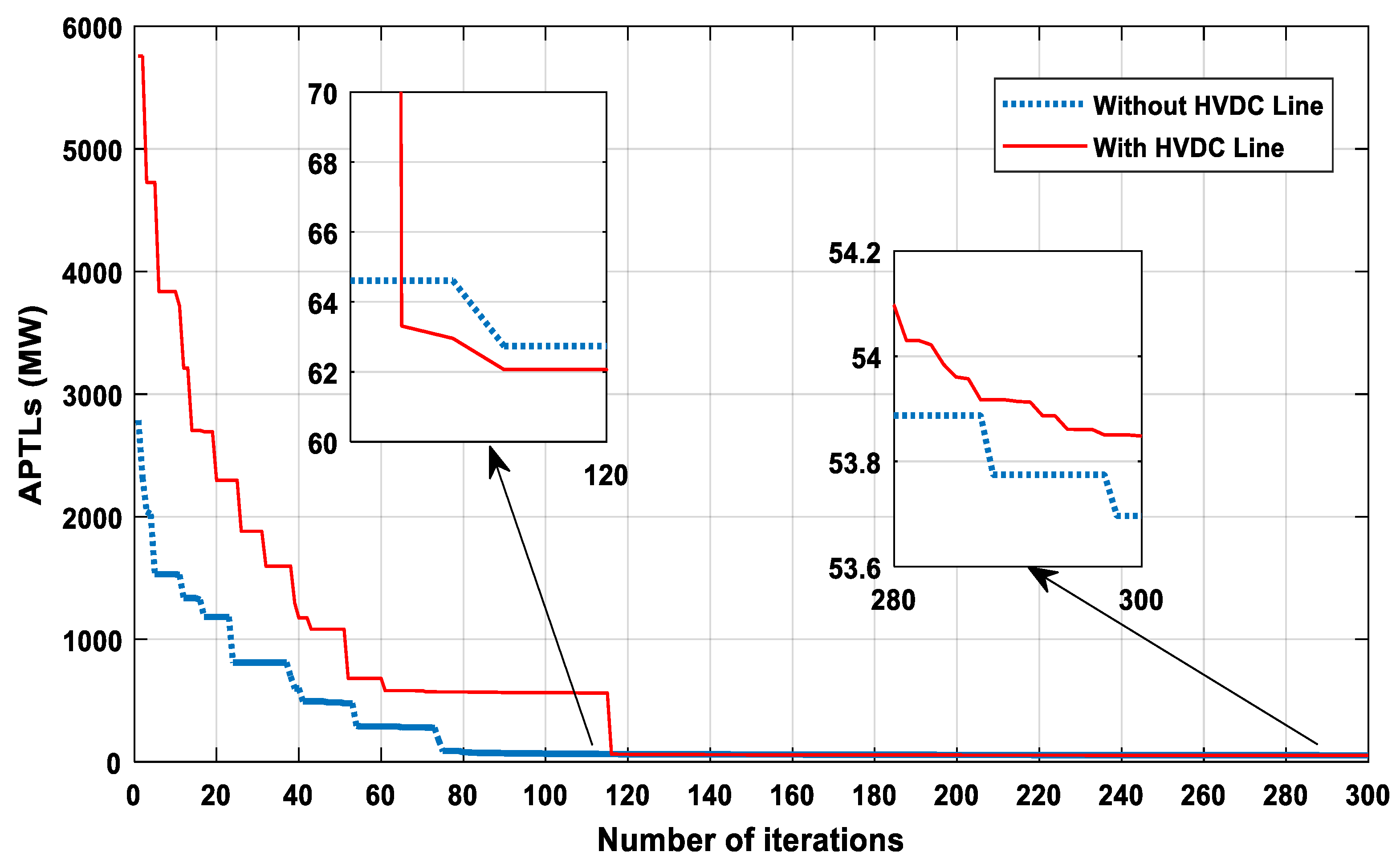
| (MW) | 59.3861 | 57.622 | 53.6965 | 53.242 | ||
| (MW) | - | 0.62 | - | 0.59 | ||
| (MW) | - | 0.01 | - | 0.01 | ||
| APTLs (MW) of AC/DC system | - | 58.2520 | - | 53.8482 | ||
| The convergence time (second) | 97.1380 | 533.601 | 123.180 | 542.842 | ||
| Methods | TGCs (USD/h) | Method Description |
|---|---|---|
| MOALO [44] | 19,355.859 | Multi-objective ant lion algorithm |
| DE [45] | 19,203.340 | Differential evolution |
| GA-ED-PS [46] | 19,199.444 | Hybrid GA-DE-PS |
| GOA [7] | 19,178.818 | Grasshopper optimization algorithm |
| GWO [47] | 19,171.958 | Grey wolf optimizer |
| SMA [7] | 19,170.205 | Slime mould algorithm |
| SABO | 18,928,4612 | Self-adaptive bonobo optimizer |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alouache, H.E.; Sayah, S.; Bosisio, A.; Hamouda, A.; Kouadri, R.; Shirvani, R. Optimal Placement of HVDC-VSC in AC System Using Self-Adaptive Bonobo Optimizer to Solve Optimal Power Flows: A Case Study of the Algerian Electrical Network. Electronics 2024, 13, 3848. https://doi.org/10.3390/electronics13193848
Alouache HE, Sayah S, Bosisio A, Hamouda A, Kouadri R, Shirvani R. Optimal Placement of HVDC-VSC in AC System Using Self-Adaptive Bonobo Optimizer to Solve Optimal Power Flows: A Case Study of the Algerian Electrical Network. Electronics. 2024; 13(19):3848. https://doi.org/10.3390/electronics13193848
Chicago/Turabian StyleAlouache, Houssam Eddine, Samir Sayah, Alessandro Bosisio, Abdellatif Hamouda, Ramzi Kouadri, and Rouzbeh Shirvani. 2024. "Optimal Placement of HVDC-VSC in AC System Using Self-Adaptive Bonobo Optimizer to Solve Optimal Power Flows: A Case Study of the Algerian Electrical Network" Electronics 13, no. 19: 3848. https://doi.org/10.3390/electronics13193848
APA StyleAlouache, H. E., Sayah, S., Bosisio, A., Hamouda, A., Kouadri, R., & Shirvani, R. (2024). Optimal Placement of HVDC-VSC in AC System Using Self-Adaptive Bonobo Optimizer to Solve Optimal Power Flows: A Case Study of the Algerian Electrical Network. Electronics, 13(19), 3848. https://doi.org/10.3390/electronics13193848






