A Graph Similarity Algorithm Based on Graph Partitioning and Attention Mechanism
Abstract
1. Introduction
2. Related Work
2.1. Graph Partitioning
2.2. Graph Neural Networks (GNN)
2.3. Graph Similarity Computation
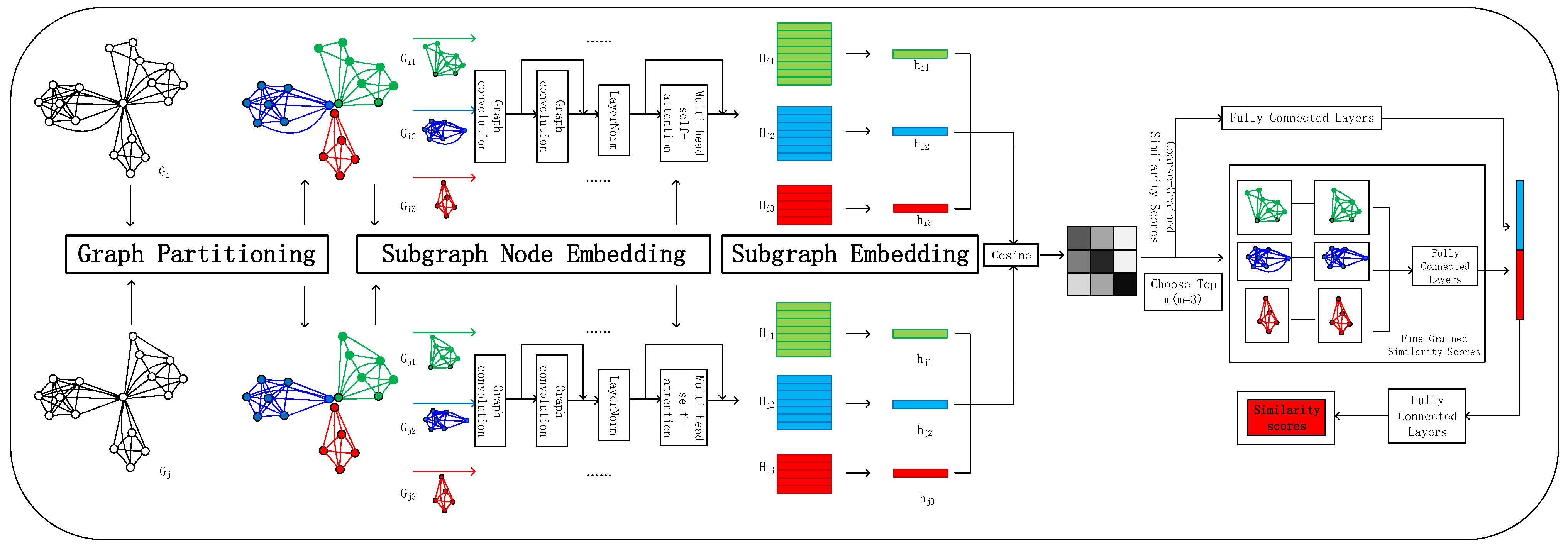
3. The Proposed Approach: APSimGNN
3.1. Problem Definition
3.2. Graph Partitioning
3.3. Subgraph Node Embedding
3.4. Subgraph Embedding
3.5. Graph Similarity Score Computation
4. Experiment
4.1. Dataset
4.2. Ground-Truth Generation
4.3. Results and Analysis
4.3.1. Baseline Methods
4.3.2. Parameter Settings
4.3.3. Evaluation Metrics
4.3.4. Result Analysis
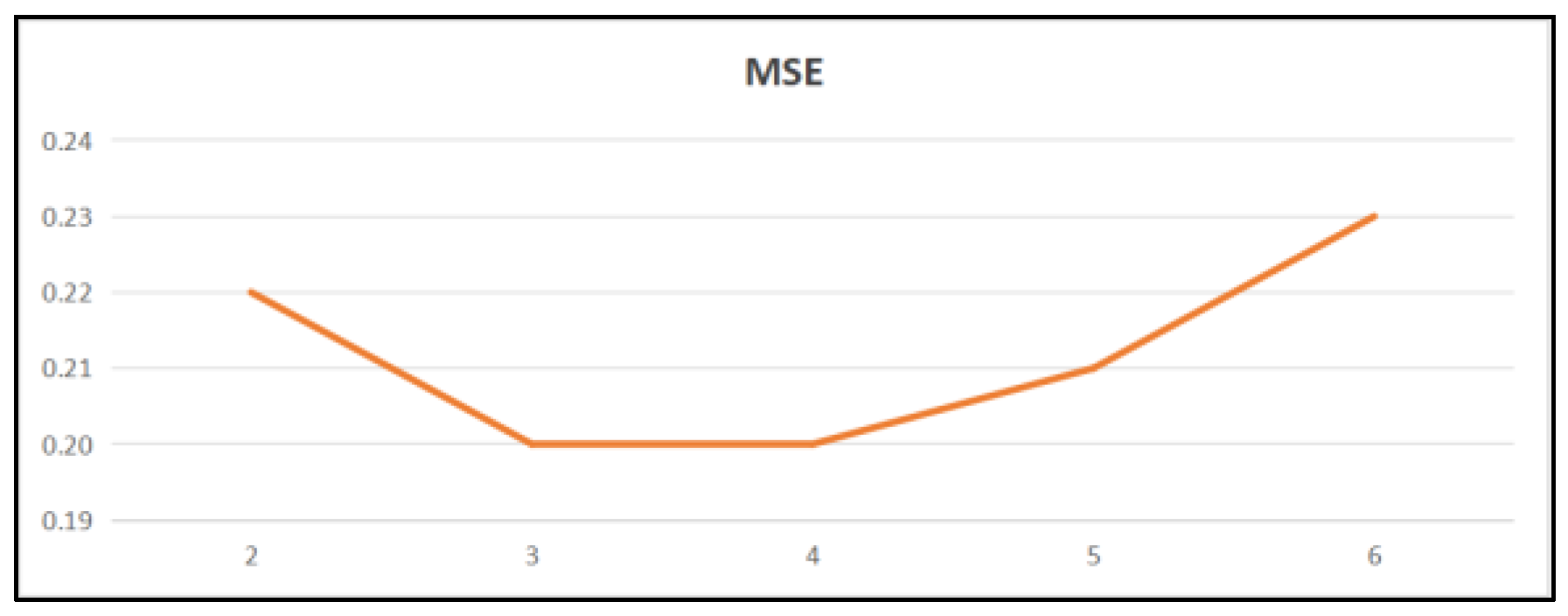
4.3.5. Parameter Optimization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miao, F.Y.; Wang, H.Z. Method for similarity join on uncertain graph database. J. Softw. 2018, 29, 3150–3163. (In Chinese) [Google Scholar]
- Blumenthal, D.B.; Boria, N.; Gamper, J.; Bougleux, S.; Brun, L. Comparing heuristics for graph edit distance computation. VLDB J. 2020, 29, 419–458. [Google Scholar] [CrossRef]
- Chang, L.; Feng, X.; Lin, X.; Qin, L.; Zhang, W.; Ouyang, D. Speeding up GED verification for graph similarity search. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020. [Google Scholar]
- Riesen, K.; Ferrer, M.; Bunke, H. Approximate graph edit distance in quadratic time. IEEE/ACM Trans. Comput. Biol. Bioinform. 2015, 17, 483–494. [Google Scholar] [CrossRef] [PubMed]
- Bunke, H. On a relation between graph edit distance and maximum common subgraph. Pattern Recognit. Lett. 1997, 18, 689–694. [Google Scholar] [CrossRef]
- Blumenthal, D.B.; Gamper, J. On the exact computation of the graph edit distance. Pattern Recognit. Lett. 2020, 134, 46–57. [Google Scholar] [CrossRef]
- Kim, J.; Choi, D.H.; Li, C. Inves: Incremental Partitioning-Based Verification for Graph Similarity Search. EDBT 2019. [Google Scholar] [CrossRef]
- Liang, Y.; Zhao, P. Similarity search in graph databases: A multi-layered indexing approach. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017. [Google Scholar]
- Blumenthal, D.B.; Gamper, J. Improved lower bounds for graph edit distance. IEEE Trans. Knowl. Data Eng. 2017, 30, 503–516. [Google Scholar] [CrossRef]
- Bai, Y.; Ding, H.; Bian, S.; Chen, T.; Sun, Y.; Wang, W. Simgnn: A neural network approach to fast graph similarity computation. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining (WSDM’19), New York, NY, USA, 11–15 February 2019. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. Adv. Neural Inf. Process. Syst. 2016, 29, 3844–3852. [Google Scholar]
- Bai, Y.; Ding, H.; Sun, Y.; Wang, W. Convolutional set matching for graph similarity. arXiv 2018, arXiv:1810.10866. [Google Scholar]
- Li, Y.; Gu, C.; Dullien, T.; Vinyals, O.; Kohli, P. Graph matching networks for learning the similarity of graph structured objects. In Proceedings of the 36th International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 3835–3845. [Google Scholar]
- Qin, Z.; Bai, Y.; Sun, Y. GHashing: Semantic graph hashing for approximate similarity search in graph databases. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 6–10 July 2020. [Google Scholar]
- Hou, Y.; Ning, B.; Hai, C.; Zhou, X.; Yang, C.; Li, G. NAGSim: A Graph Similarity Model Based on Graph Neural NetWorks and Attention Mechanism. J. Chin. Comput. Syst. 2023, 44, 1665–1671. [Google Scholar]
- Xu, H.; Duan, Z.; Wang, Y.; Feng, J.; Chen, R.; Zhang, Q.; Xu, Z. Graph partitioning and graph neural network based hierarchical graph matching for graph similarity computation. Neurocomputing 2021, 439, 348–362. [Google Scholar] [CrossRef]
- Parés, F.; Gasulla, D.G.; Vilalta, A.; Moreno, J.; Ayguadé, E.; Labarta, J.; Cortés, U.; Suzumura, T. Fluid communities: A competitive, scalable and diverse community detection algorithm. In Complex Networks & Their Applications VI. COMPLEX NETWORKS 2017; Cherifi, C., Cherifi, H., Karsai, M., Musolesi, M., Eds.; Studies in Computational Intelligence; Springer: Cham, Switzerland, 2018; Volume 689, pp. 229–240. [Google Scholar]
- Buluç, A.; Meyerhenke, H.; Safro, I.; Sanders, P.; Schulz, C. Recent advances in graph partitioning. In Algorithm Engineering. Lecture Notes in Computer Science; Kliemann, L., Sanders, P., Eds.; Springer: Cham, Switzerland, 2016; Volume 9220, pp. 117–158. [Google Scholar]
- Kaburlasos, V.G.; Moussiades, L.; Vakali, A. Fuzzy lattice reasoning (FLR) type neural computation for weighted graph partitioning. Neurocomputing 2009, 72, 2121–2133. [Google Scholar] [CrossRef]
- Adoni, H.W.Y.; Nahhal, T.; Krichen, M.; Aghezzaf, B.; Elbyed, A. A survey of current challenges in partitioning and processing of graph-structured data in parallel and distributed systems. Distrib. Parallel. Dat. 2020, 38, 495–530. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Ma, Y.; Wang, S.; Aggarwal, C.C.; Tang, J. Graph convolutional networks with eigenpooling. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD’19), New York, NY, USA, 4–8 August 2019. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful are Graph Neural Networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Qiu, J.; Chen, Q.; Dong, Y.; Zhang, J.; Yang, H.; Ding, M.; Wang, K.; Tang, J. Gcc: Graph contrastive coding for graph neural network pre-training. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD’20), New York, NY, USA, 6–10 July 2020. [Google Scholar]
- Xu, K.; Li, C.; Tian, Y.; Sonobe, T.; Kawarabayashi, K.; Jegelka, S. Representation learning on graphs with Jumping knowledge networks. In Proceedings of the 35th International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 5453–5462. [Google Scholar]
- Cai, L.; Li, J.; Wang, J.; Ji, S. Line graph neural networks for link prediction. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5103–5113. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y. Link prediction based on graph neural networks. Adv. Neural Inf. Process. Syst. 2018. [Google Scholar] [CrossRef]
- Liu, J.; Shang, X.; Song, L.; Tan, Y. Progress of Graph Neural Networks on Complex Graph Mining. J. Softw. 2022, 33, 3582–3618. (In Chinese) [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Bai, Y.; Ding, H.; Gu, K.; Sun, Y.; Wang, W. Learning-based efficient graph similarity computation via multi-scale convolutional set matching. Proc. AAAI Conf. Artif. Intell. 2020, 34, 3219–3226. [Google Scholar] [CrossRef]
- Doan, K.D.; Manchanda, S.; Mahapatra, S.; Reddy, C.K. Interpretable graph similarity computation via differentiable optimal alignment of node embeddings. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR’21), New York, NY, USA, 11–15 July 2021. [Google Scholar]
- Tan, W.; Gao, X.; Li, Y.; Wen, G.; Cao, P.; Yang, J.; Li, W.; Zaiane, O.R. Exploring attention mechanism for graph similarity learning. Knowl.-Based Syst. 2023, 276, 110739. [Google Scholar] [CrossRef]
- Yanardag, P.; Vishwanathan, S. Deep graph kernels. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’15), New York, NY, USA, 10–13 August 2015. [Google Scholar]
- Jain, N.; Liao, G.; Willke, T.L. Graphbuilder: Scalable graph etl Graphbuilder: Scalable graph etl framework. In First International Workshop on Graph Data Management Experiences and Systems (GRADES’13); ACM: New York, NY, USA, 2013. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jone, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
- Zeng, Z.; Tung, A.K.H.; Wang, J.; Feng, J.; Zhou, L. Comparing stars: On approximating graph edit distance. Proc. VLDB Endow. 2009, 2, 25–36. [Google Scholar] [CrossRef]

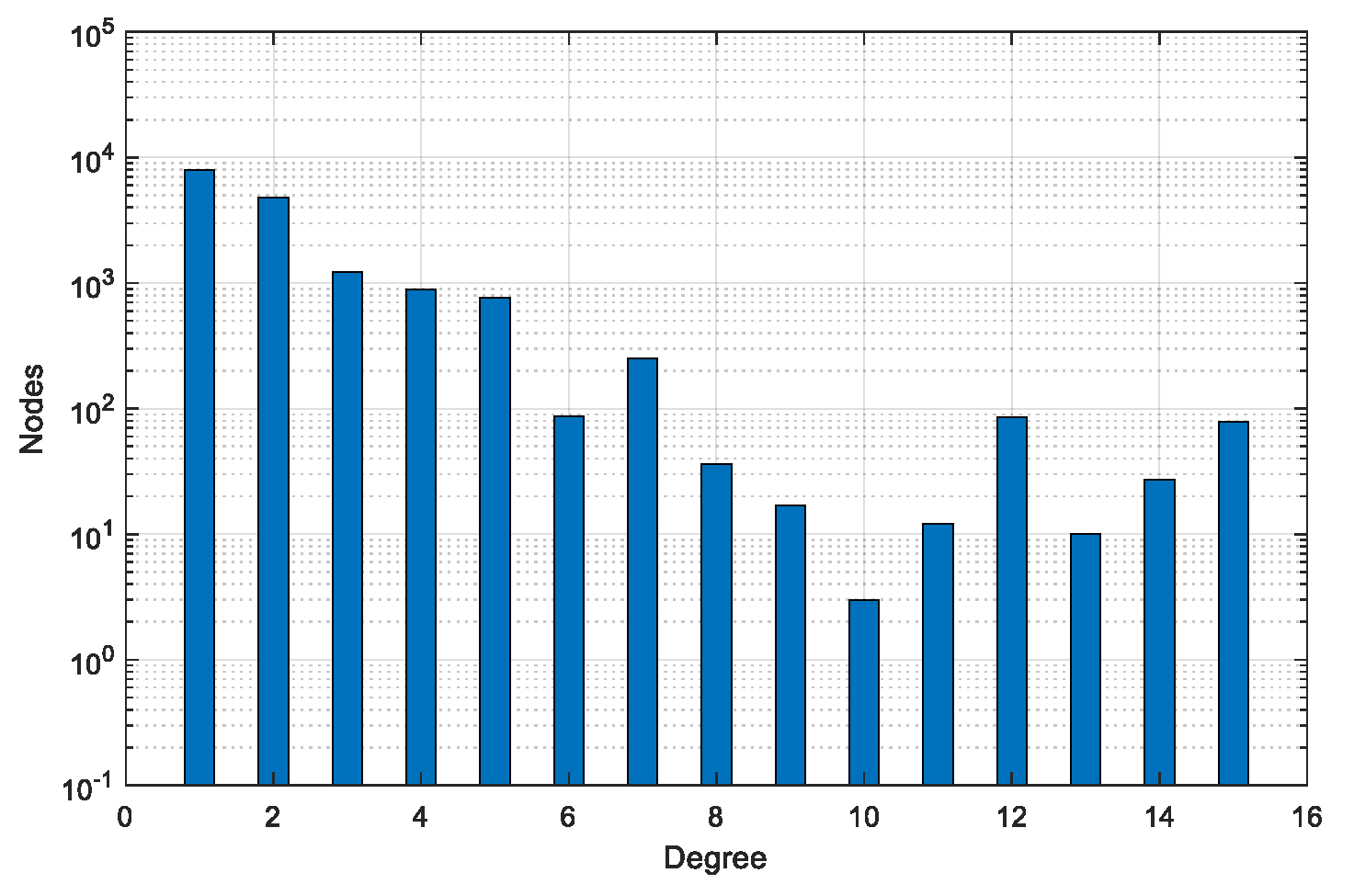
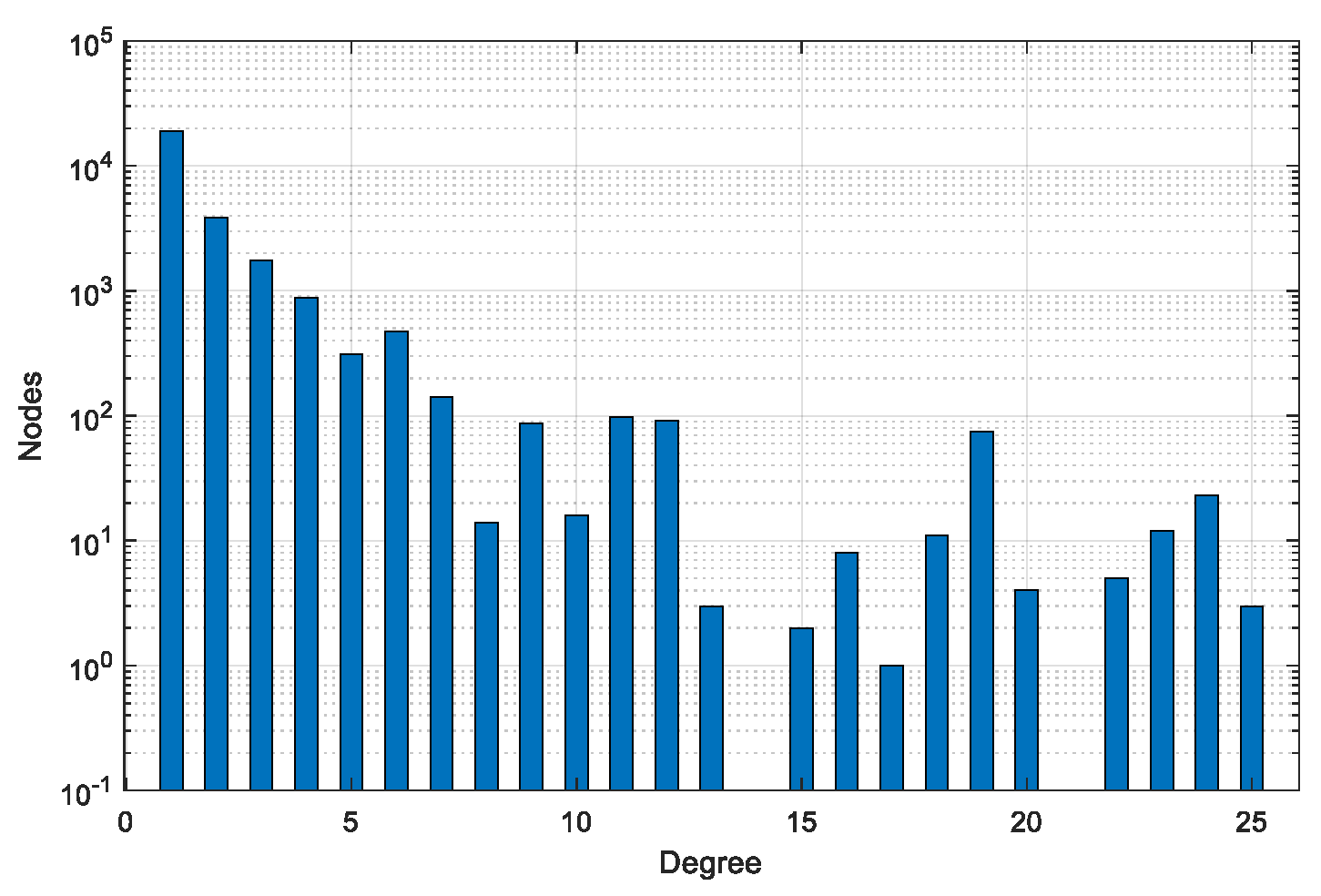
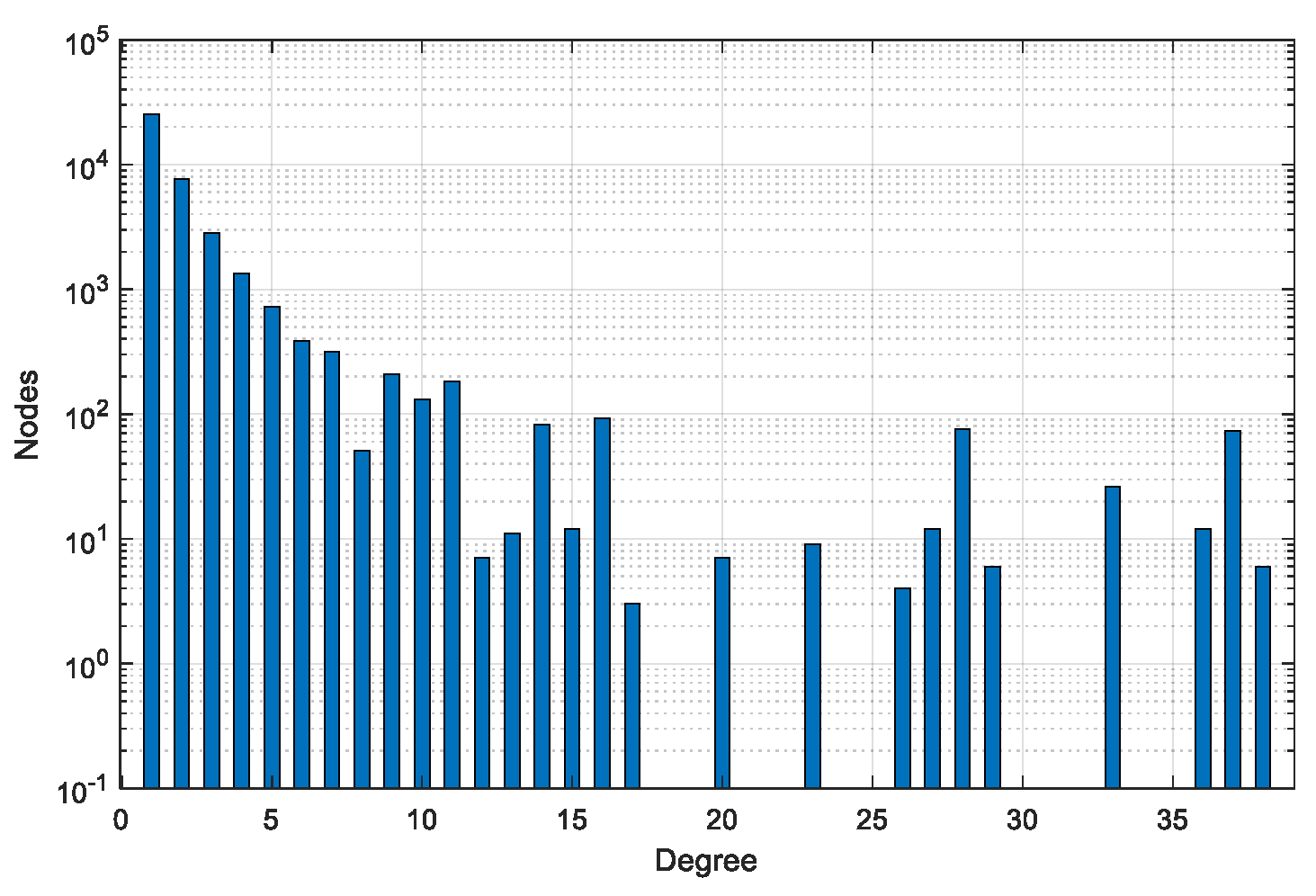
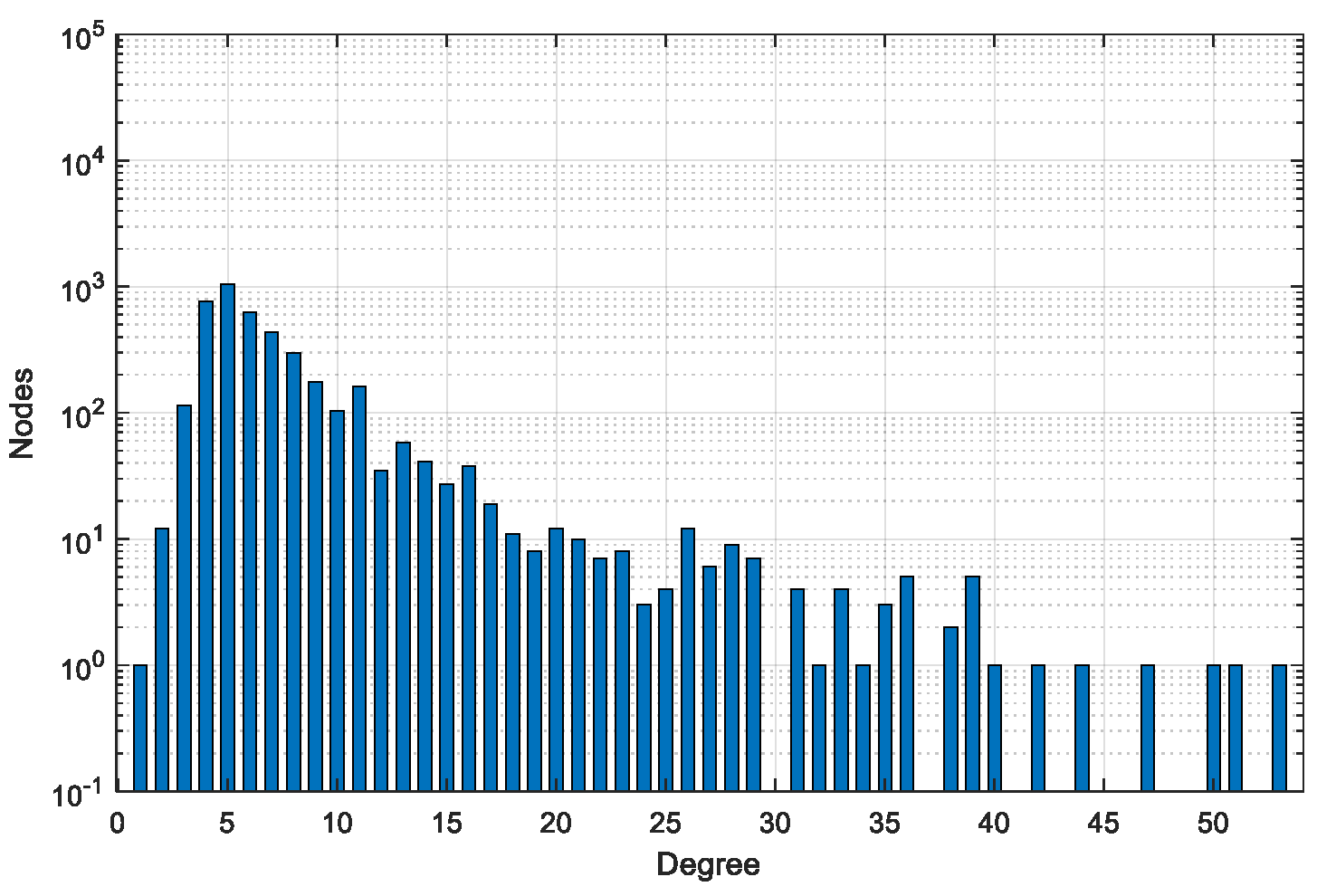

| Dataset | #Graphs | #Pairs | #Min Nodes | #Max Nodes | #Avg Nodes | #Min Edges | #Max Edges | #Avg Edges |
|---|---|---|---|---|---|---|---|---|
| BA-60 | 200 | 40,000 | 54 | 65 | 60 | 54 | 66 | 60 |
| BA-100 | 200 | 40,000 | 96 | 105 | 100 | 96 | 107 | 100 |
| BA-200 | 200 | 40,000 | 192 | 205 | 200 | 193 | 206 | 200 |
| IMDBX | 220 | 48,400 | 15 | 52 | 21 | 33 | 186 | 74 |
| IMDB | 1500 | 2,250,000 | 7 | 89 | 13 | 12 | 1467 | 66 |
| Methods | BA-60 | BA-100 | BA-200 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | ρ | τ | MSE | MAE | ρ | τ | MSE | MAE | ρ | τ | |
| GCN-Mean [11] | 0.58 | 5.39 | 0.756 | 0.532 | 1.25 | 9.09 | 0.763 | 0.533 | 2.37 | 12.78 | 0.734 | 0.488 |
| GCN-Max [11] | 1.37 | 9.14 | 0.746 | 0.523 | 1.20 | 8.54 | 0.761 | 0.530 | 2.28 | 10.76 | 0.749 | 0.516 |
| GSimCNN [12] | 0.60 | 5.61 | 0.807 | 0.604 | 0.23 | 3.25 | 0.823 | 0.616 | 0.32 | 3.58 | 0.796 | 0.568 |
| GMN [13] | 0.27 | 3.82 | 0.763 | 0.546 | 0.15 | 2.71 | 0.772 | 0.542 | 0.12 | 2.66 | 0.795 | 0.578 |
| SimGNN [10] | 0.78 | 6.58 | 0.773 | 0.567 | 0.80 | 6.93 | 0.763 | 0.538 | 0.84 | 6.19 | 0.734 | 0.488 |
| NAGSim [16] | 0.24 | 4.13 | 0.814 | 0.613 | 0.13 | 3.01 | 0.798 | 0.565 | 0.08 | 2.48 | 0.753 | 0.523 |
| PSimGNN [17] | 0.20 | 3.39 | 0.844 | 0.661 | 0.11 | 2.41 | 0.801 | 0.584 | 0.06 | 1.96 | 0.791 | 0.572 |
| APSimGNN | 0.18 | 3.32 | 0.859 | 0.632 | 0.09 | 2.21 | 0.832 | 0.613 | 0.05 | 1.88 | 0.821 | 0.596 |
| Methods | IMDBX | IMDB | ||||||
|---|---|---|---|---|---|---|---|---|
| MSE | MAE | ρ | τ | MSE | MAE | ρ | τ | |
| GCN-Mean [11] | 2.22 | 5.54 | 0.466 | 0.362 | 0.69 | 3.69 | 0.423 | 0.307 |
| GCN-Max [11] | 4.71 | 12.32 | 0.246 | 0.173 | 0.51 | 4.33 | 0.565 | 0.342 |
| GSimCNN [12] | 0.50 | 3.04 | 0.662 | 0.498 | 0.08 | 1.07 | 0.895 | 0.847 |
| GMN [13] | 0.38 | 2.73 | 0.695 | 0.553 | 0.08 | 0.97 | 0.853 | 0.818 |
| SimGNN [10] | 0.74 | 3.37 | 0.527 | 0.393 | 0.13 | 2.19 | 0.794 | 0.770 |
| NAGSim [16] | 0.45 | 2.57 | 0.683 | 0.457 | 0.11 | 1.36 | 0.832 | 0.792 |
| PSimGNN [17] | 0.31 | 2.51 | 0.723 | 0.603 | 0.07 | 0.78 | 0.859 | 0.822 |
| APSimGNN | 0.27 | 2.11 | 0.736 | 0.636 | 0.06 | 0.63 | 0.872 | 0.817 |
| Methods | BA-60 | BA-100 | BA-200 |
|---|---|---|---|
| GCN-Mean [11] | 256 | 348 | 408 |
| GCN-Max [11] | 284 | 368 | 452 |
| GSimCNN [12] | 100 | 124 | 224 |
| GMN [13] | 376 | 552 | 1500 |
| SimGNN [10] | 176 | 224 | 276 |
| NAGSim [16] | 147 | 213 | 319 |
| PSimGNN [17] | 624 | 800 | 1200 |
| APSimGNN | 553 | 616 | 824 |
| Methods | BA-60 | BA-100 | BA-200 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | ρ | τ | MSE | MAE | ρ | τ | MSE | MAE | ρ | τ | |
| APSimGNN-0 | 0.34 | 4.70 | 0.793 | 0.594 | 0.39 | 3.94 | 0.789 | 0.578 | 0.07 | 3.94 | 0.774 | 0.529 |
| APSimGNN-m | 0.28 | 4.02 | 0.825 | 0.616 | 0.12 | 2.39 | 0.814 | 0.597 | 0.06 | 2.03 | 0.793 | 0.553 |
| APSimGNN | 0.18 | 3.32 | 0.859 | 0.632 | 0.09 | 2.21 | 0.832 | 0.613 | 0.05 | 1.88 | 0.821 | 0.596 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, F.; Zhou, X.; Xiao, S.; Zhang, S. A Graph Similarity Algorithm Based on Graph Partitioning and Attention Mechanism. Electronics 2024, 13, 3794. https://doi.org/10.3390/electronics13193794
Miao F, Zhou X, Xiao S, Zhang S. A Graph Similarity Algorithm Based on Graph Partitioning and Attention Mechanism. Electronics. 2024; 13(19):3794. https://doi.org/10.3390/electronics13193794
Chicago/Turabian StyleMiao, Fengyu, Xiuzhuang Zhou, Shungen Xiao, and Shiliang Zhang. 2024. "A Graph Similarity Algorithm Based on Graph Partitioning and Attention Mechanism" Electronics 13, no. 19: 3794. https://doi.org/10.3390/electronics13193794
APA StyleMiao, F., Zhou, X., Xiao, S., & Zhang, S. (2024). A Graph Similarity Algorithm Based on Graph Partitioning and Attention Mechanism. Electronics, 13(19), 3794. https://doi.org/10.3390/electronics13193794





