Deep Learning Approach for Modeling the Power Consumption and Delay of Logic Circuits Employing GNRFET Technology
Abstract
1. Introduction
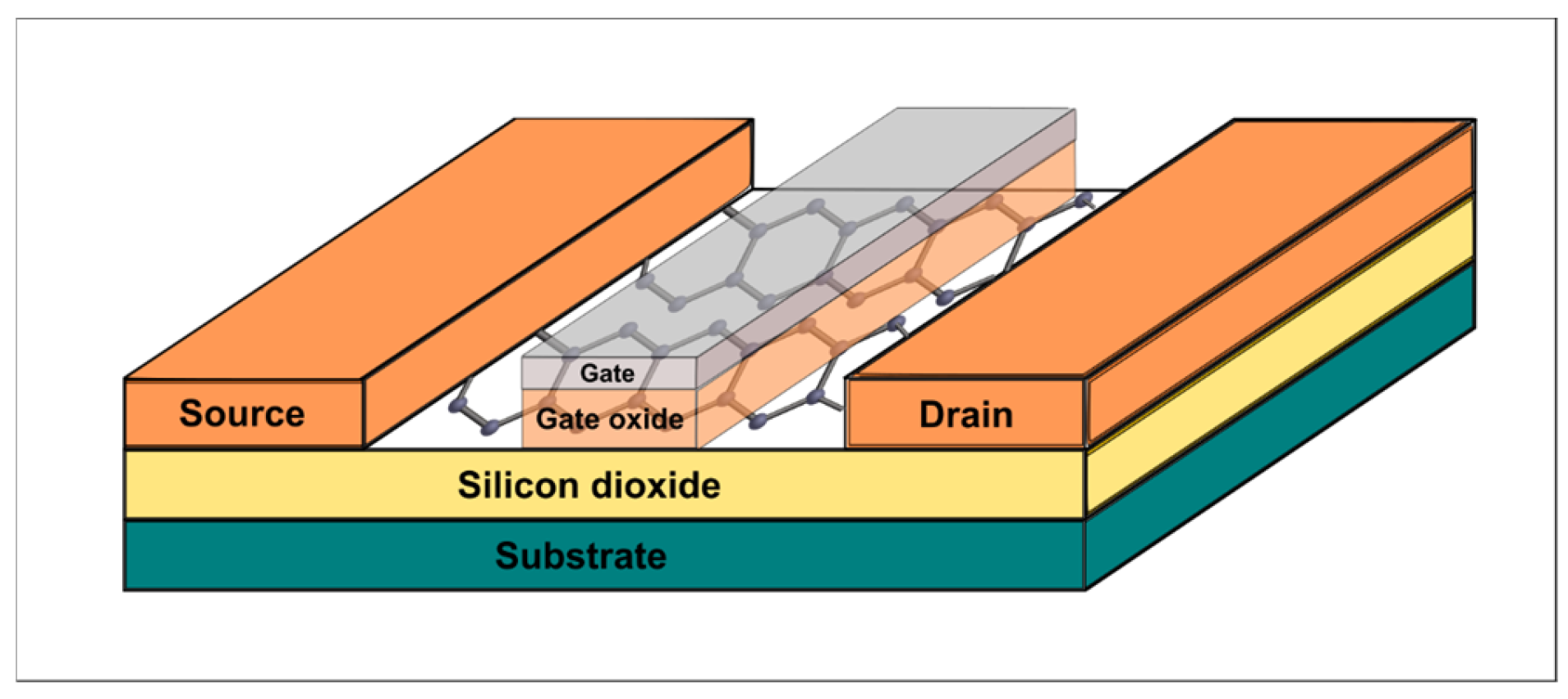
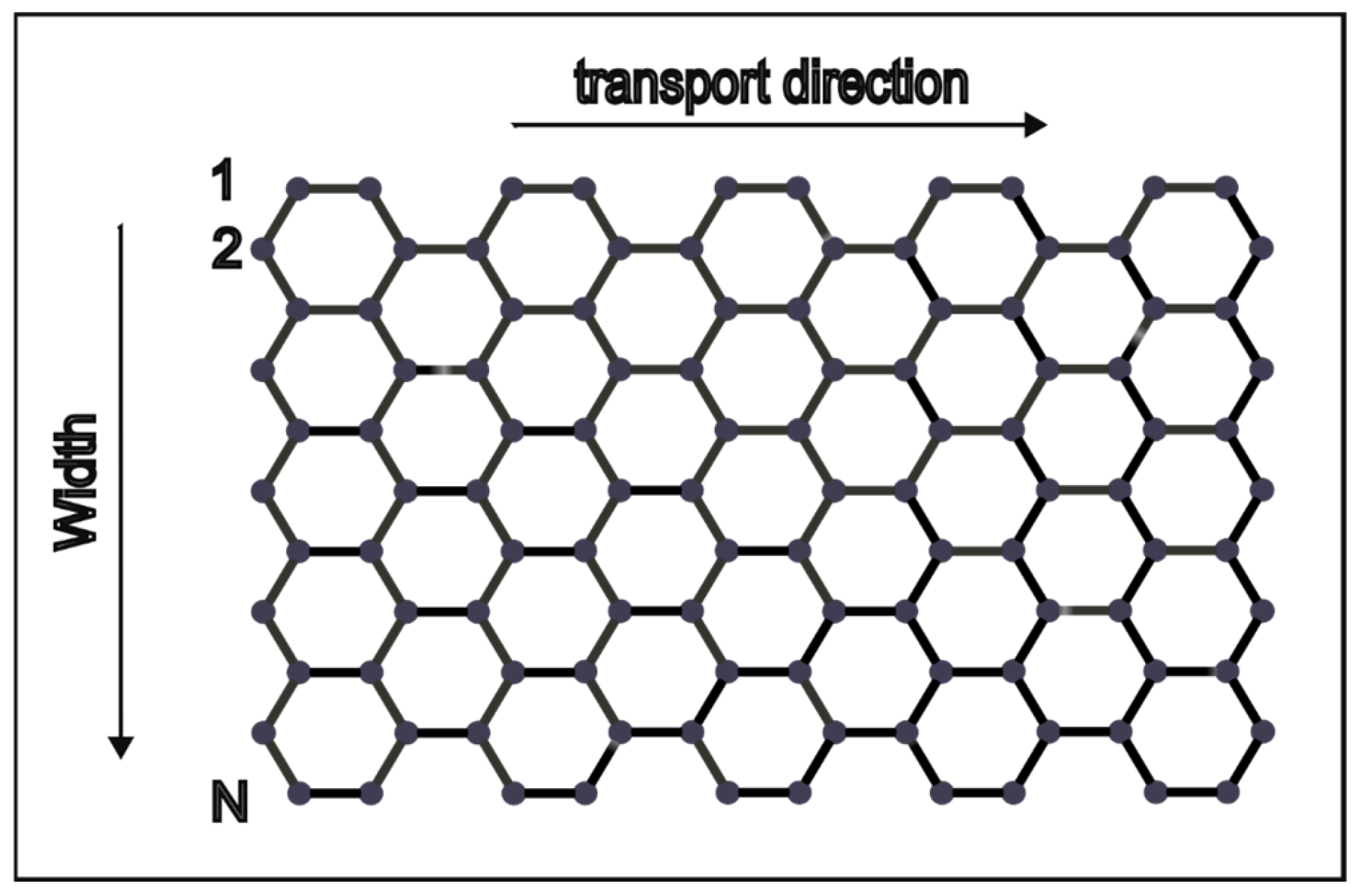
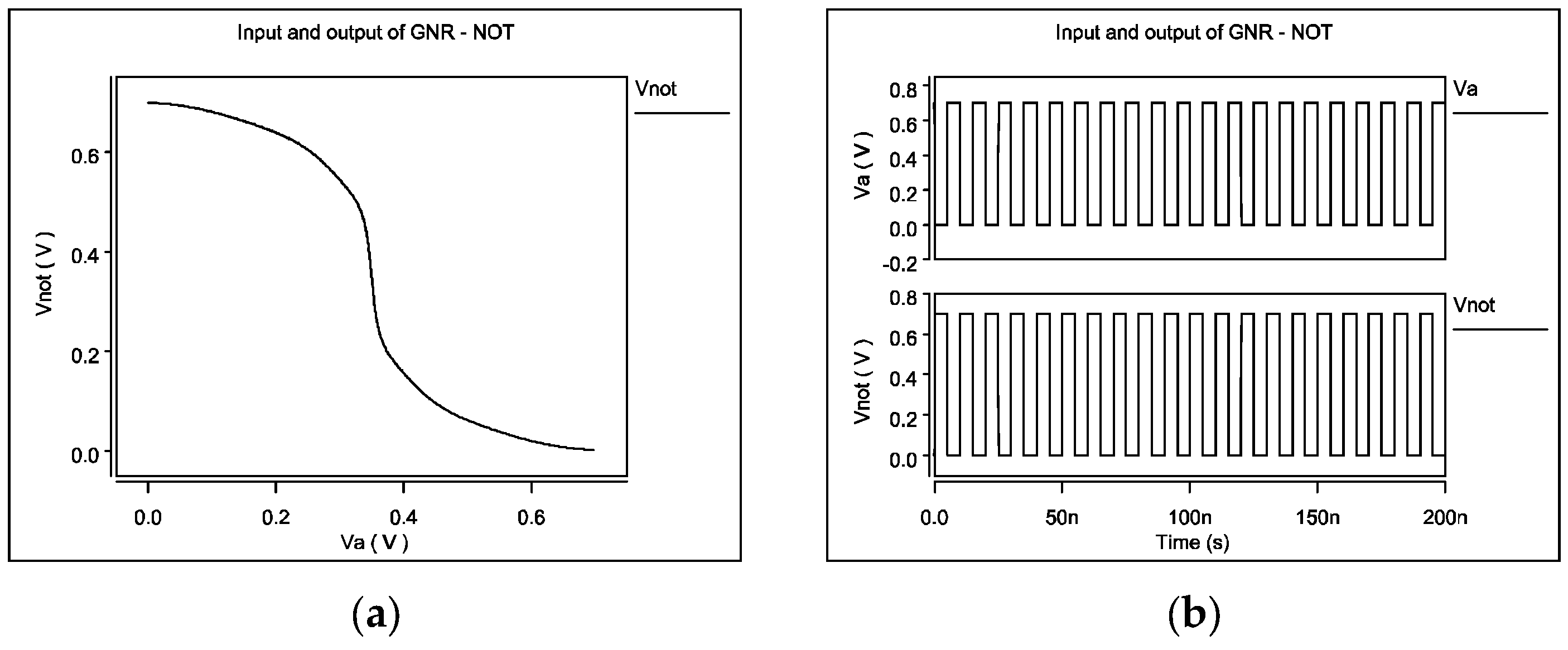
2. Description of the Utilized GNRFET Model
3. Logic Design Employing GNRFETs
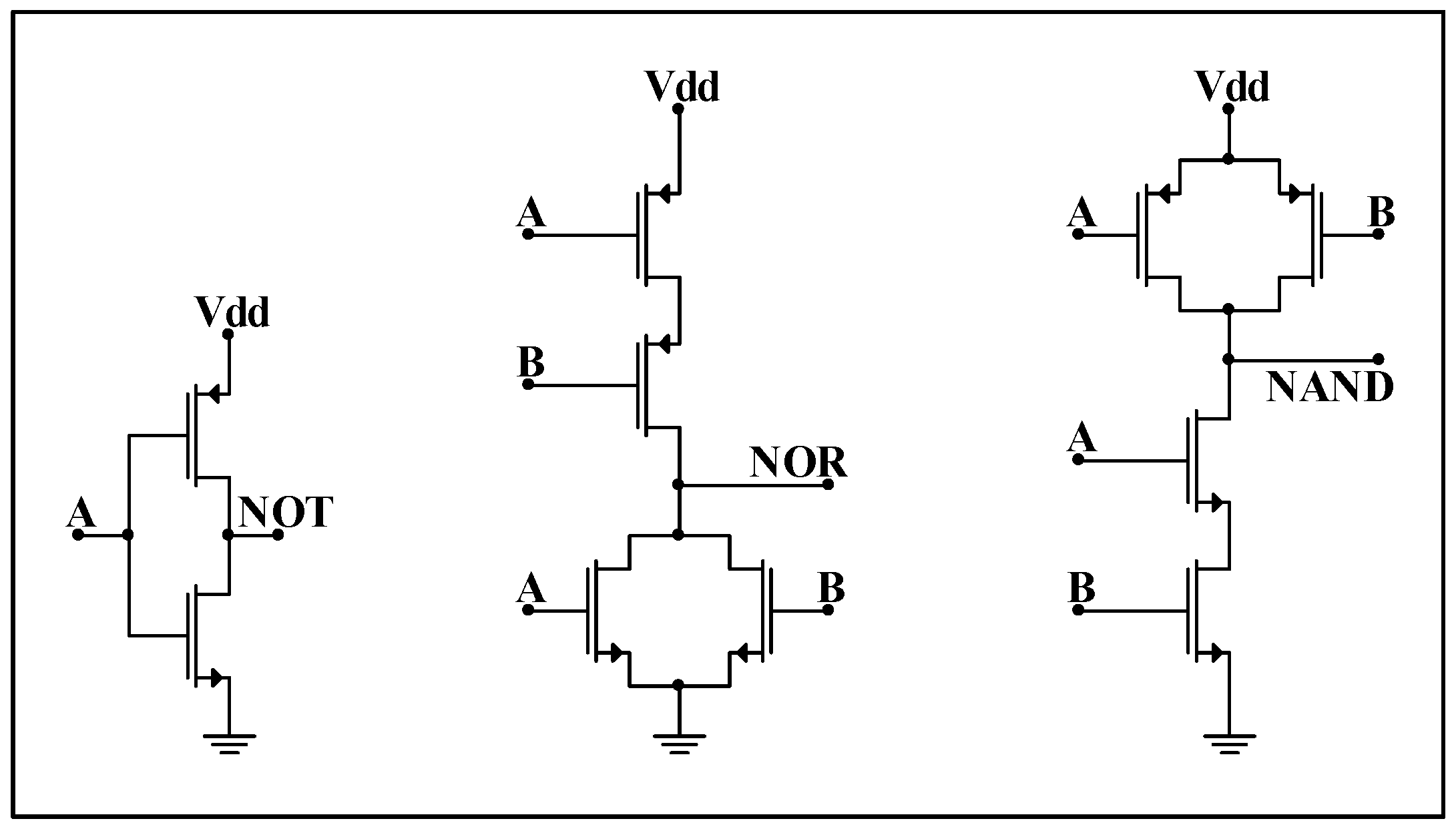
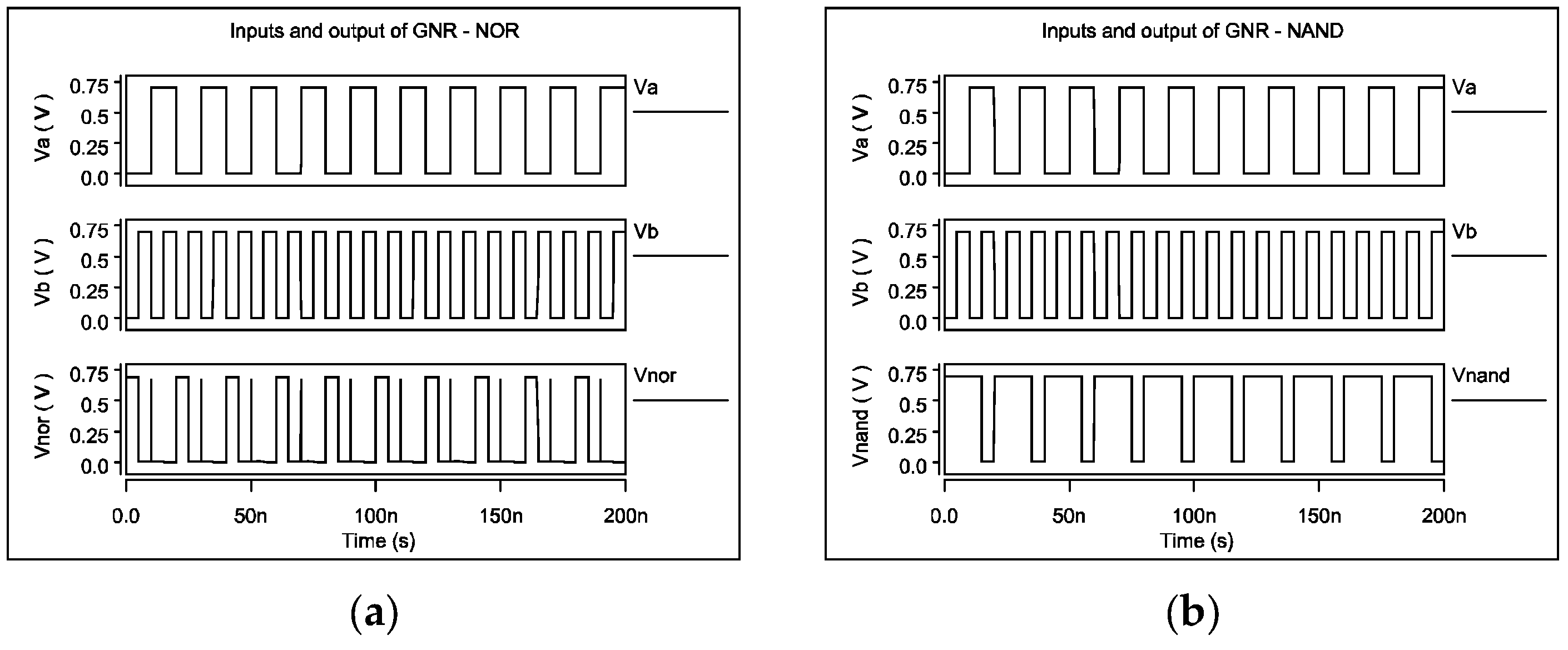
3.1. NOT, NOR and NAND Gates
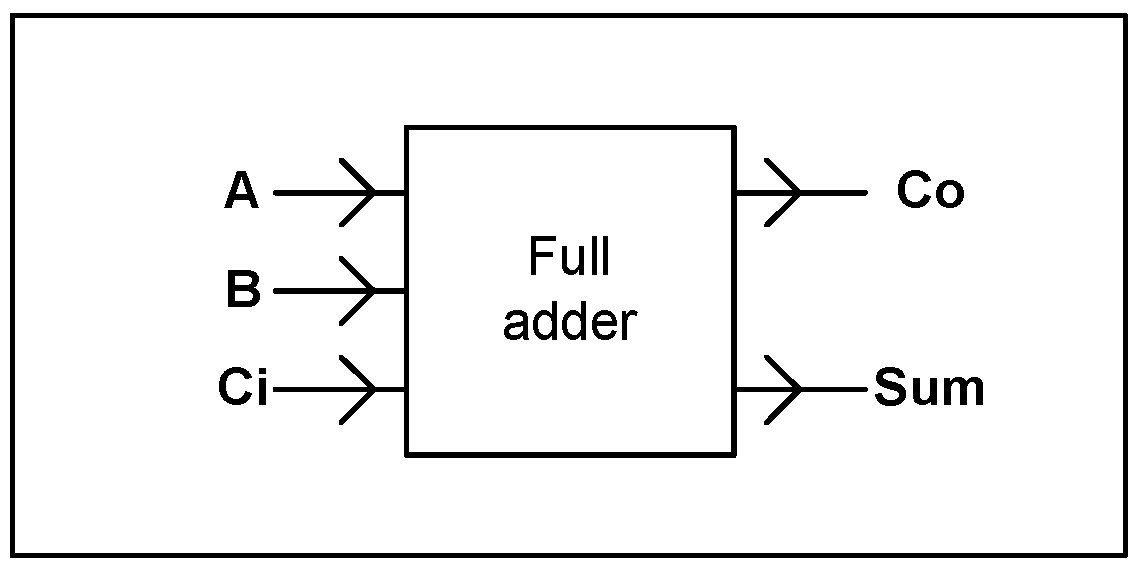
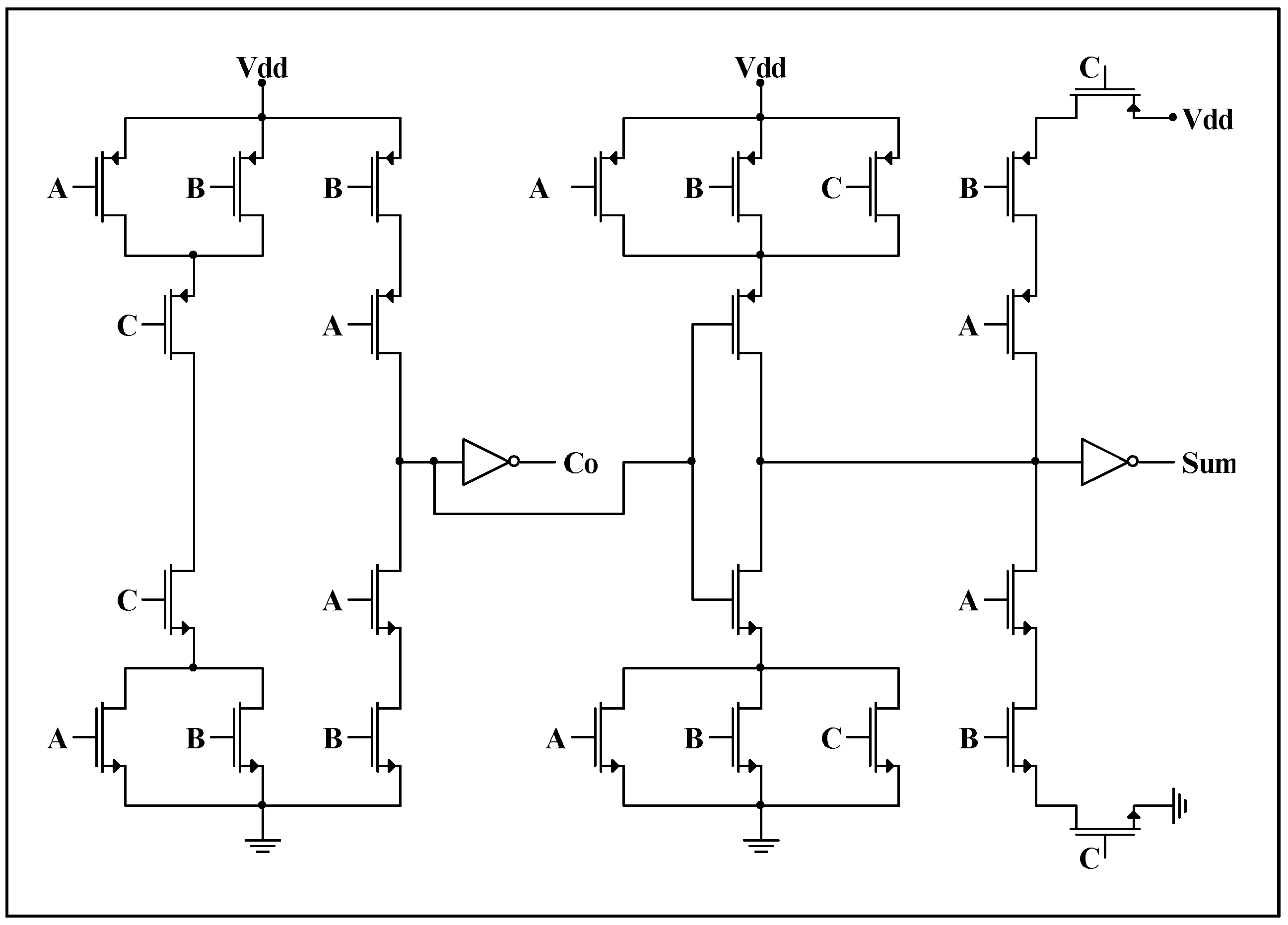
3.2. Full Adder
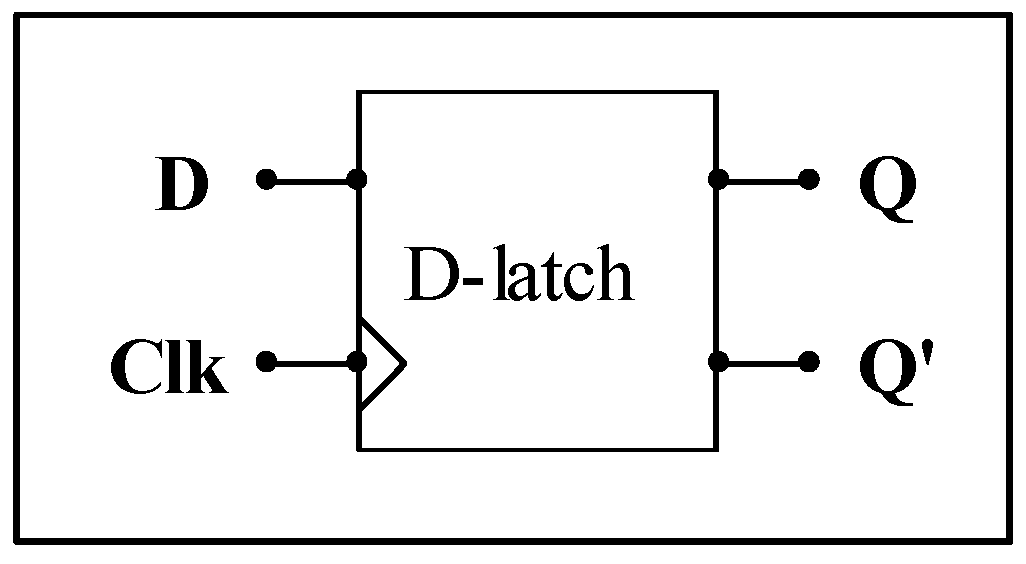
3.3. D-Latch
4. Comparison of the Performances of Silicon-Based CMOS and GNRFET-Based CMOS Logic Blocks
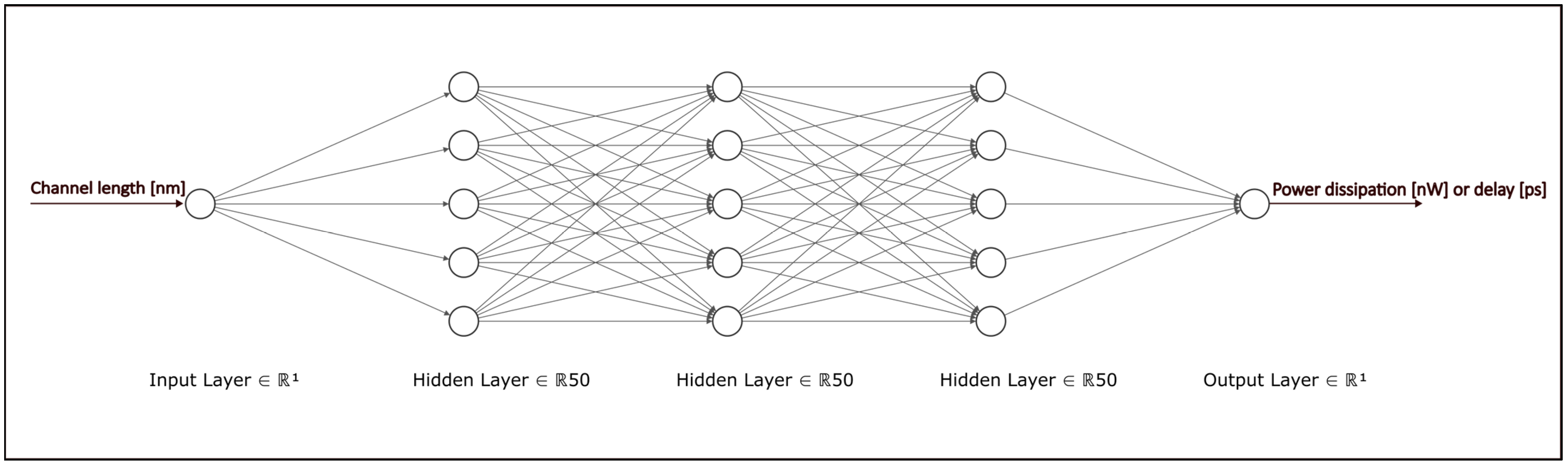
5. A Deep Learning Network Design for Power Consumption and Delay Modeling of GNRFET Logic
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Neamen, D.A. Microelectronics Circuit Analysis and Design; University of New Mexico: Albuquerque, NM, USA; McGraw-Hill: New York, NY, USA, 2010. [Google Scholar]
- Lin, J.; Hwang, Y.; Sheu, M.; Ho, C. A Novel High-Speed and Energy Efficient 10-Transistor Full Adder Design. IEEE Trans. Circuits Syst. 1-Regul. Pap. 2007, 54, 1050–1059. [Google Scholar] [CrossRef]
- Amini-Valashani, M.; Ayat, M.; Mirzakuchaki, S. Design and Analysis of a Novel Low Power and Energy-Efficient 18T Hybrid Full Adder. Microelectron. J. 2018, 74, 49–59. [Google Scholar] [CrossRef]
- Hussain, S.; Hasan, M.; Agrawal, G.; Hasan, M. A High-Performance Full Swing 1-Bit Hybrid Full Adder Cell. IET Circuit Devices Syst. 2021, 16, 210–217. [Google Scholar] [CrossRef]
- Rafik, M.; Pitchai, K. Design and Analysis of XOR-XNOR Circuit Based Modified Hybrid Full Adder. In Proceedings of the IEEE Delhi Section Conference (DELCON) 2022, New Delhi, India, 11–13 February 2022; Available online: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=9752792 (accessed on 28 June 2024).
- Rafiee, M.; Shiri, N.; Sadeghi, A. High-Performance 1-Bit Full Adder with Excellent Driving Capability for Multistage Structures. IEEE Embed. Syst. Lett. 2022, 14, 47–50. [Google Scholar] [CrossRef]
- Teotia, P.; Shah, O.A. Power and Area Efficient Sense Amplifier Based Flip Flop with Wide Voltage and Temperature Upholding for Portable IoT Applications. Inf. Midem-J. Microelectron. Electron. Compon. Mater. 2023, 53, 39–48. [Google Scholar] [CrossRef]
- Dai, G.; Xie, W.; Du, X.; Han, M.; Ni, T.; Wu, D. Memristor-Based D-Flip-Flop Design and Application in Built-In Self-Test. Electronics 2023, 12, 3019. [Google Scholar] [CrossRef]
- Khana, S.; Shahb, A.P.; Chouhanc, S.S.; Guptaa, N.; Pandeyd, J.G.; Vishvakarma, S.K. A symmetric D flip-flop based PUF with improved uniqueness. Microelectron. Reliab. 2020, 106, 113595. [Google Scholar] [CrossRef]
- Rao, K.M.; Mohanraj, J. Design a high efficient optical composite D/T flip-flop. Int. J. Syst. Assur. Eng. Manag. 2023. [Google Scholar] [CrossRef]
- Karimi, A.; Rezai, A.; Hajhashemkhani, M.M. Ultra-Low Power Pulse-Triggered CNTFET-Based Flip-Flop. IEEE Trans. Nanotechnol. 2019, 18, 756–761. [Google Scholar] [CrossRef]
- Zhao, P.; McNeely, J.B.; Golconda, P.K.; Venigalla, S.; Wang, N.; Bayoumi, M.A.; Kuang, W.; Downey, L. Low-Power Clocked-Pseudo-NMOS Flip-Flop for Level Conversion in Dual Supply Systems. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2009, 17, 1196–1202. [Google Scholar] [CrossRef]
- Wakabayashi, K.; Fujita, M.; Ajiki, H.; Sigrist, M. Electronic and Magnetic Properties of Nanographite Ribbons. Phys. Rev. B 1999, 59, 8271–8276. [Google Scholar] [CrossRef]
- Nakada, K.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 1996, 54, 17954–17961. [Google Scholar] [CrossRef] [PubMed]
- Brey, L.; Fertig, H.A. Electronic States of Graphene Nanoribbons. Phys. Rev. B 2006, 73, 235411–235418. [Google Scholar] [CrossRef]
- Yang, L.; Park, C.-H.; Son, Y.-W.; Cohen, M.L.; Louie, S.G. Quasiparticle Energies and Band Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 2007, 99, 186801–186805. [Google Scholar] [CrossRef] [PubMed]
- Adesina, N.O.; Srivastava, A.; Khan, M.A.U. Evaluating the performances of memristor, FinFET, and graphene TFET in VLSI circuit design. In Proceedings of the 2021 IEEE 11th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 27–30 January 2021; pp. 0591–0595. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Arora, V.K. Introduction to carbon nanotubes and nanoribbons. In Graphene, Nanotubes and Quantum Dots-Based Nanotechnology; Elsevier: Amsterdam, The Netherlands, 2022; pp. 231–251. [Google Scholar] [CrossRef]
- Available online: https://www.ee.iitm.ac.in/~nagendra/cadinfo.html (accessed on 28 June 2024).
- Chen, Y.-Y.; Sangai, A.; Rogachev, A.; Gholipour, M.; Iannaccone, G.; Fiori, G.; Chen, D. A SPICE-Compatible Model of MOS-Type Graphene Nano-Ribbon Field-Effect Transistors Enabling Gateand Circuit-Level Delay and Power Analysis Under Process Variation. IEEE Trans. Nanotechnol. 2015, 14, 1068–1082. [Google Scholar] [CrossRef]
- Florance, D.R.; Prabhakar, B. Design of joint reconfigurable hybrid adder and subtractor using FinFET and GnrFET technologies. Integration 2023, 88, 32–42. [Google Scholar] [CrossRef]
- Wang, L.; Fu, Y.; LaCroix, M.-A.; Chong, E.; Carusone, A.C. A 64-Gb/s 4-PAM transceiver utilizing an adaptive threshold ADC in 16-nm FinFET. IEEE J. Solid-State Circuits 2018, 54, 452–462. [Google Scholar] [CrossRef]
- Geron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Newton, MA, USA, 2019; ISBN 978-1492032649. [Google Scholar]
- Chollet, F. Deep Learning with Python; Manning: Clarendon County, SC, USA, 2017; ISBN 978-1617294433. [Google Scholar]
- Cantón Croda, R.M.; Gibaja Romero, D.n.E.; Caballero Morales, S.O. Sales prediction through neural networks for a small dataset. Int. J. Interact. Multimed. Artif. Intell. 2019, 5, 35–41. [Google Scholar] [CrossRef]
- Nassif, A.B.; Ho, D.; Capretz, L.F. Towards an early software estimation using log-linear regression and a multilayer perceptron model. J. Syst. Softw. 2013, 86, 144–160. [Google Scholar] [CrossRef]
- Fujita, T.; Sato, A.; Narita, A.; Sone, T.; Iokawa, K.; Tsuchiya, K.; Yamane, K.; Yamamoto, Y.; Ohira, Y.; Otsuki, K. Use of a multilayer perceptron to create a prediction model for dressing independence in a small sample at a single facility. J. Phys. Ther. Sci. 2019, 31, 69–74. [Google Scholar] [CrossRef]
- Walde, J.F.; Tappeiner, G.; Tappeiner, U.; Tasser, E.; Holub, H.W. Statistical aspects of multilayer perceptrons under data limitations. Comput. Stat. Data Anal. 2004, 46, 173–188. [Google Scholar] [CrossRef]
- Ingrassia, S.; Morlini, I. Neural network modeling for small datasets. Technometrics 2005, 47, 297–311. [Google Scholar] [CrossRef]


| Ci | A | B | Co | Sum | Result |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | (0)10 |
| 0 | 0 | 1 | 0 | 1 | (1)10 |
| 0 | 1 | 0 | 0 | 1 | (1)10 |
| 0 | 1 | 1 | 1 | 0 | (2)10 |
| 1 | 0 | 0 | 0 | 1 | (1)10 |
| 1 | 0 | 1 | 1 | 0 | (2)10 |
| 1 | 1 | 0 | 1 | 0 | (2)10 |
| 1 | 1 | 1 | 1 | 1 | (3)10 |
| D | Clk | Qn | Qn′ |
|---|---|---|---|
| 0 | 0 | Qc | Qc’ |
| 0 | 1 | 0 | 1 |
| 1 | 0 | Qc | Qc′ |
| 1 | 1 | 1 | 0 |
| Parame | Design | Unit | Value |
|---|---|---|---|
| Vdd = Vi+ | Both | V | 0.7 |
| Vgnd = Vi− | Both | V | 0 |
| Input wave | Both | - | Square |
| Input frequency | Both | MHz | 100 |
| R (load) | Both | MΩ | 1000 |
| Wp/Wn | MOS | nm | 14/7 |
| Wp = Wn | GNR | nm | 7/7 |
| Lp = Ln | Both | nm | 7/7 |
| Np = Nn | GNR | - | 42 |
| Circuit/Input | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| NOT-MOS | - | - | - | - | - | - | 9.41 | 692.52 |
| NOT-Fin | - | - | - | - | - | - | 0.45 | 699.27 |
| NOT-GNR | - | - | - | - | - | - | 1.61 | 698.38 |
| NOR-MOS | - | - | - | - | 0.14 | 4.46 | 7.68 | 672.52 |
| NOR-Fin | - | - | - | - | 0.00 | 0.32 | 0.43 | 697.09 |
| NOR-GNR | - | - | - | - | 0.14 | 1.43 | 1.52 | 693.58 |
| NAND-MOS | - | - | - | - | 33.36 | 695.70 | 693.38 | 699.82 |
| NAND-Fin | - | - | - | - | 1.78 | 699.39 | 699.28 | 699.95 |
| NAND-GNR | - | - | - | - | 6.39 | 698.57 | 698.48 | 699.86 |
| FA-Co-MOS | 692.44 | 688.27 | 689.14 | 11.77 | 690.32 | 12.63 | 13.28 | 9.51 |
| FA-Co-Fin | 699.27 | 699.24 | 699.24 | 0.48 | 699.25 | 0.48 | 0.49 | 0.45 |
| FA-Co-GNR | 698.35 | 698.03 | 698.04 | 1.97 | 698.03 | 1.95 | 1.96 | 1.64 |
| FA-Sum-MOS | 687.72 | 13.88 | 14.13 | 688.52 | 13.25 | 687.52 | 688.06 | 14.52 |
| FA-Sum-Fin | 699.22 | 0.50 | 0.47 | 699.24 | 0.50 | 699.24 | 699.24 | 0.52 |
| FA-Sum-GNR | 697.58 | 1.99 | 2.01 | 698.00 | 2.00 | 697.99 | 698.00 | 2.41 |
| DL-Q-MOS | - | - | - | - | 699.64 | 37.05 | 34.99 | 692.59 |
| DL-Q-Fin | - | - | - | - | 699.95 | 1.81 | 1.80 | 699.37 |
| DL-Q-GNR | - | - | - | - | 699.82 | 6.77 | 6.59 | 698.22 |
| Circuit/Input | Avg. Power (nW) | PGNR /PMOS | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|---|---|
| NOT-MOS | 1250.60 | 18.50% | - | - | - | - | - | - | 1514.80 | 986.45 |
| NOT-Fin | 625.72 | - | - | - | - | - | - | 580.42 | 671.03 | |
| NOT-GNR | 231.40 | - | - | - | - | - | - | 226.28 | 236.52 | |
| NOR-MOS | 945.39 | 24.56% | - | - | - | - | 44.56 | 735.30 | 1241.40 | 1760.30 |
| NOR-Fin | 583.61 | - | - | - | - | 28.84 | 404.76 | 567.89 | 1332.0 | |
| NOR-GNR | 232.19 | - | - | - | - | 41.22 | 204.02 | 218.75 | 464.77 | |
| NAND-MOS | 1025.00 | 22.94% | - | - | - | - | 2602.50 | 574.06 | 876.26 | 47.21 |
| NAND-Fin | 610.88 | - | - | - | - | 1153.80 | 552.27 | 660.92 | 76.50 | |
| NAND-GNR | 235.11 | - | - | - | - | 475.08 | 206.99 | 217.65 | 40.73 | |
| FA-MOS | 6570.30 | 21.38% | 4335.20 | 7731.60 | 7387.50 | 6518.90 | 6222.60 | 7505.90 | 7561.40 | 5299.20 |
| FA-Fin | 3378.30 | 2555.40 | 3700.10 | 3637.00 | 3428.30 | 3305.90 | 3711.50 | 3667.90 | 3019.80 | |
| FA-GNR | 1404.90 | 1270.50 | 1437.60 | 1458.50 | 1447.40 | 1445.70 | 1446.10 | 1470.20 | 1263.30 | |
| DL-MOS | 6790.60 | 19.50% | - | - | - | - | 7564.20 | 6465.20 | 7410.10 | 5722.60 |
| DL-Fin | 3382.10 | - | - | - | - | 3539.00 | 3080.10 | 3746.70 | 3162.50 | |
| DL-GNR | 1324.30 | - | - | - | - | 1413.00 | 1217.30 | 1443.90 | 1223.00 |
| Circuit/Delay | Average Delay | Delay Ratio (MOS/GNR) | td4 | td3 | td2 | td1 |
|---|---|---|---|---|---|---|
| NOT-MOS | 1.15 | 43.48% | - | - | 0.87 | 1.44 |
| NOT-Fin | 1.19 | - | - | 0.59 | 1.79 | |
| NOT-GNR | 0.50 | - | - | 0.45 | 0.55 | |
| NOR-MOS | 1.84 | 65.67% | - | - | none | 3.67 |
| NOR-Fin | 1.77 | - | - | none | 3.54 | |
| NOR-GNR | 1.21 | - | - | none | 2.41 | |
| NAND-MOS | 0.88 | 77.14% | - | - | 1.75 | none |
| NAND-Fin | 0.92 | - | - | 1.84 | none | |
| NAND-GNR | 0.68 | - | - | 1.35 | none | |
| FA-Co-MOS | 4.09 | 34.47% | 5.05 | 2.69 | 5.12 | 3.49 |
| FA-Co-Fin | 3.07 | 3.82 | 1.62 | 3.84 | 2.97 | |
| FA-Co-GNR | 1.06 | 1.86 | none | 0.79 | 1.59 | |
| FA-Sum-MOS | 6.73 | 18.57% | 14.07 | 8.90 | 3.63 | 0.30 |
| FA-Sum-Fin | 6.15 | 13.60 | 7.78 | 3.22 | none | |
| FA-Sum-GNR | 0.31 | none | 1.25 | none | none | |
| DL-MOS | 5.79 | 40.93% | - | - | 4.05 | 7.52 |
| DL-Fin | 5.19 | - | - | 3.68 | 6.71 | |
| DL-GNR | 2.37 | - | - | 1.99 | 2.75 |
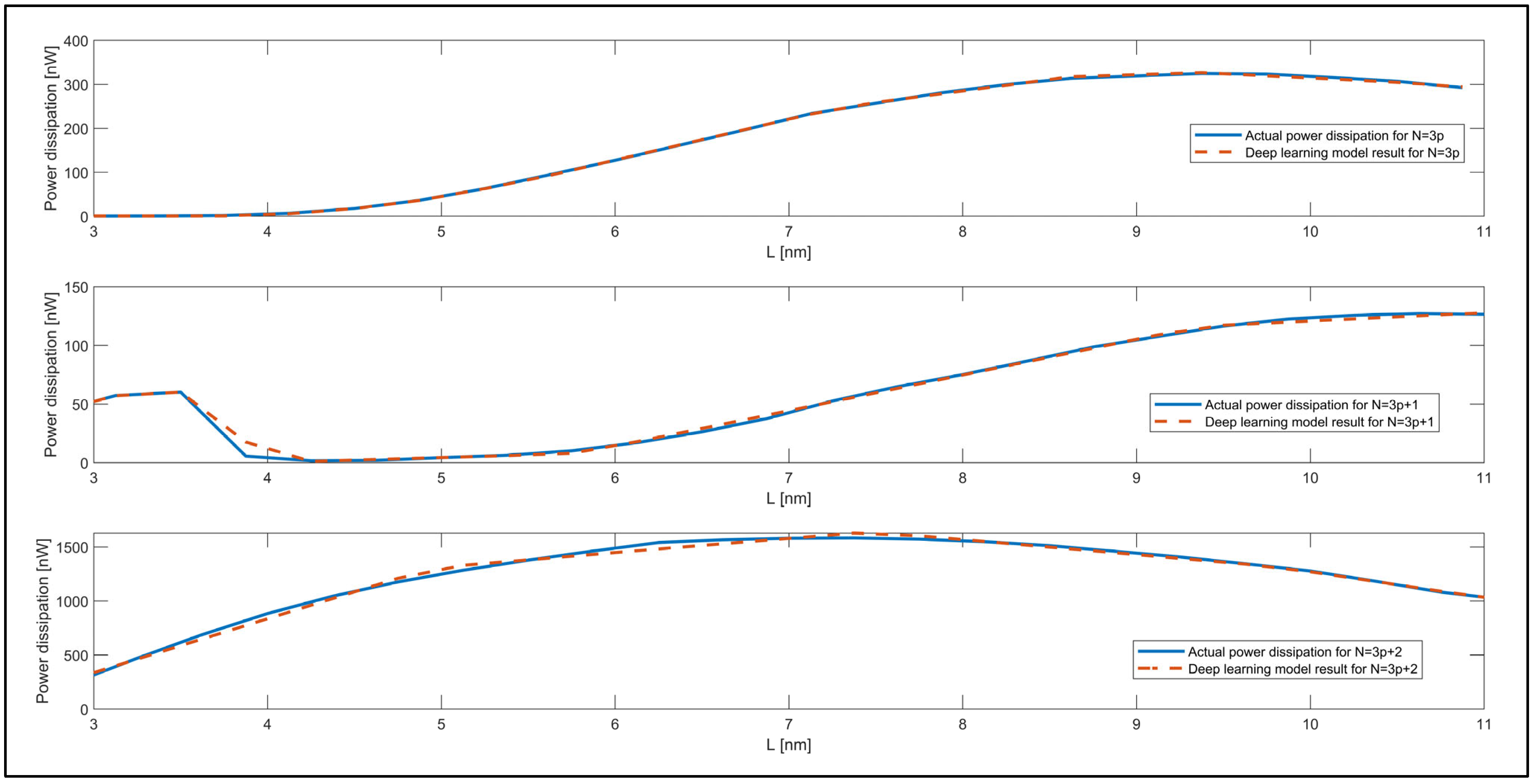
| Power Dissipation | R2 | MAPE | MAE | RMSE |
|---|---|---|---|---|
| for N = 3p | 0.99 | 0.04 | 1.42 | 1.85 |
| for N = 3p + 1 | 0.99 | 0.15 | 1.61 | 2.90 |
| for N = 3p + 2 | 0.94 | 0.03 | 3.74 | 8.23 |
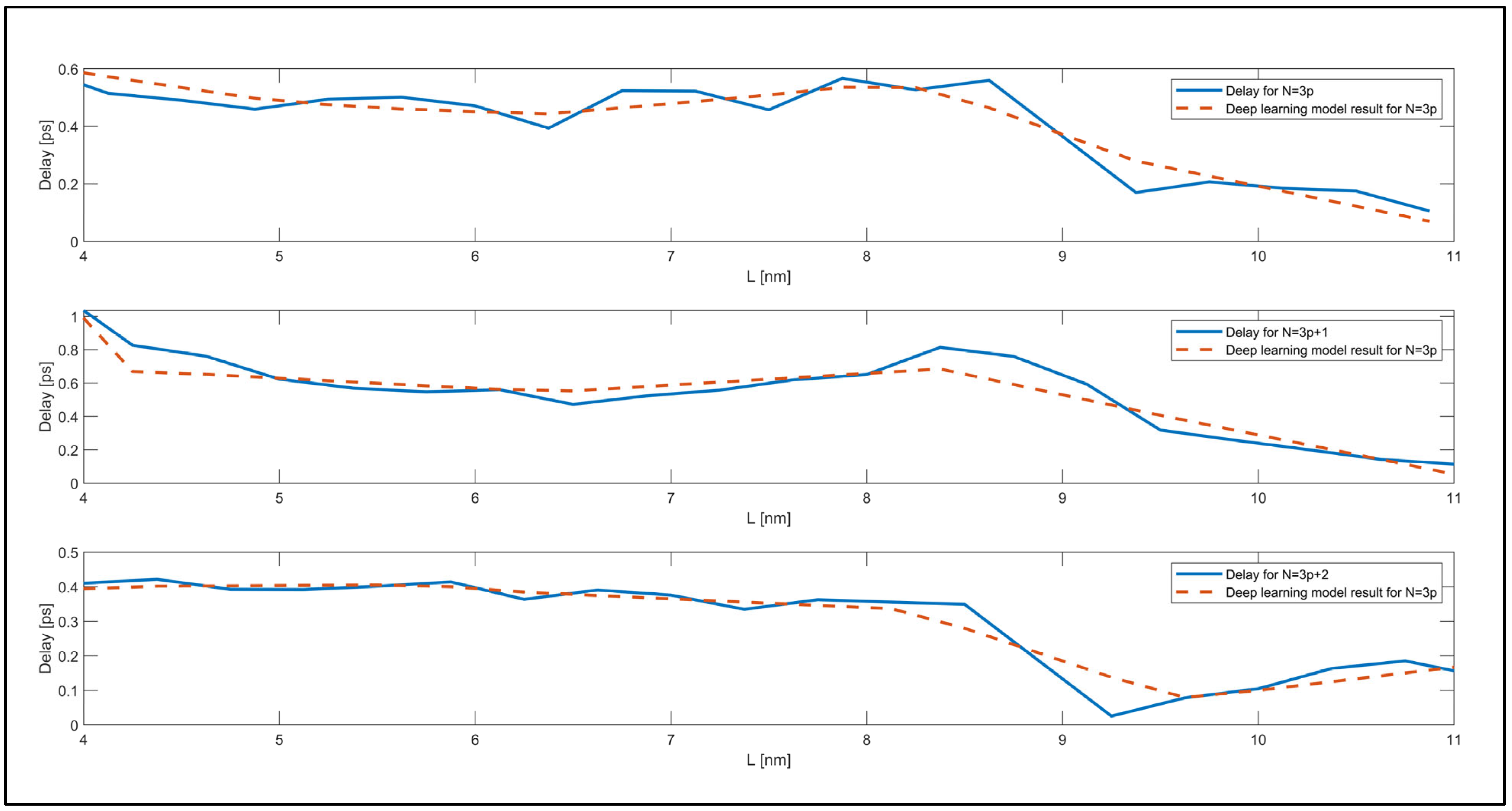
| Delay | R2 | MAPE | MAE | RMSE |
|---|---|---|---|---|
| for N = 3p | 0.86 | 0.14 | 0.05 | 0.07 |
| for N = 3p + 1 | 0.96 | 0.31 | 0.07 | 0.13 |
| for N = 3p + 2 | 0.92 | 0.27 | 0.02 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emir, R.; Yamacli, D.S.; Yamacli, S.; Tekin, S.A. Deep Learning Approach for Modeling the Power Consumption and Delay of Logic Circuits Employing GNRFET Technology. Electronics 2024, 13, 2993. https://doi.org/10.3390/electronics13152993
Emir R, Yamacli DS, Yamacli S, Tekin SA. Deep Learning Approach for Modeling the Power Consumption and Delay of Logic Circuits Employing GNRFET Technology. Electronics. 2024; 13(15):2993. https://doi.org/10.3390/electronics13152993
Chicago/Turabian StyleEmir, Recep, Dilek Surekci Yamacli, Serhan Yamacli, and Sezai Alper Tekin. 2024. "Deep Learning Approach for Modeling the Power Consumption and Delay of Logic Circuits Employing GNRFET Technology" Electronics 13, no. 15: 2993. https://doi.org/10.3390/electronics13152993
APA StyleEmir, R., Yamacli, D. S., Yamacli, S., & Tekin, S. A. (2024). Deep Learning Approach for Modeling the Power Consumption and Delay of Logic Circuits Employing GNRFET Technology. Electronics, 13(15), 2993. https://doi.org/10.3390/electronics13152993






