An Adaptive Learning Control for MIMO Nonlinear System with Nonuniform Trial Lengths and Invertible Control Gain Matrix

Abstract

In the traditional iterative learning control (ILC) method, the operational time interval is conventionally fixed to facilitate a seamless learning process along the iteration axis. However, this condition may frequently be contravened in real-time applications owing to unknown uncertainties and unpredictable factors. In essence, replicating a control system at a consistent time interval proves challenging in practical scenarios. This paper proposes an adaptive iterative learning control (AILC) method for the multi-input–multi-output (MIMO) nonlinear system with nonuniform trial lengths and an invertible control gain matrix. Compared to the existing AILC research that features nonuniform trial lengths, the control gain matrix of the system in this paper is assumed to be invertible. Hence, the general requirement in the conventional AILC method that the control gain matrix of the system is positive-definite (or negative-definite) or even known is relaxed. Moreover, the tracking reference allows it to be iteration-varying. Finally, to prove the convergence of the system, the composite energy function is introduced and to verify the validity of the AILC method, a robot movement imitation with an uncalibrated camera system is used. The simulation results show that the actual output can track the desired reference trajectory well, and the tracking error converges to zero after 30 iterations.

1. Introduction

Trajectory tracking control can be classified into two categories: repetitive tracking over a finite time interval and asymptotic tracking at infinite time intervals. Iterative learning control (ILC) [1,2,3,4,5,6,7], as an effective strategy aimed at enhancing current dynamical system performance through leveraging past experiences without requiring precise model knowledge about the controlled system, has seen substantial progress over recent decades in both theoretical development and practical applications across various domains such as rail traffic management or aircraft surface detection robotics. These demands served as the impetus for the development of the ILC method, and Arimoto et al. provided the foundational framework and theoretical validation of this method in 1984 [7]. One of the key features of ILC is its independence from precise model knowledge of the controlled system. Over the past three decades, ILC has made significant advancements in both theoretical foundations and practical applications [4,5,6].

However, in most of the existing ILC designs, it is required that the system plant, the initial state, the reference trajectory, and the trial length in the ILC process must be invariant as the iteration number increases [1,2]. To challenge the limitation of tracking identical conditions in practical ILC applications, interest in dealing with identical conditions has been increasing in the ILC community [1,8,9,10,11,12,13], especially for dealing with the identical trial length [1]. Actually, in practical terms, it is challenging to repeat a control system at regular time intervals. For example, in the flying probe testing process, if data from some critical test points are abnormal, the sample is deemed defective, and its testing is terminated. The system then automatically proceeds to test the next sample. Another example is that in the realm of fully automated precision manufacturing, semi-finished goods undergo sequential processing steps, culminating in highly integrated end products. This methodology intricately intertwines machining and inspection stages, where a flaw in any machining operation could jeopardize the entire production line’s success. Detection of an irreparable fault in a semi-finished item during an inspection phase precipitates an automatic cessation of the manufacturing process. In terms of non-repetitive trial lengths, relevant ILC algorithms [12,14,15,16] were employed utilizing average operator techniques and modified tracking errors. The robustness and convergence of the ILC errors were assessed using conventional norms.

On the contrary, the majority of research has concentrated on discrete time linear systems [17,18], primarily due to the advantageous system structure and well-developed analysis techniques for discrete random variables. While nonlinear systems were addressed in [19], they were subject to the global Lipschitz continuous condition. Hence, it is imperative to consider eliminating this condition for continuous-time systems. Furthermore, despite the widespread use of the average operator to assimilate historical data in most literature, a direct P-type controller constitutes the inherent controller structure. For general nonlinear systems, such a controller may prove inadequate for stabilizing the system.

In recent decades, the incorporation of adaptive control concepts into the design of ILC has led to the development of a significant class of ILC algorithms known as the AILC approach [20,21,22]. The main feature of the AILC approach is to estimate the uncertain control parameters between successive iterations, which are, in turn, used to generate the current control input. The AILC approach offers significant advantages in relaxing the global Lipschitz continuous condition and addressing non-identical initial states, iteration-varying reference trajectories, and external disturbances by identifying relevant system parameters during the ILC process. Liu et al. studied the iteration varying trail lengths problem based on the AILC method for continuous-time nonlinear systems [20]. However, the system was single-input single-output (SISO), and the input gain or control direction was a scalar value. An AILC scheme was proposed for continuous-time parametric nonlinear systems with iteration lengths that randomly vary [21], in which the system referred to both the SISO system and the MIMO system. Unfortunately, the control gain matrix in the MIMO system should be known in order to design the controller.

In MIMO systems, the control gain matrices (which are the derivatives of system outputs to control inputs) are typically expected to be symmetric and positive-definite (or negative-definite), as indicated by previous studies [23,24,25]. The scalar control gains of SISO dynamical systems can be viewed as specific instances of this requirement [20,26,27]. However, in practical dynamical systems such as industrial agitator tank systems and robot systems [23,24], it is common for the control gain matrices to exhibit asymmetry. The stringent requirement for strict symmetry and positive-definiteness (or negative-definiteness), or even the established requirement on the control gain matrices has significantly constrained the advancement of adaptive ILC methodology.

Based on the above description, in the conventional ILC algorithm, the time interval is limited to the fixed value in order to obtain a perfect learning process, which may often be violated due to unknown uncertainties in real-time applications. On the other hand, in the existing AILC research that refers to the nonuniform trial lengths, most of the systems refer to SISO systems. For a few MIMO systems, the control gain matrix is required to be strictly symmetric and positive-definite (or negative-definite) or even accurately known. To solve these problems, this paper aims to present a novel AILC strategy for the MIMO nonlinear system with nonuniform trial lengths and the invertible control gain matrix, in which some rough knowledge on the bounds of system uncertainties and invertible control gain matrix are often available in practical applications. A composite energy function concept is introduced to establish the convergence of AILC tracking errors and the boundedness of system signals. Moreover, the primary challenge encountered in this study is the inherent difficulty in constructing Lyapunov functions to demonstrate stability when developing adaptive control methods. Compared to the existing AILC works, this paper presents the key features and significant contributions as follows:

• Compared to the parameterized dynamical systems, a more general class of MIMO nonlinear systems with nonuniform trial lengths and iteration-varying external disturbance is used for AILC designs.
• In contrast to previous AILC studies with nonuniform trial lengths, the control gain matrix in this paper is considered indeterminate and assumed to be invertible. As a result, the conventional requirement for the control gain matrix of the system to be positive-definite (or negative-definite) or even known is relaxed in our approach.
• The tracking reference allows it to be iteration-varying. Suffering from the nonuniform trial lengths, unknown external disturbance, and iteration-varying reference, a robot movement imitation with an uncalibrated camera system is used for simulation to verify the effectiveness of this method.

The subsequent sections of this paper are structured as follows: Section 2 gives the problem formulation and mathematical preliminaries. The theorem and corresponding convergence analysis of the AILC algorithm are presented in Section 3. In Section 4, a simulation study is provided. Finally, the paper is concluded in Section 5.

Notations: In this paper, let R denote the set of real numbers, $R^n$ denote the set of n-dimensional real column vectors, and $R^{m\times n}$ denote the set of $m\times n$ real matrices. The notation spec $\left(A\right)\subset C^{-}$ represents that all the eigenvalues of A lie within the open left half of the complex plane.

2. Problem Formulation

Take into account the MIMO nonlinear system to iteration-varying reference trajectories

$${\dot{x}}_k\left(t\right)=g\left(x_k\left(t\right)\right)+B{u}_k\left(t\right)+w_k\left(t\right),t\in \left[0,T\right]$$

(1)

where $k=0,1,2,\cdots$ represents the k-th iteration of the system over $t\in \left[0,T\right]$; $x_k\left(t\right)\in R^n$ is the system state/output; whereas $u_k\left(t\right)\in R^n$ represents the control input. The nonlinear function $g\left(x_k\left(t\right)\right)\in R^n$, the control gain matrix $B\in R^{n\times n}$, and the external disturbance $w_k\left(t\right)\in R^n$ are bounded.

The tracked reference trajectories for the MIMO nonlinear system (1) are different from iteration to iteration, which are denoted as $r_{d,k}\left(t\right)\in C^1\left({\left[0,T\right]}^n\right)$ for the k-th iteration. And the repetitive tracking error $e_k\left(t\right)={\left[\begin{array}{cccc}{e}_k^{\left(1\right)}\left(t\right)& e_k^{\left(2\right)}\left(t\right)& \cdots & e_k^{\left(n\right)}\left(t\right)\end{array}\right]}^T\in R^n$ is represented as

$$e_k\left(t\right)=r_{d,k}\left(t\right)-x_k\left(t\right).$$

(2)

Throughout this paper, for an n-dimensional vector $z={\left[\begin{array}{cccc}{z}_1& z_2& \cdots & z_n\end{array}\right]}^T$$\in R^n$ or $z^T={\left[\begin{array}{cccc}{z}_1& z_2& \cdots & z_n\end{array}\right]}^T\in R^n$, the following norm of the vector is used,

$${∥z∥}_{\infty }=\underset{i}{max}\left|z_i\right|.$$

When considering a matrix $G=\left[g_{ij}\right]\in R^{n\times n}$, the norm ${∥G∥}_{m_{\infty }}$ is specified as

$${∥g∥}_{m_{\infty }}=\underset{i,j}{nmax}\left|g_{ij}\right|.$$

The proof on compatibility of the matrix norm ${∥·∥}_{m_{\infty }}$ with the vector norm ${∥·∥}_{\infty }$ is easy, and is thus omitted.

In the sequel, the following assumptions are made for the MIMO nonlinear system (1).

Assumption 1.

The function $g\left(x_k\left(t\right)\right)$ satisfies the condition of linear growth.

$${∥g\left(x_k\left(t\right)\right)∥}_{\infty }\le {\beta }_1{∥x_k\left(t\right)∥}_{\infty }+{\beta }_2,$$

(3)

where the unknown constants ${\beta }_1$ and ${\beta }_2$ satisfy $0\le {\beta }_1<+\infty$ and $0\le {\beta }_2<+\infty$.

Remark 1.

In comparison to the global Lipschitz condition commonly utilized in ILC designs for nonlinear functions, the linear growth condition is slightly more relaxed as it can be deduced from the global Lipschitz condition [25].

Assumption 2.

In the AILC process of the MIMO nonlinear system (1), the reference trajectory $r_{d,k}\left(t\right)$ and the iterative initial state $x_k\left(0\right)\in R^n$ are bounded. The initial condition satisfies $x_k\left(0\right)=r_{d,k}\left(0\right)$.

Assumption 3.

The control gain matrix $B\in R^{n\times n}$ is assumed to be invertible and the rough knowledge on B is available such that an invertible matrix $\widehat{B}\in R^{n\times n}$ can be found to make spec $\left(-B\widehat{B}\right)\subset C^{-}$, which represents that all the eigenvalues of $-B\widehat{B}$ lie within the open left half of the complex plane.

Remark 2.

In fact, Assumption 2 represents the identical iterative initial condition commonly employed in ILC designs, which means that the reference trajectory $r_{d,k}\left(t\right)$ and the iterative initial state $x_k\left(0\right)\in R^n$ both have upper and lower bounds. As for Assumption 3, it is feasible to obtain the requisite matrix $\widehat{B}$ based on the robustness of $\widehat{B}$ to the estimated error of B.

3. Adaptive AILC Designs with Convergence Analysis

In this section, we present an AILC algorithm along with its convergence analysis for the MIMO nonlinear system (1).

Based on Assumptions 1–3, an AILC algorithm (4)–(6) with two adaption parameters ${\widehat{\varphi }}_k\left(t\right)\in R^2$ is proposed as follows,

$$u_k\left(t\right)=\left\{\begin{array}{c}{\displaystyle \frac{\widehat{B}{e}_k\left(t\right){e_k}^T\left(t\right)\xi \left(e_k\left(t\right)\right){\widehat{\delta }}_k\left(t\right)}{{∥e_k\left(t\right)∥}_2^2}}{e}_k\left(t\right)\ne 0\in R^n\\ u_k\left(t^{-}\right)e_k\left(t\right)=0\in R^n\end{array}\right.$$

(4)

$${\widehat{\delta }}_k\left(t\right)=\left\{\begin{array}{c}{\widehat{\delta }}_{k-1}\left(t\right)+\mathsf{\Gamma }{\xi }^T\left(e_k\left(t\right)\right)e_k\left(t\right)\in R^2,0\le t\le {\tau }_k\\ {\widehat{\delta }}_{k-1}\left(t\right)\in R^2,{\tau }_k<t\le T\end{array}\right.$$

(5)

$$\xi \left(e_k\left(t\right)\right)=\left[\begin{array}{cc}{e}_k\left(t\right)& \mathrm{sign}\left(e_k\left(t\right)\right)\end{array}\right]\in R^{n\times 2},$$

(6)

where ${\widehat{\delta }}_{-1}\left(t\right)=0\in R^2$, $\mathrm{sign}\left(e_k\left(t\right)\right)={\left[\begin{array}{cc}\mathrm{sign}\left(e_k^{\left(1\right)}\left(t\right)\right)& \mathrm{sign}\left(e_k^{\left(2\right)}\left(t\right)\right)\cdots \mathrm{sign}\left(e_k^{\left(n\right)}\left(t\right)\right)\end{array}\right]}^T$, and $u_k\left(0^{-}\right)=0$ for $k=0,1,2,\cdots$. $\mathsf{\Gamma }\in R^{2\times 2}$ is a symmetric gain matrix, which is positive definite.

Theorem 1.

Consider the MIMO nonlinear system (1) based on Assumptions 1–3. Using the AILC algorithm (4)–(6), if the gain matrix $\widehat{B}$ makes spec $\left(-B\widehat{B}\right)\subset C^{-}$, then the tracking error $e_k\left(t\right)$ converges to zero as k goes to infinity, i.e., $\underset{k\to \infty }{lim}{e}_k\left(t\right)=0$.

Proof. 

In the subsequent discussion, the argument t in the variables $e_k\left(t\right)$, ${\widehat{\delta }}_k\left(t\right)$, and ${\tilde{\delta }}_k\left(t\right)$ is frequently omitted when it does not cause confusion. Due to the fact that $\mathrm{spec}\left(-B\widehat{B}\right)\subset C^{-}$, there exists a unique positive-definite matrix $Q=Q^T\in R^{n\times n}$ such that

$${\left(B\widehat{B}\right)}^{T}Q+Q\left(B\widehat{B}\right)=2I_n.$$

(7)

According to Assumptions 1–3, suppose that

$$\underset{0\le t\le T}{\sup }{∥Q{\dot{r}}_{d,k}\left(t\right)-Q{w}_k\left(t\right)∥}_{\infty }\le \alpha$$

(8)

$$\underset{0\le t\le T}{\sup }{∥Q∥}_{m_{\infty }}\le c,$$

(9)

we can make

$$\left\{\begin{array}{c}p=nc{\beta }_1\\ q=n\alpha +nc{\beta }_1{∥r_{d,k}\left(t\right)∥}_{\infty }+nc{\beta }_2\end{array}\right.$$

(10)

$$\delta ={\left[\begin{array}{cc}p& q\end{array}\right]}^T\in R^2,$$

(11)

$${\tilde{\delta }}_k\left(t\right)=\delta -{\widehat{\delta }}_k\left(t\right),$$

(12)

where the unknown parameters ${\beta }_1$ and ${\beta }_2$ are given in Assumption 1, and ${\widehat{\delta }}_k\left(t\right)$ is the estimated value of $\delta$ for the k-th iteration at the time t. The following process consists of three parts.

Define the Lyapunov-like composite energy function as follows.

$$V_k\left(t\right)={\displaystyle \frac{1}{2}}{{\epsilon }_k}^T\left(t\right)Q{\epsilon }_k\left(t\right)+{\displaystyle \frac{1}{2}}{\int }_0^t{\tilde{\delta }}_k^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_k\left(t\right)d\tau$$

(13)

The following proof is structured in three steps: the initial step establishes the non-increasing property of $\left\{V_k\left(t\right)\right\}$ along the iteration axis; the second step further demonstrates the bounded property of $\left\{V_k\left(t\right)\right\}$, and $e_k\left(t\right)\to 0$ as $k\to \infty$ finally shown in the last step.

Step 1: To prove the $\left\{V_k\left(t\right)\right\}$ being a non-increasing function sequence, the difference of $V_k\left(t\right)$ along the iteration axis can be written as,

$$\begin{array}{cc}\hfill \Delta V_k\left(t\right)& =V_k\left(t\right)-V_{k-1}\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{{\epsilon }_k}^T\left(t\right)Q{\epsilon }_k\left(t\right)-{\displaystyle \frac{1}{2}}{{\epsilon }_{k-1}}^T\left(t\right)Q{\epsilon }_{k-1}\left(t\right)+{\int }_0^t{\displaystyle \frac{1}{2}}\left({\tilde{\delta }}_k^T\left(\tau \right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_k\left(\tau \right)-{\tilde{\delta }}_{k-1}^T\left(\tau \right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_{k-1}\left(\tau \right)\right)d\tau \hfill \end{array}$$

(14)

It is important to note that both ${\epsilon }_k\left(t\right)$ and ${\tilde{\delta }}_k\left(t\right)$ have distinct formulations for $0\le t\le {\tau }_k$ and ${\tau }_k<t$. So, the proof is divided into two cases.

Case 1: when $0\le t\le {\tau }_k$

For the sake of simplicity, (14) is divided into several parts to discuss respectively as follows.

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}{\tilde{\delta }}_k^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_k\left(t\right)-{\displaystyle \frac{1}{2}}{\tilde{\delta }}_{k-1}^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_{k-1}\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\tilde{\delta }}_k^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_k\left(t\right)+{\displaystyle \frac{1}{2}}{\tilde{\delta }}_k^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_{k-1}\left(t\right)-{\displaystyle \frac{1}{2}}{\tilde{\delta }}_{k-1}^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_k\left(t\right)-{\displaystyle \frac{1}{2}}{\tilde{\delta }}_{k-1}^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_{k-1}\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\left({\tilde{\delta }}_k\left(t\right)-{\tilde{\delta }}_{k-1}\left(t\right)\right)}^T{\mathsf{\Gamma }}^{-1}\left({\tilde{\delta }}_k\left(t\right)+{\tilde{\delta }}_{k-1}\left(t\right)\right)\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}{\left({\widehat{\delta }}_k\left(t\right)-{\widehat{\delta }}_{k-1}\left(t\right)\right)}^T{\mathsf{\Gamma }}^{-1}\left(2{\tilde{\delta }}_k\left(t\right)+\left({\widehat{\delta }}_k^T\left(t\right)-{\widehat{\delta }}_{k-1}\left(t\right)\right)\right)\hfill \end{array}$$

(15)

Then,

$$\begin{array}{cc}\hfill & {\int }_0^t{\displaystyle \frac{1}{2}}\left({\tilde{\delta }}_k^T\left(\tau \right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_k\left(\tau \right)-{\tilde{\delta }}_{k-1}^T\left(\tau \right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_{k-1}\left(\tau \right)\right)d\tau \hfill \\ \hfill & ={\int }_0^t\left(-{\displaystyle \frac{1}{2}}{\left({\widehat{\delta }}_k\left(\tau \right)-{\widehat{\delta }}_{k-1}\left(\tau \right)\right)}^T{\mathsf{\Gamma }}^{-1}\left(2{\tilde{\delta }}_k\left(\tau \right)+\left({\widehat{\delta }}_k^T\left(\tau \right)-{\widehat{\delta }}_{k-1}\left(\tau \right)\right)\right)\right)d\tau \hfill \end{array}$$

(16)

According to adaptive law (5), as $0\le t\le {\tau }_k$, ${\widehat{\delta }}_k\left(t\right)={\widehat{\delta }}_{k-1}\left(t\right)+\mathsf{\Gamma }{\xi }^T\left(e_k\left(t\right)\right)e_k\left(t\right)$. Then, (16) can be deduced as follows.

$$\begin{array}{cc}\hfill & {\int }_0^t{\displaystyle \frac{1}{2}}\left({\tilde{\delta }}_k^T\left(\tau \right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_k\left(\tau \right)-{\tilde{\delta }}_{k-1}^T\left(\tau \right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_{k-1}\left(\tau \right)\right)d\tau \hfill \\ \hfill & ={\int }_0^t\left(-{\displaystyle \frac{1}{2}}{\left(\mathsf{\Gamma }{\xi }^T\left(e_k\left(\tau \right)\right)e_k\left(\tau \right)\right)}^T{\mathsf{\Gamma }}^{-1}\left(2{\tilde{\delta }}_k\left(\tau \right)+\mathsf{\Gamma }{\xi }^T\left(e_k\left(\tau \right)\right)e_k\left(\tau \right)\right)\right)d\tau \hfill \\ \hfill & ={\int }_0^t\left(-{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right){\tilde{\delta }}_k\left(\tau \right)-{\displaystyle \frac{1}{2}}{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right)\mathsf{\Gamma }{\xi }^T\left(e_k\left(\tau \right)\right)e_k\left(\tau \right)\right)d\tau \hfill \end{array}$$

(17)

Furthermore,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}{{\epsilon }_k}^T\left(t\right)Q{\epsilon }_k\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{e_k}^T\left(t\right)Q{e}_k\left(t\right)\hfill \\ \hfill & ={\int }_0^t{e_k}^T\left(\tau \right)Q{\dot{e}}_k\left(\tau \right)d\tau +{\displaystyle \frac{1}{2}}{e_k}^T\left(0\right)Q{e}_k\left(0\right)\hfill \\ \hfill & ={\int }_0^t{e_k}^T\left(\tau \right)Q{\dot{e}}_k\left(\tau \right)d\tau \hfill \\ \hfill & ={\int }_0^t{e_k}^T\left(\tau \right)\left(Q{\dot{r}}_{d,k}\left(\tau \right)-Q{\dot{x}}_k\left(\tau \right)\right)d\tau \hfill \\ \hfill & ={\int }_0^t{e_k}^T\left(\tau \right)\left(Q{\dot{r}}_{d,k}\left(\tau \right)-Q\left(g\left(x_k\left(\tau \right)\right)+B{u}_k\left(\tau \right)+w_k\left(\tau \right)\right)\right)d\tau \hfill \\ \hfill & ={\int }_0^t\left({e_k}^T\left(\tau \right)\left(Q{\dot{r}}_{d,k}\left(\tau \right)-Qg\left(x_k\left(\tau \right)\right)-Q{w}_k\left(\tau \right)\right)-{e_k}^T\left(\tau \right)QB{u}_k\left(\tau \right)\right)d\tau \hfill \end{array}$$

(18)

Consider ${e_k}^T\left(t\right)\left(Q{\dot{r}}_{d,k}\left(\tau \right)-Qg\left(x_k\left(t\right)\right)-Q{w}_k\left(t\right)\right)$ and $-{e_k}^T\left(t\right)QB{u}_k\left(t\right)$ in (18).

$$\begin{array}{cc}\hfill & {e_k}^T\left(t\right)\left(Q{\dot{r}}_{d,k}\left(t\right)-Qg\left(x_k\left(t\right)\right)-Q{w}_k\left(t\right)\right)\hfill \\ \hfill & \le {∥{e_k}^T\left(t\right)\left(Q{\dot{r}}_{d,k}\left(t\right)-Qg\left(x_k\left(t\right)\right)-Q{w}_k\left(t\right)\right)∥}_{\infty }\hfill \\ \hfill & \le n{∥e_k\left(t\right)∥}_{\infty }{∥Q{\dot{r}}_{d,k}\left(t\right)-Qg\left(x_k\left(t\right)\right)-Q{w}_k\left(t\right)∥}_{\infty }\hfill \\ \hfill & \le n{∥e_k\left(t\right)∥}_{\infty }\left({∥Q{\dot{r}}_{d,k}\left(t\right)-Q{w}_k\left(t\right)∥}_{\infty }+{∥Q∥}_{m_{\infty }}{∥g\left(x_k\left(t\right)\right)∥}_{\infty }\right)\hfill \\ \hfill & \le n{∥e_k\left(t\right)∥}_{\infty }\left({∥Q{\dot{r}}_{d,k}\left(t\right)-Q{w}_k\left(t\right)∥}_{\infty }+{∥Q∥}_{m_{\infty }}\left({\beta }_1{∥x_k\left(t\right)∥}_{\infty }+{\beta }_2\right)\right)\hfill \\ \hfill & \le n{∥e_k\left(t\right)∥}_{\infty }\left(\alpha +c\left({\beta }_1{∥x_k\left(t\right)∥}_{\infty }+{\beta }_2\right)\right)\hfill \\ \hfill & \le {∥e_k\left(t\right)∥}_{\infty }\left(n\alpha +nc{\beta }_1{∥r_{d,k}\left(t\right)∥}_{\infty }+nc{\beta }_1{∥e_k\left(t\right)∥}_{\infty }+nc{\beta }_2\right)\hfill \end{array}$$

(19)

Based on p and q given in (10), we have,

$$\begin{array}{cc}\hfill & {e_k}^T\left(t\right)\left(Q{\dot{r}}_{d,k}\left(t\right)-Qf\left(x_k\left(t\right)\right)-Q{w}_k\left(t\right)\right)\hfill \\ \hfill & \le {∥e_k\left(t\right)∥}_{\infty }\left(p{∥e_k\left(t\right)∥}_{\infty }+q\right)\hfill \\ \hfill & \le {e_k}^T\left(t\right)\left(p{e}_k\left(t\right)+q\mathrm{sign}\left(e_k\left(t\right)\right)\right)\hfill \\ \hfill & ={e_k}^T\left(t\right)\xi \left(e_k\left(t\right)\right)\delta \hfill \end{array}$$

(20)

Based on ${\left(B\widehat{B}\right)}^{T}Q+Q\left(B\widehat{B}\right)=2I_m$ in (7), as $e_k\left(t\right)\ne 0$, employing adaptive control law (4), finally we have

$$\begin{array}{cc}\hfill & -{e_k}^T\left(t\right)QB{u}_k\left(t\right)\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}\left({e_k}^T\left(t\right)QB{u}_k\left(t\right)+{\left(QB{u}_k\left(t\right)\right)}^T{e}_k\left(t\right)\right)\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}\left({e_k}^T\left(t\right)QB\widehat{B}{e}_k\left(t\right){\displaystyle \frac{{e_k}^T\left(t\right)\xi \left(e_k\left(t\right)\right){\widehat{\delta }}_k\left(t\right)}{{∥e_k\left(t\right)∥}_2^2}}+{\left({\displaystyle \frac{{e_k}^T\left(t\right)\xi \left(e_k\left(t\right)\right){\widehat{\delta }}_k\left(t\right)}{{∥e_k\left(t\right)∥}_2^2}}\right)}^T{e_k}^T\left(t\right){\widehat{B}}^T{B}^{T}Q{e}_k\left(t\right)\right)\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}{e_k}^T\left(t\right)\left(QB\widehat{B}+{\widehat{B}}^T{B}^{T}Q\right)e_k\left(t\right){\displaystyle \frac{{e_k}^T\left(t\right)\xi \left(e_k\left(t\right)\right){\widehat{\delta }}_k\left(t\right)}{{∥e_k\left(t\right)∥}_2^2}}\hfill \\ \hfill & =-{e_k}^T\left(t\right)e_k\left(t\right){\displaystyle \frac{{e_k}^T\left(t\right)\xi \left(e_k\left(t\right)\right){\widehat{\delta }}_k\left(t\right)}{{∥e_k\left(t\right)∥}_2^2}}\hfill \\ \hfill & =-{e_k}^T\left(t\right)\xi \left(e_k\left(t\right)\right){\widehat{\delta }}_k\left(t\right)\hfill \end{array}$$

i.e.,

$$-{e_k}^T\left(t\right)QB{u}_k\left(t\right)=-{e_k}^T\left(t\right)\xi \left(e_k\left(t\right)\right){\widehat{\delta }}_k\left(t\right)$$

(21)

It is worth noting that when $e_k\left(t\right)=0$, Equation (21) remains attainable regardless of the value taken by $u_k\left(t\right)$; thus, when $e_k\left(t\right)=0$, it follows that $u_k\left(t\right)=u_k\left(t^{-}\right)$.

Substitute (20) and (21) into (18), we obtained that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}{{\epsilon }_k}^T\left(t\right)Q{\epsilon }_k\left(t\right)\hfill \\ \hfill & \le {\int }_0^t\left({e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right)\delta -{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right){\widehat{\delta }}_k\left(\tau \right)\right)d\tau \hfill \\ \hfill & ={\int }_0^t{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right){\tilde{\delta }}_k\left(\tau \right)d\tau \hfill \end{array}$$

(22)

According to (17) and (22), we have

$$\begin{array}{cc}\hfill & \Delta V_k\left(t\right)=V_k\left(t\right)-V_{k-1}\left(t\right)\hfill \\ \hfill & \le {\int }_0^t{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right)\tilde{\delta }\left(\tau \right)d\tau -{\displaystyle \frac{1}{2}}{e_{k-1}}^T\left(t\right)Q{e}_{k-1}\left(t\right)\hfill \\ \hfill & +{\int }_0^t\left(-{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right){\tilde{\delta }}_k\left(\tau \right)-{\displaystyle \frac{1}{2}}{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right)\mathsf{\Gamma }{\xi }^T\left(e_k\left(\tau \right)\right)e_k\left(\tau \right)\right)d\tau \hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}{\int }_0^t{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right)\mathsf{\Gamma }{\xi }^T\left(e_k\left(\tau \right)\right)e_k\left(\tau \right)d\tau -{\displaystyle \frac{1}{2}}{e_{k-1}}^T\left(t\right)Q{e}_{k-1}\left(t\right)\hfill \end{array}$$

(23)

Case 2: when ${\tau }_k\le t\le T$

According to adaptive law ${\widehat{\delta }}_k\left(t\right)=\left\{\begin{array}{c}{\widehat{\delta }}_{k-1}\left(t\right)+\mathsf{\Gamma }{\xi }^T\left(e_k\left(t\right)\right)e_k\left(t\right)\in R^2,0\le t\le {\tau }_k\\ {\widehat{\delta }}_{k-1}\left(t\right)\in R^2,{\tau }_k<t\le T\end{array}\right.$ in (5), then (16) can be rewritten as

$$\begin{array}{cc}\hfill & {\int }_0^t{\displaystyle \frac{1}{2}}\left({\tilde{\delta }}_k^T\left(\tau \right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_k\left(\tau \right)-{\tilde{\delta }}_{k-1}^T\left(\tau \right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_{k-1}\left(\tau \right)\right)d\tau \hfill \\ \hfill & ={\int }_0^{{\tau }_k}\left(-{\displaystyle \frac{1}{2}}{\left({\widehat{\delta }}_k\left(\tau \right)-{\widehat{\delta }}_{k-1}\left(\tau \right)\right)}^T{\mathsf{\Gamma }}^{-1}\left(2{\tilde{\delta }}_k\left(\tau \right)+\left({\widehat{\delta }}_k^T\left(\tau \right)-{\widehat{\delta }}_{k-1}\left(\tau \right)\right)\right)\right)d\tau \hfill \\ \hfill & +{\int }_{{\tau }_k}^t\left(-{\displaystyle \frac{1}{2}}{\left({\widehat{\delta }}_k\left(\tau \right)-{\widehat{\delta }}_{k-1}\left(\tau \right)\right)}^T{\mathsf{\Gamma }}^{-1}\left(2{\tilde{\delta }}_k\left(\tau \right)+\left({\widehat{\delta }}_k^T\left(\tau \right)-{\widehat{\delta }}_{k-1}\left(\tau \right)\right)\right)\right)d\tau \hfill \\ \hfill & ={\int }_0^{{\tau }_k}\left(-{\displaystyle \frac{1}{2}}{\left({\widehat{\delta }}_k\left(\tau \right)-{\widehat{\delta }}_{k-1}\left(\tau \right)\right)}^T{\mathsf{\Gamma }}^{-1}\left(2{\tilde{\delta }}_k\left(\tau \right)+\left({\widehat{\delta }}_k^T\left(\tau \right)-{\widehat{\delta }}_{k-1}\left(\tau \right)\right)\right)\right)d\tau \hfill \\ \hfill & ={\int }_0^{{\tau }_k}\left(-{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right){\tilde{\delta }}_k\left(\tau \right)-{\displaystyle \frac{1}{2}}{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right)\mathsf{\Gamma }{\xi }^T\left(e_k\left(\tau \right)\right)e_k\left(\tau \right)\right)d\tau \hfill \end{array}$$

(24)

For this case, (22) becomes

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}{{\epsilon }_k}^T\left(t\right)Q{\epsilon }_k\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{e_k}^T\left({\tau }_k\right)Q{e}_k\left({\tau }_k\right)\hfill \\ \hfill & \le {\int }_0^{{\tau }_k}{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right){\tilde{\delta }}_k\left(\tau \right)d\tau \hfill \end{array}$$

(25)

Thus, for the second case and based on (23), we have

$$\begin{array}{cc}\hfill & \Delta V_k\left(t\right)=V_k\left(t\right)-V_{k-1}\left(t\right)\hfill \\ \hfill & \le {\int }_0^{{\tau }_k}{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right)\tilde{\delta }\left(\tau \right)d\tau -{\displaystyle \frac{1}{2}}{e_{k-1}}^T\left({\tau }_k\right)Q{e}_{k-1}\left({\tau }_k\right)\hfill \\ \hfill & +{\int }_0^{{\tau }_k}\left(-{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right){\tilde{\delta }}_k\left(\tau \right)-{\displaystyle \frac{1}{2}}{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right)\mathsf{\Gamma }{\xi }^T\left(e_k\left(\tau \right)\right)e_k\left(\tau \right)\right)d\tau \hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}{\int }_0^{{\tau }_k}{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right)\mathsf{\Gamma }{\xi }^T\left(e_k\left(\tau \right)\right)e_k\left(\tau \right)d\tau -{\displaystyle \frac{1}{2}}{e_{k-1}}^T\left({\tau }_k\right)Q{e}_{k-1}\left({\tau }_k\right)\hfill \end{array}$$

(26)

Combing (23) and (26), it can be finally acquired that

$$\begin{array}{cc}\hfill & \Delta V_k\left(t\right)=V_k\left(t\right)-V_{k-1}\left(t\right)\hfill \\ \hfill & \le -{\displaystyle \frac{1}{2}}{\int }_0^{{\tau }_k\vee t}{e_k}^T\left(\tau \right)\xi \left(e_k\left(\tau \right)\right)\mathsf{\Gamma }{\xi }^T\left(e_k\left(\tau \right)\right)e_k\left(\tau \right)d\tau -{\displaystyle \frac{1}{2}}{e_{k-1}}^T({\tau }_k\vee t)Q{e}_{k-1}({\tau }_k\vee t)\hfill \end{array}$$

(27)

where ${\tau }_k\vee t=min\left\{{\tau }_k,t\right\}$.

Then, it can be finally obtained that $\Delta V_k\left(t\right)\le 0$.

Step 2: Since

$$V_0\left(t\right)={\displaystyle \frac{1}{2}}{{\epsilon }_0}^T\left(t\right)Q{\epsilon }_0\left(t\right)+{\displaystyle \frac{1}{2}}{\int }_0^t{\tilde{\delta }}_0^T\left(\tau \right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_0\left(\tau \right)d\tau$$

(28)

Then we have,

$${\dot{V}}_0\left(t\right)={\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}\left({{\epsilon }_0}^T\left(t\right)Q{\epsilon }_0\left(t\right)\right)+{\displaystyle \frac{1}{2}}{\tilde{\delta }}_0^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_0\left(t\right)$$

(29)

From (22) and ${\epsilon }_0\left(t\right)={\lambda }_0{e}_0\left(t\right)+(1-{\lambda }_0)e_0\left({\tau }_0\right)$, it is obtained that

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{dt}}\left({e_0}^T\left(t\right)Q{e}_0\left(t\right)\right)\le {\lambda }_0{e_0}^T\left(t\right)\xi \left(e_0\left(t\right)\right){\tilde{\delta }}_0\left(t\right)$$

(30)

Substituting (30) into (29), and considering (20) and (21), further we have

$${\dot{V}}_0\left(t\right)\le {\lambda }_0{e_0}^T\left(t\right)\xi \left(e_0\left(t\right)\right){\tilde{\delta }}_0\left(t\right)+{\displaystyle \frac{1}{2}}{\tilde{\delta }}_0^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_0\left(t\right)$$

(31)

Notably, due to ${\widehat{\delta }}_{-1}\left(t\right)=0$, there is ${\widehat{\delta }}_0\left(t\right)={\widehat{\delta }}_{-1}\left(t\right)+{\lambda }_0\mathsf{\Gamma }{\xi }^T\left(e_0\left(t\right)\right)e_0\left(t\right)={\lambda }_0\mathsf{\Gamma }{\xi }^T\left(e_0\left(t\right)\right)e_0\left(t\right)$. As a result,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{2}}{\tilde{\delta }}_0^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_0\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\left(\delta -{\widehat{\delta }}_0\left(t\right)\right)}^T{\mathsf{\Gamma }}^{-1}\left(\delta -{\widehat{\delta }}_0\left(t\right)\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\delta }^T{\mathsf{\Gamma }}^{-1}\delta -{\widehat{\delta }}_0^T\left(t\right){\mathsf{\Gamma }}^{-1}\delta +{\displaystyle \frac{1}{2}}{\widehat{\delta }}_0^T\left(t\right){\mathsf{\Gamma }}^{-1}{\widehat{\delta }}_0\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\delta }^T{\mathsf{\Gamma }}^{-1}\delta -{\widehat{\delta }}_0^T\left(t\right){\mathsf{\Gamma }}^{-1}\left({\tilde{\delta }}_0\left(t\right)+{\widehat{\delta }}_0\left(t\right)\right)+{\displaystyle \frac{1}{2}}{\widehat{\delta }}_0^T\left(t\right){\mathsf{\Gamma }}^{-1}{\widehat{\delta }}_0\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\delta }^T{\mathsf{\Gamma }}^{-1}\delta -{\widehat{\delta }}_0^T\left(t\right){\mathsf{\Gamma }}^{-1}{\tilde{\delta }}_0\left(t\right)-{\displaystyle \frac{1}{2}}{\widehat{\delta }}_0^T\left(t\right){\mathsf{\Gamma }}^{-1}{\widehat{\delta }}_0\left(t\right)\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}{\delta }^T{\mathsf{\Gamma }}^{-1}\delta -{\lambda }_0{e_0}^T\left(t\right)\xi \left(e_0\left(t\right)\right){\tilde{\delta }}_0\left(t\right)-{\displaystyle \frac{1}{2}}{\widehat{\delta }}_0^T\left(t\right){\mathsf{\Gamma }}^{-1}{\widehat{\delta }}_0\left(t\right)\hfill \end{array}$$

(32)

Substituting (32) into (31), we have

$$\begin{array}{cc}\hfill & {\dot{V}}_0\left(t\right)\le {\displaystyle \frac{1}{2}}{\delta }^T{\mathsf{\Gamma }}^{-1}\delta -{\displaystyle \frac{1}{2}}{{\widehat{\delta }}_0}^T\left(t\right){\mathsf{\Gamma }}^{-1}{\widehat{\delta }}_0\left(t\right)\hfill \\ \hfill & \le {\displaystyle \frac{1}{2}}{\delta }^T{\mathsf{\Gamma }}^{-1}\delta \le M\hfill \end{array}$$

(33)

where M is a real number greater than zero.

By integrating both sides of (33), the expression for $V_0\left(t\right)$ can be derived as,

$$V_0\left(t\right)={\int }_0^t{\dot{V}}_0\left(\tau \right)d\tau \le MT$$

(34)

Step 3: It can be readily inferred from (27) that

$$\sum _{i=1}^k\Delta V_i\left(t\right)\le \sum _{i=1}^k\left(-{\displaystyle \frac{1}{2}}{e_{i-1}}^T({\tau }_i\vee t)Q{e}_{i-1}({\tau }_i\vee t)\right)$$

(35)

Thus,

$$\begin{array}{cc}\hfill & V_k\left(t\right)=V_0\left(t\right)+\sum _{i=1}^k\Delta V_i\left(t\right)\hfill \\ \hfill & \le V_0\left(t\right)+\sum _{i=1}^k\left(-{\displaystyle \frac{1}{2}}{e_{i-1}}^T({\tau }_i\vee t)Q{e}_{i-1}({\tau }_i\vee t)\right)\hfill \end{array}$$

(36)

Then, as $k\to \infty$, combining (34) and (36), we have

$$\sum _{i=1}^{\infty }{e_{i-1}}^T({\tau }_i\vee t)Q{e}_{i-1}({\tau }_i\vee t)\le 2\left(V_0\left(t\right)-V_k\left(t\right)\right)\le 2V_0\left(t\right)\le 2MT$$

(37)

From (28), it can be obviously concluded that $\underset{k\to \infty }{lim}{e}_k\left(t\right)=0$.

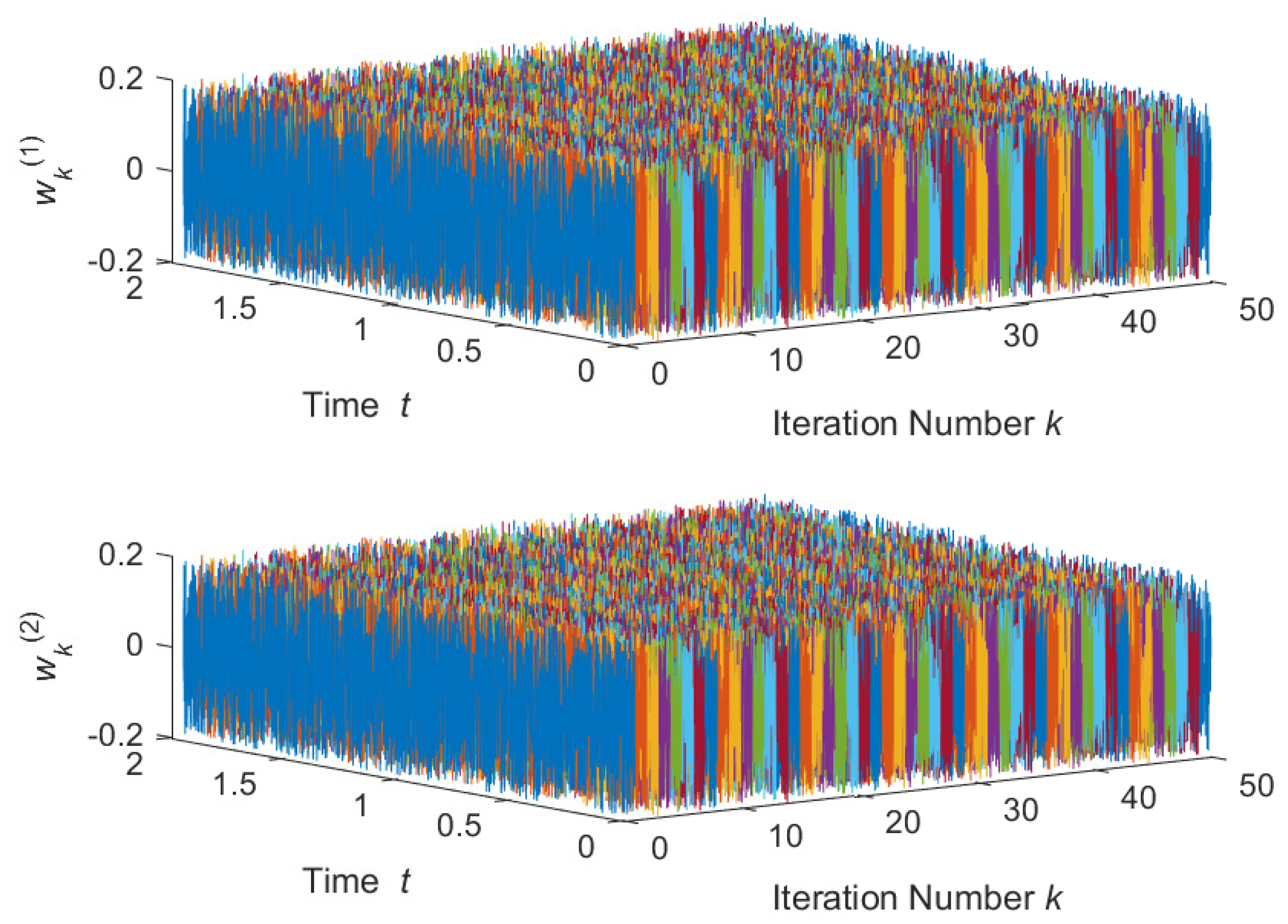
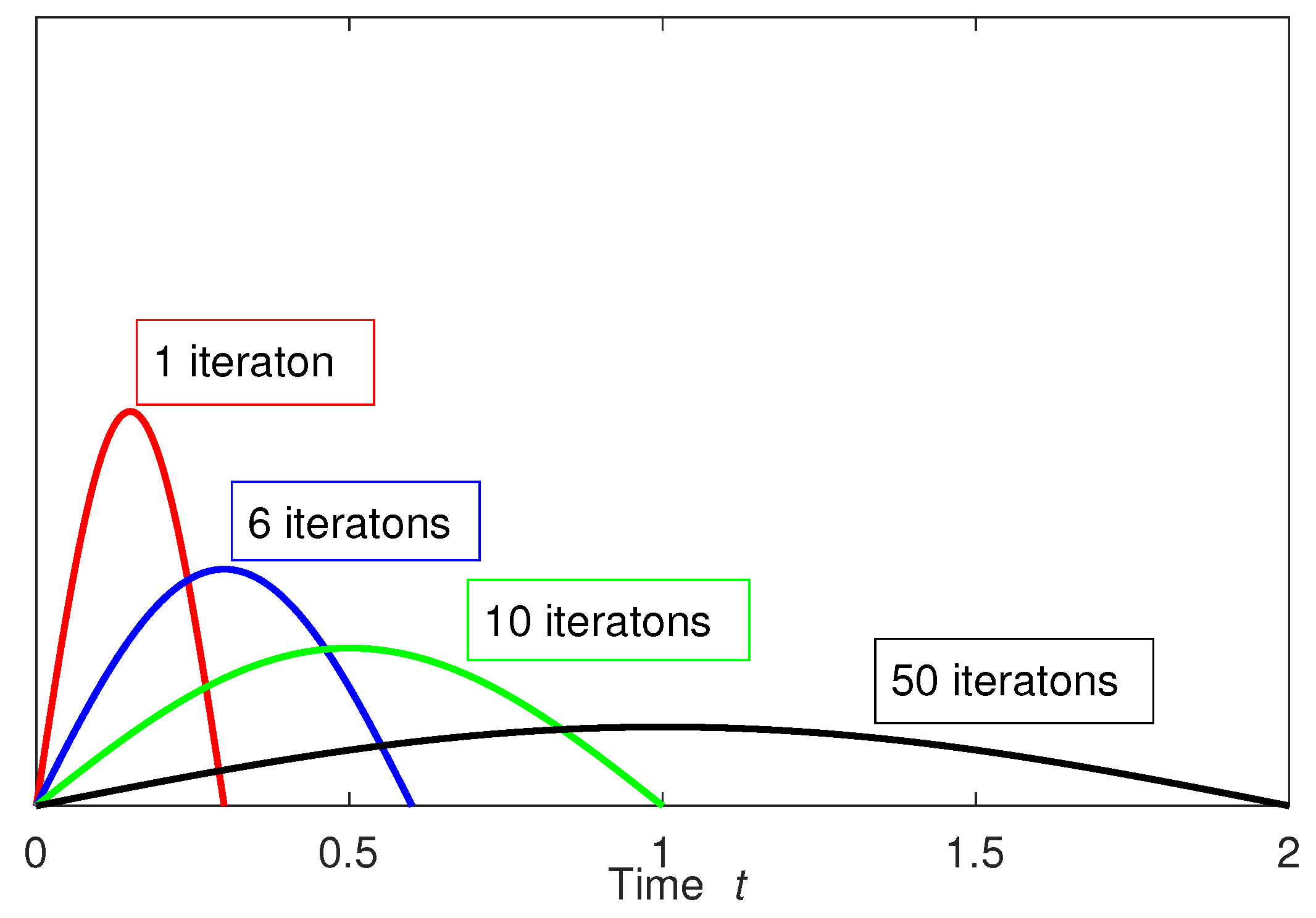
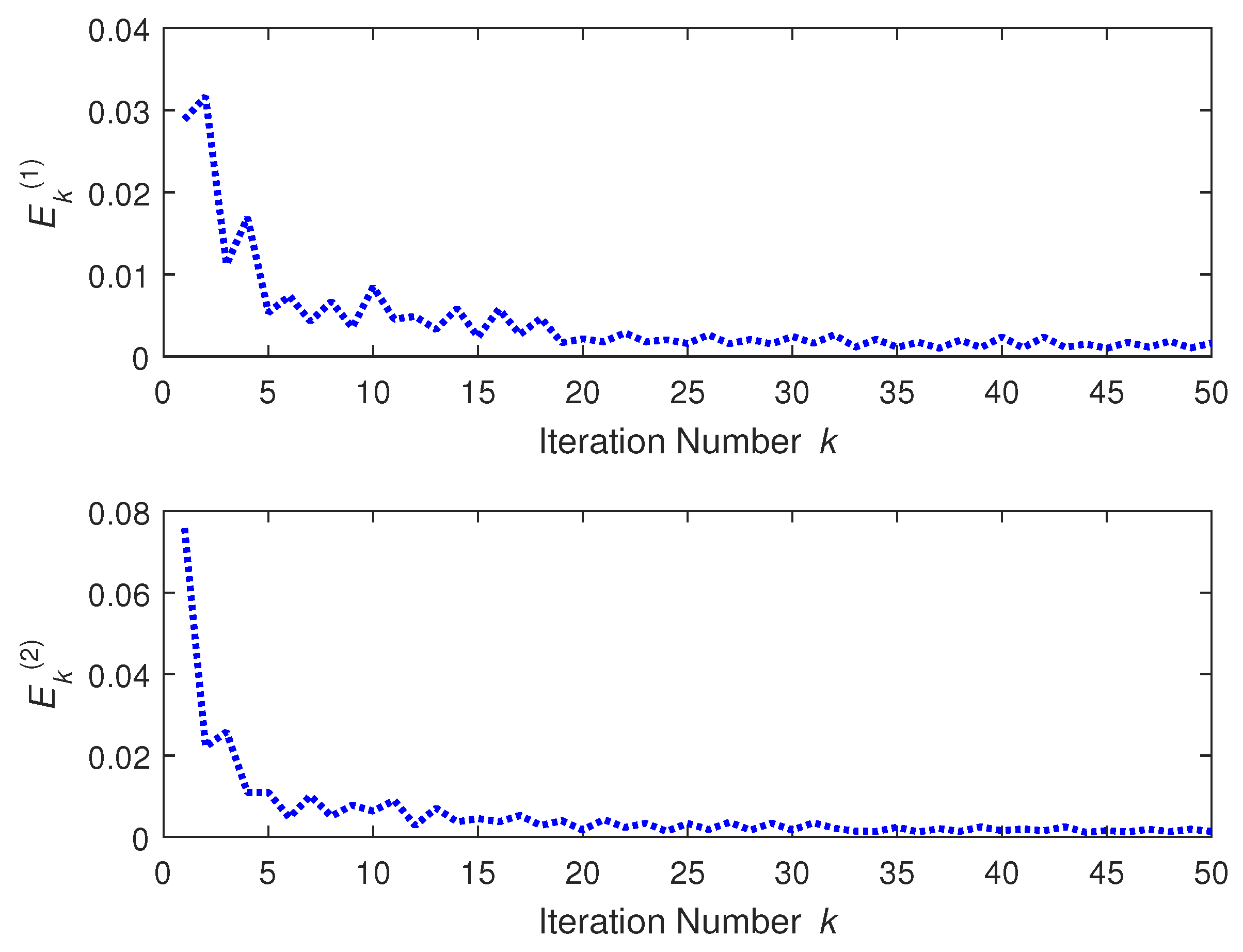
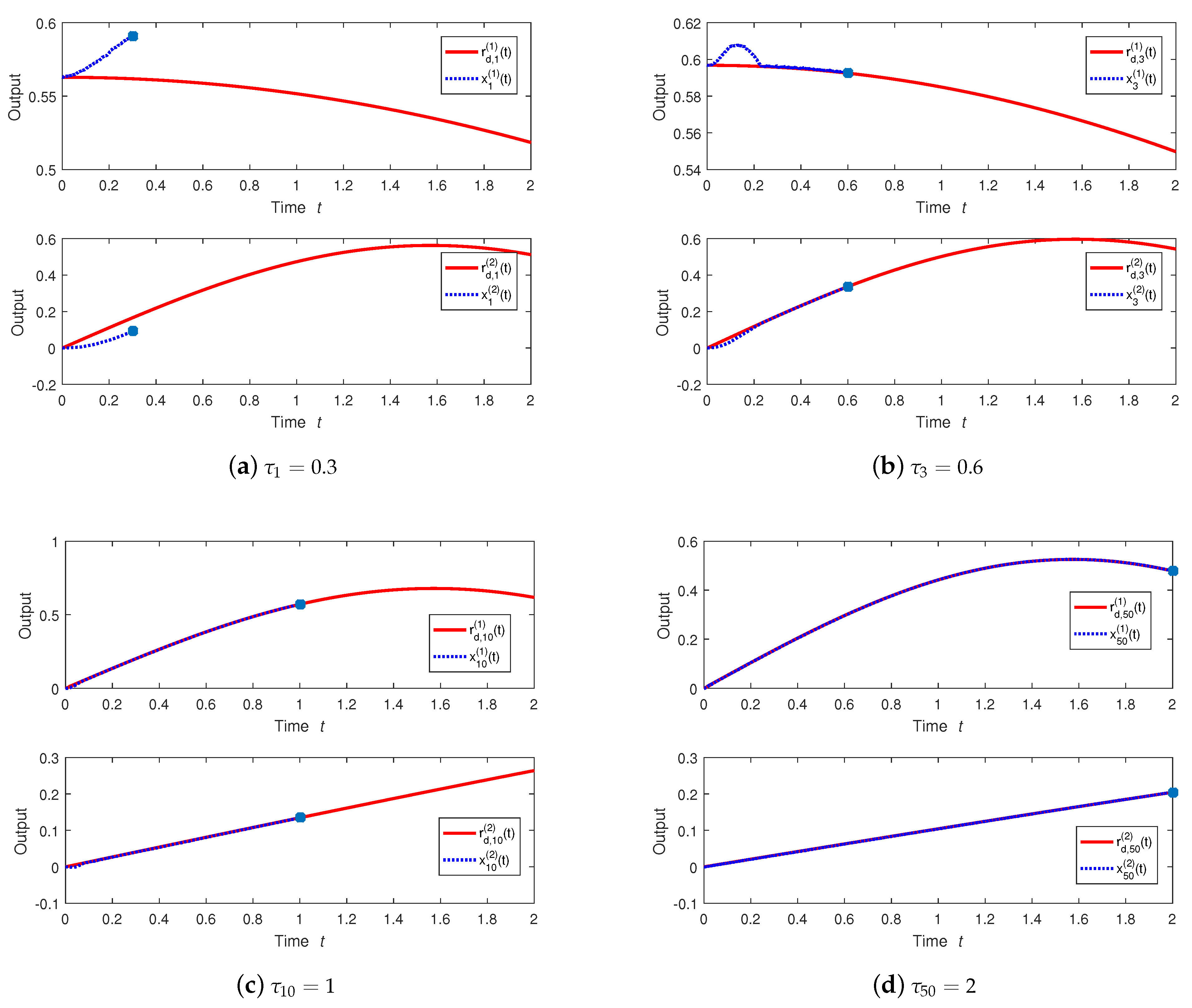
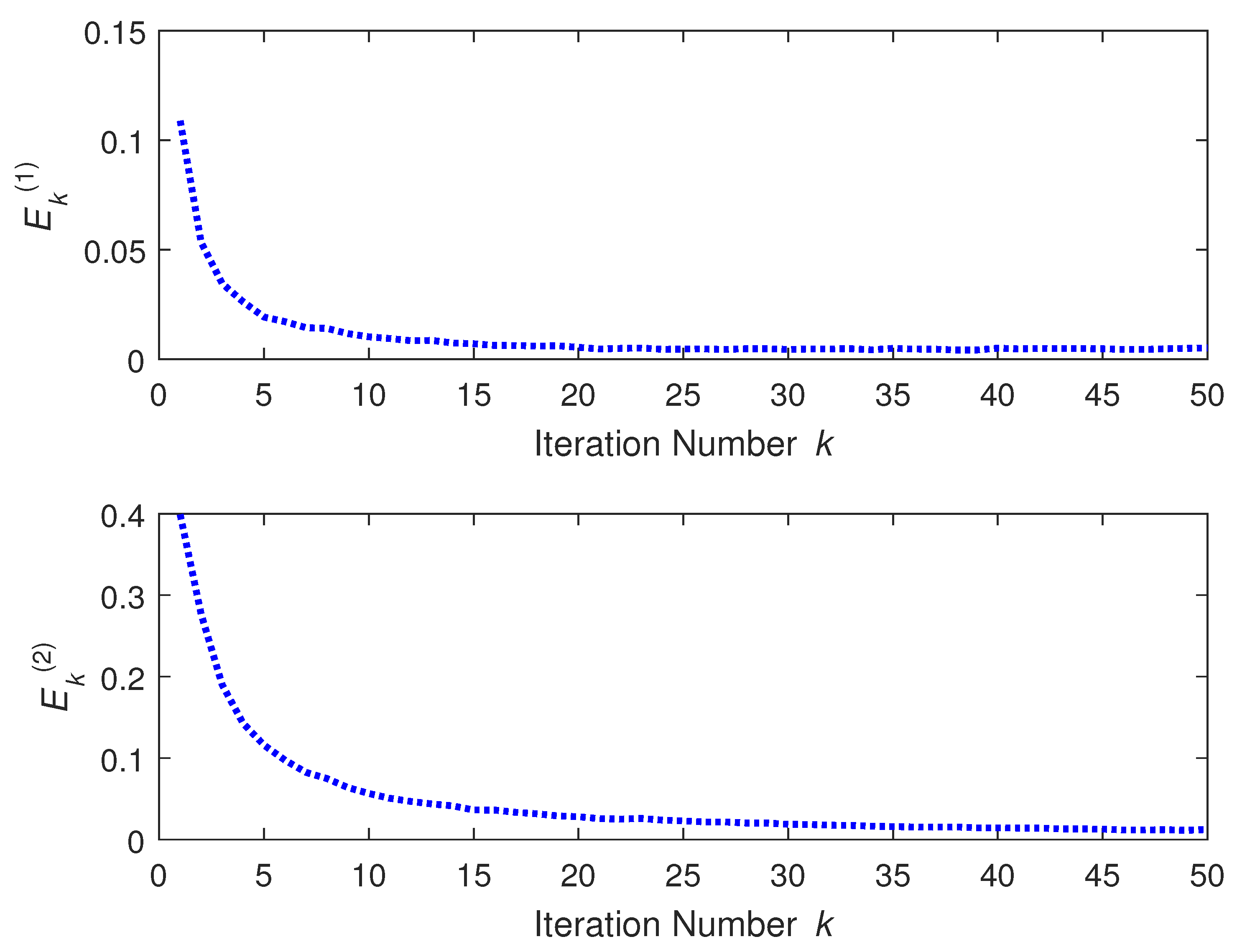
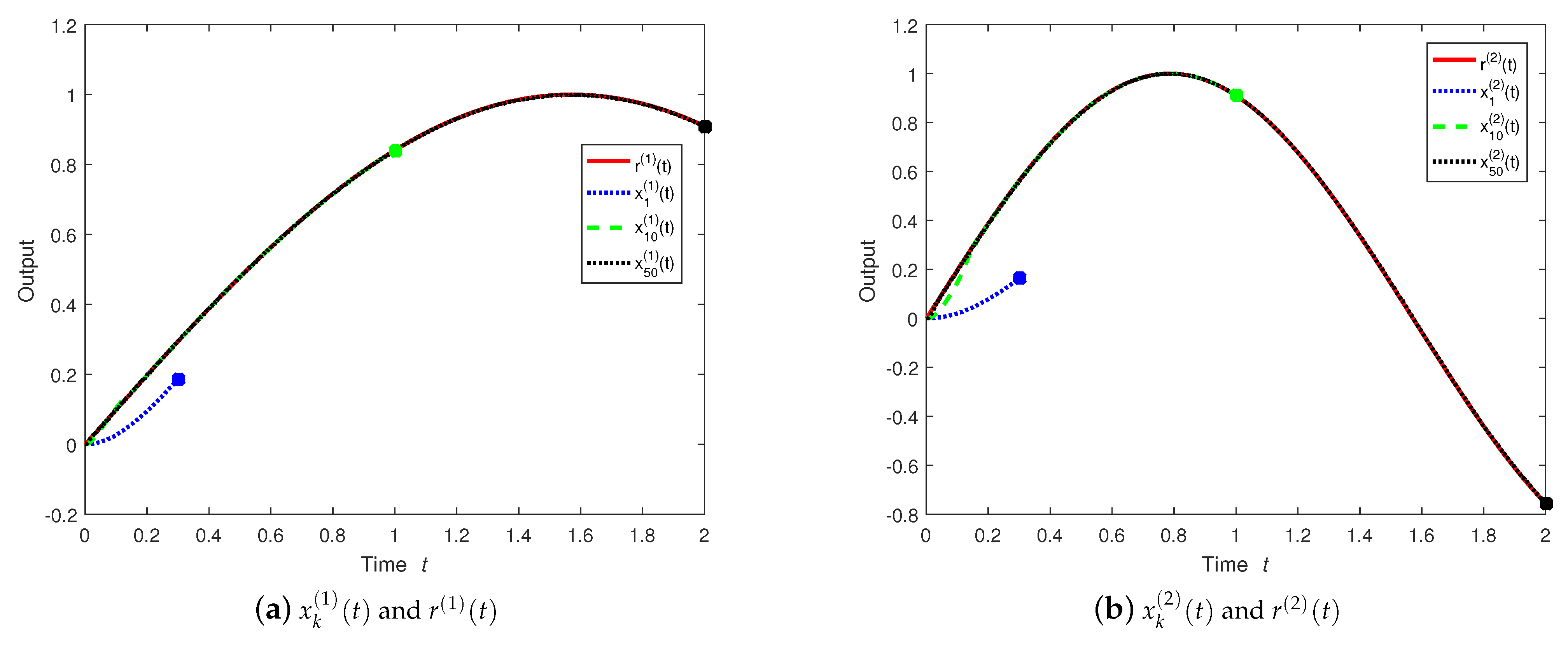
4. Illustrative Example

In a planar robot manipulator equipped with an overhead camera, the image plane aligns parallel to the work plane. When the planar robot manipulator performs repetitive tasks, it is possible to represent the projection of optical flow from the work plane to the image plane as follows.

$$\left[\begin{array}{c}{\dot{x}}_k^{\left(1\right)}\left(t\right)\hfill \\ {\dot{x}}_k^{\left(2\right)}\left(t\right)\hfill \end{array}\right]=\left[\begin{array}{c}{b}_{1}cosa-b_{1}sina\hfill \\ b_{2}sina{b}_{2}cosa\hfill \end{array}\right]\left[\begin{array}{c}{u}_k^{\left(1\right)}\left(t\right)\hfill \\ u_k^{\left(2\right)}\left(t\right)\hfill \end{array}\right]+\left[\begin{array}{c}{w}_k^{\left(1\right)}\left(t\right)\hfill \\ w_k^{\left(2\right)}\left(t\right)\hfill \end{array}\right].$$

(38)

For each $k=0,1,2,\cdots$ and for all $t\in \left[0,2\right]$, the components of disturbance $w_k\left(t\right)={\left[w_k^{\left(1\right)}\left(t\right)w_k^{\left(2\right)}\left(t\right)\right]}^T$ change uniformly within the range $\left[-0.2,0.2\right]$ as depicted in Figure 1. The scale factors of a camera are denoted by $b_1$ and $b_2$, both set to unity: $b_1=b_2=1$. The symbol a represents orientation and is assumed to take a value of $\pi /2$ without loss of generality.

The iteration-varying reference trajectories are given as

$$r_{d,k}\left(t\right)=\left\{\begin{array}{cc}{\rho }_k\times {\left[sin\left(t\right)sin\left(2t\right)\right]}^T,\hfill & kiseven\hfill \\ {\rho }_k\times {\left[exp\left(t\right)sin\left(t\right)cos\left(t\right)\right]}^T,\hfill & kisodd\hfill \end{array}\right.,t\in \left[0,2\right],$$

(39)

where the factor ${\rho }_k$ varies randomly at $\left[0.5,0.7\right]$ as shown in Figure 2. Figure 3 gives an example of varying trial lengths. From Figure 3, it can be obtained that the actual trial lengths are ${\tau }_1=0.3$, ${\tau }_6=0.6$, ${\tau }_{10}=1$, and ${\tau }_{50}=2$, respectively, where ${\tau }_{50}=2$ is the desired trial length. The initial states of the system (46) are set as $x_k^{\left(1\right)}\left(0\right)=x_{d,k}^{\left(1\right)}\left(0\right)$ and $x_k^{\left(2\right)}\left(0\right)=x_{d,k}^{\left(2\right)}\left(0\right)$, respectively. Thus, the initial tracking error of the system is $e_k\left(0\right)=x_{d,k}\left(0\right)-x_k\left(0\right)=0$. According to control law (4), the control input $u_k\left(0\right)=u_k\left(0^{-}\right)=0$ when $e_k\left(0\right)=0$. The precision of ILC tracking within the time interval $t\in \left[0,2\right]$ is assessed using the subsequent measure of maximum absolute deviation.

$$E_k^{\left(i\right)}=\underset{t\in \left[0,2\right]}{sup}\left|r_{d,k}^{\left(i\right)}\left(t\right)-x_k^{\left(i\right)}\left(t\right)\right|,(i=1,2),$$

(40)

To perform the numerical simulations for AILC tracking, the AILC algorithms (4)–(6) are used, and the controlled MIMO nonlinear system (38) are discretized with a sampling period of $0.001$. Based on the rough knowledge on the control gain matrix B in (38), the gain matrix $\widehat{B}$ involved in the AILC algorithms (4)–(6) is uniformly selected as $\widehat{B}=\left[\begin{array}{cc}-0.5& 0.866\\ 0.866& -0.5\end{array}\right]$ that makes $spec\left(-B\widehat{B}\right)\subset C^{-}$.

Figure 4 illustrates the evolution of the AILC tracking error indices $E_k^{\left(1\right)}$ and $E_k^{\left(2\right)}$ with respect to iteration k. From Figure 4, it can be seen that the AILC tracking errors converge to zero after 30 iterations. In particular, for the selected parameter value $\mathsf{\Gamma }=2I_2$, Figure 5 shows the system outputs $x_k^{\left(1\right)}\left(t\right)$ and $x_k^{\left(2\right)}\left(t\right)$ to the iteration-varying reference trajectory (39) at iterations $k=1$, $k=3$, $k=10$, and $k=50$, respectively. Figure 5a shows that the actual tracking curves cannot track the reference trajectory well at $k=1$. However, Figure 5b–d show that the actual tracking curves of states track the reference trajectory well after several iterations. The corresponding control inputs $u_{50}^{\left(1\right)}\left(t\right)$ and $u_{50}^{\left(2\right)}\left(t\right)$ are provided in Figure 6. To make it more intuitive, Figure 7, Figure 8 and Figure 9 show the situation with the fixed reference trajectory $r\left(t\right)={\left[sin\left(t\right)sin\left(0.2t\right)\right]}^T$, and Figure 8 shows that system outputs converge to the reference trajectory after 30 iterations when the system suffering from the nonuniform trial lengths.

5. Conclusions

For a class of MIMO nonlinear systems with nonuniform trial lengths and uncertain control gain matrix. Compared to the existing AILC research that features nonuniform trial lengths, the control gain matrix of the system in this paper has been assumed to be uncertain, and an AILC algorithm has been developed. By utilizing a Lyapunov-like approach with a composite energy function, the convergence of AILC tracking errors has been proven. Moreover, based on the fact that the rough knowledge of the control gain matrix and the bounds of system uncertainties are often available in practical applications, the AILC algorithm proposed in Theorem 1 involves just one adjustable variable. Finally, to verify the validity of the AILC method, a robot movement imitation with an uncalibrated camera system has been used.