Mitigation of Low Harmonic Ripples Based on the Three-Phase Dual Active Bridge Converter in Charging Station Applications
Abstract
1. Introduction
2. System Configuration and Assumptions
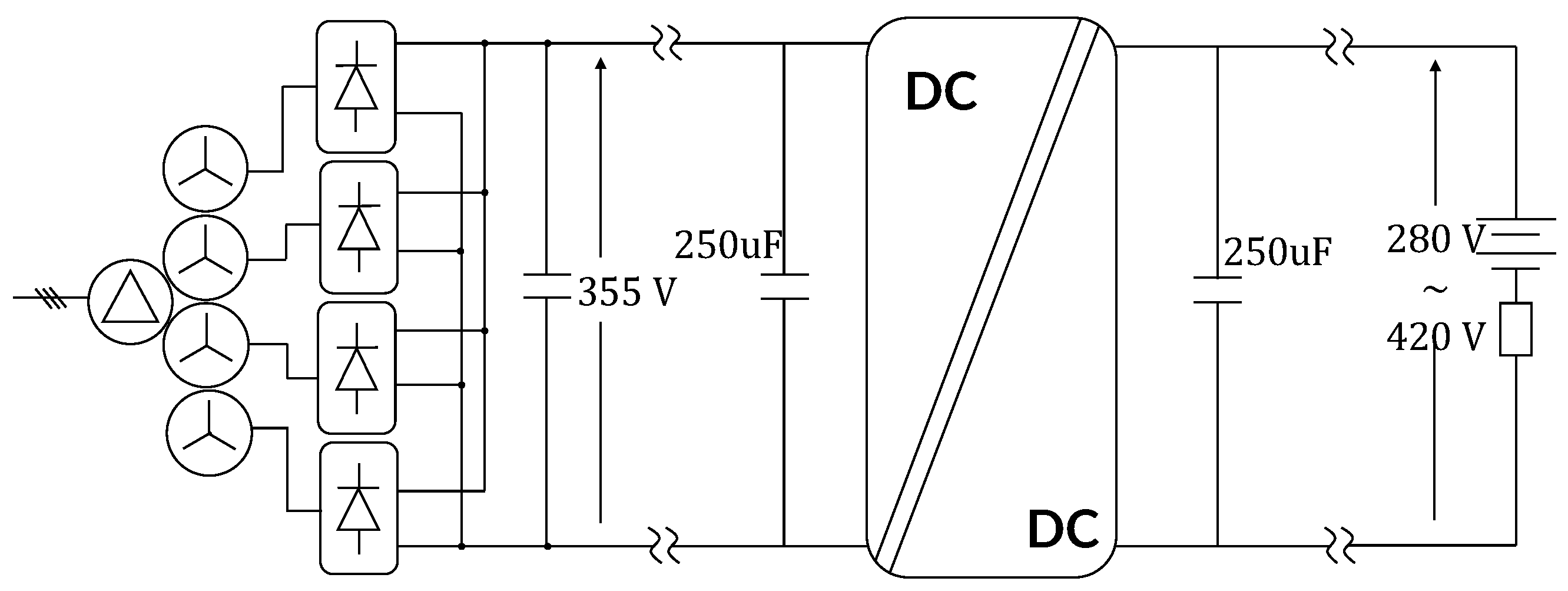
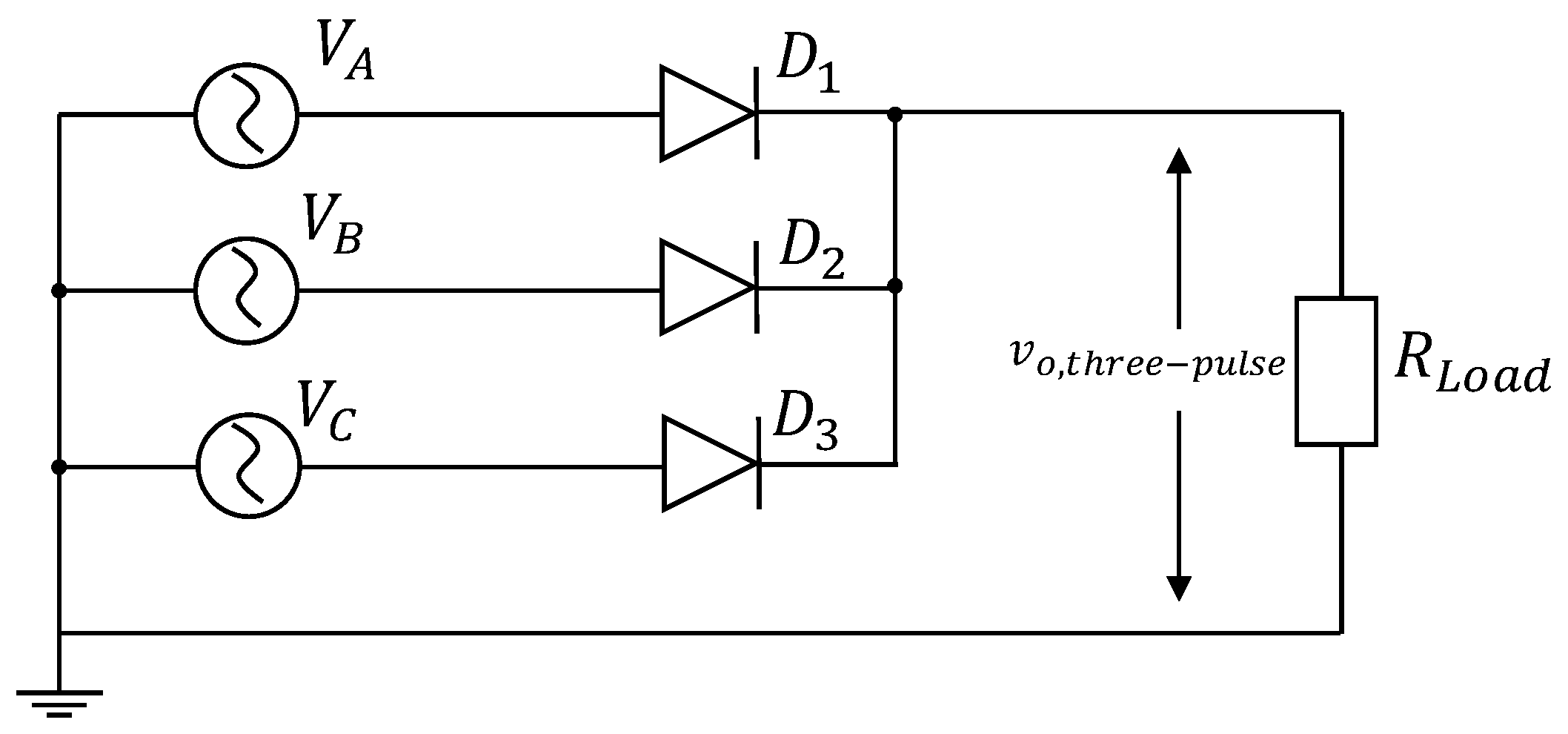
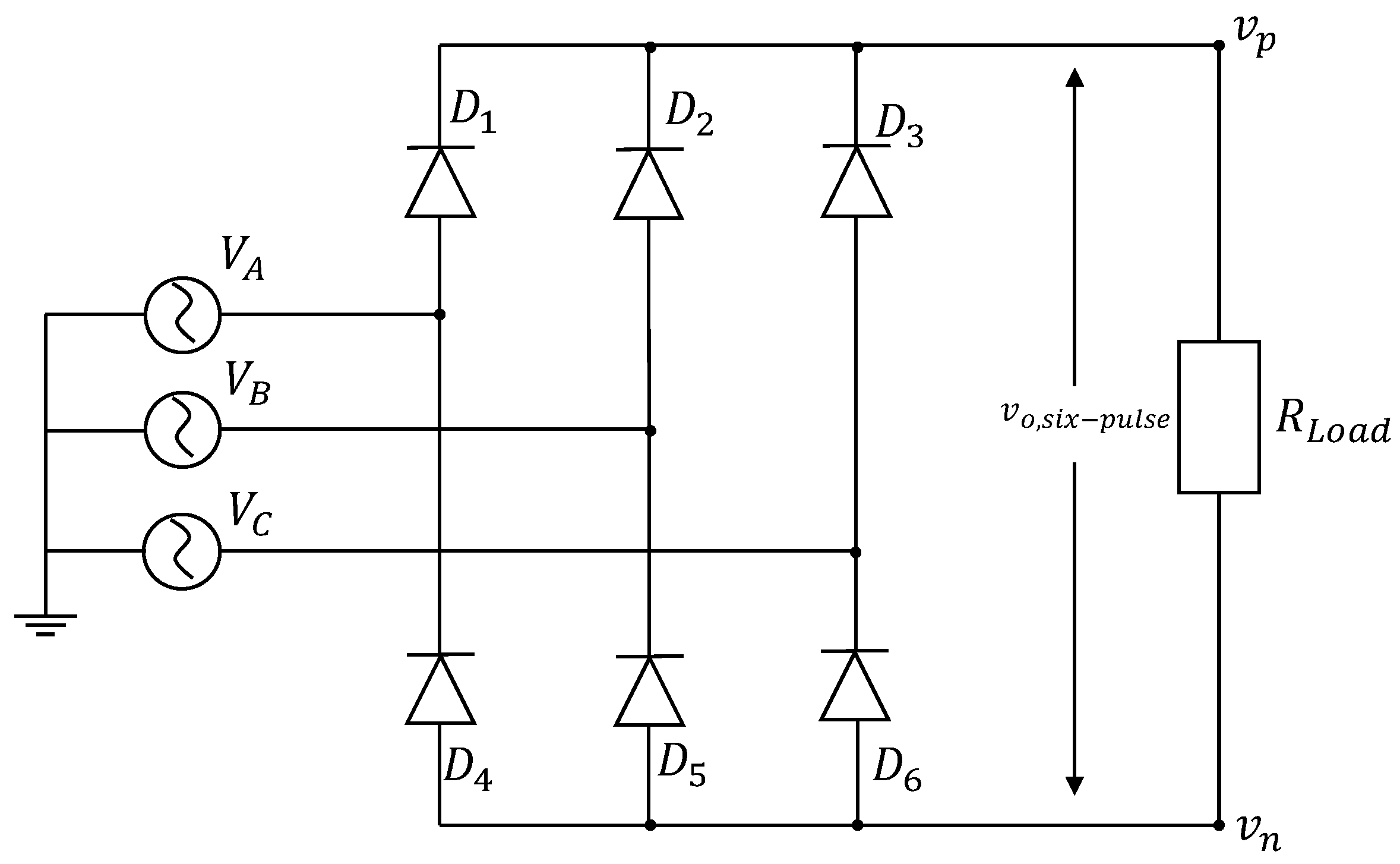
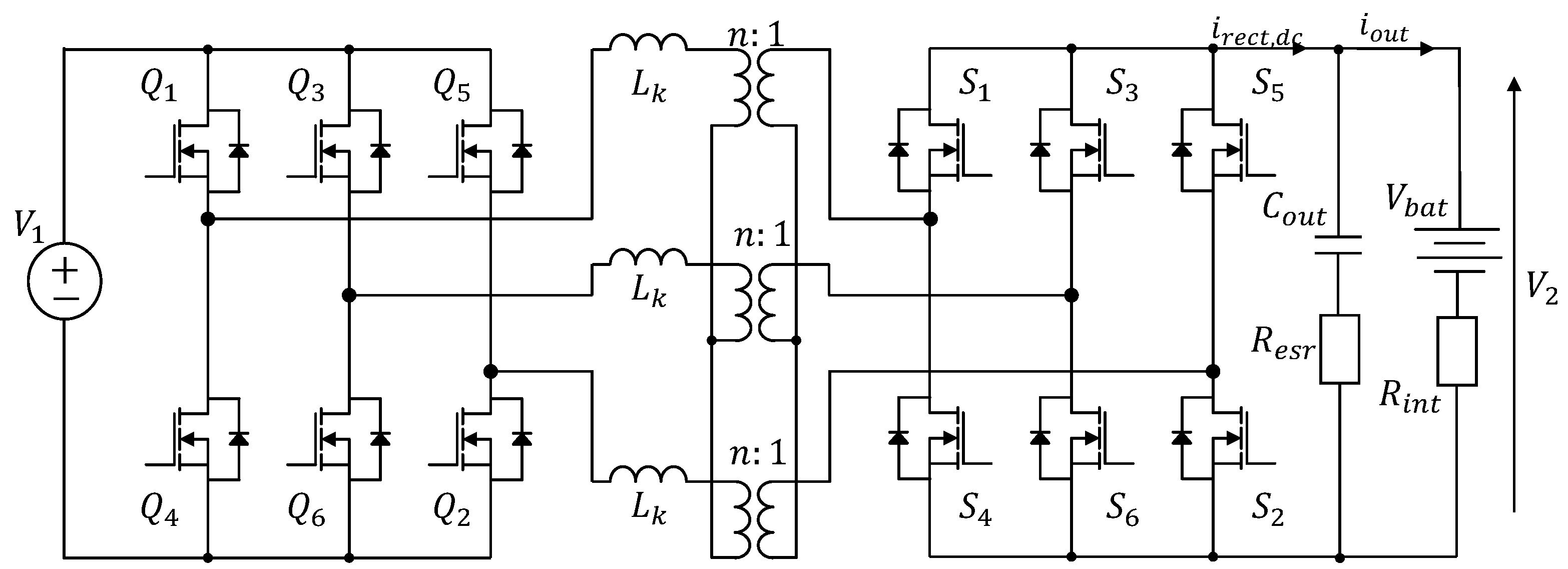
2.1. General Structure
2.2. The Three-Phase Dual Active Bridge Converter
- Series resistance of the transformer winding is ignored;
- ON resistance of the MOSFETs is ignored;
- Parameters of switches are identical;
- Parameters of transformers are identical;
- Magnetizing inductance is much higher than the leakage inductance;
- The voltage drops across the parasitic resistors are significantly smaller than the voltage of the battery;
- The AC–DC stage can be supplied with a stable output and satisfy requirements at the AC line input.
3. Modeling
4. Controller Design and the Low Harmonic Frequency Current Ripple Mitigation Algorithm
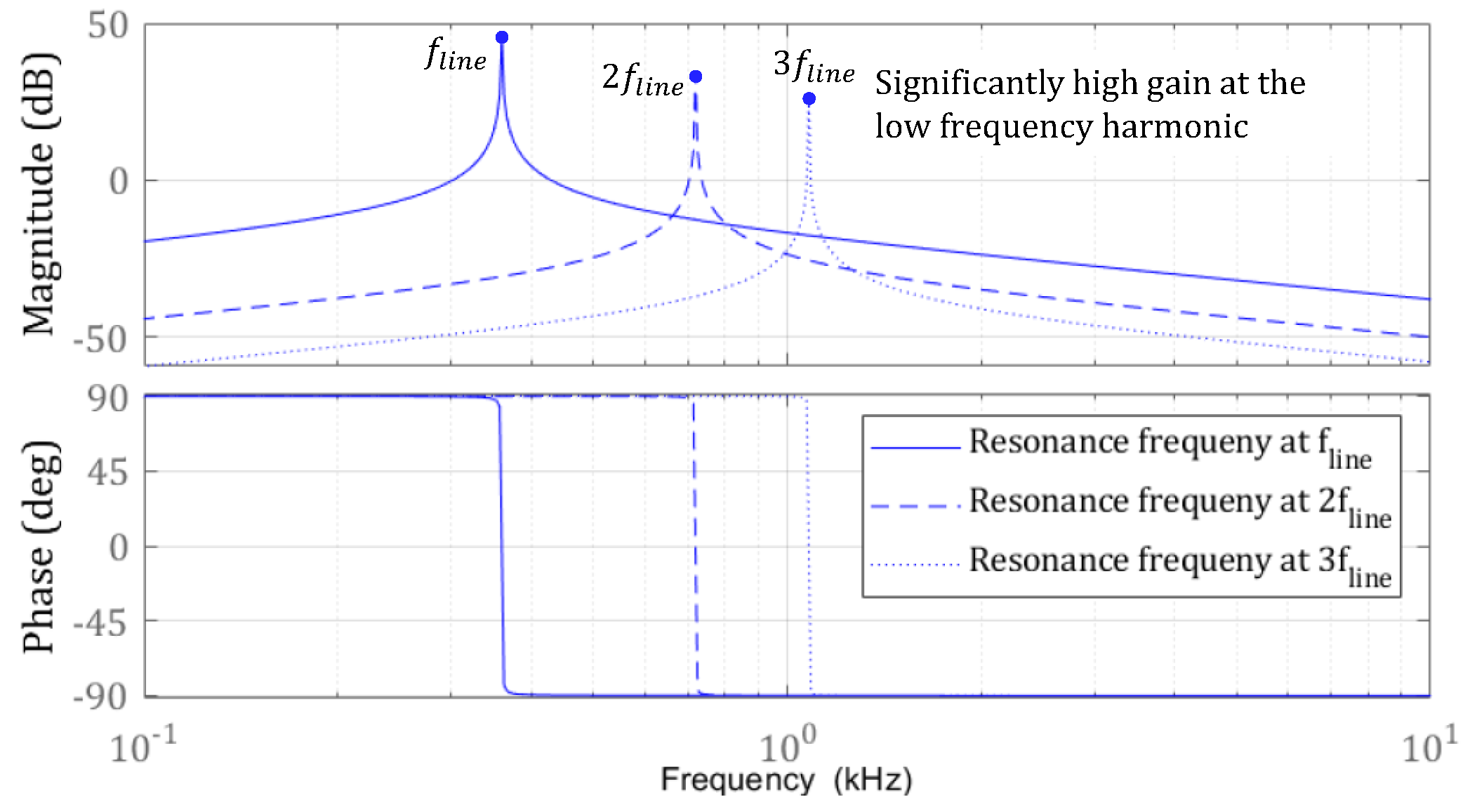
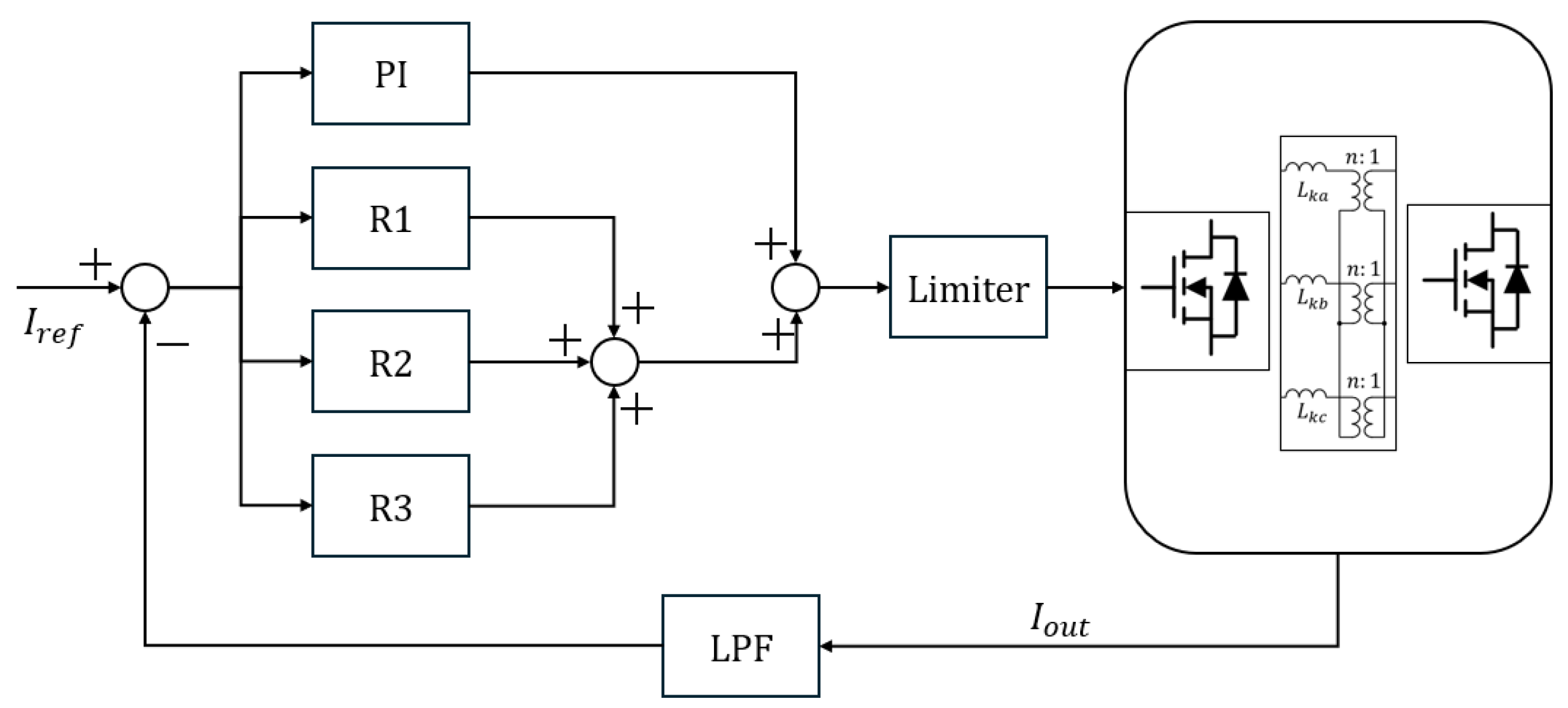
4.1. Multiple Resonance Controllers
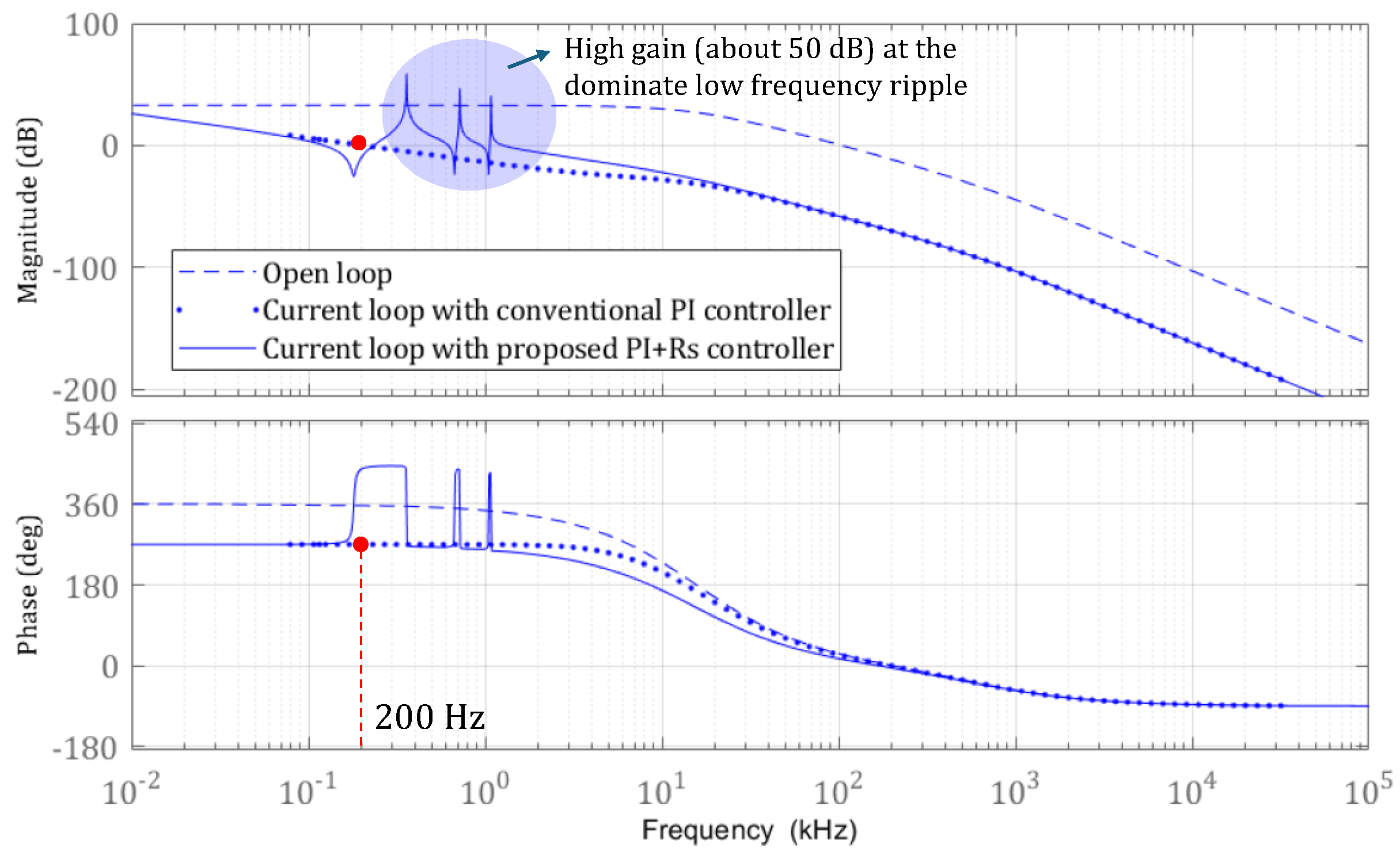
4.2. Controller Design with Harmonic Frequency Ripple Cancellation
4.3. Analyzing the Effect of THD and PF
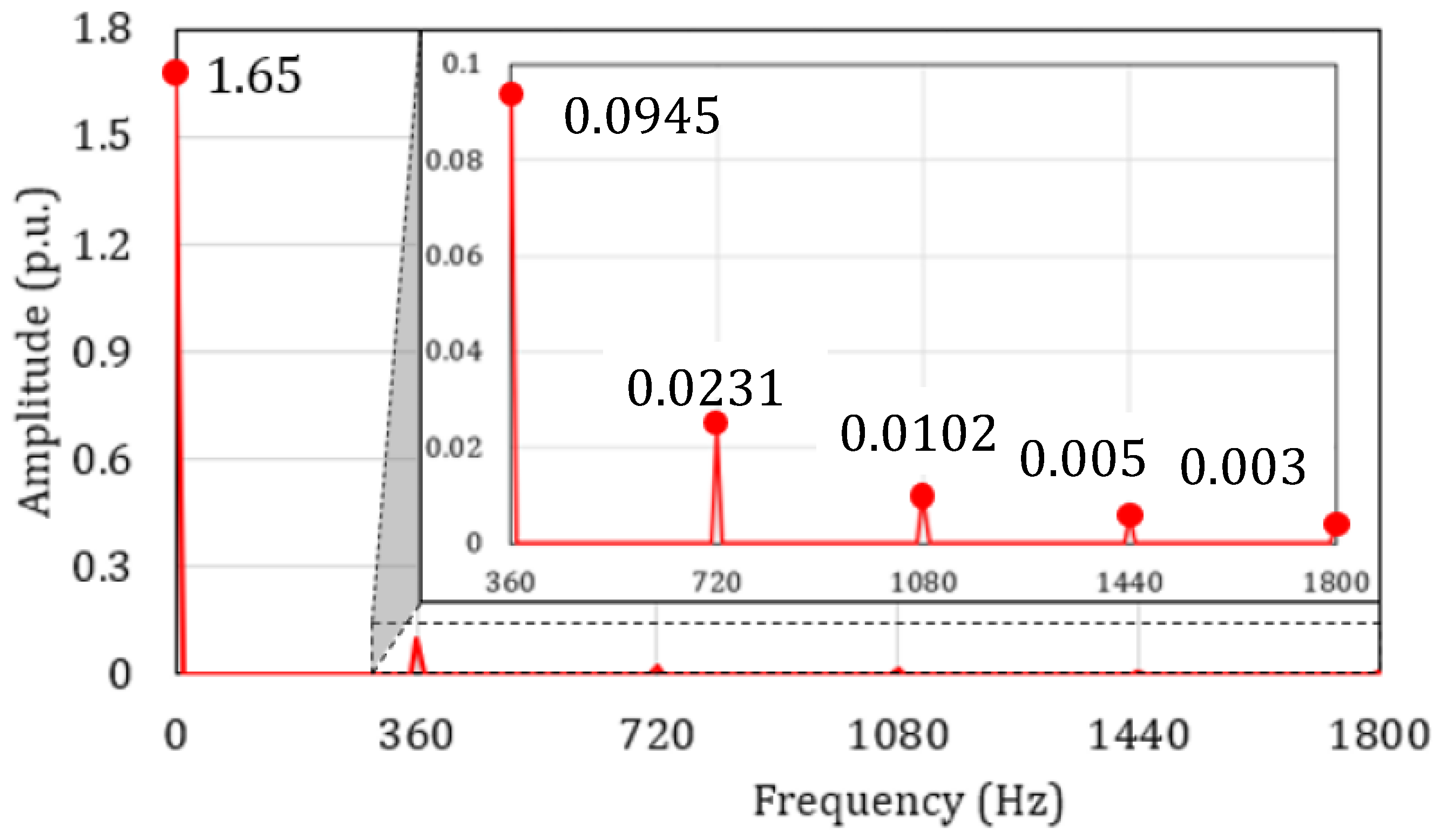
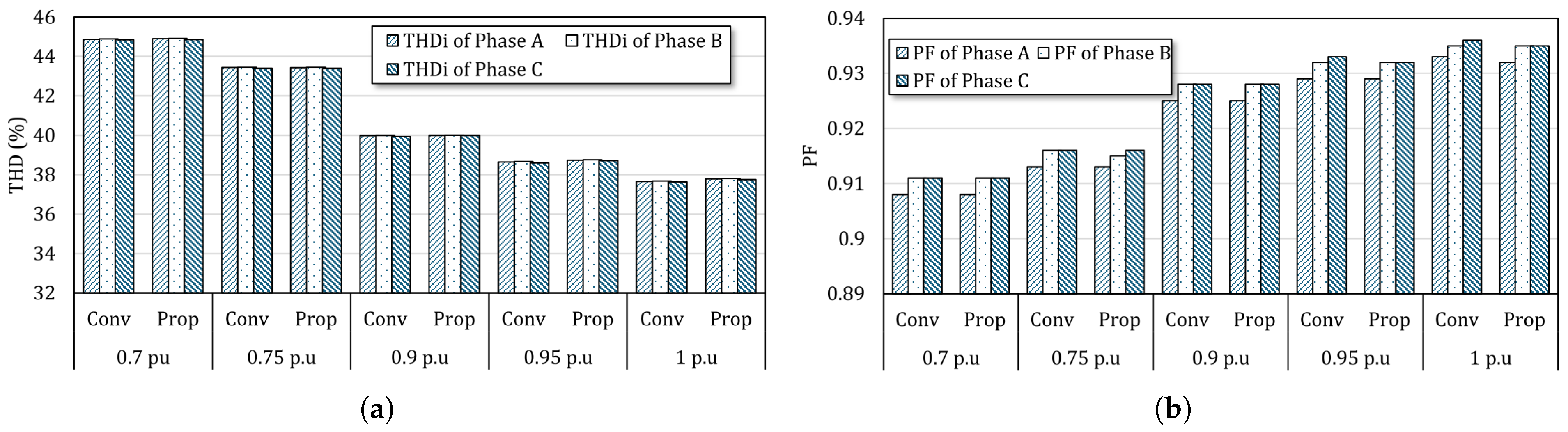
5. Experiment Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. Global EV Outlook 2023. Available online: https://www.iea.org/reports/global-ev-outlook-2023 (accessed on 1 April 2023).
- International Energy Agency. Net Zero by 2050: A Roadmap for the Global Energy Sector. 2021. Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 22 April 2024).
- Mohammed, S.A.Q.; Jung, J.W. A comprehensive state-of-the-art review of wired/wireless charging technologies for battery electric vehicles: Classification/common topologies/future research issues. IEEE Access 2021, 9, 19572–19585. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. Optimal sizing of battery energy storage system in a fast EV charging station considering power outages. IEEE Trans. Transp. Electrif. 2020, 6, 453–463. [Google Scholar] [CrossRef]
- Duan, X.; Hu, Z.; Song, Y.; Strunz, K.; Cui, Y.; Liu, L. Planning strategy for an electric vehicle fast charging service provider in a competitive environment. IEEE Trans. Transp. Electrif. 2022, 8, 3056–3067. [Google Scholar] [CrossRef]
- Rafi, M.A.H.; Bauman, J. A comprehensive review of DC fast-charging stations with energy storage: Architectures, power converters, and analysis. IEEE Trans. Transp. Electrif. 2020, 7, 345–368. [Google Scholar] [CrossRef]
- Dao, N.D.; Lee, D.C.; Phan, Q.D. High-efficiency SiC-based isolated three-port DC/DC converters for hybrid charging stations. IEEE Trans. Power Electron. 2020, 35, 10455–10465. [Google Scholar] [CrossRef]
- Bagchi, A.C.; Kamineni, A.; Zane, R.A.; Carlson, R. Review and comparative analysis of topologies and control methods in dynamic wireless charging of electric vehicles. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4947–4962. [Google Scholar] [CrossRef]
- Barsari, V.Z.; Thrimawithana, D.J.; Covic, G.A. An inductive coupler array for in-motion wireless charging of electric vehicles. IEEE Trans. Power Electron. 2021, 36, 9854–9863. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, C.; Wang, M.; Si, Y.; Liu, Y.; Lei, Q. High-efficiency high-power-density CLLC resonant converter with low-stray-capacitance and well-heat-dissipated planar transformer for EV on-board charger. IEEE Trans. Power Electron. 2020, 35, 10831–10851. [Google Scholar] [CrossRef]
- Franzese, P.; Patel, D.D.; Mohamed, A.A.; Iannuzzi, D.; Fahimi, B.; Risso, M.; Miller, J.M. Fast DC charging infrastructures for electric vehicles: Overview of technologies, standards, and challenges. IEEE Trans. Transp. Electrif. 2023, 9, 3780–3800. [Google Scholar] [CrossRef]
- Mojumder, M.R.H.; Ahmed Antara, F.; Hasanuzzaman, M.; Alamri, B.; Alsharef, M. Electric vehicle-to-grid (V2G) technologies: Impact on the power grid and battery. Sustainability 2022, 14, 13856. [Google Scholar] [CrossRef]
- Kazemtarghi, A.; Dey, S.; Mallik, A. Optimal utilization of bidirectional EVs for grid frequency support in power systems. IEEE Trans. Power Deliv. 2022, 38, 998–1010. [Google Scholar] [CrossRef]
- Khalid, H.M.; Flitti, F.; Muyeen, S.; Elmoursi, M.S.; Tha’er, O.S.; Yu, X. Parameter estimation of vehicle batteries in V2G systems: An exogenous function-based approach. IEEE Trans. Ind. Electron. 2021, 69, 9535–9546. [Google Scholar] [CrossRef]
- Zabetian-Hosseini, A.; Joos, G.; Boulet, B. Control Design for Effective Usage of Electric Vehicles in V2G-Enabled DC Charging Stations. IEEE Trans. Power Deliv. 2023, 38, 4335–4346. [Google Scholar] [CrossRef]
- Xu, Q.; Vafamand, N.; Chen, L.; Dragičević, T.; Xie, L.; Blaabjerg, F. Review on advanced control technologies for bidirectional DC/DC converters in DC microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 1205–1221. [Google Scholar] [CrossRef]
- Zeng, J.; Du, X.; Yang, Z. A multiport bidirectional DC–DC converter for hybrid renewable energy system integration. IEEE Trans. Power Electron. 2021, 36, 12281–12291. [Google Scholar] [CrossRef]
- Arya, H.; Das, M. Fast charging station for electric vehicles based on DC microgrid. IEEE J. Emerg. Sel. Top. Ind. Electron. 2023, 4, 1204–1212. [Google Scholar] [CrossRef]
- Li, L.; Xu, G.; Sha, D.; Liu, Y.; Sun, Y.; Su, M. Review of dual active bridge converters with topological modifications. IEEE Trans. Power Electron. 2023, 38, 9046–9076. [Google Scholar] [CrossRef]
- Shao, S.; Chen, L.; Shan, Z.; Gao, F.; Chen, H.; Sha, D.; Dragičević, T. Modeling and advanced control of dual-active-bridge DC–DC converters: A review. IEEE Trans. Power Electron. 2021, 37, 1524–1547. [Google Scholar] [CrossRef]
- De Doncker, R.W.; Divan, D.M.; Kheraluwala, M.H. A three-phase soft-switched high-power-density DC/DC converter for high-power applications. IEEE Trans. Ind. Appl. 1991, 27, 63–73. [Google Scholar] [CrossRef]
- Min, J.; Ordonez, M. Bidirectional resonant CLLC charger for wide battery voltage range: Asymmetric parameters methodology. IEEE Trans. Power Electron. 2020, 36, 6662–6673. [Google Scholar] [CrossRef]
- Jin, F.; Nabih, A.; Yuan, T.; Li, Q. A High Efficiency High Density Three-Phase CLLC Resonant Converter With a Universally Derived Three-Phase Integrated Transformer for On-Board Charger Application. IEEE Trans. Power Electron. 2024, 38, 9046–9076. [Google Scholar] [CrossRef]
- van Hoek, H.; Neubert, M.; Kroeber, A.; De Doncker, R.W. Comparison of a single-phase and a three-phase dual active bridge with low-voltage, high-current output. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar]
- Nguyen, D.D.; Yuktta, K.; Katou, A.; Yoshida, S. A comparison study of modulation methods for three-phase dual-active-bridge converters in battery charging applications. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition-Asia (ECCE-Asia), Singapore, 24–27 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1033–1038. [Google Scholar]
- Dong, Z.; Wang, C.; Cheng, Q. A hybrid modulation method with the maximum controllable range of the neutral-point current for three-level NPC. IEEE Trans. Transp. Electrif. 2022, 8, 4444–4455. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, Y.; Sun, X.; Zhang, Y.; Li, X. Harmonic resonance suppression strategy of the front-end VIENNA rectifier in EV charging piles. IEEE Trans. Power Electron. 2022, 38, 1036–1053. [Google Scholar] [CrossRef]
- Lan, D.; Wu, Y.; Soeiro, T.B.; Granello, P.; Qin, Z.; Bauer, P. 12-pulse Rectifier with DC-Side Buck Converter for Electric Vehicle Fast Charging. In Proceedings of the IECON 2022–48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Langella, R.; Testa, A.; Alii, E. IEEE recommended practice and requirements for harmonic control in electric power systems. In IEEE Recommended Practice; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Abidin, M.N.Z. IEC 61000-3-2 Harmonics Standards Overview; Schaffner EMC Inc.: Edsion, NJ, USA, 2006. [Google Scholar]
- Kalpana, R.; Singh, B.; Bhuvaneswari, G. A 20-pulse asymmetric multiphase staggering autoconfigured transformer for power quality improvement. IEEE Trans. Power Electron. 2017, 33, 917–925. [Google Scholar]
- Liu, Z.; Meng, F.; Yang, W. Harmonic reduction technology at DC link in star-connected-autotransformer-based multi-pulse rectifier. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Meng, F.; Yang, W.; Zhu, Y.; Gao, L.; Yang, S. Load adaptability of active harmonic reduction for 12-pulse diode bridge rectifier with active interphase reactor. IEEE Trans. Power Electron. 2015, 30, 7170–7180. [Google Scholar] [CrossRef]
- IEEE 2030.1.1; Technical Specifications of Quick Charger for the Electric Vehicle. IEEE: Piscataway, NJ, USA, 2010.
- Qin, Z.; Tang, Y.; Loh, P.C.; Blaabjerg, F. Benchmark of AC and DC active power decoupling circuits for second-order harmonic mitigation in kilowatt-scale single-phase inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 4, 15–25. [Google Scholar] [CrossRef]
- Hu, H.; Harb, S.; Kutkut, N.; Batarseh, I.; Shen, Z.J. A review of power decoupling techniques for microinverters with three different decoupling capacitor locations in PV systems. IEEE Trans. Power Electron. 2012, 28, 2711–2726. [Google Scholar] [CrossRef]
- Qin, H.; Kimball, J.W. Closed-loop control of DC–DC dual-active-bridge converters driving single-phase inverters. IEEE Trans. Power Electron. 2013, 29, 1006–1017. [Google Scholar]
- Lahyani, A.; Venet, P.; Grellet, G.; Viverge, P.J. Failure prediction of electrolytic capacitors during operation of a switchmode power supply. IEEE Trans. Power Electron. 1998, 13, 1199–1207. [Google Scholar] [CrossRef]
- Karanayil, B.; Agelidis, V.G.; Pou, J. Performance evaluation of three-phase grid-connected photovoltaic inverters using electrolytic or polypropylene film capacitors. IEEE Trans. Sustain. Energy 2014, 5, 1297–1306. [Google Scholar] [CrossRef]
- Zhang, L.; Ruan, X. Control schemes for reducing second harmonic current in two-stage single-phase converter: An overview from DC-bus port-impedance characteristics. IEEE Trans. Power Electron. 2019, 34, 10341–10358. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Bui, N.T.; Yukita, K. Design and optimization of three-phase dual-active-bridge converters for electric vehicle charging stations. Energies 2019, 13, 150. [Google Scholar] [CrossRef]
- Nguyen, D.D.; Pham, T.T.; Le, T.T.; Choi, S.; Yukita, K. A Modulation Method for Three-Phase Dual-Active-Bridge Converters in Battery Charging Applications. Sustainability 2023, 15, 5170. [Google Scholar] [CrossRef]






| Frequency | Limit Value (Ap-p) |
|---|---|
| 10 Hz or less | 1.5 |
| 5 kHz or less | 3.0 |
| 150 kHz or less | 9.0 |
| Parameters | Symbols | Value |
|---|---|---|
| Input and output Voltage | and | 100 V |
| Transformer turn ratio | n | 1:1 |
| Leakage inductance | 12.5 H | |
| Magnetizing inductance | 0.9 mH | |
| Input and output filter capacitor | 250 F | |
| Switching frequency | 50 kHz |
| Parameters | Symbol | Value |
|---|---|---|
| Input voltage | 100 V | |
| Output voltage | 100 V | |
| Power | 1.5 kW | |
| Frequency | 50 kHz | |
| Turn ratio | n | 1 (7:7) |
| Magnetizing inductance | 0.9 mH | |
| Leakage inductance | 12.5 H | |
| Wire | Lizt 1050AWG38 | |
| Core | EE42/21/15 (N87) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goto, T.; Pham, T.-T.; Nguyen, N.-D.; Yukita, K.; Nguyen, D.-D. Mitigation of Low Harmonic Ripples Based on the Three-Phase Dual Active Bridge Converter in Charging Station Applications. Electronics 2024, 13, 2527. https://doi.org/10.3390/electronics13132527
Goto T, Pham T-T, Nguyen N-D, Yukita K, Nguyen D-D. Mitigation of Low Harmonic Ripples Based on the Three-Phase Dual Active Bridge Converter in Charging Station Applications. Electronics. 2024; 13(13):2527. https://doi.org/10.3390/electronics13132527
Chicago/Turabian StyleGoto, Takuya, The-Tiep Pham, Nam-Danh Nguyen, Kazuto Yukita, and Duy-Dinh Nguyen. 2024. "Mitigation of Low Harmonic Ripples Based on the Three-Phase Dual Active Bridge Converter in Charging Station Applications" Electronics 13, no. 13: 2527. https://doi.org/10.3390/electronics13132527
APA StyleGoto, T., Pham, T.-T., Nguyen, N.-D., Yukita, K., & Nguyen, D.-D. (2024). Mitigation of Low Harmonic Ripples Based on the Three-Phase Dual Active Bridge Converter in Charging Station Applications. Electronics, 13(13), 2527. https://doi.org/10.3390/electronics13132527







