A Wideband Timing Mismatch Calibration Design for Time-Interleaved Analog-to-Digital Converters with Fast Convergence

Abstract

This paper presents a design for timing mismatch calibration in a TIADC (Time-Interleaved Analog-to-Digital Converter) with wideband inputs. By exploiting the approximately linear relationship between the autocorrelation properties of sub-ADCs and timing mismatch, we achieve rapid convergence of error estimation. A low-cost detection method is proposed based on the convergent monotonicity of the Least Mean Square (LMS) algorithm, which can automatically correct the calibration direction when the input signal goes beyond the Nyquist zone. Physical test results indicate that the spurs caused by timing mismatch can be suppressed by 26–30 dB using the proposed method.

1. Introduction

As the world enters the era of 5G (5th generation) communications and big data, the demand for information is exploding. Ultra-high-speed ADCs are widely used in modern communication systems, such as WiFi, software-defined radio, and electronic measuring instruments. A single ADC is constrained by factors such as its own structure and process, which make it unable to simultaneously meet the performance requirements of high precision, a high conversion rate, and low power consumption. In an ideal situation, the Time-Interleaved Analog-to-Digital Converter (TIADC) greatly improves the sampling rate of the system by simultaneously sampling multiple sub-channel ADCs [1,2,3,4].

However, under real-world conditions, the linearity of the TIADC system output will deteriorate significantly due to errors such as offset mismatch, gain mismatch, and timing mismatch between the channels. High-energy spurs will be generated in the output spectrum, which can reduce the SFDR and SNR and also affect the effective number of bits of the output [5]. Compared with other mismatches, timing mismatch will drastically deteriorate the performance of the TIADC system as the frequency of the input signal increases [6]. Therefore, the calibration of timing mismatches plays a vital role in the entire TIADC system. Existing calibration methods for timing mismatch errors can be divided into calibration with a reference signal and calibration with its own signal, depending on whether it includes an additional reference channel [7,8,9,10]. We can naturally divide the calibration into two steps: detection and correction. From the correction structure, it can be divided into the analog domain [11,12,13,14] and the digital domain [15,16,17]. Analog calibration typically involves utilizing a tunable delay line in the sampling clock [5,18]. The key distinction lies in the resistance [11] or capacitance [18] of the delay circuit.

Timing mismatch can be easily estimated through digital methods. These methods assume that the slope of the signal is first-order equivalent and utilize the product of the timing mismatch and the signal derivative (time deviation) in the digital domain to eliminate the error caused by the timing mismatch. The time deviation detection method can be roughly divided into two categories: one based on deterministic equalization detection [14,19] and the other based on statistical information of the input signal [10].

The time deviation detection method based on deterministic equalization, in the context of time-skew detection, is a direct and effective approach to correct the various non-ideal factors of the ADC by utilizing an additional converter for equalization as a reference [20,21]. However, referencing the ADC will lead to an increased power consumption and area. The reference converter also periodically changes the TIADC’s input impedance, resulting in additional spurious signals that depend on the signal. A digital differentiator implemented by an FIR filter can accurately calculate the slope of the input signal [22,23]. However, this method has inherent constraints and may fail to operate effectively when the input signal approaches or exceeds the Nyquist frequency. By increasing the number of taps in the FIR filter, the digital differentiator can operate over a wider Nyquist frequency range [24]. However, this method poses significant challenges regarding the digital hardware area and power consumption [25,26]. In addition to the digital differential, there is another method to obtain the slope of the signal. By using two ADCs to sample the same input but with different bandwidths, it is possible to determine the difference between the two ADCs [18]. By adding a resistor to the sampling network of the other ADC to make its sampling bandwidth different from that of the reference ADC, the disparity between the two ADCs enables the estimation of the signal slope. This method can only determine the slope of the signal when the reference ADC samples, but it cannot determine the slope at all positions. Therefore, this method is only suitable for use with analog tuning correction.

However, the digital calibration compensation method often requires a higher hardware cost to achieve a better compensation accuracy as the frequency of the input signal increases [27]. Using multipliers operating at high clock frequencies will result in a significant power consumption penalty. Most of the aforementioned methods impose restrictions on the frequency of the input signal, which cannot exceed the Nyquist zone [11,14,17]. This limitation hampers the TIADC system in undersampling scenarios.

In this paper, a wideband timing mismatch calibration design for a TIADC with fast convergence is proposed. We accelerate the convergence process of timing mismatch estimation by tracking the sign information of the sub-ADC’s autocorrelation properties. A low-cost direction correction module based on convergence monotonicity is introduced into the TIADC system to address the issue of incorrect calibration direction when the input signal exceeds the Nyquist zone.

The rest of this paper is organized as follows: Section 2 describes the implementations of the proposed calibration design and presents the simulation results. Section 3 reports physical test results. The conclusion is drawn in Section 4.

2. The Proposed Calibration Design

We assume that the offset and gain mismatches have already been corrected and only focus on the timing mismatch. The detailed system block diagram is shown in Figure 1, where Sub-ADC1, Sub-ADC2, ..., Sub-ADCN represent N sub-channel ADCs of the TIADC system [5]. These sub-channel ADCs are driven by the output of the clock generator, as illustrated in Figure 2. The variable delay line is composed of a switched capacitor array, with their status being switched by the error estimate D_calib generated by the error estimation module. The convergence direction monitor module is introduced to detect and correct the convergence direction.

2.1. Timing Mismatch Estimation and Compensation

We take a traditional two-channel TIADC as an example. The timing mismatch is shown in Figure 3.

Take the CH1 as the reference channel. Let x₁ be the sampled value of CH1 at time t, x₂ be the sampled value of CH2 at the ideal sampling time t + T_s/2, x′₂ be the sampled value of CH2 at the sampling time t + T_s/2 + ∆t with timing mismatch ∆t, and x₃ be the sampled value of CH1 at time t + T_s. In the case of ∆t ≪ T_s, the error value between CH1 and CH2 can be presented as follows [11]:

$${\mathit{error}}_{\mathrm{1,2}}=E\left[{\left(x_2^{\prime }-x_1\right)}^2\right]-E\left[{\left(x_3-x_2^{\prime }\right)}^2\right]\approx {\left.-4\mathsf{\Delta }y\frac{dR\left(\tau \right)}{d\left(\tau \right)}\right|}_{\tau =T_s}$$

(1)

where E represents expectation and R represents the cross-correlation function of T_s. To simplify the calculation and reduce the hardware costs, the expectation is replaced by the cumulative average, and the square operation is replaced by the absolute value. Based on the LMS algorithm [20,22], error_1,2 can be estimated as follows,

$${\mathit{error}}_{\mathrm{1,2}}[n]= {\mathit{error}}_{\mathrm{1,2}}[n-1]+\mu \left(\left|x_3-x_2^{\prime }\right|-\left|x_2^{\prime }-x_1\right|\right)$$

(2)

where µ indicates the step size, as we know, which is a trade-off between the convergence speed and accuracy. The block diagram of the timing mismatch estimation is shown in Figure 4.

After obtaining the estimated value of the error between channels, the error value is mapped to a control code word. The correction feedback loop adjusts the switched capacitor array in sub-ADCs based on the control code word mentioned above. This can help adjust the sampling clock delay for each channel, minimizing timing discrepancies between channels.

The traditional estimation method can achieve stable convergence when µ is small enough. However, this is often accompanied by the issue of a slow convergence speed. Additionally, when the input signal goes beyond the Nyquist zone, the traditional estimation method will fail due to an incorrect calibration direction.

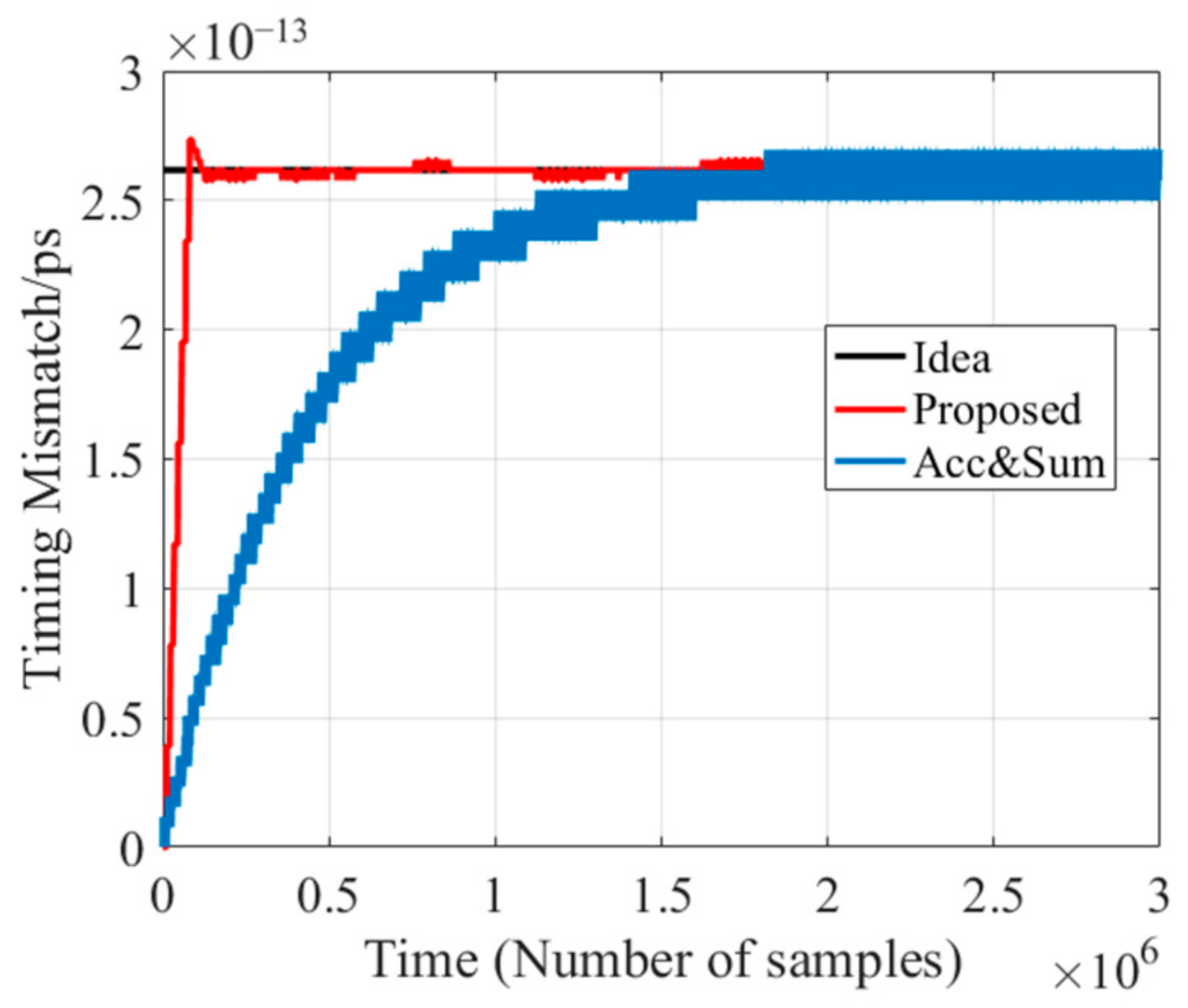
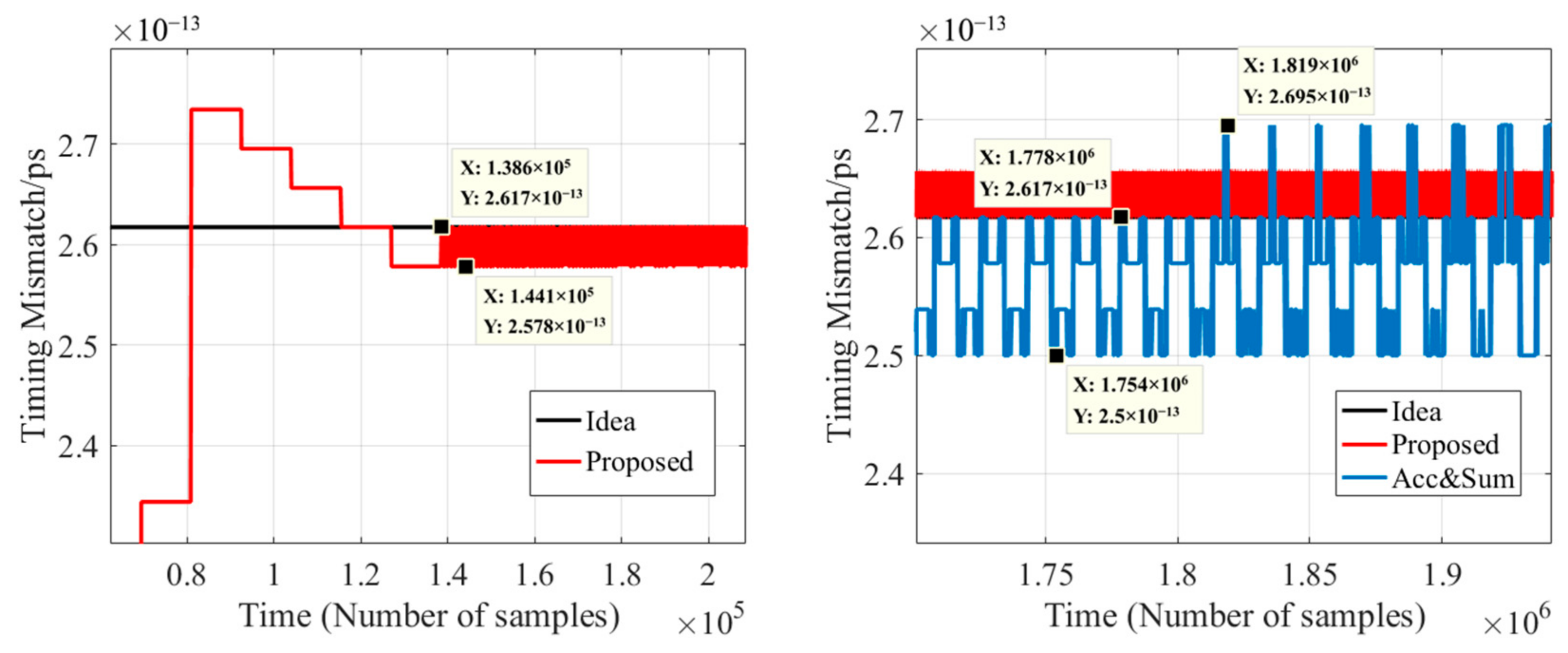
2.2. Mismatch Estimation Fast Convergence

The linear relationship in (1) indicates that the error_1,2 will change sign in an overcompensated condition. In our method, we perform a window averaging operation on the iteration quantity and obtain its sign information.

Let

$$\alpha =\frac{1}{N}\sum _{k=1}^N\mu \left(\left|x_3-x_2^{\prime }\right|-\left|x_2^{\prime }-x_1\right|\right)$$

(3)

We can rewrite (2) as

$${\mathit{error}}_{\mathrm{1,2}}\left[n]={\mathit{error}}_{\mathrm{1,2}}\right[n-1]+\mathit{sign}(\mathsf{\alpha })·\mathit{Step}\_\mathit{value}.$$

(4)

Then, the convergence process can be divided into three parts: 1. the fast approach part; 2. the reverse correction part; and 3. the oscillation convergence part. In the fast approach part, we choose a constant large step value to rapidly reach the overcompensated condition. When the sign of α is inverted, we select a small step value that corresponds to 1 LSB of the delay line control codeword, and then proceed to the reverse correction part. This process will continue until the sign of α inverse changes again, indicating that we have neared the final convergence value. At this point, the iterative formula will be replaced by (2) to achieve the oscillation convergence phase.

We constructed a two-channel 14-bit TIADC model with timing mismatch, operating at 2 GS/s in Simulink v9.2. The delay compensation utilizes a variable delay line array with an accuracy of 1 ps and is mapped to an 8-bit control codeword. The calibration algorithm implemented in Verilog HDL code performs behavioral co-simulation. The entire simulation platform is illustrated in Figure 5. On the left, within the red dashed box, is the SIMULINK mathematical model of the two-channel time-interleaved ADC and ideal delay line. On the right, within the blue dashed box, is the Verilog HDL code design for timing mismatch calibration. This section also includes a data-type conversion module for converting between floating-point and fixed-point numbers.

The input frequency signal is normalized to a frequency of f_s1 = 0.11f_s, respectively. The inter-channel timing mismatch is set to ∆t/Ts = 0.0026. Figure 6 shows the convergence speed comparison between the proposed method and the traditional method, where µ is set to 2−7. It can be seen from Figure 7 that the convergence accuracy of the two methods is within ±2 LSB delay line control codeword precision. The spectra of the TIADC output are shown in Figure 8. The simulation results show that the proposed method drastically reduces the convergence time and effectively inhibits timing mismatch spurs.

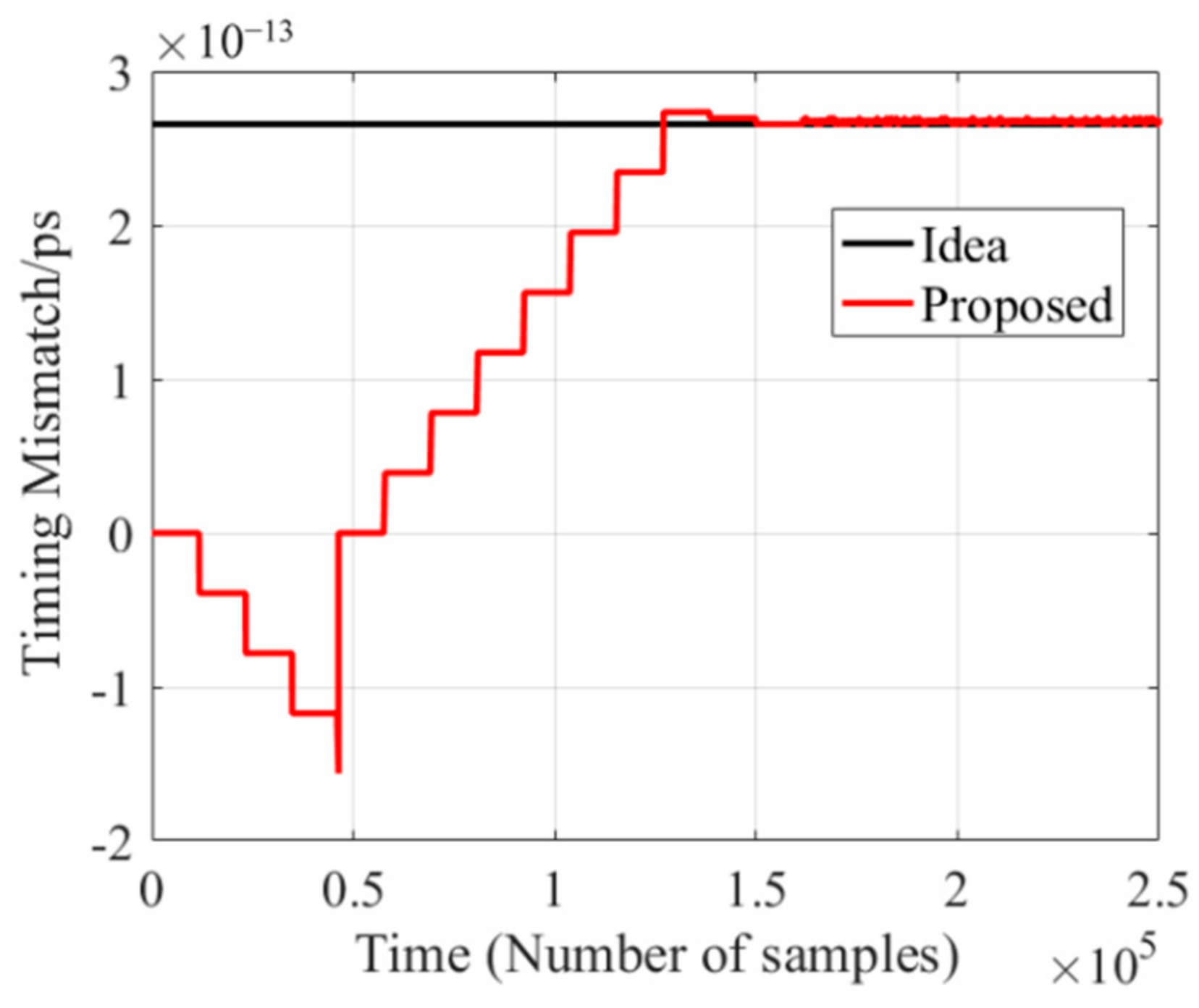
2.3. Calibration Direction Auto Correction

It can be shown from [28] that the derivative of the autocorrelation is given by

$${\left.\frac{dR\left(\tau \right)}{d\left(\tau \right)}\right|}_{\tau =T_s}={\int }_{-\infty }^{+\infty }\left(2\pi f\right)S_x(f)\sin (2\pi f\tau )df$$

(5)

where S_x(f) represents a real input signal spectrum and exhibits an even symmetry. We can recognize from Figure 9 that when the signal spectrum is located in different Nyquist zones, the sign of Equation (5) exhibits a reverse periodicity due to the sine function.

The simulation results of input signals at different frequencies from the first to the second Nyquist zone are shown in Figure 10.

The opposite sign will lead to the wrong convergence direction, which can cause the calibration to fail. According to the LMS principle [11,20,22], we know that when the convergence is in the right direction, α will gradually decrease and eventually converge to the oscillation’s final value. When the signs are opposite, the incorrect convergence direction will cause error_1,2 to increase further. At the same time, due to the approximately linear relationship between α and error_1,2, α will also increase. Based on this rule, we introduce a simple method to correct the convergence direction. At the beginning of the calibration, we use a two-window period to monitor the monotonic variation in error_1,2. If error_1,2 continuously and monotonically increases, this indicates that the current calibration direction is incorrect. In this case, we abandon all the steps taken and reverse the calibration direction. Following the simulation conditions in Section 2.1 and changing the input frequency to f_s2 = 0.66fs, the entire process of convergence direction calibration is illustrated in Figure 11. It can be seen from Figure 11 that the estimation error is reset to 0 after the direction of convergence briefly goes in the wrong direction. Then, the estimation error converges in the correct direction and eventually stabilizes around the ideal error value. The spectra of the TIADC output are shown in Figure 12, and the timing mismatch is effectively suppressed.

The input signal covers the entire first and second Nyquist zones for verification, as shown in Figure 13. The results show that the proposed calibration method in this paper is still applicable for wideband inputs, and the spurious-free dynamic range (SFDR) is significantly improved compared to the case without calibration.

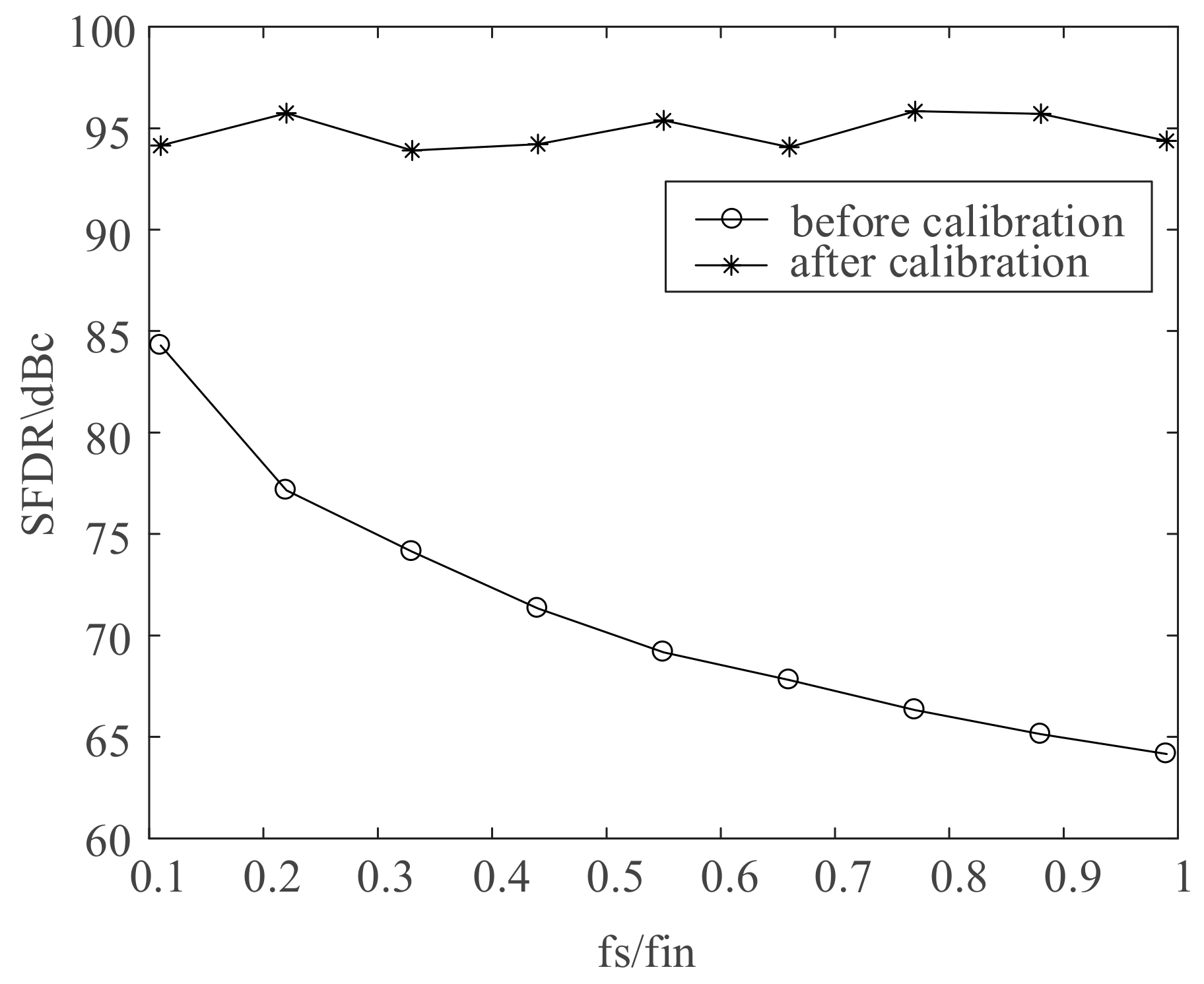
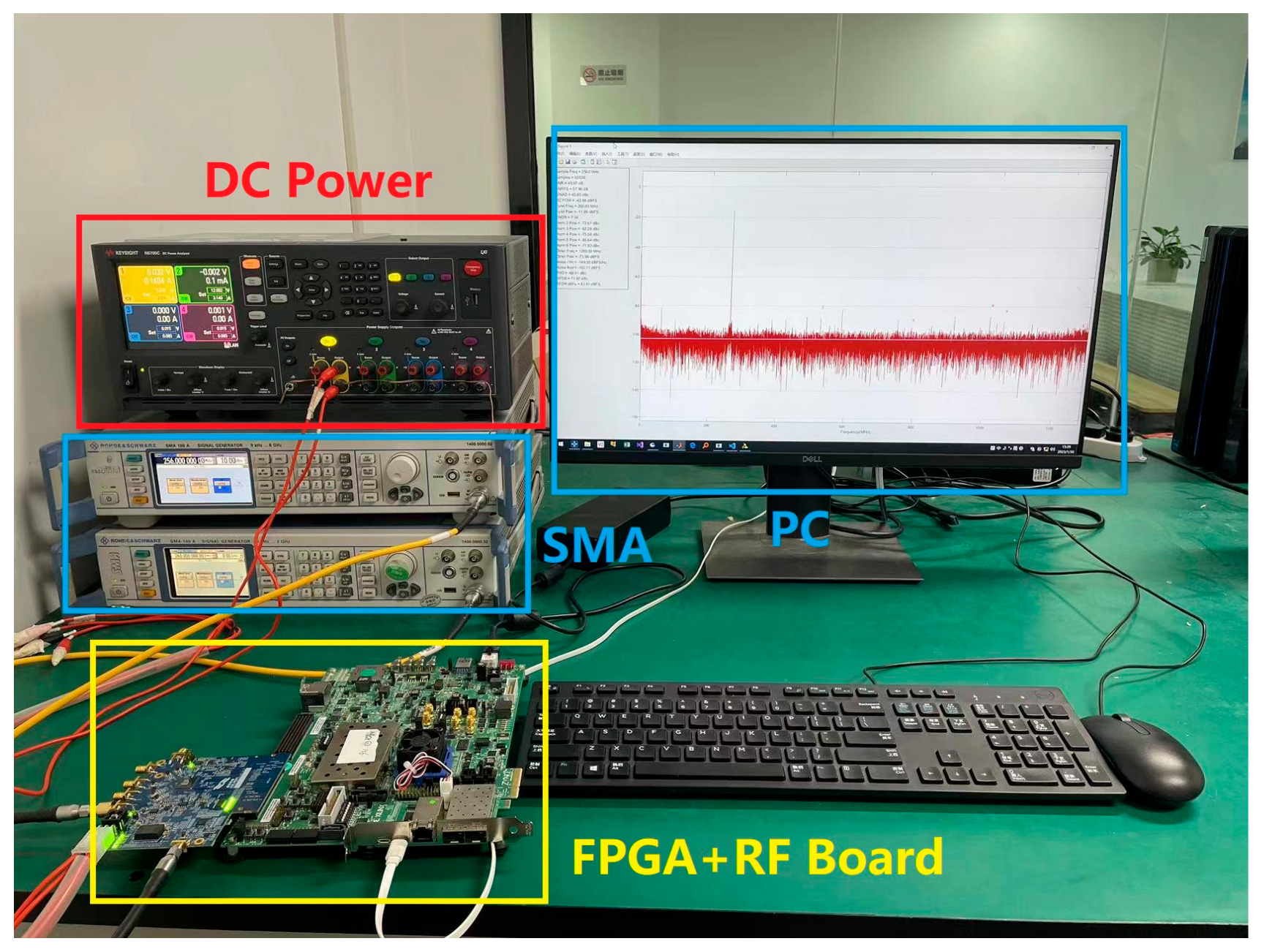
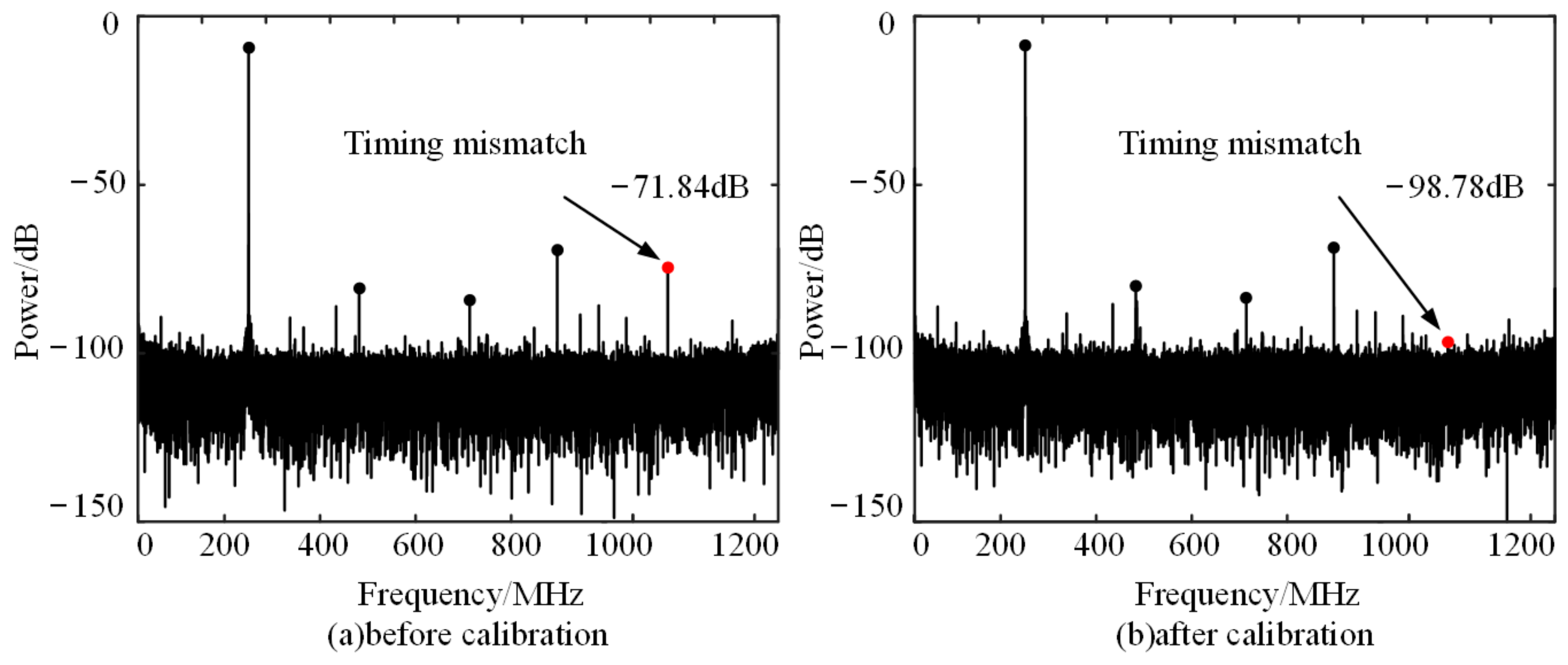
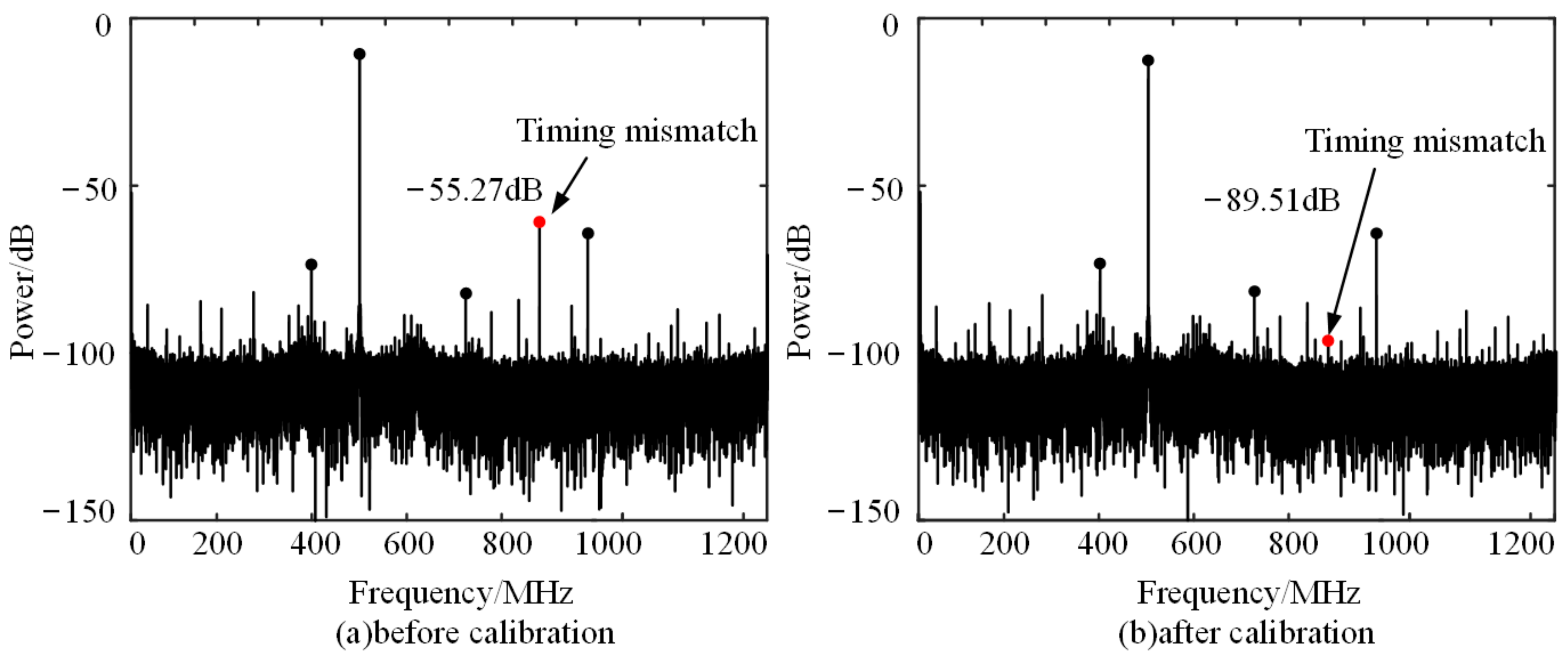
3. Physical Test Results

The two-channel 14-bit 2.56-GS/s TIADC, including the timing mismatch correction and compensation circuits, was fabricated using 28 nm digital CMOS technology. The die photograph of the 2T/3R RF transceiver chip, which incorporates three TIADCs and was primarily intended for small base stations, is depicted in Figure 14, with the design section highlighted by a red dotted box.

The setup of the entire physical test bench is shown in Figure 15. It includes a PC running MATLAB 2018b software for processing sampled data, an FPGA board connected to an RF board for data acquisition, a DC power supply for system operation, and two SMA connectors used for providing a reference clock and input signals, respectively.

Figure 16 and Figure 17 display the measured output spectra with 0.221 GHz and 2.101 GHz inputs before and after calibration.

The measurement results show that the proposed method can achieve excellent calibration results. The spurs caused by the timing mismatch are significantly reduced when the input signal is in the first or second Nyquist zones.

The design features compared to those in reference papers are listed in

Table 1. Comparison with references.

Design Features	[9]	[29]	[14]	[17]	[11]	This Work
Estimation type	Digital	Digital	Digital	Digital	Digital	Digital
Correction type	Digital	Digital	Analog	Digital	Analog	Analog
Reference channel	None	Yes	Yes	None	None	None
Input signal exceed	No	No	No	No	No	Yes
Nyquist zone
Convergence time (samples)	1.2 M	>1 M	250 K	430 K	382 K	140 K
Mismatch spur (dBFS)	−80 *	<−71	<−80 *	<−72 *	<−60	<−85

* Simulation result.

. The proposed method in this paper achieves excellent mismatch spur suppression while converging faster. And thanks to the automatic direction correction design, the input signal of the proposed method can exceed the Nyquist zone.

4. Conclusions

In this paper, we have proposed a low-complexity calibration design for TIADC timing mismatch. By utilizing the sign information of the sub-ADC’s autocorrelation properties, the convergence process is accelerated compared to traditional methods. Furthermore, a low-cost automatic direction correction design is proposed to ensure the accuracy of the calibration algorithm even when the input signal exceeds the Nyquist zone. The effectiveness of the proposed method in this paper is demonstrated through simulation and physical testing, and the spurious effects caused by timing mismatch can be suppressed by 26–30 dB. However, the calibration design proposed in this paper also has some limitations and shortcomings. Due to its reliance on the autocorrelation statistical characteristics of the input signal, it requires the input signal frequency to be coprime with the TIADC sampling frequency. Additionally, the selection of large step-size iteration constants during the initial fast approach part and the iteration parameter µ during the final oscillation convergence part needs careful consideration based on practical circumstances to achieve the best calibration results.