Abstract
Cognitive radio inspired non-orthogonal multiple access (CR-NOMA) networks are a research focus in the wireless communication field. The secure communication of wireless networks has become a pressing issue due to the openness of the wireless channel. Multiple-antenna technology can enhance the secrecy performance in CR-NOMA networks, thus we propose a multiple-input-single-output (MISO) CR-NOMA network where the base station (BS) is equipped with multiple antennas, while others have a single antenna in the paper. The BS serves three secondary users in the presence of an eavesdropper and a primary user. We propose two transmit antenna selection (TAS) schemes, namely the space-time transmission (ST) scheme and the maximum channel capacity (MCC) scheme, respectively. Firstly, we obtain an exact closed-form expression for the secrecy outage probability (SOP) of three secondary users and the overall SOP of the networks with the two schemes, respectively. To gain further insights, the present study analyzes the asymptotic SOP performance to analyze the relationship between the network parameters and secrecy outage performance. Based on this, we propose a power allocation algorithm to further improve the secrecy outage performance of the networks. Finally, we verify the analyses with Monte Carlo simulations. The numerical and simulation results demonstrate that: (1) The MCC scheme outperforms the ST scheme on the secrecy outage performance. (2) The proposed power allocation algorithm optimizes the secrecy outage performance of the networks. (3) There exists a sole respective optimal power allocation factor for a BS different transmission power.
1. Introduction
The future communication network is poised to revolutionize the capabilities of smart cities and the Internet of Things by leveraging global coverage, 10 GB communication capacities, and real-time communication. Nevertheless, the proliferation of access devices has compounded the need for more spectrum resources. To address the problem of spectrum shortage, non-orthogonal multiple access (NOMA) and cognitive radio (CR) technologies have emerged as promising solutions to enhance the efficiency of spectrum utilization in future wireless networks [1,2,3,4,5]. These technologies offer unique advantages for mitigating the problem of spectrum resources, and their significance in the field is widely recognized.
1.1. Related Works
By integrating the benefits of NOMA and CR technologies, researchers have proposed a CR-NOMA network based on spectrum sharing mode in their works [6,7]. The study has focused on the connection outage performance of secondary users, revealing that the connection reliability of the CR-NOMA network surpasses that of the orthogonal multiple access (OMA) based on a CR network. These findings underscore the potential of CR-NOMA as a promising approach to improve the performance of future wireless networks in terms of connectivity and reliability.
The issue of wireless network security has become a prominent research focus, as users’ confidential information is vulnerable to eavesdropping in wireless network channels. Based on information security theory, physical layer security (PLS) technology has emerged as a practical solution [8,9]. In recent studies [10,11], the security communication concerns in CR-NOMA networks have been investigated from the PLS perspective. Specifically, the authors investigated the secrecy performance of the CR-NOMA network in the presence of multiple primary users under the PLS scenario, where secondary users were considered potential eavesdroppers [10]. Moreover, [11] investigated the secrecy outage probability (SOP) of one secondary user in CR-NOMA networks under the quality-of-service (QoS) and security constraints of the primary user.
Nonetheless, a notable limitation of the aforementioned studies is that the base station (BS) is equipped with only a single antenna, thus prompting researchers to shift their focus towards multi-antenna networks and investigate various transmit antenna selection (TAS) schemes to enhance secrecy outage performance [12,13,14,15,16,17,18]. For example, in [12], Nandan et al. proposed a zero-forcing-beamforming (ZFBF) technique to enhance the secrecy performance in multiple-antenna CR-NOMA networks. In [13,14], the SOP of secondary users in cooperative multiple-input-single-output (MISO) CR-NOMA networks were examined, with consideration given to the absence of a direct link between the secondary transmitting BS and secondary users, and the provision of a relay for cooperative signal transmission. Moreover, Zhu et al. proposed a space-time transmission (ST) scheme and a maximum channel capacity (MCC) scheme [15], which served as the basis for LEI et al.’s study on the SOP of two secondary users in the MISO-NOMA network with STT and MCC schemes. Simulation results shown that the secrecy performance with STT and MCC schemes were substantially better than that of a single-antenna NOMA system [16]. In [17,18], artificial noise and relay-assisted cooperative technology were applied to NOMA networks with ST and MCC schemes, further enhancing the secrecy outage performance of the system. However, it is worth noting that [15,16,17,18] were conducted solely in non-cognitive scenarios.
In order to further improve the spectrum efficiency and secrecy outage performance of next-generation wireless networks, researchers have turned their attention to the power allocation (PA) problem. For instance, the authors proposed a power allocation algorithm for single-input-single-output (SISO) NOMA systems to enhance the secrecy sum rate of the secondary networks [19]. In [20], the authors examined the optimization problem of secrecy outage probability (SOP) for both primary users and random secondary users in a CR-NOMA network. In [21], a machine-learning algorithm was proposed to minimize the SOP of the secondary networks in cooperative CR-NOMA systems. Simulation results indicated the superiority of the proposed PA algorithm in terms of achievable SOP.
The primary limitation of the aforementioned studies pertains to the analysis of secrecy performance in two-user networks implementing either NOMA or CR-NOMA schemes. Notably, the primary objective of NOMA technology is to ensure optimal performance while serving a maximum number of users, thereby not being recommended for use in two-user scenarios. However, the derivation of the mathematical model becomes increasingly complex as the number of users grows, which poses a significant challenge. Presently, investigations into the performance of three-user CR-NOMA networks remain in their nascent stages [22,23]. The authors of the studies have demonstrated superior performance in connection outage probability and achievable capacity for such networks [23].
1.2. Motivation and Contribution
In view of the inspiration mentioned earlier and to the best of our knowledge, the evaluation of secrecy outage performance in CR-NOMA networks employing MCC and ST schemes is an outstanding issue. Consequently, we propose a novel multiple-antenna CR-NOMA network architecture, wherein the secondary base station (BS) transmits signals to three secondary users while accounting for the presence of an eavesdropper over Rayleigh fading channels. The transmission strategy considers interference caused by the secondary network to the primary user (PD) and adopts a power constraint to ensure QoS of PD. This approach not only enhances the spectrum utilization of the network, but also ensures the security of the transmitted data. The article’s primary contributions can be condensed as follows:
- We investigate the secrecy outage performance for MISO-CR-NOMA networks with MCC and ST schemes. The exact closed-form expressions for the SOP of secondary users are derived. To obtain further insights, we conduct the asymptotic analysis of SOP for MCC and ST schemes when the transmitted power of BS reaches the QoS constraint;
- Based on the secrecy outage performance with MCC and ST schemes, we study the problem of optimal power allocation and minimum SOP, and design a simulated-annealing (SA) algorithm based on the QoS constraint to solve the problem;
- Through theoretical analysis and Monte Carlo simulation verification, we compare the secrecy outage performance of the overall secondary network and every secondary user with the ST scheme and the MCC scheme, verifying the accuracy of the optimal power allocation algorithm. It is shown that: (1) The MCC scheme outperforms the ST scheme in secrecy outage performance; (2) the proposed power allocation algorithm optimizes the secrecy outage performance of the secondary user network; and (3) the optimal power allocation factor changes when the BS transmission power changes.
1.3. Structure
The subsequent sections of this paper are structured as follows. Section 2 describes the system model. The investigation of the secrecy outage performance for single-antenna BS is presented in Section 3. Section 4 and Section 5 detail the TAS schemes and provide the exact and asymptotic closed-form expressions for the SOP of secondary networks. Section 6 proposes the SA algorithm. In Section 7, we showcase representative numerical results based on the analytical findings and SA optimization models. Finally, Section 8 concludes this article.
2. System Model
Based on Figure 1, we contemplate a downlink CR-NOMA network including a secondary base station (BS), a primary user (PD), a set of secondary users: (the farthest user), (the remote user) and (the near user), a passive eavesdropper (E). Because BS has strong computing power and volume, we assume that BS is equipped with M-antennas; instead, PD, , , and E are equipped with a single antenna because of their limited spatial and power consumption. The model is founded on the following assumptions, which are without loss of generality:
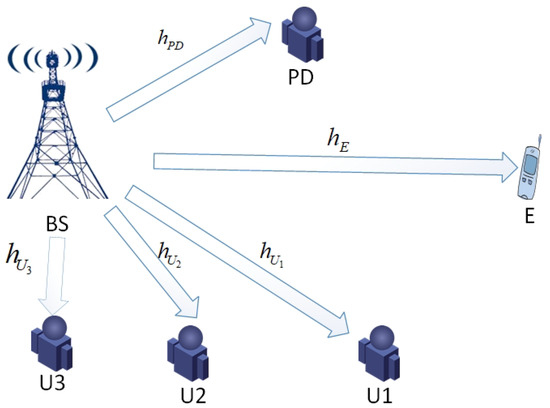
Figure 1.
Network model.
- (1)
- Considering the channel from BS to the D, where , let and represent the small-scale fading and large-scale path-loss of the BS→D, channel. It is assumed that all channels are independent of each other and exhibit Rayleigh block flat fading. Therefore, the channel gain of small-scale fading () follows independent exponential distribution with the mean of . The model of large-scale fading is , where means the path-loss constant, represents the distance between BS and D, means the reference distance, and means the path-loss exponent. To simplify symbols, we refer to the modeling of [24], let , follows an exponential distribution with unit mean. Consequently, the channel coefficient follows an independent exponential distribution with the mean of .
- (2)
- All channels are subjected to an additive white Gaussian noise (AWGN) characterized by a zero mean and a variance of . In line with [25], we consider the absence of channel state information (CSI) of the primary base station (PBS) at the secondary users. Consequently, owing to the Central Limit Theorem, we can regard the interference resulting from PBS as AWGN having a zero mean and a variance of . To simplify symbols, let .
In this network, the superimposed signal sent by BS in NOMA mode is
where , and represents the signals sent by BS to secondary users , and , respectively. , and are power distribution coefficients (). According to the NOMA transmission principle, since the distance from to BS is closer than to BS, is also closer than , and it is assumed that .
When BS sends signals to secondary users, the signal received by secondary users can be expressed as
where is the channel coefficient from BS to link, is BS transmit power, and is AWGN with the variance of .
In order to ensure the QoS of the primary user, we consider the transmit power of the BS to be constrained by both BS peak transmission power and peak interference power, which is expressed as
where is BS peak transmission power, Q is interference temperature, and indicates the interference channel gain between BS to PD.
Firstly, we describe the signal-to-interference-plus-noise ratio (SINR) and signal-to-noise ratio (SNR) at and E according to successive interference cancellation (SIC) technology.
- (1)
- At : directly decodes its own signal , and the signal and are regarded as interference, the SINR of can be given as
- (2)
- At : In order to decode , first needs to decode , then eliminate the interference caused by with the help of SIC technology, and finally decode with as the interference signal. To facilitate the analysis of secrecy outage performance, we posit that exhibits effective decoding , thus the SINR of can be given as
- (3)
- At : Similar to the decoding process of , needs to decode and successfully eliminate interference before decoding , we assume that can successfully decode and , and the SNR of can be given as
- (4)
- At E: We assume that E has SIC capabilities similar to and to detect multi-user data. and are considered as interference noise when they eavesdrop on . is successfully eliminated through SIC, and is regarded as interference noise when it eavesdrops on . and are successfully eliminated when they eavesdrop on . Thus, we have
3. Secrecy Outage Performance of SISO-CR-NOMA Network
In this section, we consider the circumstance of the SISO-CR-NOMA network, i.e., , the BS is equipped with one antenna. The SOP results obtained in this section can replace many complex expressions in the MISO network, which is easier to understand more intuitively, and it can be used as a benchmark for comparison, making it easier to understand the secrecy outage performance improvement brought by TAS schemes. First, we explain the secrecy capacity and SOP, then derive the exact closed-form of the secondary user’s SOP in the SISO-CR-NOMA network.
Secrecy capacity can be defined as the disparity between the channel capacity of the BS-User transmission link and the BS-E eavesdropping link [14]. Therefore, the secrecy capacity of is
where , , .
SOP is defined as the probability that secrecy capacity is less than the secrecy communication rate [16]. The SOP of can be expressed as
where is the secrecy communication rate of .
In order to derive the SOP of , we first need to obtain the cumulative distribution function (CDF) of , , and BS-PD interference channel gain , the CDF of (, ) and expressed as
By deriving the CDF above (10)–(13), the probability density function (PDF) of the variable and can be obtained, respectively.
Substituting the above CDF and PDF into Equations (8) and (9), the following conclusions can be obtained:
Theorem 1.
The SOP of secondary users , and in the SISO-CR-NOMA network are expressed as
where , , ,, , , , ,, , , .
Proof.
Please see Appendix A. □
According to [26,27], given the assumption that E’s interest lies solely in the information of a particular user within the system, the probability of selecting said user is equal among all users, i.e., . However, BS lacks knowledge regarding which user E intends to eavesdrop on. Therefore, the overall SOP of three secondary users in the CR-NOMA network can be expressed as
Proof.
Please see Appendix B. □
4. Secrecy Outage Performance of MISO-CR-NOMA Network
This section analyzes the secrecy outage performance of the secondary users with MCC and ST schemes.
4.1. The Maximum Channel Capacity Scheme
In general, the CSI of the links between the BS and secondary users can be relayed to the former through a combination of signaling and channel feedback mechanisms [24]. In contrast, E remains in a passive operational state, such that no exchange of information exists between it and the BS. Thus, it is considered that the CSI of BS and secondary user links are available at BS, while the CSI of the BS to E link is not available. To this end, the MCC scheme is proposed to maximize the SNR, or alternatively, SINR of the secondary users while concurrently ensuring that the QoS requirements of PD are upheld. Specifically, the optimal transmit antenna for the signal of BS transmitted to the secondary is identified as the one that maximizes the channel capacity. Assuming no loss of generality, we contemplate that the i-th () transmit antenna of BS is selected as the best antenna to transmit signal with power . Next, we analyze three situations, called max-, max- and max-, respectively.
4.1.1. max-
In this one, the i-th transmit antenna at the BS is selected such that the channel capacity of the BS– is maximized, which means , is the received instantaneous SINR at from the i-th antenna at S, and the symbol “M1” represents max-. The CDF and PDF of correspond identically to Equations (10) and (14). Then, the CDF and PDF of can be obtained as
It is noteworthy that the selection of the i-th transmits antenna for entails the random selection of a transmit antenna for , , PD, and E. As a result, the CDF and PDF of , and in this scenario are identical to those of the SISO-CR-NOMA network, i.e., (11)–(13) and (15)–(17), respectively. Similar to the derivation of the single-antenna case, we can obtain Theorem 2.
Theorem 2.
The SOP of secondary users , and with max- of MCC scheme in the MISO-CR-NOMA network are expressed as
where, .
4.1.2. max-
Similarly, in order to maximize the channel capacity of the communication link of the BS–, the i-th transmit antenna at the BS is deliberately selected. To simplify the layout, the SOP of secondary users with max- circumstances are given as
where , .
The proof is omitted since the deductions follow similar steps to max-.
4.1.3. max-
Similar to max- and max-, the SOP of secondary users with max- circumstances can be obtained as:
4.2. The Space-Time Transmission Scheme
First, BS uses space-time coding [15] technology to encode the secondary user signal. All antennas of BS participate in signal coding and send the signal to the secondary users receiving node. To ensure the QoS of PD, the total transmit power of all antennas are limited to . To simplify the calculation, consider the equal power distribution method, and assume that the transmitting power of each antenna of BS is [16]. The CDF of ( , ) and are expressed as
Similar to the derivation of the SOP with MCC scheme, we can obtain Theorem 3.
Theorem 3.
The SOP of secondary users , and with ST scheme in the MISO-CR-NOMA network are expressed as
where , , , .
5. Asymptotic Secrecy Outage Performance Analysis
Due to the complexity of the aforementioned secondary user’s SOP expression, it is difficult to find the relationship between SOP and system parameters intuitively. Next, we analyze the asymptotic SOP performance of secondary users and discuss the relationship between SOP and system parameters.
We assume , hence the transmit power of the BS depends on the QoS constraints of the PD. With some simple algebraic manipulations and observation, we can easily obtain the exact asymptotic SOP expression of the secondary users.
5.1. SISO-CR-NOMA Network
The asymptotic SOP of secondary users with the single-antenna network are as follows:
Proof.
Please see Appendix C. □
5.2. MISO-CR-NOMA Network
Similar to the derivation process of SOP in the SISO-CR-NOMA network, we can easily obtain the SOP for multiple-antenna networks.
5.2.1. MCC Scheme
The asymptotic SOP of secondary users with max- are as follows:
The asymptotic SOP of secondary users with max- are as follows:
The asymptotic SOP of secondary users with max- are as follows:
5.2.2. ST Scheme
The asymptotic SOP of secondary users with the ST scheme are as follows:
By observing the above expressions, we can reach a useful understanding as follows:
Remark 1.
As increases, the SOP of the secondary users is finally constant because the QoS of the PD limits the maximum transmit power. From (3), we can obtain the current transmission power of BS as .
Remark 2.
Combining Remarks 1 and 2, in the next section, we find the minimum overall SOP in the CR-NOMA network by optimizing the power allocation coefficient to maximize the advantages of the TAS schemes.
6. Power Optimization with SA Algorithm
Common optimization algorithms in CR-NOMA networks include golden search, simulated annealing (SA), and gradient descent. Compared with previous algorithms, the SA algorithm has the advantages of simple description and high running efficiency. Thus, we consider the SA algorithm to solve the minimum overall SOP of secondary network problems based on the maximum BS transmit power under QoS constraints.
We formulate this optimization problem as follows:
where constraint condition C1 is the power coefficient requirements of SIC technology, and constraint conditions C2 and C3 represent the total power constraints allocated by the BS to the superimposed signal.
Since the objective function given in is highly non-linear, and this optimization problem contains the equality constraints, we transform the constraints C1 and C2 into a penalty function and then construct a new objective function. The new optimization problem is given as
where , represents penalty coefficient, represents external penalty function. Then, we can use the SA algorithm (shown as Algorithm 1) for solving (64).
| Algorithm 1 The SA Algorithm to solve (64). |
Input:
|
In the upcoming section, we will conduct a simulation verification and analyze the SA algorithm’s superiority in terms of convergence speed.
7. Simulation Results
This section simulates the above-mentioned theoretical derivation and algorithm, then uses the theoretical curve and simulation results to analyze the influence of system parameters on the secrecy outage performance index. We use samples per Monte Carlo simulation to ensure sufficient statistical confidence. Unless otherwise specified, we set the power coefficient 0.6, 0.3, 0.1, numbers of BS transmit antenna , distance between receiving nodes of secondary users, primary users and eavesdropper and BS 300 , 200 , 100 , 100 , 700 , the reference distance 1 , the path-loss constant 1, the path-loss exponent , interference temperature −10 , total noise power 0.001 , and secondary users secrecy communication rate 0.5 . For brevity, “M1”, “M2” and “M3” mean “max-”, “max-” and “max-”, “Ana” means “Analysis”, “Sim” means “Simulation” and “Asym” means “Asymptotic analysis” in all figures.
7.1. Validation of Analysis and Performance Comparison
In Figure 2, we compare the secrecy outage performance of three secondary users with various TAS schemes, numbers of antennas, and secrecy communication rates in the CR-NOMA network. The analytical results are based on Section 3 and Section 4, and the asymptotic results are based on Section 5. From Figure 2, we can obtain the following views: (1) The results of the theoretical analysis and Monte Carlo simulation are very consistent, which verifies the correctness of theoretical analysis. (2) With the ST and MCC schemes for all secondary users in Figure 2d,e, we increase the secrecy communication rate of each secondary user, i.e., , , , the overall SOP of the secondary network will increase, and the secrecy outage performance will deteriorate. This is due to the fact that when the , , and increase, the outage threshold of , , and also increase correspondingly. (3) For the overall SOP of the secondary network, the max- of the MCC scheme is far superior to other schemes. The intuitive reason is that in the signal transmission process, is the farthest user, and its SOP is relatively high, which greatly impacts the overall SOP. (4) When the BS is equipped with multiple-antenna, the secrecy outage performance of secondary users is significantly better than that of the SISO-CR-NOMA network.
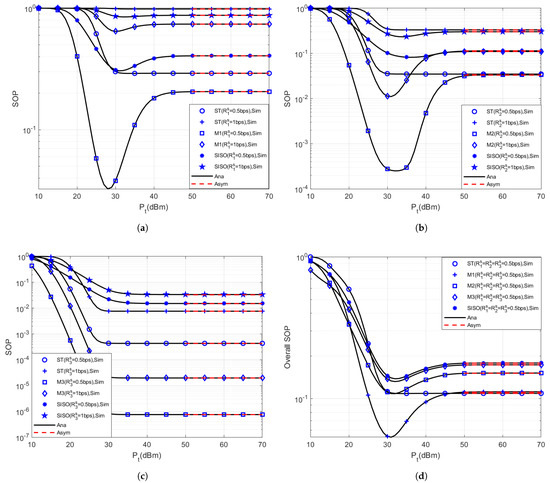
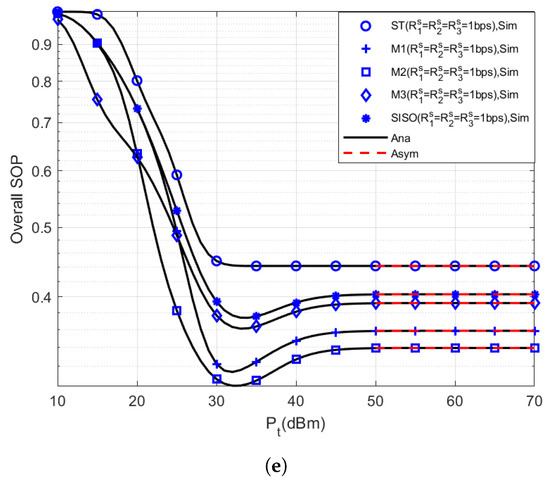
Figure 2.
The secrecy outage performance of secondary users with various TAS schemes, numbers of antennas, and secrecy communication rates. (a) SOP of ; (b) SOP of ; (c) SOP of ; (d,e) overall SOP with different secrecy communication rates.
In Figure 3, we compare the SOP of the MCC and ST schemes in different interference temperatures. From Figure 3a,b, as can be seen, with the increase of , the SOPs of and present a curve trend that first decreases, then increases. It can be explained by features of SIC technology and QoS constraints of PD. As with Formulas (4), (5) and (7), when signal is used as interference, uses SIC to decode its own signal. With the increase of to a certain value, the influence of on user channel capacity begins to exceed other parameters such as the power distribution coefficient and channel gain, so the interference effect of becomes stronger, the user channel capacity and eavesdropping channel capacity decrease synchronously, the security capacity decreases, the SOP increases, and the secrecy performance drops sharply. Meanwhile, with the increase of , SOP is finally constant. This result verifies the correctness of Section 5. Because the transmission power of BS is constrained by the QoS of PD. By comparing Figure 2d and Figure 3d, we found that reducing Q can reduce the interference between signals simultaneously, improving the network’s secrecy outage performance.
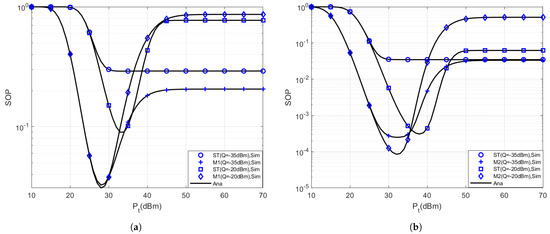
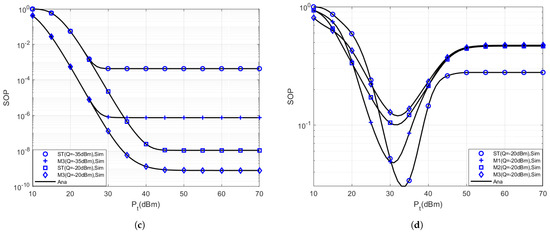
Figure 3.
The secrecy outage performance of secondary users with various TAS schemes and interference temperature. (a) SOP of ; (b) SOP of ; (c) SOP of ; and (d) overall SOP.
7.2. Insights on Optimal Solution
In Figure 4, we study the relationship between the power allocation coefficient and SOP of secondary users with various TAS schemes in = 20 and 30 . From Figure 4, as continues to increase, overall SOP presents a trend of first decreasing and then increasing in the MCC and ST schemes. Table 1 provides the optimal transmit allocation coefficient found by the SA algorithm to minimize the overall SOP with different . We set the initial temperature , the final temperature , the cooling coefficient , and the inner loop has 200 samples to iterate at the same time. This setting is conducive to finding more accurate results, but the iteration time will be slightly longer. Interestingly, different correspond to different optimal power allocation factors. This is because affects signal and interference strength, resulting in a non-linear change in SINR. Combined with the analysis of Table 1 and Figure 4, the SA algorithm we proposed to find the optimal power parameters is reasonable and correct.
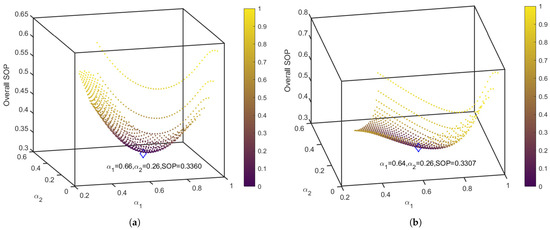
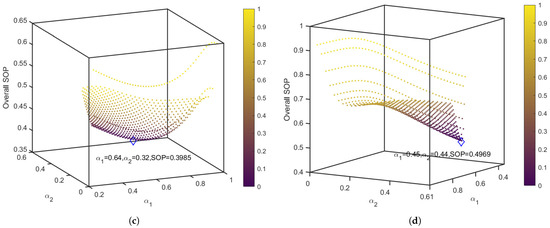
Figure 4.
The SOPs of secondary users with various TAS schemes based on SA algorithm. (a) Overall SOP with max of MCC scheme; (b) overall SOP with max of MCC scheme; (c) overall SOP with max of MCC scheme; and (d) overall SOP with ST scheme.

Table 1.
Optimal power allocation coefficients for different TAS schemes with different (in dBm).
For more valuable insights, we compared the overall SOP of the system for fixed power allocation and optimal power allocation with 20 , as Table 2. We found that the secrecy outage performances of max- and max- of the MCC scheme are better, and the SOPs of max- in the MCC and ST scheme are higher in the fixed power allocation, which is not conducive to secrecy communication. The overall secrecy outage performance with different TAS schemes obtained after optimization based on the SA algorithm has relatively improved, and the optimization effect of the ST scheme is the best.

Table 2.
Comparison of optimized secrecy outage performance.
Figure 5 shows the convergence rate of the overall SOP of the secondary network optimized by the SA algorithm for different TAS schemes. We observe that the MCC scheme converges faster than the ST scheme, among which max- is the fastest.
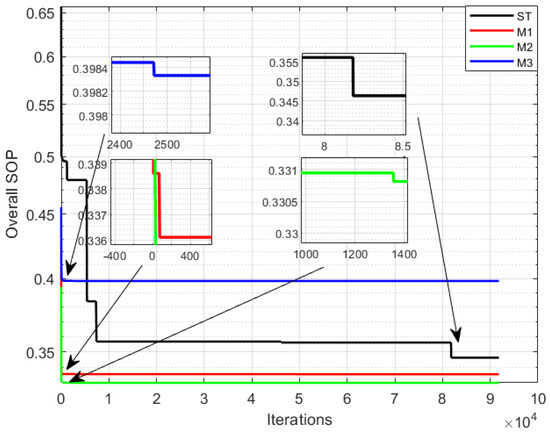
Figure 5.
Iterative convergence rate of SA algorithm.
8. Conclusions
In this paper, the secrecy outage performance of the multi-antenna three secondary users CR-NOMA network is studied, and the exact closed-form SOP expressions of secondary users with a single-antenna scheme, MCC scheme, and ST scheme are derived, respectively. Then, the asymptotic performance of SOP is analyzed, and the relationship between system parameters and secondary user secrecy outage performance is obtained. Finally, an SA optimization algorithm is proposed, and the optimal power allocation coefficient and secrecy outage probability of each TAS scheme are obtained. The simulation results verify the correctness of the theoretical analysis and obtain some valuable conclusions. The results of our work prove that the security advantages of using the MCC scheme and ST scheme to prevent eavesdropping will be beneficial to the design of practical CR-NOMA systems with TAS. The secondary users with multiple-antenna are considered in our future work, and the secrecy outage performance of multiple-user is further studied.
Author Contributions
Conceptualization, J.J.; methodology, S.L.; software, S.L.; validation, S.L.; data curation, S.L.; writing—original draft preparation, S.L.; writing—review and editing, S.L. and J.J.; supervision, S.L. and J.J.; project administration, S.L. and J.J.; funding acquisition, S.L. and J.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (no. 61650103), the Natural Science Foundation of Guangxi (no. 2018GXNSFAA281161).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CR | Cognitive radio |
| OMA | Orthogonal multiple access |
| NOMA | Non-orthogonal multiple access |
| MISO | Multiple-input single-output |
| SISO | Single-input single-output |
| BS | Base station |
| TAS | Transmit antenna selection |
| ST | Space-time transmission |
| MCC | Maximum channel capacity |
| SA | Simulated-annealing |
| SOP | Secrecy outage probability |
| CDF | Cumulative distribution function |
| Probability density function | |
| PLS | Physical layer security |
| QoS | Quality-of-service |
| PA | Power allocation |
| CSI | Channel state information |
| SINR | Signal-to-noise-plus-interference ratio |
| SNR | Signal-to-noise ratio |
| AWGN | Additive white Gaussian noise |
Appendix A. Proof of Theorem 1
The derivation method of SOP for and is the same, and we present the SOP calculation steps for and here.
Appendix B. Proof of (21)
Drawing upon the pertinent tenets of probability theory, it can be inferred that:
Appendix C. Proof of asymptotic SOP (48)
When , the incomplete gamma function has the following properties: . Therefore, when the peak transmission power of BS , we have , and the upper limit of the integration for the statistical average of the interference channel gain variable approaches positive infinity, i.e.,. Simplifying according to the above two steps, the SOP of can be simplified as (48). Similarly, we can easily derive asymptotic SOP expressions for other users.
References
- Dai, L.; Wang, B.; Ding, Z.; Wang, Z.; Chen, S.; Hanzo, L. A survey of non-orthogonal multiple access for 5G. IEEE Commun. Surv. Tutor. 2018, 20, 2294–2323. [Google Scholar] [CrossRef]
- Hassan, M.; Singh, M.; Hamid, K.; Saeed, R.; Abdelhaq, M.; Alsaqour, R.; Odeh, N. Enhancing NOMA’s Spectrum Efficiency in a 5G Network through Cooperative Spectrum Sharing. Electronics 2023, 12, 815. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Peng, Y.; Dong, Y.; Zhao, C. Performance analysis of intelligent CR-NOMA model for industrial IoT communications. CMES Comput. Model. Eng. Sci. 2020, 125, 239–257. [Google Scholar] [CrossRef]
- Ghous, M.; Abbas, Z.H.; Hassan, A.K.; Abbas, G.; Baker, T.; Al-Jumeily, D. Performance analysis and beamforming design of a secure cooperative MISO-NOMA network. Sensors 2021, 21, 4180. [Google Scholar] [CrossRef]
- Singh, S.; Bansal, M. On the outage performance of overlay cognitive STBC-NOMA system with imperfect SIC. IEEE Wirel. Commun. Lett. 2021, 10, 2587–2591. [Google Scholar] [CrossRef]
- Luo, L.; Li, Q.; Cheng, J. Performance analysis of overlay cognitive NOMA systems with imperfect successive interference cancellation. IEEE Trans. Commun. 2020, 68, 4709–4722. [Google Scholar] [CrossRef]
- Kumar, V.; Ding, Z.; Flanagan, M.F. On the performance of downlink NOMA in underlay spectrum sharing. IEEE Trans. Veh. Technol. 2021, 70, 4523–4540. [Google Scholar] [CrossRef]
- Wu, Y.; Khisti, A.; Xiao, C.; Caire, G.; Wong, K.K.; Gao, X. A survey of physical layer security techniques for 5G wireless networks and challenges ahead. IEEE J. Sel. Areas Commun. 2018, 36, 679–695. [Google Scholar] [CrossRef]
- Tefera, M.K.; Jin, Z.; Zhang, S. A Review of Fundamental Optimization Approaches and the Role of AI Enabling Technologies in Physical Layer Security. Sensors 2022, 22, 3589. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Z.; Yang, W.; Cai, Y.; Ding, Z.; Song, Y. Secure transmission design in HARQ assisted cognitive NOMA networks. IEEE Trans. Inf. Forensics Secur. 2020, 15, 2528–2541. [Google Scholar] [CrossRef]
- Ahmad, N.; Sidhu, G.A.S.; Khan, W.U. A Learning Based Framework for Enhancing Physical Layer Security in Cooperative D2D Network. Electronics 2022, 11, 3981. [Google Scholar] [CrossRef]
- Nandan, N.; Majhi, S.; Wu, H.C. Secure beamforming for MIMO-NOMA-based cognitive radio network. IEEE Commun. Lett. 2018, 22, 1708–1711. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Nguyen, N.L.; Nguyen, N.T.; Le, A.T.; Ha, N.D.X.; Do, D.T.; Voznak, M. Reliable and secure transmission in multiple antennas hybrid satellite-terrestrial cognitive networks relying on NOMA. IEEE Access. 2020, 8, 215044–215056. [Google Scholar] [CrossRef]
- Zhao, F.; Hao, W.; Guo, H.; Sun, G.; Wang, Y.; Zhang, H. Secure Energy Efficiency for mmWave-NOMA Cognitive Satellite Terrestrial Network. IEEE Commun. Lett. 2022, 27, 283–287. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, Y.; Wang, G.; Yao, Y.D.; Karagiannidis, G.K. On secrecy performance of antenna-selection-aided MIMO systems against eavesdropping. IEEE Trans. Veh. Technol. 2015, 65, 214–225. [Google Scholar] [CrossRef]
- Lei, H.; Zhang, J.; Park, K.H.; Xu, P.; Ansari, I.S.; Pan, G.; Alomair, B.; Alouini, M.S. On secure NOMA systems with transmit antenna selection schemes. IEEE Access 2017, 5, 17450–17464. [Google Scholar] [CrossRef]
- Pei, X.; Yu, H.; Wen, M.; Li, Q.; Ding, Z. Secure outage analysis for cooperative NOMA systems with antenna selection. IEEE Trans. Veh. Technol. 2020, 69, 4503–4507. [Google Scholar] [CrossRef]
- Shim, K.; Do, T.N.; Nguyen, T.V.; da Costa, D.B.; An, B. Enhancing PHY-security of FD-enabled NOMA systems using jamming and user selection: Performance analysis and DNN evaluation. IEEE Internet Things J. 2021, 8, 17476–17494. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.M.; Yang, Q.; Ding, Z. Secrecy sum rate maximization in non-orthogonal multiple access. IEEE Commun. Lett. 2016, 20, 930–933. [Google Scholar] [CrossRef]
- Wei, L.; Jing, T.; Fan, X.; Wen, Y.; Huo, Y. The secrecy analysis over physical layer in NOMA-enabled cognitive radio networks. In Proceedings of the IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018. [Google Scholar]
- Tran, H.; Dang, V.H.; Niyato, D.; Cuong, D.N.; Luong, N.C.; So-In, C. Outage Probability Minimization in Secure NOMA Cognitive Radio Systems with UAV Relay: A Machine Learning Approach. IEEE Trans. Cogn. Commun. Netw. 2022, 9, 82–98. [Google Scholar]
- Auyo, A.M.; Babale, S.A.; Bello, L.M. Effect of Inspired CR-NOMA Power Allocation on Bit Error Rate For Three User NOMA system. In Proceedings of the 2022 IEEE Nigeria 4th International Conference on Disruptive Technologies for Sustainable Development (NIGERCON), Lagos, Nigeria, 17–19 May 2022. [Google Scholar]
- Fang, Z.; Hu, J.; Lu, Y.; Ni, W. Three-user cooperative NOMA transmission. IEEE Wirel. Commun. Lett. 2019, 9, 465–469. [Google Scholar] [CrossRef]
- Do, T.N.; da Costa, D.B.; Duong, T.Q.; An, B. Improving the performance of cell-edge users in NOMA systems using cooperative relaying. IEEE Trans. Commun. 2018, 66, 1883–1901. [Google Scholar] [CrossRef]
- Arzykulov, S.; Tsiftsis, T.A.; Nauryzbayev, G.; Abdallah, M. Outage performance of cooperative underlay CR-NOMA with imperfect CSI. IEEE Commun. Lett. 2018, 23, 176–179. [Google Scholar] [CrossRef]
- Xiang, Z.; Yang, W.; Pan, G.; Cai, Y.; Song, Y. Physical layer security in cognitive radio inspired NOMA network. IEEE J. Sel. Top. Signal Process. 2019, 13, 700–714. [Google Scholar] [CrossRef]
- Song, Y.; Yang, W.; Xiang, Z.; Wang, H.; Cao, F. Research on cognitive power allocation for secure millimeter-wave NOMA networks. IEEE Trans. Veh. Technol. 2020, 69, 13424–13436. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).