Distributed Adaptive Consensus Output Tracking Problem of Nonlinear Multi-Agent Systems with Unknown High-Frequency Gain Signs under Directed Graphs

Abstract

This paper deals with the consensus output tracking problem for multi-agent systems with unknown high-frequency gain signs, in which the subsystems are connected over directed graphs. The subsystems may have different dynamics, as long as the relative degrees are the same. A new type of Nussbaum gain is first presented to tackle adaptive consensus control of network-connected systems without the knowledge of the high-frequency gains. Adaptive laws and internal models are then proposed to handle the uncertainties and unknown parameters. An integral Lyapunov function based on sufficient conditions is finally introduced to tackle the asymmetry of the Laplacian matrix of directed graphs, into which we incorporate the new Nussbaum gain and the adaptive internal model to design the controller. It is apparent that the control scheme and the adaptive laws are fully distributed, which means that only the relative information of the neighbourhood subsystems’ outputs is used, and the simulation results validate the effectiveness of the control design, whereby they guarantee the asymptotic convergence of errors to zero as well as the boundedness of the state variables.

1. Introduction

With the development of computing, communication and sensing, having multiple control agents working together to accomplish collective group behaviours can significantly improve their operational effectiveness. Due to its potential applications in various fields such as satellite formation flying, robotics and electric power systems, consensus output regulation of multi-agents has received great attention from the systems and control community. Consensus output regulation of multi-agents is to have a group of agents connected together in a networkto asymptotically follow a prescribed trajectory and/or maintain asymptotic rejection of disturbances [1,2]. In the formulation of cooperative control, there are two types of methods: centralised and distributed methods. Due to the limited perception capabilities of agents and sensors, implementing a centralised controller is considered too expensive in practice. The distributed method, which depends on information of agents and their neighbours, brings more benefits [3,4].

As a result, the output tracking or regulation problem of multi-agent systems has attracted great attention in recent years. In terms of these multi-agent systems, they are always uncertain, and the uncertainties can be general nonlinear functions and can be input-related and/or input-unrelated. Adaptive control algorithms are developed to deal with unknown parameters in the systems. One of the important tools is the backstepping method. The general adaptive algorithms for input-related uncertainties and backstepping are developed with virtual coefficients equal to one, or under the assumption that the coefficients containknown signs. These signs, called control directions or high-frequency gains, indicate motion directions of system under any control, and knowledge of these signs makes robust control design much easier [5]. However, when not all state variables are measurable, and when large uncertainties exist in systems, it is difficult to detect the high-frequency gain directly. Thus, it makes sense to devise an adaptive control method to eliminate the requirements on the sign of the high frequency gain and to implement for the output tracking or regulation problem [6,7,8,9,10]. In terms of a network of connected systems with multiple subsystems, the existing control design for an individual system with unknown high-frequency gain would not be able to establish the boundedness of all the variables in the adaptive consensus output tracking/regulation problem since each subsystem could move in different directions. Additionally, the communication between agents can be undirected and directed; the asymmetric connection in a directed graph remains an obstacle to extending adaptive schemes beyond undirected graphs to fully distributed adaptive consensus control. Thus, the adaptive consensus control problem of unknown nonlinear systems on directed graphs with unknown control directions drew our attention [11,12].

In ref. [13], consensus global output regulation was discussed for several classes of nonlinear multi-agent systems. The controller presented in the above study was not fully distributed. A fully distributed consensus adaptive output regulation for a class of nonlinear uncertain multi-agent systems with unknown leader was addressed in [14], where the authors combined an adaptive internal model and a robust control to handle the unknown parameters in the leader systems. Designing fully distributed controllers for heterogeneous multi-agent systems with general directed graphs to achieve consensus output regulation is much more complicated and is still open, though a case with nominal and one with uncertain linear subsystems were first studied in ref. [15,16].In recent years, the consensus output regulation of a class of network-connected dynamic systems, in which all the system parameters were completely unknown, including the high frequency gain signs, were considered intensively [17,18]. The consensus global output regulation problem of second-order nonlinear multi-agent systems subject to the unknown control directions was then presented in ref. [19]. Inthe novel distributed controllers based on the Nussbaum-type dynamic gain, the adaptive control techniques can not only handle the unknown control directions but also the uncertain parameters that belong to any unknown and non-compact set, and the arbitrary unknown control directions do not need to be identical. For the consensus output regulation of a class of general nonlinear systems with unknown high-frequency gains, a new Nussbaum gain with a potentially faster rate was proposed in ref. [20], such that the boundedness of system parameters can be established by the paradoxical argument even if the Nussbaum gain parameter for only one of the subsystems becomes unbounded. This removes the assumption of known lower and upper bounds of the control coefficients in ref. [21]. However, the above works were based on undirected graphs; the consensus output regulation for nonlinear systems with unknown high-frequency gains under directed graphs is still challenging. Additionally, some other control approaches recently came to our attention because they proved to be successful in various applications: use of multi-parametric quadratic programming in fuzzy control systems [22]; nonlinear optimal control of oxygen and carbon dioxide levels in blood [23]; test platform and graphical user interface design for vertical take-off and landing of drones [24].

In this paper, the consensus output tracking problem of a class of network-connected uncertain nonlinear agents by output feedback is considered. Each agent is a minimum-phase SISO system with a relative degree of 1, unknown parameters and unknown control directions, and the connecting graph between the subsystems is directed. Inspired by using the Nussbaum gain [7] to tackle the unknown high-frequency gain sign and adaptive laws to solve the parameters uncertainties, a new control scheme is specified as follows. Due to the asymmetry of the Laplacian matrices, a distributed adaptive controller based on a newly designed Lyapunov function together with a novel Nussbaum gain and an adaptive internal model are proposed to achieve consensus output tracking in the sense that the subsystem outputs asymptotically follow a reference signal. The presented adaptive control only uses relative output measurements and the local information of the connection to each subsystem, and hence the proposed control scheme is fully distributed. The contributions of this paper are at least two-fold. First, contrary to previous works, the parameters of each agent in this paper are completely unknown and the connection between the subsystems is direct, which makes the design of Nussbaum gain, the internal model and the Lyapunov function much more challenging because of the asymmetry of the Laplacian matrices. Second, the adaptive protocols proposed in this paper depend only on the relative output information, which is much more difficult compared to the adaptive protocols that rely on the relative states of neighbouring subsystems.

This paper is organized as follows. Section 2 describes the mathematics model of the distributed adaptive consensus output tracking problem of a set of unknown nonlinear subsystems with unknown control directions under directed graphs. The state transformation is introduced in Section 3. Section 4 presents a new adaptive internal model, the design of consensus controllers and the stability analysis based on the novel Lyapunov function. In addition, simulation examples are demonstrated in Section 5.

2. Problem Statement

Consider a group of N unknown nonlinear subsystems over a directed interaction topology, of which the dynamics of the i-th, $i=1,\dots ,N$ subsystem are described by

$$\begin{array}{cc}\hfill {\dot{x}}_i& =A{x}_i+b{u}_i+\theta (y_i,d),\hfill \\ \hfill y_i& =C{x}_i,\hfill \end{array}$$

(1)

with $\theta ,b,C^T\in {\mathbb{R}}^n$ and

$$A=\left[\begin{array}{ccccc}0& 1& 0& \dots & 0\\ 0& 0& 1& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \dots & 1\\ 0& 0& 0& \dots & 0\end{array}\right],b=\left[\begin{array}{c}{b}_1\\ ⋮\\ b_n\end{array}\right],C^T=\left[\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right],$$

where $x_i\in {\mathbb{R}}^n$ is the state vector, with n being a known positive constant integer representing the order of the subsystems. $u_i,y_i\in \mathbb{R}$ are the input and output of the ith subsystem, and $b\in {\mathbb{R}}^n$ and $d\in {\mathbb{R}}^q$ are vectors of unknown parameters, with b being a Hurwitz vector with $b_1\ne 0$, which denotes that the relative degree of the system is 1. $\theta :\mathbb{R}\times {\mathbb{R}}^q\to {\mathbb{R}}^n$ contains unknown nonlinear functions; each element is a polynomial of its variables and satisfies $\theta (0,d)=0$. In terms of the reference signal, it can be expressed as

$$\begin{array}{cc}\hfill {\dot{x}}_0& =A{x}_0+b{u}_0+\theta (y_0,d),\hfill \\ \hfill y_0& =C{x}_0,\hfill \end{array}$$

(2)

with a constant control input $u_0$. We define the output tracking errors as

$$e_i=y_i-y_0,i=1,\dots ,N.$$

(3)

A directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ is introduced to demonstrate the communication topology among the subsystems, where $\mathcal{V}=\{1,\dots ,N\}$ is the vertex set and $\mathcal{E}$ denotes the edge set. A vertex represents an agent, and each edge represents a connection. As for the graph $\mathcal{G}$, its adjacent matrix S has elements $s_{ij}=1$ if there is a path from subsystem j to subsystem i, and $s_{ij}=0$ otherwise. The Laplacian matrix L is defined as $l_{ii}={\sum }_{j=1}^N{s}_{ij}$ and $l_{ij}=-s_{ij}$ when $i\ne j$. A directed graph is strongly connected if there is a directed path from every vertex to every other vertex. Not all the subsystems have access to $y_0$, and they rely on the network connections to achieve the consensus output tracking. We use a diagonal matrix $\Delta$ = $\mathrm{diag}({\delta }_1,\dots ,{\delta }_N)$ to denote the access to $y_0$ in the way that if ${\delta }_i=1$, the ith subsystem has access to the value of $y_0$ for the control design, and ${\delta }_i=0$ otherwise.

The distributed adaptive consensus output tracking problem considered in this paper is to use the relative information $y_i-y_j,i\ne j$ of neighbouring subsystems to design a distributed adaptive controller to ensure that the output tracking errors $e_i$ for $i=1,\dots ,N$ converge to zero under any initial condition of the system in the state space, i.e., the convergence of the subsystem outputs $y_i$ to the common function $y_0$, that is

$$\underset{t\to \infty }{lim}{e}_i\left(t\right)=0,i=1,\dots ,N.$$

(4)

We make the following assumptions about the interactions among the subsystems and the exosystem.

Assumption 1.

The invariant zeros of $\{A,b,C\}$ are stable, for $i=1,\dots ,N$, and all the subsystems have the same sign but completely unknown high-frequency gains.

Assumption 2.

The directed graph $\mathcal{G}$ among the N subsystems is strongly connected and at least one subsystem has access to $y_0$.

Assumption 3.

For the nonlinear function ϕ, the following condition holds:

$$\parallel \theta (y_i,d)-\theta (y_0,d){\parallel }^2\le {\gamma }_{\theta }(e_i^2+e_i^{2q}),$$

(5)

where ${\gamma }_{\theta }$ is a positive real number and q is a known positive integer.

Remark 1.

Note that the subsystem (1) is in the standard nonlinear output feedback form. The geometric conditions that any general nonlinear systems can be transformed to such a structure have been verified in [25].

Remark 2.

Assumption 3 is clearly satisfied for linear systems with unknown parameters. The nonlinear functions involved in ${\theta }_i$ are polynomials with $\theta (0,d)=0$, and the unknown parameters are constant. In such a case, Assumption 3 is then satisfied.

3. Preliminaries

Before proposing the adaptive control, some preliminary results are introduced. We consider a state transform to extract the internal dynamics of (1) with ${\overline{x}}_i\in {\mathbb{R}}^{n-1}$ given by

$${\overline{x}}_i=x_{i,2:n}-\frac{b_{2:n}}{b_1}{y}_i,$$

(6)

where ${(·)}_{2:n}$ refers to the vector or matrix formed by the 2nd row to the nth row. With the coordinates $({\overline{x}}_i,y_i)$, (1) is rewritten as

$$\begin{array}{cc}\hfill {\dot{\overline{x}}}_i& =B{\overline{x}}_i+\phi (y_i,\varphi ),\hfill \\ \hfill {\dot{y}}_i& =g^T{\overline{x}}_i+{\phi }_y(y_i,\varphi )+b_1{u}_i,\hfill \end{array}$$

(7)

where the unknown parameter vector $\varphi ={[d^T,b^T]}^T$, $g=[1,0,\dots ,0]\in {\mathbb{R}}^{n-1}$, and B is the left companion matrix of b given by

$$B=\left[\begin{array}{cccc}-b_2/b_1& 1& \dots & 0\\ -b_3/b_1& 0& \dots & 0\\ ⋮& ⋮& ⋮& ⋮\\ -b_{n-1}/b_1& 0& \dots & 1\\ -b_n/b_1& 0& \dots & 0\end{array}\right],$$

(8)

and

$$\begin{array}{cc}\hfill \phi (y_i,\varphi )& =B\frac{b_{2:n}}{b_1}{y}_i+{\theta }_{2:n}(y_i,d)-\frac{b_{2:n}}{b_1}{\theta }_1(y_i,d),\hfill \\ \hfill {\phi }_y(y_i,\varphi )& =\frac{b_2}{b_1}{y}_i+{\theta }_1(y_i,d).\hfill \end{array}$$

Note that B is the Hurwitz vector from Assumption 1, and that it is easy to check that $\phi (0,\theta )=0$ and ${\phi }_y(0,\theta )=0$.

Before moving on to present the main control scheme of this paper, we first introduce a property of Laplacian matrix. For notational convenience, we let $Q=L+\Delta$. Under Assumption 2, it is not difficult to verify that Q is a nonsingular M-matrix [26], which satisfies the following property.

Lemma 1.

There exists a positive diagonal matrix $\overline{G}$ with $\overline{G}$ = $\mathit{diag}\{{\overline{g}}_1,\dots ,{\overline{g}}_N\}$ [27] , such that

$$\overline{G}Q+Q^T\overline{G}\ge {\gamma }_{c}I,$$

(9)

for some positive real number ${\gamma }_c$.

Let us denote the consensus output tracking error as

$${\zeta }_i=\sum _{j=1}^N{s}_{ij}(y_i-y_j)+{\delta }_i(y_i-y_0),i=1,\dots ,N.$$

(10)

It can be obtained that

$$\begin{array}{cc}\hfill {\zeta }_i& =\sum _{j=1}^N{s}_{ij}(e_i-e_j)+{\delta }_i{e}_i\hfill \\ \hfill & =\sum _{j=1}^N{q}_{ij}{e}_j,\hfill \end{array}$$

(11)

where $q_{ij}$ denotes the $(i,j)$-th entry of the matrix Q. The above equation Equation (11) can be represented in the vector form, $\zeta =Qe$, where $\zeta ,e\in {\mathbb{R}}^N$ are the vectors with ${\zeta }_i$ and $e_i$ as elements, respectively. Clearly, ${\zeta }_i$ is available to the control design for the ith subsystem.

A useful result relating $\zeta$ and e is shown in the following lemma for the stability analysis.

Lemma 2.

With $\zeta =Qe$, the following inequality holds for any positive integer m,

$$\sum _{i=1}^N{e}_i^{2m}\le U^{m-1}{\sigma }^{2m}\left(Q\right)\sum _{i=1}^N{\zeta }_i^{2m},$$

(12)

where $\sigma \left(Q\right)$ denotes the square root of the eigenvalue of $Q^{H}Q$.

Proof. 

$$\begin{array}{cc}\hfill \sum _{i=1}^N{\zeta }_i^{2m}& =U{\left({\left[\frac{1}{U}\sum _{i=1}^N{\left({\zeta }_i^2\right)}^m\right]}^{\frac{1}{m}}\right)}^m\hfill \\ \hfill & \ge U{\left(\left[\frac{1}{U}\sum _{i=1}^N\left({\zeta }_i^2\right)\right]\right)}^m\hfill \\ \hfill & =U^{1-m}{(\parallel \zeta \parallel }^2{)}^m=U^{1-m}{(\parallel Qe\parallel }^2{)}^m\hfill \\ \hfill & \ge U^{1-m}{\sigma }^{-2m}\left(Q\right){\parallel e\parallel }^{2m}\hfill \\ \hfill & \ge U^{1-m}{\sigma }^{-2m}\left(Q\right){\left(\sum _{i=1}^N{e}_i^2\right)}^m\hfill \\ \hfill & \ge U^{1-m}{\sigma }^{-2m}\left(Q\right)\sum _{i=1}^N{e}_i^{2m},\hfill \end{array}$$

from which (12) is obtained. □

For the leader, the internal dynamics have the same formulation as (7), the only change is from index i to 0. Then, letting ${\tilde{x}}_i={\overline{x}}_i-{\overline{x}}_0$, the subsystem dynamics in (1) can be rewritten as

$$\begin{array}{cc}\hfill {\dot{\tilde{x}}}_i& =B{\tilde{x}}_i+\widetilde{{\phi }_i},\hfill \\ \hfill {\dot{e}}_i& =g^T{\tilde{x}}_i+{\tilde{\phi }}_{i,y}+b_1(u_i-u_0),\hfill \end{array}$$

(13)

where ${\tilde{\phi }}_i=\phi (y_i,\varphi )-\phi (y_0,\varphi ),{\tilde{\phi }}_{i,y}={\phi }_y(y_i,\varphi )-{\phi }_y(y_0,\varphi )$.

4. Distributed Consensus Control Algorithm Design

In this section, a distributed adaptive output feedback control law will be designed, which stabilizes the augmented system (13) globally under the assumption that the control direction $b_1$ is completely unknown.

4.1. A Novel Nussbaum-Type Function

When high-frequency gains are completely unknown, Nussbaum gain functions $N\left(\kappa \right)$ are applied in the adaptive control, which have the properties that

$$\begin{array}{cc}\hfill \underset{\kappa \to \pm \infty }{lim}sup\frac{1}{\kappa }{\int }_0^{\kappa }N\left(s\right)ds& =+\infty ,\hfill \\ \hfill \underset{\kappa \to \pm \infty }{lim}inf\frac{1}{\kappa }{\int }_0^{\kappa }N\left(s\right)ds& =-\infty ,\hfill \end{array}$$

(14)

where $\kappa \to \pm \infty$ denotes $\kappa \to +\infty$ and $\kappa \to -\infty$, and the control input takes the form $u=N\left(\kappa \right)\overline{u}$. Then, the control design is continued with $\overline{u}$, such that a condition in the following form is obtained for a single-input system,

$$V\left(t\right)\le V\left(0\right)+{\int }_0^{\kappa }(b_{\rho }N\left(s\right)-1)ds+r\left(t\right),$$

(15)

where V is a positive definite function, $\kappa \left(t\right)$ is a continuous function with $\kappa \left(0\right)=0$, $r\left(t\right)$ is a bounded function and $b_{\rho }$ is the unknown high-frequency gain. The boundedness of $\kappa$ and subsequently the boundedness of V can be established by seeking a contradiction using (15) if the Nussbaum function satisfies (14). Commonly used Nussbaum-type functions include ${\kappa }^{2}cos\left(\kappa \right),{\kappa }^{2}sin\left(\kappa \right)$ and $e^{k^2}cos\left(\kappa \right)$ [28]. For consensus control, there are N unknown control directions, and we aim at a condition

$$V\left(t\right)\le V\left(0\right)+\sum _{i=1}^N{\int }_0^{{\kappa }_i}(b_{i,\rho }N\left(s_i\right)-1)d{s}_i+r\left(t\right),$$

(16)

similar to (15), but with multiple continuous functions ${\kappa }_i$. However, it is not clear how to use existing Nussbaum-type functions to tackle the consensus problem of multi-agent systems whose control directions are unknown. The reason is that multiple Nussbaum-type function terms would coexist in the same conditional inequality and ${\kappa }_i$s are independent. Thus, we expect a function which grows faster, such that one of the ${\kappa }_i$s is dominant for the positive definite condition for consensus control in (16).

Through an enormous number of experiments and calculations, the following kind of Nussbaum gain for consensus output tracking problem is considered:

$$N\left(\kappa \right)=e^{\frac{{\kappa }^2}{2}}({\kappa }^2+2)sin\kappa .$$

(17)

The following lemma shows that this kind of Nussbaum gain can be used to prove that one of the ${\kappa }_i$s can be dominant for the positive definite condition of the Lyapunov function.

Lemma 3.

With the Nussbaum gain shown in (17), the boundedness of ${\kappa }_i$ and V can be established from (16).

Proof. 

Let $W\left(\kappa \right)={\int }_0^{\kappa }N\left(s\right)ds$, then it can be obtained that

$$W\left(\kappa \right)=e^{\frac{{\kappa }^2}{2}}(\kappa sin\left(\kappa \right)-cos\left(\kappa \right))+1.$$

(18)

From trigonometric properties, it can be shown that $W\left(\kappa \right)$ takes local minima at $\kappa =2n\pi$ and local maxima at $\kappa =(2n+1)\pi$. Hence, for $2n\pi <\kappa \le 2(n+1)\pi$, we have

$$-e^{\frac{{\left(2(n+1)\pi \right)}^2}{2}}+1\le W\left(\kappa \right)\le e^{\frac{{\left((2n+1)\pi \right)}^2}{2}}+1.$$

In order to seek a contradiction, suppose that at least one of the ${\kappa }_i$s becomes unbounded. Then, at the time interval $[0,t_f)$, there exists an increasing sequence $\left\{t_n\right\},n=0,1,\dots ,$ defined by

$$t_n=\left\{\begin{array}{cc}\underset{1\le i\le N}{min}\left\{t:|{\kappa }_i\left(t\right)|=(2n+1)\pi \right\},\hfill & \mathrm{if}\mathrm{sgn}\left(b_{i,\rho }\right)=-1,\hfill \\ \underset{1\le i\le N}{min}\left\{t:|{\kappa }_i\left(t\right)|=2(n+1)\pi \right\},\hfill & \mathrm{if}\mathrm{sgn}\left(b_{i,\rho }\right)=1.\hfill \end{array}\right.$$

(19)

Clearly, ${lim}_{n\to \infty }{t}_n=t_f$. Since the sign of $b_{i,\rho }$ is the same, the analysis can be divided into two parts, i.e., $\mathrm{sgn}\left(b_{i,\rho }\right)=1$ and $\mathrm{sgn}\left(b_{i,\rho }\right)=-1$.

For the case $\mathrm{sgn}\left(b_{i,\rho }\right)=1$, substituting (19) into (16) together with (18), the value of V at time $t=t_n$ satisfies

$$\begin{array}{cc}\hfill V\left(t_n\right)& =V\left(0\right)+\sum _{i=1}^N{b}_{i,\rho }W\left({\kappa }_i\left(t_n\right)\right)-\sum _{i=1}^N{\kappa }_i\left(t_n\right)+r\left(t_n\right),\hfill \\ \hfill & \le V\left(0\right)+\underline{b}(-e^{\frac{{\left(2(n+1)\pi \right)}^2}{2}}+1)+(N-1)\overline{b}(e^{\frac{{\left((2n+1)\pi \right)}^2}{2}}+1)+r\left(t_n\right),\hfill \end{array}$$

(20)

where $\underline{b}={min}_{i=1}^N\left\{b_{i,\rho }\right\}$ and $\overline{b}={max}_{i=1}^N\left\{b_{i,\rho }\right\}$. With

$$\begin{array}{cc}\hfill & -\underline{b}{e}^{\frac{{\left(2(n+1)\pi \right)}^2}{2}}+(N-1)\overline{b}{e}^{\frac{{\left((2n+1)\pi \right)}^2}{2}}\hfill \\ \hfill & =-\underline{b}{e}^{\frac{{\left((2n+1)\pi \right)}^2}{2}}\left(e^{\frac{(4n+3){\pi }^2}{2}}-\frac{(N-1)\overline{b}}{\underline{b}}\right),\hfill \end{array}$$

(21)

we have

$$V\left(t_n\right)\le -\underline{b}{e}^{\frac{{\left((2n+1)\pi \right)}^2}{2}}\left(e^{\frac{(4n+3){\pi }^2}{2}}-\frac{(N-1)\overline{b}}{\underline{b}}\right)+\overline{r}\left(t_n\right),$$

(22)

where $\overline{r}\left(t_n\right)$ is bounded. As $e^{\frac{(4n+3){\pi }^2}{2}}$ will dominate any bounded function with sufficient large n, we can conclude from (22) that $V\left(t_n\right)<0$ for sufficiently large n. This is a contradiction, as $V\left(t\right)$ is a positive definite function. Hence, none of the ${\kappa }_i$s becomes unbounded, and therefore boundedness of the ${\kappa }_i$s and V is established.

For the case $\mathrm{sgn}\left(b_{i,\rho }\right)=-1$, the proof can be carried out in the same way as for the case $\mathrm{sgn}\left(b_{i,\rho }\right)=1$, and is omitted here. □

4.2. Control Law Design

Denote ${\displaystyle N\left({\kappa }_i\right)=e^{{\kappa }_i^2/2}({\kappa }_i^2+2)sin\left({\kappa }_i\right),i=1,\dots ,N}$, which is a type of Nussbaum function proposed in last subsection.

We consider the closed-loop system composed of (13) and the following control laws

$$\begin{array}{cc}\hfill u_i& =\beta N\left({\kappa }_i\right){\overline{u}}_i+{\xi }_i,\hfill \\ \hfill {\dot{\kappa }}_i& ={\gamma }_c(h_i+{\rho }_i)({\zeta }_i+{\zeta }_i^{2m-1}){\overline{u}}_i,{\kappa }_i\left(0\right)=0,\hfill \end{array}$$

(23)

for $i=1,\dots ,N$, where $\beta$ is a positive real design parameter, ${\gamma }_c$ is illustrated in (9), and

$${\overline{u}}_i=-(h_i+{\rho }_i)({\zeta }_i+{\zeta }_i^{2m-1}),$$

(24)

with ${\rho }_i={\zeta }_i^2$. $h_i$ and ${\xi }_i$ are generated by

$$\begin{array}{cc}\hfill {\dot{h}}_i& ={\gamma }_h({\zeta }_i^2+{\zeta }_i^{2m}),h_i\left(0\right)=h_0,\hfill \\ \hfill {\dot{\xi }}_i& =-{\xi }_i+u_i,\hfill \end{array}$$

(25)

with ${\gamma }_h,h_0$ being any known positive constants. Note that $h_i$ can be viewed as an adaptive gain. Then, there exists a Lyapunov function candidate $V\left(t\right)$, such that, along the trajectory of the closed-loop system,

$$\begin{array}{cc}\hfill \dot{V}& \le \sum _{i=1}^N(\beta b_{1}N\left({\kappa }_i\right)-1){\dot{\kappa }}_i+c\left(t\right),\hfill \end{array}$$

(26)

where $c\left(t\right)$ is a bounded function.

Theorem 1.

Suppose Assumptions 1–3 hold. The network-connected nonlinear systems with subsystem dynamics (1), and the control input (23) together with the adaptive laws (24) and (25) solve the distributed adaptive consensus output tracking control problem with unknown control directions under directed graphs, in the sense that the trakcing error e asymptotically converges to zero with the boundedness of all states.

Proof. 

Let the auxiliary internal model be

$${\tilde{\eta }}_i=u_0-{\xi }_i+b_1^{-1}{e}_i,$$

(27)

then from (13) and (25) it can be shown that

$${\dot{\tilde{\eta }}}_i=-{\tilde{\eta }}_i+b_1^{-1}{e}_i+b_1^{-1}{g}^T{\tilde{z}}_i+b_1^{-1}{\tilde{\phi }}_{i,y}.$$

(28)

The closed-loop subsystem dynamics of $e_i$ can be obtained as

$$\begin{array}{cc}\hfill {\dot{e}}_i& =g^T{\tilde{x}}_i+{\tilde{\phi }}_{i,y}-(h_i+{\rho }_i)({\zeta }_i+{\zeta }_i^{2m-1})\hfill \\ \hfill & +(\beta b_{1}N\left({\kappa }_i\right)-1){\overline{u}}_i-b_1{\tilde{\eta }}_i+e_i.\hfill \end{array}$$

(29)

Furthermore, we design the Lyapunov function candidate as

$$\begin{array}{cc}\hfill V_{\zeta }& =\sum _{i=1}^{N}2{\overline{g}}_i\left(h_i\left(\frac{{\zeta }_i^2}{2}+\frac{{\zeta }_i^{2m}}{2m}\right)+\left(\frac{{\zeta }_i^4}{4}+\frac{{\zeta }_i^{2m+2}}{2m+2}\right)\right)\hfill \\ \hfill & +\frac{1}{2{\gamma }_h}\sum _{i=1}^N{(h_i-h^{*})}^2,\hfill \end{array}$$

(30)

where ${\overline{g}}_i$ is defined as in Lemma 1 and $h^{*}$ is a constant to be determined later. Using (13) and (23), we have

$$\begin{array}{cc}\hfill {\dot{V}}_{\zeta }& =\sum _{i=1}^{N}2{\overline{g}}_i(h_i+{\rho }_i)({\zeta }_i+{\zeta }_i^{2m-1})\sum _{i=1}^N{q}_{ij}{\dot{e}}_j\hfill \\ \hfill & +\sum _{i=1}^N{\overline{g}}_i\left({\zeta }_i^2+\frac{{\zeta }_i^{2m}}{m}\right){\dot{h}}_i+\frac{1}{{\gamma }_h}\sum _{i=1}^N(h_i-h^{*}){\dot{h}}_i\hfill \\ \hfill & =\sum _{i=1}^{N}2{\overline{g}}_i(h_i+{\rho }_i)({\zeta }_i+{\zeta }_i^{2m-1})\sum _{j=1}^N{q}_{ij}\left(\beta b_{1}N\left({\kappa }_j\right)-1\right){\overline{u}}_j\hfill \\ \hfill & +2{\zeta }^T(\mathcal{H}+\rho )(I_N+{\rho }^{m-1})\overline{G}Q\left((I_N\otimes g^T)\tilde{x}+{\tilde{\Psi }}_y\right)\hfill \\ \hfill & -{\zeta }^T(\mathcal{H}+\rho )(I_N+{\rho }^{m-1})(\overline{G}Q+Q^T\overline{G})(I_N+{\rho }^{m-1})(\mathcal{H}+\rho )\zeta \hfill \\ \hfill & +{\gamma }_h\left(\rho +\frac{{\rho }^m}{m}\right)\overline{G}(\rho +{\rho }^m)+{\zeta }^T\mathcal{H}(I_N+{\rho }^{m-1})\zeta -h^{*}\sum _{i=1}^N({\zeta }_i^2+{\zeta }_i^{2p})\hfill \\ \hfill & +2{\zeta }^T(\mathcal{H}+\rho )(I_N+{\rho }^{m-1})\overline{G}\left(-b_{1}Q\tilde{\eta }+Qe\right),\hfill \end{array}$$

(31)

where $e={[e_1^T,\dots ,e_N^T]}^T,\zeta ={[{\zeta }_1^T,\dots ,{\zeta }_N^T]}^T,\tilde{x}=[{\tilde{x}}_1^T,\dots ,$ ${\tilde{x}}_N^T{]}^T,\tilde{\eta }={[{\tilde{\eta }}_1^T,\dots ,{\tilde{\eta }}_N^T]}^T,{\tilde{\Psi }}_y={[{\tilde{\phi }}_{1,y}^T,\dots ,{\tilde{\phi }}_{N,y}^T]}^T,\mathcal{H}=\mathrm{diag}(h_1,\dots ,h_N)$ and $\rho =\mathrm{diag}({\rho }_1,\dots ,{\rho }_N)$.

Note that $\zeta =Qe$, and that from (9), (23) and Young’s inequality, we have

$$\begin{array}{cc}\hfill {\dot{V}}_{\zeta }& \le \sum _{i=1}^N(\beta b_{1}N\left({\kappa }_i\right)-1){\dot{\kappa }}_i-\frac{8}{12}{\gamma }_c{\parallel (\mathcal{H}+\rho )(I_N+{\rho }^{m-1})\zeta \parallel }^2\hfill \\ \hfill & +\frac{12}{{\gamma }_c}\left(\parallel \overline{G}{Q\parallel }^2\parallel \tilde{x}{\parallel }^2+\parallel \overline{G}{Q\parallel }^2\parallel {\tilde{\Psi }}_y{\parallel }^2+\parallel b_1\overline{G}{Q\parallel }^2{\parallel \tilde{\eta }\parallel }^2\right.\hfill \\ \hfill & +\left.\parallel \overline{G}{\parallel }^2{\parallel \zeta \parallel }^2\right)+{\gamma }_h\left(\rho +\frac{{\rho }^m}{m}\right)\overline{G}(\rho +{\rho }^m)\hfill \\ \hfill & +{\zeta }^T\mathcal{H}(I_N+{\rho }^{m-1})\zeta -h^{*}\sum _{i=1}^N({\zeta }_i^2+{\zeta }_i^{2m}).\hfill \end{array}$$

(32)

Similar to [29], we can obtain that

$${\gamma }_h\left(\rho +\frac{{\rho }^m}{m}\right)\overline{G}(\rho +{\rho }^m)\le \frac{{\gamma }_c}{12}{\parallel (\mathcal{H}+\rho )(I_N+{\rho }^{m-1})\zeta \parallel }^2+\nu \left({\gamma }_c\right)\rho ,$$

(33)

where $\nu :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ is a function that depends on unknown parameters. We used

$${\zeta }^T\mathcal{H}(I_N+{\rho }^{m-1})\zeta \le \frac{{\gamma }_c}{12}\parallel (\mathcal{H}+\rho )(I_N+{\rho }^{m-1}){\zeta \parallel }^2+\frac{3}{{\gamma }_c}{\parallel \zeta \parallel }^2,$$

(34)

and from Assumption 3, it can be shown that there exists a positive real constant ${\nu }_y$, such that

$$\frac{12}{{\gamma }_c}{\parallel {\tilde{\Psi }}_y\parallel }^2\le {\gamma }_y\sum _{i=1}^N(e_i^2+e_i^{2m})\le {\nu }_y\sum _{i=1}^N({\zeta }_i^2+{\zeta }_i^{2m}).$$

(35)

From (32)–(35), we have

$$\begin{array}{cc}\hfill {\dot{V}}_{\zeta }& \le \sum _{i=1}^N(\beta b_{1}N\left({\kappa }_i\right)-1){\dot{\kappa }}_i-\frac{{\gamma }_c}{2}{\parallel (\mathcal{H}+\rho )(I_N+{\rho }^{m-1})\zeta \parallel }^2\hfill \\ \hfill & +\frac{12}{{\gamma }_c}\left(\parallel \overline{G}{Q\parallel }^2\parallel \tilde{x}{\parallel }^2+\parallel b_1\overline{G}{Q\parallel }^2{\parallel \tilde{\eta }\parallel }^2\right)-\left(h^{*}-\frac{3}{{\gamma }_c}\right.\hfill \\ \hfill & \left.-\parallel \overline{G}{Q\parallel }^2{\nu }_y-\frac{12}{{\gamma }_c}{\parallel \overline{G}\parallel }^2-\nu \left({\gamma }_c\right)\right)\sum _{i=1}^N({\zeta }_i^2+{\zeta }_i^{2m}).\hfill \end{array}$$

(36)

To analyse the dynamics of ${\tilde{x}}_i$, let

$$V_x=\sum _{i=1}^N{\tilde{x}}_i^T{P}_x{\tilde{x}}_i.$$

(37)

Since B is a Hurwitz vector, there exists a positive definite matrix $P_x$, such that

$$P_{x}B+B^T{P}_x=-3I.$$

From (13), it can be obtained that

$$\begin{array}{cc}\hfill {\dot{V}}_x& =-3\sum _{i=1}^N{\parallel {\tilde{x}}_i\parallel }^2+2\sum _{i=1}^N{\tilde{x}}_i^T{P}_x{\tilde{\phi }}_i\hfill \\ \hfill & ⩽-2\parallel \tilde{x}{\parallel }^2+{\parallel P_x\parallel }^2{\mu }_{\phi }\sum _{i=1}^N({\zeta }_i^2+{\zeta }_i^{2m}),\hfill \end{array}$$

(38)

where ${\mu }_{\psi }$ is a positive real constant.

Then, we consider the stability of ${\tilde{\eta }}_i$. Let

$$V_{\eta }=\sum _{i=1}^N{\tilde{\eta }}_i^2,$$

(39)

then from (28), it can be obtained that

$$\begin{array}{cc}\hfill {\dot{V}}_{\eta }& =-2\sum _{i=1}^N{\tilde{\eta }}_i^2+2\sum _{i=1}^N{\tilde{\eta }}_i(b_1^{-1}{e}_i+b_1^{-1}{g}^T{\tilde{x}}_i+b_1^{-1}{\tilde{\phi }}_{i,y})\hfill \\ \hfill & ⩽-\sum _{i=1}^N{\tilde{\eta }}_i^2+3\sum _{i=1}^N\left(\frac{1}{b_1^2}{e}_i^2+\frac{{\parallel g\parallel }^2}{b_1^2}{\parallel {\tilde{x}}_i\parallel }^2+\frac{1}{b_1^2}{\mu }_{{\phi }_y}\sum _{i=1}^N({\zeta }_i^2+{\zeta }_i^{2m})\right)\hfill \\ \hfill & ⩽-\parallel \tilde{\eta }{\parallel }^2+3\frac{{\parallel g\parallel }^2}{b_1^2}{\parallel \tilde{x}\parallel }^2+3\left(\frac{1}{b_1^2}{\parallel Q^{-1}\parallel }^2+\frac{1}{b_1^2}{\mu }_{{\phi }_y}\right)\sum _{i=1}^N({\zeta }_i^2+{\zeta }_i^{2m}),\hfill \end{array}$$

(40)

where ${\mu }_{{\phi }_y}$ is a positive real constant.

Finally, let

$$V=V_{\zeta }+2{\delta }_1{V}_{\eta }+{\delta }_2{V}_x,$$

(41)

where ${\delta }_1$ and ${\delta }_2$ are positive constants, satisfying

$$\begin{array}{cc}\hfill {\delta }_1& =\frac{12}{{\gamma }_c}{\parallel b_1\overline{G}Q\parallel }^2,\hfill \\ \hfill {\delta }_2& =6\frac{{\delta }_1{\parallel g\parallel }^2}{b_1^2}+\frac{12}{{\gamma }_c}{\parallel \overline{G}Q\parallel }^2\hfill \end{array}$$

and setting

$$\begin{array}{cc}\hfill h^{*}& ={\delta }_3+\parallel \overline{G}{Q\parallel }^2{\nu }_y+\frac{12}{{\gamma }_c}{\parallel \overline{G}\parallel }^2+\nu \left({\gamma }_c\right)+\frac{3}{{\gamma }_c}\hfill \\ \hfill & +{\delta }_2{\parallel P_x\parallel }^2{\mu }_{\phi }+6{\delta }_1\left(\frac{1}{b_1^2}{\parallel Q^{-1}\parallel }^2+\frac{1}{b_1^2}{\mu }_{{\phi }_y}\right),\hfill \end{array}$$

where ${\delta }_3$ is a positive constant. Then, we can obtain that

$$\begin{array}{cc}\hfill \dot{V}& \le \sum _{i=1}^N(\beta b_{1}N\left({\kappa }_i\right)-1){\dot{\kappa }}_i-{\delta }_3\sum _{i=1}^N({\zeta }_i^2+{\zeta }_i^{2m})\hfill \\ \hfill & -{\delta }_2\parallel \tilde{x}{\parallel }^2-{\delta }_1{\parallel \tilde{\eta }\parallel }^2.\hfill \end{array}$$

(42)

The proof is completed based on above analysis. □

We will now show that, using the Lyapunov-like function $V\left(t\right)$ and the inequality (26), the stability of closed-loop multi-agent systems can be established. For convenience, a lemma is given below.

Lemma 4.

Let $V\left(t\right)$ and ${\kappa }_i\left(t\right),i=1,\dots ,N$, be smooth functions defined on $[0,t_f)$ with $V\left(t\right)\ge 0$ and ${\kappa }_i\left(0\right)=0$. Additionally, let $N\left({\kappa }_i\right)=e^{{\kappa }_i^2/2}({\kappa }_i^2+2)sin\left(k_i\right)$. If the following inequality

$$\begin{array}{cc}\hfill V\left(t\right)& \le V\left(0\right)+\sum _{i=1}^N{\int }_0^t\beta b_{1}N\left({\kappa }_i\left(\tau \right)\right){\dot{\kappa }}_i\left(\tau \right)d\tau \hfill \\ \hfill & -\sum _{i=1}^N{\int }_0^t{\dot{\kappa }}_i\left(\tau \right)d\tau +r\left(t\right),\hfill \end{array}$$

(43)

where r represents some suitable constant holds for any $t\in [0,t_f)$, then $V\left(t\right),{\kappa }_i\left(t\right)$ for $i=1,\dots ,N$ and ${\sum }_{i=1}^N{\int }_0^t\beta b_1$$N\left({\kappa }_i\left(\tau \right)\right){\dot{\kappa }}_i\left(\tau \right)d\tau$ are bounded on $[0,t_f).$

Using Lemma 4 and Theorem 1, we can conclude that, for any given initial condition, all ${\kappa }_i\left(t\right),1\le i\le N$, in the closed-loop system are bounded on $[0,t_f)$. Moreover, $V\left(t\right),{\sum }_{i=1}^N{\int }_0^t\beta b_{1}N\left({\kappa }_i\left(\tau \right)\right)$${\dot{\kappa }}_i\left(\tau \right)d\tau$ are bounded on $[0,t_f)$. Since $V\left(t\right)$ is a proper positive definite function in ${\zeta }_i,{\tilde{x}}_i$ and ${\tilde{\eta }}_i,i=1,\dots ,N$, ${\zeta }_i,{\tilde{x}}_i$ and ${\tilde{\eta }}_i,i=1,\dots ,N$, are bounded on $[0,t_f).$ Therefore, finite-time escape cannot occur and $t_f=\infty$, that is ${\zeta }_i,{\tilde{x}}_i$ and ${\tilde{\eta }}_i,i=1,\dots ,N$, are bounded for all $t\ge 0$. As a result, from (29), ${\dot{e}}_i,i=1,\dots ,N$ are bounded for all $t\ge 0$. Using Barbalat’s lemma, we can show that ${lim}_{t\to \infty }{e}_i\left(t\right)=0$ for $i=1,\dots ,N$.

5. Simulation Example

In this section, an example is provided to verify the effectiveness of the proposed adaptive consensus output tracking control design. The considered system is a connection of four subsystems; each of them is described by a second-order state-space model as

$$\begin{array}{cc}\hfill {\dot{x}}_{i,1}& =x_{i,2}+d(y_i-0.3y^3)+b_1{u}_i,\hfill \\ \hfill {\dot{x}}_{i,2}& =-\frac{y_i}{d}+b_2{u}_i,\hfill \end{array}$$

(44)

with $y_i=x_{i,1}$, where $d,b_1$ and $b_2$ are unknown positive real parameters. Note that, when $u_i=0$, the system is a van der Pol oscillator and its trajectories are bounded. Hence, it can be shown that Assumption 3 is satisfied with $q=3$. For the reference signal, the formation is the same as (44) but with $u_0=2$. Then, we assume the interaction graph among the subsystems is

$$\mathcal{G}=\left[\begin{array}{cccc}0& 0& 1& 0\\ 1& 0& 0& 0\\ 0& 0& 0& 1\\ 0& 1& 0& 0\end{array}\right],$$

and only subsystems 1 and 3 have access to $y_0$. Thereby the result Q is given by

$$Q=\left[\begin{array}{cccc}2& 0& -1& 0\\ -1& 1& 0& 0\\ 0& 0& 2& -1\\ 0& -1& 0& 1\end{array}\right].$$

According to Lemma 4, the distributed adaptive controller is designed according to the format in(23)–(25) for $i=1,\dots ,4$.

A simulation study with the parameters $b_1=b_2=1$, ${\gamma }_c=1,\beta =1$ and ${\gamma }_h=5$ was carried out. The parameter d is set as

$$d=\left\{\begin{array}{c}0.2\mathrm{for}0\le t\le 30,\hfill \\ 2\mathrm{for}t\ge 30,\hfill \end{array}\right.$$

so that two different limit cycles are used as the trajectories of the reference signal.

The simulation results of the subsystems’ outputs and states are shown in Figure 1, Figure 2, Figure 3 and Figure 4 and show the adaptive gains ${\kappa }_i$ and the tracking errors. It can be seen that both the output and the states, which are shown in Figure 1 and Figure 2, respectively, converge to the reference signal trajectory with the values ${[2,-1]}^T$. Figure 3 shows that the adaptive gains are bounded; the tracking errors are shown in Figure 4. The control inputs are shown in Figure 5 and a specific control input is shown in Figure 6. It is also noted that the trajectories are different after 30 s in the simulation, due to the change in the value of d.

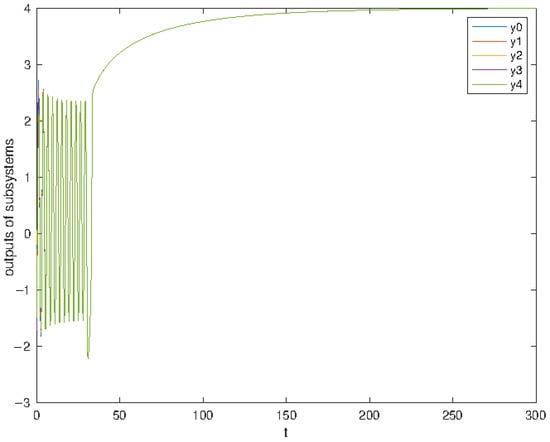
Figure 1. The subsystem outputs $y_i,i=0,\dots ,4$.

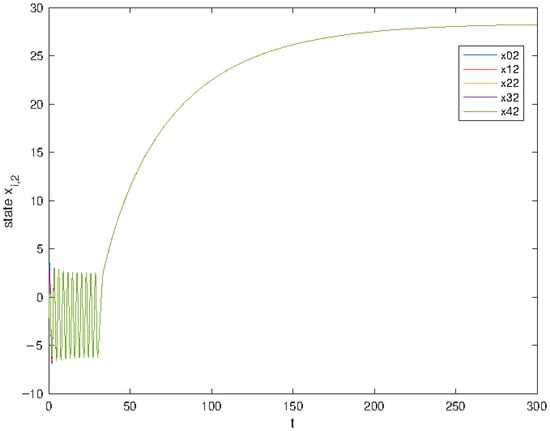
Figure 2. The subsystem states $x_{i,2},i=0,\dots ,4$.

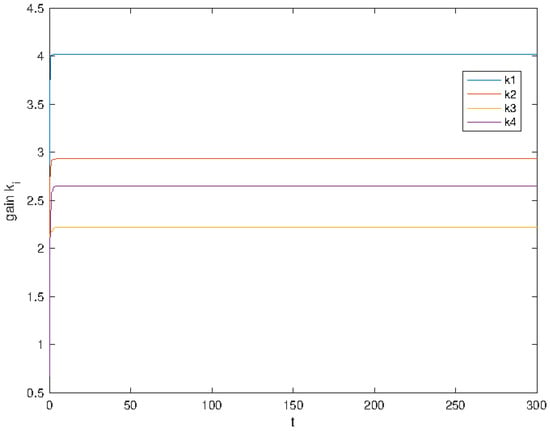
Figure 3. The adaptive gains ${\kappa }_i,i=1,\dots ,4$.

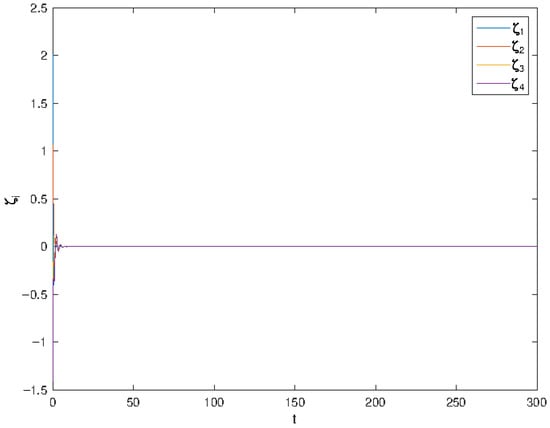
Figure 4. The tracking errors ${\zeta }_i,i=1,\dots ,4$.

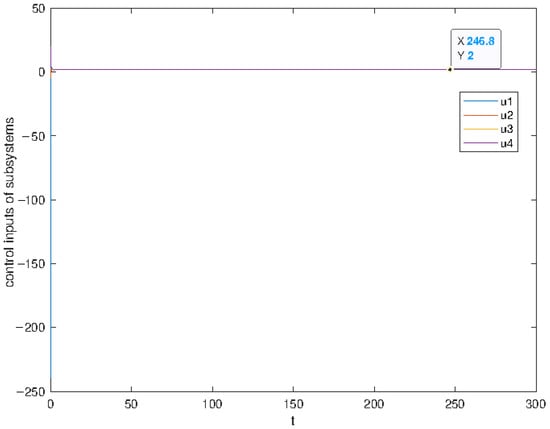
Figure 5. The control inputs $u_i,i=1,\dots ,4$.

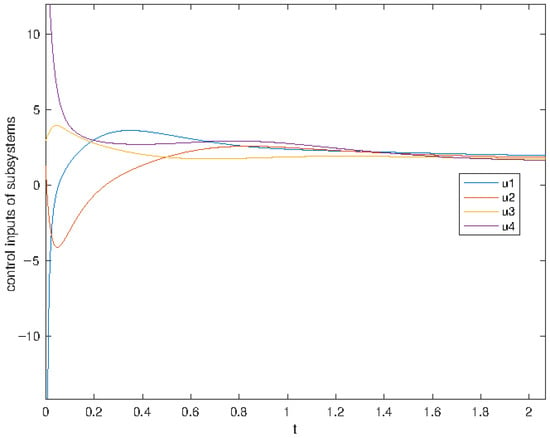
Figure 6. The control inputs $u_i,i=1,\dots ,4$ when t between 0 and 2 s.

6. Conclusions

In this paper, we propose a new distributed adaptive control design to solve the consensus output tracking problem for strongly connected nonlinear multi-agent systems with unknown control directions. The asymmetry of the Laplacian matrices becomes the obstacle in the control design. To address this issue, a novel integral Lyapunov function is proposed along with adaptive internal models and Nussbaum gains. The presented new internal models are used to generate the contribution of the desired input compensation to the state variable, which are then used in the control design. These internal models, along with adaptive laws and Nussbaum gains, account for unknown connectivity and unknown parameters in the subsystems’ dynamics. The proposed schemes only depend on the relative output information of the subsystems in the directed graph, and a distinct feature is that they can be designed by each agent in a fully distributed way. Finally, the adaptive laws and control design ensure the asymptotic convergence of output tracking errors of the subsystems to zero. Simulations were employed to demonstrate the validity of the theoretical results.

7. Future Work

In this paper, consensus output tracking for a class of nonlinear systems under directed graphs was studied. The reference signal with constant input is much more conservative. How to design a distributed adaptive consensus controller if the reference is a periodic signal with unknown parameters is more challenging as, because of the asymmetry of Laplacian matrices, the construction of the Lyapunov function becomes more difficult. The $\sigma$-modification method might work. Besides, the adaptive event-triggered control based on the frequency of data transmission proposed in [30,31,32] might be a way to achieve the disturbance rejection theoretically. Further analysis to tackle these problems is a topic of future research.

In the real world, some phenomena might be well described by discontinuous dynamics; for example, in the physical field, the characteristics of an ideal diode possessing a very high slope in the conducive region can be precisely modelled by a discontinuous system. It is necessary for us to investigate multi-agent systems with discontinuous nonlinear dynamics. Recently, the consensus of fractional multi-agent systems with discontinuous inherent nonlinear dynamics was discussed in [33,34], with a new convex function and the inherent nonlinear dynamics satisfying the local nonlinear Hölder growth property in a neighbourhood of continuous points.

Time delays widely exist in practical multi-agent systems due to the time taken for transmission of signals, transport of material, etc. The presence of time delays, if not considered in the controller design, may seriously degrade the performance of the controlled systems, may even cause the loss of stability. One basic idea for tackling an input delay is to predict the evolution of a state variable for the delay period and then use the predicted state for control. The state prediction is based on the explicit solution of the state equation, which consist of the zero input and the zero state solutions. However, the zero state solution involves the integral of the past control input and causes difficulty in control implementation.

An alternative method based on the prediction is to ignore the troublesome zero state solution, and use the zero input solution as the prediction, which is referred to as the truncated prediction [35]. By transforming the Laplacian matrix into the real Jordan form, sufficient conditions are needed such that the proposed control algorithms can achieve the consensus. Therefore, by using the truncated prediction feedback for consensus output regulation of nonlinear multi-agent systems with input delay draws our attention.