1. Introduction
As an important branch of optimization, combinatorial optimization plays a significant role in management and economics, computer science, artificial intelligence, biology, engineering, etc. [
1]. The traveling salesman problems (TSPs) are the main subject of combinatorial optimization problems, in which the goal is to find a closed route through all the cities once, and only once. This problem is equivalent to finding a Hamilton circuit with the minimum distance. The TSP, and its variants, such as asymmetric TSPs (ATSPs) [
2], clustered TSPs (CTSPs) [
3], dynamic TSPs (DTSPs) [
4], multiple TSPs (MTSPs) [
5], and wandering salesman problems (WSPs) [
6], have wide applications in laser engraving [
7], integrated circuit design [
8], transportation [
9], energy saving [
10], logistics problems [
11], communication engineering [
12], and medical waste transportation, which is closely related to the COVID-19 pandemic [
13]. The TSP was first considered in mathematical format in 1930 to solve a school bus routing problem, and then spread by researchers of Rand corporation. However, these problems were first considered only dozens of cities, but with the increase in applications, the scale of the problems may exceed millions [
14].
Although the description of TSP is simple, it has been proven as NP-Hard, which means that the time required to obtain the exact solution for TSP will increase exponentially when the size of the problem aggrandizes. Lots of algorithms have been developed for TSPs, and they can be split into four categories: exact methods, approximation algorithms, intelligence algorithms, and heuristics algorithms. The exact solver, such as brute-force search, linear programming [
15], dynamic programming [
16], brand and bound [
17], brand and cut [
18], and cutting plane [
19] are powerful tools for small scale TSPs. However, the computational complexity of an exact algorithm is very huge, such that solving the instance with 85900 nodes will take over 136 CPU-years by Concorde, which is a mature exact solver for TSPs [
20]. Since there is no efficient exact solution to any NP-hard problem, numerous efficient approximation solutions are presented for finding efficient approximation solutions in polynomial time complexity and with provable solution quality [
21]. Although such algorithms can obtain high approximation ratio such as
for Euclidean TSPs [
22] and
for TSPs [
23], the running times of these approaches, even though asymptotically polynomial, can be rather large, see [
24].
The intelligence algorithms are inspired by the nature world and have high capabilities to approximate the global optimal for optimization problems. Evolutionary algorithm (EA) [
25], ant colony optimization algorithm (ACO) [
26], ant colony system (ACS) [
27], shuffled frog leaping algorithm (SFLA) [
28], simulated annealing algorithm (SA) [
29], particle swarm optimization (PSO) [
30], and other well-known algorithms [
31,
32] all belong to intelligence algorithms. The novel intelligence algorithm can be employed to solve the problem with
nodes with high quality in an hour on a retail computer, but it is still hard to tackle while the scale is larger [
33]. There are two main drawbacks of intelligent algorithms: one is that they frequently converge to the local optimum; the other one is that the parameters affect the solution quality deeply but usually can only be determined empirically [
34]. The main heuristic algorithms for TSPs can be grouped into the Lin–Kernighan family and stem-and-cycle family; they could provide high-quality solutions for nearly 2 million cities’ problems [
35]. For higher quality solutions and lower running time, some researchers combined intelligence algorithms and heuristics algorithms; see [
36,
37,
38] and the reference therein.
Genetic algorithm (GA) was proposed by Holland in 1975, the basic idea stems from “survival of the fittest” in evolutionism. Most types of GAs contain three main segments: selection operator, crossover operator, and mutation operator. Due to the high effectiveness and versatility of GAs, they have been widely employed to solve TSPs and other challenging optimization problems [
39]. However, there are still several doubts about TSPs, including premature convergence, population initialization, problem encoding, etc. [
40].
On the other hand, crossover operators have a significant influence on the performance of GA and are a key factor in global searching and convergence speed. As a matter of fact, various crossover operators have been proposed for TSP, including partially mapped crossover (PMX) [
41], ordered crossover (OX) [
42], cycle crossover (CX) [
43], sequential constructive crossover operator (SCX) [
44], completely mapped crossover operators (CMX) [
45], and others based on heuristic algorithms such as bidirectional heuristic crossover operator (BHX) [
46]. Additionally, merging GAs with local search or heuristic algorithms will reveal both of their advantages, including high convergence speed and the capacity for global optimization; therefore, it has been a hot topic of study [
36,
47,
48].
Although the size of TSPs are larger than
, seeking a high quality solution is extremely difficult, even the high powerful implementation of the Lin–Kernighan heuristic (LKH) maintained by Helsgaun [
49] will take over an hour on a
nodes instance, see the experiments in [
33] and
Table 1. In addition, even a small improvement in quality can take a long time; the question of how to obtain an acceptable approximation solution in a reasonable time is more useful in real-world applications [
50]. Thus, a new series of two-layered algorithms has been proposed, and the fundamental concepts of them can be divided into two categories. The first type of them is to use various clustering techniques to divide the cities into small groups, calculate the sub-TSPs within those groups, and then merge the groups into a Hamilton cycle [
51,
52,
53]. The other one is to determine the start and end points for each small group after clustering firstly, and then solve the fixed start and end points of TSPs, which are also called WSPs; finally, combine all the groups [
54]. These algorithms are much faster than algorithms without clustering and can solve 180 K size TSP within a few hours [
7].
Naturally, two-layered algorithms can be developed to be three-layered or multiple-layered; very recent works can be seen in [
55,
56]. Admittedly, in order to fully utilize all the CPUs of computers, parallelizability is becoming extremely essential for algorithms designed to solve large and complicated problems. Some parallel algorithms for TSPs can be seen in [
57,
58].
In this paper, in order to develop a fast, easy implementation and high parallelizability algorithm for TSPs, an adaptive layered clustering framework with improved genetic algorithms (ALC_IGA) is supposed. This algorithm is not only an improvement of GA, but also an extension of the two-layered and three-layered methods in the references [
7,
51,
55] for TSPs. The key contributions of this study are as follows:
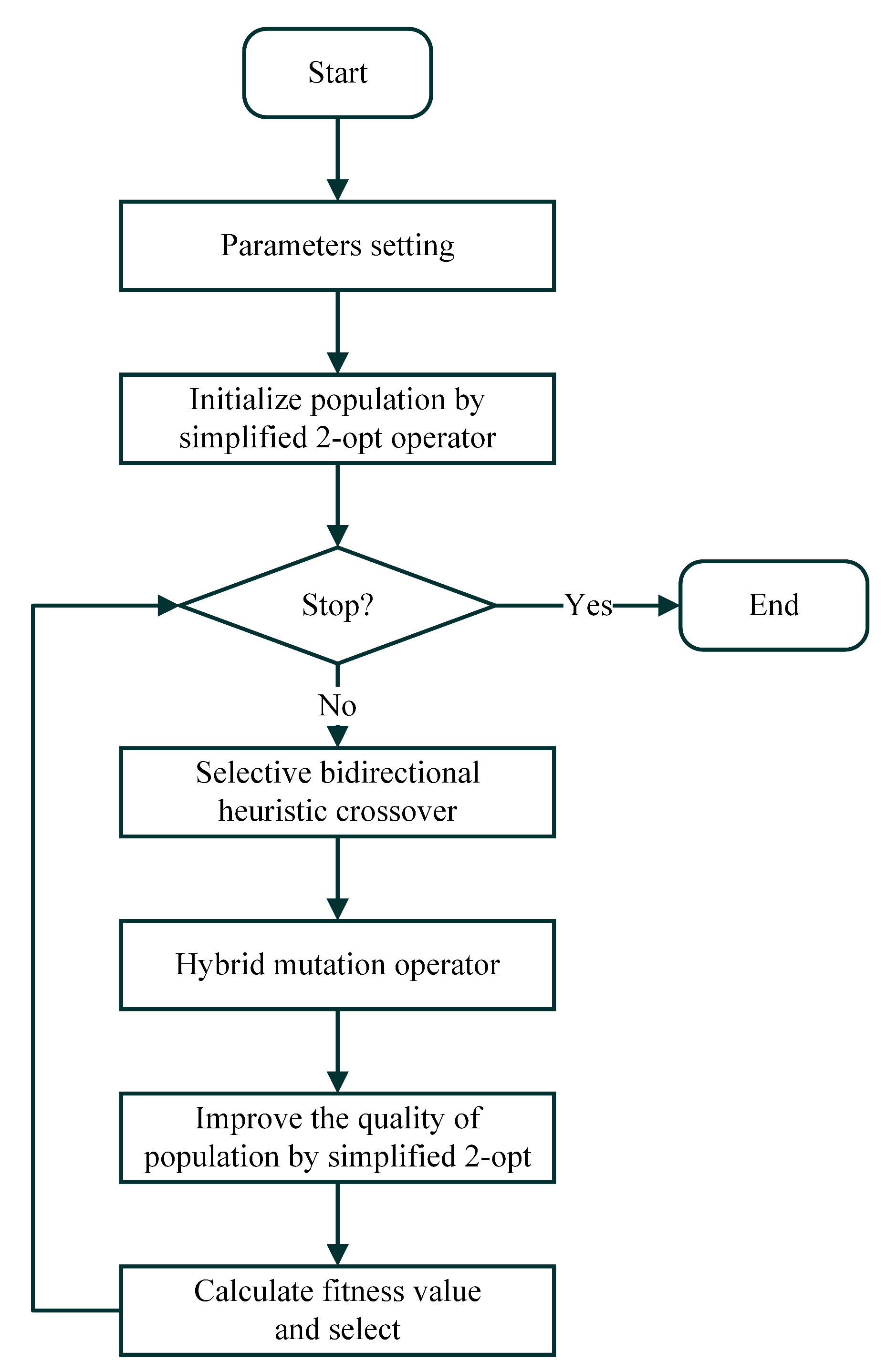
An improved genetic algorithm (IGA) integrated with hybrid selection, a selective BHX crossover operator, and simplified 2-opt local search has been proposed; a numerical comparison of IGA, GA, and ACS on TSPs shows the high performance of IGA.
Plentiful numerical results also prove the effectiveness of the novel IGA for solving the WSPs.
An adaptive layered clustering framework is proposed to break down a large-scale problem into a series of small-scale problems. The computational complexity of the ALC_IGA is between and ; moreover, the parallelability of it has been discussed.
We show a numerical experiment for parameters tuning of the proposed ALC_IGA; the results reveal that the larger the parameter set, the higher the solution quality that is obtained, but a longer time is required.
Dozens of two-dimensional Euclidean instances have been tested with ALC_IGA and some two-layered algorithms, and the results show that ALC_IGA has advantages in terms of accuracy, stability and convergence speed over the two-layered algorithms proposed by [
7,
51].
Lots of large-scale instances ranging in size from to have been tested, and the results show that the parallel ALC_IGA is more than four times faster than the other three compared algorithms, and obtains the best solution in the most cases. The results on very large-scale TSPs, with sizes ranging from to , also demonstrate the excellent effectiveness of ALC_IGA.
The remainder of the paper is organized as follows: a brief literature review of some related concepts is presented in
Section 2; the main procedures of IGA are shown in
Section 3; the details ALC_IGA are discussed in
Section 4; the results of experimental analyses and algorithms comparisons are shown in
Section 5; A summary of this paper and future works are listed in
Section 6.
4. The Framework of ALC_IGA for Large-Scale TSPs
In recent years, some two-layered algorithms have been proposed, and they significantly reduce the time expenditure for large-scale TSPs [
7,
51]. Liang et al. [
55] recently proposed a three-layered algorithm with
k-means and indicated that it outperforms some two-layered algorithms by numerical experiments. Notwithstanding, both two-layered and three-layered algorithms may still have medium-scale or large-scale groups. Naturally, this will require a significant amount of time to solve the underlying problems. Thus, upgrading the two-layered and three-layered algorithms to the adaptive layered algorithm stands to reason.
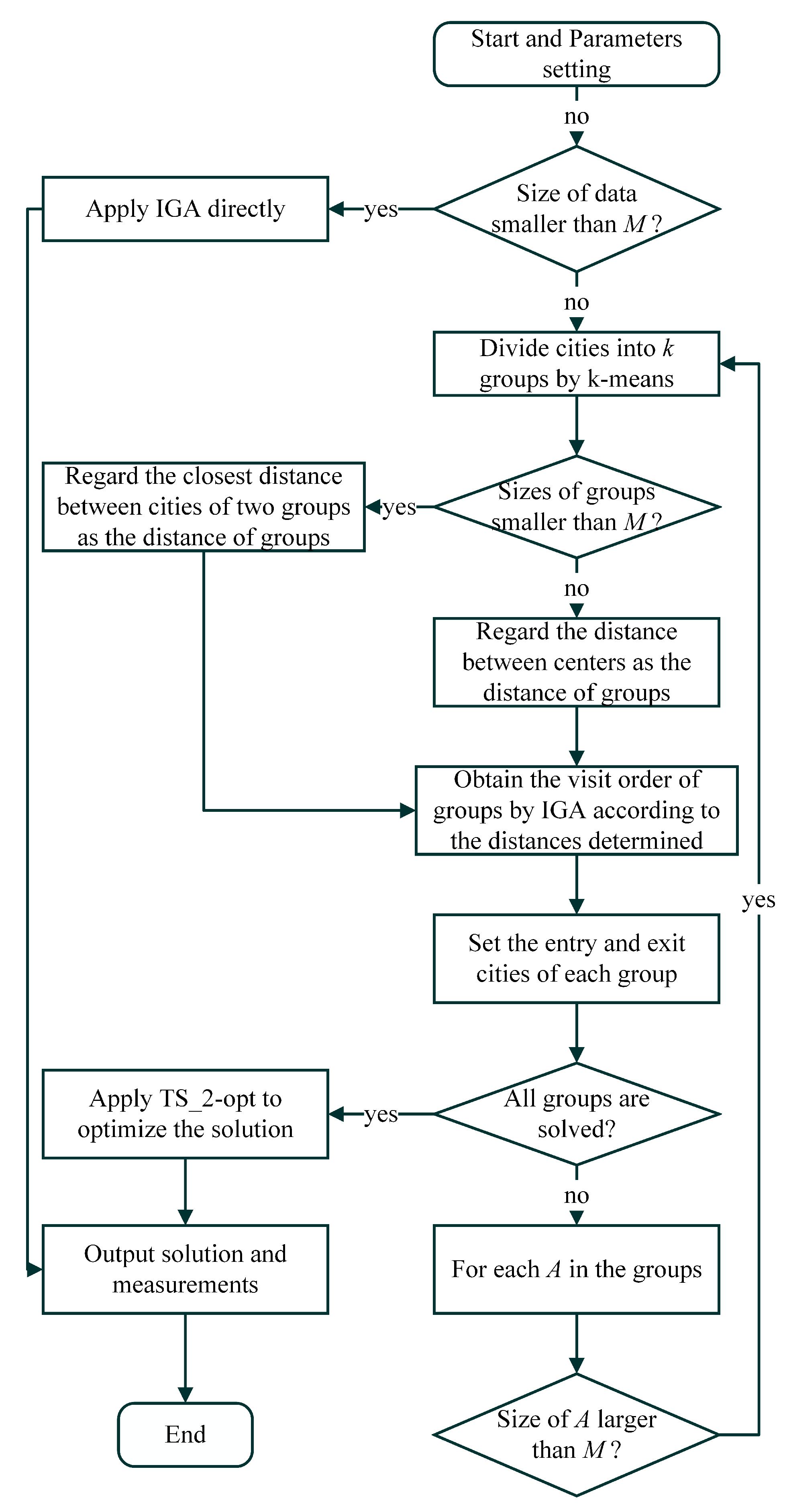
We propose a brand new framework for adaptive layered clustering that takes into account the IGA created in the previous section. The framework is divided into two parts: the first is applying clustering and IGA to initialize the solution, and the second is optimizing the initial solution. Based on our new algorithm, the large-scale TSPs can be transformed into solving some TSPs and WSPs that are smaller than the specified size. The processing flows are illustrated in
Figure 2, and the details of solution initialization and optimization are represented subsequently in
Section 4.1 and
Section 4.2.
4.1. Solution Initialization
In the solution initialization phase, we combine the adaptive layered clustering and IGA. For each cluster that is larger than the specified size, k-means will be applied to divide the problem into some small clusters and then determine the number of layers, visit order, entry cities, and exit cities of the sub-clusters. When the size of a cluster is smaller than the specified size, IGA is used to determine the Hamiltonian path from the entry node to the exit node within the cluster. When the size of a cluster is larger than the specified size, k-means is used again to split the cluster. These processes are repeated until the paths of all clusters are determined. Then, combining all sub-paths, and we obtain the initial feasible path.
The procedure of main steps of the solution initialization phase is illustrated in
Figure 2. Its pseudo-code is given in Algorithm 6.
| Algorithm 6 Solution initialization framework. |
Input: A TSP problem G, the size N of G, the nodes are designated by , a positive integer M, and denote the size of by . Output: The initial solution for TSP G.
- 1:
if
then - 2:
Apply IGA to solve G, and output the solution . - 3:
else - 4:
Divide the problem G into clusters by k-means. - 5:
Denote the groups by , the coordinate vectors of centers are , the sizes of groups marked as . - 6:
if then - 7:
Set as , where , , , . - 8:
Use IGA to solve the distance matrix M and record the visited order . - 9:
else - 10:
Obtain the visited order by IGA for solving . - 11:
end if - 12:
for in do - 13:
Find the last visit group and the next visit group . - 14:
Set as the nearest city in to , and set as the nearest city to . - 15:
if = then - 16:
Set as the second nearest city to . - 17:
end if - 18:
end for - 19:
while some groups are unsolved do - 20:
for in do - 21:
if is unsolved then - 22:
if then - 23:
Apply IGA to obtain the shortest route from to . - 24:
else - 25:
Divide the into clusters by k-means. - 26:
Denote the groups by , the coordinate vectors of centers are , the sizes of groups marked as . - 27:
Find the visited order by the same method in lines 6–11. - 28:
Set the entry and exit cities of each groups by the same method mentioned in lines 12–18. - 29:
end if - 30:
end if - 31:
end for - 32:
end while - 33:
Organize the visit orders, entry cities, exit cities, and the internal route of each cluster, and output the initial feasible path . - 34:
end if
|
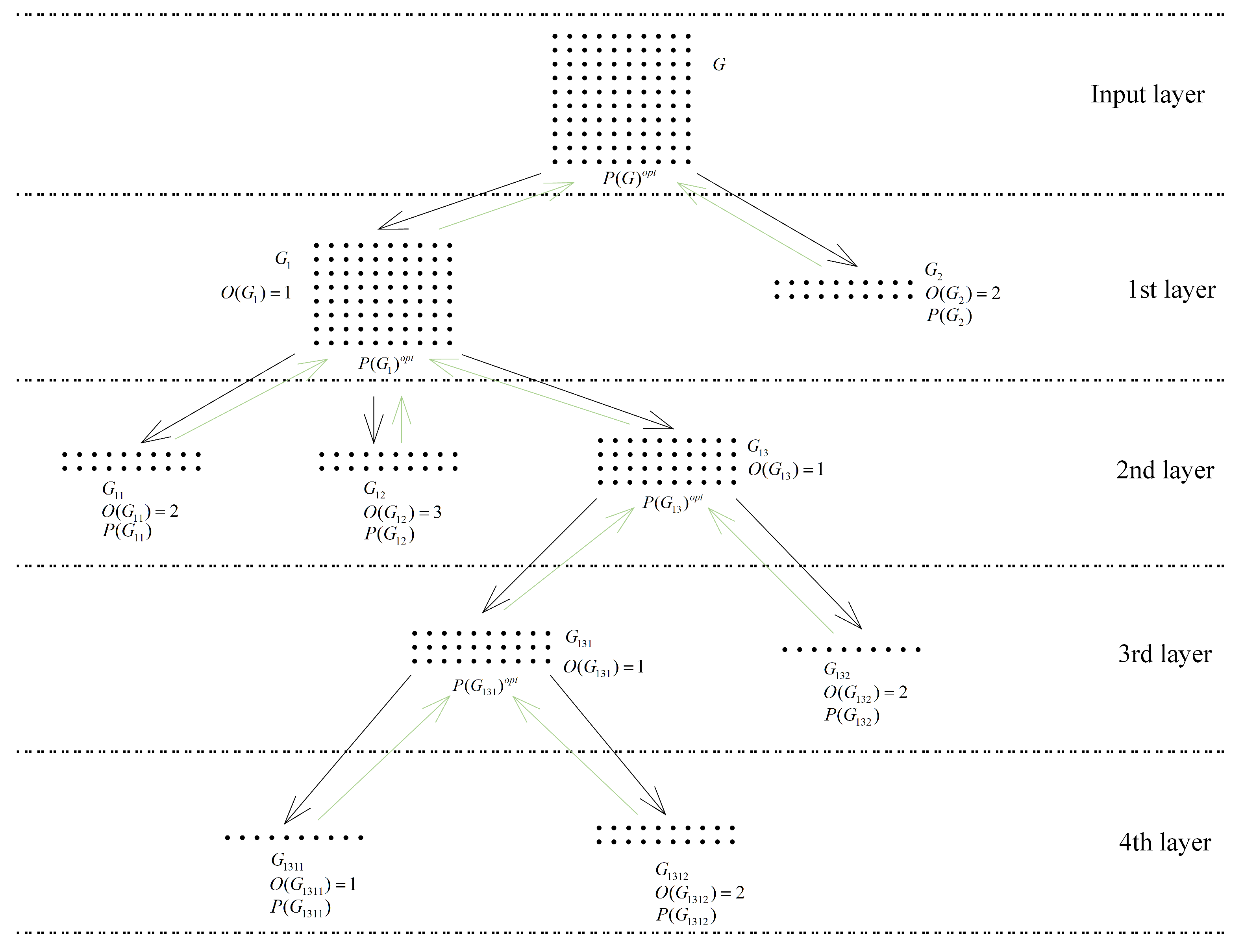
Remark 2. We point out that there are many different clustering techniques, which makes it hard to select the ideal clustering strategy for TSPs. The results in [64] indicate that the simple grid-based methods are better than the k-means methods. Because the numerical experiments are only focused on one particular instance, we still use the standard k-means as models. An example of a 100-cities TSP and
M set to 20 is shown in
Figure 3. In the first layer, the cities have been divided into two groups
by
k-means, and the visit order found by IGA is
and
. On the one hand, since the size of
equals
M, the visit route
of the 20 cities in
could be solved by IGA quickly. On the other hand, because there are 80 cities in
, that is larger than
M, so
needs to be divided into small groups again. Repeat the procedures are until all of the group sizes are less than
M, resulting in six groups and four layers being determined during the solution initialization phase. To combine the six routes, first, from the bottom layer, connect
with
sequentially, and obtain
. Then, in the third layer, connect
with
, then
. Following these steps, the path for the 100-cities TSP is eventually
.
4.2. Two Phases 2-Opt for Solution Optimization
Because of the clustering algorithm used, the solution obtained in the solution initialization stage is a little rough and can be continue to be optimized. In [
66], Liao and Liu first applied the 2-opt and 3-opt operators to optimize the initial route with the clustering algorithm involved, and the numerical studies show a marked improvement when
k-opt is used. Nevertheless, when the number of cities in the problem is exceptionally enormous, the
k-opt struggles to work.
To improve the quality of the initial solution in an affordable time, a two-phase simplified 2-opt algorithm (TS_2-opt) is given in Algorithm 7. The TS_2-opt is aimed to optimize the routes and orders of all the groups which belong to a cluster at a higher layer. Once the solution is initialized, TS_2-opt is used to optimize the route of each group in the penultimate layer and repeated layer by layer until the top layer is optimized. Depicted in
Figure 3, the green lines show the workflow of solution optimization. Firstly, from the bottom layer, the routes
and
are combined by TS_2-opt to the local optimal routes
. Then, the two routes in the third layer also are optimized to
by using TS_2-opt. Follow these steps until the final solution
is obtained.
| Algorithm 7 Two-phase simplified 2-opt algorithm. |
Input: A batch of groups , suppose the order of them is , and the travel routes of them . Initialize parameters: The first phase max iteration ; the second phase max iteration ; the length selected for optimization R. Output: An optimized route for .
- 1:
Compute the distance of the tour . - 2:
for = 1 to do - 3:
Randomly generated two different integers , between . - 4:
Denote the route between and as ; denote the route between and as ; denote the route between and as . - 5:
Inverse , denote the new route as . - 6:
Generate two routes and , where is combined by the last R elements of and the first R elements of ; is combined by the last R elements of and the first R elements of . Denote the new order of groups as , the sizes of groups is noted as . - 7:
The Algorithm 5 with max iteration number is applied to optimize and . Denote the new routes as and . - 8:
Replace and in with and , respectively. Denote the new route as . - 9:
Compute the distance of . - 10:
if then - 11:
Assign to . - 12:
Divide into h segments , here is equal to . - 13:
end if - 14:
Replace by . - 15:
end for - 16:
Output .
|
Suppose there are three groups
belonging to the same higher group
, and the visit orders of them are
, respectively.
Figure 4 illustrates the major processing of TS_2-opt in detail. Each cluster is represented by a different color, whereas the start and end locations are marked by larger shapes. In Step 1 of
Figure 4, the three routes are arranged by order and assume the
is chosen, then the path of
is inverted. In Step 2, the segments at the junctions of the clusters are determined according to
R, where
R equals 5 for simplicity. The next step is to optimize the two segments provided by Step 2. In Step 4, three new routes are generated according to Step 3 and the input routes. Once all four steps have been completed, return to Step 1 until the termination condition is met.
We note that the purpose of the TS_2-opt is not to reach the global optimal, but rather to optimize the visit orders and junctions between groups that belong to the same group at the higher layer. Despite sacrificing some precision, the computation speed of TS_2-opt is very fast, which is critical in large-scale TSPs.
4.3. Parallelizability and Computational Complexity Analysis
We show the highly parallelizable capability of the proposed ALC_IGA. In the phase of solution initialization, the operations for clusters are independent in each layer; the operations of subgroups that do not belong to the same cluster in different layers are also independent. As an illustration, there are three tasks in the third layer shown in
Figure 3; find the visit route for
and
, and apply
k-means to divide
into small groups. As they are stand-alone, if there are three or more cores of the CPU, they can be computed on different cores simultaneously. Furthermore, if
k-means is faster than the other two tasks, then the computations of
and
in the next layer can also be allocated to the free cores even if
and
are still being calculated.
In the second phase of ALC_IGA, solution optimization also can be parallelized, but the parallel effectiveness is not as high as in the first phase. Firstly, the complex calculation in solution optimization is only the optimization of the junctions, but there are only two junctions in each iteration, so parallel computing is unnecessary. Secondly, the optimization of the solution starts from the bottom and ends at the top layer, but the higher-layer optimizations must wait for lower-layer optimizations to finish. In the example shown in
Figure 3, there is only one task in the fourth layer, which is connecting
and
. Because the route of
is not determined before the computation of the fourth layer is finished, the free cores can not be used to combine
and
in the third layer.
Notwithstanding, parallel techniques can be used in each layer to speed up computation while the scale of the problem is very large. The computational complexity of the major stages of the proposed ALC_IGA is presented in the remainder of this subsection.
We recall that the time complexity of k-means is known as , where N is the number of points, K is the number of clusters, I is the specified max iterations, and D is the number of dimensions. For the sake of simplicity, we assume that there are n nodes in the TSP, and m and k are two positive integers, is the max run time of the IGA for solving m-nodes TSP, I and D are fixed. After that, we look at the time complexity in two parts.
In the best-case scenario, we assume that , and each use of clustering divides the cluster into m sub-clusters, where the number of nodes of each sub-cluster is equal. Firstly, in the second layer, the IGA well is used once to obtain the visited cluster order, and in the third layer, it is m times. We deduce that the total times of IGA are , and by we have , then the upper bound of the total time of IGA is , which is . Secondly, in the top layer, the time complexity of k-means is ; in the second layer, the time complexity of k-means is , which is . Subsequently, we can infer that the time complexity of each layer is always . Note that when there are layers, then the total time complexity of ALC_IGA is , and since the m is a given constant, the time complexity of ALC_IGA is .
In the worst case, each cluster ends up with groups that contain a single city and a single group that contains all the other cities. It can be seen that in this condition, the numbers of k-means and IGA are both far more than the best scenario. Suppose , then there will be k times clustering and times IGA. The time of IGA applied is no more than , it is . Similar to the best-case analysis, the computational complexity of clustering in the worst condition is ; by some calculation, we obtain that the time complexity of the k-means used is . Accordingly, the computational complexity of ALC_IGA in the worst condition is .
In summary, the computational complexity of the ALC_IGA ranges from
to
. The computational complexity of ALC_IGA is closer to
, however, in the majority of cases. This is supported by the numerical experiments presented in
Section 5.
Remark 3. Comparing with the algorithms in [7,51,55], we note briefly that ALC_IGA exhibits several innovations and advantages as follows: As a tool for solving sub-TSPs, IGA has been improved in some aspects based on existing techniques, and has shown significant improvements compared to GA [51] and ACS [7] on small-scale TSP problems; see the experiments in Section 5. ALC_IGA only requires attention to one parameter: the maximum number of clusters for k-means. This simplicity is more convenient than that of two- or three-layered algorithms and is crucial for solving large-scale TSPs.
Based on the characteristics of layered-clustering computation, we have proposed a fast fine-tuning algorithm; this step has not been introduced in [7,51,55]. By applying adaptive layered clustering, we are able to analyze the time complexity of ALC_IGA, which is still challenging to in the case of two or three-layered algorithms.
5. Numerical Results and Discussions
Four-part numerical experiments are presented in this paper to illustrate the effectiveness of ALC_IGA. First,
Section 5.4 shows that IGA is substantially superior to GA and ACS in terms of accuracy and convergence speed. The implications of the primary parameter setting performance on ACL_IGA are examined in the second part. The third part proves the superiority of ALC_IGA on middle-scale benchmark datasets over two two-layered algorithms from the literature. The last part proves the excellent performance and parallelizability of the proposed ALC_IGA in comparison to some representative algorithms.
5.1. Experimental Setting
In this study, all experiments were computed on a Dell PowerEdge R620 with two Intel Xeon E5-2680V2 10-core processors and 64.0 GB of 1066 MHz DDR3 memory under Windows 10 OS. The speed of all cores is locked to 2.80 GHz without turbo boost technology and disabled hyperthreading to ensure the fairness and stability of the numerical experiments. All the programs are edited and run on MATLAB R2020a, the used parallel technique is the parallel computing toolbox in MATLAB, and only the experiments in
Section 5.7 were run in parallel. By default, each instance was computed 20 times under the same setting. In detail, if the algorithm was single-threaded, the instance on 20 cores was executed simultaneously; if the algorithm was multi-threaded, they were run one by one. The sources of GA, ACS [
27], IGA, two-level genetic algorithm (TLGA) [
51], TLACS [
7], and ALC_IGA are published on GitHub (
https://github.com/nefphys/tsp, published on 4 January 2023), and the instances involved are also on this repository.
5.2. Benchmark Instances
For various experimental tasks, the instances are classified into three categories: small-scale TSPs , medium-scale TSPs , and large-scale TSPs . Small-scale TSPs were used to study the effectiveness of IGA, middle-scale TSPs were employed to tune parameters and compare ALC_IGA with TLACS and TLGA in a single thread, and large-scale TSPs were adopted to compare ALC_IGA with some relevant algorithms in parallel and verify the efficiency of ALC_IGA.
5.3. Evaluation Criteria
The following are the evaluation criteria for the algorithmic analyses on instances:
The minimum objective value among all runs: .
The average objective value among all runs: .
The standard deviation of results among all runs: .
The best known solution of the instance: .
The deviation percentage of
is defined by:
The deviation percentage of
is defined by:
The running time in seconds while was found.
The average of the running time in seconds among all runs: .
The count of the best , , , and are denoted as , , , and .
5.4. Performance Comparison of IGA, GA, and ACS
In addition to clustering, the most time-consuming part of ALC is eliminating the sub-TSPs. That is why the IGA proposed. To illustrate that IGA is efficient on TSPs, a comparison of IGA, GA, and ACS is imperative, and 42 small-scale benchmark instances were used in this numerical comparison. The parameters setting of IGA were as follows: the population was set to 0.4 times the number of nodes; the maximum number of iterations for S_2-opt was set to 20 times the number of nodes; the parameters of selection operator,
and
, were set to 0.15 and 0.5; and the probability of mutation was set to 0.05. The population size of GA was set to 0.8 times the size of the instance and the mutation number was always set at three individuals. The parameters setting of ACS is as same as the literature [
7]. Finally, the termination condition for the three compared algorithms is when there has been no improvement in the population for
X iterations. In this experiment,
X were set to 100, 100, and
for IGA, ACS, and GA, respectively. The results of the comparison without parallelization are displayed in
Table 2, and various evaluation criteria were considered, including
,
,
,
,
,
,
,
, and the average value for
,
, and
.
From
Table 2, the
of IGA, GA, and ACS are
,
, and
, respectively. It is clear that the innovative IGA consistently produces superior results over GA and ACS. Additionally, the average computation time of IGA is the least in 97% instances, and its stability also has a far higher level than the other two algorithms. More specifically, the average
of IGA is 0.27%, but GA and ACS are 2.79% and 5.19%, respectively, 10 times and 19 times of IGA. In almost all cases, the
of IGA is less than 2%, but GA and ACS are often greater than 5%, especially ACS, and even greater than 10% in some instances. In the view of stability, the average of the evaluation criteria
of IGA is 125.45, only 22.56% of GA and 63.52% of ACS. The average computation time of IGA is 90.43 s, which is less than one-sixth as long as GA or half as long as ACS. The above discussion indicates that all the accuracy and the convergence speeds of IGA are substantially superior to the traditional GA and ACS, which proves that the proposed IGA can reduce the computation time and improve the solution of ALC_IGA.
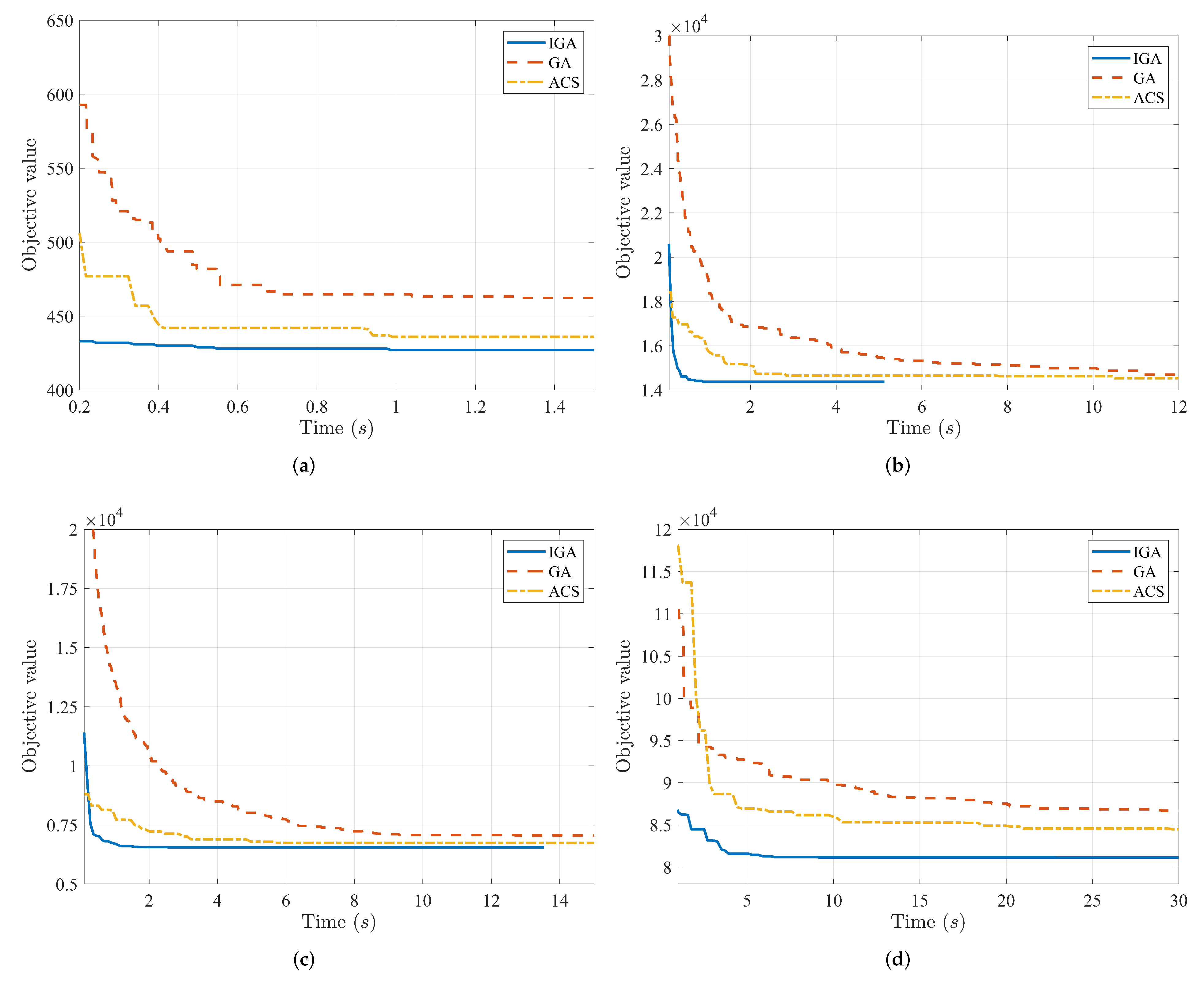
In
Figure 5, the convergence speeds of IGA, GA, and ACS are compared under four instances with sizes ranging from 51 to 226. It can be observed that the convergence speed of IGA in the initial stage is much faster than that of GA and ACS. This is due to the heuristic crossover SBHX and the local search S_2-opt combined in IGA.
We know that the suggested IGA can be utilized to solve WSP as stated in
Section 3, with just a minor adjustment to the distance between the start and end cities. In this part, to validate the effectiveness of IGA for WSP, the 42 instances in
Table 2 were re-investigated. The start and end cities of these instances were determined using the first and last elements of the best known solutions provided by TSPLIB and TSP test data, and the distances between start and end cities were set to −
. The benchmark algorithm is the famous TSP solver LKH proposed by Helsgaun [
49]. The results, which include
,
,
,
,
,
,
, and
are shown in
Table 3.
It is clear from
Table 3 that the IGA can produce the solution of WSP with a high level of accuracy. We note that all
are lower than 1% and 18 out of 42 are as good as LKH. The
of 25 out of 42 instances produced by IGA are less than 0.1%, and all the
are lower than 1%. The outcomes on WSPs are even superior to those of IGA on TSPs in some aspects. In detailed, the averages of
,
, and
are 0.2%, 134.28, and 81.83, respectively. By comparison, they are 0.27%, 125.45, and 90.43 on TSPs, that indicating that the IGA is able to find better solutions on WSPs in a shorter time than on TSPs. Especially on d493, the average execution time
of IGA on WSPs is only 473.19, whereas it is 650.09 on TSPs.
According to the aforementioned analyses, the proposed IGA significantly outperforms GA and ACS in terms of convergence speed, solution quality, and stability. Additionally, on the WSP, which appeared more often in ALC_IGA, IGA also performed very well.
5.5. Parameters Tuning for ALC_IGA
The solution initialization phase of ALC_IGA shown in
Section 4.1 shows that the main parameter of ALC_IGA in only the first phase is
M, which limits the time required to solve TSP or WSP less than
. The results from the previous subsection show that, under ordinary situations, the IGA can handle TSPs with less than 100 nodes in 6 s and solve TSPs with less than 150 nodes in 20 s. Consequently, a decent
M should not go beyond 150 too much. In order to choose a favorable
M for ALC_IGA to balance the computation time and quality of solution, numerical comparison of
M was set to 50, 100, and 150 on 45 instances, which are considered in this subsection. These instances were medium-scale, with sizes ranging from
to
. Due to the fact that the distribution of nodes greatly affects the clustering effect, in order to fairly study the influence of
M on the results of ALC_IGA, a variety of instances coming from TSPLIB, TSP test data, and TNM data were studied in this experiment. In the following subsections of this paper, the termination condition of IGA is set to when there has been no improvement in the population for 30 iterations, and the other parameters are as same as in the last
Section 5.7. Denote the ALC_IGA with
as ALC_IGA50, ALC_IGA100, and ALC_IGA150, respectively; the major five evaluation criteria
,
,
,
,
and
of the results, which ran without parallelization, are presented in
Table 4.
From
Table 4, the
of the ALC_IGA50, ALC_IGA100, and ALC_IGA150 are
,
, and
, respectively. As can be seen, the ALC_IGA50 is the fastest, whereas the ALC_IGA150 algorithm usually produces the best results. When the size of instance is less than
, ALC_IGA50 has the minimum
and
on fl1400, and ALC_IGA10 has the lowest
on dca1389 and dkd1973. However, the
and
of ALC_IGA150 on the three instances are all less than 10%, and this is still a respectable result. When the instance size is larger than
, the ALC_IGA50 and ALC_IGA100 only perform better than the ALC_IGA150 on TNM instances. Concerning specifics, the ALC_IGA50 works well on Tnm2002 and Tnm4000, the ALC_IGA100 excels on Tnm6001, Tnm8002, and Tnm10000, but the ALC_IGA150 provided the best result on the large instance of Tnm20002. The results of ALC_IGA150 are therefore superior to those of ALC_IGA50 and ALC_IGA100 in TSPLIB and TSP test data, and it is still a suitable approach for TNM data. The average of
and
for the three algorithms shown at the bottom of
Table 4 also support this.
Furthermore, considering the algorithms’ running times, the mean of of ALC_IGA50 is 91.02, which is three-fifths of the time taken by ALC_IGA100 and two-fifths of ALC_IGA-150. This indicates that the fastest algorithm is ALC_IGA50, and the ratio of running time hardly changes with the size of the instance. However, even the slowest proposed ALC_IGA150 could handle the nodes instance with just approximately 10% deviation percentage in the same amount of running time as the IGA, which can only solve the instance with a size of roughly 400 nodes. The fastest ALC_IGA50, which is more than 60 times faster than the IGA, can deal with nodes in the same amount of time. Thus, the high efficiency of ALC_IGA has been verified.
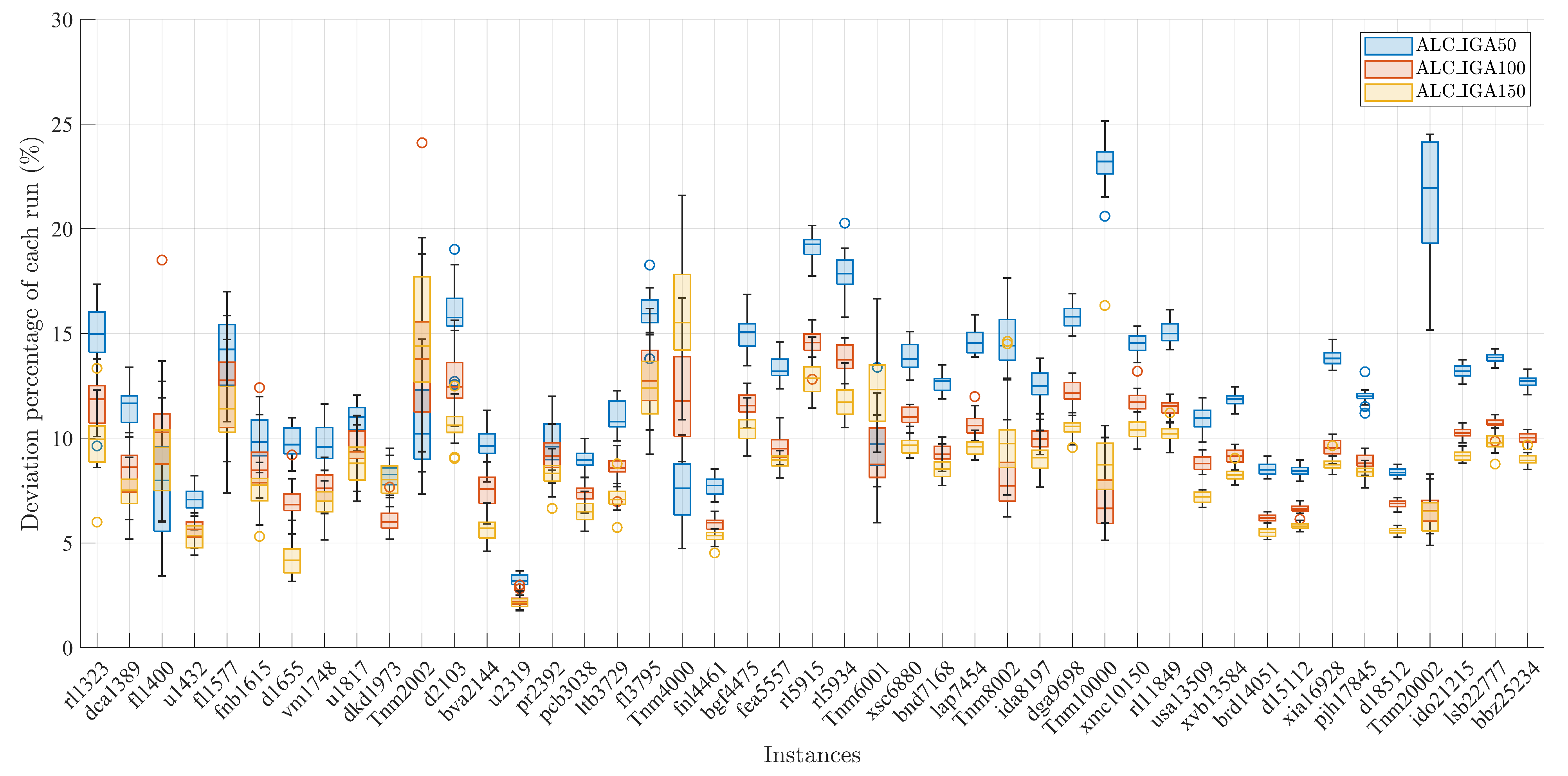
Figure 6 displays the deviation percentage of each run among all instances. It is noteworthy that for all three algorithms, most of the deviation percentages are under 20%. In particular, the deviation percentages of the ALC_IGA100 and ALC_IGA150 are less than 10% in the majority of instances. Furthermore, the figure also reveals that the ALC_IGA100 and ALC_IGA150 have many overlapping regions, indicating that the performance of the two algorithms is roughly equivalent.
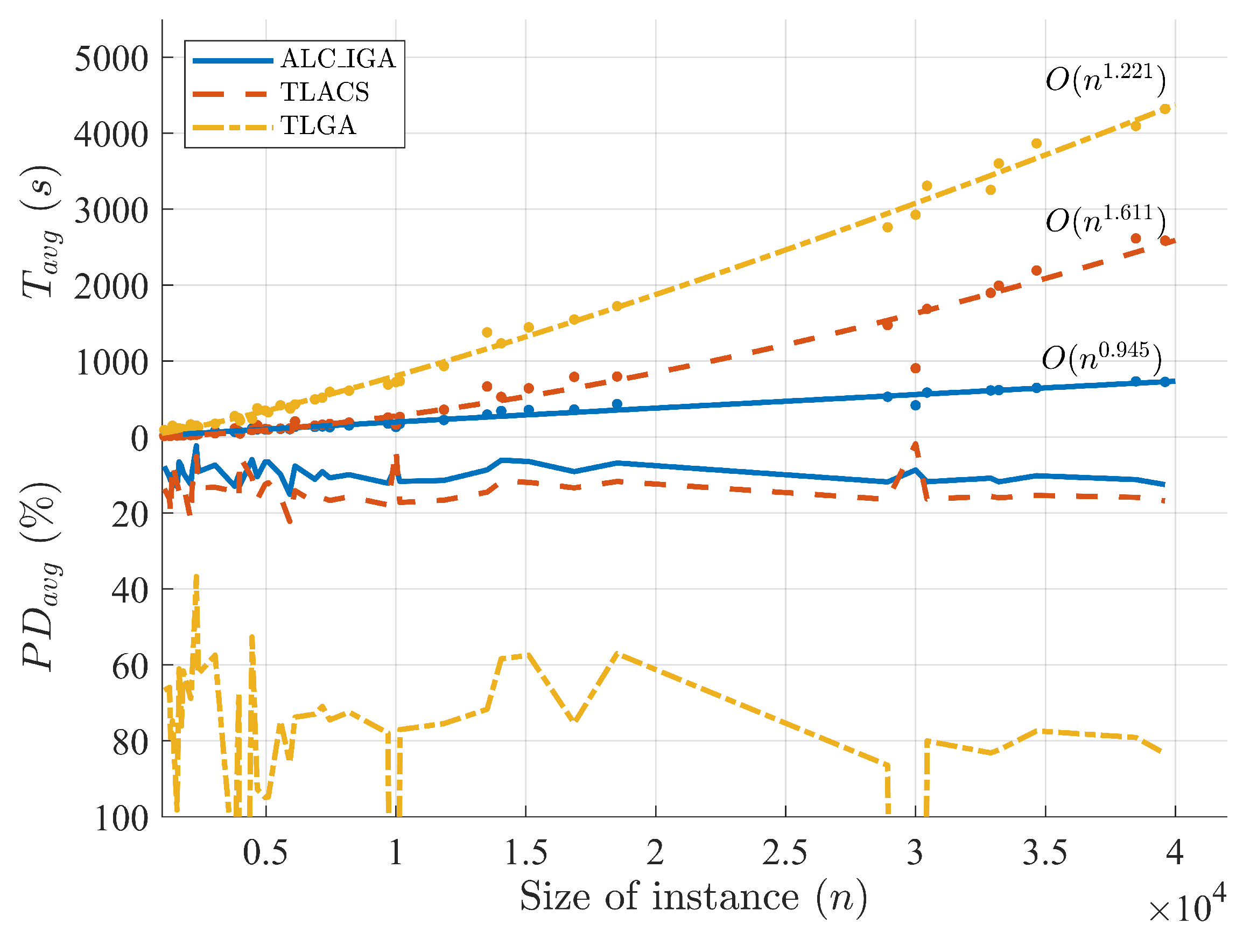
Additionally, the relationship between the running time of ALC_IGA and the value of
M is taken into account. The average execution time for the instances of the three algorithms is plotted in
Figure 7 in different colors. In order to discuss the computational complexity of the algorithms, the exponential curve fitting for each group was calculated. Because the computation time of ALC_IGA150 is larger than the other two, its slope shown in the figure is undoubtedly the steepest. The approximated time complexities of ALC_IGA50, ALC_IGA100, and ALC_IGA150 are
,
, and
, respectively, which are all extremely close to the linear computational complexity
. With 95% confidence bounds, the upper bound of the computational complexity for ALC_IGA50 is 1.0326, and the other two are 1.0963 and 1.151. The statistical outcomes of curve fitting are shown in
Table 5. It can be seen that all three fitting models have high confidence, especially the
of ALC_IGA50, which is over 0.99. The above results prove the computational complexity analysis of the proposed ALC_IGA in
Section 4.3.
To sum up, the quality of the solution obtained by ALC_IGA has a strong relationship with the data distribution and the value of M. On the other hand, the larger M is set, the longer the computation time required by ALC_IGA according to the numerical experiments. In most cases, setting M to 100 is a typical compromise choice to balance computation time and quality.
5.6. ALC_IGA Compared with Two-Layered Algorithms
The effectiveness of ALC_IGA on medium-scale problems was confirmed in
Section 5.5, although it is unclear whether it is superior to the other layered algorithms. To illustrate the performance of ALC_IGA, the proposed ALC_IGA was compared with two typical algorithms, which were TLGA [
51] and TLACS [
7]. The TLGA and TLACS were re-coded in Matlab, and to be fair, the running time and the solution quality were improved to be better than the literature. The main parameters were set as follows: the
M of ALC_IGA was set to 100; the numbers of cluster centers of TLACS and TLGA were automatically adjusted according to the size of the instance; the termination conditions of ALC_IGA, TLACS, and TLGA were that when there has been no improvement of the solution for 30, 30, and 100 iterations, respectively. All of the algorithms were implemented in single-thread. There were 45 medium-scale instances whose sizes ranging from
to
were investigated in this experiment.
As is shown in
Table 6, the evaluation criteria
of ALC_IGA are
, the
of TLACS are
, and
of TLGA are
. First of all, it is pointed out that TLGA has no advantage in all instances compared with the other two algorithms in terms of solution quality and convergence speed. The TLACS obtained the four best
and five best
among all 45 instances. In detail, TLACS outperforms ALC_IGA on fl1400 and fl1577, but ALC_IGA defeats TLACS on fl3795. The other three instances where TLACS performs better are all hard-to-solve instances [
69]. That is because the fewer clusters generated, the better solution produced, which is according to the results in
Section 5.5. The averages of
and
for ALC_IGA are 8.51 and 9.74, whereas for TLACS and TLGA, they are 12.89 and 14.10, and 88.84 and 102.43, respectively. The analyses above verify that the accuracy of ALC_IGA is superior to TLACS and TLGA in all scenarios except for TNM instances.
From
Table 6, the average values of
of ALC_IGA, TLACS and TLGA are 209.98, 489.48, and 1020.86 s. It can be seen that the proposed ALC_IGA is much faster than the other two algorithms. In detail, when the size of the instance is less than
, TLACS is faster than ALC_IGA in most cases. When the size of the instance is between
and
, the running times of ALC_IGA and TLACS are very close. When the size of the instance is larger than
, the proposed ALC_IGA has huge advantages, especially when the problem size is greater than
, as the computation time of ALC_IGA is less than one-third of TLACS and less than one-fifth of TLGA.
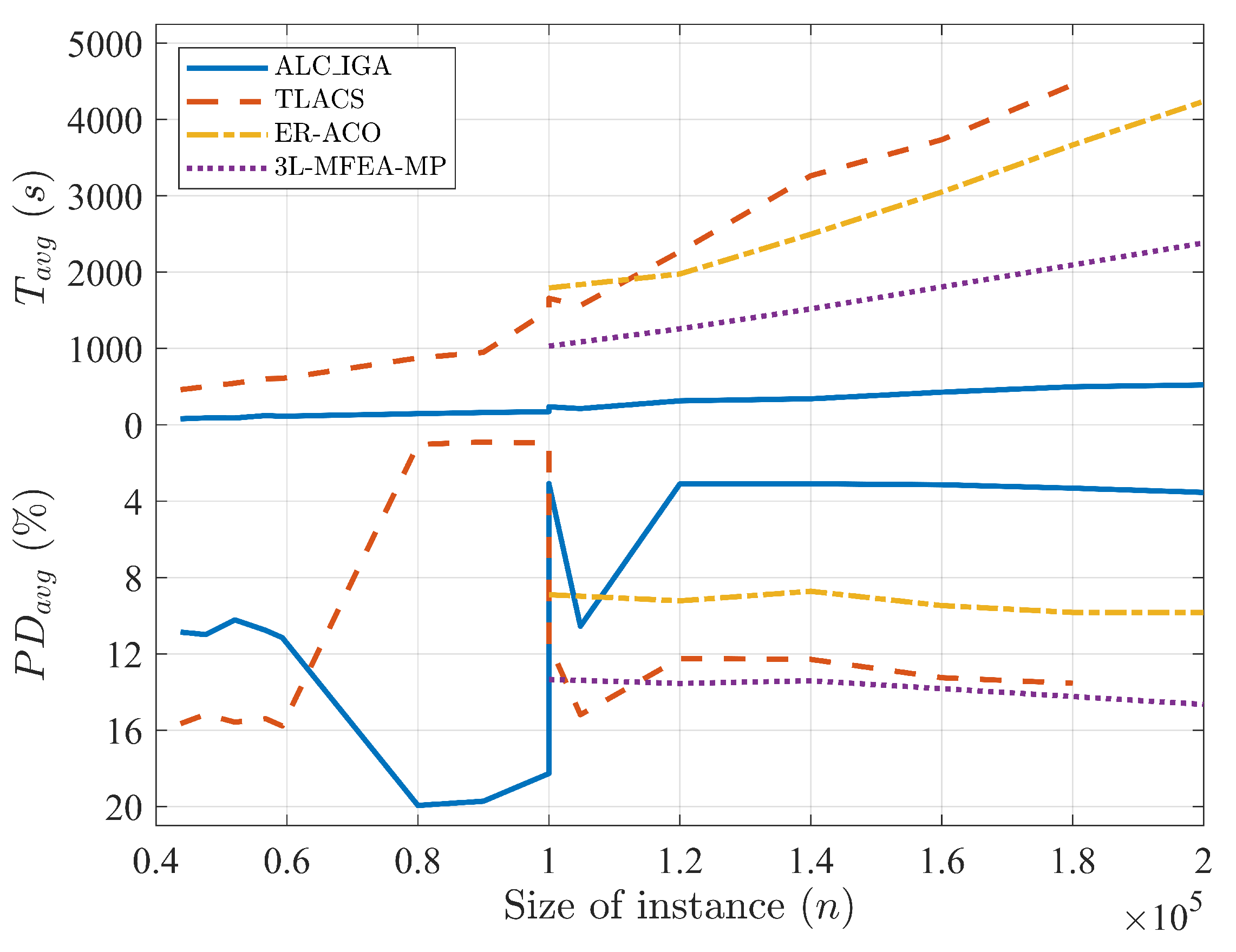
Figure 8 converts a large amount of data in
Table 6 into an explicit image. The real lines represent the
and
of ALC_IGA. It is closer to the horizontal axis, which means that the ALC_IGA has a high performance in accuracy and convergence speed. The results of the run times for ALC_IGA, TLACS, and TLGA with exponential curve fittings were
,
, and
. This reveals that the gap in computation time between ALC_IGA and the other two algorithms will increase as the size of the problem increases.
5.7. Results on Large-Scale TSP Instances
In this section, to investigate the performance of ALC_ IGA in large-scale instances, the new ALC_IGA is compared to the TLACS [
7], an accelerating genetic algorithm evolution via ant-based mutation and crossover (ER-ACO) [
32] and a 3L-MFEA-MP [
55]. The ALC_IGA and TLACS were implemented in Matlab R2022a and parallelized by the parallel computing toolbox in Matlab. The ER-ACO was set on an AMD Ryzen 2700 CPU with 16 threads in parallel. The parallel 3L-MFEA-MP was coded in Python, and it was implemented on a server with a 24-core Intel Xeon CPU and 96 GB RAM. The sizes of the 15 involved instances range from
to
.
The results and five evaluation criteria
,
,
,
, and
are shown in
Table 7. Compared to ALC_IGA with TLACS, the advantage of ALC_IGA in running time is apparent again. The running time of ALC_IGA is roughly one-sixth of TLACS when the problem size is around
, but when the size approaches
, the running time of it is just one-ninth of TLACS. The performance of ALC_IGA is better than TLACS in most conditions, but TLACS works pretty well on TNM instances.
There are four instances compared with 3L-MFEA-MP; results shown in
Table 7 reveal that the performance of it is very close to TLACS, and the difference between them in terms of
and
is about 2%, whereas, compared with ALC_IGA, the 3L-MFEA-MP is far worse than it in terms of convergence speed and solution quality. On the involved six instances, the
and
of the novel intelligence algorithm ER-ACO exceeded ALC_IGA by 2.5 times. Additionally, the proposed ALC_IGA runs significantly faster than ER-ACO.
Figure 9 shows the average computation times and deviation percentages of the four algorithms. It is clear that ALC_IGA performs well in most situations and is significantly faster than the others. According to the results illustrated in
Section 5.5, the only drawback of ALC_IGA is on TNM instances, which can be improved by setting
M larger.
Finally, the results of ALC_IGA under
M set to 50, 100, and 150 for five huge instances are also given. The ara238025, lra498378, and lrb744710 are three instances containing hundreds of thousands of nodes, which are the very large-scale integration instances of TSP test data. The Santa, which has 1437195 cities, as a benchmark instance for large-scale TSPs, has been investigated thoroughly by several well-known solvers in [
64]. Gaia was published by William Cook in 2019 and includes two million coordinates of stars.
Five evaluation criteria and the averages of them are presented in
Table 8. It shows again that the larger the
M set, the better the solution obtained and the longer computation time needed. For ALC_IGA50, ALC_IGA100, and ALC_IGA150, the averages of
are 13.944, 11.122, and 10.308, respectively, which are extremely close to the average of
. This illustrates the strong stability of ALC_IGA, which the average of
has also proven. While
M was set to 50 or 100, the
nodes instance can be handled within 1 h on our implement, and even the large three-dimensional Gaia can be fixed within 1.5 h.
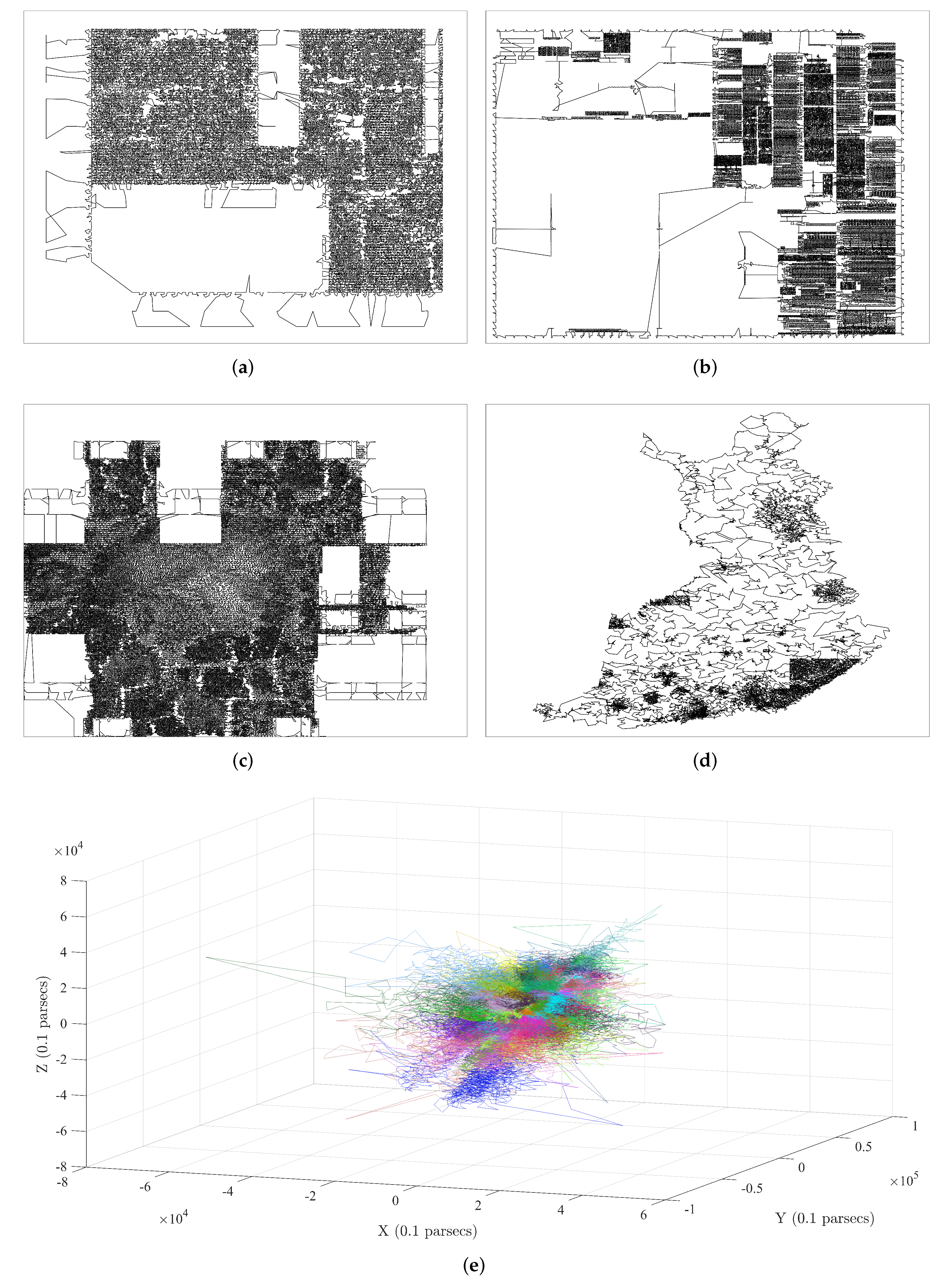
Figure 10 depicts the best solutions obtained by the ALC_IGA with
.
6. Conclusions and Discussion
Inspired by two-layered [
7,
51] and three-layered [
55] algorithms for TSPs, ALC_IGA with high parallelizability is proposed to solve large-scale TSPs with millions of nodes in this paper. In the first phase, ALC_IGA ensures that all sub-TSPs and sub-WSPs are smaller than the specified size through
k-means repeatedly applied, thereby reducing the computation time. In the second phase, the TS_2-opt is developed to rapidly improve the initial solution. The IGA is also proposed for small-scale TSPs and WSPs, with the following significant modifications: the polygynandry-inspired SBHX is designed for high convergence speed; the S_2-opt for balancing convergence speed and falling into local optimum is created. According to the study, the computational complexity of ALC_IGA is between
and
.
The numerical results on 42 instances show that the proposed IGA is better than both GA and ACS in terms of convergence speed and accuracy, and it performs better on WSP than on TSP. According to the numerical results on lots of instances from diverse sources, in most conditions, ALC_IGA outperforms TLGA, TLACS, and 3L-MFEA-MP and the novel ER-ACO in terms of precision, stability, and computation speed. The worst situation of ALC_IGA is on the hard-to-solve TSP instances, where the errors are still less than 20% and can be improved by adjusting the parameters.
Mariescu-Istodor and Fränti [
64] compared three types of algorithms for solving the large-scale Santa problem within 1 h on an enterprise server without parallelization. They achieved a high-quality solution (111,636 km) using their LKH and grid clustering implement (
https://cs.uef.fi/sipu/soft/tspDiv.zip, accessed on 20 March 2023), which outperforms the best result (121,831 km) obtained by ALC_IGA with parallelization. Moreover, it is worth noting that LKH without clustering achieved a 108,996 km solution, which is over 12% better than our result. As a result, we give the following suggestions for future research:
It is worth combining the adaptive layered clustering framework with LKH and some new techniques in [
64] and other references.
Investigate the impact of different clustering algorithms on the quality of solutions.
Explore better tuning algorithm to enhance solution quality.
Extending ALC_IGA to tackle large-scale ATSPs, CTSPs, DTSPs, and other related problems would also be meaningful.