Range Deception Jamming Performance Evaluation for Moving Targets in a Ground-Based Radar Network
Abstract
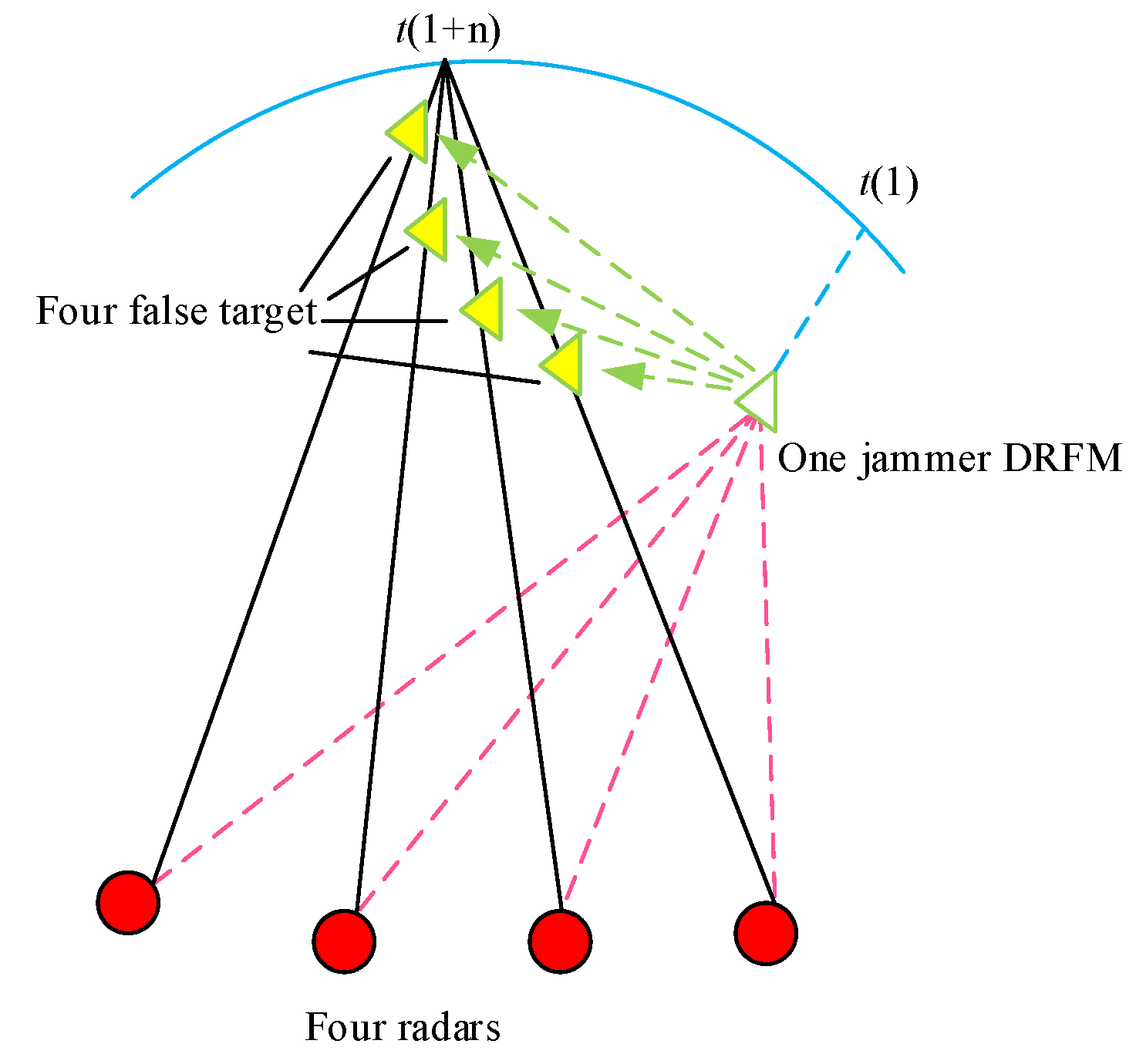
:1. Introduction
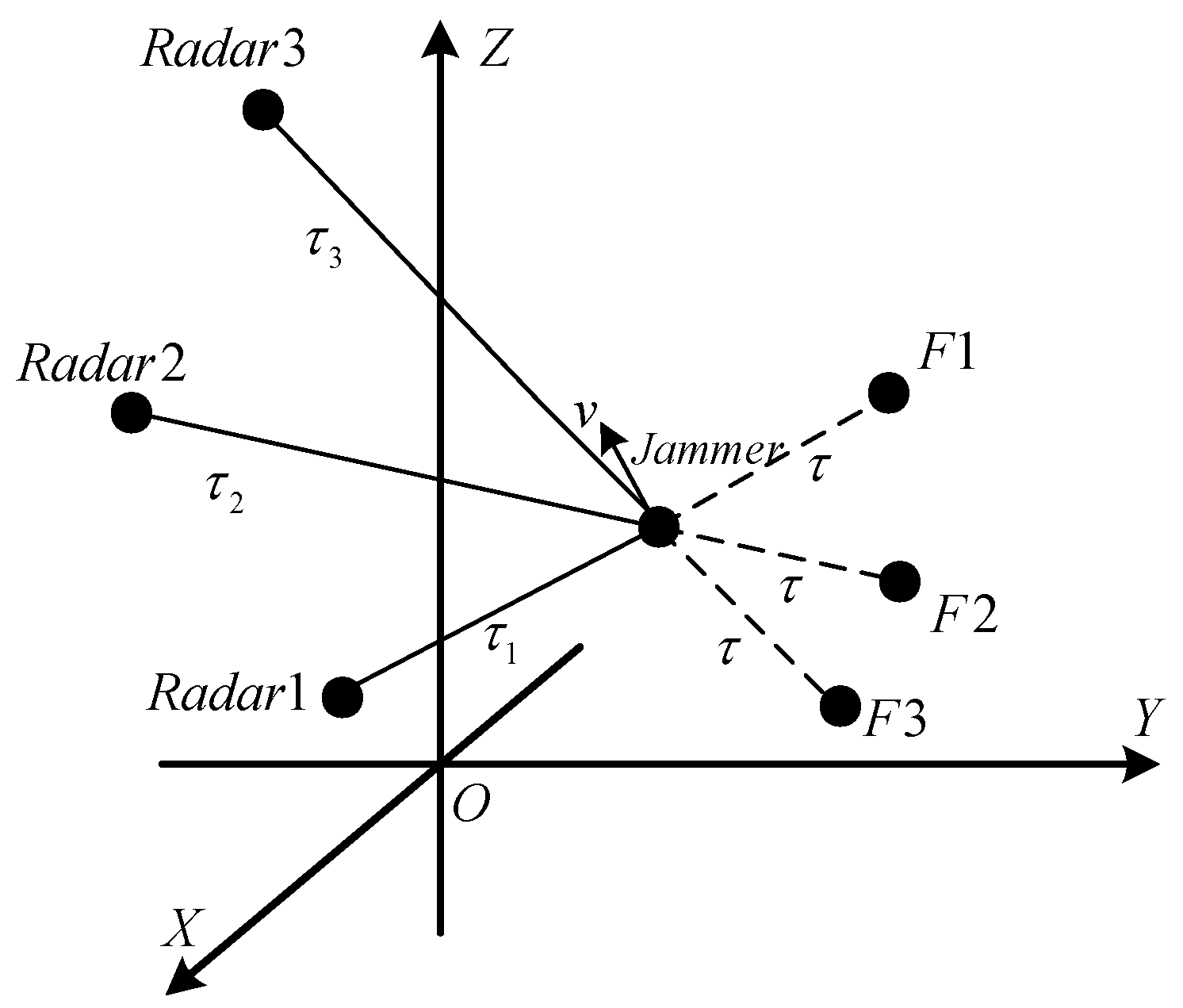
2. Signal Model
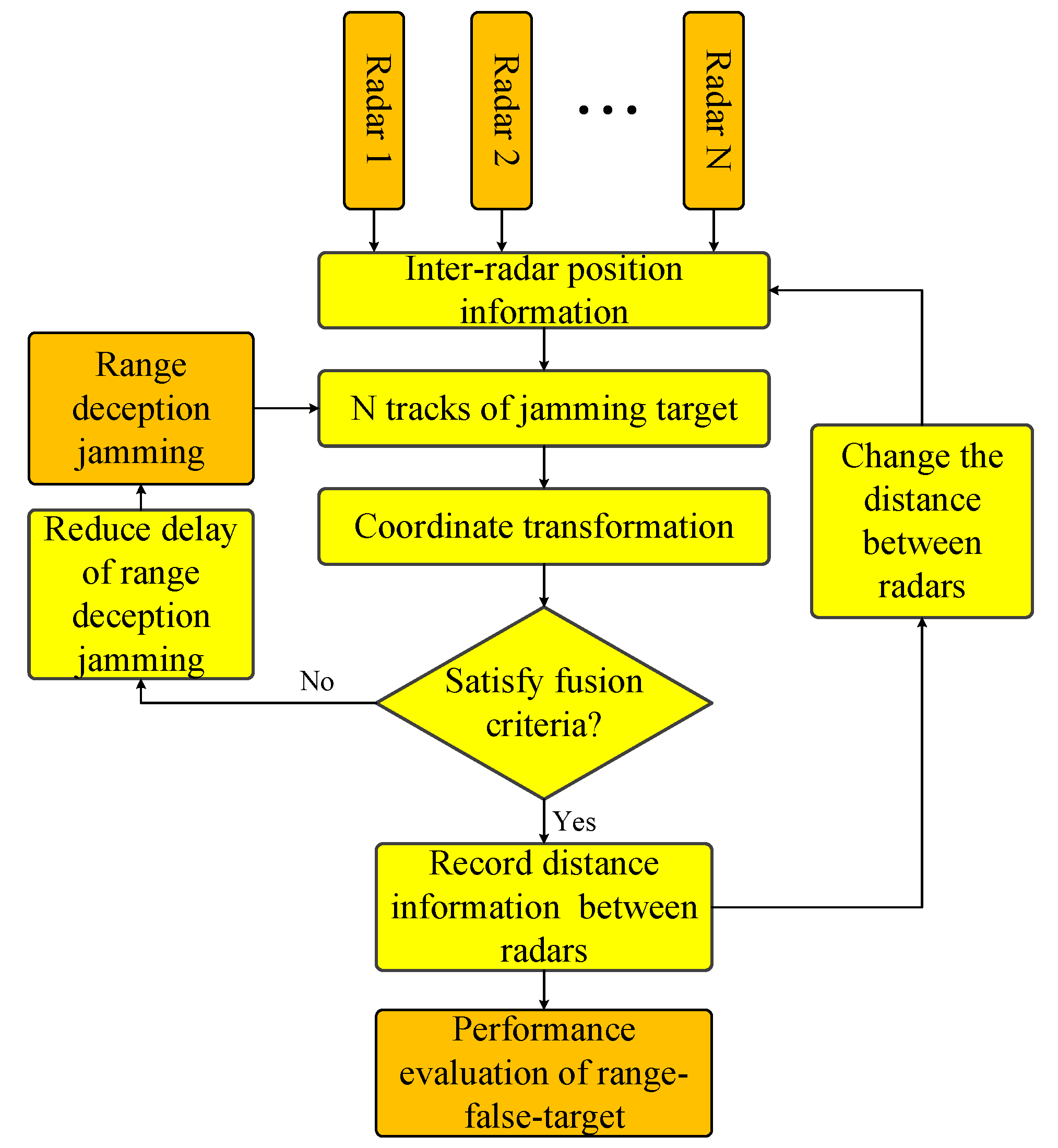
3. Range Deception Jamming Performance Evaluation Method for Ground-Based Radar Network
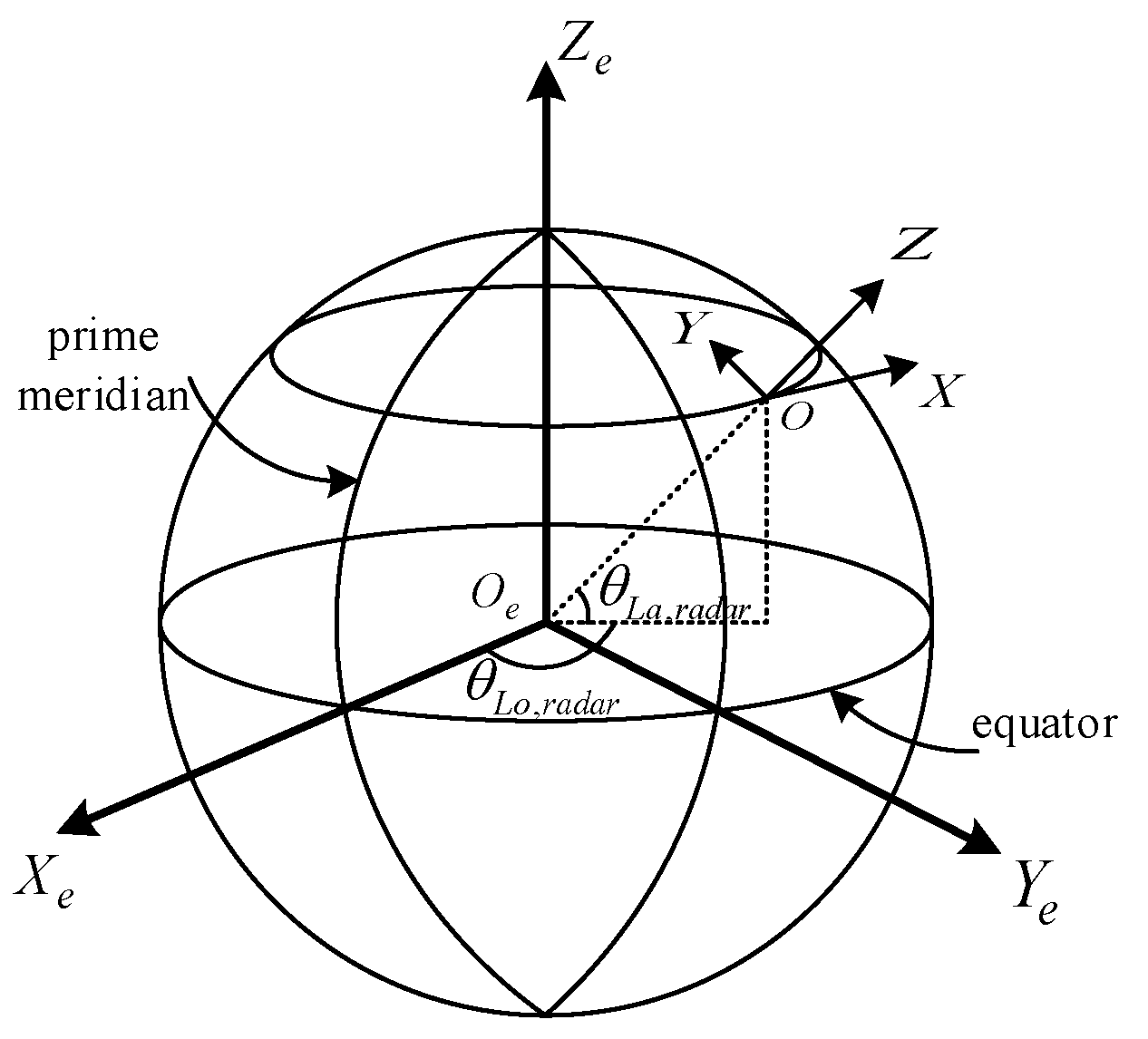
3.1. Radar Coordinate Transformation
3.2. Parameter Estimation
3.2.1. Range Estimation
3.2.2. Angle Estimation
3.3. Interpolation Operation
3.4. Track Fusion
4. Simulation Experiment Analysis
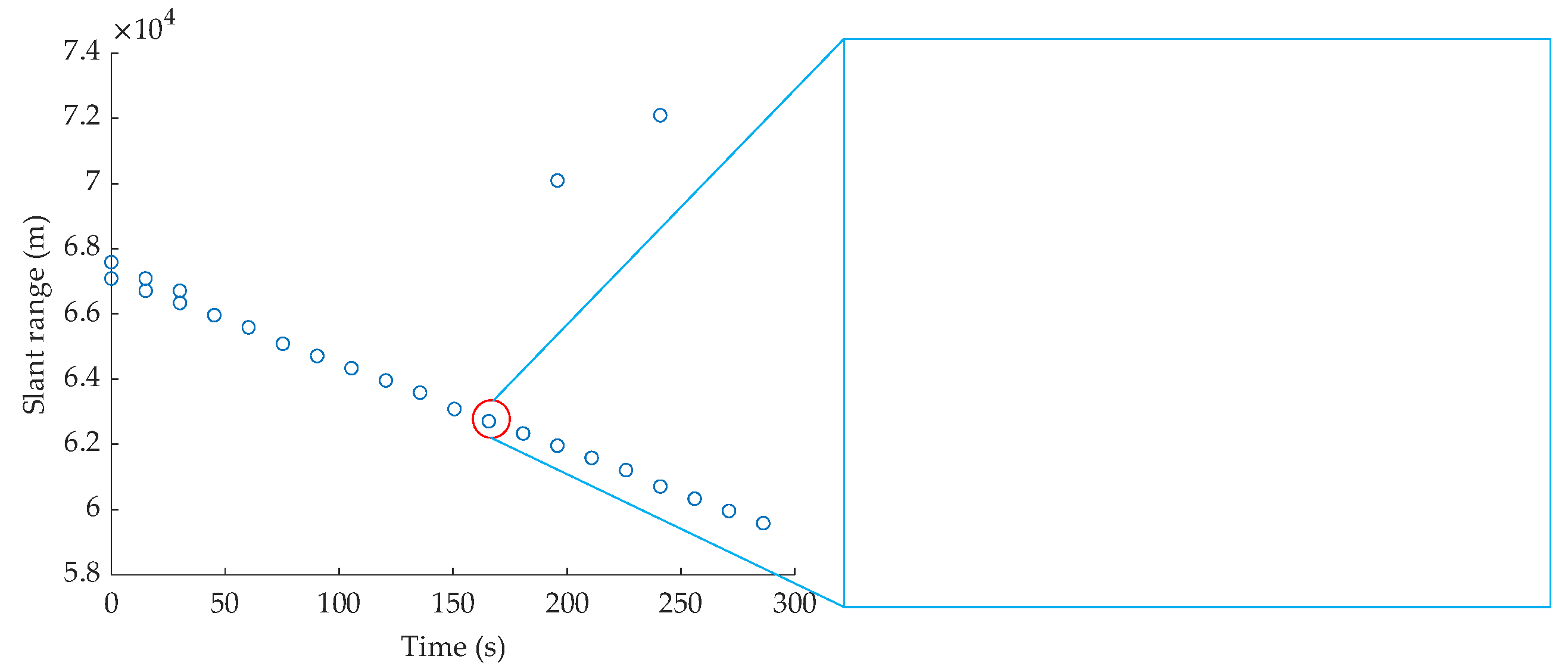
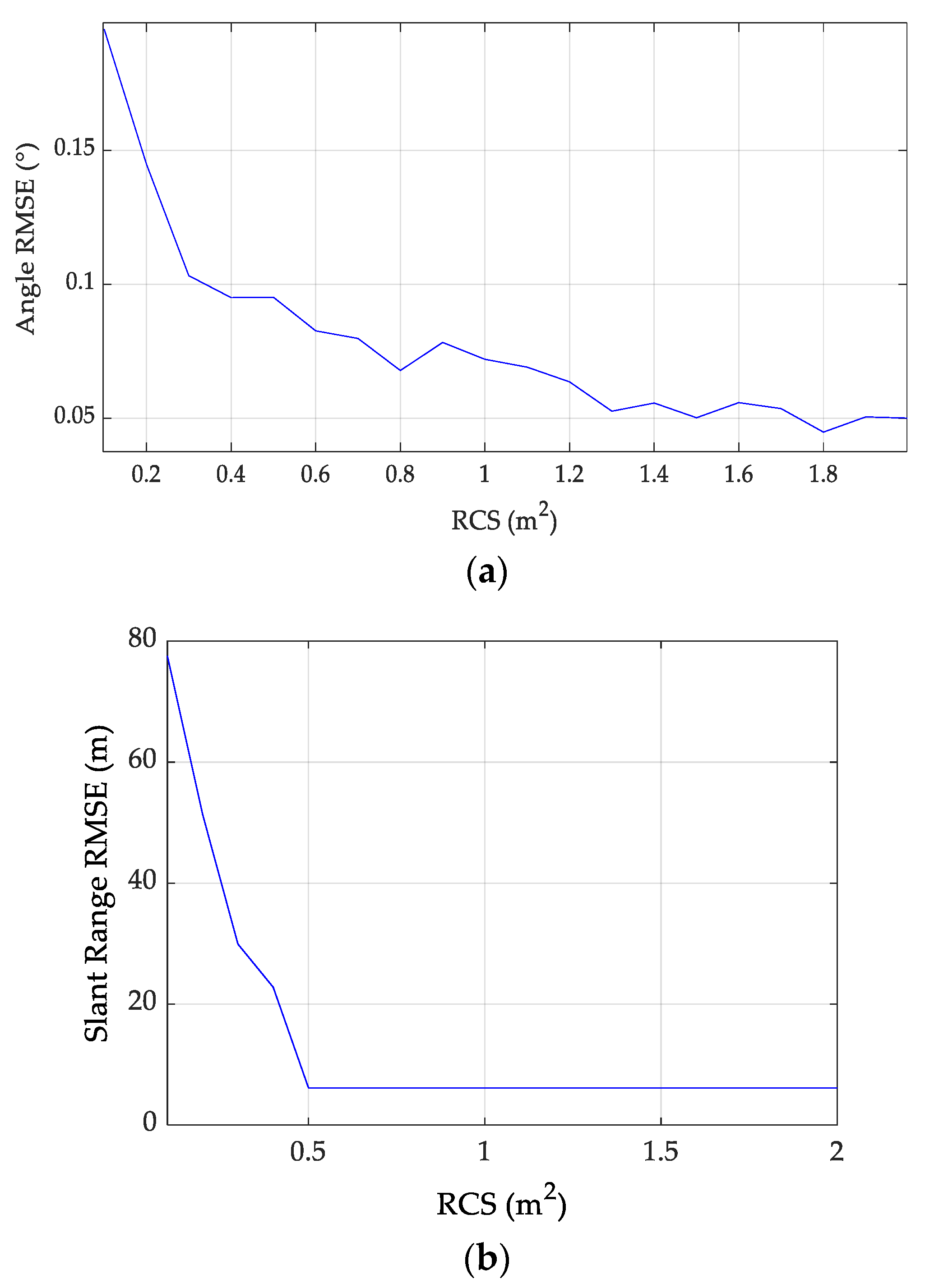
4.1. Simulation Analysis of Radar Slant Range and Angle Measurement Errors
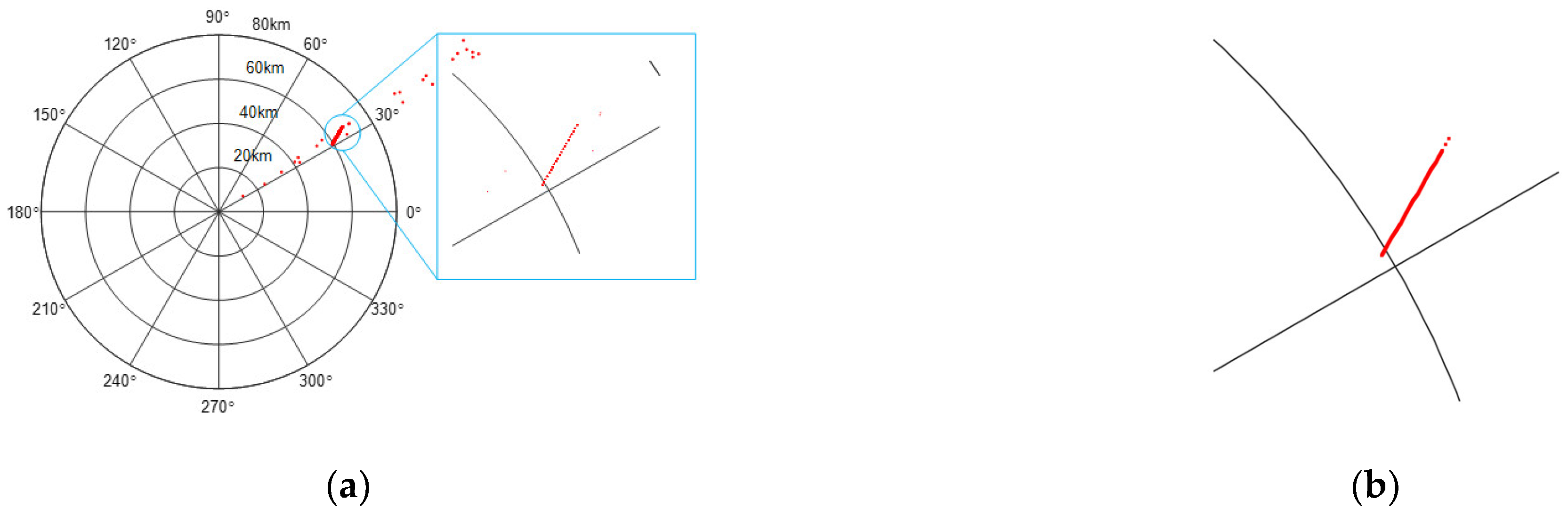
4.2. True Target Track Fusion Analysis
4.3. Jamming Range Delay Boundary Analysis
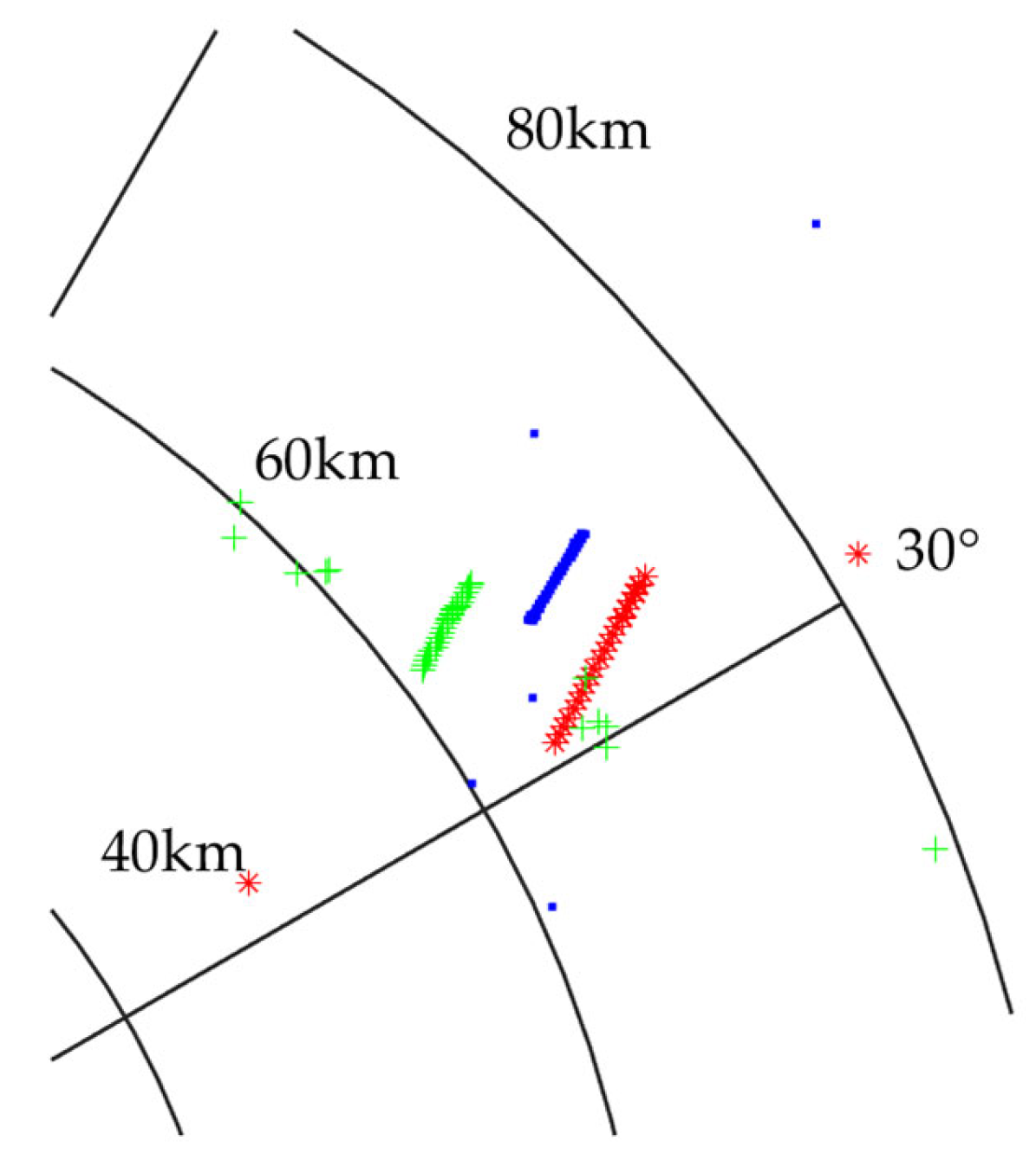
4.3.1. Two-Radar System
4.3.2. Three-Radar System
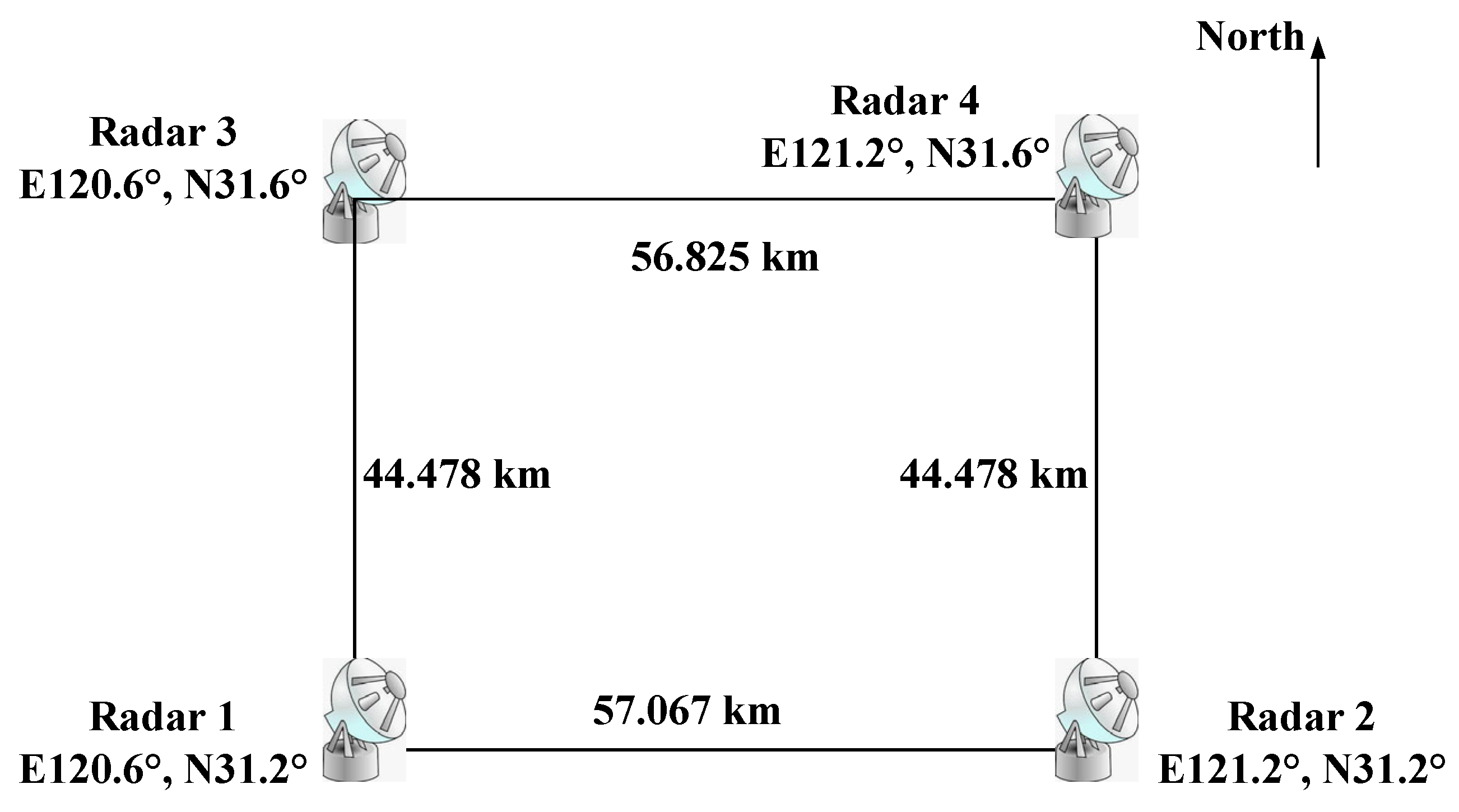
4.3.3. Four-Radar System
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Acronyms | Description |
| ECM | electronic countermeasure |
| ECCM | electronic counter-countermeasure |
| DRFM | digital radio frequency memory |
| RCS | radar cross-section |
| PRF | pulse repetition frequency |
| CFAR | constant false alarm rate |
| CA-CFAR | cell averaging constant false alarm rate |
| RMSE | root mean squared error |
| FFT | fast Fourier transform |
| IFFT | inverse fast Fourier transform |
References
- Zhu, X.-L. Design Efficiency Evaluation Index System of Radar Networking System. Shipboard Electron. Countermeas. 2019, 42, 48–51. [Google Scholar]
- Skolnik, M.I. Radar Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Tao, F.; Kojima, N. A new method for fabricating cell-embedded ECM capsules and ECM-loaded spheroids. In Proceedings of the 2015 International Symposium on Micro-NanoMechatronics and Human Science (MHS), Nagoya, Japan, 23–25 November 2015; pp. 1–3. [Google Scholar]
- Saha, P.K.; Shekhar, S.; Laxmi, V.; Thakura, P.R. Improved Speed Response of ECM Drive Using Antiwindup Concept. In Proceedings of the 2019 3rd International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019; pp. 286–289. [Google Scholar]
- Ji, Z.; Wang, G.; Zhang, X.; Sun, D. Technique of anti-multi-range-false-target jamming for radar network based on double discrimination. In Proceedings of the 2016 CIE International Conference on Radar, Guangzhou, China, 10–13 October 2016; pp. 1–5. [Google Scholar]
- Akhtar, J. Orthogonal block coded ECCM schemes against repeat radar jammers. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1218–1226. [Google Scholar] [CrossRef]
- Zhao, Z.C.; Wang, X.S.; Xiao, S.P. Cooperative deception jamming against radar network using a team of UAVs. In Proceedings of the 2009 IET International Radar Conference, Guilin, China, 20–22 April 2009; pp. 1–4. [Google Scholar]
- Huang, C.; Chen, Z.; Duan, R. Novel discrimination algorithm for deceptive jamming in polarimetric radar. Proc. Int. Conf. Inf. Technol. Softw. Eng. 2013, 210, 359–365. [Google Scholar]
- Yang, Y.; Da, K.; Zhu, Y.; Xiang, S.; Fu, Q. Consensus based target tracking against deception jamming in distributed radar networks. IET Radar Sonar Navig. 2023. ahead of print. [Google Scholar] [CrossRef]
- Liang, X.; Zhang, Q.; Luo, Y. The research of deceptive jamming of missile warhead based on micro-Doppler effect. J. Proj. Rocket. Missiles Guid. 2011, 31, 56–67. [Google Scholar]
- Zhao, S.; Liu, N.; Zhang, L.; Zhou, Y.; Li, Q. Discrimination of deception targets in multistatic radar based on clustering analysis. IEEE Sens. J. 2016, 16, 2500–2508. [Google Scholar] [CrossRef]
- Wang, Z.; Li, T.; Liu, J. Radar Jamming Effect Analysis Based on Bayesian Inference Network with Adaptive Clustering. IEEE Sens. J. 2021, 21, 15153–15160. [Google Scholar] [CrossRef]
- Lv, B.; Song, Y.; Zhou, C.-Y. Study of multistatic radar against velocity-deception jamming. In Proceedings of the 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11 September 2011; pp. 1044–1047. [Google Scholar]
- Zhang, S.; Zhou, Y.; Zhang, L.; Zhang, Q.; Du, L. Target Detection for Multistatic Radar in the Presence of Deception Jamming. IEEE Sens. J. 2021, 21, 8130–8141. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; Zhou, Y.; Liu, N. Signal fusion-based algorithms to discriminate between radar targets and deception jamming in distributed multiple-radar architectures. IEEE Sens. J. 2015, 15, 6697–6706. [Google Scholar] [CrossRef]
- Cui, Z.; Hou, Z.; Yang, H.; Liu, N.; Cao, Z. A CFAR Target-Detection Method Based on Superpixel Statistical Modeling. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1605–1609. [Google Scholar] [CrossRef]
- Kuang, C.; Wang, C.; Wen, B.; Hou, Y.; Lai, Y. An Improved CA-CFAR Method for Ship Target Detection in Strong Clutter Using UHF Radar. IEEE Signal Process. Lett. 2020, 27, 1445–1449. [Google Scholar] [CrossRef]
- Oraizi, H.; Fallahpour, M. Sum, Difference and Shaped Beam Pattern Synthesis by Non-Uniform Spacing and Phase Control. IEEE Trans. Antennas Propag. 2011, 59, 4505–4511. [Google Scholar] [CrossRef]
- Fan, X.; Liang, J.; Jing, Y.; So, H.C.; Geng, Q.; Zhao, X. Sum/Difference Pattern Synthesis with Dynamic Range Ratio Control for Arbitrary Arrays. IEEE Trans. Antennas Propag. 2022, 70, 1940–1953. [Google Scholar] [CrossRef]
- Han, X.; He, H.; Zhang, Q.; Yang, L.; He, Y.; Li, Z. Main-Lobe Jamming Suppression Method for Phased Array Netted Radar Based on MSNR-BSS. IEEE Sens. J. 2022, 22, 22972–22984. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Willett, P.K.; Tian, X. Tracking and Data Fusion: A Handbook of Algorithms; YBS Publishing: Storrs, CT, USA, 2011. [Google Scholar]
- Nouri, M.; Mivehchy, M.; Sabahi, M.F. Novel anti-deception jamming method by measuring phase noise of oscillators in LFMCW tracking radar sensor networks. IEEE Access 2017, 5, 11455–11467. [Google Scholar] [CrossRef]
- Chen, H.; Kirubarajan, T. Performance limits of track-to-track fusion versus centralized estimation: Theory and application. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 386–400. [Google Scholar] [CrossRef]
- Gao, X.; Chen, J.; Tao, D.; Li, X. Multi-sensor centralized fusion without measurement noise covariance by variational Bayesian approximation. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 272–718. [Google Scholar] [CrossRef]
- Feng, X.; Zhao, Y.-N.; Zhao, Z.-F.; Zhou, Z.-Q. Cognitive tracking waveform design based on multiple model interaction and measurement information fusion. IEEE Access 2018, 6, 30680–30690. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, G.; Guan, C.; Tan, S. A Biased Track Association Algorithm Based Modified Global Nearest Neighbor Algorithm. J. Proj. Rocket. Missiles Guid. 2012, 32, 167–170. [Google Scholar]
- You, H. Radar Data Processing and Application, 1st ed.; Publishing House of Electronics Industry Press: Beijing, China, 2009. [Google Scholar]
- Zhao, Y.-L.; Wang, X.-S.; Wang, G.-Y.; Liu, Y.-H.; Luo, J. Tracking Technique for Radar Network in the Presence of Multi-Range-False-Target Deception Jamming. Acta Electron. Sin. 2007, 35, 454–457. [Google Scholar]
- Rao, B.; Gu, Z.; Nie, Y. Deception Approach to Track-to-Track Radar Fusion Using Noncoherent Dual-Source Jamming. IEEE Access 2020, 8, 50843–50858. [Google Scholar] [CrossRef]
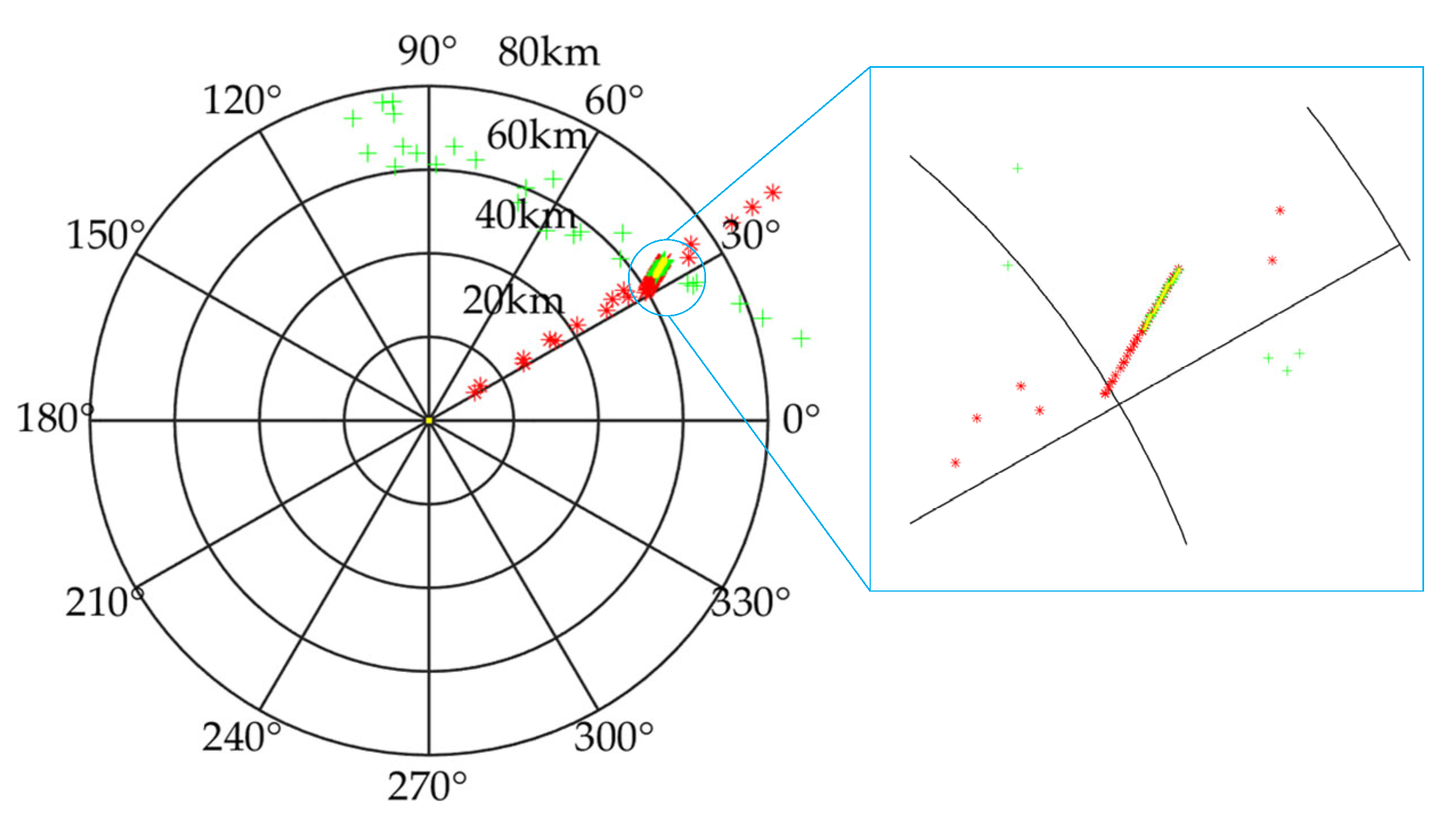
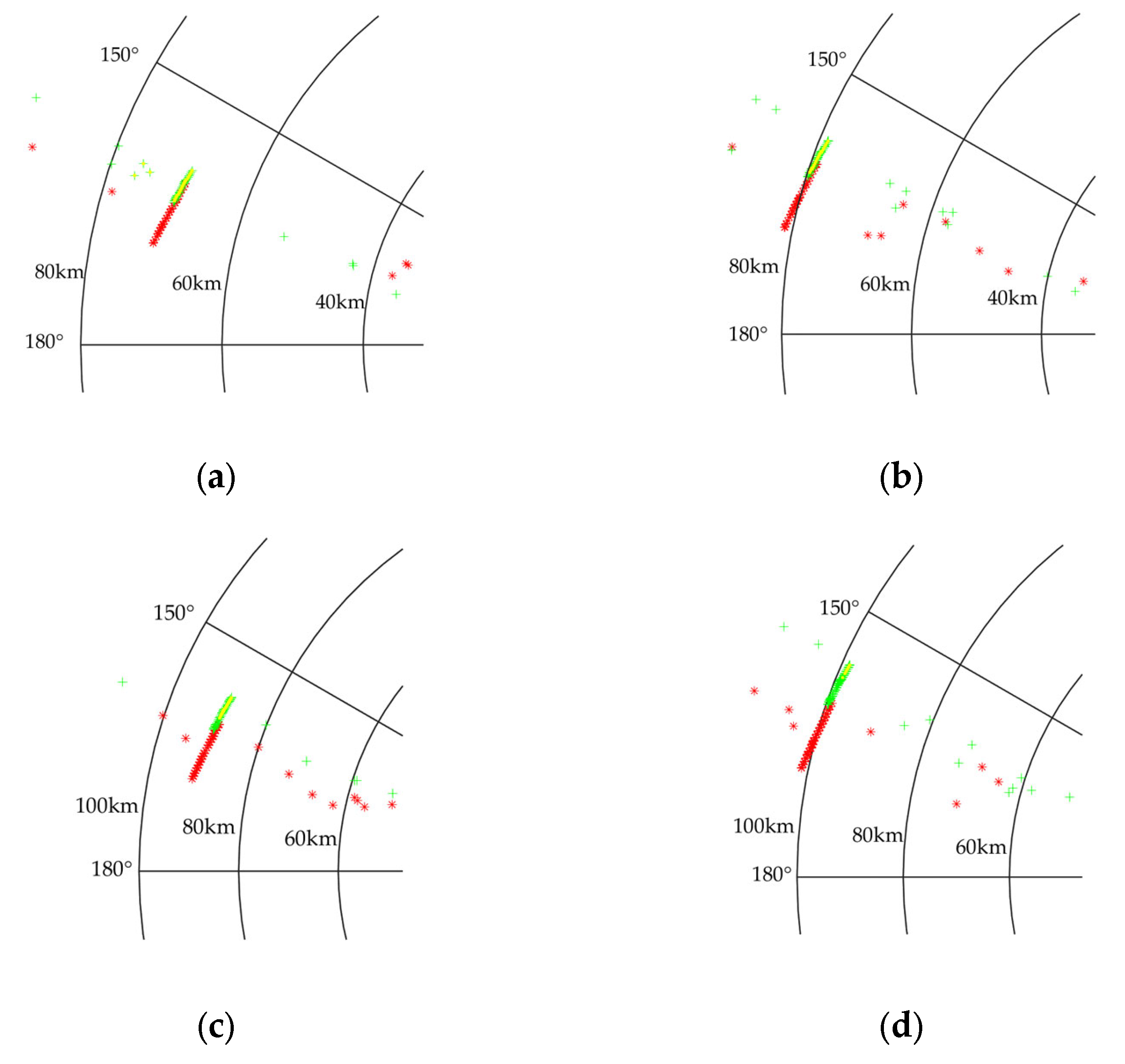
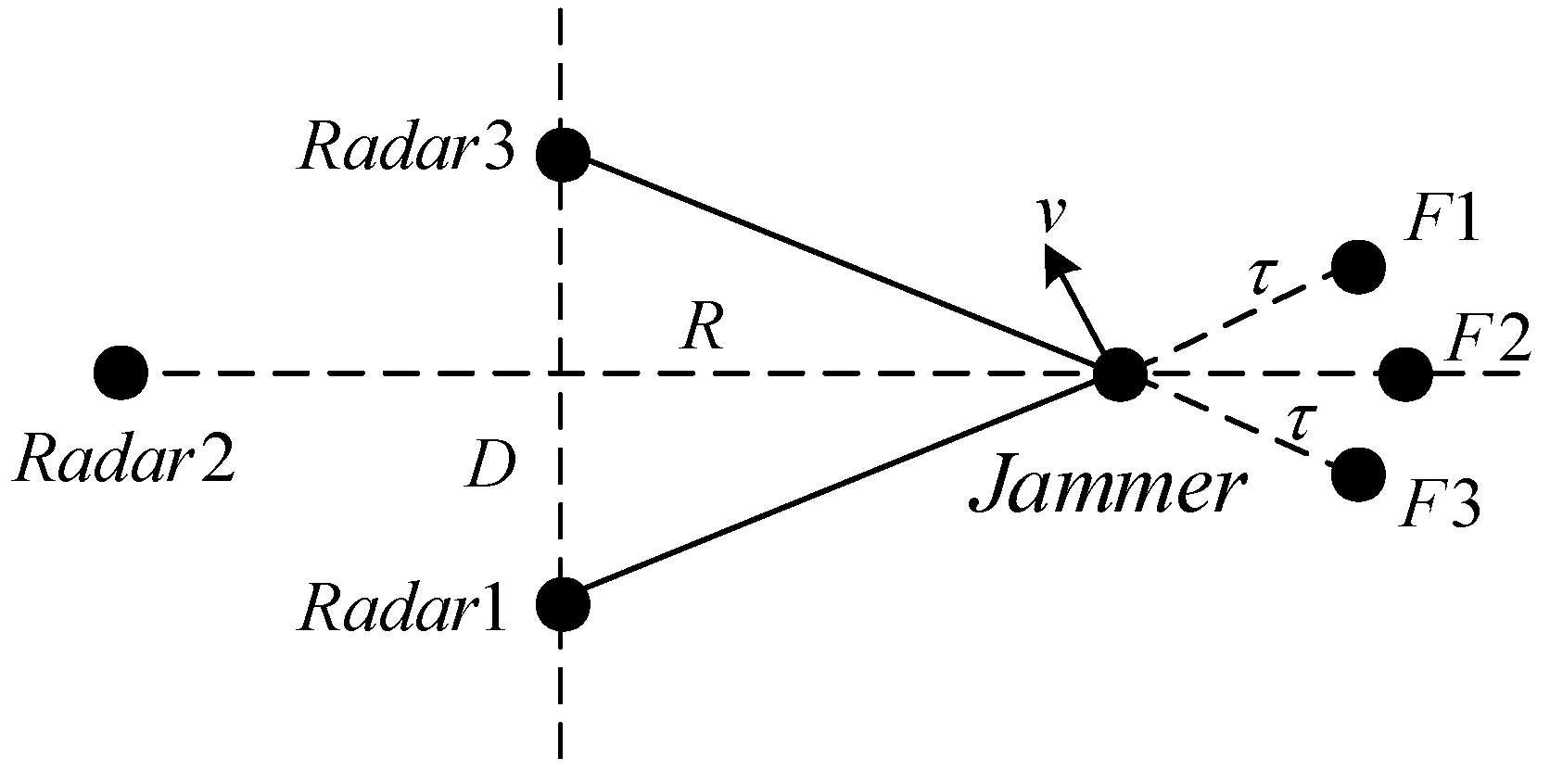
| Position | Carrier Frequency | RCS (m2) | Rotating Velocity (r/min) | Antenna Azimuth Size (m) | |
|---|---|---|---|---|---|
| Radar 1 | E120.8, N30.7 | 800 MHz | 1.818 | 8 | 7.3 |
| Radar 2 | E120.5, N31.1 | 1.3 GHz | 0.978 | 6 | 6.3 |
| Radar 3 | E120.6, N31.5 | 3 GHz | 0.925 | 4 | 4.3 |
| Parameters | Value |
|---|---|
| Radar peak power | 150 kW |
| Transmit signal bandwidth | 1 MHz |
| PRF | 500 Hz |
| Duty ratio | 0.07 |
| Antenna range size | 4.3 m |
| System loss | 7 dB |
| Noise factor | 3 dB |
| Carrier Frequency | RCS (m2) | Antenna Azimuth Size (m) | RMSE of Slant Range (m) | RMSE of Angle (°) | |
|---|---|---|---|---|---|
| Radar 1 | 800 MHz | 1.818 | 7.3 | 3.8 | 0.045 |
| Radar 2 | 1.3 GHz | 0.978 | 6.3 | 3.8 | 0.08 |
| Radar 3 | 3 GHz | 0.925 | 4.3 | 3.8 | 0.10 |
| Distance of Fixed Radar from Target (km) | Two-Radar Distance (km) | Jamming Range Delay (km) | Fusion Rate | Successful Fusion |
|---|---|---|---|---|
| 38.2 | 1.1 | 20 | 83.5% | √ |
| 40 | 93.5% | √ | ||
| 60 | 82.9% | √ | ||
| 80 | 80.1% | √ | ||
| 8.9 | 20 | 87.9% | √ | |
| 40 | 83.1% | √ | ||
| 60 | 77.3% | × | ||
| 80 | 70.3% | × | ||
| 11 | 20 | 87.2% | √ | |
| 30 | 90.2% | √ | ||
| 35 | 76.6% | × | ||
| 40 | 76.6% | × | ||
| 16.7 | 10 | 87.3% | √ | |
| 20 | 77.5% | × | ||
| 30 | 66.8% | × | ||
| 40 | 57.9% | × | ||
| 22 | 10 | 82.6% | √ | |
| 20 | 72.3% | × | ||
| 30 | 60.0% | × | ||
| 40 | 25.4% | × | ||
| 45.4 | 5 | 80.7% | √ | |
| 10 | 50.0% | × | ||
| 15 | 18.0% | × | ||
| 89 | 0.2 | 88.9% | √ | |
| 0.3 | 89.2% | √ | ||
| 0.4 | 76.9% | × | ||
| 0.5 | 63.4% | × | ||
| 72.8 | 11 | 20 | 85.6% | √ |
| 40 | 85.1% | √ | ||
| 60 | 89.3% | √ | ||
| 22 | 10 | 84.9% | √ | |
| 15 | 62.3% | × | ||
| 20 | 41.9% | × | ||
| 30 | 0 | × | ||
| 33 | 5 | 81.8% | √ | |
| 10 | 78.9% | × | ||
| 15 | 50.3% | × | ||
| 20 | 19.6% | × | ||
| 53.6 | 3 | 84.2% | √ | |
| 5 | 79.3% | × | ||
| 10 | 62.5% | × | ||
| 15 | 0 | × |
| Frequency Band | Carrier Frequency | Wavelength (m) | RCS (m2) | Rotating Velocity (r/min) | Azimuth Size (m) | |
|---|---|---|---|---|---|---|
| Radar 1 | 1 MHz | 800 MHz | 0.3750 | 1.8185 | 8 | 7.3 |
| Radar 2 | 1 MHz | 800 MHz | 0.3750 | 1.8185 | 8 | 7.3 |
| Radar 3 | 1 MHz | 3 GHz | 0.1000 | 0.925 | 4 | 4.3 |
| The Distance of R (km) | Distance between Radar 1 and Radar 3 | Distance between Radar 2 and Radar 3 | Jamming Range Delay | Fusion Rate of Tracks Detected by Radar 1 and Radar 3 | Fusion Rate of Tracks Detected by Radar 2 and Radar 3 | Final Fusion Rate |
|---|---|---|---|---|---|---|
| 67.7 km | 33.4 km | 33.2 km | 1 km | 97.1% | 98.5% | 96.6% |
| 3 km | 73.8% | 86.7% | 61.8% | |||
| 5 km | 11.3% | 84.1% | 11.6% | |||
| 10 km | 0 | 78.8% | 0 | |||
| 86.6 km | 33.4 km | 33.2 km | 1 km | 100% | 100% | 100% |
| 3 km | 97.5% | 100% | 97.3% | |||
| 5 km | 92.6% | 95.2% | 90.8% | |||
| 10 km | 84.6% | 92% | 81.2% | |||
| 15 km | 35.4% | 87.8% | 24.6% |
| Radar Position (°) | Frequency Band | Carrier Frequency | Wavelength (m) | RCS (m2) | Rotating Velocity (r/min) | Azimuth Size (m) | |
|---|---|---|---|---|---|---|---|
| Radar 1 | E120.6, N31.2 | 1 MHz | 800 MHz | 0.3750 | 1.8185 | 8 | 7.3 |
| Radar 2 | E121.2, N31.2 | 1 MHz | 800 MHz | 0.6818 | 1.8185 | 8 | 7.3 |
| Radar 3 | E120.6, N31.6 | 1 MHz | 3 GHz | 0.1000 | 0.925 | 4 | 4.3 |
| Radar 4 | E121.2, N31.6 | 1 MHz | 3 GHz | 0.1000 | 0.925 | 4 | 4.3 |
| Distance between Radar 1 and Radar 3 | Distance between Radar 2 and Radar 3 | Distance between Radar 4 and Radar 3 | Jamming Range Delay | Fusion Rate of Tracks Detected by Radar 1 and Radar 3 | Fusion Rate of Tracks Detected by Radar 2 and Radar 3 | Fusion Rate of Tracks Detected by Radar 4 and Radar 3 | Final Fusion Rate |
|---|---|---|---|---|---|---|---|
| 44.5 km | 72.3 km | 56.8 km | 1 km | 95% | 100% | 100% | 92.5% |
| 2 km | 91.4% | 97.4% | 100% | 88.4% | |||
| 3 km | 90.5% | 89.3% | 96.1% | 46.7% | |||
| 5 km | 79.8% | 0 | 80.3 | 0 | |||
| 10 km | 47.1% | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ling, Q.; Huang, P.; Wang, D.; Xu, H.; Wang, L.; Liu, X.; Liao, G.; Sun, Y. Range Deception Jamming Performance Evaluation for Moving Targets in a Ground-Based Radar Network. Electronics 2023, 12, 1614. https://doi.org/10.3390/electronics12071614
Ling Q, Huang P, Wang D, Xu H, Wang L, Liu X, Liao G, Sun Y. Range Deception Jamming Performance Evaluation for Moving Targets in a Ground-Based Radar Network. Electronics. 2023; 12(7):1614. https://doi.org/10.3390/electronics12071614
Chicago/Turabian StyleLing, Qing, Penghui Huang, Donghong Wang, Huajian Xu, Lingyu Wang, Xingzhao Liu, Guisheng Liao, and Yongyan Sun. 2023. "Range Deception Jamming Performance Evaluation for Moving Targets in a Ground-Based Radar Network" Electronics 12, no. 7: 1614. https://doi.org/10.3390/electronics12071614
APA StyleLing, Q., Huang, P., Wang, D., Xu, H., Wang, L., Liu, X., Liao, G., & Sun, Y. (2023). Range Deception Jamming Performance Evaluation for Moving Targets in a Ground-Based Radar Network. Electronics, 12(7), 1614. https://doi.org/10.3390/electronics12071614







