Hybrid Precoding Applied to Multi-Beam Transmitting Reconfigurable Intelligent Surfaces (T-RIS)
Abstract
1. Introduction and Motivations
- (i)
- We derive an analytical propagation model that includes a T-RIS propagation channel and constraints on the resolution of the phase shifters. The obtained model is general and can be easily adapted to most use cases by setting the array geometry, the illumination law, and the pertinent radiation patterns for the focal sources and unit cells.
- (ii)
- (iii)
- We propose and compare two methods to optimize the T-RIS: (i) maximization of the per-user gain (RF-only approach), and (ii) maximization of the per-user rate (hybrid approach). To this end, we fix the array geometry and the set of unit cells (1-bit design) and then we determine the optimal focal distance, i.e., the distance between the lens and the focal sources, with respect to the two aforementioned metrics.
- (iv)
- We provide an evaluation of the two metrics for four served users with imperfect channel knowledge, with an emphasis on the impact of the beam codebook size.
2. System Model
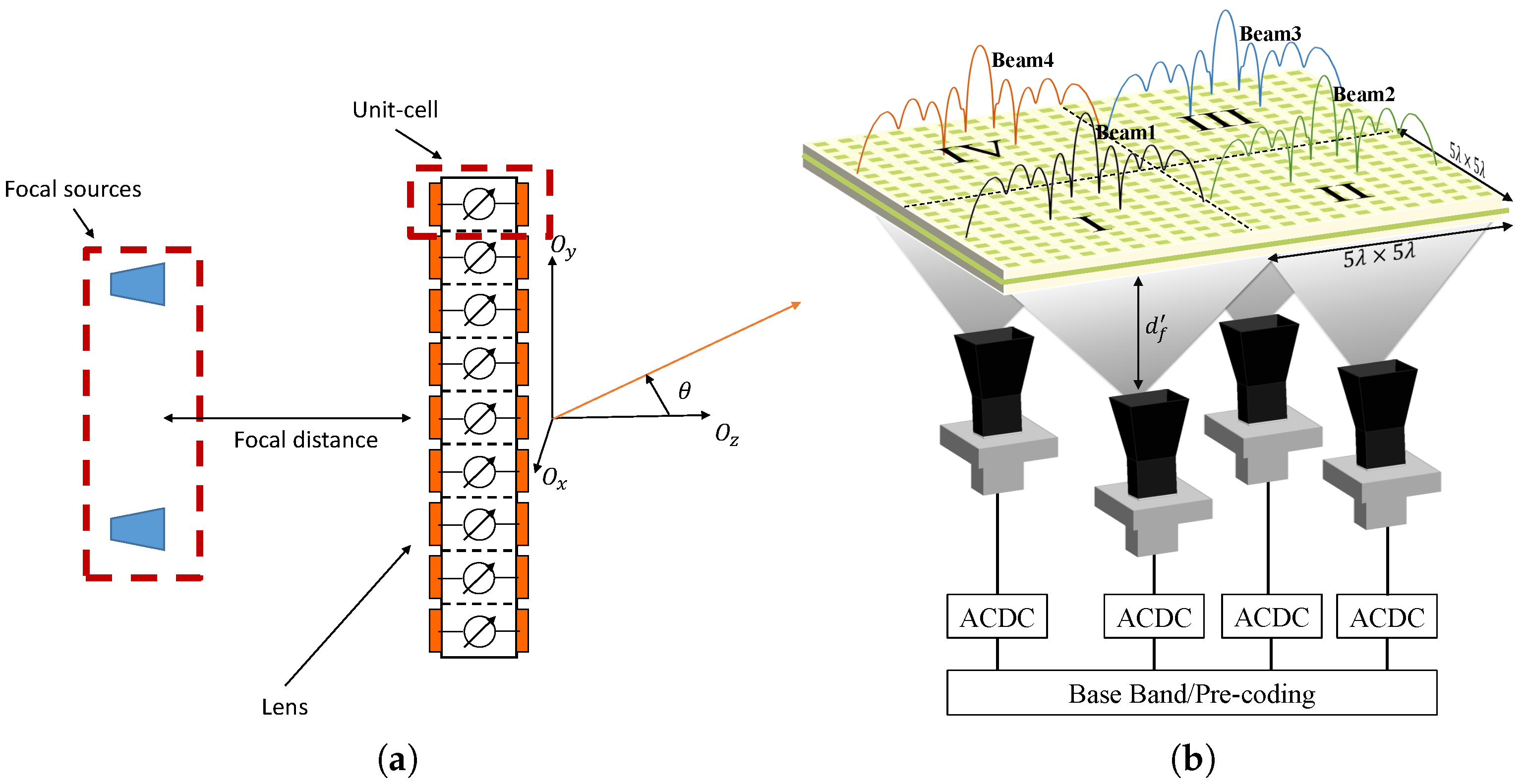
2.1. Coordinate System
2.2. Analytical Model: T-RIS
2.3. Analytical Model: Over-the-Air Propagation Channel
2.4. Baseband System Model
3. Problem Formulation and Precoder Design
3.1. Problem Formulation
3.2. RF Precoder
3.3. Equivalent Channel and Digital Precoder
3.4. Optimization of T-RIS Structure
- Gain optimization:The T-RIS structure is determined by maximizing the antenna array gain, as defined in (19). By doing so, is the only function of the RF precoder.The optimization problem can thus be expressed as follows:
- Capacity optimization:Another proposed method is to directly optimize the T-RIS structure to maximize the per-user capacity (8). Contrary to the optimization of the gain, the IUI is taken into account here and, therefore, so is the impact of the ZF precoder. The optimization problem can be stated as follows :
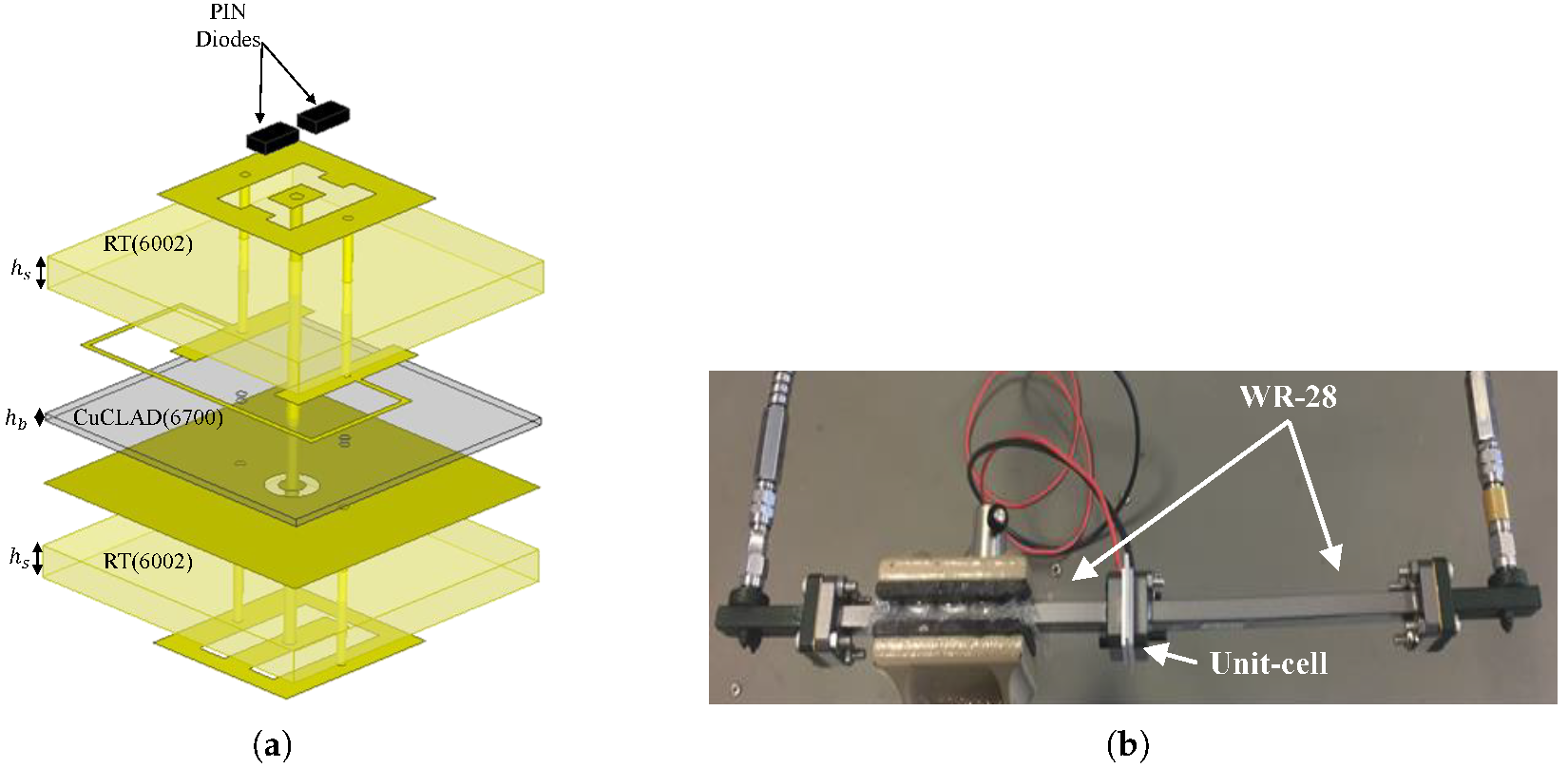
4. Unit-Cell Design and Characterization
4.1. Unit-Cell Design and Frequency Behavior
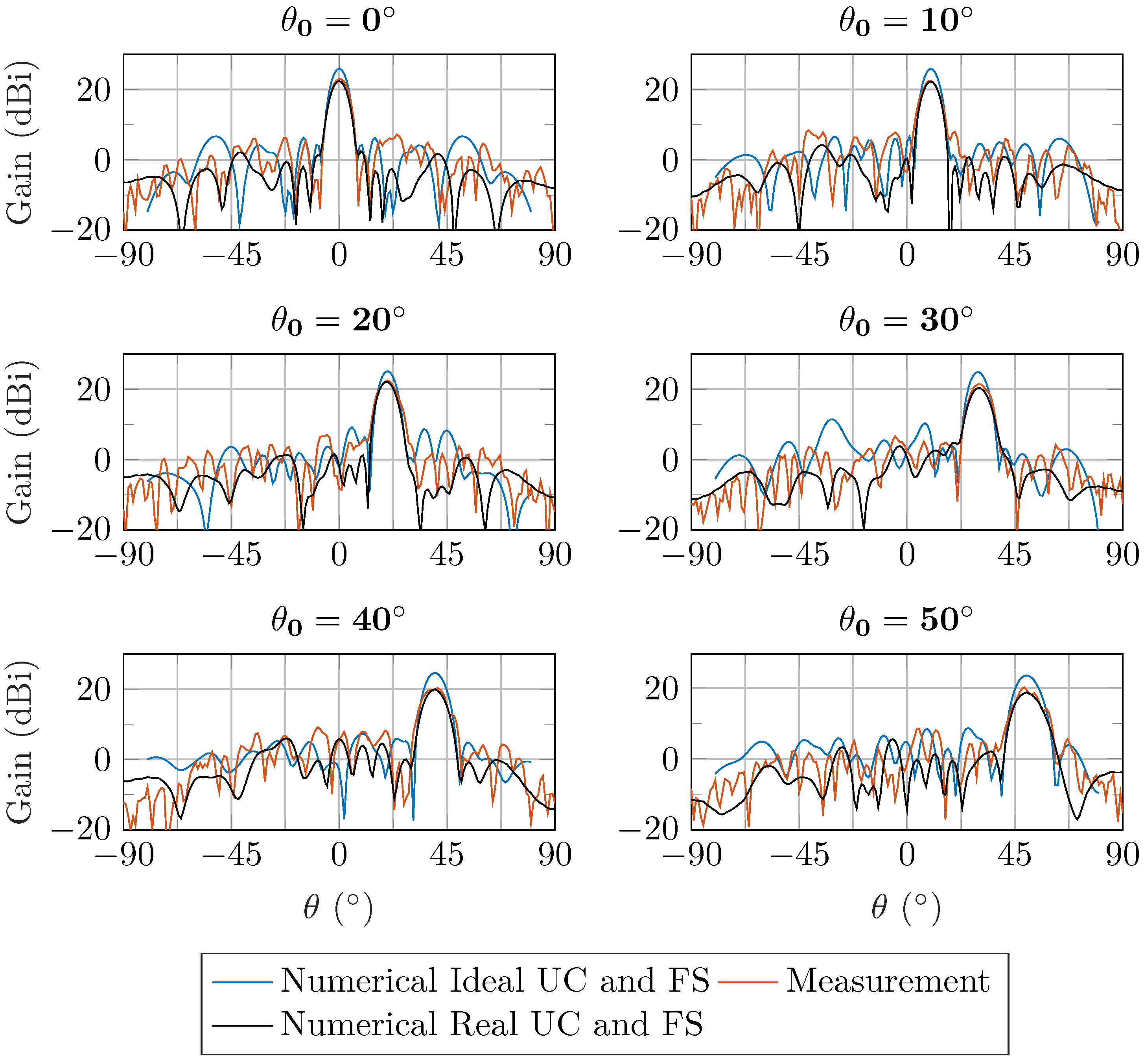
4.2. Validation of the Proposed Model
5. Multi-User Performance Evaluation
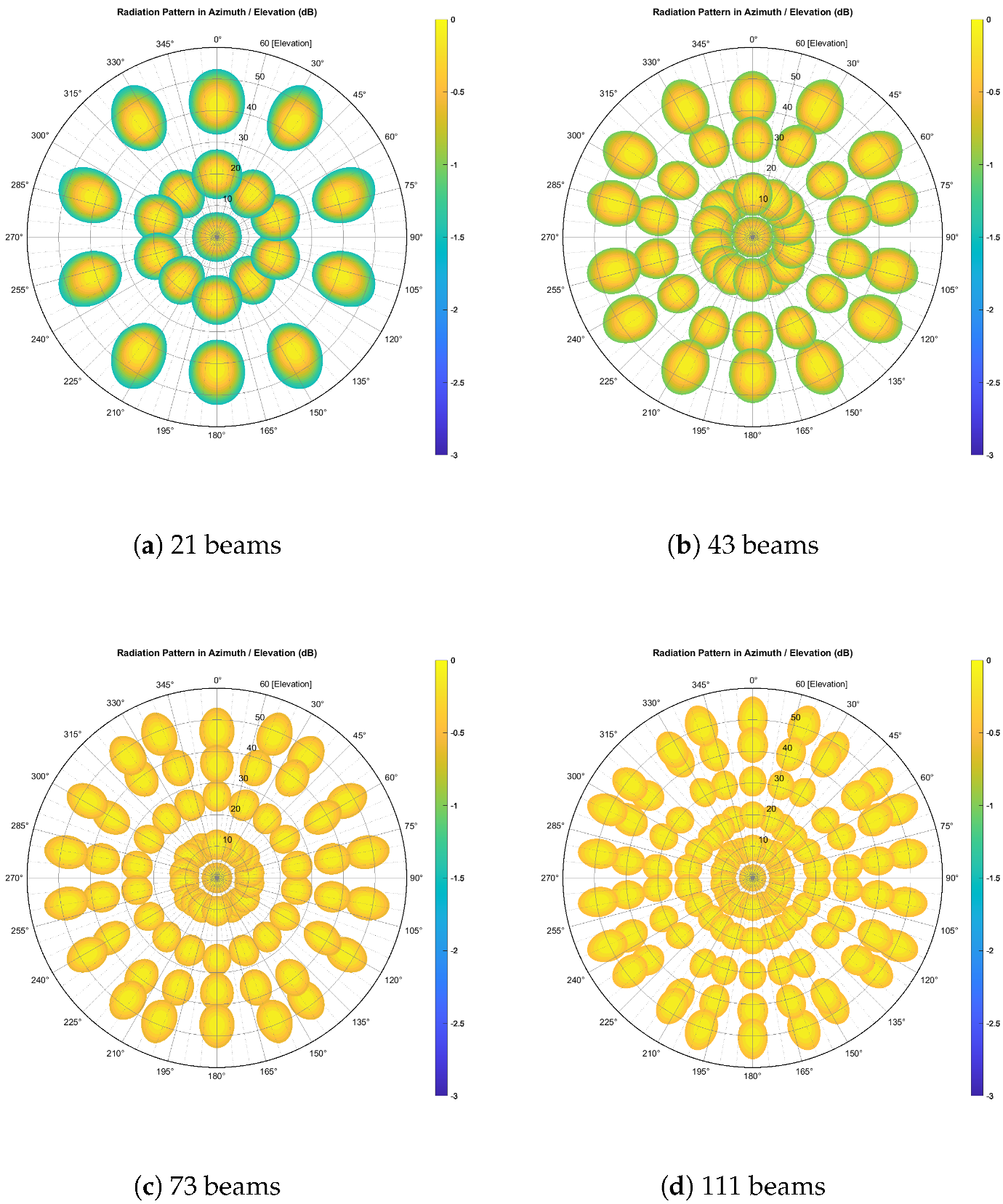
5.1. Definitions of Scenarios
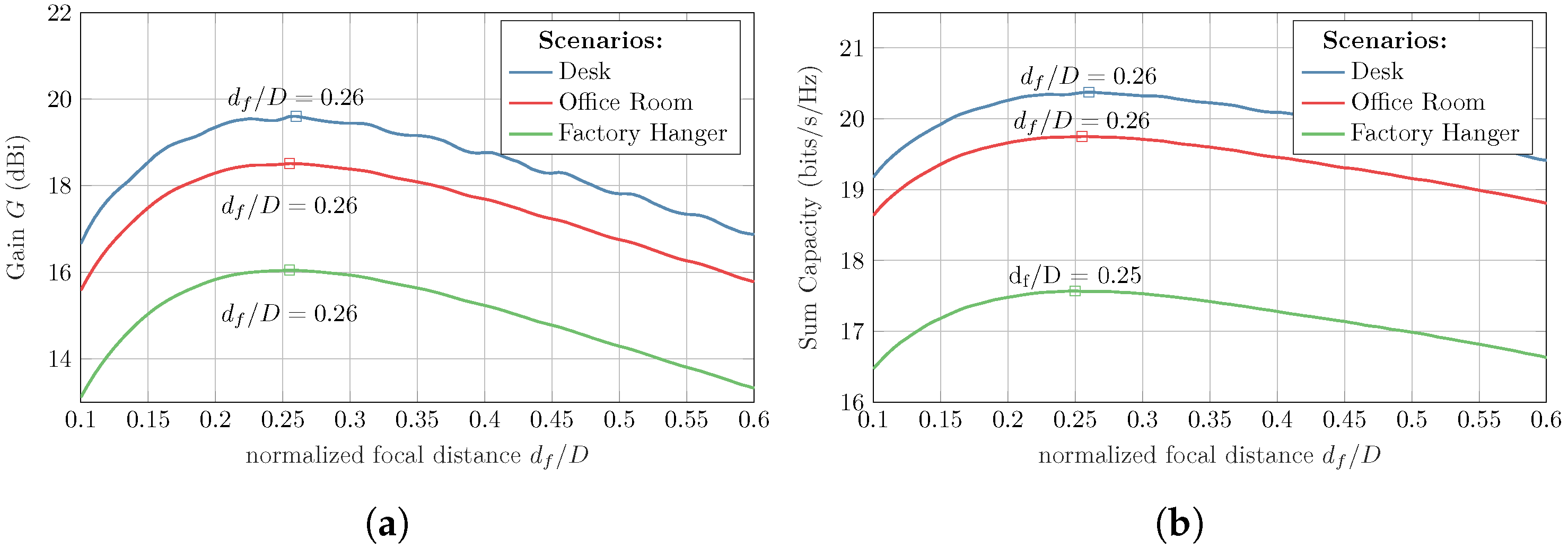
5.2. Optimal Focal Distance
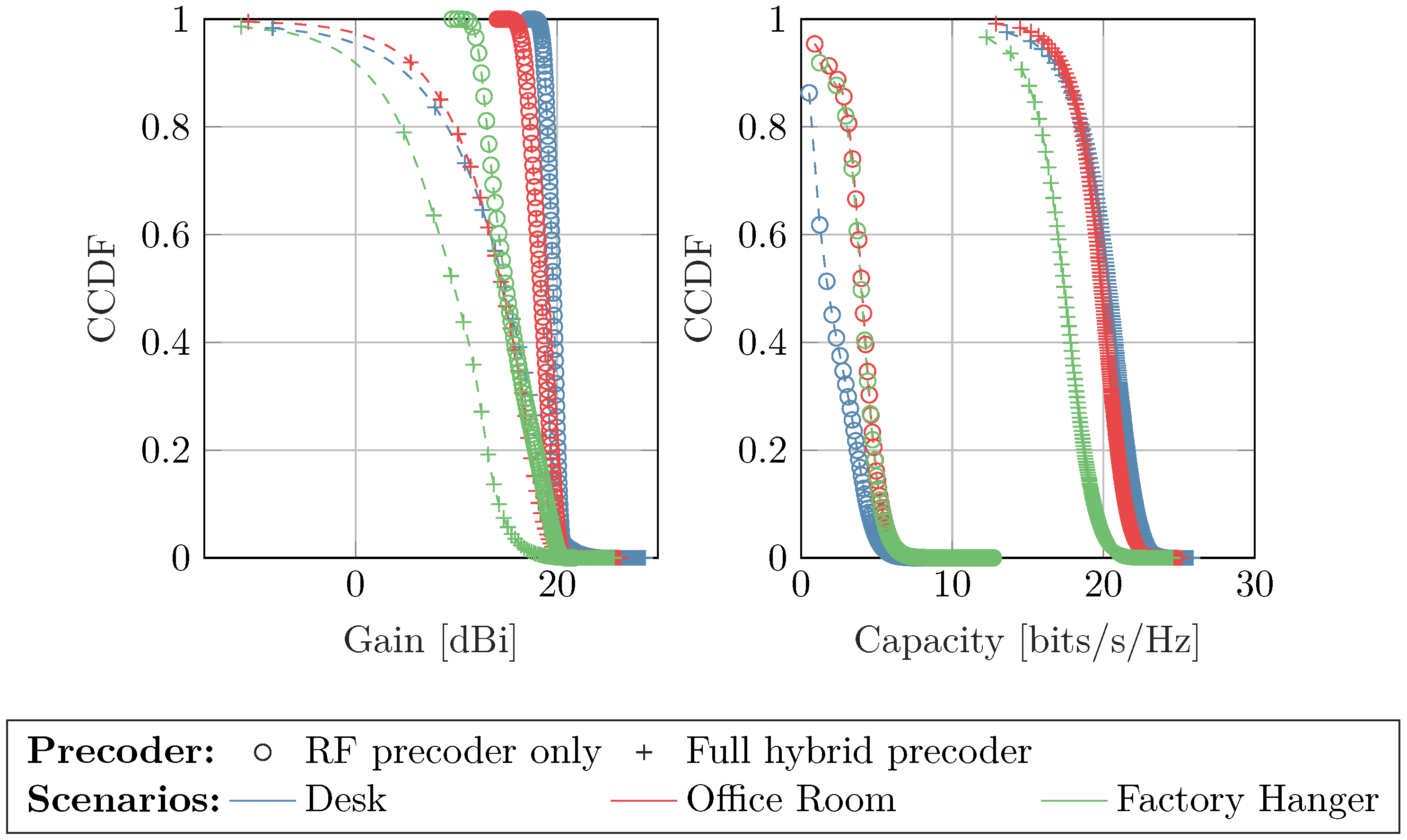
5.3. Codebook-Aware Optimization
6. Conclusions and Perspectives
Perspectives
- (i)
- Power allocation: We observed during the performance evaluation that low, complex ZF can strongly attenuate user streams when beam overlapping occurs. It limits the TX gain and, by extension, the coverage. We believe that a solution with improved power efficiency would greatly improve system performance.
- (ii)
- Source and unit-cell radiation pattern: One challenge for T-RIS is to limit its form factor and investigate systems with reduced focal distances. However, to do so, it is necessary to consider more accurate modeling of sources and unit-cell radiation patterns. In this case, it is possible to use models derived from measurements.
- (iii)
- Wideband transmissions and beam split: With the rise in frequency, signal bandwidth increases and some wideband-induced effects can occur such as beam split. Beam split means that the beam direction moves with the frequency, which induces a power loss and higher IUI. This effect must be taken into account for high-mmWave and sub-THz system design.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Busari, S.A.; Huq, K.M.S.; Mumtaz, S.; Dai, L.; Rodriguez, J. Millimeter-Wave Massive MIMO Communication for Future Wireless Systems: A Survey. IEEE Commun. Surv. Tutor. 2018, 20, 836–869. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter Wave Mobile Communications for 5G Cellular: It Will Work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Jornet, J.M.; Han, C. Terahertz band: Next frontier for wireless communications. Phys. Commun. 2014, 12, 16–32. [Google Scholar] [CrossRef]
- Ayach, O.E.; Rajagopal, S.; Abu-Surra, S.; Pi, Z.; Heath, R.W. Spatially Sparse Precoding in Millimeter Wave MIMO Systems. IEEE Trans. Wirel. Commun. 2014, 13, 1499–1513. [Google Scholar] [CrossRef]
- Niu, Y.; Li, Y.; Jin, D.; Su, L.; Vasilakos, A.V. A survey of millimeter wave communications (mmWave) for 5G: Opportunities and challenges. Wirel. Netw. 2015, 21, 2657–2676. [Google Scholar] [CrossRef]
- Heath, R.W.; González-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An Overview of Signal Processing Techniques for Millimeter Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Basar, E.; Di Renzo, M.; De Rosny, J.; Debbah, M.; Alouini, M.S.; Zhang, R. Wireless Communications Through Reconfigurable Intelligent Surfaces. IEEE Access 2019, 7, 116753–116773. [Google Scholar] [CrossRef]
- Pradhan, C.; Li, A.; Song, L.; Vucetic, B.; Li, Y. Hybrid Precoding Design for Reconfigurable Intelligent Surface Aided mmWave Communication Systems. IEEE Wirel. Commun. Lett. 2020, 9, 1041–1045. [Google Scholar] [CrossRef]
- He, J.; Wymeersch, H.; Sanguanpuak, T.; Silven, O.; Juntti, M. Adaptive Beamforming Design for mmWave RIS-Aided Joint Localization and Communication. In Proceedings of the IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Seoul, Republic of Korea, 6–9 April 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Reis, J.R.; Vala, M.; Caldeirinha, R.F.S. Review Paper on Transmitarray Antennas. IEEE Access 2019, 7, 94171–94188. [Google Scholar] [CrossRef]
- Padilla, P.; Muñoz-Acevedo, A.; Sierra-Castañer, M.; Sierra-Pérez, M. Electronically Reconfigurable Transmitarray at Ku Band for Microwave Applications. IEEE Trans. Antennas Propag. 2010, 58, 2571–2579. [Google Scholar] [CrossRef]
- Jamali, V.; Tulino, A.M.; Fischer, G.; Müller, R.R.; Schober, R. Intelligent Surface-Aided Transmitter Architectures for Millimeter-Wave Ultra Massive MIMO Systems. IEEE Open J. Commun. Soc. 2021, 2, 144–167. [Google Scholar] [CrossRef]
- Koutsos, O.; Madi, R.; Foglia Manzillo, F.; Smierzchalski, M.; Clemente, A.; Sauleau, R. Recent Achievements on Passive and Beam Steering Transmitarrays at Millimeter Waves. In Proceedings of the International Symposium on Antennas and Propagation (ISAP), Taipei, Taiwan, 19–22 October 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Molisch, A.F.; Ratnam, V.V.; Han, S.; Li, Z.; Nguyen, S.L.H.; Li, L.; Haneda, K. Hybrid Beamforming for Massive MIMO: A Survey. IEEE Commun. Mag. 2017, 55, 134–141. [Google Scholar] [CrossRef]
- Sohrabi, F.; Yu, W. Hybrid Digital and Analog Beamforming Design for Large-Scale Antenna Arrays. IEEE J. Sel. Top. Signal Process. 2016, 10, 501–513. [Google Scholar] [CrossRef]
- Wang, Z.; Li, M.; Li, H.; Liu, Q. Hybrid Beamforming with One-Bit Quantized Phase Shifters in mmWave MIMO Systems. In Proceedings of the IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Leus, G.; Heath, R.W. Limited Feedback Hybrid Precoding for Multi-User Millimeter Wave Systems. IEEE Trans. Wirel. Commun. 2015, 14, 6481–6494. [Google Scholar] [CrossRef]
- Zhao, L.; Kwan Ng, D.W.; Yuan, J. Multiuser precoding and channel estimation for hybrid millimeter wave MIMO systems. In Proceedings of the IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Su, X.; Jiang, Y. Optimal Zero-Forcing Hybrid Downlink Precoding for Sum-Rate Maximization. IEEE Wirel. Commun. Lett. 2022, 11, 463–467. [Google Scholar] [CrossRef]
- Nicholls, J.G.; Hum, S.V. Full-Space Electronic Beam-Steering Transmitarray With Integrated Leaky-Wave Feed. IEEE Trans. Antennas Propag. 2016, 64, 3410–3422. [Google Scholar] [CrossRef]
- Tang, J.; Xu, S.; Yang, F.; Li, M. Design and Measurement of a Reconfigurable Transmitarray Antenna with Compact Varactor-Based Phase Shifters. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 1998–2002. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.B.; Gong, C.Y.; Dong, S.Y.; Wang, S.Y.; Wang, H.P.; Cui, T.J. Design of Programmable Transmitarray Antenna With Independent Controls of Transmission Amplitude and Phase. IEEE Trans. Antennas Propag. 2022, 70, 8086–8099. [Google Scholar] [CrossRef]
- Frank, M.; Lurz, F.; Weigel, R.; Koelpin, A. Electronically Reconfigurable 6×6 Element Transmitarray at K-Band Based on Unit Cells With Continuous Phase Range. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 796–800. [Google Scholar] [CrossRef]
- Clemente, A.; Dussopt, L.; Sauleau, R.; Potier, P.; Pouliguen, P. 1-Bit Reconfigurable Unit Cell Based on PIN Diodes for Transmit-Array Applications in X-Band. IEEE Trans. Antennas Propag. 2012, 60, 2260–2269. [Google Scholar] [CrossRef]
- Yu, H.; Li, P.; Su, J.; Li, Z.; Xu, S.; Yang, F. Reconfigurable Bidirectional Beam-Steering Aperture With Transmitarray, Reflectarray, and Transmit-Reflect-Array Modes Switching. IEEE Trans. Antennas Propag. 2023, 71, 581–595. [Google Scholar] [CrossRef]
- Wang, X.; Qin, P.Y.; Tuyen Le, A.; Zhang, H.; Jin, R.; Guo, Y. Beam Scanning Transmitarray Employing Reconfigurable Dual-Layer Huygens Element. IEEE Trans. Antennas Propag. 2022, 70, 7491–7500. [Google Scholar] [CrossRef]
- Xiao, Y.; Yang, F.; Xu, S.; Li, M.; Zhu, K.; Sun, H. Design and Implementation of a Wideband 1-Bit Transmitarray Based on a Yagi–Vivaldi Unit Cell. IEEE Trans. Antennas Propag. 2021, 69, 4229–4234. [Google Scholar] [CrossRef]
- Dai, X.; Wu, G.; Luk, K. A Wideband Low-Profile Reconfigurable Transmitarray Using Magnetoelectric Dipole Elements. IEEE Trans. Antennas Propag. 2022, 70, 8008–8019. [Google Scholar] [CrossRef]
- Di Palma, L.; Clemente, A.; Dussopt, L.; Sauleau, R.; Potier, P.; Pouliguen, P. Circularly-polarized reconfigurable transmitarray in Ka-band. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), Davos, Switzerland, 10–15 April 2016; pp. 1–2. [Google Scholar] [CrossRef]
- Vilenskiy, A.; Makurin, M.; Lee, C.; Ivashina, M.V. Reconfigurable Transmitarray With Near-Field Coupling to Gap Waveguide Array Antenna for Efficient 2-D Beam Steering. IEEE Trans. Antennas Propag. 2020, 68, 7854–7865. [Google Scholar] [CrossRef]
- Cheng, C.C.; Lakshminarayanan, B.; Abbaspour-Tamijani, A. A Programmable Lens-Array Antenna with Monolithically Integrated MEMS Switches. IEEE Trans. Microw. Theory Tech. 2009, 57, 1874–1884. [Google Scholar] [CrossRef]
- Dai, L.; Wang, B.; Wang, M.; Yang, X.; Tan, J.; Bi, S.; Xu, S.; Yang, F.; Chen, Z.; Di Renzo, M.; et al. Reconfigurable Intelligent Surface-Based Wireless Communications: Antenna Design, Prototyping, and Experimental Results. IEEE Access 2020, 8, 45913–45923. [Google Scholar] [CrossRef]
- Diaby, F.; Clemente, A.; Sauleau, R.; Pham, K.T.; Dussopt, L. 2 Bit Reconfigurable Unit-Cell and Electronically Steerable Transmitarray at Ka -Band. IEEE Trans. Antennas Propag. 2020, 68, 5003–5008. [Google Scholar] [CrossRef]
- Foglia Manzillo, F.; Smierzchalski, M.; Reverdy, J.; Clemente, A. A Ka-band Beam-Steering Transmitarray Achieving Dual-Circular Polarization. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), Dusseldorf, Germany, 22–26 March 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Gharbieh, S.; Clemente, A.; Milbrandt, J.; Reig, B. Phase Change Material Based Reconfigurable Transmitarray: A Feasibility Study. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Venkatesh, S.; Lu, X.; Saeidi, H.; Sengupta, K. A high-speed programmable and scalable terahertz holographic metasurface based on tiled CMOS chips. Nat Electron 2020, 3, 785–793. [Google Scholar] [CrossRef]
- Liang, L.; Xu, W.; Dong, X. Low-Complexity Hybrid Precoding in Massive Multiuser MIMO Systems. IEEE Wirel. Commun. Lett. 2014, 3, 653–656. [Google Scholar] [CrossRef]
- Clemente, A.; Di Palma, L.; Diaby, F.; Dussopt, L.; Pham, K.; Sauleau, R. Electronically-Steerable Transmitarray Antennas for Ka-Band. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–4. [Google Scholar]
- Clemente, A.; Dussopt, L.; Sauleau, R.; Potier, P.; Pouliguen, P. Focal Distance Reduction of Transmit-Array Antennas Using Multiple Feeds. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1311–1314. [Google Scholar] [CrossRef]
- Mudonhi, A.; D’Errico, R.; Oestges, C. Indoor mmWave Channel Characterization with Large Virtual Antenna Arrays. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 15–20 March 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Jung, J.S.; Park, C.Y.; Oh, J.H.; Song, H.K. Intelligent Reflecting Surface for Spectral Efficiency Maximization in the Multi-User MISO Communication Systems. IEEE Access 2021, 9, 134695–134702. [Google Scholar] [CrossRef]
- Di Palma, L. Reconfigurable Transmitarray Antennas at Millimeter-Wave Frequencies. Ph.D. Thesis, Université Rennes 1, Rennes, France, 2015. [Google Scholar]


| Frequency | Reconfigurable Device | Phase Quantization | References |
|---|---|---|---|
| C-band | Varactors | continuous | [20,21] |
| C-band | Varactors and PIN diodes | 16-bit | [22] |
| X-band | PIN diodes | 1-bit | [24,25] |
| Ku-band | PIN diodes | 1-bit | [26,27,28] |
| K-band | Varactors | continuous | [23] |
| Ka-band | PIN diodes | 1-bit | [29,30] |
| Ka-band | MEMS switches | 2-bit | [31] |
| Ka-band | PIN diodes | 2-bit | [32,33,34] |
| D-band | PCM-based switches | 1-bit | [35] |
| 300 GHz | CMOS switches | 8-bit | [36] |
| Unit Cell | Insertion Loss (dB) at 28.0 GHz | −2 dB Bandwidth (% @ 27.0 GHz) | −3 dB Bandwidth (% @ 27.0 GHz) |
|---|---|---|---|
| Carrier Frequency | GHz |
| Lens | uniform square grid |
| unit cells | |
| size with cm | |
| 1-bit phase quantization | |
| omnidirectional antennas | |
| Focal Source | |
| square arrangement with distance | |
| horn antennas 10 dBi gain () |
| Desk | Office Room | Factory Hanger | |
|---|---|---|---|
| Max aperture | 20 | 60 | 80 |
| Radius [m] | |||
| Area [m] |
| Scenarios: | Desk | Office Room | Factory Hanger | ||
|---|---|---|---|---|---|
| Codebook size | Reference | ||||
| 21 | ref opt. | ||||
| c-a opt. | |||||
| 43 | ref opt. | ||||
| c-a opt. | |||||
| 73 | ref opt. | ||||
| c-a opt. | |||||
| 111 | ref opt. | ||||
| c-a opt. | |||||
| Scenarios: | Desk | Office Room | Factory Hanger | |
|---|---|---|---|---|
| Codebook | Reference | |||
| 21 | ||||
| 43 | ||||
| 73 | ||||
| 111 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demmer, D.; Foglia Manzillo, F.; Gharbieh, S.; Śmierzchalski, M.; D’Errico, R.; Doré, J.-B.; Clemente, A. Hybrid Precoding Applied to Multi-Beam Transmitting Reconfigurable Intelligent Surfaces (T-RIS). Electronics 2023, 12, 1162. https://doi.org/10.3390/electronics12051162
Demmer D, Foglia Manzillo F, Gharbieh S, Śmierzchalski M, D’Errico R, Doré J-B, Clemente A. Hybrid Precoding Applied to Multi-Beam Transmitting Reconfigurable Intelligent Surfaces (T-RIS). Electronics. 2023; 12(5):1162. https://doi.org/10.3390/electronics12051162
Chicago/Turabian StyleDemmer, David, Francesco Foglia Manzillo, Samara Gharbieh, Maciej Śmierzchalski, Raffaele D’Errico, Jean-Baptiste Doré, and Antonio Clemente. 2023. "Hybrid Precoding Applied to Multi-Beam Transmitting Reconfigurable Intelligent Surfaces (T-RIS)" Electronics 12, no. 5: 1162. https://doi.org/10.3390/electronics12051162
APA StyleDemmer, D., Foglia Manzillo, F., Gharbieh, S., Śmierzchalski, M., D’Errico, R., Doré, J.-B., & Clemente, A. (2023). Hybrid Precoding Applied to Multi-Beam Transmitting Reconfigurable Intelligent Surfaces (T-RIS). Electronics, 12(5), 1162. https://doi.org/10.3390/electronics12051162






