Abstract
Ride sharing is a service that enables users to share trips with others, conserving energy, decreasing emissions and reducing traffic congestion. Selecting a suitable partner for a user based on the their trip data is essential for the service, but it also leads to privacy disclosure, e.g., the user’s location and trajectory. Many privacy-preserving solutions for ride sharing services have been proposed, which are based on cryptographic technology and provide accurate matching services. However, these encryption-based algorithms are very complicated and difficult to calculate. In hot spots, such as stations, airports and sport gymnasiums, a large number of users may apply for a ride sharing service in short space of time, which will place huge pressure on the service provider. Using traditional matching methods increases the matching time and leads to a less favorable user experience. To solve these problems, we model them, aiming to maximize the vehicle’s carrying capacity and propose a lightweight privacy-preserving ride matching scheme for selecting feasible partners during busy periods with a large number of requests. To achieve this, we make use of the homomorphic encryption technique to hide location data and design a scheme to calculate the distances between users in road networks securely and efficiently. We employ a road network embedding technique to calculate the distance between users. Moreover, we use travel time instead of space distance, which makes matching more accurate. Further, with the encrypted itineraries of users, the service provider selects potential ride share partners according to the feasibility of time schedules. We use ciphertext packing to reduce overhead, improving the efficiency of ride matching. Finally, we evaluate our scheme with simulation and demonstrate that our scheme achieves an efficient and accurate matching service. It only takes a few seconds to complete the matching, and the matching accuracy is higher than 85 percent in most cases.
1. Introduction
With increasing demand on traffic, congestion is becoming increasingly serious, especially in rush hour. As part of the Internet sharing economy trend, ride sharing services (RSSs) have been developed rapidly, which not only mitigates traffic pressure greatly, but also reduces carbon emissions [1]. Thanks to the widespread use of smart phones and accurate digital maps, many online ride hailing services (RHS) have been developed, such as DiDi, Lyft and Uber [2]. The RHS enables a user to use their smart phone to hail a taxi in a short time. As reported in [3], these ride services, including RSS and RHS, have been used by 30 percent of citizens in America, surpassing the traditional way of travel. The market share is expected to exceed USD 200 billion by 2025. In 2021, the sales volume of the global ride sharing market reached USD 38.2 billion, and is expected to reach USD 126.8 billion in 2028, with a CAGR of 19.8% (2022–2028).
Although ride sharing services can bring convenience to users’ travel, they also bring unprecedented privacy risks to their users’ information security [4]. As the service depends on mature positioning technology, users must submit their location information to the platform if they want to book a taxi through smart phone application, such as boarding and alighting locations. In addition, compared with traditional cruise taxis, the ride sharing service platform can easily collect the travel tracks of millions of passengers every day. Using data mining technology, it can infer a large amount of passenger privacy information from these travel records, such as the passenger’s home address or work location, and even their hobbies [5]. However, the service provider is not fully trusted. It may sell the collected information from users for monetary reasons while providing services. Furthermore, if the service platform is attacked, such information will be completely disclosed to unauthorized organizations or individuals. In extreme cases, if such information is used by criminals, passengers’ personal property, social reputation and even life safety may be threatened. Some media have reported the harm of privacy disclosure of the ride sharing system. Therefore, in order to achieve the long-term development of the ride sharing economy, a solution to the problems of location privacy and the disclosure of ride sharing services is urgently required. In the ride sharing service, protecting location privacy means that the departure and destination of passengers (or any other place related to the ride) will not be disclosed to anyone [6].
In order to solve the problem of privacy disclosure, different privacy-preserving plans for ride services (ride hailing and ride sharing) have been proposed in the past few years, based on encryption techniques [7] or location obfuscation methods [8]. By using spatial masking [9], differential privacy [10], k-anonymity technology [11], location obfuscation methods are efficient to protect location privacy. However, they sacrifice the accuracy of the location and provided inferior services. On the other hand, encryption-based solutions, such as Searchable Symmetric Encryption [12] and Private Set InterSection [13], provide accurate location services and privacy preservation. Homomorphic encryption (HE) schemes can provide a ride matching service by calculating the distance between users over the encrypted data while protecting the location privacy of users. However, these algorithms have high computational complexity, and the operations of encryption, decryption and computation cost too much time. Moreover, with a large amount of service requests, the calculation complexity increases fast with order . The SP has to execute a lot of calculations on encrypted ciphertexts. In hot spot areas, a large number of users may apply for a ride sharing service in a short time. Considering that many people come out of a railway station or a gymnasium after a sports game or a concert, respectively, there are many requests in short time, as shown in Figure 1. In order to provide a ride matching service, the system has to encrypt the location information of all users and calculate the travel distance of different matching combinations. It takes much time to encrypt data and calculate the distance, which is not acceptable.
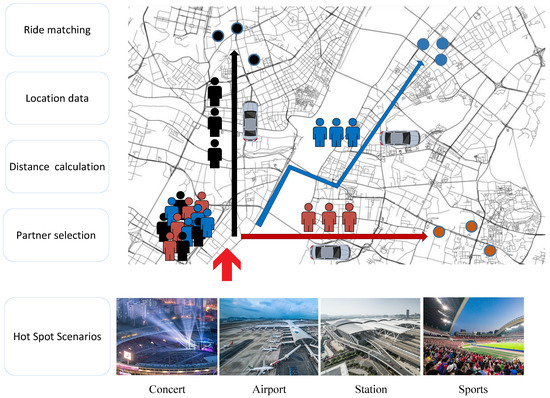
Figure 1.
Example scenario of hot spots.
In this article, we investigate the issue of privacy preservation and ride matching algorithms in hot spot areas. Our aim is to enable the RSS to provide a ride matching service efficiently and accurately while protecting location privacy. To provide accurate matching, we propose a privacy protection method based on the road network distance. The users encrypt their location and this is transmitted to the server. The distance is calculated under homomorphic encryption by the server. By this means, the location privacy is protected. We analyze the problem from both the macro- and micro-level perspectives and provide the matching criterion. To improve efficiency, the map is divided into small areas and users are filtered before matching according to their trip and schedules. The server matches users within the same areas. We also use ciphertexts packing to reduce communication overhead and computational complexity. The contributions of this paper are summarized below:
- We formulate the problem to maximize the vehicle’s carrying capacity and propose a privacy-preserving ride matching scheme. Our scheme can calculate the road network distance between users to provide ride matching services without knowing the users’ location.
- We propose an efficient scheme that can quickly provide ride matching results to deal with a large number of ride sharing services in hot spot area. The users are pre-selected according to their trip and schedules before matching. We use ciphertexts packing to reduce communication overhead.
- We evaluate the scheme and the experimental results demonstrate that our scheme provides accurate matching service within acceptable time. Our scheme can provide travel time saving and reduce the overall energy consumption.
The remainder of this paper is organized as follows. In Section 2, we summarize the previous research work. In Section 3, we introduce the system model, analyse the location privacy threats, and explain the design goals of the proposed scheme in this paper. We introduce the formulation of the problem and give our proposed scheme in Section 4. We give the security analysis of our proposed scheme and evaluate the performance in Section 5. Finally, we draw the conclusion in Section 6.
2. Related Work
Although the ride service has many advantages, few users are willing to use it if they do not solve the privacy problems that users worry about. Therefore, providing privacy protection is one of the key technologies for the success of ride service. Many schemes have been proposed to solve the privacy protection problem of ride service. We provide a summary of location privacy-preserving schemes for ride service in Table 1.
One tradition method is based on spatial and temporal obfuscation. Friginal et al. [14] introduce the privacy-preserving problem of ride sharing service and proposed a dynamic framework. In [15], a cloaking based method is proposed. He et al. [10] utilise the differential privacy technique, which can meet the personalized privacy needs of users. In [5], the pick up position is optimised to obfuscate the location. Literature [16] considers the concept of k anonymity and l diversity. The upload position is to select a close Point of Interest (POI) from l randomly selected POIs, which is within a given radius. This method ensures that the exposed location is spatially accessible. These non-cryptographic solutions are fast and easy to implement. However, they may sacrifice the accuracy.
The follow-up works utilise cryptographic technique to protect users’ location information. Pham et al. [9] first introduce an encrypted scheme for ride hailing service. Later, they improve their scheme, which supports easy payment and reputation assessment [1]. In [17], Nabil et al. discussed the segmentation of shared RSS tasks. Users would take different vehicles to complete the journey. In [18], Vignesh et al. considered the community matching scenario, which not only consisted of the travel factor, but also personal preferences, such as the age, gender, smoking and so on. In [19], a privacy protection scheme without a trusted third party was proposed. The bilinear pairing scheme was used to encrypt the road network distance, and a searchable encryption scheme was designed. However, these schemes are based on spatial mapping or Euclidean Distance. The matching result is not accurate according to road network. Luo et al. [2] introduce a scheme for ride hailing service based on road network. They utilise RNE and Garbled Circuit to compute the distance between uses [20]. In [4], an online ride matching scheme is proposed. Later, some blockchain based schemes are proposed, which support smart contract and reputation assessment [7,21]. These solutions focus on one-to-one matching, which are not practical in reality as one vehicle can deliver several passengers.

Table 1.
Summary of privacy-preserving schemes that address location privacy.
Table 1.
Summary of privacy-preserving schemes that address location privacy.
| Reference | Technique | Characteristic |
|---|---|---|
| [5,10,14,15,16] | obfuscation method such as k-anonymity | Fast and easy to implement |
| [1,9] | Homomorphic encryption | Euclidean Distance calculation and reputation assessment |
| [17,18,19] | Spatial mapping | Flexible matching and personal preference |
| [2,4] | Road network distance | Accurate location; one-to-one matching |
| [7,21] | Blockchain | Smart contract and reputation assessment system |
3. Models and Problem Definition
In this section, we first introduce the system model, followed by an analysis of the location privacy threats currently faced by ride sharing systems, and finally identify the design goals of the solution proposed in this paper.
3.1. System Model
In this paper, we consider an RSS system that allows the users to request a ride sharing matching from the service provider. The ride sharing system is composed of three parties: the authority, the service provider, and the users, as shown in Figure 2.
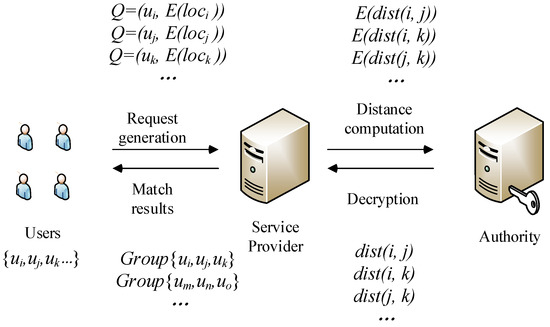
Figure 2.
System model.
- Users: Each user has a smart phone with a built-in positioning system, where he can get their location anytime and anywhere. At the same time, the user has installed the ride sharing application and completed the registration. A ride sharing query message includes their identity and location information. represents a user’s identity and denotes the user’s location information, including pick-up and drop off locations. A user submits their encrypted query to the service provider to request nearby users who can ride together.
- Service Provider: The ride matching service provider (SP) is responsible for calculating the distance and providing ride matching service. It divides the road network into small areas and calculates the distance matrix of the road network. After receiving the user’s request, the SP calculates the distance between different users with the encrypted location data. For example, represents the encrypted distance between user i and user j. The SP sends the encrypted distance to the authority to get data decrypted. Based on the decrypted distance, the SP gives the matching result , which means user i, j and k share the same ride.
- Authority: The authority is responsible for the registration of users. It provides efficient key management for a wide range of password operations. It decrypts the distance data and sends the result back to the SP. The authority is an independent third party and will not conspire with the SP, thus ensuring the privacy of the service.
3.2. Threat Model
In general, most users are are honest and sensitive. They submit valid requests and provide real encrypted locations to the SP. Users do not want any party (including the SP and other users) to know their travel information. However, there are a few malicious users. They may attempt to capture some sensitive information about others. Further, the SP is also considered as semi-honest. That is, it tries to collect user information while providing services. We also assume that there is no collusion between different parties. We mainly consider the following typical attacks launched by the SP and users:
- The SP may try to accurately track users in their daily activities, such as the boarding and alighting locations recorded by the system. According to the travel information collected, it may perform large-scale inference attacks to learn additional user privacy information, such as the user’s home and work address, behavior and interests.
- The malicious users may attempt to capture some sensitive information, including personal information and travel data. They may perform replay attacks. They will apply for ride services. After obtaining the matching results, they cancel the ride request. By repeating this, they may collet many travel information of different users.
3.3. Design Goal
Under the above discussion of system model and threat model, our proposed scheme should achieve the following objectives, for the problem of location privacy disclosure in the ride sharing system.
3.3.1. Function
The system should provide accurate ride matching results. That is, the SP could find the nearby users and forms a team by using road distance. To achieve this goal, the SP should support distance measurement between users with encrypted location.
3.3.2. Privacy Preservation
The location of each user should be protected. In the whole matching process, the service provider should not know any information about the user’s location, and users should not know any information about their partners’ locations before they reach a ride agreement.
3.3.3. Efficient
The scheme should be fast and efficient, that is, the computation cost and communication overhead should be low enough to enable the ride share matching in real time. Therefore, it can still provide matching results quickly in the scenario of a large number of service requests in hot spot areas.
4. Problem Formulation and Proposed Scheme
In this section, we first introduce the formulation of the problem and then propose our scheme.
4.1. Problem Formulation
In order to give reasonable matching results, we analyze the problem from both macro- and micro-level perspectives.
From a macro perspective, the system tends to maximize transport capacity, which means the car transports more customers with fewer detours. As a result, fuel consumption and carbon emissions are reduced. Transport capacity is defined as the number of riders in a car. Therefore, the system will assign users with similar destinations to the same vehicle [22].
From a micro perspective, the users are willing to participate in ride sharing as they benefit from it in multiple ways, including time and money. In hot spot areas, users have to wait for a long time for a vehicle because there are a large number of ride service requests. Users can save waiting time through ride sharing while they may suffer more traffic time as the vehicle take a detour to send different users. Thus, users hope to travel with users with similar destinations.
Using the above analysis, we arrive at the same conclusion from both the macro-level and micro-level perspectives—that users with similar destinations will take the same vehicle. We use the definition of travel time saving (TSS) from the literature [23] and provide detailed problem modeling derivation. TTS means the time saving brought by ride sharing. To reduce detours, the TTS should be positive. The problem is to find a set of users to maximize the TSS.
The problem is denoted as:
For rider , we suppose the driver sends i first and then j and k. The TTS can be calculated as:
where is the pick-up location for all users, , and are the drop off locations for users and represents the distance between two users in road network. The constraint means that the users should benefit from ride sharing. Specifically, user j and k should pay less money as they wait for the driver sending the other user.
As shown in Equation (2), we can see that the TTS is the difference between the sum of travel distance without ride sharing and the sum of the distance between different user. The former part is constant according to the users’ location. Our goals can be transformed to calculate the minimum distance between different users, that is, the users are close to each other, which is consistent with our previous analysis that we need to find users with similar destinations.
In many papers, a widely used scheme to measure map distance is the Euclidean distance. The distance between any two nodes A and B is evaluated by their Cartesian coordinates :
Obviously, this is not well fitted in the road network. A vehicle cannot run through buildings to move straight from A to B. It has to move along the roads. Researchers propose a Manhattan distance on a gird network. The distance is the sum up of vertical and horizontal distances.
However, there are seldom strict grid road networks in reality. Many roads are not vertical or horizontal, which will effect the distance calculation accuracy directly. The distance should be calculated by the sum up of road segments along the trajectory. Moreover, there are some one-way streets. Suppose there is a one-way street from node A to node B. We denote as the distance from node A to node B and as the distance from node B to node A. We can easily get . Because a driver can drive directly from A to B but has to make a detour to drive back from B to A.
In order to calculate the distance between users more accurately in road network, we use the road network embedding (RNE) technology proposed by Shahabi [24]. We define the road network as a weighted directed graph , where the node set V represents intersections of roads or road ends, and E is a set of directed edges connecting two nodes. As the road network is stable, we can easily get the distance between any two nodes and , and form a spatial distance matrix , where denotes the distance from node to .
Suppose user u is located in the road segment connecting node s and node t; the distance between u and any node can be be calculated by the following formula:
Note that the location of u can be expressed by the distance matrix when there are enough reference points .
With all the locations of users described by distance matrix, the distance between two users a and b can be approximated as:
To be more accurate, we need to consider the traffic condition. It takes long time to go when there is heavy traffic. Similarly, we can obtain a temporal distance matrix , where denotes the driving time from node to . The travel time matrix is represented as
For simplicity, we denote a sketch of user as,
Then we have
4.2. Proposed Scheme
In this section, we will illustrate how our proposed scheme works. Figure 3 shows the workflow our scheme, which consists of four stages.
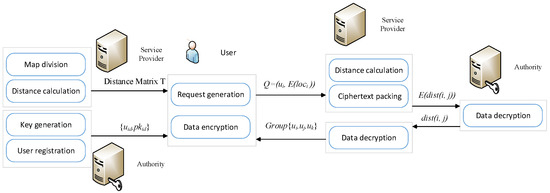
Figure 3.
The workflow of our scheme.
- (1)
- System initialization: The authorized authority generates a public key and a private key according to the encryption algorithm. The generated keys will be assigned to the designated user. The SP divides the road network into small areas and calculates the distance matrix of the road network.
- (2)
- User Registration: The users use phone number or other personal information to register their personal identity. The service provider will encrypt the registration information.
- (3)
- Request Generation: Users generate and submit the requests to the SP in encrypted form.
For a user i with request , they encrypt the location data, where and stand for the start location and the destination location. The user sends the encrypted request to the server.
In order to protect users’ location privacy, we use homomorphic encryption technology to encrypt users’ location information. Homomorphic encryption (HE) is a kind of encryption scheme which has a special property—homomorphism. It allows a third party (e.g., cloud, service provider) to perform certain computable functions on the encrypted data while preserving the features of the function and format of the encrypted data [25]. As an example for an additively HE scheme, for plaintext and ,
where E denotes the encryption function and ⨁ stands for a certain operation. One can obtain by using and without knowing and explicitly.
There are many encryption algorithms that achieve homomorphism. According to the supported the types and times of operations, all these algorithms can be divided into the following three categories: (1) Partially homomorphic encryption (PHE) supports infinite addition or multiplication operations, such as RSA [26]. (2) Somewhat homomorphic encryption (SHE, sometimes abbreviated as SWHE), such as BGN cryptosystem [27], supports finite combination of different operations. (3) Fully homomorphic encryption (FHE) supports all operations without any limits, such as Gentry09 [28].
Generally, due to the limited operation supported, the complexity of the PHE scheme is low. Paillier cryptosystem is a PHE [29] scheme, which can achieve additive homomorphism. In this paper, we will use Paillier cryptosystem to encrypt the location data of drivers and riders.
Key Generation . Choose two large prime numbers p and q, the two numbers are the same length, and . Compute . Choose a random number , such that , where The public key is and the private key is .
Encryption. Suppose a plaintext and choose a random number . The ciphertext can be calculated as
Decryption. Given a ciphertext , the plaintext is derived as
The Paillier cryptosystem has additive Homomorphism. For any , we have the following properties,
The modified Paillier cryptosystem was proposed to make decryption lightweight. As we know, the plaintext space of the Paillier cryptosystem is much smaller than the space of ciphertext. Thus, we adopt the plaintext packing technique to significantly reduce computation cost and communication cost. The basic idea of ciphertext packing is introduced as follows. Suppose are -bit integers, their corresponding ciphertexts are . We construct the packed ciphertext by
We only need one decryption to obtain the packed plaintext
and then recover .
In this paper, we set the modulus N used in Paillier cryptosystem to 1024 bits, the bit length of is 32 bits.
We construct the packed ciphertext by
The corresponding packed plaintext is
- (4)
- Ride Matching: The SP computes the distances between different users based on encrypted location data, and then transmit the encrypted distance to the authority. After the distance is decrypted, the result is sent back to the SP. The SP selects a set of users with the maximum TTS.
Based on the properties of homomorphism encryption, the SP can calculate the travel time between different users,
The SP sends to the authority to get data decrypted. After ciphertext decryption, the SP get and calculate the minimum of .
As discussed above, we reach a conclusion that the system will assign users with similar destinations to the same vehicle. Therefore, the matching result depends on which users are in the vicinity, without worrying about the other users far away. By filtering unnecessary users, the server only needs to calculate the distance between users in a small area and give the matching result. It greatly reduces the amount of data to be calculated, thus saving the matching time. Therefore, a simple method is to divide the map into small areas. The SP executes matching algorithm only among users within the same area. As we mention in the first stage, the SP divides the road network into small areas and calculates the distance matrix of the road network. Therefore, the matching will be performed among users in the specified area according to the SP. However, as shown in Figure 4, some users fail to find a match or their group is not full. Then the zone is increased and the remaining users perform the second round of matching. Moreover, we set a threshold for the matching process. When the distance between two users is longer than , the users will not share the same vehicle as it is not worthwhile.
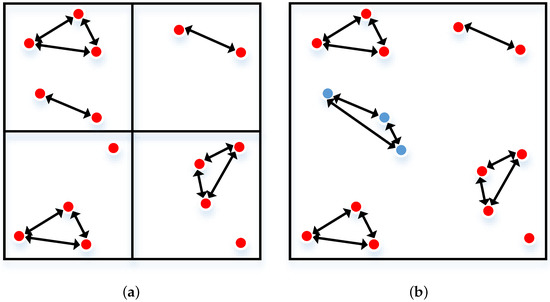
Figure 4.
Example of multiple rounds of matching process. (a) Users (depicted as red points) match in a small range; (b) The remaining users (depicted as blue points) perform the second round of matching.
5. Performance Evaluation
5.1. Security Analysis
In this section, we outline the security analysis of our proposed scheme according to the different types of attacks mentioned above.
To obtain a ride service, users have to register their identities to the service provider and upload their trip information. In the service request phase, users will encrypt their location information according to the road network distance matrix provided by the server, and send it to the platform. The SP calculates the distance between different users according to their encrypted location data. Although the service provider can know the map area to which the user belongs, the specific location of the user is encrypted. The server can only obtain the user’s rough location information and cannot infer the user’s specific location.
In our ride sharing system, a malicious external attacker may be disguised as a legitimate user and obtain the personal information of a legitimate user by issuing a ride sharing request and then canceling it. However, in the design of this scheme, the matching process is completed based on homomorphic encrypted data. The attacker can only know the nearest matching partner, but cannot obtain the specific information of other users. From the design details of the scheme, it is clear that the service provider only stores users’ encrypted phone numbers. Without the private key, the external attacker cannot obtain any information about the user; this can only be accessed through the encrypted phone number.
5.2. Simulation Result
In this section, we evaluate the practicability of our scheme in urban scenarios. We analyze the performance from three aspects: complexity, accuracy and benefit. For complexity, we show how fast our scheme works, which is vital in a hot spot scenario. We also evaluate how accurate the matching is. It is the core of ride matching service. Finally, we show how we benefit from ride matching. It is the motivation this service. We run the simulations with MATLAB(manufatured by The MathWorks, USA) and the parameters are listed in Table 2.

Table 2.
Experimental Parameters.
- (1)
- Complexity Analysis
First, we evaluate the performance of our scheme in terms of communication and computation costs. This depends on how long time ride matching takes. For the Paillier cryptosystem, one encryption requires two exponentiations and one multiplication, while one decryption requires one exponentiation. We set N and g to 1024 bits and 160 bits and the ciphertext is 2048 bits.
Table 3 and Table 4 summarize the computation and communication cost of our scheme and the basic original scheme. In the original scheme, the user location is encrypted and sent to the service provider to complete the distance calculation and user matching. In our improved scheme, the complexity of the matching algorithm is reduced and the communication cost is saved through space division and ciphertext packing. According to the discussion above, we know users with similar destinations will take the same vehicle. So we divide the map into small areas and make ride matching among users in the same area. This way, the number of users is decreased.

Table 3.
Communication overhead and computation cost.

Table 4.
Communication overhead and computation cost.
For a user, its cost depends on the dimension of the road network matrix. In order to get service, the user has to upload location data and encrypt all of the pieces. The more data uploaded by the user, the more accurate the ride matching. However, there are more calculations with the increase in uploaded data. With the data packing technique, there needs to be only one or two layers of encryption instead of layers of encryption. Moreover, the packet length is reduced. Therefore, both the communication cost and computation cost is significantly reduced.
- (2)
- Accuracy Analysis
In this section, we compare the performance of our scheme with that of the other four schemes. Among them, the ORide [1] and pRide [2] solutions provide the ride hailing service, while PSRide [4] and PRIS [23] provide ride sharing services. The ride hailing service provides a match between a user and several drivers. The SP finds the nearest driver to the specific user. In a ride sharing service, the schedule and itinerary of a user is considered. The matching criterion is to find two users with a similar itinerary. ORide and PRIS are based on Euclidean distance, while pRide and PSRide are based on road distance. We consider the characteristics of the road network and use travel time to measure the distance between users. We use matching accuracy to evaluate the performance of distance calculation in different schemes. The more precisely the distance between users is calculated, the more accurate the matching result, and the better the users’ service.
Figure 5 illustrates the matching accuracy under different dimension of the road network matrix. The matching accuracy of pRide and our scheme rises as the dimension increases, because when users upload more location information, the system can calculate the distance between users more accurately and provide accurate matching services. We can see the accuracy in our scheme is above 90% if the dimension reaches 12, which is practical in daily life. The ORide scheme is based on European distance, so the accuracy is lower than the other two schemes in most cases. Our scheme considers the complexity and time variations of the road network and, therefore, has the best performance.
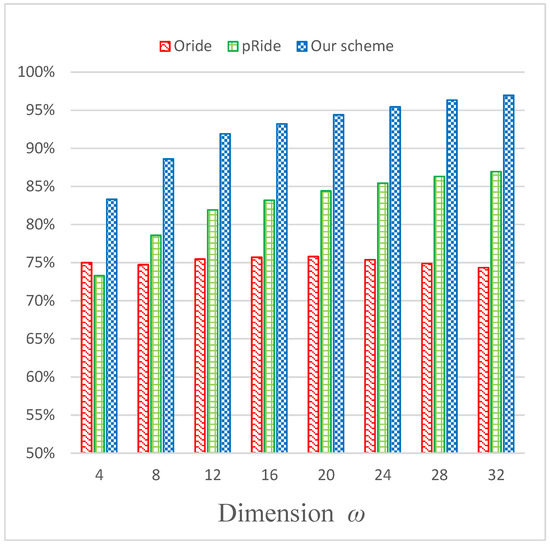
Figure 5.
Matching accuracy under different dimension of the road network.
As shown in Figure 6, the matching accuracy gradually rises as the user density increases, since there are more users around each other. The accuracy of our scheme is always higher than 90%, which is much higher than other schemes, as we consider the complexity and time variations of the road network due to the the road network distance.
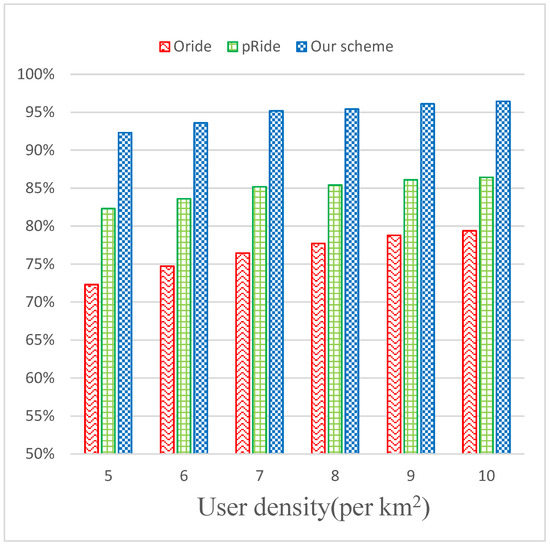
Figure 6.
Matching accuracy under different user density.
- (3)
- Benefit Analysis
In this part, we show how the system and users benefit from the ride sharing service with respect to transport capacity and fuel consumption reduction.
The matching distribution under different user density is shown in Figure 7, which depicts the transport capacity. With the increase in user density, there are more users in the matched group. The proportion of groups containing three users increases and the proportion of un-grouped users decreases. When there are fewer users, the destinations of users are sparse and scattered. The matching is not easily completed. When the user density increases, there are more users in the partition zone, which makes matching easier. The proportion of groups containing three users is about 80 percent when the user density reaches 7 users per km, which means the matching scheme is effective.
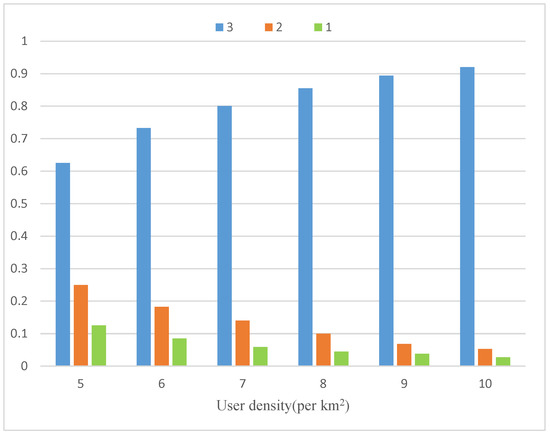
Figure 7.
Matching distribution under different user density.
Figure 8 depicts the execution time of PRIS, PSRide and our scheme under different user densities. With the increase in user density, the server has to execute more computation due to the greater number of potential match users. Our scheme is much more efficient, since PRIS and PSRide do not consider the scenario of massive numbers of users. For each match, our scheme takes less than 10 seconds in most cases, while the other schemes require tens of seconds to find partners.
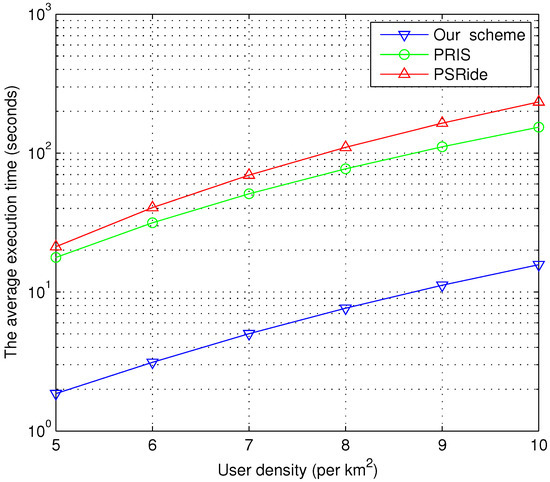
Figure 8.
Impact of the user density on execution time.
The average TTS per vehicle is shown in Figure 9, which means the the fuel consumption reduction brought by the ride sharing. We can see the average TTS of all the schemes increases with user density. With the increase in user density, their are more potential user matches. Some ungrouped users find matching partners. The matching result is more accurate. Our scheme is much more efficient, since PRIS and PSRide do not consider the scenario of massive numbers of users matching.
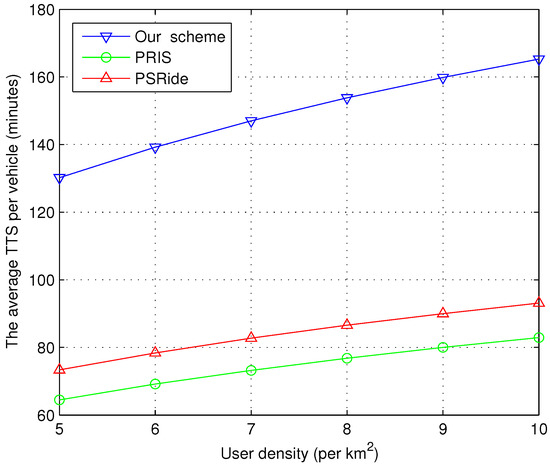
Figure 9.
Impact of user density on average TTS per vehicle.
6. Conclusions
In this paper, we studied the issue of privacy preservation for massive ride-share matching and proposed a lightweight scheme based on the road network. We utilized a homomorphic encryption technique to hide location data and designed a secure and effective scheme to calculate the distance between users in the road network to achieve ride sharing matching service. Moreover, we consider space division and ciphertext packing to decrease communication and computation costs. The simulation results have shown that our scheme can achieve 90% ride matching accuracy while maintaining a fast matching speed. Our scheme also performed well when considering travel time savings and energy consumption reduction. In future work, we will use blockchain technology to establish a trust evaluation mechanism for users and design a privacy-preserving matching algorithm.
Author Contributions
Conceptualization, Q.L. and H.W.; methodology, Q.L.; software, Q.L.; validation, Q.L., H.W. and C.D.; formal analysis, Q.L.; investigation, Q.L.; resources, Q.L.; data curation, Q.L.; writing—original draft preparation, Q.L.; writing—review and editing, Q.L., H.W. and C.D.; visualization, Q.L.; supervision, Q.L.; project administration, Q.L.; funding acquisition, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Fundamental Research Funds for the Central Universities (2022JBQY004), China Postdoctoral Science Foundation (2021TQ0028, 2021M700369), and Beijing Natural Science Foundation (L211013).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RSS | Ride Sharing Service |
| RHS | Ride Hailing Service |
| PoI | Point of Interest |
| SP | Service Provider |
| TSS | Travel Time Saving |
| RNE | Road Network Embedding |
| HE | Homomorphic Encryption |
| PHE | Partially Homomorphic Encryption |
| SHE | Somewhat Homomorphic Encryption |
| FHE | Fully Homomorphic Encryption |
References
- Pham, A.; Dacosta, I.; Endignoux, G.; Pastoriza, J.R.T.; Huguenin, K.; Hubaux, J.P. ORide: A Privacy-Preserving yet Accountable Ride-Hailing Service. In Proceedings of the 26th USENIX Security Symposium (USENIX Security 17); USENIX Association: Vancouver, BC, Canada, 2017; pp. 1235–1252. [Google Scholar]
- Luo, Y.; Jia, X.; Fu, S.; Xu, M. pRide: Privacy-Preserving Ride Matching Over Road Networks for Online Ride-Hailing Service. IEEE Trans. Inf. Forensics Secur. 2019, 14, 1791–1802. [Google Scholar] [CrossRef]
- Clewlow, R.R.; Mishra, G.S. Disruptive Transportation: The Adoption, Utilization, and Impacts of Ride-Hailing in the United States; Working Paper Series; Institute of Transportation Studies, University of California: Davis, CA, USA, 2017. [Google Scholar]
- Yu, H.; Jia, X.; Zhang, H.; Yu, X.; Shu, J. PSRide: Privacy-Preserving Shared Ride Matching for Online Ride Hailing Systems. IEEE Trans. Dependable Secur. Comput. 2019, 18, 1425–1440. [Google Scholar] [CrossRef]
- Goel, P.; Kulik, L.; Ramamohanarao, K. Optimal Pick up Point Selection for Effective Ride Sharing. IEEE Trans. Big Data 2017, 3, 154–168. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, H.; Yu, X.; Du, X.; Guizani, M. PGRide: Privacy-Preserving Group Ridesharing Matching in Online Ride Hailing Services. IEEE Internet Things J. 2021, 8, 5722–5735. [Google Scholar] [CrossRef]
- Baza, M.; Lasla, N.; Mahmoud, M.M.E.A.; Srivastava, G.; Abdallah, M. B-Ride: Ride Sharing with Privacy-Preservation, Trust and Fair Payment Atop Public Blockchain. IEEE Trans. Netw. Sci. Eng. 2021, 8, 1214–1229. [Google Scholar] [CrossRef]
- Hua, J.; Tong, W.; Xu, F.; Zhong, S. A Geo-Indistinguishable Location Perturbation Mechanism for Location-Based Services Supporting Frequent Queries. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1155–1168. [Google Scholar] [CrossRef]
- Pham, A.; Dacosta, I.; Jacot-Guillarmod, B.; Huguenin, K.; Hajar, T.; Tramer, F.; Gligor, V.; Hubaux, J.P. PrivateRide: A Privacy-Enhanced Ride-Hailing Service. Proc. Priv. Enhancing Technol. 2017, 2017, 38–56. [Google Scholar] [CrossRef]
- He, Y.; Ni, J.; Yang, L.T.; Wei, W.; Deng, X.; Zou, D.; Ahmed, S.H. Differentially Private Tripartite Intelligent Matching Against Inference Attacks in Ride-Sharing Services. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22583–22595. [Google Scholar] [CrossRef]
- Niu, B.; Li, Q.; Zhu, X.; Cao, G.; Li, H. Achieving k-anonymity in privacy-aware location-based services. In Proceedings of the IEEE INFOCOM 2014–IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 754–762. [Google Scholar]
- Fu, Z.; Wu, X.; Guan, C.; Sun, X.; Ren, K. Toward Efficient Multi-Keyword Fuzzy Search Over Encrypted Outsourced Data With Accuracy Improvement. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2706–2716. [Google Scholar] [CrossRef]
- Dong, C.; Chen, L.; Wen, Z. When Private Set Intersection Meets Big Data: An Efficient and Scalable Protocol. In Proceedings of the 2013 ACM SIGSAC Conference on Computer & Communications Security, CCS ’13, Berlin, Germany, 4–8 November 2013; Association for Computing Machinery: New York, NY, USA, 2013; pp. 789–800. [Google Scholar]
- Friginal, J.; Gambs, S.; Guiochet, J.; Killijian, M.O. Towards privacy-driven design of a dynamic carpooling system. Pervasive Mob. Comput. 2014, 14, 71–82. [Google Scholar] [CrossRef]
- Chow, C.Y.; Mokbel, M.F.; Liu, X. A peer-to-peer spatial cloaking algorithm for anonymous location-based service. In Proceedings of the 14th Annual ACM International Symposium on Advances in Geographic Information Systems, Arlington, VA, USA, 10–11 November 2006; p. 171. [Google Scholar]
- Martelli, F.; Renda, M. Enhancing Privacy in Ride-Sharing Applications Through POIs Selection. In Proceedings of the 2022 IEEE 23rd International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Belfast, UK, 14–17 June 2022; pp. 444–449. [Google Scholar]
- Nabil, M.; Mahmoud, M.; Sherif, A.; Alsharif, A.; Abdallah, M.M. Efficient and Privacy-Preserving Ride Sharing Organization for Transferable and Non-Transferable Services. IEEE Trans. Dependable Secur. Comput. 2018, 18, 1291–1306. [Google Scholar] [CrossRef]
- Vignesh, R.; Samhitha, B.K.; Suja, C.M.; Divya, S. Privacy-preserving Ride Sharing Scheme with Global Social Network for vehicles using Big Data. Indian J. Sci. Technol. 2018, 11, 21. [Google Scholar] [CrossRef]
- Xie, H.; Guo, Y.; Jia, X. A Privacy-preserving Online Ride-hailing System without Involving a Third Trusted Server. IEEE Trans. Inf. Forensics Secur. 2021, 16, 3068–3081. [Google Scholar] [CrossRef]
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd Annual IEEE Symposium on Foundations of Computer Science, Chicago, IL, USA, 3–5 November 1982. [Google Scholar]
- Baza, M.; Mahmoud, M.; Srivastava, G.; Alasmary, W.; Younis, M. A Light Blockchain-Powered Privacy-Preserving Organization Scheme for Ride Sharing Services. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020. [Google Scholar]
- Ruch, C.; Lu, C.; Sieber, L.; Frazzoli, E. Quantifying the Efficiency of Ride Sharing. IEEE Trans. Intell. Transp. Syst. 2021, 22, 5811–5816. [Google Scholar] [CrossRef]
- He, Y.; Ni, J.; Wang, X.; Niu, B.; Li, F.; Shen, X. Privacy-Preserving Partner Selection for Ride-Sharing Services. IEEE Trans. Veh. Technol. 2018, 67, 5994–6005. [Google Scholar] [CrossRef]
- Shahabi, C.; Kolahdouzan, M.R.; Sharifzadeh, M. A Road Network Embedding Technique for K-Nearest Neighbor Search in Moving Object Databases. GeoInformatica 2003, 7, 255–273. [Google Scholar] [CrossRef]
- Acar, A.; Aksu, H.; Uluagac, A.S.; Conti, M. A Survey on Homomorphic Encryption Schemes: Theory and Implementation. ACM Comput. Surv. 2018, 51, 1–35. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Boneh, D.; Goh, E.J.; Nissim, K. Evaluating 2-DNF Formulas on Ciphertexts. In Proceedings of the Theory of Cryptography; Kilian, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 325–341. [Google Scholar]
- Gentry, C. A fully homomorphic encryption scheme. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2009. [Google Scholar]
- Paillier, P. Public-Key Cryptosystems Based on Composite Degree Residuosity Classes. In Proceedings of the Advances in Cryptology—EUROCRYPT ’99; Stern, J., Ed.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 223–238. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).