Abstract
This paper analyses the multi-objective design of an inductor for a DC-DC buck converter. The core volume and total losses are the two competing objectives, which should be minimised while satisfying the design constraints on the required differential inductance profile and the maximum overheating. The multi-objective optimisation problem is solved by means of a population-based metaheuristic algorithm based on Artificial Immune Systems (AIS). Despite its effectiveness in finding the Pareto front, the algorithm requires the evaluation of many candidate solutions before converging. In the case of the inductor design problem, the evaluation of a configuration is time-consuming. In fact, a non-linear iterative technique (fixed point) is needed to obtain the differential inductance profile of the configuration, as it may operate in conditions of partial saturation. However, many configurations evaluated during an optimisation do not comply with the design constraint, resulting in expensive and unnecessary calculations. Therefore, this paper proposes the adoption of a data-driven surrogate model in a pre-selection phase of the optimisation. The adopted model should classify newly generated configurations as compliant or not with the design constraint. Configurations classified as unfeasible are disregarded, thus avoiding the computational burden of their complete evaluation. Interesting results have been obtained, both in terms of avoided configuration evaluations and the quality of the Pareto front found by the optimisation procedure.
1. Introduction
The innovations in the field of semiconductor devices have paved the way for the diffusion of efficient switch-mode power supplies. In recent years, wide bandgap materials, such as silicon carbide (SiC) and gallium nitride (GaN) devices, enabled the design of high switching frequency power converters, going towards the MHz range [1]. The improvements in the power semiconductor involve higher current and voltage ratings and lower conduction and switching losses, allowing power electronics converters with high efficiency and power density. However, a power electronic converter is not only made up of semiconductor devices. Every converter structure requires the use of passive components, and in particular, magnetic elements. The research in magnetic materials for power electronics did not experience the same growth rate as semiconductor devices since the magnetic technology field had already reached a higher degree of maturity in the past. For this reason, the goals of maximising power density and efficiency should be addressed by better exploiting the available materials and technologies. The design of inductors for power electronic converters represents a significant challenge that involves the evaluation of the compromise between conflicting goals, defined by the high efficiency and the high power density requirements [2,3,4,5,6,7]. The present analysis is focused on the output inductor of DC-DC buck converters. In this topology, the inductor has to ensure an acceptable current ripple in the entire current range of the application. In addition, the devices should guarantee low losses to ensure high conversion efficiency and reduced volume to minimise the size of the converter [8]. However, a significant obstacle to the miniaturisation is represented by the saturation of the magnetic core [9]. In this converter topology, inductors are subject to a magnetic field bias caused by the non-zero average current. The DC magnetic field bias leads to the operation of the core material towards the saturation region of the magnetisation curve. This condition implies that the differential permeability drops to values considerably lower than the initial one, causing a reduction in the differential inductance of the component. Conventionally, the operation in the partially saturated condition has been considered undesirable due to the criticalities introduced by the non-linear behaviour of the inductor. In order to avoid inductor saturation, the standard design rules of inductors for DC-DC converters lead to oversized cores, which do not allow the proper exploitation of magnetic material. However, design configuration operating in partial saturation allows for further reduction in the core dimension, accepting a limited increase in the total losses [9,10,11,12,13,14]. Figure 1 represents a set of design configurations (each dot in the plane represents the results of one configuration) obtained considering only the operation in linear conditions (yellow dots), compared to the ones that are achievable, including the operation in partial saturation (blue dots). As shown, the operation in partial saturation allows the exploitation of smaller core volumes, which would not result in feasible configurations considering only the linear operation [15].
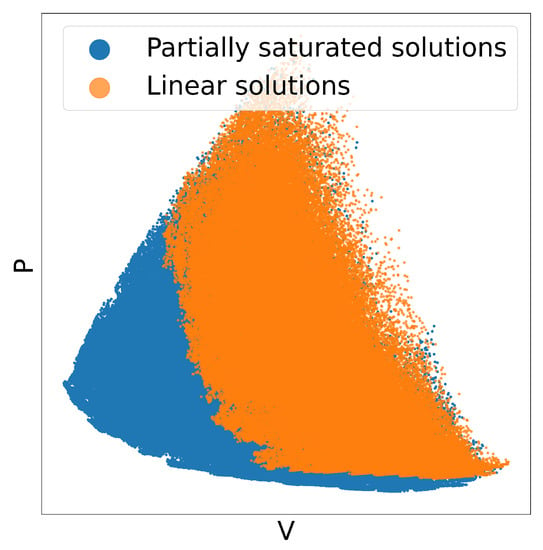
Figure 1.
Qualitative comparison of the solutions evaluated considering the operation in linear and in partial saturation conditions, in the space of the total losses and the core volume. The maximum magnetic flux density considered for the linear operation is 0.2 T.
However, the design of partially saturated inductors requires adopting a non-linear model to evaluate the differential inductance profile of the devices. This task is particularly time-consuming since it requires the solution of the non-linear equivalent reluctance model of the part by means of iterative techniques. The computational effort required by these iterative techniques represents a significant burden when the design optimisation of the inductor is carried out as a multi-objective optimisation problem (given the two conflicting objectives of volume and losses). The multi-objective design of inductors has already been treated in literature [16,17,18,19,20], and it is usually solved by means of population-based metaheuristic approaches. Despite their effectiveness, these approaches typically require the evaluation of many designs before converging. However, many of the designs evaluated during the optimisation procedure (up to 50%) are revealed to be unfeasible since they do not comply with the design constraints on the operative inductance or maximum overheating [21]. Avoiding these unnecessary calculations could then increase the speed of convergence of the optimisation. Therefore, this paper proposes the adoption of a data-driven surrogate model to handle the design constraints in a pre-selection phase of the optimisation. In this approach, the designs generated during the optimisation are first classified by the surrogate model as compliant or not with the design constraints. Configurations classified as unfeasible are disregarded, thus avoiding the computational burden of their complete evaluation.
This paper is structured as follows: in Section 2, the methodology adopted for the design of inductors for DC-DC buck converters is presented and, in Section 3, the specifications of the proposed test case are described. The multi-objective optimisation approach to the design problem is proposed in Section 4 and further described in Appendix A. Section 5 presents the classifier-based approach for the constraint handling of the proposed multi-objective optimisation problem, while Section 6 discusses the achieved results of the proposed methodology. In Section 7, the conclusions of the proposed research are reported.
2. Design Procedure of Inductors for DC-DC Converters
Given the specifications of the converter, defined by the maximum operating current, the input and output voltages, the switching frequency, and the maximum current ripple, the required operating inductance can be computed. In particular, a tolerance range over the prescribed inductance value can be defined. A non-linear reluctance model can be adopted for the preliminary evaluation of the differential inductance profile of the design configurations [22]. The non-linear problem is solved through the polarisation fixed point (FP) technique [23]. The loss evaluation can be performed through analytical computations. In particular, the assumption of neglecting the AC winding losses can be stated, and the winding losses can be determined by computing the DC resistance of the winding [22]. Concerning the losses of the magnetic core, the improved Generalised Steinmetz Equation (iGSE) allows computing the losses under an arbitrary waveform [24,25]. For the sake of clarity, it should be noted that the DC magnetic field bias, typical in inductors operating in DC-DC converters, involves an increase in magnetic losses. The parameters of the iGSE can be adjusted as a function of the applied premagnetising field [26]. However, the dependence of the parameters on the DC bias field has to be investigated with experimental measurements at different frequencies, magnetic flux density, and premagnetising field values. In addition, these parameters are generally not reported by manufacturers. This lack of information forces the designer to neglect the effect of the DC bias on the core loss increase, knowing that the computed value will be underestimated. A further requirement for an output inductor of a DC-DC buck converter is controlled overheating during regular operation. The appropriate estimation of the inductor heating requires also knowing the positioning of the other components on the PCB of the converter and the thermal specifications of the surrounding materials to implement a thermal finite element simulation. However, a preliminary estimation of the temperature rise caused by the inductor losses can be performed considering a natural convection heat transfer condition, with a uniform heat flux density over the outer surface of the core exposed to air.
3. Statement of the Design Problem
The multi-objective optimisation approach is performed on the test case of the simplified model described in Section 2. The selected geometry is the double-E core, and the adopted core material is the N87 ferrite. The specifications of the evaluated case study are reported in Table 1.

Table 1.
Design specifications of the test case problem.
The design variables, shown in Figure 2, are the three geometrical dimensions of the core (width A, height of the single E core B, and central column’s extension F) [27], the air gap’s length g, and the number of turns N. In order to reduce the number of design variables, the cross-section of the central column is assumed to be square and twice as wide as the cross-section of the outer ferromagnetic paths.
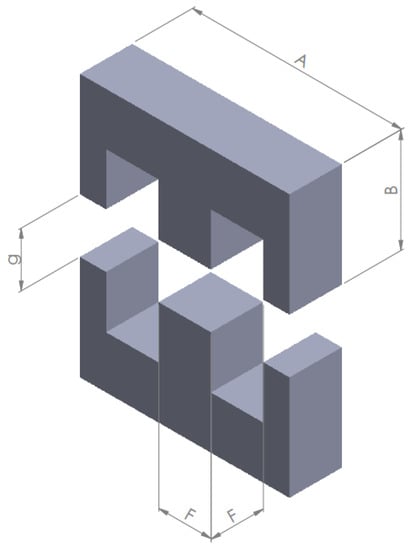
Figure 2.
Three-dimensional representation of the double-E core geometry. The design variables are: the width of the E core A, the height of a single E-core B, the extension of the central column F, and the air gap’s length g.
The geometric design variables can take real values in a fixed range, while the number of turns is an integer quantity. The ranges considered for the design variable are defined in Table 2:

Table 2.
Ranges adopted for the design variables.
A design configuration is feasible only if its differential inductance profile can ensure a feasible current ripple. For this reason, a series of constraints are put on the differential inductance profile, defined as follows:
- Lower bound, ;
- Upper bound, ;
- Inductance drop limit, ;
where is the initial value of the differential inductance, while the other parameters present in the constraints are defined in Table 3.

Table 3.
Parameters adopted in the feasibility constraints of the design problem.
The constraints on the differential inductance profile are represented in Figure 3. The first two conditions define a bandwidth for the admissible inductance values that guarantee the current ripple limits. The third condition refers to the saturation of the inductor. As mentioned in Section 1, solutions that operate in partial saturation help to reduce the core dimension. However, an inductor that goes towards the deep saturation makes the current control critical and implies higher core losses due to the high DC bias magnetic field. A limit to the acceptable saturation rate is fixed with respect to the initial inductance value to avoid this issue. Therefore, a given design configuration must be compliant with the following constraint, given by the intersection of the three:
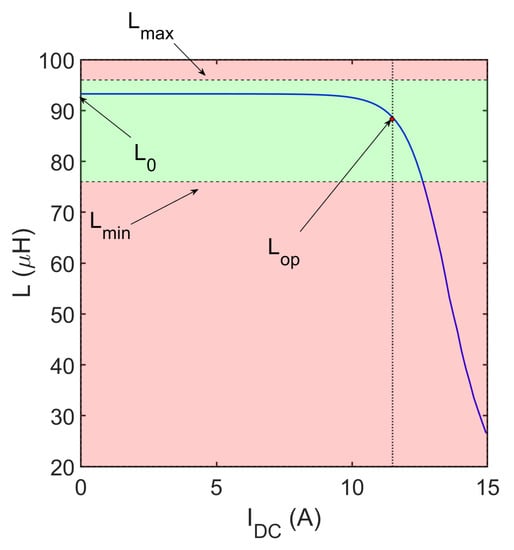
Figure 3.
Differential inductance profile of a design configuration as a function of the output current of the converter. The bandwidth of the admissible inductance value is highlighted in green. The proposed case represents a solution operating in partial saturation.
Another constraint is represented by the maximum over-temperature the core can tolerate, which can be defined as follows:
where T is the over-temperature reached by the core during operation. The value of is also shown in Table 3.
4. Multi-Objective Optimisation Approach
The optimisation problem is configured as the search for the core volume V and total losses P minimisation, complying with the constraints defined in (1) and (2) and reported in Table 3. The two objectives are typically conflicting: a strategy that reduces volume will inevitably result in higher losses. In particular, as presented in [22], for a specific core size and a given switching frequency, a minimum loss configuration can be identified, defined by an adequately selected number of turns and air gap length configuration. In a multi-objective optimisation approach, not a single optimal solution is searched, but rather the set of non-dominated solutions (Pareto front or set, if considered in the objectives or variables space, respectively). A solution can be loosely defined as non-dominated when it is not possible to improve one of the objectives without worsening another one. Once the Pareto set is known, selecting a configuration with low losses and a non-negligible volume or vice-versa depends on the designer’s specific requirements.
Several algorithms have been proposed in the literature to search the Pareto front in a multi-objective algorithm. Population-based algorithms based on metaheuristics, such as Artificial Immune Systems (AIS) [28,29], have proven effective in reproducing the Pareto front on different benchmark problems. However, these algorithms require numerous objective function evaluations before convergence. In the inductor design problem, the evaluation of the objective function requires the computation of the total losses and the component size, which are not particularly costly operations if approached as in [22]. The computation of the constraints in (1) requires the solution of the equivalent non-linear reluctance model proposed in [22], computed with the iterative fixed point technique.
The method adopted in this paper to solve the multi-objective optimisation problem is the Vector Immune System (VIS) presented in [28,29]. This approach exploits AIS, which is intrinsically well-suited to the solution of multi-objective optimisation problems since it maintains the diversity in the population of solutions during the procedure. This method performs well compared to other well-established multi-objective optimisation methods [28,29], such as the widely adopted Non-dominated Sorting Genetic Algorithm II (NSGA-II) [16,18,30].
In brief, the algorithm is based on a population of antibodies that represent candidate solutions to the optimisation problem. All the antibodies representing non-dominated solutions found throughout the procedure are kept in a memory set. The objective is to recreate the true Pareto front (which is unknown) through the known Pareto front (the memory set). The antibodies are evolved through two loops:
- An outer loop (network), where randomly generated configurations are introduced in the population (exploration);
- An inner loop (clonal selection), where the population is improved by means of local mutations (exploitation).
- Further details about the optimisation algorithm can be found in Appendix A.
During the optimisation procedure, new design configurations are generated (both randomly and from local mutations). Each configuration must undergo a series of steps to assess its feasibility and then evaluate the objectives:
- 1.
- First, the geometric consistency is checked (e.g., non-negative area of the core’s windows). An inconsistent configuration is discarded and replaced by a new one if it was randomly generated. Otherwise, if the configuration is a clone (mutated from a feasible configuration), the mutation is gradually reduced until the solution is feasible again.
- 2.
- 3.
- The remaining candidate solutions are evaluated in terms of objectives (volume and total losses).
- The clouds of points in Figure 4 represent all the design configurations explored during a complete run of the optimisation procedure on the test problem, in the objectives space (volume V and total losses P, on the x and y axes, respectively). The colour depends on the feasibility of the configurations and distinguishes those configurations compliant with the design constraints (i.e., good, orange points) from those that are unfeasible (i.e., bad, blue points). Two graphs are reported to further distinguish between parent configurations (Figure 4a) and clones (Figure 4b). It can be noticed that only a small percentage of the configurations generated randomly (parents) is feasible. Clones, instead, have higher chances of complying with the design constraints since they originate from local mutations of feasible configurations.
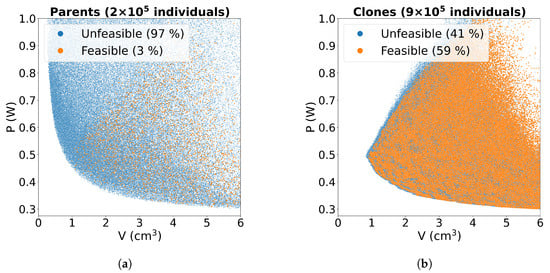 Figure 4. Representation in the objectives space (total losses and core volume) of all the design configurations explored during a run of the VIS multi-objective optimisation algorithm. The orange dots represent the feasible configurations (good), while the blue dots are the unfeasible ones (bad): (a) generated randomly (parents); (b) generated by local mutations of the parents (clones). The total number of parents and clones evaluated and the percentages of good/bad ones are shown.
Figure 4. Representation in the objectives space (total losses and core volume) of all the design configurations explored during a run of the VIS multi-objective optimisation algorithm. The orange dots represent the feasible configurations (good), while the blue dots are the unfeasible ones (bad): (a) generated randomly (parents); (b) generated by local mutations of the parents (clones). The total number of parents and clones evaluated and the percentages of good/bad ones are shown.
Considering the whole run, about 50% of the design configurations explored proved to be unfeasible, resulting in expensive and unnecessary calculations. Indeed, about five hundred thousand fixed-point evaluations could have been avoided. This work aims to adopt a data-driven surrogate model of the feasibility constraints in (1) and (2) to speed up the algorithm. The surrogate model should classify newly generated configurations as compliant or not with the design constraint, based only on the values assumed by the design variables. Configurations classified as unfeasible can then be disregarded, thus avoiding the computational burden of their evaluation.
5. Surrogate Modelling of Constraints for Pre-Selection
The surrogate model must face a binary classification task, as it has to predict if a configuration complies or not with the design constraints. In order to examine the classification task, the same configurations as in Figure 4 can be represented in the design space. Only three variables are considered (extension of the central column F, air gap’s length g and number of turns N, which mainly influence the design’s feasibility), to allow a three-dimensional representation. In this way, it is possible to visualise and highlight the feasibility region in the design space.
Figure 5a shows the feasible (orange points) and unfeasible (grey points) configurations, among those generated randomly. Wide regions of the design space can be easily identified, where only unfeasible configurations can be found. Figure 5b shows instead the feasible and unfeasible (blue points) configurations, among those generated from local mutations of feasible configurations. Since the mutations introduced are small, the figure is able to represent the interface between the feasibility region and the rest of the design space, which does not appear to be uniformly shaped. Since this interface is narrow and largely nonlinear, the classification task is challenging.
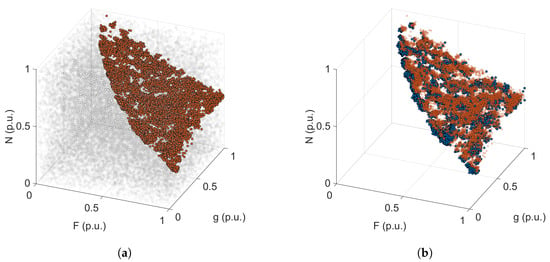
Figure 5.
Representation in a design sub-space identified by the number of turns, the extension of the central column and the air gap length, of all the configurations explored during a run of the VIS multi-objective optimisation algorithm. All the feasible configurations (orange dots) are compared to (a) the unfeasible configurations generated randomly (grey dots); (b) the unfeasible solutions generated with local mutations (blue dots).
5.1. AIS-Based Classifier
Different approaches can be adopted to face this binary classification problem, but as a first attempt, a classifier based on an AIS [31] has been used. As with any supervised method, this classifier uses previous observations to make predictions on unknown data. These previous observations, that serve as a training data set, are labelled data, i.e., configurations whose compliance with the design constraints has already been evaluated. Therefore, each training sample represents a design configuration D, which is identified by the array of the design variables, and is assigned a label y, defined as follows:
The AIS classifier presented in [31] is a supervised method that is based on the concepts of antigens and antibodies. These are both characterised by a value of the and a corresponding label y, which may be unknown in the case of antigens. The training samples are used to create a collection of labelled antigens. The AIS is instead composed of a series of antibodies called memory cells. Each memory cell covers a certain region of the design space or a sub-space, and it is associated with a unique label. The training phase consists of the interactions between the AIS and the training antigens: each memory cell is locally mutated to optimise its capability to recognise the antigenic patterns (i.e., arrays in the design space, or in a sub-space) whose associated label y matches the label predicted by the antibody. At the end of the training phase, each antibody has a recognition region, which is a sphere in the design space, or a sub-space. An antibody is activated when an antigen falls in its recognition region. Therefore, when unknown antigens (unseen and unlabelled data) are presented to the AIS, a collective response is created by combining the response of the activated antibodies. The latter is the label predicted by the AIS classifier.
The rationale behind the choice of this classifier is the common structure with the VIS algorithm, as they are both based on AIS. This can open up interesting possibilities in terms of online training, where the AIS is continuously improved by means of new configurations evaluated during the optimisation procedure, in order to better cover the design space. Nevertheless, in future developments of this research activity, other approaches will be defined to solve the classification problem.
5.2. Effects of the Classifier on the Optimisation
The adoption of the surrogate model in the optimisation process consists of the classification (feasible/unfeasible) of each new configuration generated, prior to its evaluation by means of the fixed point technique. Configurations classified as unfeasible are disregarded and not evaluated with the FP iterative method. Configurations that were classified as feasible are evaluated instead by means of the FP. Since the response of the classifier may be incorrect, combining the responses of the classifier and of the FP evaluation, a confusion matrix such as the one in Figure 6 can be built. The latter contains the different combinations of the classifier-FP responses to a given design configuration, which can be summarised as follows:

Figure 6.
Confusion matrix of the responses given by the classifier system and the evaluation with the FP iterative technique. The traffic lights highlight the effect of the response on the optimisation process: green stands for a correct classification, yellow for an incorrect evaluation that should not affect the output of the optimisation, and red for an incorrect classification which could negatively affect the final result.
- True positives: feasible configurations that are correctly classified as positive.
- False positives: unfeasible configurations wrongly classified as positives. Since they are evaluated with the FP during the optimisation, the incorrect classification implies unnecessary calculation that slows down the procedure.
- True negatives: unfeasible configurations correctly classified as negative, which can be correctly disregarded in the optimisation process.
- False negatives: feasible configurations wrongly classified as negatives, which are therefore disregarded during the optimisation. This is the worst case since it implies discarding solutions potentially belonging to the Pareto Front.
5.3. Evaluation of the Classifier’s Performance
The proposed AIS-based classifier system must be trained on a data set of previously evaluated configurations. The definition of the data set is a critical task that can strongly influence classification accuracy. Figure 4a shows that in the proposed problem, randomly generated configurations are mostly unfeasible. Hence, a training data set generated randomly would be strongly unbalanced, which could result in a weak accuracy. To this end, over 80,000 configurations were generated to extract around 2500 feasible samples. From the remaining (unfeasible) configurations, 2500 were extracted to form a balanced data set that uniformly covers the design space. It should be noted that, for the training of the classifier system, a non-negligible number of conventional feasibility evaluations is required to build up a consistent data set. However, the computational time required for the training is considerably lower than the one required in an optimisation execution. In addition, the classifier training can be generalised for optimisation problems related to different inductance constraints. If the non-linear computation is generalised to a given core geometry and air gap value, the equivalent reluctance profile can be obtained as a function of the applied magnetomotive force. The computed profile is not strictly related to a given inductance value since different numbers of turns allow several differential inductance profiles for the same geometry-air gap combination. From a single set of non-linear problem solutions, different training data sets for different inductance profile constraints can be obtained by relating the computed non-linear reluctance profile to the number of turn values admissible for the considered optimisation problem, further improving the computational efficiency of the proposed approach. After the training phase, a test run of the VIS optimisation has been executed to evaluate the effectiveness of the trained classifier in the multi-objective optimisation process. Therefore, each configuration generated is evaluated both by means of the FP method and the classification approach. Table 4 shows the results of this analysis, divided by parents and clones.

Table 4.
Classifier performances in feasibility evaluation.
Some highlights can be made on the results of the analysis:
- The high percentage of true negatives (around 97%) in the randomly generated configurations considerably reduces the number of FP evaluations in this phase. Despite the high rate of false positives, the low number of total positives identified by the classifier among the parent results in a significant reduction in the unnecessary evaluations of the FP.
- The good performance in the classification of negatives among parents is motivated by the presence of wide areas of unfeasible configurations in the design space (Figure 5a).
- As previously discussed (Figure 5b), the classification task is much harder in the proximity of the interface between the feasibility region and the rest of the design space. Most configurations generated from local mutations are located in this area. This explains the poor performance of the classifier in the clones. In particular, while around 200,000 FP evaluations are saved by correct classification of unfeasible configurations (true negatives), an equivalent number of feasible configurations are wrongly disregarded.
- The percentage of false positives in clones is smaller than in parents. However, around 150,000 configurations are unnecessarily evaluated.
6. Evaluation of the Surrogate Modelling Approach
The AIS-based classifier shows interesting performances in reducing FP evaluations. To further investigate these aspects, a comparison of the results for three different approaches is proposed:
- Execution of VIS optimisation method without a classifier ().
- Application of the classifier only on randomly generated configurations ().
- Application of the classifier both on randomly generated and locally mutated configurations. ().
- For each of the presented cases, 30 optimisation executions are performed. The first result is the average number of FP evaluation calls, reported in Figure 7, in which separated results are reported for the classification of parents and clones.
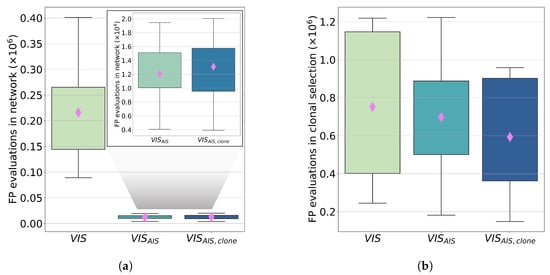 Figure 7. Box plots of the FP executions in the 30 runs of the three tested approaches. The pink diamonds represent the mean value of each case: (a) describes the FP evaluations for the randomly generated cells. A zoom of the results for the two classifier approach is reported in the upper right corner; (b) describes the FP evaluations for the locally mutated cells.
Figure 7. Box plots of the FP executions in the 30 runs of the three tested approaches. The pink diamonds represent the mean value of each case: (a) describes the FP evaluations for the randomly generated cells. A zoom of the results for the two classifier approach is reported in the upper right corner; (b) describes the FP evaluations for the locally mutated cells.
Figure 7a highlights the considerable advantage of adopting the classifier on the randomly generated elements. A considerable FP evaluation saving can be observed since 97% of the parents generated in VIS optimisation are unfeasible. As previously mentioned, the distribution of the unfeasible randomly generated solutions in the design variable space leads to a classification accuracy of 99% on true negative elements. By observing Figure 7b, the adoption of the classifier on clones allows us to reduce the FP iterations, but this result can be further improved by reducing the bad recognition of unfeasible solutions. Figure 8 reports the total FP calls for the three cases.
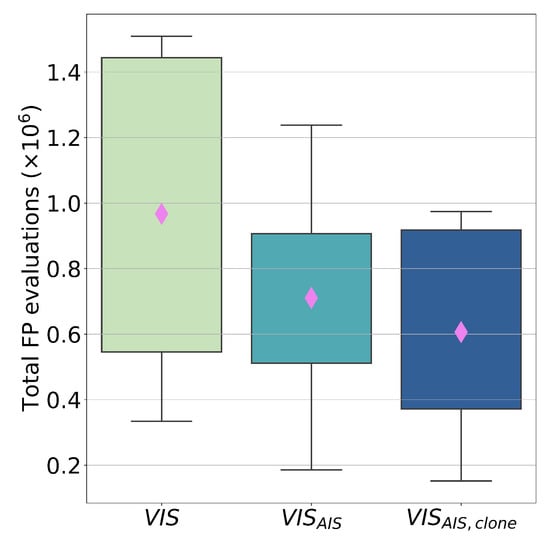
Figure 8.
Box plot of the total FP executions in the 30 runs of the three tested approaches. The pink diamonds represent the mean value of each case.
As previously mentioned, about 50% of the configurations generated in the VIS optimisation are unfeasible, and thus a perfect classifier allows for avoiding, on average, 500,000 FP calls. The results show that the tested classifier avoids 260,000 calls when applied only on randomly generated solutions and avoids 360,000 calls when applied both on parents and clones. These results are quite satisfactory but can still be improved by adopting a more effective classification system in the region of the locally mutated cells. Other considerations can be studied by observing the Pareto Fronts obtained through the three proposed approaches, reported in Figure 9.
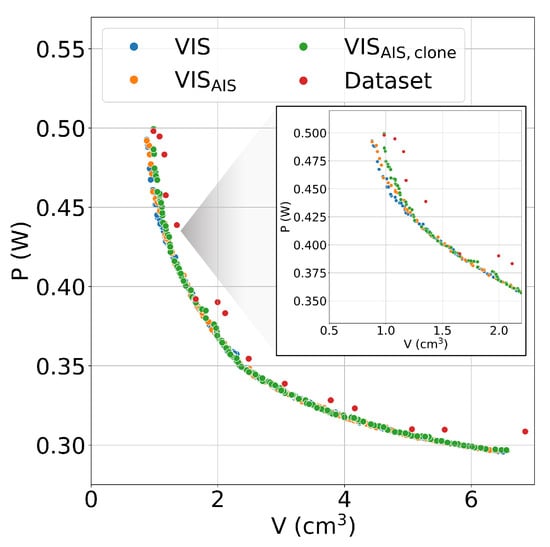
Figure 9.
Pareto fronts of the analysed design case, obtained with the three proposed approaches. The reported fronts are computed by combining the solutions of the 30 executions performed in each case. In addition, the Pareto front of the training-test data set is reported. A zoom of the Pareto fronts in the region of small volumes is also reported to highlight the marked differences in this area.
The proposed Pareto Fronts are defined by selecting the non-dominated solutions between the results of the 30 runs for each tested approach. In addition, the Pareto Front of the randomly generated configurations adopted for the training-test data set of the classifier is reported. As shown, practically none of the configurations in the data set belong to the true Pareto Front.
A substantial overlapping of the three fronts can be observed, except for the region of the lowest volume cores. Clearly, in these regions, the constraint evaluations became more critical for two reasons: The first is related to the core saturation, which is more likely to happen for small volume cores, which are attractive for the operation in partial saturation. The second is related to the maximum over-temperature. A small core solution belonging to the Pareto Front is characterised by non-negligible total losses and a reduced outer surface for heat dissipation that can lead to exceeding the thermal limit fixed by the application specification. It is apparent from Figure 9 how the adoption of the classifier on parents and clones involves a worsening of the Pareto Front, which can be motivated by the high percentage of false negatives classifications in clones. As previously described, false negative configurations are wrongly disregarded in optimisation. The number of wrongly disregarded configurations is about 200,000, and these may include design solutions belonging to the Pareto Front. The worsening of the Pareto Front can be analytically evaluated by considering some performance measurements. In particular, the Reverse Generational Distance (RGD) is evaluated. This performance index computes the distance for each solution in the Pareto True to the closest solution in the Pareto known. The mean value over the True Front is then considered:
Since the Pareto True cannot be analytically evaluated for the presented case, the following assumption is made: the Pareto True is defined as the set of non-dominated solutions evaluated in all the 90 runs performed with the three different approaches. The other considered Pareto quality index is the Spacing (S), which measures how well the solutions of the Pareto Known are distributed. The Spacing is defined as:
where is the mean value of all .
Figure 10 shows the results for the two presented performance measures.
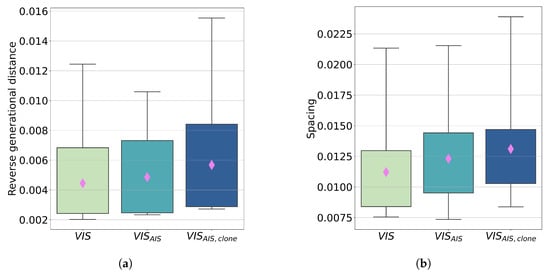
Figure 10.
(a) Box plots of the reverse generational distance index for the 30 runs of the three tested approaches. The pink diamonds represent the mean value of each case; (b) Box plot of the spacing index for the 30 runs of the three tested approaches. The pink diamonds represent the mean value of each case.
A lower value for S and RGD is related to a better quality of the obtained Pareto Front. The Spacing is not particularly affected by the adoption of the classifier since it is mainly determined by the characteristic of the VIS methodology adopted. On the other side, the RGD gets worse as the influence of the classification on the optimisation process increases. In particular, the worst behaviour is found with the adoption of the classifier on parents and clones. As seen before, the wrong classification of the small volume solutions determines a higher distance of the Pareto Fronts obtained with this approach, with respect to the Pareto True that in this region is totally determined by the solutions obtained with the VIS method without classification on the constraint evaluation.
7. Conclusions
The adoption of a classification-based constraint handling in the design of inductors for DC-DC converters aims to reduce the number of time-consuming computations required by the conventional feasibility evaluation approaches, represented by the solution of non-linear equivalent reluctance models or, in a more detailed design procedure, electromagnetic finite element simulations. In this paper, as a first attempt, an Artificial Immune System-based classifier has been selected. The obtained performances indicate the opportunity to considerably reduce the required feasibility evaluation with conventional time-consuming approaches, still obtaining good results in terms of quality indexes of the optimisation process. The evaluated design problem highlights the highly unbalanced nature of the data set available for the classifier training due to the majority of unfeasible configurations in a randomly generated design space. In future developments of this research activity, other classification strategies will be explored to better deal with the unbalanced nature of the problem.
Author Contributions
Conceptualization, G.L., C.S.R., M.R. and L.S.; methodology, G.L., C.S.R., M.R. and L.S.; software, G.L. and L.S.; investigation, G.L. and L.S.; writing—original draft preparation, G.L., C.S.R., M.R. and L.S.; writing—review and editing, G.L., C.S.R., M.R. and L.S.; supervision, C.S.R. and M.R.. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Let us consider a general definition of a multi-objective optimisation problem (MOOP), that can be stated as the search of:
where is the vector of the decision variables, which can assume values in the design space and is the vector of the objective functions (m is the number of optimisation objectives). A feasible region is identified within the design space by the intersection of equality and inequality constraints.
Typically, different objectives are contrasting and cannot be minimised at the same time; hence, a unique solution cannot be found. The solution of the MOOP then consists in finding the set of non-dominated solutions (Pareto set or front if referring to the variables or objectives space, respectively). A solution dominates another solution (), if:
VIS is an AIS-based algorithm [29] that solves a MOOP by attempting to reproduce the Pareto front. Antibodies represent candidate solutions to the MOOP: an antibody contains both the array of the values assumed by the design variables and its image in the objectives space (array of the values of the m objective functions evaluated in ). The algorithm considers a set of candidate solutions (population). A memory set contains all the non-dominated solutions found throughout the optimisation process. The population is improved through a series of steps aimed at maximising the fitness of the antibodies. The latter measures the goodness of an antibody and depends on the dominance relations within the population: if a solution is non-dominated, its fitness is 1, if it is dominated by all the other solutions in the set, its fitness is 0. The antibodies are also evaluated in terms of affinity, which is instead a measure of the distance between antibodies in the objectives space (normalised). In order to maintain diversity and cover the Pareto front more uniformly, the algorithm eliminates antibodies whit high affinity. The basic structure of the algorithm can be depicted as follows:
- 1.
- An initial population of configurations (antibodies ) is randomly generated.
- 2.
- A memory set is also created, initially empty, where all the non-dominated solutions found during the search are stored.
- 3.
- The memory set is built through a network loop, where for iterations or until a stop criterion is reached:
- (a)
- The fitness f of all antibodies in the current population is evaluated, also including the antibodies eventually present in the memory set.
- (b)
- The current population is improved through a clonal selection loop, where for iterations or until a stop criterion is reached:
- i.
- The antibodies in the current population (parents) are replicated into clones;
- ii.
- Each clone is then locally mutated. The random mutation is evaluated as follows: , where is a mutation amplitude parameter and f the fitness of the parent (lower fitness corresponds to larger mutations);
- iii.
- The fitness of the clones is evaluated, also including the antibodies eventually present in the memory set;
- iv.
- The clone with the highest fitness is selected and it replaces the parent in the next generation if it has higher fitness.
- (c)
- The current population and the memory set are merged and their affinity is calculated.
- (d)
- Network selection is performed, removing antibodies with high affinity. The affinity threshold is evaluated as follows: , where m is the number of objectives and is the desired size of the memory set.
- (e)
- The memory set is updated with the non-dominated solutions, among those that survived the network selection.
- (f)
- A fraction (with respect to the current size of the population) of randomly generated new configurations is introduced in the population to increase the exploration of the design space.
- 4.
- The final memory set is taken as the Pareto set of the problem.
- The values of the parameters adopted in all the runs of the VIS optimisation are shown in Table A1.

Table A1.
Values adopted for the parameters of VIS in all optimisation runs.
Table A1.
Values adopted for the parameters of VIS in all optimisation runs.
| Parameter | Value |
|---|---|
| Initial population size, | 50 |
| Number of clones, | 5 |
| Desired size of the memory set, | 100 |
| Number of network loops, | 50 |
| Number of clonal selection loops, | 10 |
| Mutation amplitude factor, | 0.02 |
| Fraction of new antibodies, | 0.4 |
References
- Rashid, M.H. (Ed.) Power Electronics Handbook, 4th ed.; Energy Engineering and Power Technology, Butterworth-Heinemann, an imprint of Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Hurley, W.G.; Wölfle, W.H. Transformers and Inductors for Power Electronics: Theory, Design and Applications; Reprinted with Corrections ed.; Wiley: Chichester, UK, 2014. [Google Scholar]
- McLyman, C.W.T. Transformer and Inductor Design Handbook, 4th ed.; CRC Press: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Hurley, W.G.; Duffy, M.C.; Acero, J.; Ouyang, Z.; Zhang, J. 17—Magnetic Circuit Design for Power Electronics. In Power Electronics Handbook, 4th ed.; Rashid, M.H., Ed.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 571–589. [Google Scholar] [CrossRef]
- Biela, J.; Badstuebner, U.; Kolar, J.W. Impact of Power Density Maximization on Efficiency of DC–DC Converter Systems. IEEE Trans. Power Electron. 2009, 24, 288–300. [Google Scholar] [CrossRef]
- Mühlethaler, J. Modeling and Multi-Objective Optimization of Inductive Power Components. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2012. [Google Scholar] [CrossRef]
- Calderon-Lopez, G.; Scoltock, J.; Wang, Y.; Laird, I.; Yuan, X.; Forsyth, A.J. Power-Dense Bi-Directional DC–DC Converters With High-Performance Inductors. IEEE Trans. Veh. Technol. 2019, 68, 11439–11448. [Google Scholar] [CrossRef]
- Guillod, T.; Papamanolis, P.; Kolar, J.W. Artificial Neural Network (ANN) Based Fast and Accurate Inductor Modeling and Design. IEEE Open J. Power Electron. 2020, 1, 284–299. [Google Scholar] [CrossRef]
- Kaiser, J.; Dürbaum, T. An Overview of Saturable Inductors: Applications to Power Supplies. IEEE Trans. Power Electron. 2021, 36, 10766–10775. [Google Scholar] [CrossRef]
- Milner, L.; Rincón-Mora, G.A. Small saturating inductors for more compact switching power supplies. IEEJ Trans. Electr. Electron. Eng. 2012, 7, 69–73. [Google Scholar] [CrossRef]
- Musumeci, S.; Solimene, L.; Ragusa, C.S. Identification of DC Thermal Steady-State Differential Inductance of Ferrite Power Inductors. Energies 2021, 14, 3854. [Google Scholar] [CrossRef]
- Scirè, D.; Lullo, G.; Vitale, G. Non-Linear Inductor Models Comparison for Switched-Mode Power Supplies Applications. Electronics 2022, 11, 2472. [Google Scholar] [CrossRef]
- Di Capua, G.; Femia, N.; Stoyka, K. Validation of inductors sustainable-saturation-operation in switching power supplies design. In Proceedings of the 2017 IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 242–247. [Google Scholar] [CrossRef]
- Martins, S.; Seidel, A.R.; Perdigão, M.S.; Roggia, L. Core volume reduction based on non-linear inductors for a PV DC–DC converter. Electr. Power Syst. Res. 2022, 213, 108716. [Google Scholar] [CrossRef]
- Gareau, J.; Emadi, A.; Bilgin, B. Power Inductor Optimization Using Non-linear Magnetization Characteristics. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 992–999. [Google Scholar] [CrossRef]
- Sudhoff, S.D. Power Magnetic Devices: A Multi-Objective Design Approach, 2nd ed.; IEEE Press Series on Power and Energy Systems; Wiley: Hoboken, NJ, USA, 2022. [Google Scholar]
- Wang, X.; Zeng, H.; Gunasekaran, D.; Peng, F.Z. Multi-objective design and optimization of inductors: A generalized software-driven approach. In Proceedings of the 2016 IEEE 17th Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Cale, J.; Sudhoff, S.D.; Chan, R.R. Ferrimagnetic Inductor Design Using Population-Based Design Algorithms. IEEE Trans. Magn. 2009, 45, 726–734. [Google Scholar] [CrossRef]
- Wallmeier, P. Pre-optimization of linear and nonlinear inductors using area-product formulation. In Proceedings of the Conference Record of the 2002 IEEE Industry Applications Conference, 37th IAS Annual Meeting (Cat, No.02CH37344), Pittsburgh, PA, USA, 13–18 October 2002; Volume 4, pp. 2445–2450. [Google Scholar] [CrossRef]
- Stratta, A.; Gottardo, D.; di Nardo, M.; de Lillo, L.; Empringham, L.; Espina, J.; Johnson, M. Automated design of integrated inductive components for DC-DC converters. In Proceedings of the 2021 IEEE Design Methodologies Conference (DMC), Bath, UK, 14–15 July 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Solimene, L. Investigation of Inductive Components for Power Electronics Applications. Ph.D. Thesis, Politecnico di Torino, Torino, Italy, 2022. [Google Scholar]
- Solimene, L.; Ragusa, C.S.; Musumeci, S. The role of materials in the optimal design of magnetic components for DC–DC converters. J. Magn. Magn. Mater. 2022, 564, 170038. [Google Scholar] [CrossRef]
- Chiampi, M.; Chiarabaglio, D.; Repetto, M. An accurate investigation on numerical methods for nonlinear magnetic field problems. J. Magn. Magn. Mater. 1994, 133, 591–595. [Google Scholar] [CrossRef]
- Reinert, J.; Brockmeyer, A.; De Doncker, R. Calculation of losses in ferro- and ferrimagnetic materials based on the modified Steinmetz equation. IEEE Trans. Ind. Appl. 2001, 37, 1055–1061. [Google Scholar] [CrossRef]
- Li, J.; Abdallah, T.; Sullivan, C. Improved calculation of core loss with nonsinusoidal waveforms. In Proceedings of the Conference Record of the 2001 IEEE Industry Applications Conference, 36th IAS Annual Meeting (Cat, No.01CH37248), Chicago, IL, USA, 30 September–4 October 2001; Volume 4, pp. 2203–2210. [Google Scholar] [CrossRef]
- Muhlethaler, J.; Biela, J.; Kolar, J.W.; Ecklebe, A. Core Losses Under the DC Bias Condition Based on Steinmetz Parameters. IEEE Trans. Power Electron. 2012, 27, 953–963. [Google Scholar] [CrossRef]
- OCLC: 1197739030; Ferrite Cores. Guidelines on Dimensions and the Limits of Surface Irregularities. Part 8. British Standards Institution: London, UK, 2019.
- Freschi, F.; Repetto, M. Multiobjective Optimization by a Modified Artificial Immune System Algorithm. In Proceedings of the Artificial Immune Systems; Lecture Notes in Computer Science; Jacob, C., Pilat, M.L., Bentley, P.J., Timmis, J.I., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 248–261. [Google Scholar] [CrossRef]
- Freschi, F.; Repetto, M. VIS: An artificial immune network for multi-objective optimization. Eng. Optim. 2006, 38, 975–996. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Dudek, G. An Artificial Immune System for Classification With Local Feature Selection. IEEE Trans. Evol. Comput. 2012, 16, 847–860. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).