Abstract
In the era of digital OT (Operating Theatre), the developments in Robot-Assisted Surgery (RAS) can greatly benefit the medical field. RAS is a method of technological advancement that uses surgical robots to assist complicated surgeries. Its implementation improves the ability of the specialised doctors to perform surgery to a great extent. This paper addresses the dynamics and control of the highly non-linear 3DOF surgical robot manipulator in the occurrence of external disturbances and uncertainties. The integration of non-linear robust SMC (Sliding Mode Control) with smoothing mechanism, FOPID (Fractional-Order Proportional Integral Derivative) controller and fuzzy controller provides a high degree of robustness and minimal chatter. The addition of type-2 fuzzy logic to the controller, named intelligent T2F-SFOSMC (Type-2 Fuzzy-Smoothing Fractional Order Sliding Mode Controller), improves the system’s performance by ruling out the disturbances and uncertainties. The prototype model is developed in a laboratory and its outcomes are validated on OP5600: a real-time digital simulator. The simulation results and experimental results of the proposed T2F-SFOSMC are compared with conventional controllers, which illustrates the efficacy and superiority of the proposed controller’s performance during the typical situation of surgery. The proposed T2F-SFOSMC outperforms conventional controllers by providing greater precision, stability and robustness to time-varying nonlinear multi-incision trajectory.
1. Introduction
Medical robotics is closely linked to human health. Day by day, the use of robotics in medicine is becoming widespread, as it has different benefits in the medical profession. In recent years, RAS has proven to be a booming field. The introduction of robotics in the medical field has substituted the traditional surgical course of action. To carry out difficult, minimally invasive surgical (MIS) operations, surgical robots [1] have high precision and dexterousness. The efficacy and scope of MIS is improved by surgical robotics, as some of the advantages of robotic surgery include the requirement for smaller incisions, greater precision and capacity to replicate identical movements, reduced bleeding, reduced pain, reduced scarring, quicker healing period and a shorter stay in the hospital [2]. In the 1960s, NASA introduced telerobotics for surgery for different uses, such as assistive devices and supporting manipulators, for the first time. Their objective was to provide astronauts with medical assistance [3].
Owing to coupling and nonlinearities effects in the robotic system, apt motion control for surgical robots is a difficult task [4]. For surgical robots, a novel control is presented in this paper. SMC is an efficient robust nonlinear control because of its invariance property towards the system. It deals with the design of the controller to handle uncertainties to achieve robust performance and stability under various assumptions to track the system’s time varying trajectory [4,5,6].
SMC offers robustness and satisfactory monitoring efficiency to disturbances [7,8]. However, it has many drawbacks: optimum sliding surface selection is intricate; sensitive to noise; chattering causes saturation and heating in the different mechanical parts of a surgical robot; composite non-linear dynamics [6,9,10]. Even if the PID (Proportional Integral Derivative) controllers have low tracking performance, they offer better reliability and stability than the SMC controller. Thus, the combo of the advantages of both PID and SMC control guarantees stability and good monitoring performance. Because of increased number of gain parameters, FOPID controllers [11,12] are superior to PID controllers, improving efficiency and flexibility. The coupling of FOPID and SMC would consequently be helpful in increasing the efficiency and robustness of the system [6,13].
Conventional controllers work well for single incisions and linear trajectories. In the case of time-varying and nonlinear trajectory, conventional controllers fail. Chattering, however, remains the major hindrance to the application of sliding mode control and prominently impairs the controlled manipulator’s tracking performance. The chatter obtained through the SMC is attenuated by the smoothing function and the fuzzy logic controller [14,15,16,17,18]. A fuzzy logic controller is an intelligent controller that quantifies linguistic variables using fuzzy logic. It imitates the human decision-making process. They are used in energy management, smart watering system, robots, autonomous vehicles, etc., [19,20,21]. The T1F-SFOSMC (Type-1 Fuzzy-SFOSMC) cannot deal with the uncertainties present in the system because it employs type-1 fuzzy sets that are certain [22]. In order to deal with uncertainty, the type-2 variable MFs (Membership Functions) are used instead of fixed MFs, i.e., type-2 fuzzy control. Type-2 fuzzy logic controllers combined with SMC have also been found to be efficient in other applications such as DC-DC converters [22], aerial vehicles [23,24], wind turbines [25], etc. Uncertainty due to sensor measurement, ageing effect, friction, inertia, geometric parameters, backlash, etc., has an impact on a surgical manipulator’s positioning error. Therefore, the T2F-SFOSMC has been proposed for robot-assisted surgery to ensure precise needle placement and an automated surgical procedure. It employs type-2 fuzzy sets [26,27,28,29,30], including FOU (Footprint of Uncertainty), which provides an additional DOF to handle uncertainties more effectively. In addition, the gain parameters of controllers are found using PSO [31,32,33] (particle swarm optimisation). This paper proposes the T2F-SFOSMC of 3DOF master-slave surgical robot for the application of RAS. Detailed simulation work has been carried out in MATLAB Simulink environment for the practical purpose. In addition, the prototype model has been developed in a laboratory and the results of trajectory tracking with chatter reduction have been validated in real time using OP5600 (Opal-RT: a real-time digital simulator).
The major contributions of the paper are as follows:
- (1)
- Surgical robot, dynamic with robust controllers.
- (2)
- Design, implementation and validation of controllers for robust tracking during typical surgical situation using OP5600.
- (3)
- Proposed T2F-SFOSMC is compared with the existing traditional SMCs based on the time response parameters for time-varying nonlinear multi-incision trajectory in the presence of uncertainties.
The paper’s prompt is structured in the following way—Section 2 discusses the 3DOF surgical robot manipulator model. In Section 3, the different controllers for surgical manipulators are conferred, and Section 4 illustrates and discusses simulation results followed by experimental validation on OP5600, i.e., real-time digital simulator in Section 5. In addition, the last section concludes the paper’s work.
2. Surgical Robot’s Dynamic Model
The paper emphases on motion control of the surgical robots, as illustrated in Figure 1. This motion-controlled manipulator will be of great help in the surgical process. Each joint of the surgical manipulator provides relative motion between the links. The different controllers have been intended to control the position of the surgical manipulator.
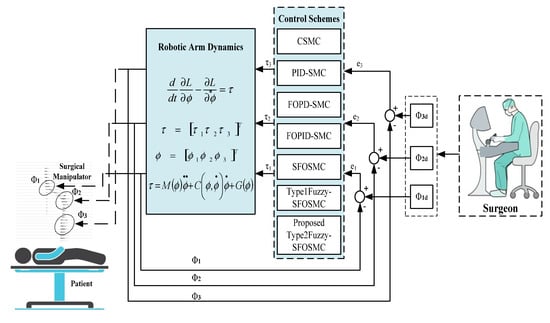
Figure 1.
Outline of the work.
The dynamic model of a three links-three joints surgical robot manipulator is represented in Figure 2. The basics of the dynamics of the manipulator are well known and are more specifically represented in the below derivation. For an n-DOF robot manipulator, the Euler–Lagrange equation is [4]:
where denote position, velocity and acceleration of the manipulator’s joint, τ is input control torque, is inertia matrix, is gravity vector,is coriolis/centripetal matrix andis disturbance vector.
where ΔA, ΔB, ΔD are the uncertainties present in the system; and. For the 3DOF surgical manipulator,
where is the angle between the base and first link of the robotic manipulator, is the angle between second link and first link of the robotic manipulator and is the angle between third link and second link of the robotic manipulator. τ1, τ2 and τ3 are the resultant torques applied on joint1, joint2 and joint3, respectively, of the surgical manipulator. The various controllers intended to control the position of the surgical manipulator are discussed in detail in the following section.
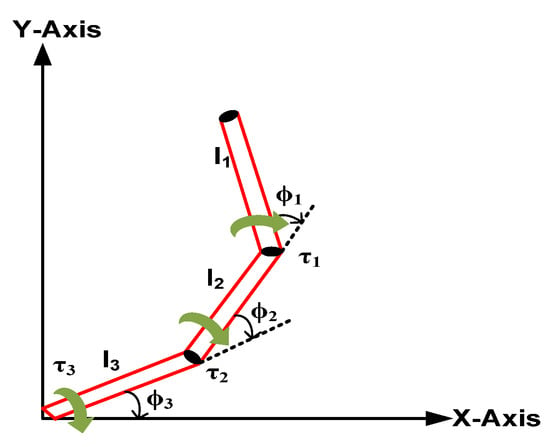
Figure 2.
3DOF robotic manipulator.
3. Different Controllers for Surgical Manipulators
Various controllers are designed to control the joints’ positions, which cause torque to be generated and applied to the surgical manipulator’s joints, as presented in Figure 1. These are discussed in detail below.
3.1. CSMC (Conventional Sliding Mode Controller)
CSMC [6,10] is a non-linear controller applicable to nonlinear MIMO (Multiple-Input-Multiple-Output) systems. It deals with the uncertain systems and withstands external disturbances [8,9]. Since CSMC offers robustness and stability, its inclusion in a surgical robot is required. The robotic control with CSMC is a good approach to attain set-point problems [5].
The CSMC has a PD-based sliding surface that has proportional (Kp) plus derivative (Kd) terms to respond rapidly with an error change, which is specified by [6,10]:
As is well known, the control law of CSMC is the combo of reaching control () and equivalent control () that is given as
To determine the equivalent control, take the derivative of sliding surface, i.e.,
The equivalent torque is given by
where and .
In addition, the reaching control of the control law is given by
Now, the computed-torque control law [6] from Equations (3)–(5) is
The four traditional controllers, i.e., CSMC, PID-SMC, FOPD-SMC and FOPID-SMC, are shown in Figure 3 and discussed in our paper [6].
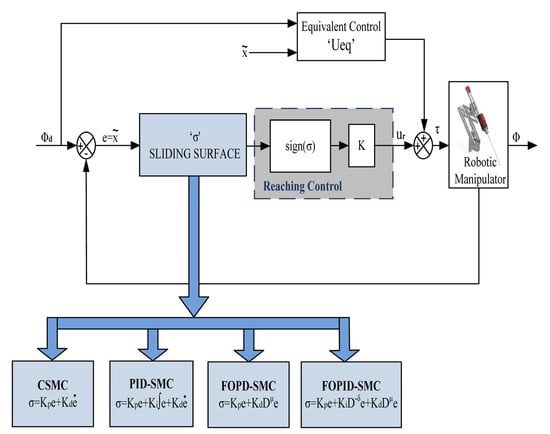
Figure 3.
Conventional SMC controllers for surgical manipulators.
3.2. PID-SMC
The PID-SMC [4,6] controller has a PID-based sliding surface. The incorporation of the integral term into the sliding surface with the derivative term minimises the error, specified in the following equation [6,12]:
Now, the computed-torque control law for the 3DOF surgical robot from Equations (6) and (7) is
3.3. FOPD-SMC
The FOPD-SMC [6] controller has an FOPD (Fractional Order Proportional Derivative)-based sliding surface that has an additional fractional-order derivative. Its sliding surface is defined by:
Substitute the sliding surface ‘σ’ in Equation (6) to obtain the computed-torque control law for the 3DOF surgical manipulator:
3.4. FOPID-SMC
The FOPID-SMC controller has a sliding surface based on the FOPID (Fractional Order Proportional Integral Derivative) with proportional, derivative, integral terms and two additional parameters viz. fractional integration order (δ) and fractional derivative order (µ) [6,11,12,13]. This integration of additional parameters enhances the system’s accuracy and flexibility. The FOPID-based sliding surface is specified by [6,12]:
Substitute the sliding surface ‘σ’ in Equation (6) to obtain the computed-torque control law for the 3DOF surgical manipulator:
3.5. SFOSMC (Smoothing Fractional Order SMC)
The conventional SMC has a discontinuous sign(σ) function that introduces oscillations into the system, which is an unwanted phenomenon called chattering. This causes the heating and saturation of the different mechanical parts of the surgical manipulator. The smoothing function, i.e., the saturation function (sat(σ)) is used to overcome this problem instead of the signum function, as it would remove the chatter by integrating the boundary layer into the control [5,6,9].
This boundary layer introduction and chatter minimization in the FOPID-SMC is known as smoothing FOPID-SMC. In this paper, η (boundary layer thickness) is taken as 0.15 to mitigate the chattering. Therefore, the sat function [5,6] can be characterised as:
The computed-torque controller for surgical manipulators is given by:
From Equations (8) and (9),
The infinite switching introduces undesired chattering in the system. This chatter concern is alleviated by the implementation of fuzzy logic control. Therefore, the proposed fuzzy-SFOSMC controller is designed to make the system more robust and chatter free. The SFOSMC and proposed fuzzy-SFOSMC control schemes are shown in Figure 4.
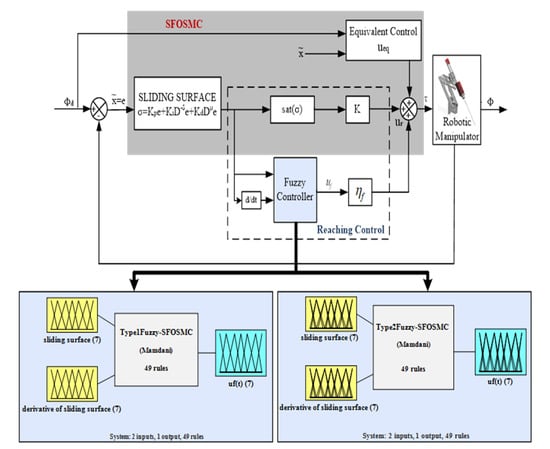
Figure 4.
SFOSMC, T1F-SFOSMC and proposed T2F-SFOSMC controllers for surgical manipulators.
3.6. T1F-SFOSMC
The theory of Artificial Intelligence (AI) has been applied often in sliding mode-controlled systems in recent years. One of the more prominent implementations of the fuzzy-logic theory is the FLC (Fuzzy Logic Controller) [14,15,16,17,18]. Uncertain, noisy and non-linear systems can be brought under control with this controller. The blending of Type-1 FLC and SFOSMC is referred as T1F-SFOSMC (in Figure 4), which includes the advantages and features of both the controllers.
The Type-1 FLC consists of a fuzzifier (binary to fuzzy conversion), fuzzy rules, an inference engine and a defuzzifier (fuzzy to binary conversion). The Mamdani fuzzy inference engine is used in this paper to alleviate the chattering. The max-min aggregation and the centroid method are used for defuzzification. The reaching control law of the fuzzy controller is specified by:
where u1f(t) is the output of fuzzy-SFOSMC and η1f(t) is the normalising factor. The uf(t) is the normalisation of the sliding surface and derivative of the sliding surface. The input and output MFs (Membership Functions) of the fuzzy-SFOSMC are 2D functions as presented in Figure 5a–c, respectively. The input and output MFs are further split into seven fuzzy sets: “PS (Positive Small), PM (Positive Medium), PB (Positive Big), Z (Zero), NM (Negative Medium), NB (Negative Big) and NS (Negative Small)” [4].
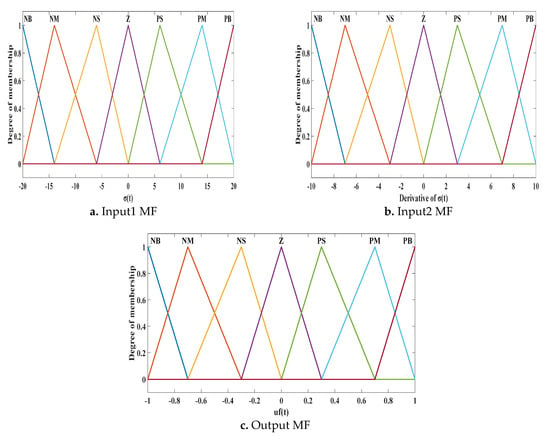
Figure 5.
Fuzzy−SFOSMC Parameters.
These fuzzy membership functions are defined in the fuzzy rules:
where and are the input fuzzy-set labels and Bi is the output fuzzy-set label. The rule matrix table for the T1F-SFOSMC’s reaching control is displayed in Table 1.

Table 1.
Rule matrix for T1F-SFOSMC and proposed T2F-SFOSMC.
The complete T1F-SFOSMC control law is computed as:
3.7. Proposed T2F-SFOSMC
Uncertainty due to sensor measurement, ageing effect, friction, inertia, geometric parameters, backlash, etc., has an impact on a surgical manipulator’s positioning error. The type-1 fuzzy is not capable of handling uncertainties [19]. Therefore, the extended version of T1F, i.e., T2F, handles the uncertainties present in the membership function definition and linguistic variables [26,27]. In order to deal with uncertainty, the type-2 variable MFs are used instead of fixed MFs. A fuzzy logic system is considered to be a T2F system that uses at least one T2F set [28,29,30]. The amalgamation of Type-2 FLC and SFOSMC is referred to as T2F-SFOSMC (in Figure 5), which includes the advantages and features of both the controllers.
The Type-2 FLC comprises of a fuzzifier (binary to fuzzy conversion), fuzzy rules, an inference engine, a type reducer and a defuzzifier (fuzzy to binary conversion). The Mamdani fuzzy inference engine is used in this paper to alleviate the chattering.
Let be the T2F set having x as a primary variable in X domain, v as a secondary variable in Jx domain and µÃ as a secondary MF value [28].
FOU is the region of uncertainty between LMF (lower MF, i.e., ) and UMF (upper MF, i.e., ).
These fuzzy membership functions are defined in the fuzzy rules:
where and are the input T2F sets labels, is the output T2F set label and i is the number of rules. The rule matrix table for the proposed T2F-SFOSMC’s reaching control is displayed in Table 1.
The type-2 FLC has high computational cost compared to type-1 FLC due to type reduction. It is the process to obtain the centroid of fuzzy inference system by converting T2F set to T1F. Here, the Karnik–Mendel type-reduction method is used that determines two end points (ufl and ufr) of centroid (C) [28].
where
L and R are switch-points [28], as switching is between LMF and UMF and .
The max-min aggregation and the centroid method are used for defuzzified output, i.e., specified by:
Thus, the T2F-SFOSMC deals with uncertainties that increase the system’s robustness and performance.
The reaching control law of the proposed controller is specified by:
where u2f(t) is the output of T2F-SFOSMC and η2f(t) is the normalising factor. The u2f(t) is the normalisation of the sliding surface and derivative of the sliding surface. The input and output MFs of the T2F-SFOSMC are shown in Figure 6a–c, respectively.
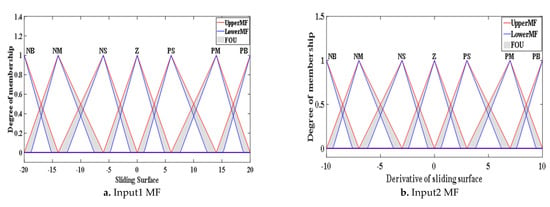
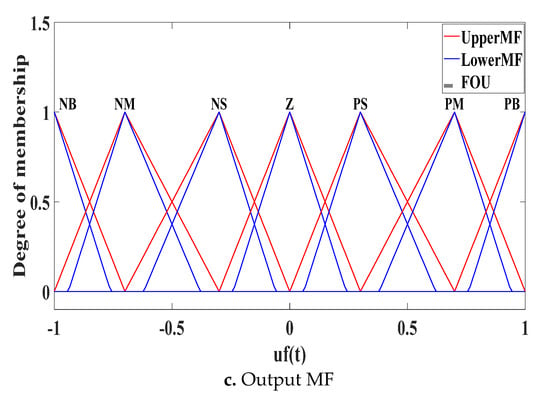
Figure 6.
T2F−SFOSMC parameters.
The complete T2F-SFOSMC control law is computed as:
where
where σ is the FOPID-based sliding surface whose parameters (KP, KI, KD, µ, δ) are found using PSO [31,32,33]. The objective of PSO is to minimize the error; therefore, its objective function is represented by:
4. Materials and Methods
All of the seven controllers discussed are implemented during surgery for a typical situation. It can be clearly seen that the results of the SMC controllers have a chattering problem. This is resolved by using the proposed T2F-SFOSMC controller, as chattering is eliminated due to the existence of the saturation function and FLC.
Conventional controllers work well for single incisions and linear trajectories. In the case of time-varying and nonlinear trajectory, conventional controllers fail. Even chattering in the transient period degrades the performance of conventional controllers. Multiple incisions must be performed on the patient where incision time and depth of incision must be considered. For simulating these surgical situations with nonlinear incision trajectory, an intelligent T2F-SFOSMC is implemented to a master-slave surgical robot. In order to check the transient response of the slave, quick transmission from one incision to another is applied on the patient. Fast response time, precise incision at appropriate location and chattering-free operation is an essential requirement for the case under study. That is why an intelligent nonlinear T2F-SFOSMC control methodology has been developed, implemented and validated on the prototype model for ensuring the satisfactory performance of the master-slave surgical robot.
The predefined trajectories provided by the master robot to the 3DOF-slave robot during surgery are as follows: Φ1d = 1 + tanh(5 ∗ cos(2.5 ∗ (u − 0.5))), Φ2d = 1 + tanh(5 ∗ cos(2.5 ∗ (u − 1))) and Φ3d = 1 + tanh(5 ∗ cos(2.5 ∗ (u − 1.5))) [5]. The slave robot will follow these nonlinear trajectories efficiently.
For Validation on OP5600 (Real-Time Digital Simulator)
The OP5600 is a real-time high performance digital simulator. It has a multicore processor, digital and analog I/O channels. It is equipped with a fast Xilinx Artix-7 FPGA that provides supremacy in simulations and enhances the accuracy of the system. The multiple-core processor allows the simulation to execute at very high speed.
The host system is installed with Opal-RT software, i.e., RT-LAB. RT-LAB is integrated with MATLAB Simulink and the system is connected to the OP5600 digital simulator via Ethernet. DSO (Digital Storage Oscilloscope) DL750 connected to OP5600 via probes captured the results as illustrated in Figure 7.

Figure 7.
Experimental setup.
5. Results and Discussion
The slave robot follows the master robot’s commands successfully. O is the initial position of the slave robot that takes 0.25 s to move the tool to the body, 1 s to the incision, 0.25 s to retract the tool and 1 s to move the tool from O to P in Figure 8.
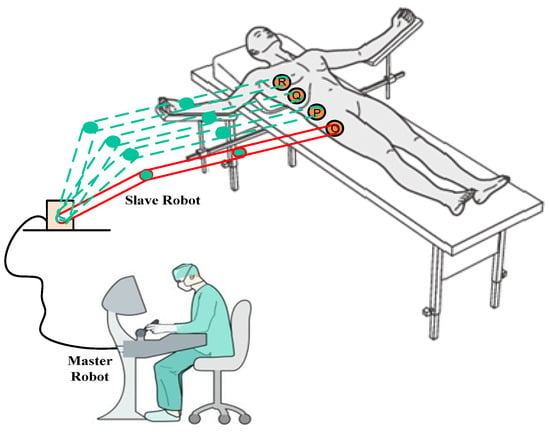
Figure 8.
Case study for RAS with nonlinear incision trajectory.
5.1. Typical Situation during Surgery
The simulation results of the 3DOF surgical manipulator are shown in Figure 9, Figure 10 and Figure 11 representing trajectories tracking, tracking errors and sliding surfaces of the manipulator, respectively. It is observed that the proposed T2F-SFOSMC has better tracking compared to other controllers, namely CSMC, PID-SMC, FOPD-SMC, FOPID-SMC, SFOSMC and T1F-SFOSMC. Because the proposed intelligent T2F-SFOSMC has minimum overshoot and undershoot and minimum tracking error, it improves system performance.
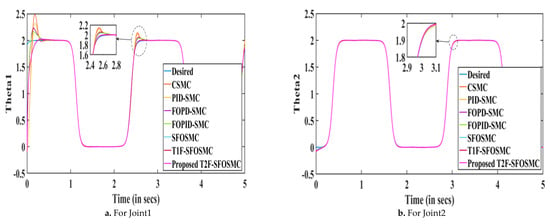
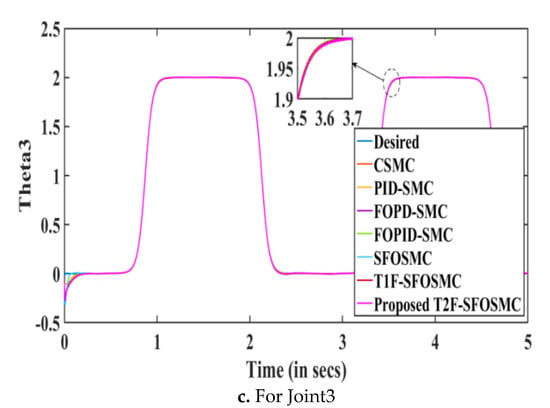
Figure 9.
Trajectory tracking of the 3DOF surgical manipulator for Joint1, Joint2 and Joint3.
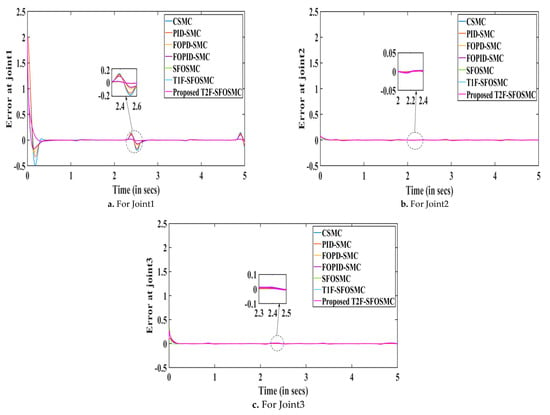
Figure 10.
Trajectory tracking errors of the 3DOF surgical manipulator at Joint1, Joint2 and Joint3.
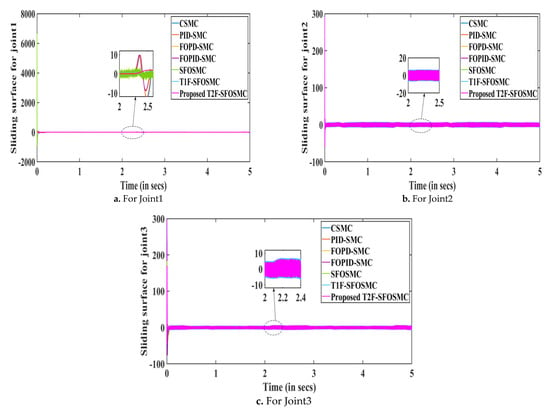
Figure 11.
Sliding surfaces for Joint1, Joint2 and Joint3 of the 3DOF surgical manipulator.
The time response parameters of various controllers for the 3DOF surgical manipulator’s joint1 have been displayed in Table 2. It is observed that the proposed T2F-SFOSMC has greater precision, minimum overshoot and undershoot, minimum integral square error (ISE) and better tracking compared to other controllers for nonlinear multi-incision trajectory, which are the primary requirements of a surgical robot. The achieved accuracy is less than 1mm, which is within the permissible limit. Similarly, the parameters can be found for other joints also. The gain parameters of discussed controllers are displayed in Table 3, which are found using PSO.

Table 2.
Time response parameters of various controllers for the 3DOF surgical manipulator’s Joint1 for 1st and 2nd cycle.

Table 3.
Gain parameters for different controllers.
At times 0.6 s and 2.5 s, disturbances occur, causing the output characteristic to deviate from the desired characteristic, as shown in Figure 12. At 0.68 s and 2.6 s, the proposed T2F-SFOSMC controlled manipulator’s response returns to the desired trajectory faster, indicating that the proposed controller against disturbances has the minimum deviation.
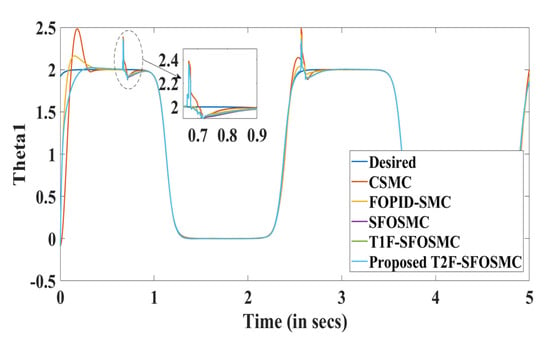
Figure 12.
Trajectory tracking of the 3DOF surgical manipulator for Joint1 with disturbances.
5.2. Validation of Typical Situation During Surgery on OP5600
During surgery, motion control is very crucial. The simulation findings for this situation (explained in Section 5.1) are validated on Opal-RT OP5600. The experimental results for CSMC, PID-SMC, FOPD-SMC, FOPID-SMC, SFOSMC, T1F-SFOSMC and proposed T2F-SFOSMC of the 3DOF surgical manipulator for Joint1, Joint2 and Joint3 are illustrated in Figure 13, Figure 14 and Figure 15, respectively, which are captured in DSO. The following sub-figures show the desired trajectory (), actual trajectory (), tracking error (e) and sliding surface (s) of all three joints of the 3DOF surgical manipulator. Figure 13, Figure 14 and Figure 15 demonstrate that the proposed T2F-SFOSMC controlled 3DOF surgical manipulator has less tracking error, less transients, less chattering, more precision and better trajectory tracking than previous controllers, even for repeated identical motions and uncertainties, which are the primary requirements of a surgical robot.
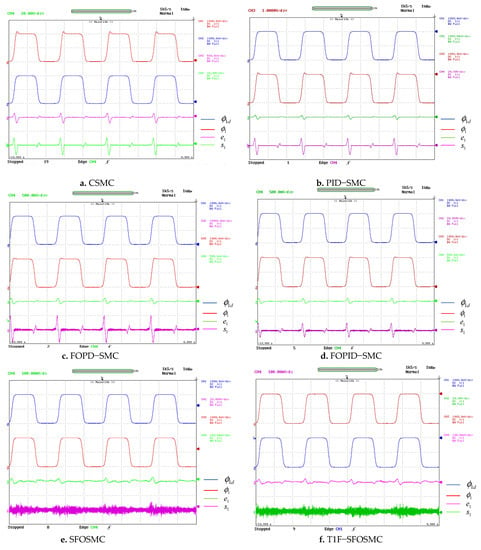
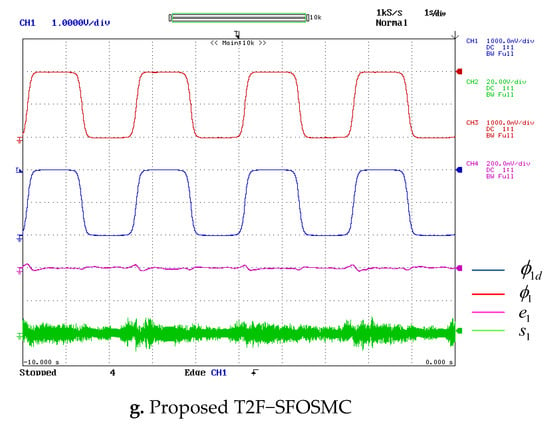
Figure 13.
Trajectory tracking of the 3DOF surgical manipulator for Joint1.
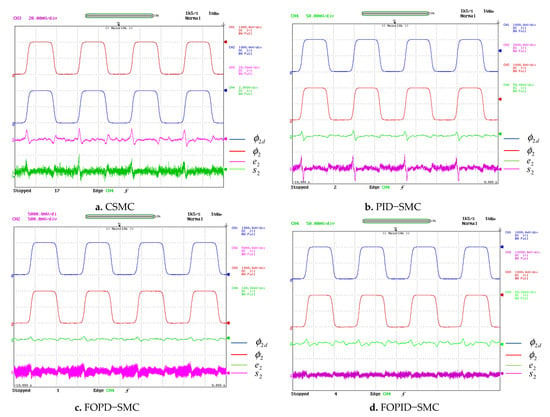
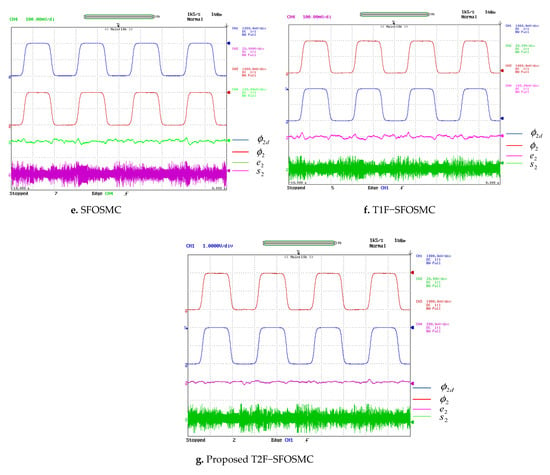
Figure 14.
Trajectory tracking of the 3DOF surgical manipulator for Joint2.
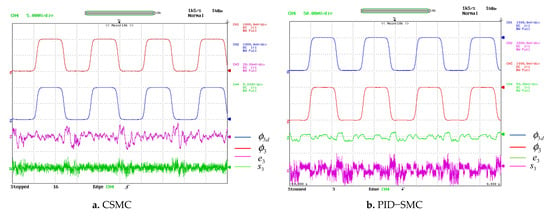
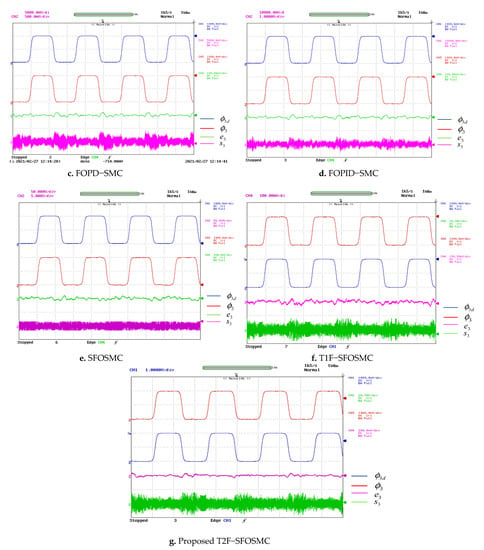
Figure 15.
Trajectory tracking of the 3DOF surgical manipulator for Joint3.
6. Conclusions
In this paper, various controllers for a three link surgical manipulator have been discussed. From the aforementioned findings, it can be inferred that the proposed T2F-SFOSMC controller for the slave robot follows the commands of the master robot efficiently. The CSMC controller has an overshoot of 24.25% and an undershoot of 4.3633%, which has been minimized to a significant degree, i.e., 0.1699% and 0.0587% by using the T2F-SFOSMC controller. The achieved accuracy is less than 1mm, which is within the permissible limit. The proposed intelligent T2F-SFOSMC controller provides greater precision, stability and robustness to time varying nonlinear multi-incision trajectory among all the controllers in the occurrence of external disturbances and uncertainties, which are the primary requirements of surgical robots. Both simulation results and experimental results exemplify that the proposed controller has minimal error of tracking and better transient response with less chattering than other conventional controllers.
Author Contributions
Conceptualization, Methodology, Investigation, Data Curation, Validation, Writing: S.S. Resources, Review, Editing, Supervision: P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Upon request to corresponding author.
Conflicts of Interest
No conflicts of interest.
References
- Kawashima, K.; Kanno, T.; Tadano, K. Robots in laparoscopic surgery: Current and future status. BMC Biomed. Eng. 2019, 1, 12. [Google Scholar] [CrossRef] [PubMed]
- Subido, E.D.; Pacis, D.M.; Bugtai, N.T. Recent technological advancements in laparoscopic surgical instruments. AIP Conf. Proc. 2018, 1933, 040007. [Google Scholar]
- Corliss, W.R.; Johnsen, E.G. Teleoperator Controls. An AEC-NASA Technology Survey; NASA SP-5070; NASA Technology Utilization: Washington, DC, USA, 1968. [Google Scholar]
- Qureshi, M.S.; Swarnkar, P.; Gupta, S. A supervisory on-line tuned fuzzy logic based sliding mode control for robotics: An application to Surgical Robots. Robot. Auton. Syst. 2018, 109, 68–85. [Google Scholar] [CrossRef]
- Qureshi, M.S.; Kaki, G.N.; Swarnkar, P.; Gupta, S. Robust control techniques for master–slave surgical robot manipulator. In Harmony Search and Nature Inspired Optimization Algorithms; Springer: Singapore, 2018; pp. 599–609. [Google Scholar]
- Sachan, S.; Swarnkar, P. Design of smoothing FOPID sliding mode controlled robotic manipulator for Robotic-assisted Surgery. Int. J. Recent Technol. Eng. 2019, 8, 5002–5007. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, L.; Wang, Z.; Xia, Y. Continuous finite-time control for uncertain robot manipulators with integral sliding mode. IET Control Theory Appl. 2018, 12, 1621–1627. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Piltan, F.; Sulaiman, N.; Rashidi, M. Design and implementation of sliding mode algorithm: Applied to robot manipulator-a review. Int. J. Robot. Autom. (IJRA) 2011, 2, 265–282. [Google Scholar]
- Gopal, M. Nonlinear control structures. In Digital Control and State Variable Methods, 3rd ed.; Tata McGraw-hill: Noida, India, 2010; pp. 575–581. [Google Scholar]
- Shah, P.; Agahse, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Varma, A.; Sachan, S.; Swarnkar, P.; Nema, S. Comparative analysis of conventional and meta-heuristic algorithm based control schemes for single link robotic manipulator. In Intelligent Computing Techniques for Smart Energy Systems: Proceedings of ICTSES 2018; Springer: Singapore, 2019; Volume 607, pp. 39–44. [Google Scholar] [CrossRef]
- Tejado, I.; Djari, A.; Vinagre, B.M. Two strategies for fractional sliding mode control of integer order systems by system augmentation: Application to a servomotor. IFAC Pap. OnLine 2017, 50, 8103–8108. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Qureshi, M.S.; Singh, P.; Swarnkar, P.; Goud, H. Robotics solutions to combat novel corona virus disease2019 (COVID-19). SSRN 2020. [Google Scholar] [CrossRef]
- Spong, M.W.; Vidyasagar, M. Robot Dynamics and Control; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Sarkhel, P.; Banerjee, N.; Hui, N.B. Fuzzy logic based tuning of PID controller to control fexible manipulators. Springer Nat. Appl. Sci. 2020, 2, 1–11. [Google Scholar] [CrossRef]
- Avazpour, M.R.; Piltan, F.; Ghiasi, H. Intelligent trajectory control of robotic-assisted surgery. Int. J. Hybrid Inf. Technol. 2015, 8, 73–90. [Google Scholar]
- Wu, H.; XU, Z. Fuzzy logic in decision support: Methods, applications and future trends. Int. J. Comput. Commun. Control 2020, 16. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, J.; Zheng, W. Trajectory tracking for an autonomous airship using fuzzy adaptive sliding mode control. J. Zhejiang Univ. SCIENCE C 2012, 13, 534–543. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, Y.; Zhu, Z.; Zheng, W. Positioning control for an unmanned airship using sliding mode control based on fuzzy approximation. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2014, 228, 2627–2640. [Google Scholar] [CrossRef]
- Medhaffar, H.; Derbel, N. Fuzzy second-order sliding mode control design for a two-cell DC-DC converter. Math. Probl. Eng. 2020, 2020, 1693971. [Google Scholar] [CrossRef]
- Al-Mahturi, A.; Santoso, F.; Garratt, M.A.; Anavatti, S.G. Self-learning in aerial robotics using type-2 fuzzy systems: Case study in hovering quadrotor flight control. IEEE Access 2021, 9, 119520–119532. [Google Scholar] [CrossRef]
- Yang, Y.; Niu, Y.; Lam, H.-K. Sliding Mode Control for Networked Interval Type-2 Fuzzy Systems via Random Multiaccess Protocols. IEEE Trans. Fuzzy Syst. 2022. [Google Scholar] [CrossRef]
- Lahlou, Z.; Ben, K.M.; Boumhidi, I. Sliding mode controller based on type-2 fuzzy logic PID for a variable speed wind turbine. Int. J. Syst. Assur. Eng. Manag. 2019, 10, 543–551. [Google Scholar] [CrossRef]
- Nafia, N.; Kari, A.E.; Ayad, H.; Mjahed, M. Robust interval type-2 fuzzy sliding mode control design for robot manipulators. Robotics 2018, 7, 40. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning—1. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Mendel, J.M. On KM algorithms for solving type-2 fuzzy set problems. IEEE Trans. Fuzzy Syst. 2013, 21, 426–446. [Google Scholar] [CrossRef]
- Naderolasli, A.; Chatraei, A. One DOF robot manipulator control through type-2 fuzzy robust adaptive controller. J. Autom. Mob. Robot. Intell. Syst. 2019, 13, 65–70. [Google Scholar] [CrossRef]
- Humaidi, A.J.; Najem, H.T.; Al-Dujaili, A.Q.; Pereira, D.A.; Ibraheem, I.K.; Azar, A.T. Social spider optimization algorithm for tuning parameters in PD-like interval type-2 fuzzy logic controller applied to a parallel robot. Meas. Control 2021, 54, 303–323. [Google Scholar] [CrossRef]
- Goud, H.; Swarnkar, P. Investigations on metaheuristic algorithm for designing adaptive PID controller for continuous stirred tank reactor. MAPAN 2019, 34, 113–119. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Chao, K.-H.; Hsieh, C.-C. Photovoltaic Module Array Global Maximum Power Tracking Combined with Artificial Bee Colony and Particle Swarm Optimization Algorithm. Electronics 2019, 8, 603. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).