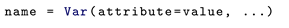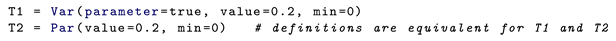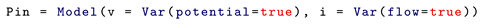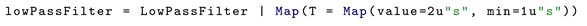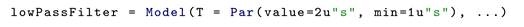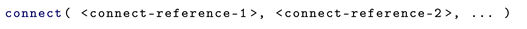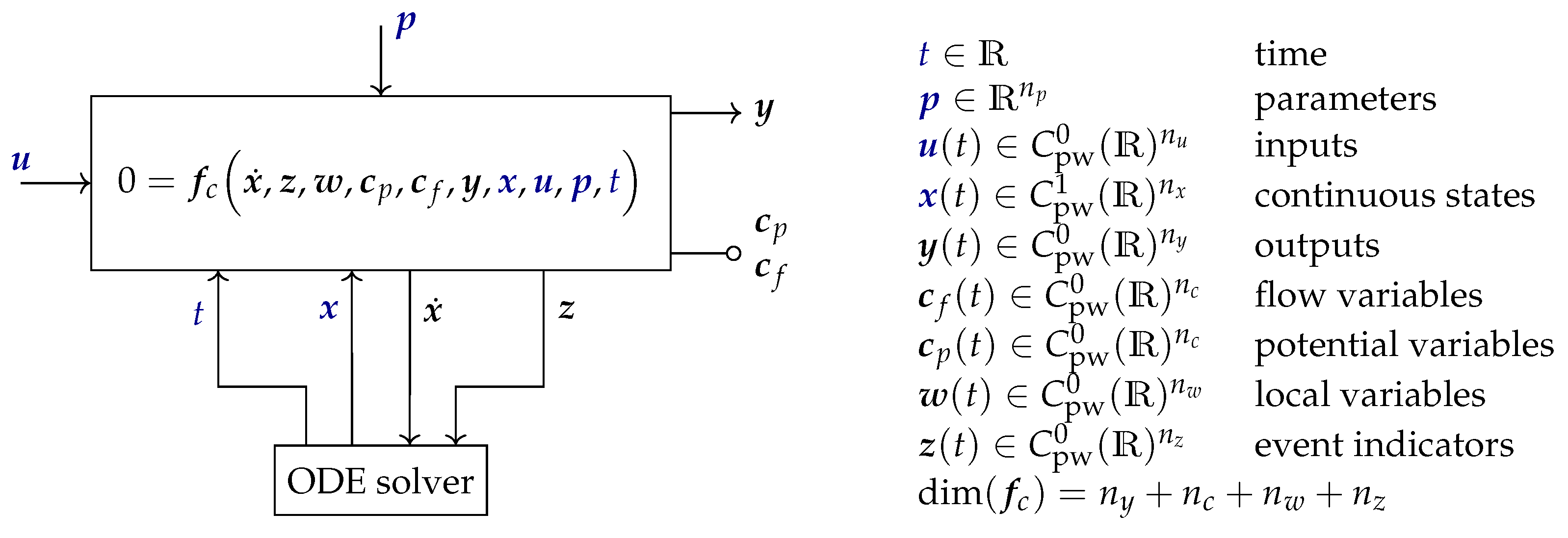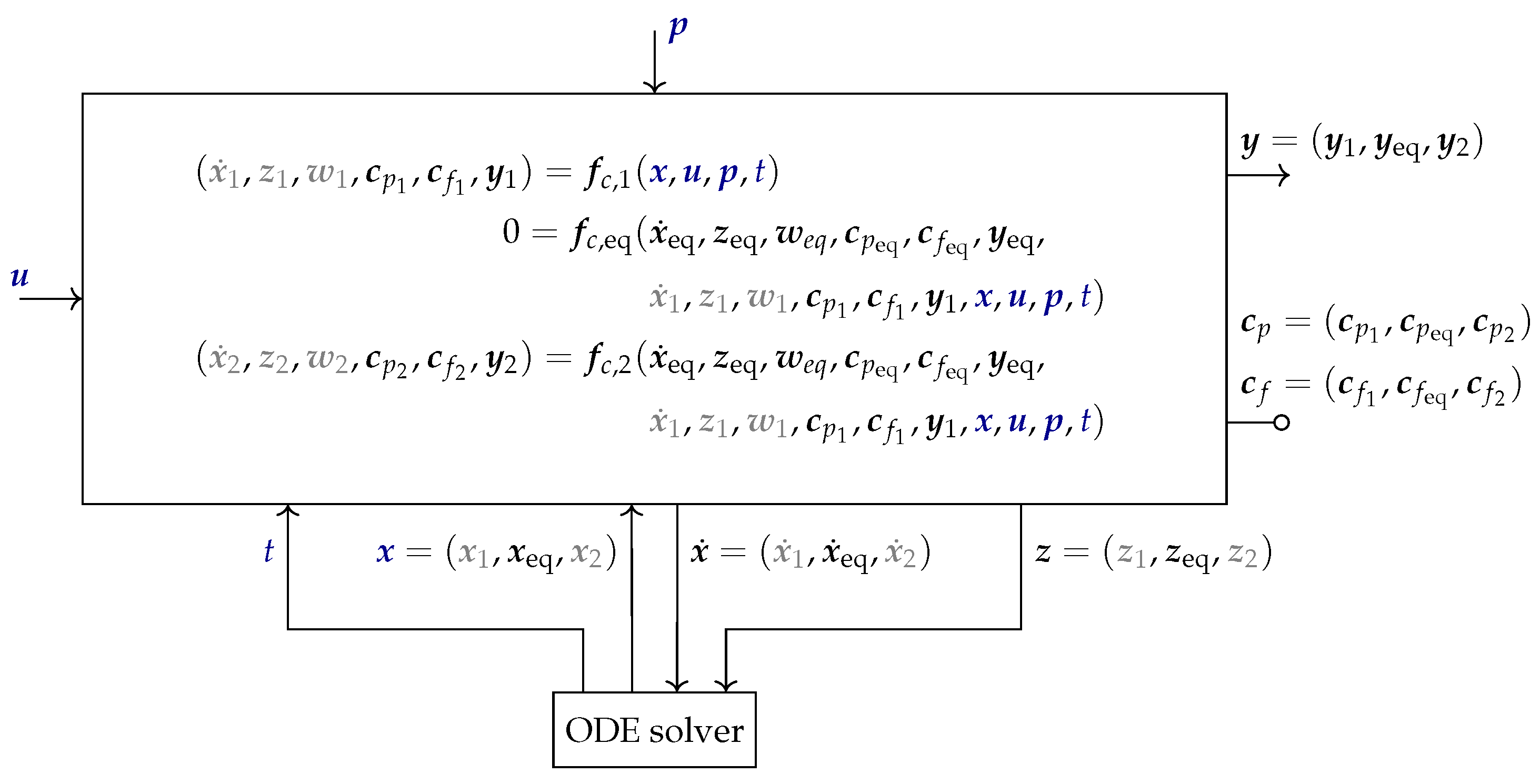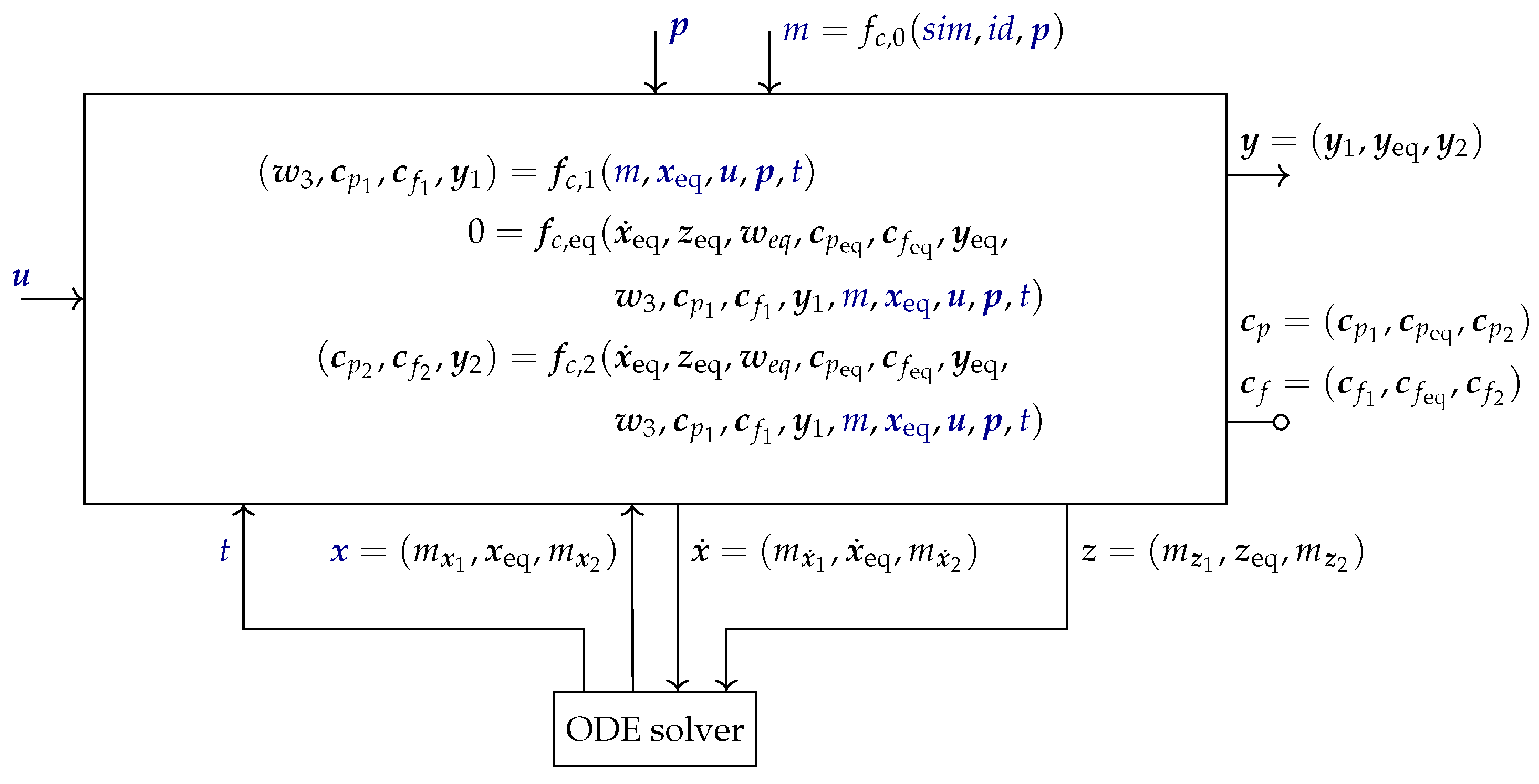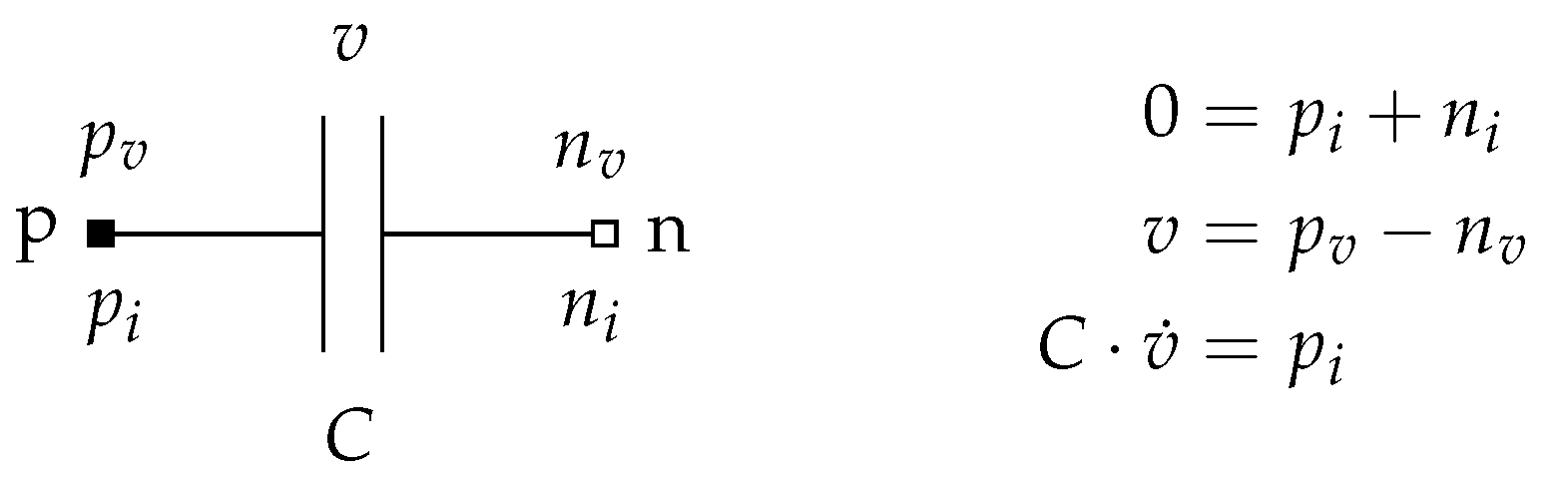1. Introduction
The standardized, declarative and equation-based Modelica language [
1] and the open source and commercial tools supporting Modelica [
2] are in widespread use in scientific and industrial applications to model, simulate and design cyber-physical systems. Modelica can be seen as a format to define large sets of differential, algebraic and discrete equations in a standardized way on a high, user-friendly level.
Modelling languages that are declarative and equation-based have the principle advantage that complex models can be defined on a high level because sophisticated symbolic algorithms allow automatic transformation into a low-level format that can be solved with standard numerical solvers for ODEs (ordinary differential equations). The principle drawbacks are that (a) the approach does not scale for large systems because the equations of
n instances of a model component are present
n times in the generated code, and (b) specialized modelling techniques and algorithms that are successfully utilized in various physical domains cannot be directly applied. For example, the multibody community has designed specialized methods for efficient simulation of 3D-mechanical systems ( see, e.g., [
3]) that cannot be directly utilized by an equation-based language.
Modia [
4] is an experimental, open source modelling and simulation system that is used to develop new approaches to overcome the limitations of declarative, equation-based modelling languages, for example, by combining equation-based modelling with domain-specific algorithms, especially from the multibody and fluid fields, or by using very simple, yet powerful, language semantics that define models with hierarchical collections of name/value pairs. Modia consists of a set of Julia packages, most importantly of packages Modia.jl (
https://github.com/ModiaSim/Modia.jl, accessed on 13 January 2023) and Modia3D.jl (
https://github.com/ModiaSim/Modia3D.jl, accessed on 13 January 2023), and relies heavily on the powerful programming language Julia [
5] and the Julia eco-system (
https://julialang.org/, accessed on 13 January 2023).
In this article, we present a new approach to modelling and simulating equation-based systems where variables can appear and disappear during a simulation without re-generation and re-compilation of code when the numbers of equations and states change during events. The method is presented in a generic, mathematical way and can be in principle applied to all types of declarative, equation-based modelling languages, such as Modelica. A concrete implementation is given for Modia, together with several applications that are based on this new feature.
Equation-based languages define models with DAEs (differential algebraic equations). With structural analysis methods such as the Pantelides algorithm [
6] or Pryce’s ∑-method [
7], along with further symbolic transformation techniques, it is possible to transform DAEs to ODEs that can be solved with standard numerical methods.
Variable-structure systems are models where equations change during simulation. The idea of multi-mode modelling is to define model components with state machines where component equations change whenever a transition to another state occurs; see, e.g., [
8]. One difficulty is to efficiently treat such models. Another difficulty is that a transition can lead to Dirac impulses. Benveniste, Caillaud et al. [
9,
10,
11] extended the structural analysis with the Pantelides algorithm and Pryce’s ∑-method for multi-mode models. In [
11], it is demonstrated how a multi-mode Modia model is treated by re-generating and re-compiling code on-the-fly with Julia when a state transition occurs and initializing in the new states even if Dirac impulses occur.
Höger [
12] also worked on Pryce’s ∑-method for variable-structure modelling. Zimmer [
13] used a run-time interpreter to process the DAE equations at run-time, when the structure and/or the DAE index was changing. The limitations of this approach are that impulsive behaviour is not supported and that the simulation time is one or more orders of magnitude larger than if compiled code is used. Pepper et al. [
14] described the semantics of variable-structure modelling with state machines. Mehlhase [
15] provided a Python-based approach where transitions can be made between pre-defined models. Elmqvist, Mattsson et al. [
8,
16] proposed high-level descriptions of multi-mode models in Modelica by extending the synchronous clocked state machines to continuous-time state machines.
Tinnerholm et al. [
17] provided a Julia-based implementation of Modelica called OpenModelica.jl that supports variable-structure systems. A distinction is made between an explicit and an implicit variable structured system. For the explicit variable structured system the transition between states of the system are explicitly encoded by the user. Thus, all equations and variables of the system are known beforehand and the compiler and the simulation runtime need to process the entire model at once. For the implicit variable structured systems predefined events trigger a re-compilation of the model with Julia on-the-fly during simulation.
All current proposals for variable-structure systems either need to know the entire models for all modes beforehand and switch between these models during simulation, or the entire model is newly processed and code re-generated and re-compiled (or interpreted) whenever the equation structure is changed. In this article, several novel features are introduced that overcome current limitations:
The sizes of array equations can be changed after code generation. A simple example is shown in
Section 2, where the parameter matrices of an LTI (Linear Time-Invariant) system can still be provided with different dimensions after generation and compilation of code.
Built-in model components are introduced that scale for large systems because the component equations are split into a (usually) large part that is encoded in a small set of pre-compiled functions and into a (usually) small part in form of standard equations which is processed with the entire model. A simple example is shown in
Appendix B.1, where the core part of a discretized partial differential equation is present in pre-compiled functions and the (acausal) component is defined with four scalar equations that are independent of the discretization.
Variables and equations of built-in model components can appear and disappear during simulation, without re-generation and re-compilation of code, provided these variables and equations are part of the pre-compiled functions. Simple examples are shown in
Appendix B, where (a) the number of volumes of a discretized partial differential equation can be changed after generation and compilation of code, and (b) the number of equations and states of a two-stage rocket are changed during simulation due to the separation of stages.
The limitation of the new approach is that built-in components cannot be designed for arbitrary (useful) connection scenarios. For example, built-in components cannot be used in a way so that one or more of its pre-compiled functions need to be differentiated. Therefore, the approach is not as general as if all equations of an entire model are newly processed when the model’s structure is changing. However, the class of systems that can be practically handled is still large and has the advantage that it scales for large systems and leads to efficient simulations because code is not re-generated and re-compiled on-the-fly during simulation.
This article is organized as follows: An overview is given in
Section 2 of how to handle Modia models where the number of states changes after the model code is generated and compiled but before simulation begins. In
Section 3 and
Section 4, a new, general method is described in which states and other variables can be introduced and removed during simulation without having to re-generate and re-compile the model code. This approach is specialized for 3D mechanical systems in
Section 5, and two applications of multibody systems with dynamically changing degrees of freedom are presented in
Section 6. Additionally, in
Appendix A, a short overview of Modia is given, and in
Appendix B, other examples with the new approach are provided.
2. Changing Number of States after Model Translation
In this section, an overview is given of how the symbolic and simulation engine of Modia can treat models where the number of states can be changed after generation and compilation of the model’s code and before simulation is started.
Appendix A gives an overview of the modelling language Modia. In
Section 4, models are treated in which the number of states can be changed during simulation. All this is done without re-translation, and the simulation speed is therefore hardly influenced when using these new techniques.
Traditional object-oriented modelling languages, in particular, the Modelica language, define variable types and array sizes precisely. This information is used by the symbolic engine when generating code that is compiled into binary form. Modia does this differently in order to take full advantage of the Julia language. In particular, the goal is that Modia models can use all variable types that can be described with Julia. Since Julia has a very rich type system with type inference, it makes no sense that a language such as Modia tries to replicate this very powerful underlying engine. As a consequence, the Modia language and Modia’s symbolic engine do not have the complete information about the variable types because a variable type can be determined in the Julia compiler inference pass.
For this reason, a Modia model basically defines a set of unknown variables, without necessarily knowing the types of these variables, and a set of equations, along with a set of known variables (=parameters). Note, an unknown variable might also be an instance of a mutable Julia struct, as will be shown below. The basic requirement is that the number of unknown variables and the number of equations must be equal. For example, if a variable is a vector, then an equation must be present that is able to compute this vector. Whether this requirement is fulfilled or not might only be detected by the Julia compiler during compilation of the generated model code, or even only during execution of the model code. Furthermore, a variable is typically treated as one symbol and the associated equation as one symbol-equation, even if the symbol is an array. Two examples are given in Listing 1.
| Listing 1. An array equation must be defined for an array variable and an array must be declared
with an init or start array value when its sizes cannot be inferred. |
![Electronics 12 00500 i001 Electronics 12 00500 i001]() |
As a consequence, the size of a variable typically has no influence on the symbolic engine or the code generation: The generated equations are basically the same, whether a variable is a scalar or has, let us say, 1000 elements. Note, all this is different to current Modelica tools, where variables and equations are typically scalarized before symbolic processing takes place (e.g., a vector of 1000 elements is replaced by 1000 scalars, so 1000 symbols are used in the symbolic engine).
Array sizes of parameters and of variables defined with init or start attributes can be changed in Modia after code generation, provided they are not defined as static arrays. Some examples are given in Listing 2.
| Listing 2. Examples of array equations. The sizes of the statically sized arrays A1, y1 cannot be changed after compilation. The sizes of arrays A1, y1 can be changed after compilation. |
![Electronics 12 00500 i002 Electronics 12 00500 i002]() |
A1,y1 are statically sized arrays, and their dimensions cannot be changed after @instantiateModel(..) has been called. In contrast, A2,y2 are standard Julia arrays, and their dimensions can be changed with the merge attribute of the simulate!(..) command after compilation of the generated getDerivatives function.
In the generated function getDerivatives, the statically sized state vector y1 is always newly generated by utilizing the corresponding elements from the model state vector _x in the SVector constructor. This constructor allocates memory on the stack, and operations on y1 are efficiently implemented in package StaticArrays. New arrays needed in calculations are automatically constructed again on the stack (which is an efficient operation). For example, Julia’s multiple dispatch feature will deduce at compile time, that A1 * y1 is a static array (because A1 and y1 are static arrays and the operator * is overloaded to return a static array), and therefore, var"der(y1)" is generated on the stack as a static array.
Auxiliary memory _m.x_vec[1] is allocated for the state vector y2 whenever the merge-attribute has been processed. Before function getDerivatives is called, the corresponding elements of the model state vector _x are copied into _m.x_vec[1], and this vector is then accessed with the alias name y2 due to y2 =_m.x_vec[1] (y2 is a reference to _m.x_vec[1]). The generated array equations’ code does not depend on the array sizes of the involved variables. The drawback of non-static arrays is that intermediate computations, and left-hand side variables such as var"der(y2)", allocate new memory on the heap, whenever the corresponding statements are executed. If there are many such statements, this can reduce the efficiency of the simulation. In the next section, built-in components are introduced that do not have this drawback. Arrays used in functions of built-in components operate on memory that is allocated once on the heap and not in every model evaluation.
3. Built-In Components
In this and the next section, a new, general method for handling equation-based models is described, where states and other variables can be introduced and removed during simulation without re-generation and re-compilation of the model code. The method is described in a generic, mathematical way and is practically demonstrated with an implementation in Julia/Modia. In principle, the method can also be used for other modelling systems, for example, in an extended version of Modelica.
To simplify the description and focus on the new technique, time-discrete systems, time events, event iteration, and super-dense time (see, e.g., [
1] Appendix B and [
18] Section 3.1) are not discussed in this article. However, in the Modia implementation, these features are included.
3.1. Acausal Components
Declarative, equation-based modelling languages, such as Modelica or Modia, define acausal component models as shown in
Figure 1. In this context, acausal means that interface variables are present that are neither inputs nor outputs of the component (
in
Figure 1). Instead, the connection between a component and the symbolic transformation defines the order equations are evaluated, and whether an interface variable is provided to the component equations or is computed by the component equations.
In
Figure 1, the following definitions are used: Let
be the set of real numbers and assume
.
is the space of functions which are bounded and
k-times continuously differentiable in
; see, e.g., [
19]. This means
is the function space of 1-time continuously differentiable functions.
is the function space of continuous functions. Furthermore, due to events, there are non-continuous jumps.
is the space of piecewise (pw) one-time continuously differentiable functions in
n dimensions, and
is the space of piecewise (pw) continuous functions in
n dimensions.
Figure 1 shows the minimal smoothness requirements of the variables. Depending on the structure of the equations
and how the component is connected with other components, higher smoothness might be required; see, e.g., [
20].
An acausal component, according to
Figure 1, consists of a set of implicit equations
, e.g., the equations in the
equation section of a Modelica model or the equations in the quoted vector that are assigned to variable
equations in a Modia model. It can be connected with other components via inputs
u, outputs
y, and connectors containing pairs of potential
and flow variables
. As usual, when connecting potential and flow variables via connectors, the corresponding potential variables are set equal, and the sum of the corresponding flow variables is set to zero. It is required that a connector has only equal pairs of potential and flow variables to ensure that any connection of acausal components is globally balanced. In other words, the number of equations and the number of unknowns of any set of connected components is equal, provided every component is locally balanced. A component is called locally balanced if
and
. For details, see [
21].
The equations of all components of a model, together with the connection equations, form a set of DAEs. The set of DAEs is transformed into a set of ODEs and is solved by an ODE integrator. In every model evaluation, the time
t and the continuous states
x are supplied to the model by the solver. Using the symbolically processed equations, the derivative of the states
and the event indicators
z are calculated and returned to the solver. Hereby, linear and/or non-linear algebraic equation systems might be solved within the model; see, e.g., [
1] Appendix B.
3.2. Acausal Components with Pre-Translated Mathematical Functions
Elmqvist [
22] proposes a generic method to split the equations of an acausal component (see
Figure 1) into causal and acausal partitions. The intuition is that the causal partitions are always evaluated in the same order, regardless of how the component of
Figure 1 is connected with other components. These partitions are sorted, explicitly solved for the unknowns, and pre-translated. In contrast, the evaluation order of the acausal partition depends on the actual connection of the component, and this partition is kept as an implicit equation system. The method of Elmqvist defines the causal partitions as mathematical functions where the states and state derivatives are known in the calling environment. It is then possible that the symbolic engine differentiates these functions if needed. In this article a variant of this method is used, where the information about states and state derivatives is hidden in these functions and then a symbolic engine cannot differentiate these functions any more, resulting in limitations on how a component can be utilized in an overall model. The benefit of this variant is that the number of states can be changed during simulation without influencing the symbolic transformation and code generation of the overall model.
For certain cases, it is possible to find better partitioning (smaller acausal part) if special connection topologies are being considered. For example, a component without potential and flow variables (input/output block) is usually used in a way that the inputs are provided externally, and the outputs are computed from the component equations. Partitioning is then performed for this common situation. All equations can be sorted and solved for the unknowns, and the entire code can be pre-translated. When the inverse of an input/output block shall be determined, the outputs are provided externally, and the inputs are computed from the component equations. It could be that this inverse model cannot be determined from a pre-translated block, because it may be necessary to differentiate equations and this is not possible if the information about the states is hidden in the pre-translated block as done below.
If all code of a pre-translated block is included in one function, an implicit equation system might occur when connecting the block, whereas no implicit equation system might occur if the code is included in two functions. For an example, see [
18] Figure 5. This example demonstrates that even if a partitioning in causal and acausal parts is made, there is still the difficulty of deciding whether to put all causal code in one or in several functions.
If potential and flow variables are present in a component, common connection scenarios are that either the potential or flow variables or a combination of both are provided externally. In order to prepare for all these cases,
implicit dummy equations
are defined. Every element of every argument appears in every equation of
, so (
1) has full incidence of all of its arguments. Mathematically, (
1) defines a large set of potential connection possibilities. Note, more general scenarios could be treated, if
u and
y would be arguments of
too. However, this results usually in a larger acausal part. Sorting the following equations,
under the assumption that
are known and utilizing only structural information (whether a variable appears or does not appear in an equation, see, e.g., (
https://modiasim.github.io/ModiaBase.jl/stable/Tutorial.html, accessed on 11 December 2022, Sections 1.1–1.4), results in a sorted set of equations that has at least one implicit equation system,
that cannot be split into smaller implicit equation systems by sorting. All equations of (
1) are included in (
3) because (
1) has full incidence. Equations
are a subset of
and form the acausal part of the component because these equations are needed to compute all the arguments of
, and so the potential and flow variables of
Figure 1. All other sorted equations can be explicitly solved (possibly by solving linear and/or non-linear equation systems) and packed into functions
that are called either before or after (
3). Removing (
1) from the sorted equations results in
Figure 2.
Note, the unknown variables
of
Figure 1 are split into three parts; for example,
, where
is an output argument of function
,
is computed from the implicit equation system
, and
is an output argument of function
. Furthermore,
might be split in several functions, depending on the expected usage scenarios. When the acausal component of
Figure 2 is connected with other components and the overall model is
sorted,
is called before equations
are evaluated, because all output arguments of
are (possible) arguments of
. Function
is called afterwards, because variables computed by
and
are (possible) input arguments of
.
The big advantage of an acausal component according to
Figure 2 is that functions
can be pre-translated once in advance, so that symbolically processing an overall model, and generation and compilation of code, can be made much more efficiently as with the original formulation of
Figure 1.
3.3. Acausal Built-In Components
In order that the number of variables, and especially the number of states, can change during simulation
without re-generating and re-compilation of code, the scheme from the previous subsection is changed by storing the
grey variables of
Figure 2 inside an internal memory
m; see
Figure 3.
In the sequel, such components are called acausal built-in components. Contrary to the previous figures in this section,
in
Figure 3 are no longer mathematical functions but functions of a programming language where argument
m is both an input and an output argument to the respective function. The memory
m is exchanged between the functions
. Function
copies states
from the solver into
m. Functions
copy the state derivatives
and the event indicators
from these functions to the solver.
One issue is that the states
x and the output variables
of function
are (possibly) present in
, as seen in
Figure 2. It would then not be possible to add or remove these variables during simulation without re-translation. In such a case, re-formulations are needed, e.g., by computing some part of the expressions present in
in a function that has the memory
m as argument, so that variables
are no longer visible in
. It might also be necessary to hide some of these variables in (new) local, algebraic variables
that are returned from
and used in
; see
Figure 3.
The big benefit of an acausal built-in component is that the hidden states
and their derivatives are not visible in the model equations. Consequently, it is in principle possible to change the number of states during simulation, as is shown in
Section 4. Furthermore, the code parts inside functions
are pre-translated and present once, independent of the number of instances of the built-in component that are used in a model. As a result, the effort to symbolically process and translate the equations can be drastically reduced. A drawback of acausal built-in components with internal memory
m is that they might be used in a way requiring one to differentiate functions
, which is not possible due to this memory.
A simple acausal built-in component of an electrical capacitor is discussed in
Section 3.4. A more involved acausal built-in component describing heat transfer in a rod is discussed in
Appendix B.1.
3.4. Application: Capacitor
In
Figure 4, an equation-based model of a capacitor is shown that is defined by three equations. A Modia implementation of this model is given in
Appendix A.2.
Additionally, the same model is defined as (a) an acausal component with mathematical functions and (b) as a built-in component with functions of a programming language (that have internal memory) in the form of pseudo-code in
Table 1. Note, function
of the built-in component is called once during setup of the simulation run. This function allocates a record or a struct that holds the internal memory
m for the component and copies the parameters into this memory.
This capacitor model is just used as demonstration of the principle, due to its simplicity. The formulation as a built-in component does not give an advantage, because the equation section has four equations, and the function bodies are tiny, whereas the pure equation-based model consists of three equations. Note, when two capacitors defined as built-in components with internal memory are connected in parallel, then both capacitors return the respective state from function . Since the parallel connection introduces an equation , an implicit equation system with three equations for two unknowns is present. Therefore, such a model will be rejected (the issue is that due to the parallel connection, can be computed from , but then cannot be a state as defined in the built-in component).
4. Changing the Number of States during Simulation
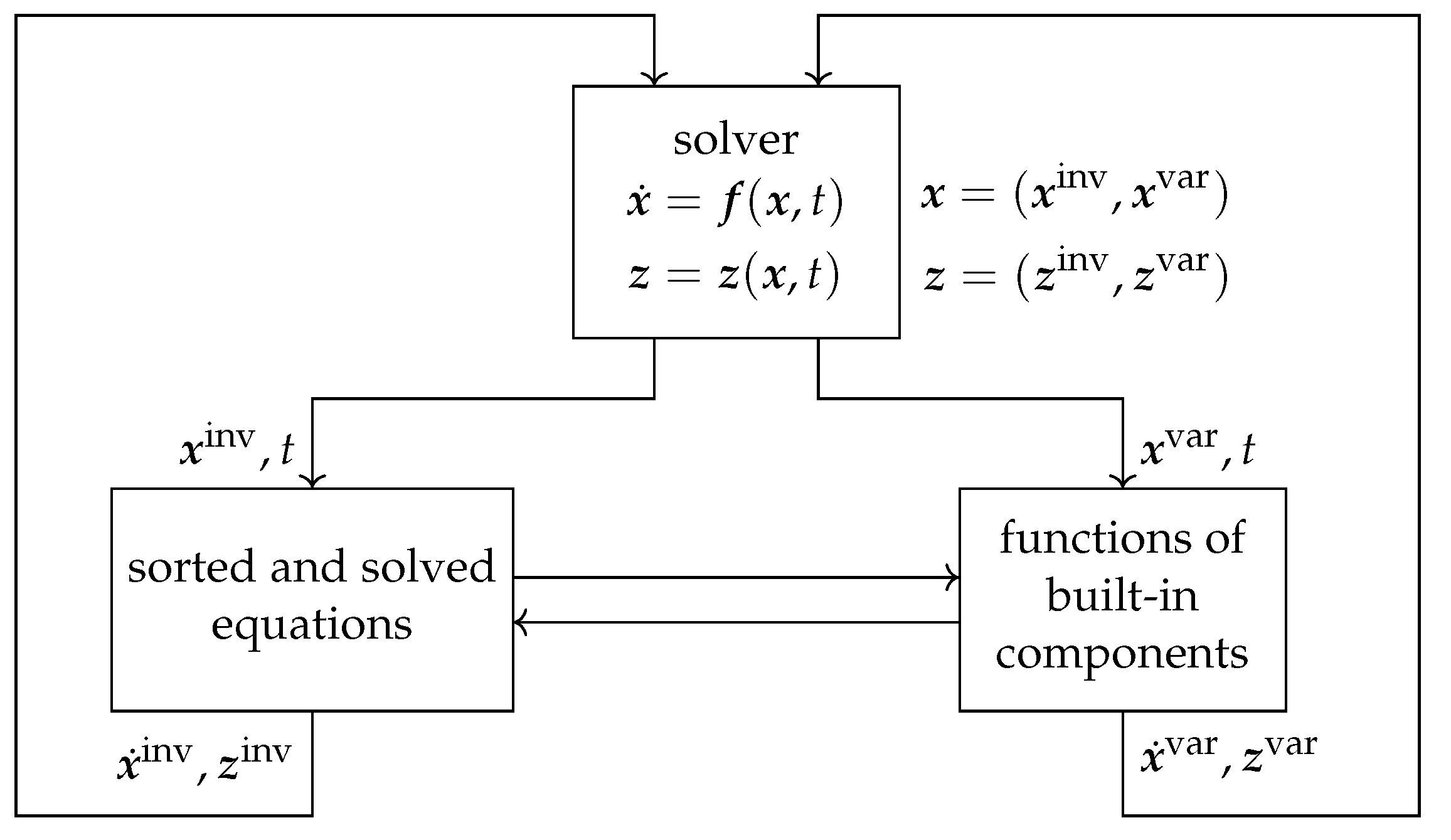
In order that the number of states can be changed during simulation (without newly generating and translating code) the generic concept sketched in
Figure 5 is used. The variables of the solver (state vector
x and the vector of event indicators
z) are split into an invariant and a variant part:
and
. The dimensions of the invariant parts were fixed before the simulation starts. The dimensions of the variant parts can change during events in the simulation. The variables of a model are characterized by the following attributes:
Invariance (inv): Variable name, type, and number of dimensions are fixed before translation. The dimensions of an invariant variable (e.g., length of a vector) can be changed before simulation starts. The solver provides vector to the model function that contains the sorted and solved equations. The elements of are copied into the elements of the invariant state variables of the model. The computed derivatives of the invariant state variables are copied into vector and the computed invariant event indicators are copied into before the model’s function returns. All variables defined and used in an equation section are invariant variables. This includes all input/output arguments of the called functions.
Variant (var): Variables can appear and existing variables can disappear during events. The type and the number of dimensions of a variant variable cannot be changed after it is first introduced in a simulation run. However, its dimensions (e.g., the length of a vector) can be changed at event initiation. All model variables defined inside functions of built-in components are variant variables. Before a variant state variable of the model is used in a function of a built-in component, its elements are retrieved from vector provided by the solver. After the derivatives of variant state variables of a model are computed, they are copied into vector provided by the solver.
As defined above, all variables present in the sorted and solved equations, including the variables that are input/output arguments of built-in component functions, must be invariant variables. Under this restriction, it is possible to sort and solve the equations of all components/built-in components and generate/translate code, provided (a) the symbolic transformation algorithms treat an array as one symbol during the assignment phase, as sketched in
Section 2, and (b) no function of a built-in component needs to be differentiated. Note, this implies that all names, types, and number of dimensions of all interface variables of a component (
of
Figure 1) are fixed before translation starts and cannot be changed after translation.
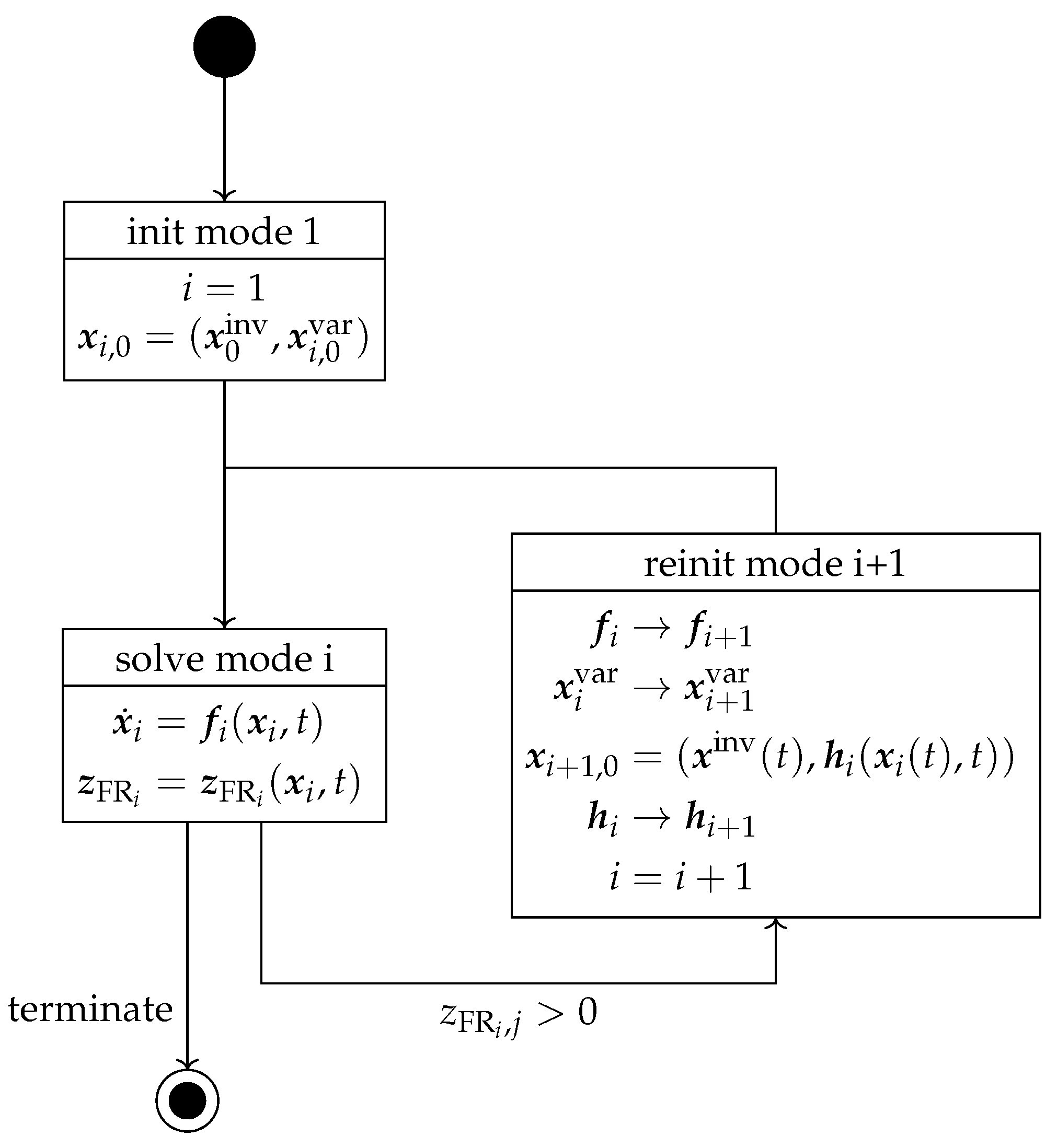
A simulation run is partitioned into phases that are called segments or modes, as sketched in
Figure 6.
A run starts with mode
, and the corresponding system is initialized with the initial states
. The ODE
of actual mode
i is solved until either a termination condition is reached or a full restart (FR) event indicator
becomes positive. In the latter case, the system switches to the next mode
with potentially new equations and potentially different variant states than in the previous mode. Initial values
in mode
are (a) the invariant states at the current time instant
t of mode
i,
; and (b) initial variant states that are computed from the states of mode
i with function
. Reinitialization is a complex topic because Dirac impulses can occur. For more details, see [
11] Section 4, in which a general reinitialization method for a large class of multi-mode systems is presented. In all the examples discussed in this article, Dirac impulses do not occur, so reinitialization in these cases is straightforward. The re-initialized mode is solved until it is terminated or another full restart event is triggered. Note, the number of modes is usually not known in advance.
Since variables may appear and disappear at events and theses changes are not known in advance, new schemes are needed to store result data. In [
23], such a proposal is given, introducing signal tables as a format for exchanging data associated with simulations based on dictionaries and multi-dimensional arrays with
missing values. This format was developed and evaluated with the open source Julia package SignalTables (
https://github.com/ModiaSim/SignalTables.jl, accessed on 12 December 2022) and is used in Modia.
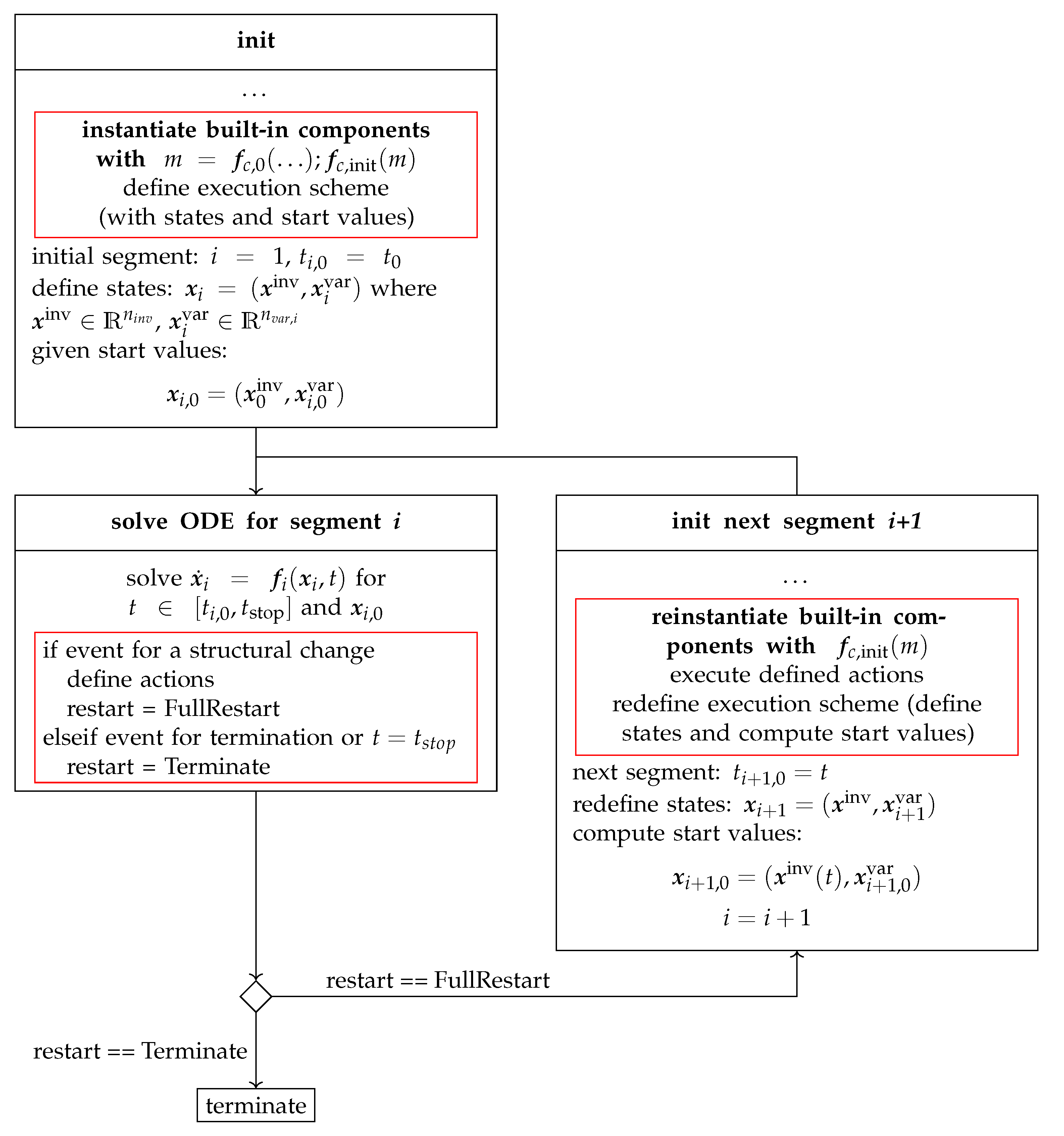
The general scheme presented above is implemented in Modia. Some details of the Modia implementation are shown in
Figure 7. Typically, whenever the number of equations changes at an event, some internal data structure must be updated that is used to efficiently compute the equations of a built-in component. This internal data structure is constructed from the dictionary of the Modia
Model that defines the interface and the equations of the built-in component. This data structure and the functions to evaluate it are called the execution scheme in
Figure 7.
When the model is initialized in mode
, the execution scheme for mode
is defined, together with the variant states and their start values. The ODE
of the actual segment
i is solved for
and its start values
until
is reached, or an event for a structural change is triggered. In the latter case,
actions are defined and stored internally in the built-in components that define how to construct mode
. More details and examples for execution schemes and actions are given in
Section 5.3 and
Appendix B.2. When the built-in component is reinstantiated in mode
, the execution scheme is redefined, together with new states
and their start values
. Afterwards, the ODE for segment
is solved. Applications of changing number of states during simulation are given in
Section 6 and
Appendix B.2.
5. Segmented Simulation with Built-In Component Modia3D
5.1. Overview Modia3D
The open source Julia package Modia3D (
https://github.com/ModiaSim/Modia3D.jl, accessed on 17 January 2023, release v0.12.0) is a multibody tool for 3D mechanical systems implemented as a built-in component of Modia and can therefore be combined with other Modia components. Modia3D is targeted for solvers with adaptive step-size control to compute results close to real physics including collision handling using the Minkowski portal refinement (MPR) algorithm [
24,
25] and collision response for elastic contacts [
26,
27,
28]. Furthermore, it is inspired by the generic component-based design pattern of modern game engines, allowing very flexible and modular definitions of 3D systems: A coordinate system located in 3D is used as a container with optional components (geometry, solid and collision properties, visualization data, light, camera, etc.); see [
29], Unity [
30], Unreal Engine [
31], and three.js [
32].
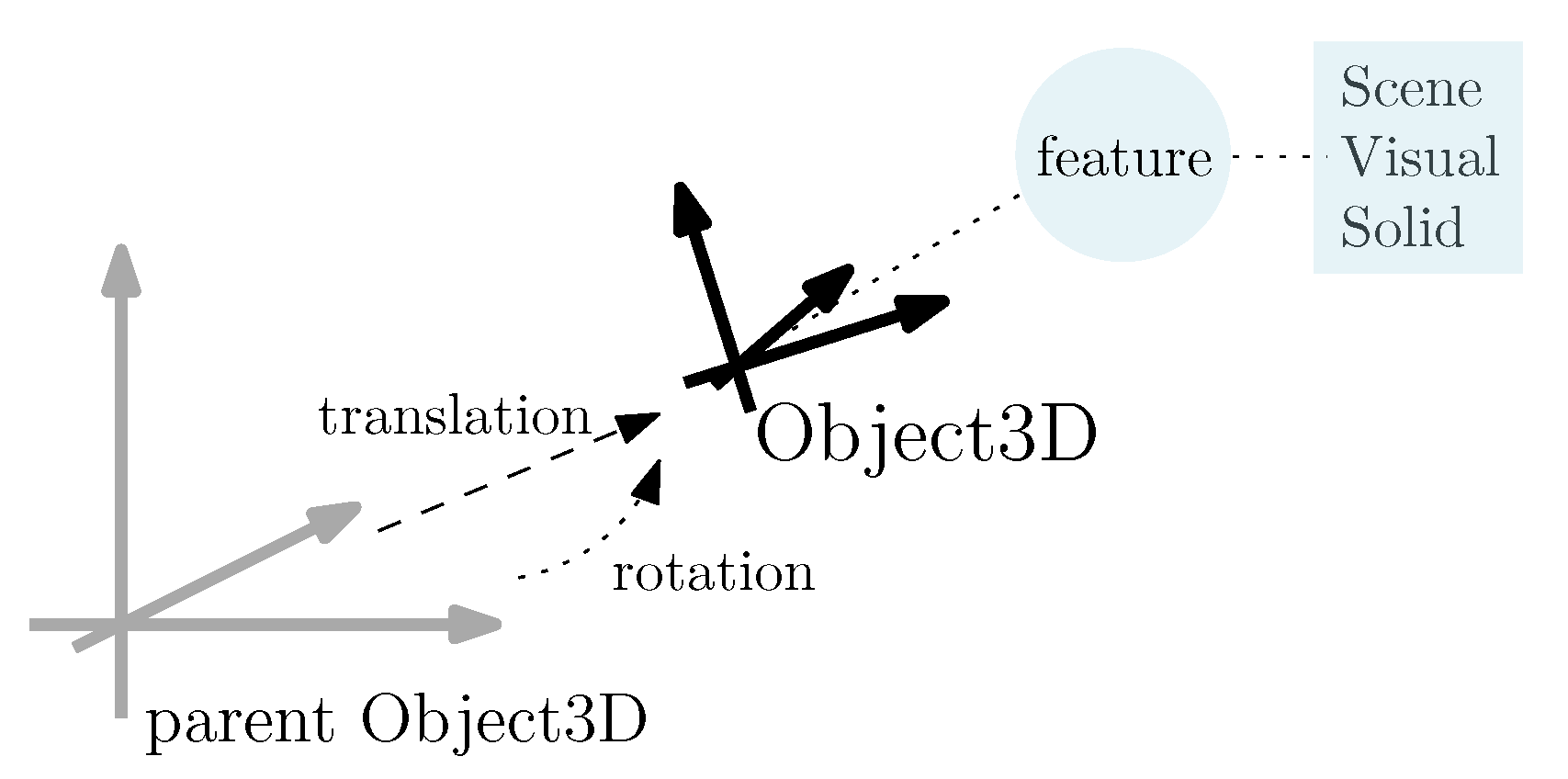
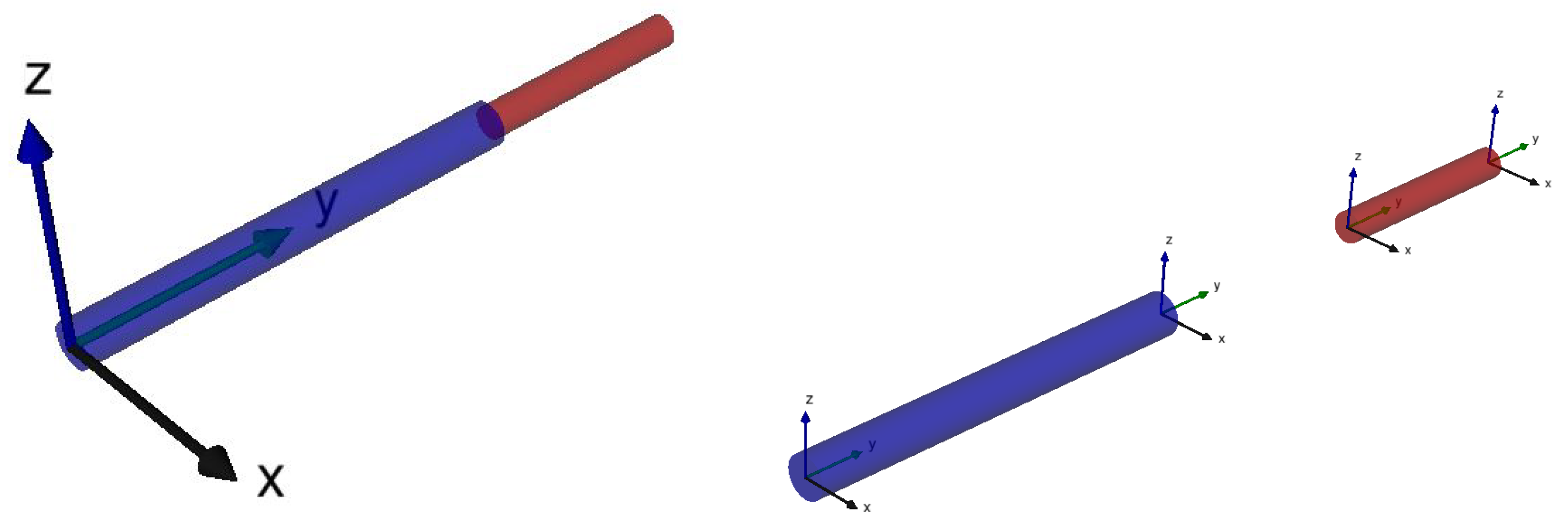
The core component of Modia3D is an
Object3D. It is a coordinate system moving in 3D with associated optional features; see
Figure 8. An Object3D’s position and orientation is defined relative to an optional parent Object3D by translation and rotation. The Object3D with feature
Scene is the root of all other Object3Ds and defines a global inertial system. The feature
Visual is for 3D animation and defines shapes such as box, sphere, cylinder, beam, and 3D meshes with visualization properties. The feature
Solid defines solid bodies. It has mass properties and can be considered in collision situations if
collision = true is set. It can have a shape and visualization properties. For a more extended description, see [
4] and the Modia3D Tutorial (
https://modiasim.github.io/Modia3D.jl/stable/, accessed on 11 December 2022).
An example of a simple pendulum model (
https://github.com/ModiaSim/Modia3D.jl/blob/main/test/Tutorial/Pendulum3.jl, accessed on 14 December 2022) with damping in its joint is given in Listing 3 with the already described features of the Modia3D built-in component. The remaining elements of the Pendulum use predefined models of a small Modia library: the Modelica.Mechanics.Rotational library. In particular, a rotational 1D
Damper is connected to a fixed point and to the flange of the revolute joint, see Listing 4, to model damping in the joint.
| Listing 3. Simple damped pendulum defined with constructors of Modia3D (Object3D, Revolute-WithFlange) and equation based components of Modia (Damper, Fixed). |
![Electronics 12 00500 i003 Electronics 12 00500 i003]() |
| Listing 4. Definition of a Modia3D revolute joint containing a Modia 1D rotational flange that can be
connected with Modia components. |
![Electronics 12 00500 i004 Electronics 12 00500 i004]() |
Modia3D offers two kinds of joints: The first kind of joints contains Modia equation sections with invariant variables, including invariant states, according to
Figure 5. These joints are visible for Modia and cannot be removed or added during simulation. In order that state constraints can be defined and index reduction on invariant states can be performed, the interface to the Modia3D functionality is designed to define differential equations only on the Modia side in Modia equation sections. The definition of a
RevoluteWithFlange joint (a revolute joint that has a Modia 1D rotational
Flange) is shown in Listing 4; for more details, see [
4]. During the instantiation of an overall model, the model is traversed, and each built-in component can inject equations into the model definition that is used during symbolic processing. As a result, in Listing 5, the code generated for the pendulum of Listing 3 is shown.
| Listing 5. Generated code for pendulum of Listing 3. |
![Electronics 12 00500 i005 Electronics 12 00500 i005]() |
As can be seen, the states _x of the solver are copied into the Modia variables phi and w of the revolute joint which are in turn passed to function Modia3D.setStatesRevolute!(..) of the Modia3D built-in component.
The joints of the second kind define variant variables, including variant states, according to
Figure 5, which are visible only in the built-in component Modia3D. These variables can be added or removed during simulation. For example, an Object3D has an optional keyword
fixedToParent with a default value of true. In this case, the Object3D is rigidly connected to its parent Object3D; this means it has zero degrees of freedom. If the value is set to false, the Object3D is allowed to move freely with respect to its parent, meaning it has 6 degrees of freedom and 12 variant states. At events, keyword
fixedToParent can be changed from
false to
true and vice versa, as will be shown below.
5.2. Super-Objects
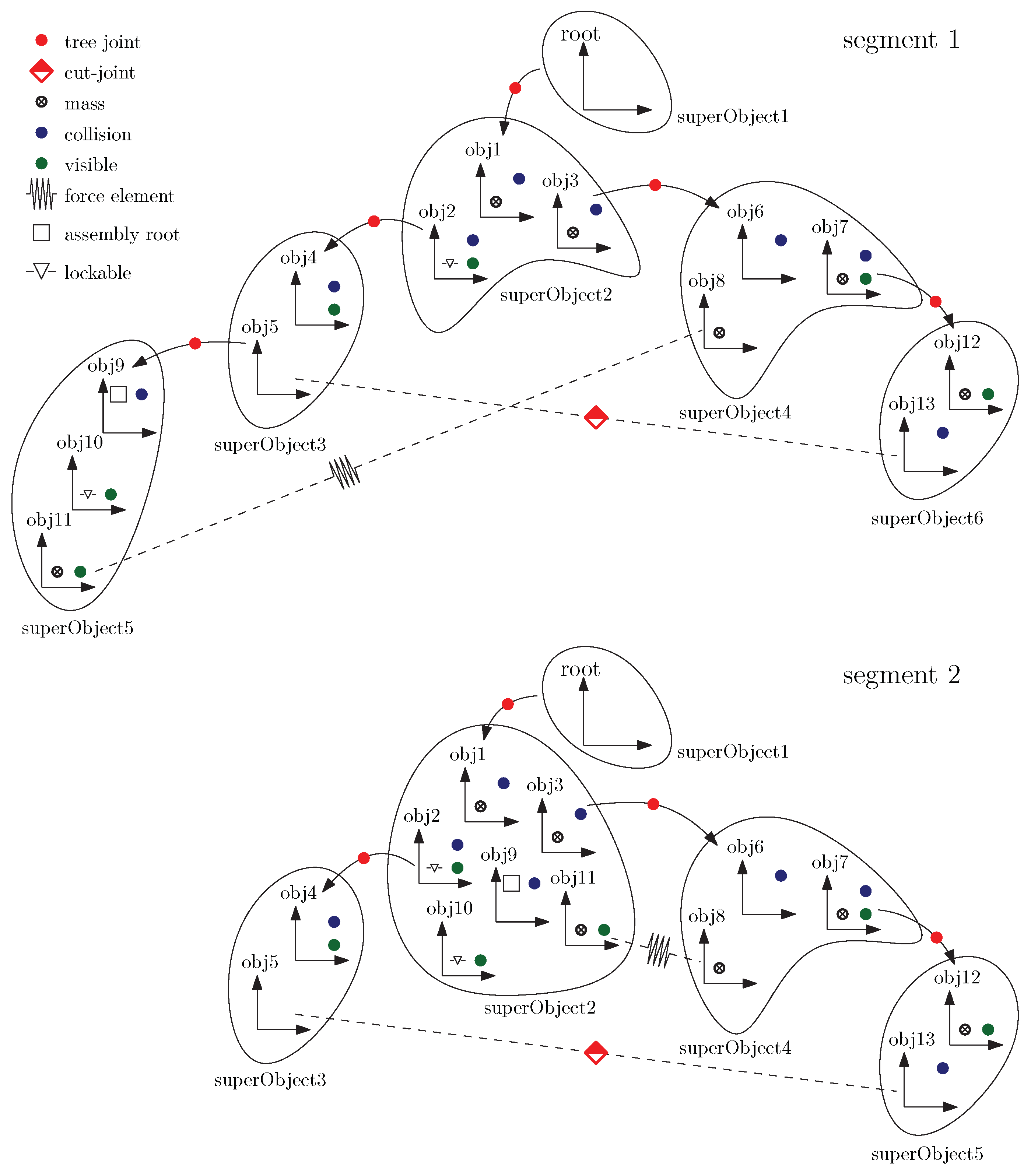
Rigidly connected Object3Ds are grouped together into so-called super-objects [
33]. An example is given in
Figure 9. Super-objects are disjunct via joints. Based on the features of Object3Ds in super-objects, different actions are performed: For example, all Object3Ds in the same super-object cannot collide with each other, but they can collide with all other Object3Ds that are enabled for collision handling. A common mass, common inertia tensor, and common center of mass are computed for a super-object taking into account the mass properties of all Object3Ds inside this super-object. For further information, see [
33].
An Object3D can be marked to be the root of an assembly, or it can be marked to be lockable. As an example,
Figure 9 shows 14 Object3Ds. In segment 1, they are grouped into six super-objects at initialization. If defined in an action program, two Object3Ds (e.g., obj2 and obj10, which are both defined as lockable Object3Ds) are locked, and a full restart is triggered, resulting in a new segment 2, as shown in
Section 5.3, if the two Object3Ds are close to each other. During re-instantiation of segment 2, see
Figure 7, the internal data structure of the Modia3D built-in component is regenerated, resulting in five super-objects in
Figure 9. This is a very cheap operation in the milli-seconds range. More details are given in
Section 5.3.
5.3. Segmented Simulation of Modia3D Models
In this subsection, a brief overview is given how Modia3D supports the generic segmented simulation method of
Figure 7. At initialization, the Modia3Ds execution scheme is built up based on the Modia3Ds model definitions; see
Figure 9. All information about the multibody systems’ components (e.g., Object3Ds, joints, and solids; for an example, see Listing 3) and their functionality (e.g., collision properties) is sorted and mapped to an internal data structure with super-objects that can be efficiently evaluated during simulation. This execution scheme includes the definitions of the states of the multibody systems and of its initial values that are deduced from the utilized joints. The execution scheme is executed during the simulation of the current segment, until one of the defined actions requests a full restart for a structural change at the time of an event or when the simulation is terminated. If a full restart is required, the execution scheme is restructured, as shown in the example of
Figure 9 (basically, this means that some internal data structures are changed).
Rigidly connected Object3Ds can form an assembly by setting
assemblyRoot = true for the freely moving Object3D, i.e.,
fixedToParent = false. All rigidly connected children of such an Object3D belong to the assembly. Additionally, any Object3D, whether it is part of an assembly or not, can be a locking mechanism by setting
lockable = true in the Object3D constructor. In
Figure 9, segment 1, superObject5 is an assembly because obj9 is marked as an assembly root. This assembly is able to interact with superObject2 because obj10 of the assembly and obj9 of superObject2 have
lockable = true defined.
Actions on a Modia3D model and especially on assemblies are executed according to the construction sketched in Listing 6; for an application, see Listing 7. A collection of action commands is defined in a Julia function (e.g., modelProgram). This function is passed as actions argument to the Modia3D constructor ModelActions that returns a reference (e.g., currentAction) to an internal data structure. This data structure is passed to executeActions, which is called in a Modia equations section.
| Listing 6. Defining actions for a Modia3D built-in model with commands of Table 2 and Table 3 to interact
with Modia. |
![Electronics 12 00500 i006 Electronics 12 00500 i006]() |
The action commands in
Table 2 increase or decrease the number of degrees of freedom, and therefore trigger a full restart of a new segment. If the number of degrees of freedom increases, new states are defined, and their initial values are computed based on the last configuration. Two actions (
ActionAttach, ActionReleaseAndAttach) are only possible if the referenced lockable Object3Ds are close together and the relative velocity and angular velocity are close to zero. Currently, the following cases are treated:
A freely moving assembly is rigidly connected to an Object3D with ActionAttach. This action reduces the number of degrees of freedom by 6.
If an assembly has at least two lockable Object3Ds (objA, objB) and is rigidly connected via objA, this rigid connection is removed, and another rigid connection via objB is introduced with ActionReleaseAndAttach. This action does not affect the number of degrees of freedom but changes the structure of the super-objects.
A rigidly connected assembly, i.e., rigid connection to an Object3D, is unlocked with ActionRelease to get a freely moving assembly. This action increases the number of degrees of freedom by six.
An assembly that is either freely moving or is rigidly connected to an Object3D is deleted with ActionDelete. All Object3Ds of this assembly are removed from the Modia3D model.
Whenever one of these actions is executed, the internal data structure with its super-objects must be restructured because the relations and connections between parents and their children have changed. As a result of this restructuring, objects may no longer be able to collide with each other, or the common mass properties of super-objects may have changed.
To initialize the next segment, a full restart is triggered in
Figure 9 (segment 1) with
ActionAttach(..., obj10, obj2), see
Table 2, provided both lockable Object3Ds (obj2 and obj10) are close to each other. Hereby, the joint connecting obj9 with obj5 is removed and obj10 is rigidly connected to obj2. The re-instantiation reduces the number of super objects and states and results in the execution scheme of
Figure 9 (segment 2).
Other Modia3D actions that can be utilized but do not result in a full restart are listed in
Table 3.
6. Applications
Two applications with segmented simulations with the built-in component Modia3D are presented in this section. The first one deals with a two-stage rocket where the two stages are separated after a while. The second application is a robot where gripping and releasing actions are modelled with dynamically changing degrees of freedom.
6.1. Two-Stage Rocket
In
Appendix B.2, an extremely simplified model of a two-stage rocket with mass points is shown, implemented as a Modia built-in component. The same model was implemented as a Modia3D model in Listing 7. The full code is available from (
https://github.com/ModiaSim/Modia3D.jl, accessed on 17 January 2023, release v0.12.0, TwoStageRocket3D.jl). In Listing 7, one stage is modelled with submodel
RocketStage consisting of a cylinder with lockable Object3Ds at the top and at the bottom and a thrust at the bottom. Model
TwoStageRocket builds up the rocket system with the
world object, two instances of
RocketStage, and a
ModelActions constructor that defines the actions with function rocketProgram:
Initially, the two stages are not rigidly connected. At initialization, the top of stage1 and the bottom of stage2 are attached with
ActionAttach(actions, "stage1.top", "stage2.bottom"); see the visualization in the left part of
Figure 10.
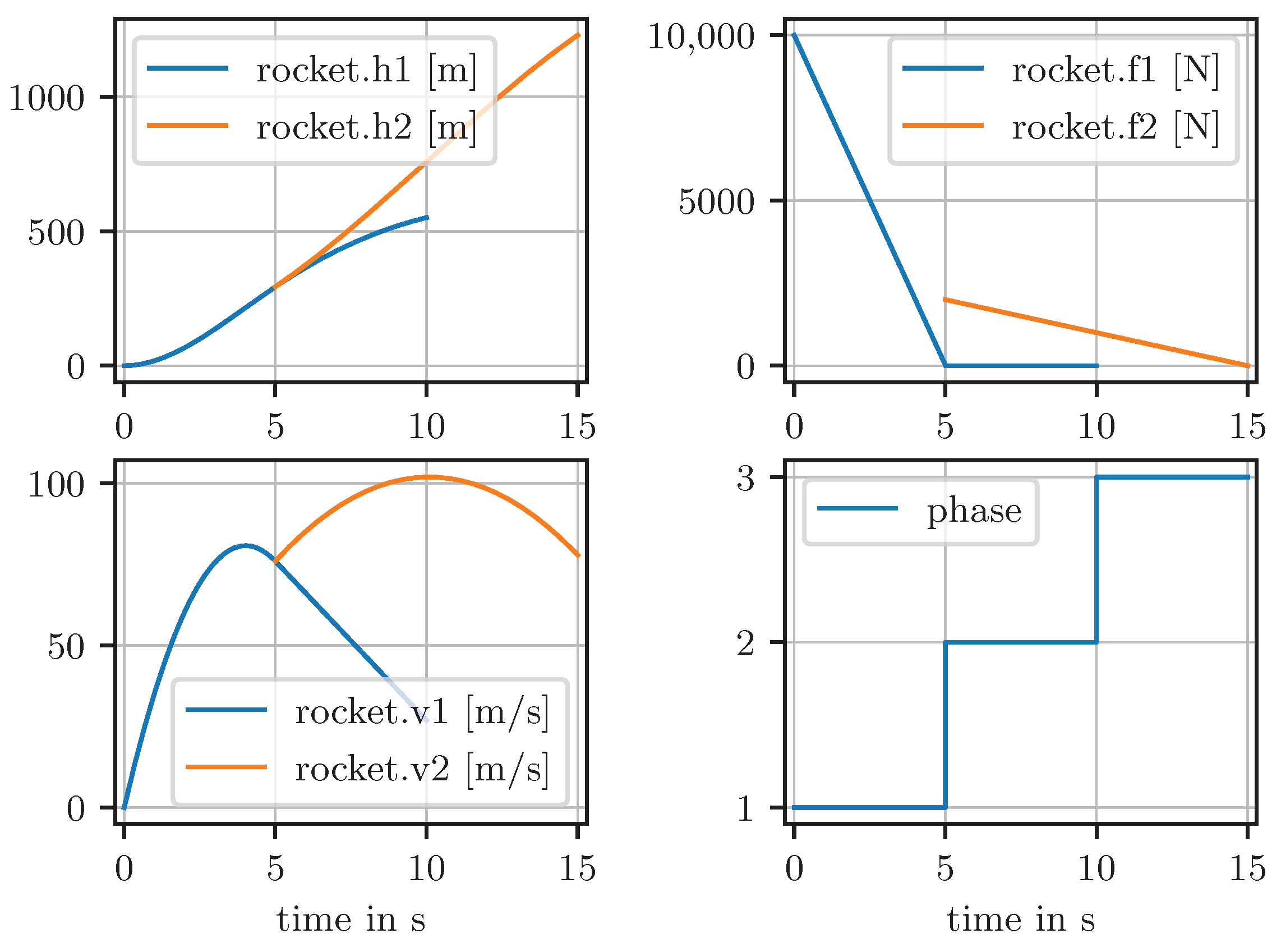
An event is triggered after 5 s with EventAfterPeriod(actions, 5) to release state1.top from state2.bottom with ActionRelease(actions, "stage1.top"). This separates the two stages. Furthermore, thrust1 is switched off.
Again, an event is triggered after 5 s with
EventAfterPeriod(actions, 5); see the right part of
Figure 10. Since the movement of stage1 is no longer of interest in this scenario,
state1.top and all Object3Ds connected to it are deleted with
ActionDelete(actions, "stage1.top"). Thus, stage1 is removed from the simulation run.
Plots of the relevant variables are shown in
Figure 11.
| Listing 7. Modia3D model of a simple two stage rocket. The stages are instances of sub-model
RocketStage that is a cylinder of length L, diameter d, mass m, with lockable Object3Ds at the top and
at the bottom, and a thrust at the bottom. |
![Electronics 12 00500 i007 Electronics 12 00500 i007]() |
6.2. Gripping Robot
The new support of segmented simulations in Modia3D allows one to carry out gripping operations without elastic contact handling. For example, an assembly A is locked at object B (meaning, A is lying on B) and is then gripped from an object C, and then A is released from B and is locked (so rigidly fixed) to C. The advantage of this procedure is that collision handling issues can be avoided. For example, simulations can be performed with larger tolerances and fine-tuning of the details of the gripping operations, and the transport of the gripped object is no longer required. Thus, the simulation is faster and more robust, and the setup of the scenario is easier (see Scenario 2). It is also possible to model gripping operations that are not based on frictional contacts but use rigid mechanical connections, such as a bayonet lock. The drawback is that the details of the gripping are not modelled, but this could be essential, e.g., when designing a control system that carries out an assembly task.
This approach is demonstrated with a gripping operation of a KUKA YouBot robot. This robot has a five degrees of freedom arm and was manufactured in the years 2010–2016. The robot was modelled with Modia (drive trains and controllers) and with Modia3D (3D mechanics); see [
4].
Scenario 1: Adding and removing states during simulation. Therefore, a slightly different version of model [
4] was created for this article; see (
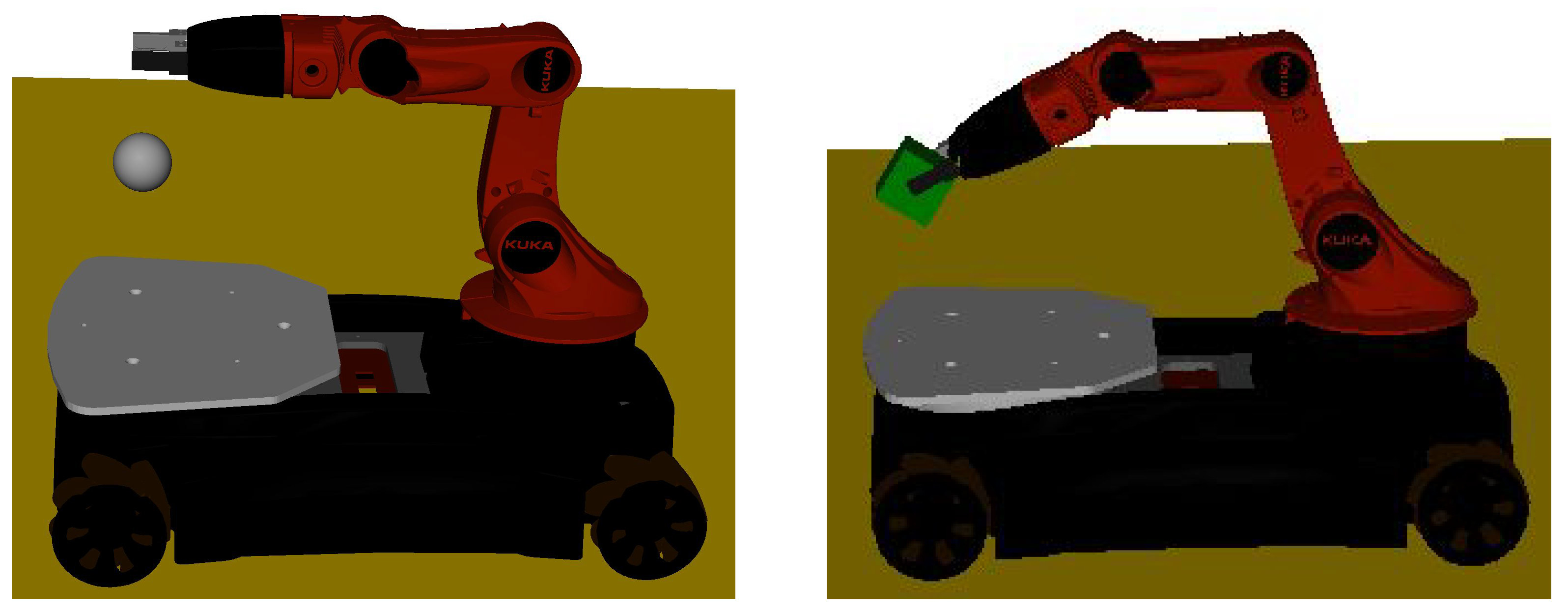
https://github.com/ModiaSim/Modia3D.jl, accessed on 17 January 2023, release v0.12.0, YouBotDynamicState.jl) using the approach sketched above. Listing 8 shows parts of the action commands, and
Figure 12 (left) shows a screenshot of the animation. The transportation procedure started with a free sphere lying on the plate of the robot (six DoF) that became rigidly attached (zero DoF) for transportation by the robot’s gripper, until it was released and fell freely downwards (six DoF), bouncing on the plate. This application combined the benefits of segmented simulation for the gripping and transportation of the sphere (no collision handling) with the collision response of the freely bouncing sphere.
| Listing 8. Action definitions for the KUKA YouBot robot. The transportation procedure starts with
initializing a new reference path for driving 5 arm angles and the gripper itself, with unique names,
initial positions, and maximum angular velocity vmax, and maximum angular acceleration amax of
the revolute joints. The arms and gripper are driven to the given points to rigidly attach the resting
sphere with the gripper. The robot transports the rigidly attached sphere until it is released, falls
freely and bounces on the plate. |
![Electronics 12 00500 i008 Electronics 12 00500 i008]() |
Scenario 2: Transportation of a sphere by segmented simulation compared to collision handling. Thus, a sphere was gripped by a robot and transported, until it was released and placed on a plate. Finally, it was gripped and transported again. This procedure was modelled (a) with a segmented simulation (
https://github.com/ModiaSim/Modia3D.jl, accessed on 17 January 2023, release v0.12.0, YouBotFixSphere.jl) and (b) with collision handling (
https://github.com/ModiaSim/Modia3D.jl, accessed on 17 January 2023, release v0.12.0, YouBotSphereTransport.jl). The simulation of (a) took about 0.22 s, whereas the simulation of (b) took about 6.67 s on a standard notebook. Therefore, the simulation time of (a) was about 30 times faster than (b). The reason is that (a) was basically a non-stiff system where the solver could use large step-sizes, and the time for the reconfiguration of the multibody system (for gripping and releasing) was negligible, whereas (b) was a stiff system, since the gripper held the sphere via elastic contact and friction forces that varied during the transportation, and therefore, the solver had to use much smaller step-sizes.
Scenario 3: Transportation of a box by segmented simulation. The models of scenario 3 were similar to those of scenario 2, but only the sphere was replaced by a box; see
Figure 12, right. The simulation time of model (a) with segmented simulation was approximately the same as that of scenario 2. It is not possible to simulate model (b) with a box, because Modia3D collision handling currently only supports point contacts with elastic contact laws due to the used MPR algorithm. For parallel or nearly parallel surfaces, such as a box and gripper, or box and plate, no unique point contact can be computed that is continuous over time, as required from an adaptive step-size control.
7. Conclusions
This article introduced a new method to extend declarative, equation-based modelling systems so that variables can appear and disappear during simulation without re-generation and re-compilation of code when the numbers of equations and states change during events. This was introduced in a generic, mathematical way and was demonstrated with an extended version of Modia and of Modia3D. The main advantages of this approach are (a) that the modeller does not need to define in advance how the system changes the equations because this is decided at run-time and (b) that the transformation to a new mode is typically very efficient, because no code needs to be newly generated and compiled on the fly. This is, in particular, the case for the multibody built-in component Modia3D, which allows a superfast re-arrangement of the execution scheme for a new mode and opens up new applications, because gripping operations are much more efficient and more robust as sketched with the scenarios of the previous section.
As a side-effect, it is now possible to implement acausal components in Modia that consist to a large extent of pre-translated functions that can, for example, hide space discretization schemes of PDEs (partial differential equations) from equation-based code and its transformation algorithms, so that, for example, the number of discretization elements can be changed after code generation and even during simulation. This was demonstrated with heat transfer in a rod and can be generalized for many more PDE-based components, especially for thermo-fluid systems. It is planned to support much more models of this kind in Modia. Another benefit is that the transformation of a model into ODE form and generation and compilation of code is much faster with such built-in components, especially for large models with many states, because the core part of the equations is compiled once, independently of how many instances of the component are used in a model.
A drawback of this method is that the manual implementation of built-in components is quite involved, when compared to the simple definition of pure equation-based components. In the future, it might be possible to automatically transform a higher-level component description to a built-in component. Furthermore, built-in components cannot be used in an arbitrary way. For example, it is usually not possible to invert a model that contains built-in components, even if this would work for the underlying, pure equation-based version of the model. In the future, it would be also useful to combine the technique of built-in components with on-the-fly translation during simulation.