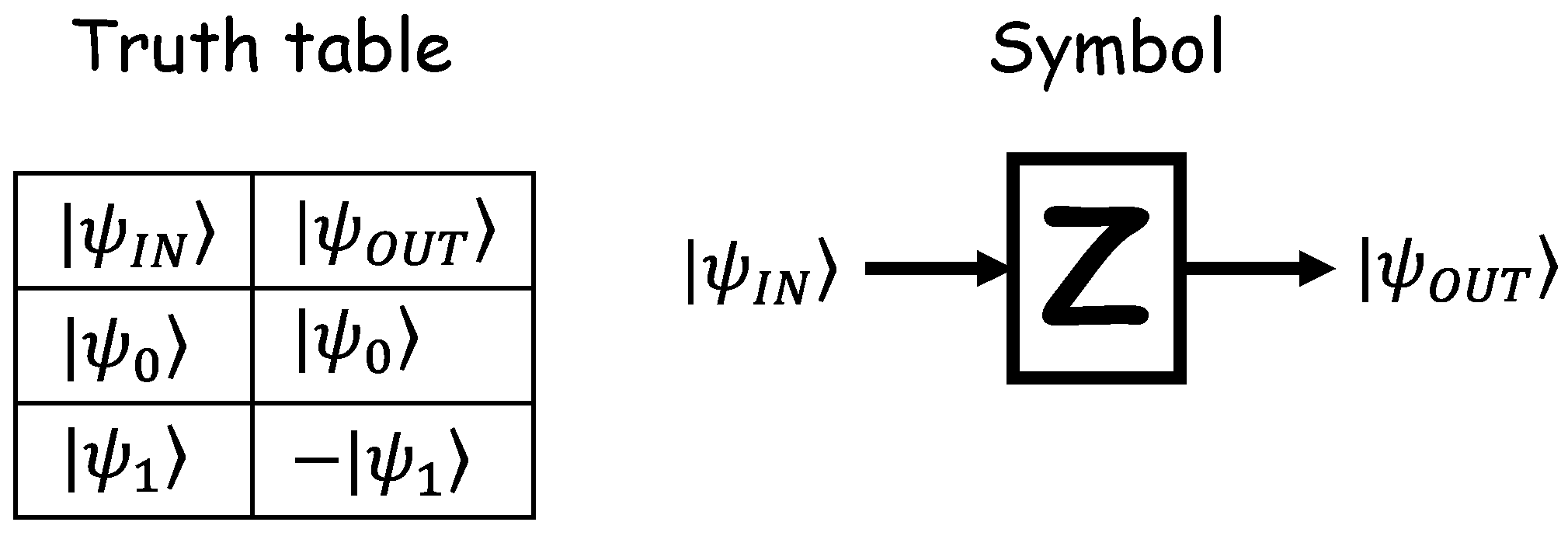
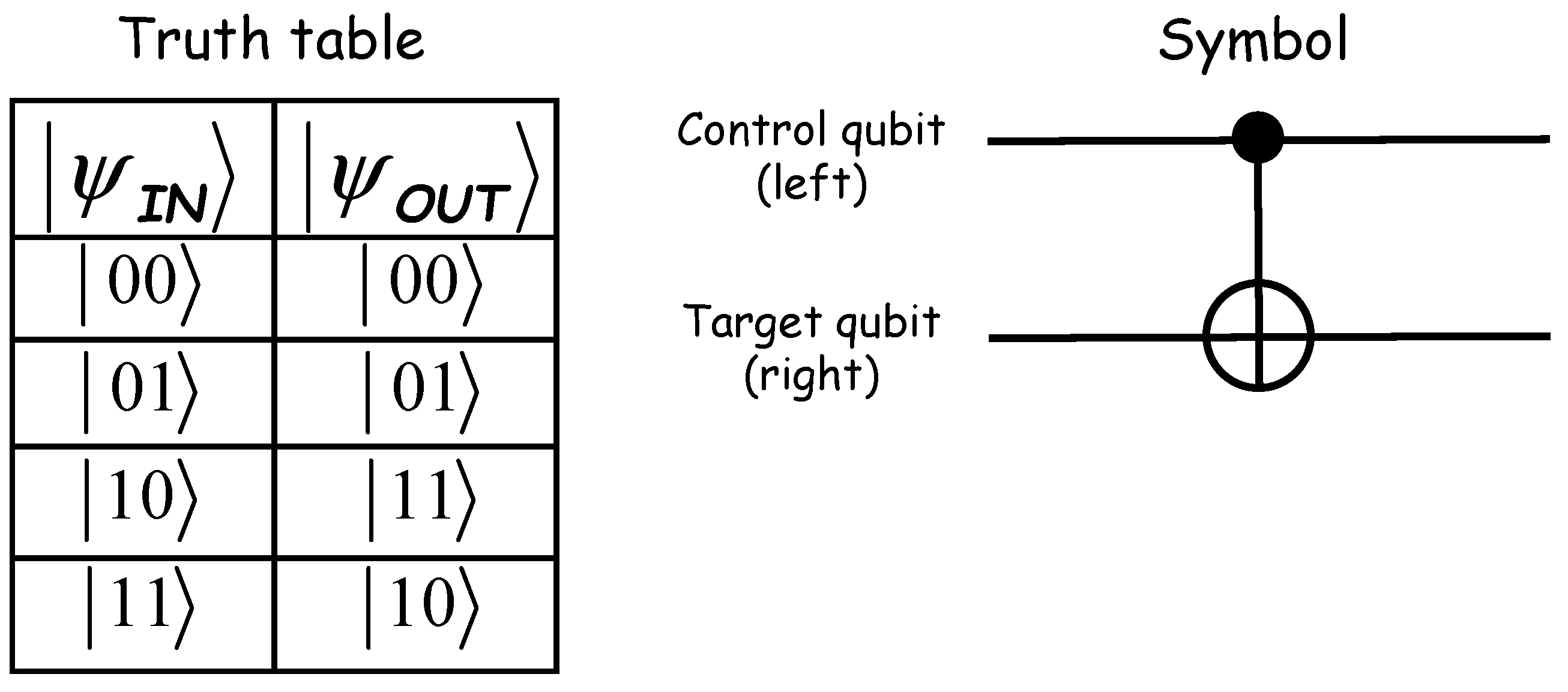
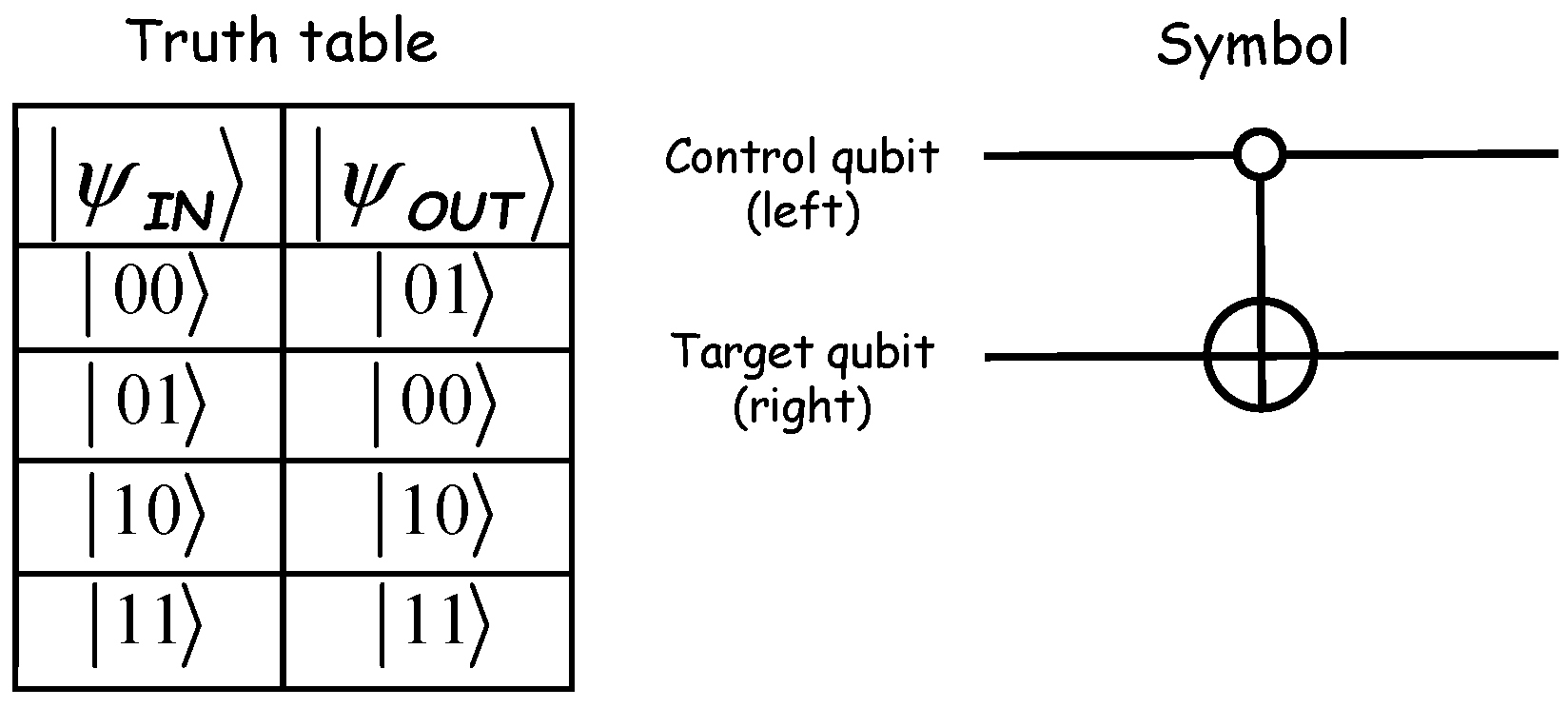
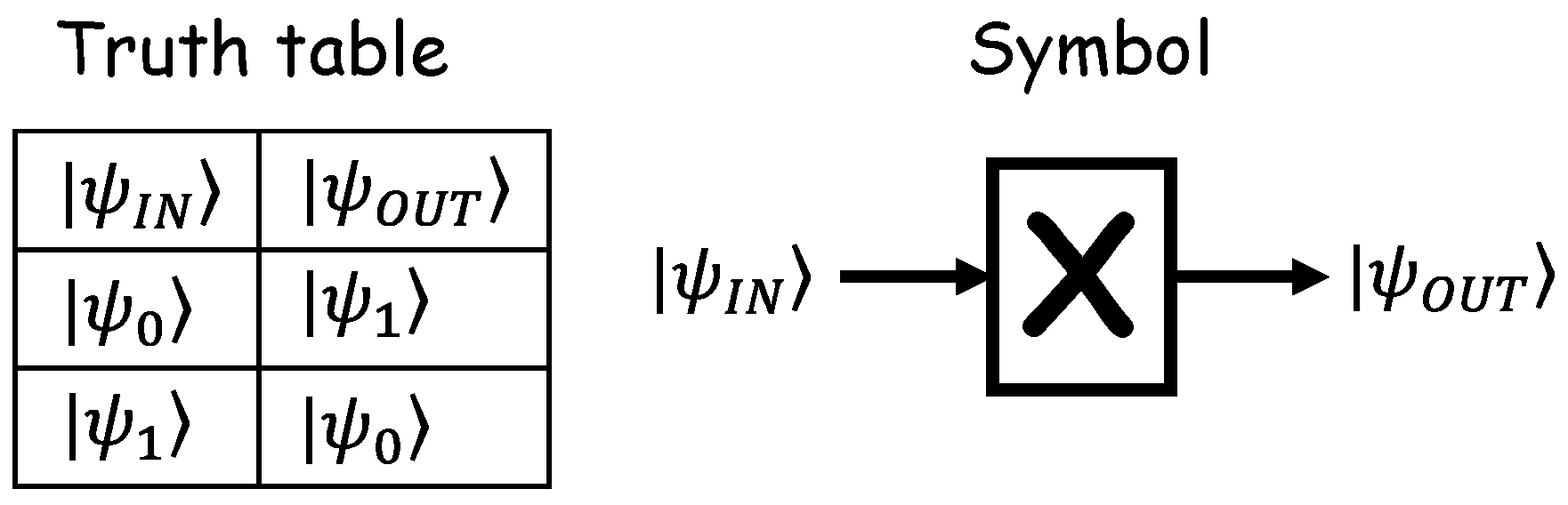1. Introduction
Despite the traditional dominance of a hydrocarbon-based global economy, the first two decades of the XXI century witnessed a substantial influence of information technology on the geopolitical scale. According to the Forbes survey of June 2023, three out of the top five global companies in terms of market capitalization (MCAP) operate within the information and communication technology (ICT) sector, with a collective consolidated MCAP of about USD 6300 billion [
1]. One company only, positioned third in the ranking with an MCAP of about USD 2000 billion, operates in the field of fossil energy resources. The fifth company is involved in the field of online retail, with an MCAP of about USD 1100 billion.
The dawn of the silicon-based digital information era can be conventionally marked in 1971, with the release of the first commercial poly-silicon gate, self-aligned MOSFET microprocessor [
2]. Since that year, the strong synergy between microelectronics and computer science has fundamentally reshaped the technological landscape.
Data and artificial intelligence (AI) are the main drivers of actual information technology. AI algorithms, in their various flavors, are only a side of the equation. The other side is specialized AI chips (e.g., neuromorphic processors), tailored to specific software and business requirements. In this area of AI-oriented microelectronics, quantum processing units (QPUs) are gaining increasing interest. Indeed, they enable the actual execution of quantum algorithms. These algorithms, leveraging the laws of quantum mechanics (QM), pave the way to efficient solutions of mathematical or optimization problems, which, due to their non-deterministic polynomial nature, are not attackable even by the best classical algorithms, because the solution time or the required resources increase exponentially with the problem size [
3]. This is exemplified by the world-famous Shor algorithm for prime number factorization [
4]. Quantum algorithms offer the possibility to speed up calculations that would require a prohibitive amount of time using a classical approach. For instance, the Harrow–Hassidim–Lloyd (HHL) quantum algorithm promises exponential speed-ups in solving linear equation systems [
5]. In 2023, the historical company Rolls-Royce signed agreements with ICT companies to develop quantum algorithms aimed at addressing the notably hard differential fluid dynamic equations crucial for the design of efficient avionic turbojet engines [
6]. Quantum algorithms also hold the potential to speed up AI software technologies like deep learning and machine learning when applied to massive datasets [
7]. It is worth noting that quantum algorithms can be emulated on traditional microprocessors but at the cost of a significant loss of efficiency [
8]. Consequently, major players in the ICT sector, including IBM [
9,
10,
11,
12,
13], Honeywell [
14], Intel [
9,
15,
16,
17,
18], Google [
9,
19,
20,
21], IonQ [
22,
23], and Rigetti [
24], are investing significant efforts in gaining expertise and capabilities to fabricate their own QPU.
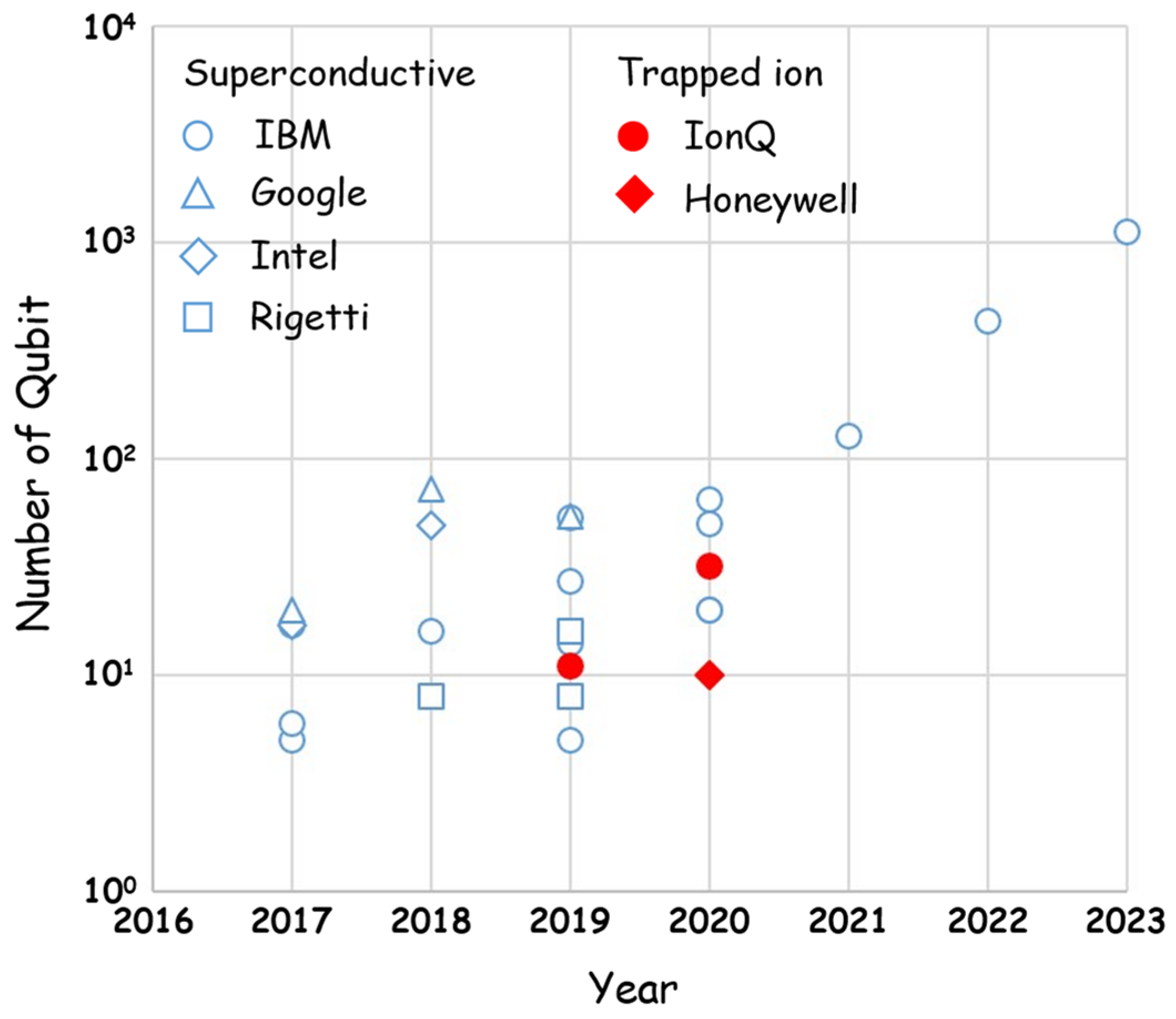
Figure 1 shows that these endeavors have led to an exponential increase over time in the quantum bits (or qubits), the quantum counterparts of the traditional bits, hosted in a single QPU. The IBM roadmap envisions a QPU with 4158 qubits in the near future and approximately 100,000 qubits in the next decade [
25]. Regardless of the more or less rigorous definition of quantum supremacy, a 100,000-qubit QPU is estimated as a landmark for the addressing of engineering problems of practical relevance.
Any two-state quantum-mechanical system can encode a qubit. Examples include the presence/absence of charge in a couple of quantum dots (QDs) (charge qubit) [
26], the spin orientation of an electron confined in a QD (electron spin qubit) [
27], the presence/absence of a Cooper pair in a superconductive island (transmon qubit), the clockwise/counter-clockwise current flow around a superconductive loop (flux qubit) [
28], or the ground/excited states of a radio frequency (RF)-trapped ion (trapped ion qubit) [
29]. All these qubits need to work at cryogenic temperatures to preserve their quantum properties.
Figure 1 reveals that the superconductive qubit is the current predominant choice. Often fashioned as transmons, superconductive qubits offer several compelling advantages, including lower sensitivity to charge noise, greater tolerance against fabrication variations, engineerable properties, and compatibility with the current complementary metal oxide semiconductor (CMOS) microelectronics manufacturing processes. The size is the main drawback of the transmon qubits. Essentially, a transmon is an anharmonic oscillator designed with capacitors, inductors, and Josephson junctions acting as a non-linear inductor. Because of all these inductors and capacitors, transmons exhibit a footprint that is orders of magnitude larger than that of QDs. On the other hand, charge qubits offer both small footprints and CMOS compatibility, but they suffer from a sensitivity to charge noise. Lower sensitivity can be achieved by magnetically coupling the qubit, as in the case of the electron spin qubit, which also offers small footprints and CMOS compatibility. The drawback of the spin qubit is a slower operating speed compared to the charge qubit, mainly because the magnetic coupling is weaker than the electric one [
26].
Here, it is worth remarking that, in light of
Figure 1, the IBM prediction of achieving a 100,000-qubit QPU by 2033 may sound excessively conservative. The exponential trend in
Figure 1, with its slope of about 1dec/2 years, could indicate that this milestone could be achieved in about 4–5 years from the present. The necessity for the individual addressing of each qubit within the QPU may partially support this conservative position.
The current practice, widely adopted in several research labs, involves generating the control and readout signals using off-QPU room temperature circuitry. This approach is conceivable only for a limited number of qubits. When dealing with a large number of qubits (e.g., 100,000), it is mandatory to envisage a solution based on a chipset constituted by, at least, a quantum chip for the QPU and a classical chip for the control and readout circuitry. The classical chip should stay as close as possible to the QPU. It should thus operate at cryogenic temperatures. Moreover, the number of cables connecting the quantum microprocessor to the classical microprocessor running the software should be kept as low as possible.
In this perspective, CMOS integrated circuits offer a promising solution, as Reilly suggested in 2015 [
30] and Charbon investigated in 2017 [
31]. Presently, several high-tech companies are investing in cryogenic CMOS integrated chipsets for their quantum microprocessors [
32]. Consequently, they also share the need for electronics engineers for the design of cryogenic CMOS chipsets. This situation is reminiscent of the early years of the XXI century, when the proliferation of radio frequency mobile devices for telecommunications induced the need for radio frequency integrated circuit (RFIC) designers. The above-presented overview emphasizes the dynamic nature of the field, necessitating a quantitatively and qualitatively more advanced migration of quantum concepts from physics to electronics engineering. The fundamentals of electron devices for electronics engineers typically do not require systematically resorting to QM. Once the origin of the conduction and valence bands is explained by means of the simple 1931 Kronig–Penney model and the Fermi–Dirac statistics are introduced, QM concepts are no longer necessary. However, this is not the case for electronics engineers in charge of designing cryogenic CMOS chips for a quantum microprocessor. These cryogenic circuits should control and read out devices that are intrinsically single quantum objects, not reducible to a semi-classical collective behavior. To design them effectively, electronics engineers need to grasp quantum physics concepts and communicate effectively with physicists. In the current early development phase of quantum computing hardware, a close and rigorous collaboration between physicists and electronics engineers is indeed mandatory, similar to the cooperation that occurred in the fifties and sixties of the past century during the growth of microelectronics [
33,
34].
The aim of the present paper is to introduce the fundamental components of a QPU, specifically the quantum gates, using a mathematical formalism as accessible as possible for electronics engineers.
Section 2 addresses the nature of a quantum microprocessor by leveraging the notion of a finite-state machine, a concept familiar to electronics engineers.
Section 3 introduces the Bloch sphere together with other generalities about a qubit.
Section 4 focuses on the physics of the single-electron-spin qubit and
Section 5 deduces the main one-qubit quantum gates. In the same way,
Section 6 addresses the physics of the two-electron-spin qubit, and
Section 7 deduces the main two-qubit quantum gates. The electron spin qubit has been chosen, in virtue of its potential as an attractive option for future QPUs, given its advantages such as lower charge noise sensitivity, a small footprint, and compatibility with CMOS technology. Here, it is worth reminding the reader that the electron spin qubit was the first qubit suggested for quantum computation in 1998 by DiVincenzo [
27]. Charge qubits have been ruled out as they currently appear less appealing. Superconductive qubits and trapped ion qubits have also been excluded, despite their presence in
Figure 1, due to their more complex mathematical treatment, which does not well fit the goals of the present paper.
Section 8 reports on the Deutsch quantum algorithm with the aim of giving evidence that a quantum microprocessor may speed up the solution of mathematical problems. Eventually,
Section 9 ends the paper by summarizing key points and by drawing some conclusions.
2. On the Nature of a Quantum Microprocessor
From a general point of view, a microprocessor can be described as a finite-state machine whose behavior is controlled by a program that implements an algorithm. In the case of a classical microprocessor, the machine state can be stored in a bank of latches, each memorizing a single bit.
In the simple case of the four-state machine in
Figure 2, this bank, and thus, the state of the finite-state machine, can be mathematically represented as a vector. Meanwhile, a matrix, dubbed the transition state matrix, describes how the state evolves over time after the execution of each step in the algorithm. The entries of the matrix can be either 1 or 0. Programming the machine means specifying the entries in the transition state matrix. For each column, the sum of all entries should be 1, ensuring that the machine always has a path to transition from its current state to a future one. For instance, the red dashed line in the figure shows that the current state S
2 leads to the future state S
4. It is worth remarking that, for a finite-state machine, it is praxis to introduce the terms of current and future states because the microprocessor is a clocked electronics system. In the frame of quantum physics, it is more common to use the terms input and output state.
The future state vector can be calculated by multiplying the transition state matrix by the current vector state.
Similarly, by assuming that S
1 is the initial state and that the algorithm ends after three steps, one can calculate the final state S
Final by means of three products carried out from the right to the left:
Considering the deterministic nature of the final result, it is sufficient to execute the algorithm only once to determine the output of the algorithm.
Now, let us shift the perspective slightly by interpreting the 1 and 0 values of the entries of the matrix in
Figure 2 as transition probabilities of 100% and 0%, respectively. If you enter the matrix with the state S
2, you have a 100% probability (certain event) of reaching the state S
4 and a 0% probability (impossible event) of reaching any other state. Under this probabilistic interpretation,
Figure 3 shows that the entries of the transition matrix can also assume fractional values while still fulfilling the constraint that the sum of their values in each column should be 1. This means that the microprocessor evolves certainly from the current state to some future state, reachable with a given probability. The finite-state machine therefore proceeds as a Markov process.
Using the example in
Figure 3, the transition probability from the current state S
1 to the future states S
2 and S
3 is 50% with a consolidated probability of 100%. Even when the current state is certain, the future state is not deterministic. The future state vector is therefore a vector of probabilities, with its entries summing to 1, indicating that the future state of the machine is certainly one out of the possible four states.
Like the previous case, the future state vector can be calculated by multiplying the current state vector by the transition matrix. Assuming that S
1 in
Figure 2 is the initial state of the microprocessor and that the algorithm ends after three steps, the final state S
Final is as follows:
Please note that the sum of all the entries in the probability vector for the final state equals 1. As in the case in
Figure 2, at the end of each algorithm execution, you observe only one of the four possible states. Nevertheless, since the microprocessor behaves like a random state machine, you cannot predict the output state. If you desire to observe the output of the algorithm, that is, the final state vector in Equation (2), you need to run the algorithm several times and calculate the resulting statistics. If the algorithm addresses some specific problem, the most reliable solution is the one with the highest probability state; for instance, the state S
4 in Equation (2). A higher difference in probability among the possible states implies a higher confidence in the achieved solution. In the simple examples addressed above, Equations (1) and (2) show that the deterministic and the stochastic algorithms yield the same solution. Nevertheless, in principle, the random algorithm may offer solutions that are not conceivable with a deterministic algorithm.
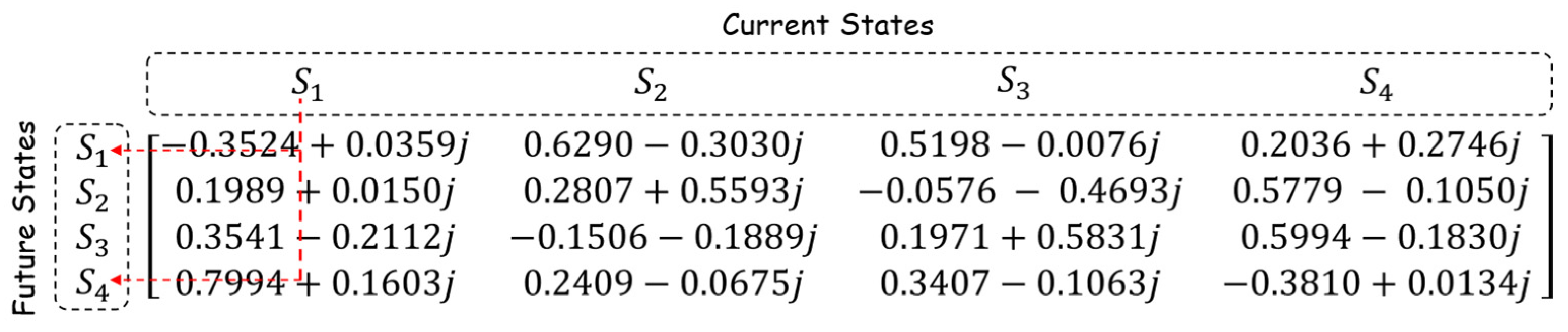
The entries of the state transition matrix in
Figure 3 are real-valued, classical probabilities. Now, let us assume that they are complex-valued, as depicted in
Figure 4. In QM, the complex-valued entries are probability amplitudes, and according to the 1926 Born interpretation [
35], their squared modules represent probabilities. Consequently, the constraint on the entries is that the sum of their squared modules should be 1 for each column.
The matrix
in
Figure 4 describes a quantum microprocessor. As for the matrix in
Figure 3, the above constraint guarantees that the microprocessor evolves certainly from the current state to some future state, reachable with a given probability. The probabilities of reaching the future states S
1, S
2, S
3, and S
4 from the current state S
1 are |−0.3524 + j0.0359|
2 ≅ 0.1255, |0.1989 + j0.0150|
2 ≅ 0.0398, |0.3541 − j0.2112|
2 ≅ 0.1700, and |0.7994 + j0.1603|
2 ≅ 0.6647, respectively, with an aggregate probability of 100%. Note that j is the imaginary unit.
The final state S
Final reached by a quantum algorithm still can be calculated by means of matrix products. Still assuming that S
1 is the initial state and the algorithm envisages three steps, S
Final is as follows:
Also in the present case, the algorithm yields S
4 as the solution to the problem because its probability of
is the highest one. Here, it is worth noting that, in the frame of the QM, the probability vector and the state transition matrix correspond to the state vector |ψ〉
and the operator Â, respectively [
36]. Following John Wheeler, in QM, an operator  can be considered as an engine that receives an input state vector |ψ
IN〉 and generates an output state |ψ
OUT〉 [
37]. By adopting this physics lexicon, Equation (3) should be commented on in terms of input and output states, corresponding to the current and future state terms, respectively, in the electronics engineering lexicon.
For a better understanding of the nature of the quantum microprocessor, it may be useful to compare the above description with the historical experiment involving fringe patterns generated on a photographic plate by electrons passing through a double slit [
38]. In this experiment, the same patterns were obtained by exposing a photographic plate, for a short time, to an electron beam or, for a longer time, to single electrons. In the analogy proposed here, each single execution of the algorithm corresponds to the launch of a single electron through the double slit. The single electron strikes the photographic plate at an unpredictable position, much like the outcome of a single algorithm execution. On the other hand, the final fringe pattern corresponds to the final probability state vector in Equation (3). The final fringe pattern results from averaging the positions where electrons struck the plate after numerous single-electron launches. Similarly, the final probability state vector is calculated by averaging across multiple single outcomes. This highlights that the quantum microprocessor shares with QM the fact of being inductive with respect to single events but predictive for collective events [
39].
Although similar considerations could also be carried out for the stochastic microprocessor in
Figure 3, the relevant difference between the stochastic and the quantum microprocessors is that only in Equation (3) can destructive interferences occur in the various sums of products, because j
2 = −1. On the other hand, in Equation (2), the sums can only be additive, because the entries of the matrix are all positive, real-valued probabilities. By referring to the double-slit experiment, since the pattern generated in this experiment is equivalent to the output of the quantum algorithm, it is possible to conclude that, for a given problem, there are solutions attainable (attainable patterns) only when probabilities carry a phase.
3. The Bloch Sphere
In his book, Dirac introduced the so-dubbed “ket” notation |〉 for the state vector [
40]. So, for the four states in
Figure 2, you can write |ψ
i〉 = S
i for i = 1…4. For a qubit, which exhibits two possible basis states, you can formulate the following:
Unlike the classical bit, which can be in only one of the two possible states, in force of the QM Postulates (see, for instance, [
36]), the qubit can be in a state |ψ〉, which is the superposition of the two basis states |ψ
0〉 and |ψ
1〉:
where α(t) and β(t) are time-variant, complex-valued probability amplitudes. The QM Postulates require also that |α(t)|
2 + |β(t)|
2 = 1. With α(t) and β(t) in the polar form, you obtain the following:
Equation (6) takes the following form:
Equation (7) can be split into two mathematical forms depending on the gathered phase:
Because of Euler’s formula e
jy = cos(y) + jsin(y), the two above mathematical expressions can be rewritten as follows:
Since |α|
2 + |β|
2 = 1 should be true, Equations (8) and (9), respectively, yield
where it is accounted that cos
2(x) + sin
2(x) = 1. From Equations (8) and (9), respectively, it is thus possible to write
When z(t) = r
α(t), x(t) = r
β(t)cos[Φ
β(t) − Φ
α(t)], and y(t) = r
β(t)sin[Φ
β(t) − Φ
α(t)] are defined for Equation (10) and, in the same way, z(t) = r
β(t), x(t) = r
α(t)cos[Φ
α(t) − Φ
β(t)], and y(t) = r
α(t)sin[Φ
α(t) − Φ
β(t)] are defined for Equation (11), Equations (10) and (11) assume the compact form x(t)
2 + y(t)
2 + z(t)
2 = 1, which describes a unitary sphere in the three-dimensional Cartesian space (x, y, z), dubbed the Bloch sphere. On the other hand, by remembering the relationship of the Cartesian coordinates with the spherical ones in
Figure 5 with r = 1, that is, x = sinθcosΦ, y = sinθsinΦ, and z(t) = cosθ, for Equation (10), you obtain the following:
from which
Similarly, for Equation (11), you obtain the following:
from which
Equations (12)–(17) allow for writing Equations (8) and (9) by means of the angles θ and Φ:
where the Euler formula has been applied again.
It is now worth noting that for θ = 0, you obtain the following:
while for =π/2, you obtain the following:
Since the complex exponential multiplying the states does not impact the module of the probability amplitudes, because their module is 1, Equations (20)–(23) suggest that the possible states of the qubit can be described with θ spanning the interval [0… π/2]. On the Bloch sphere, this can be accounted for by reformulating Equations (18) and (19) as follows:
The two angles θ and Φ allow for representing all the qubit states on the Bloch sphere.
Equations (24) and (25) show that the qubit state vector is, in general, a complex-valued vector, of which Equations (4) and (5) are special cases. In Dirac’s notation, the complex transposed state is symbolized with 〈|, dubbed the “bra” [
40]. So, for instance, the bras for Equations (4) and (5) are as follows:
It is straightforward to observe that 〈ψi|ψj〉 is 1 if i = j and 0 otherwise. Mathematically speaking, the states |ψ0〉 and |ψ1〉 are orthonormal with respect to the product 〈.|.〉. Physically speaking, the two states are distinguishable.
Eventually, it is worth noting that the complex transposed of z|ψ〉 is 〈ψ|z*, with z* being the complex conjugate of the complex number z. As a consequence, when taking into consideration Equations (26) and (27), the bra of Equation (6) is as follows:
4. Physics of the One-Electron-Spin Qubit
In the semi-classical description of the atom, the electron revolves in a circular orbit around the nucleus. It thus possesses an orbital angular moment L and, since it carries charge, also an orbital magnetic moment μ
L = −g
LqL/2m, where q and m are the charge and the mass of the electron, respectively [
36]. The term g
L is the electron orbital g-factor about equal to 1. In their effort to explain the Stern–Gerlach experiment [
36], in 1925, Goudsmit and Uhlenbeck assigned an intrinsic spin angular moment S to the electron. Here, it is worth quoting Uhlenbeck’s words from [
41]: “It was then that it occurred to me that, since (as I have learned) each quantum number corresponds to a degree of freedom of the electron, the fourth quantum number must mean that the electron had an additional degree of freedom, in other words the electron must be rotating.” In analogy to L and μ
L, Goudsmit and Uhlenbeck associated an intrinsic magnetic moment μ
S with S [
36]:
where g
S is the electron spin g-factor, about equal to 2, and S
X, S
Y, and S
Z are the components of
S in a Cartesian reference system. Since the components of
S are physical observables, the QM Postulates (see, for instance, [
36]) associate the operators Ŝ
X, Ŝ
Y, and Ŝ
Z with them:
where ħ is the reduced Planck’s constant and
is the imaginary unit. As in
Figure 4, Equations (30)–(32) describe the operators Ŝ
X, Ŝ
Y, and Ŝ
Z in a matrix notation. These matrices are known as the X, Y, and Z Pauli matrices. The substitution of Equations (30)–(32) into Equation (29) yields
where
x,
y, and
z are the unitary vectors of the Cartesian axis. As in the Stern–Gerlach experiment, you need a magnetic field to make the quantization observable. The potential energy
−μS·B is the total energy of an electron with an intrinsic magnetic moment
μS, confined in a QD, and in the presence of a magnetic field
B. In virtue of Equation (33) and of the QM Postulates (see, for instance, [
36]), to this energy corresponds the following Hamiltonian operator Ĥ:
where B
X, B
Y, and B
Z are the components of
B and μ
B = qħ/2m is the Bohr magneton. Still after the QM Postulates, the electron spin qubit evolves in obedience to the following Schrödinger equation:
where the state of the electron has been described after Equation (6). Equation (35) is equivalent to the following system of differential equations:
The component B
z is a DC large value B
0 corresponding to the strong magnet used by Stern and Gerlach to induce the spatial quantization. On the other hand, the other two components B
x and B
y are time-variant and have an amplitude value of B
1 much lower than B
0. In this way, you can write
Note that B
x and B
y describe a magnetic field rotating on a plane normal to the z axis. The substitution of Equation (37) into Equation (36) yields
The mathematical form of Equation (38) can be simplified by remembering the Euler formula and by introducing the frequencies ω
0 = gμ
BB
0/2ħ and ω
1 = gμ
BB
1/2ħ:
The frequencies 2ω
0 and 2ω
1 are known as the Larmor and Rabi frequencies, respectively. The writing of Equation (39) in matrix form reveals the two frequencies −ω
0 and ω
0 on the main diagonal, corresponding, respectively, to the two energy levels -ħω
0 and ħω
0 exhibited by the qubit:
A quantum of electromagnetic energy of frequency ω = 2ω0 thus stimulates the transition from one state to the other. The condition ω = 2ω0 is known as the resonance condition.
For the initial conditions α(t = 0) = 0 and β(t = 0) = 1 and under the condition ω = 2ω
0, the solution of Equation (39) is as follows (see
Appendix A):
A comparison of Equation (41) with Equations (24) and (25) shows that Equation (25) is most apt to describe on the Bloch sphere the effect of the rotating magnetic field on the state |ψ〉. The state vector of the qubit rotates around the x axis (Φ = −π/2), as depicted on the left in
Figure 6, at an angular speed equal to the Rabi frequency 2ω
1.
On the other hand, for the initial conditions α(t = 0) = 1 and β(t = 0) = 0, still under the condition ω = 2ω
0, the solution of Equation (39) is as follows (see
Appendix A):
In this case, Equation (24) well depicts the effect of the rotating magnetic field on |ψ〉. Like Equation (41), Equation (42) also shows that the state vector of the qubit rotates around the x axis (Φ = −π/2) at an angular speed equal to the Rabi frequency 2ω1.
Let us assume a magnetic field with the following components:
The difference between Equations (43) and (37) is in the Bx and By components, with Bx (By) in Equation (37) being in quadrature with Bx (By) in Equation (43).
The substitution of Equation (43) into Equation (36) yields
where the reader is reminded that ω
0 = gμ
BB
0/2ħ and ω
1 = gμ
BB
1/2ħ. As for Equation (40), the matrix form of Equation (44) highlights the two frequencies −ω
0 and ω
0 on the main diagonal, corresponding to the two energy levels of the qubit.
For the initial conditions α(t = 0) = 0 and β(t = 0) = 1 and under the resonance condition ω = 2ω
0, the solution of Equation (44) is as follows (see
Appendix B):
A comparison of Equation (45) with Equations (24) and (25) shows that Equation (25) is the most proper to describe on the Bloch sphere the effect of the rotating magnetic field on |ψ〉. The state vector of the qubit rotates around the y axis (Φ = −π), as depicted on the right in
Figure 6, at an angular speed equal to the Rabi frequency 2ω
1.
On the other hand, for the initial conditions α(t = 0) = 1 and β(t = 0) = 0, still under the resonance condition ω = 2ω
0, the solution of Equation (44) is as follows (see
Appendix B):
In this case, Equation (24) better captures the effect of the rotating magnetic field on |ψ〉. As in Equation (45), the state vector of the qubit rotates around the y axis (Φ = 0) at an angular speed equal to the Rabi frequency 2ω1.
Table 1 collects Equations (41), (42), (45), and (46) by clearly showing the dependence of the time evolution law of |ψ〉 on the carrier phase and the initial condition.
6. Physics of Two-Electron-Spin Qubits
Let us consider a couple of electrons, both confined in a QD. After Equation (29), the intrinsic spin magnetic dipole moments
μS1 and
μS2 of the two electrons can be expressed as follows:
where S
1X, S
1Y, and S
1Z (S
2X, S
2Y, and S
2Z) are the components of the electron spin
S1 (
S2) along the axis of an (x, y, z) Cartesian reference system.
Let us assume that the two electron spins are in the presence of a magnetic field and they interact. As the electrons are confined in a QD, the total energy of the physical system coincides with its potential energy, which is equal to Σ
i,j = x,y,zJ
ij S
1iS
2j−
μS1·B1−
μS2·B2, where J
ij is the coupling between the two spins. The QM Postulates (see, for instance, [
36]) lead to the following quantum Hamiltonian of the system:
By adopting an isotropic Heisenberg interaction as in [
42], for which J
ij ≠ 0 if i = j and J
ij = 0 otherwise, the above Hamiltonian becomes simpler, and the resulting Schrödinger equation is as follows:
Since two coupled qubits form the physical system, there are four basis states. As in
Figure 2 and by extension of Equations (4) and (5), you can write
Similarly, by extension of Equations (26) and (27), you can write
As in the case of the single qubit, the four states are also distinguishable, because they are orthonormal; that is, 〈ψi|ψj〉 is 1 if i = j and 0 otherwise.
In virtue of the QM Postulates (see, for instance, [
36]), the generic state |ψ〉 of the two interacting qubits is the superposition of the four states |ψ
1〉, |ψ
2〉, |ψ
3〉, and |ψ
4〉:
where α(t), β(t), γ(t), and δ(t) are time-variant, complex-valued probability amplitudes. Equation (81) is an extension of Equation (6). In addition, the QM Postulates also require |α(t)|
2 + |β(t)|
2 +|γ(t)|
2 + |δ(t)|
2 = 1. As an extension of Equations (30)–(32), the components of the spin operators
Ŝ1 and
Ŝ2 are given by the following tensorial products between the Pauli matrix and the identity matrix I:
As the vectors of a tensorial product space are calculated from vectors of a lower-dimensional space, higher-dimensional operators are calculated as tensorial products of lower-dimensional operators [
37]. In particular, in Equation (82), the tensorial product of the operator Â
X with the unitary operator I describes a higher-dimensional operator acting on the x component of the first (left) spin but not on the second (right) spin. Similarly, in Equation (85) the tensorial product of the operators I and Â
X describes a higher-dimensional operator acting on the x component of the second (right) spin but not on the first (left) spin. In the same way, you can comment on the remaining equations.
The substitution of Equations (82)–(87) into Equation (72) yields
Once the matrix products and sums are calculated, remembering that qħ/2m is the Bohr magneton μ
B, the above equation takes the following form:
It is worth noting that Equation (88) matches with the Hamiltonian reported in [
42] for ħ = 1; gμ
B = 1; and B
1x = B
2x = B
x, B
1y = B
2y = B
y, B
1z = B
2z = B
z, J
xx = J
x, J
yy = J
y, and J
zz = J
z. By assuming, for the sake of straightforwardness, J
ZZ ≠ 0 and J
xx = J
yy = 0, one can reduce Equation (88) to
It is worth noting that the above conditions on the coupling describe the Ising interaction, which is another typical interaction addressed in the literature for interacting spin systems [
43]. To make the two qubits addressable singularly with a microwave pulse of the proper frequency, the DC large magnetic field B
z component should be different for the two qubits; that is, B
1z = B
01 and B
2z = B
02. The integration of a Cobalt micro-magnet close to the QD makes that possible [
44]. In addition, since the two qubits are usually irradiated with the same microantenna [
45], it is reasonable to assume that the components B
x and B
y of the magnetic field rotating on the xy plane are the same for the two qubits, so B
1x = B
2x = B
1cosωt and B
1y = B
2y = B
1sinωt. Under the above assumptions, Equation (89) takes the following form:
where it was noticed that
By spotting the two Larmor frequencies 2ω
01 = gμ
BB
01/ħ and 2ω
02 = gμ
BB
02/ħ, and the Rabi frequency 2ω
1 = gμ
BB
1/ħ, the above equation can be rewritten as follows:
where J = ħJ
zz/4. As in Equation (40), Equation (90) also exhibits on the main diagonal the frequencies corresponding to the energy levels of the system, of which are four.
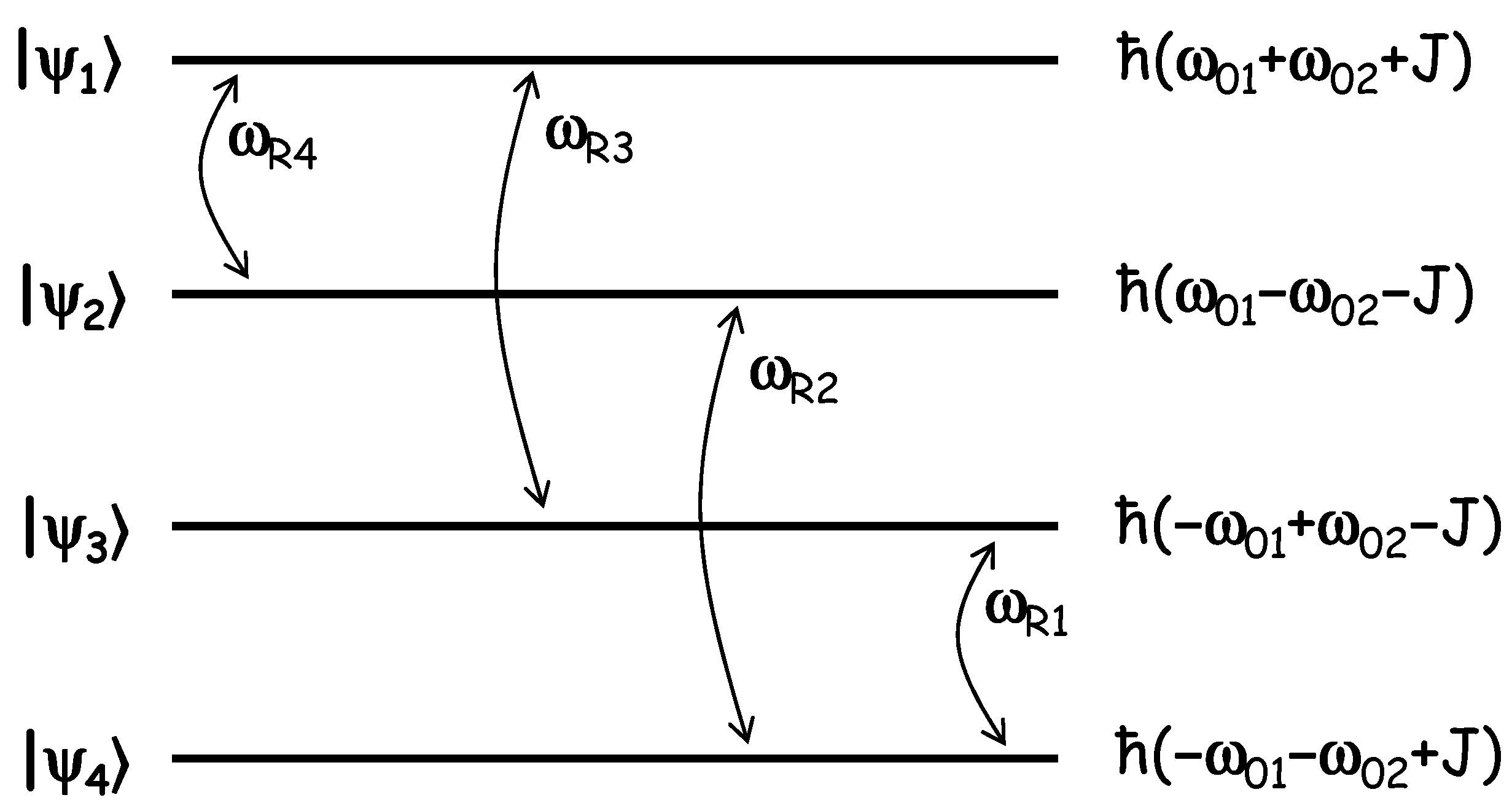
Figure 11 shows that, like in the case of the single qubit, the differences between the energy levels identify four resonance frequencies: ω
R1 = 2(ω
02 − J), ω
R2 = 2(ω
01 − J), ω
R3 = 2(ω
01 + J), and ω
R4 = 2(ω
02 + J).
These resonance frequencies can be put into evidence in Equation (90) by means of the following definitions:
from which
The substitution of Equations (92)–(95) into Equation (90) leads to a more compact form:
or, equivalently, to the following system of differential equations:
Unlike the system of coupled differential equations for the one qubit in Equations (39) and (44), the coefficients in Equation (96) are time-dependent, making it hard to find a solution [
46]. Nevertheless,
Section 5 pointed out that the one-qubit quantum gates are obtained by exciting the qubit with an electromagnetic field oscillating at the resonance frequency, by which the qubit is stimulated to transit between the two states.
Figure 11 thus suggests that the two-qubit system also transits between two out of the four states, when excited with an electromagnetic field at a frequency ω equal to one out of the four resonance frequencies. For instance, the system transits between the two states |ψ
4〉 and |ψ
3〉 when ω = ω
R1. Numerical solutions, obtained by means of Matlab, support these conclusions.
Figure 12 shows the results obtained for ω
01 = 0.6 GHz, ω
02 = 0.5 GHz, and J = 0.3 GHz, corresponding to ω
R1 = 0.4 GHz, ω
R2 = 0.6 GHz, ω
R3 = 1.8 GHz, and ω
R4 = 1.6 GHz.
Figure 12 depicts the obtained state occupation probabilities for a two-qubit system in the initial state |ψ
0〉 = |ψ
4〉. The frequency ω
1 was kept equal to 5 MHz. In
Figure 12, it was considered that, in force of Equation (91), |α(t)|
2 = |x(t)|
2, |β(t)|
2 = |y(t)|
2, |γ(t)|
2 = |z(t)|
2, and |δ(t)|
2 = |w(t)|
2.
In the upper left corner, because of Equation (81), the figure shows that the two-qubit system oscillates between the two states |ψ
3〉 and |ψ
4〉 with an oscillation period of 628 ns, corresponding to the Rabi frequency, while the occupation probabilities |α(t)|
2 and |β(t)|
2 of the other two states remain very small. In the lower left corner, the figure shows that the condition |α(t)|
2 + |β(t)|
2 +|γ(t)|
2 + |δ(t)|
2 = 1 is fulfilled, even if with a very small numerical error, which slowly increases, because it is time-integrated. The numerical results in
Figure 12 therefore support the picture that the two-qubit system transits between two states when excited with an electromagnetic field at a resonance frequency. The same results are obtained for |ψ
0〉 = |ψ
3〉 and ω = ω
R1.
These considerations suggest an approximation for the last two differential equations in Equation (90) as follows:
Equation (97) is formally identical to Equation (39). Consequently, the results reported in
Table 1 can be used by replacing ω
0 with ω
R1/2, because the resonance frequency for the one qubit is 2ω
0, and the states |ψ
0〉 and |ψ
1〉 with the states |ψ
3〉 and |ψ
4〉, respectively.
Table 2 depicts the resulting equations.
Figure 13 shows the numerically calculated state occupation probabilities for a two-qubit system in the initial state |ψ
0〉 = |ψ
4〉 and the electromagnetic pulse frequency ω = ω
R2. As in the case of
Figure 12, ω
01 = 0.6 GHz, ω
02 = 0.5 GHz, J = 0.3 GHz, and ω
1 = 5 MHz were kept. Again, in agreement with
Figure 11, the two-qubit system transits between the two states |ψ
4〉 and |ψ
2〉 while, similarly to the previous case, the occupation probabilities |α(t)|
2 and |γ(t)|
2 of the other two states remain very small. Also, in
Figure 13, the condition |α(t)|
2 + |β(t)|
2 + |γ(t)|
2 + |δ(t)|
2 = 1 is fulfilled unless there is a very small numerical error. The same results are obtained for |ψ
0〉 = |ψ
2〉 and ω = ω
R2. Also in the present case, it is therefore possible to approximate the second and fourth differential equations in Equation (90) as follows:
Again, the couple of differential equations obtained in Equation (98) are formally identical to Equation (39) describing the dynamic of one qubit with ω
R2/2 replacing ω
0 and the states |ψ
2〉 and |ψ
4〉 in the place of the states |ψ
0〉 and |ψ
1〉, respectively. Consequently, from
Table 1, the equations describing the dynamic of the two-qubit system excited with an electromagnetic field oscillating at the resonance frequency ω
R2 are as reported in
Table 3.
Identical behavior of the state occupation probabilities, still in agreement with
Figure 11, and the same considerations are found for the case of the two-qubit system in the initial state |ψ
1〉 and excited with an electromagnetic frequency ω = ω
R3 or ω = ω
R4. The following
Table 4 and
Table 5 report the mathematical expressions describing the corresponding time evolution of the two-qubit state.
8. A Simple Quantum Algorithm: Deutsch’s Algorithm
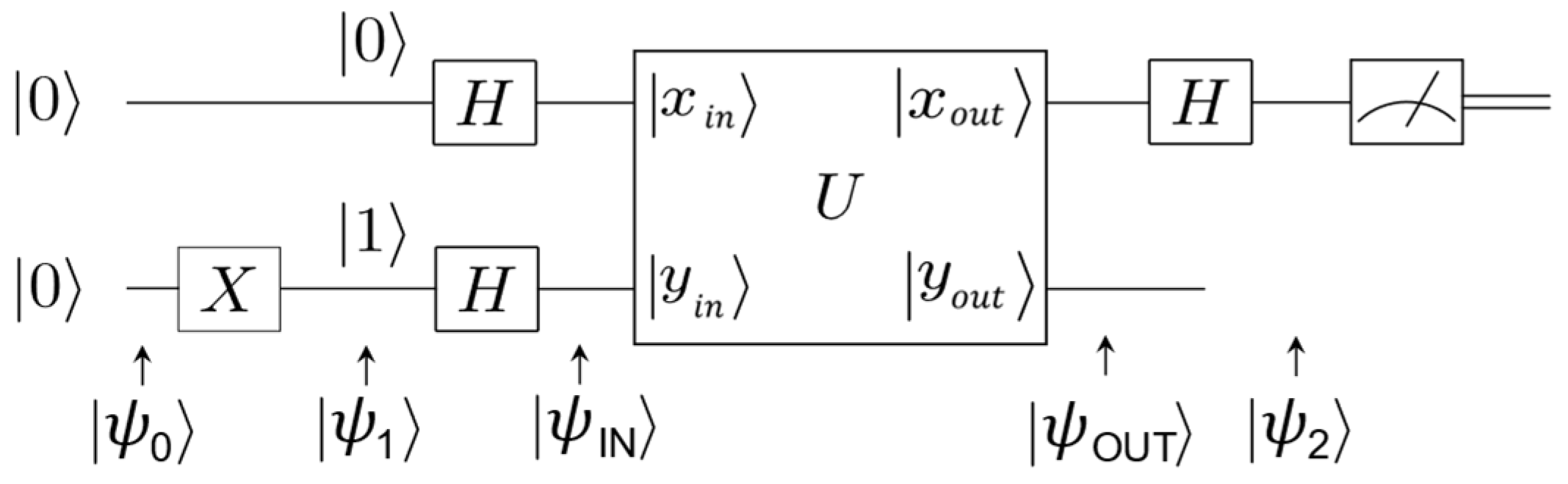
The analogy between the quantum microprocessor and the double-slit experiment in
Section 2 pointed out that a quantum algorithm makes solutions that are not accessible to a classical algorithm possible. To provide evidence of this statement, let us consider the physical system (oracle) depicted in
Figure 20. It operates, by means of the unitary operator U, on the input two-qubit state
, and it generates the output two-qubit state
with
In addition, let
f be a scalar function
f: {0,1}→{0,1} such that
, where
(
) if
(
),
(
) if
(
), and
is the XOR operation.
Let us introduce the problem of determining if the above function
f is constant, that is,
f(0) =
f(1), or balanced, that is,
f(0) ≠
f(1). To solve this problem for a given oracle, you need to calculate, for both
and
, first
and then
from
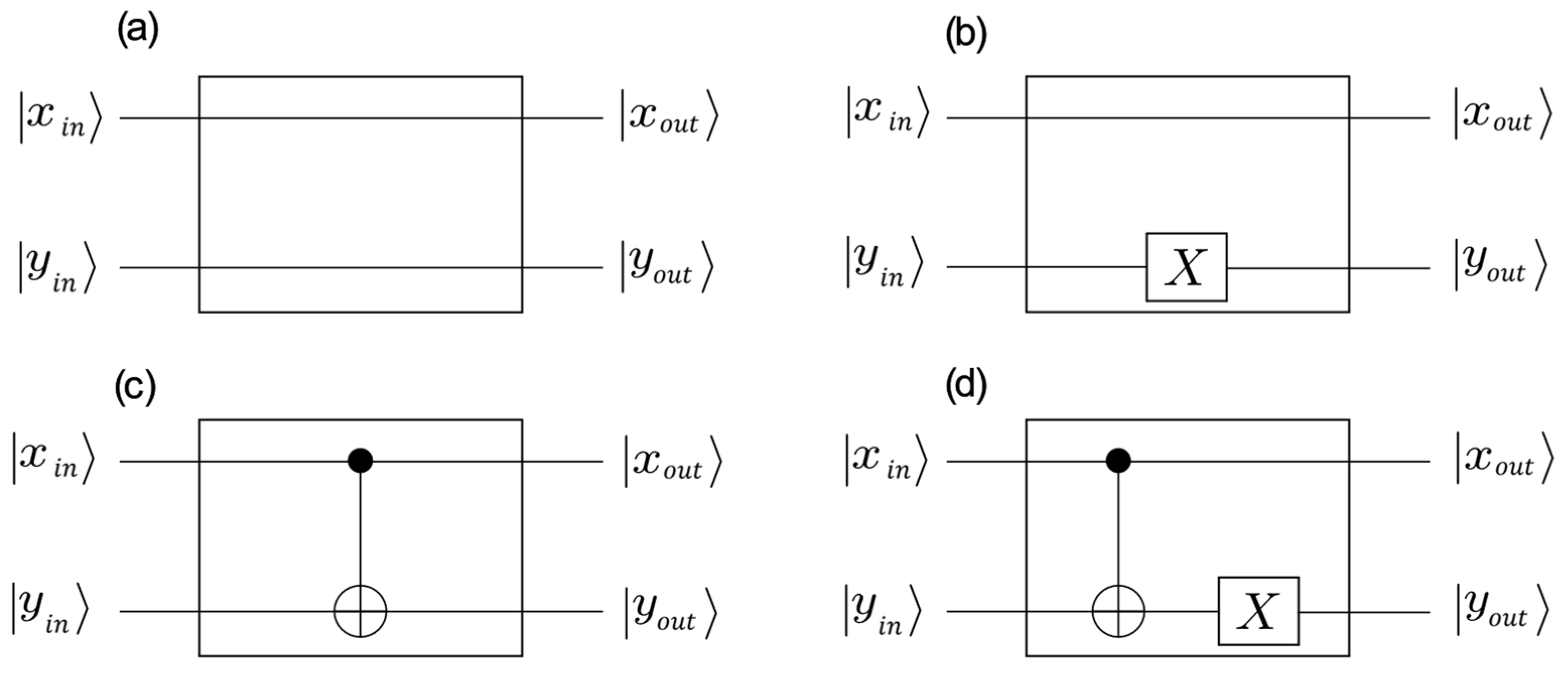
. For the sake of clarity, let us address the oracles in
Figure 21.
Table 7 details the calculation for the case (a) for which U = I
I, where I is the unitary operator used for Equations (82)–(87). Since
, by forcing
, you obtain
f(0) =
f(1) = 0. For the oracle in
Figure 21a, the function
f is thus constant.
For the oracle in
Figure 21b, U = I
, where
is the Pauli X gate operator in Equation (52).
Table 8 provides the detailed calculation. The rightmost column shows that also in the present case, the function
f is constant but with
f(0) =
f(1) = 1.
On the other hand, for the oracle in
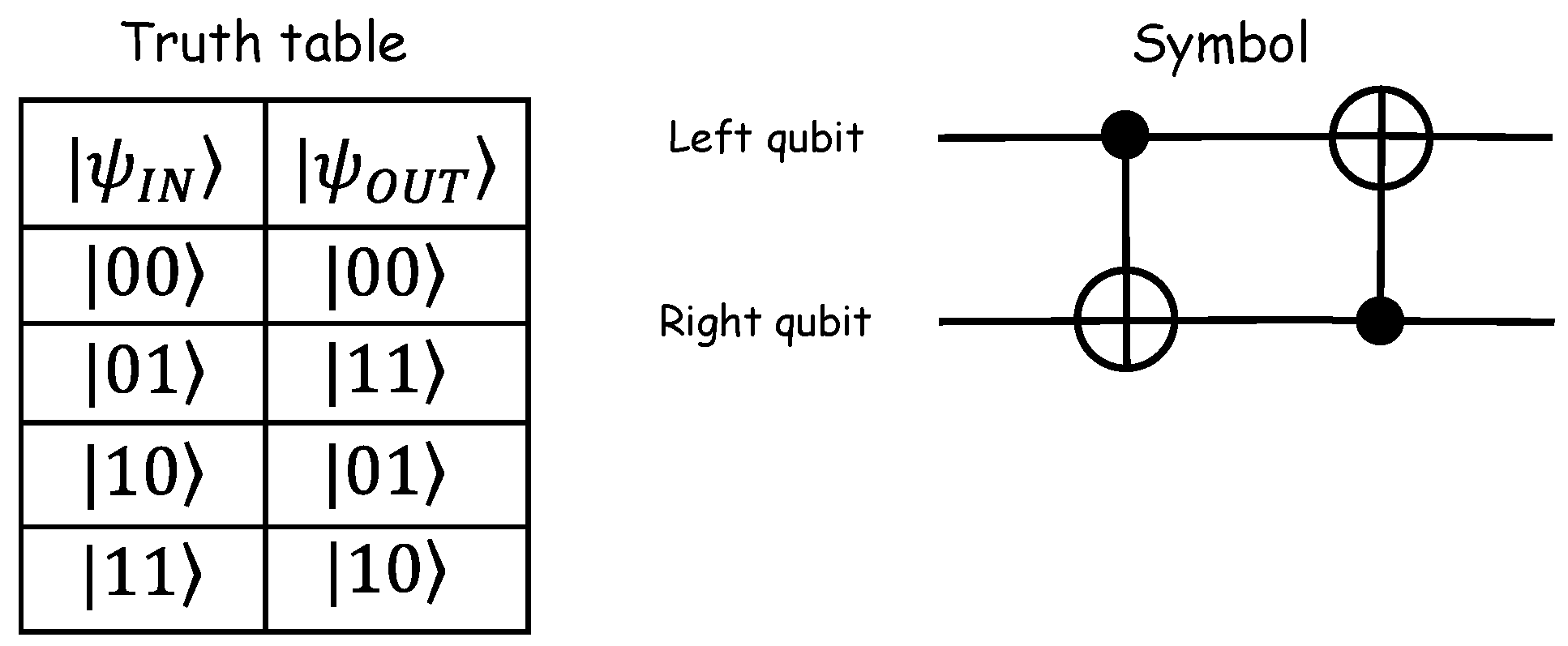
Figure 21c, for which U is the CNOT operator
in Equation (104), the calculation in
Table 9 shows that the function
f is balanced.
Table 10 shows that also for the oracle in
Figure 21d, for which U = I
, the function
f is balanced.
All the above examples in
Table 7,
Table 8,
Table 9 and
Table 10 share the need to calculate the function
f twice, that is, for
and
, before concluding whether the function is constant or balanced.
Deutsch’s quantum algorithm, depicted in
Figure 22, allows the same information to be obtained, but by performing just a single measurement. For the sake of formal briefness, the short notation
for the tensorial product
is adopted in the following.
First, you apply the operator I
to the initial state
to obtain the state
that then is subjected to the operator
, where
is the Hadamard operator in Equation (69). In this way, the state
at the input of the oracle is as follows:
As
, the state
at the output of the oracle is thus
or, by separating for
f constant or balanced,
Eventually, the application of the operator
to the output state
yields
which can be expressed in a more compact form, since
if
, and
if
:
Equations (123) and (124) show that measuring the first qubit is sufficient to draw conclusions about the function
f. The Deutsch quantum algorithm therefore speeds up the solution of the problem under investigation because a single measurement is required instead of two as in
Table 7,
Table 8,
Table 9 and
Table 10.
9. Conclusions
The core of the present paper has been the mathematical–physical description of one- and two-qubit quantum gates, in the case of qubits encoded by using spin states of electrons confined within quantum dots. The matrices representing these quantum gates have been deduced from the solution of the Schrödinger equation by employing a mathematical formalism designed to be as accessible as possible for electronics engineers who do not enjoy the more speculative formalism of theoretical physics.
The deduction clearly reveals that, from a physical standpoint, quantum gates are obtained by applying a microwave pulse with the appropriate frequency and duration to manipulate the electron spins. This understanding holds significant importance as it provides the conceptual foundation for electronics engineers responsible for designing the radio frequency integrated circuits that control the qubits.
In addition, the paper has also described the nature of a quantum microprocessor within the frame of a finite-state machine, a common notion to any electronics engineer. In particular, the analogy between the behavior of a quantum finite-state machine and the historical experiment of the fringe patterns clearly points out the quantum nature of the quantum microprocessor. The considerations carried out in
Section 2, together with the contents of
Section 5 and
Section 7, suggest that a quantum microprocessor can be considered as a very sophisticated interferometric engine that is controlled by a precise sequence of microwave pulses operating on the same qubit network. From this point of view, a quantum microprocessor is similar to a musical instrument. It is the sequence (quantum algorithm) with which you excite the instrument (the qubit network) that generates the musical motif (the output of the quantum microprocessor).
This simplifies the task for a designer, enabling a clearer understanding of the purpose of the circuits they are designing and how a quantum computation occurs at the physical level. These insights are crucial, as they empower a designer to gain a deeper understanding and make informed judgments regarding the specifications under which they are tasked with designing cryogenic integrated circuitry for a quantum processor.
In conclusion, since, on the one hand, several textbooks on quantum computing introduce quantum gates as pure mathematical objects without providing their mathematical–physical background, while, on the other hand, physics textbooks address qubit physical systems with a mathematical formalism, which is challenging for electronics engineers to follow, it is the authors’ opinion that the present paper may contribute to demystifying quantum microprocessors for electronics engineers. It is also the authors’ opinion that the present paper may enhance the information exchange between engineers and physicists who collaborate in the development of quantum microprocessors, a research field of significant interest in microelectronics today.
As a final remark, it is worth observing that the methodology employed in the present paper for electron spin qubits may be extended to superconductive qubits. In the case of a single superconductive qubit, Bardin and colleagues have indeed presented a Hamiltonian in a matrix form that bears similarities to Equation (40) [
48]. Similarly, in the case of two capacitive-coupled superconductive qubits, Krantz and collaborators have reported a Hamiltonian with a structure akin to the Hamiltonian for two spins coupled by an exchange interaction [
49], which is similar to Equation (72). This leads to the conclusion that the methodology adopted in the present paper can be extended to other physical implementations of qubits.